Elipsoida obrotowa jako powierzchnia odniesienia

Elipsoida obrotowa jest powierzchnią, którą można opisać analitycznie i określić w
przybliżeniu kształt Ziemi. Dlaczego stosujemy elipsoidę obrotową jako
powierzchnię aproksymującą bryłę Ziemi oraz parametry elipsoidy GRS’80 podane
zostały w poprzednich wykładach.
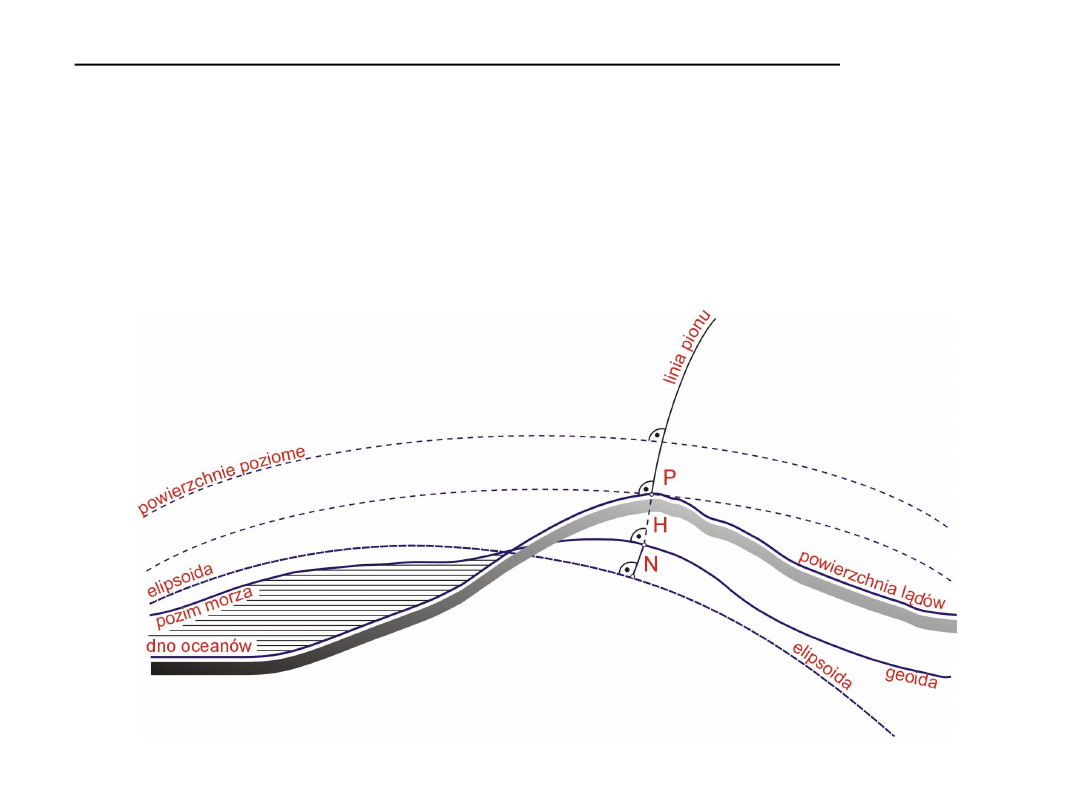
Wzajemne relacje pomiędzy geoidą (powierzchnią odniesienia niwelacji) a
elipsoidą podane są na rysunku.

Powierzchnie odniesienia: geoida i elipsoida

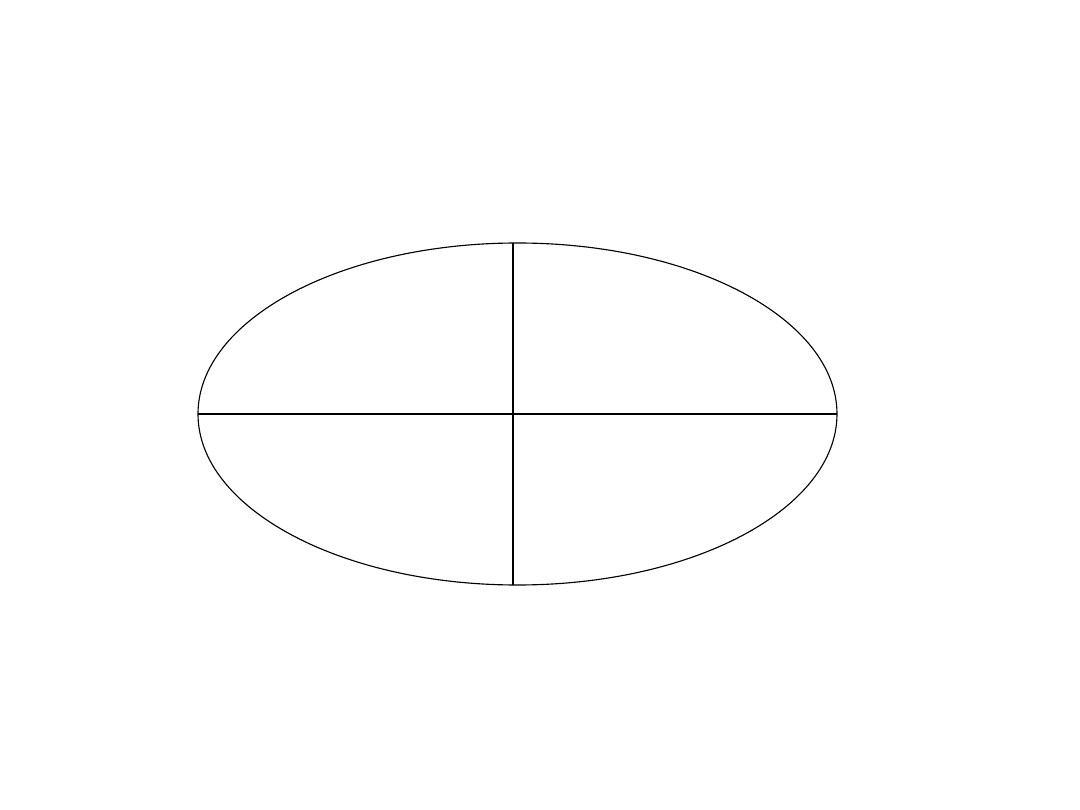
Kształt i rozmiar elipsoidy określone są za pomocą

a – duża półoś
b – mała półoś

a

b

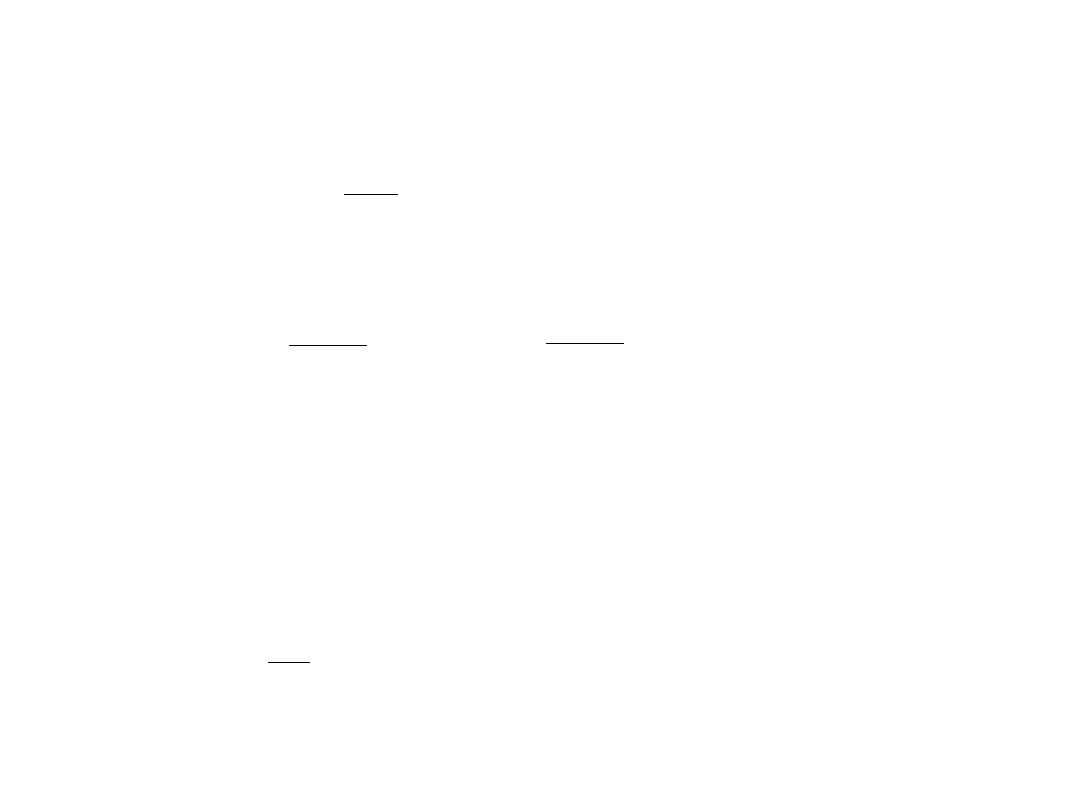
Określamy parametry pochodne

1. Spłaszczenie

f

a

b

a

f





2. Pierwszy i drugi mimośród e

2

i e’

2

2

2

2

2

a

b

a

e





2

2

2

2

'

b

b

a

e





Dla przypomnienia elipsoida GRS’80 ma następujące parametry

1

257

,

298





f

m

a

137

378

6



A więc w przybliżeniu

300

1



f

km

b

a

21





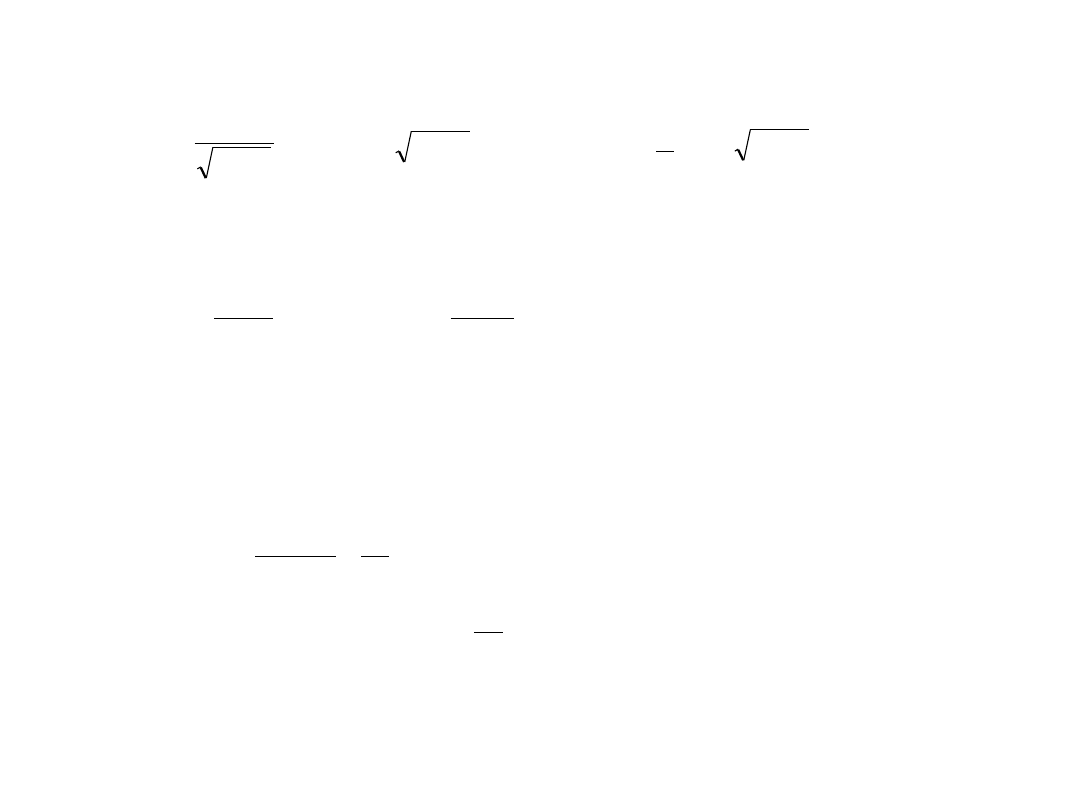
Można wykazać następujące związki:

2

1 e

b

a





2

1 e

a

b





2

1

1

1

e

a

b

f

















1

'

1

1

2

2







e

e

2

2

2

1

'

e

e

e





2

2

2

'

1

'

e

e

e





2

2

2

f

f

e





stąd

f

e

2

2



Równanie elipsoidy obrotowej ma postać

1

z

2

2

2

2

2







b

a

y

x

Wprowadzając oznaczenia

2

2

2

'

1 e

b

a









lub

2

1

1 e

z







Otrzymamy równanie w następującej postaci:

2

2

2

2

a

z

y

x









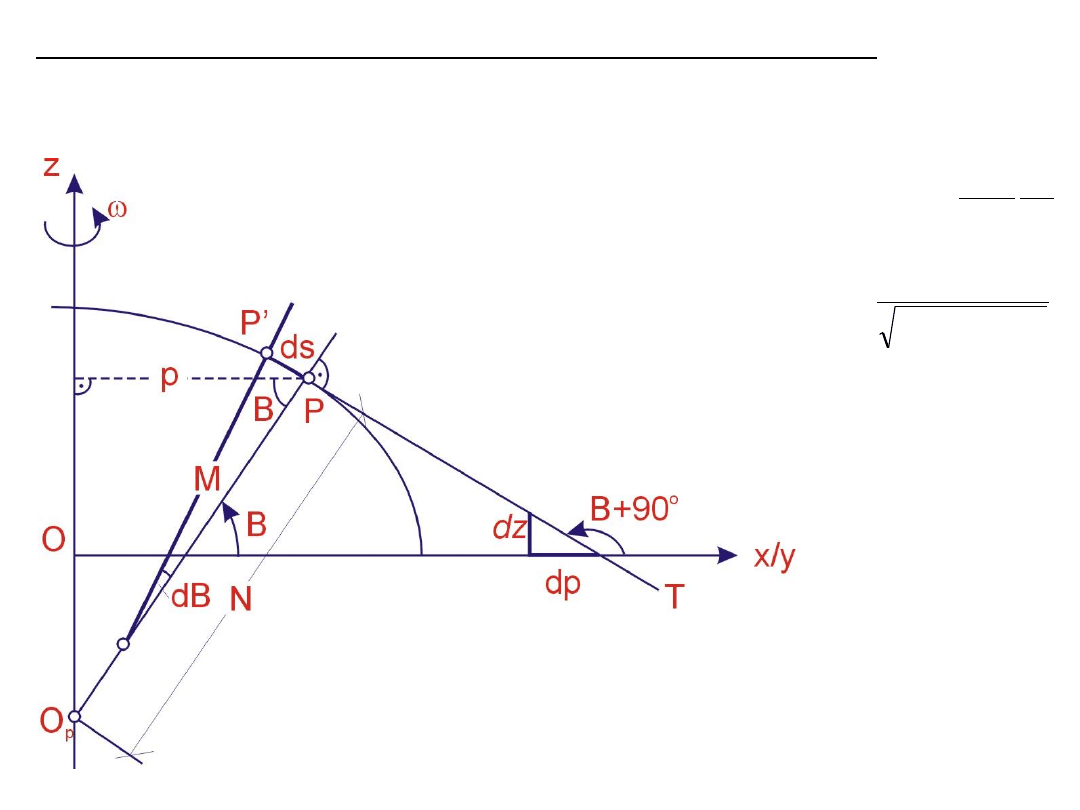
Przekroje normalne elipsoidy obrotowej i jej krzywizny

1. Promień krzywizny południka

M

Promień krzywizny południka

M

dB

dp

B

M

sin

1



albo też









3

2

2

2

sin

1

1

B

e

e

a

M







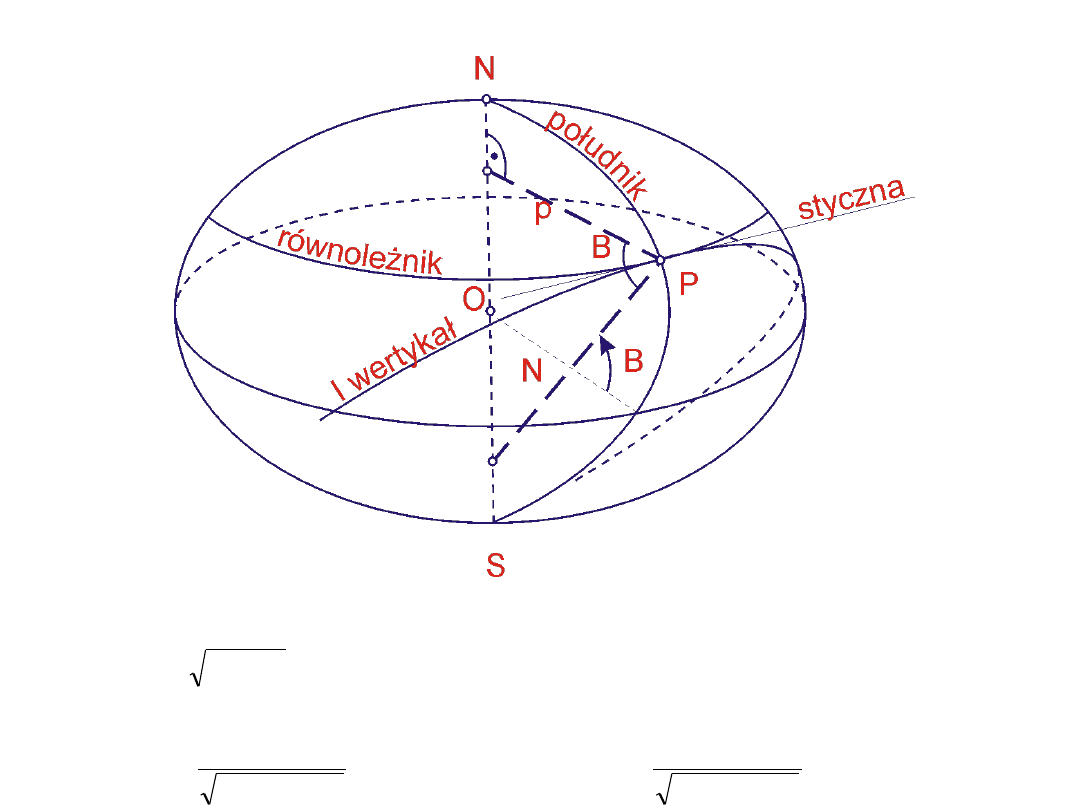
2. Promień krzywizny pierwszego wertykału

Promień równoleżnika

B

N

y

x

p

cos

2

2







oraz ponieważ

B

e

B

a

p

2

2

sin

1

cos





otrzymamy

B

e

a

N

2

2

sin

1





3. Średni promień krzywizny

Korzystając z twierdzenia Eulera

N

A

M

A

R

A

2

2

1

sin

cos







gdzie

A

R

- promień krzywizny przekroju normalnego w azymucie A

Możemy napisać wzór na średni promień krzywizny







2

0

2

2

sin

cos

2





dA

A

M

A

N

MN

R

S

Zaś po rozwiązaniu otrzymamy

MN

R

S



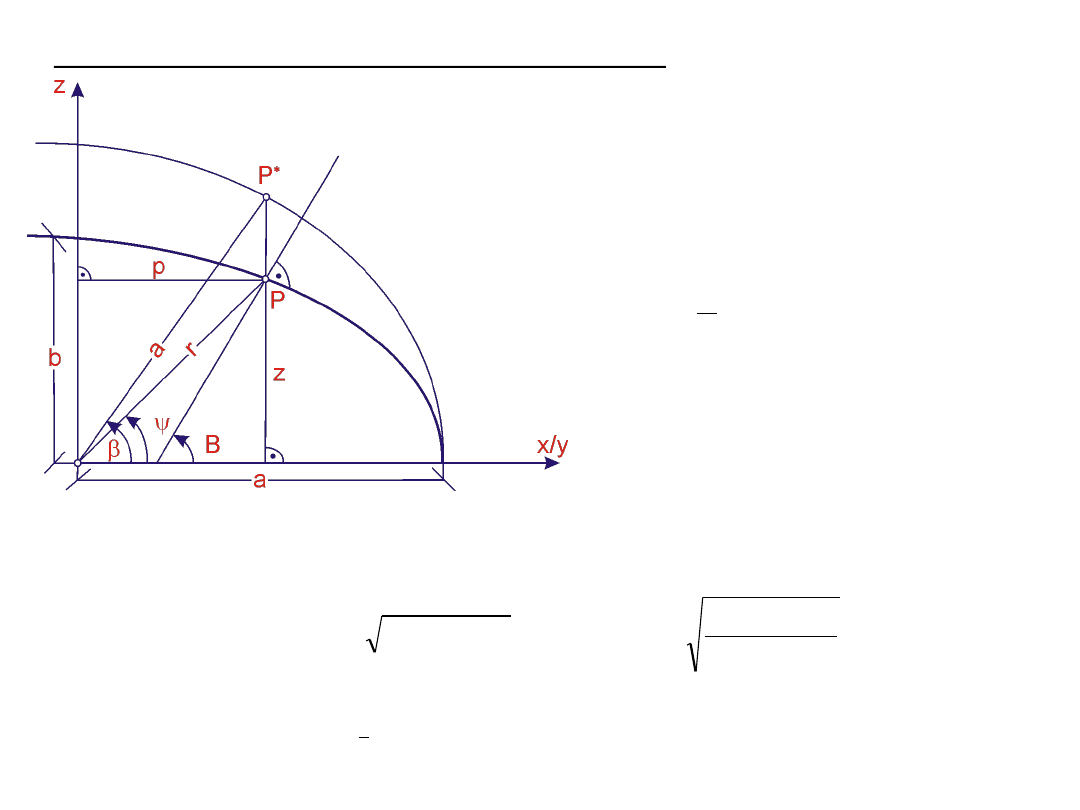
Szerokość geocentryczna i zredukowana

Szerokość geodezyjna, geocentryczna i zredukowana

p

2

tan





lub





B

e tan

1

tan

2







Szerokość geocentryczna pozwala na określenie współrzędnych prostokątnych
punktów leżących na powierzchni elipsoidy



















































sin

sin

sin

cos

cos

L

L

r

z

y

x

r

gdzie

2

2

2

z

y

x

r







lub



2

2

2

cos

1

1

e

e

a

r







Wzór na tan



można przekształcić i otrzymamy wtedy

B

e

B

2

sin

2

2







dla



45



B

otrzymamy wartość maksymalną









'

6

.

11

45

max









B

B



Szerokość zredukowana

B

p

a

tan

tan

2

2







B

e

B

2

sin

4

1

2







Maksymalna wartość tej różnicy wynosi









'

8

,

5

45

max









B

B



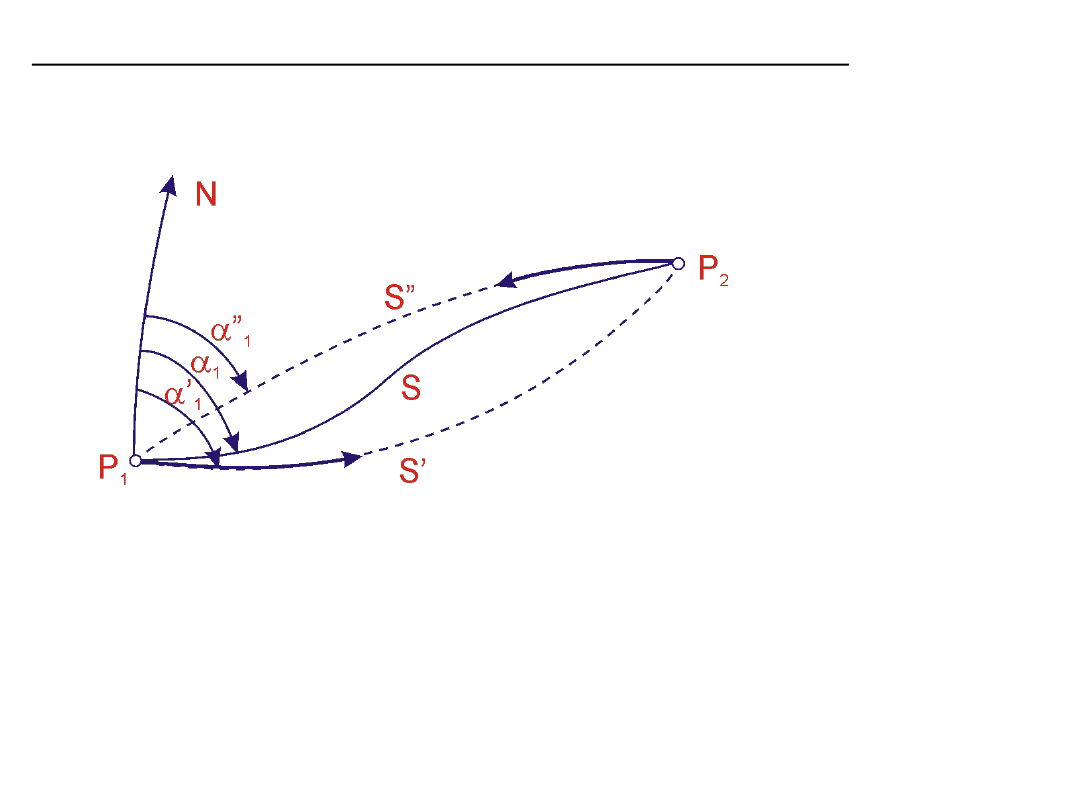
Linia geodezyjna na powierzchni elipsoidy obrotowej

Linia geodezyjna (geodetyka) – najkrótsza odległość pomiędzy dwoma
punktami na elipsoidzie

Wzajemne położenie linii geodezyjnej i przekrojów normalnych

Dla odległości S = 50km rozbieżność przekrojów normalnych





"

2

,

0

"

'

1

1









Równanie linii geodezyjnej (równanie Clairauta)

c

A

B

N



sin

cos

gdzie

A

a

c

sin

cos





Linię geodezyjną i przekroje normalne charakteryzują następujące wzory

1

1

2

2

2

2

1

1

2

sin

cos

12

'





B

a

s

e

a





B

a

s

e

s

s

4

4

5

4

cos

360

'





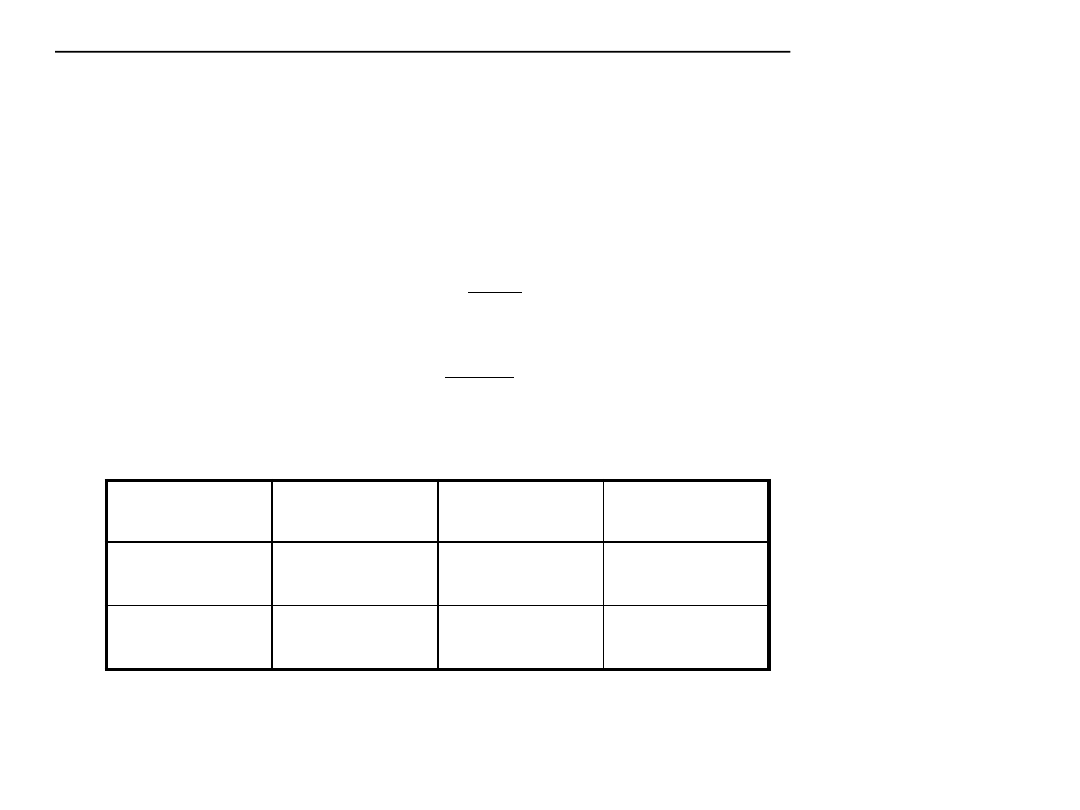
Na których podstawie można wyliczyć:

S=

100 km

200 km

0,028”

1

1

'







s

s



'

50 km

0,007”

0,112”

11

10

2





10

10

9





8

10

2



