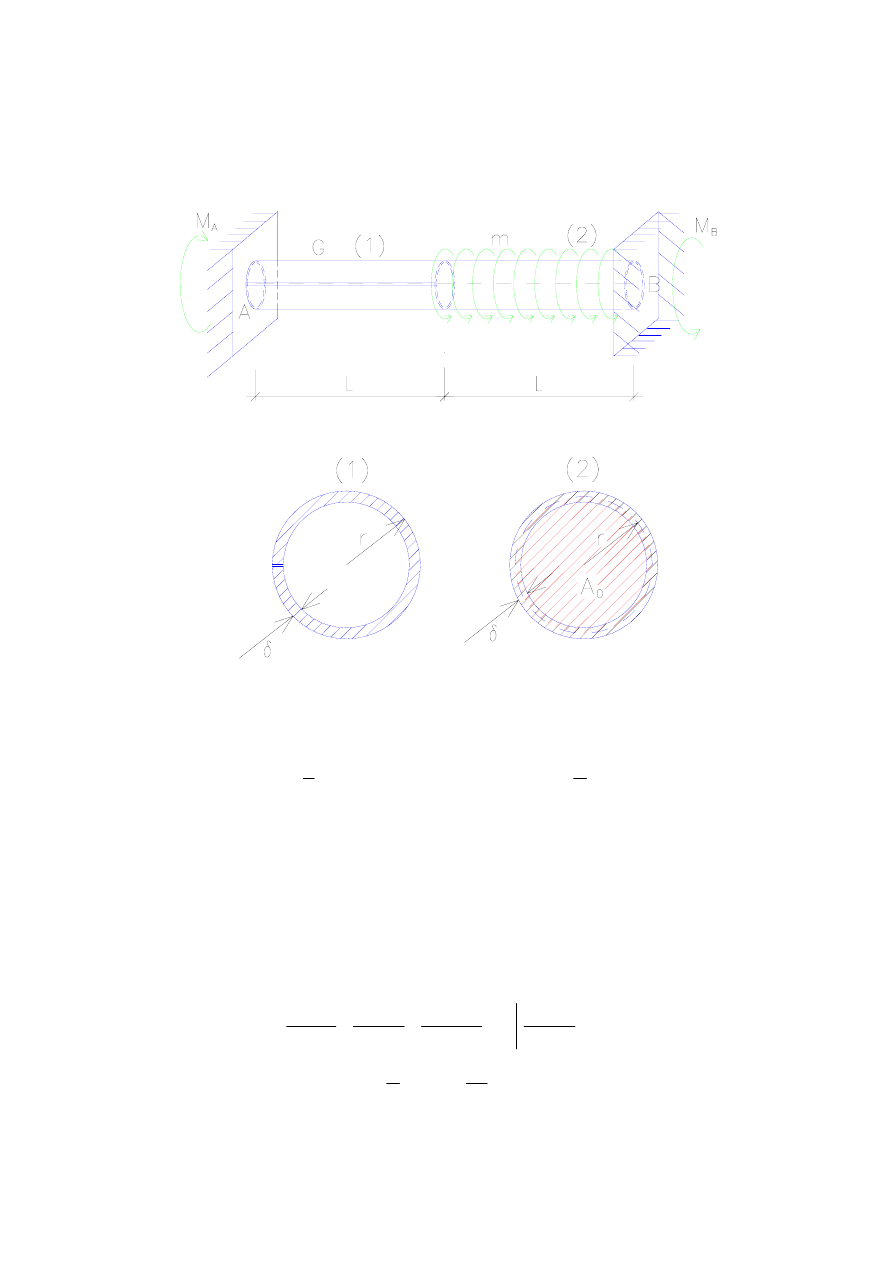
Przykład 7.5. Naprężenia styczne pręta skręcanego
Znaleźć naprężenia styczne w obu częściach pręta cienkościennego skręcanego.
Rysunek 1. Pręt skręcany
Rysunek 2. Przekroje poprzeczne pręta
Sztywności:
(
)
3
1
3
2 δ
πr
G
GJ
S
=
,
(
)
(
)
2
1
3
2
3
2
=
=
δ
δ
π
r
GJ
r
G
GJ
S
S
(1)
Warunek równowagi:
ml
M
M
B
A
=
−
(2)
Warunki przemieszczeniowe:
0
=
A
ϕ
,
ϕ
0
=
B
(3)
Obliczamy:
(
) (
)
(
)
(
)
l
GJ
GJ
ml
GJ
l
M
GJ
l
M
S
S
S
A
S
A
B
2
2
2
2
1
0
2
⋅
=
−
+
=
ϕ
(4)
2
1
3
2
ml
r
M
A
=
+
δ
(5)
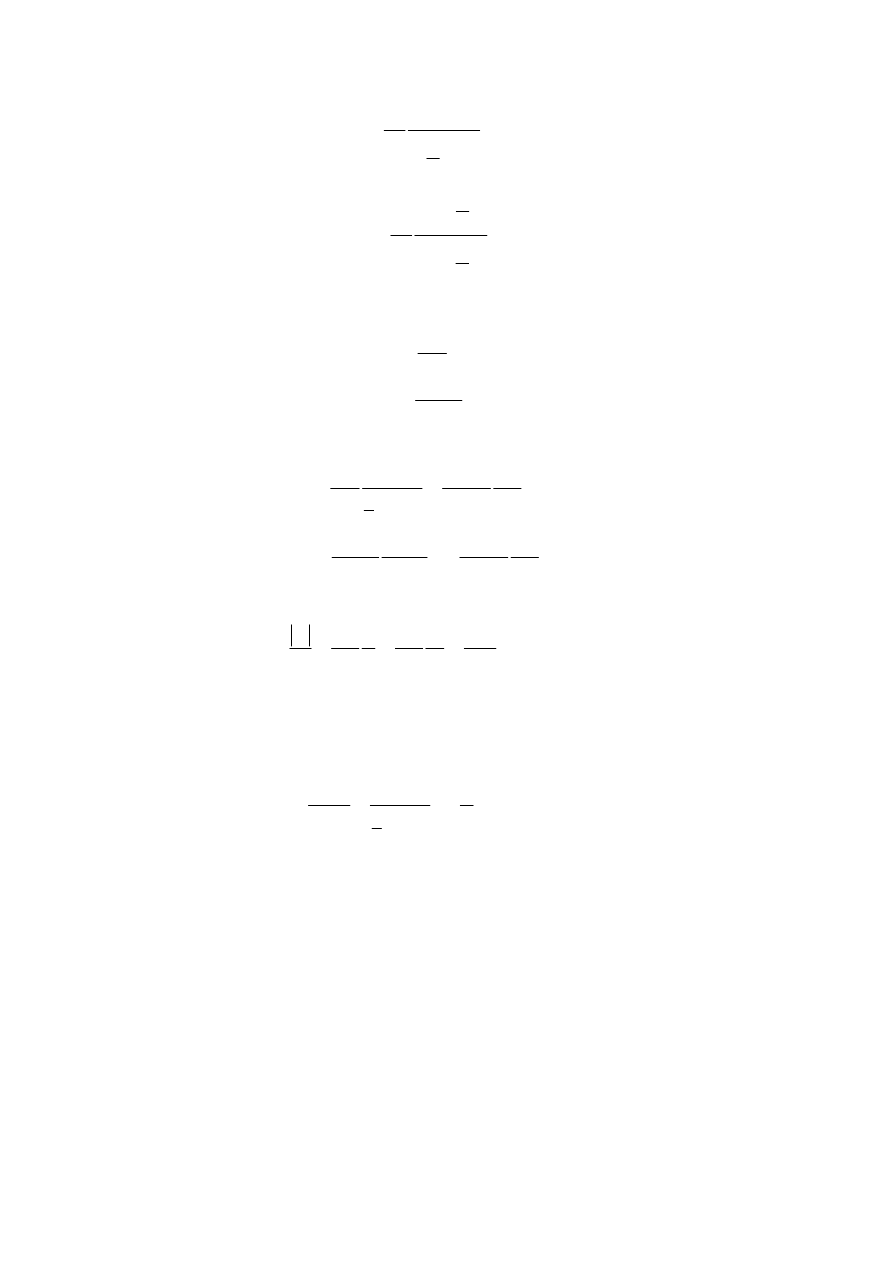
1
3
1
2
2
+
=
δ
r
ml
M
A
,
2
2
3
1
6
1
2
+
+
−
=
δ
δ
r
r
ml
M
B
.
(6)
Jeśli
to:
10
/
=
δ
r
602
ml
M
A
=
,
602
601ml
M
B
−
=
.
(7)
Naprężenia
r
ml
r
ml
2
2
1
1204
3
2
3
1
1
602
δ
π
π
δ
τ
=
=
,
δ
π
δ
π
τ
2
2
2
1204
601
2
1
602
601
r
ml
r
ml
−
=
−
=
(8)
Stosunek naprężeń:
20
3
1
.
60
10
1
3
601
3
601
1
2
≈
=
=
=
r
δ
τ
τ
(9)
Sztywności części drugiej jest 300 razy większa, lecz naprężenia w tej części są 20 razy
większe od naprężeń w części pierwszej.
Jeżeli porównać wskaźniki wytrzymałości obu części, to otrzymujemy:
( )
( )
30
3
2
3
1
2
2
2
1
2
=
=
=
δ
π
δ
δ
π
r
r
r
W
W
S
S
.
(10)
2