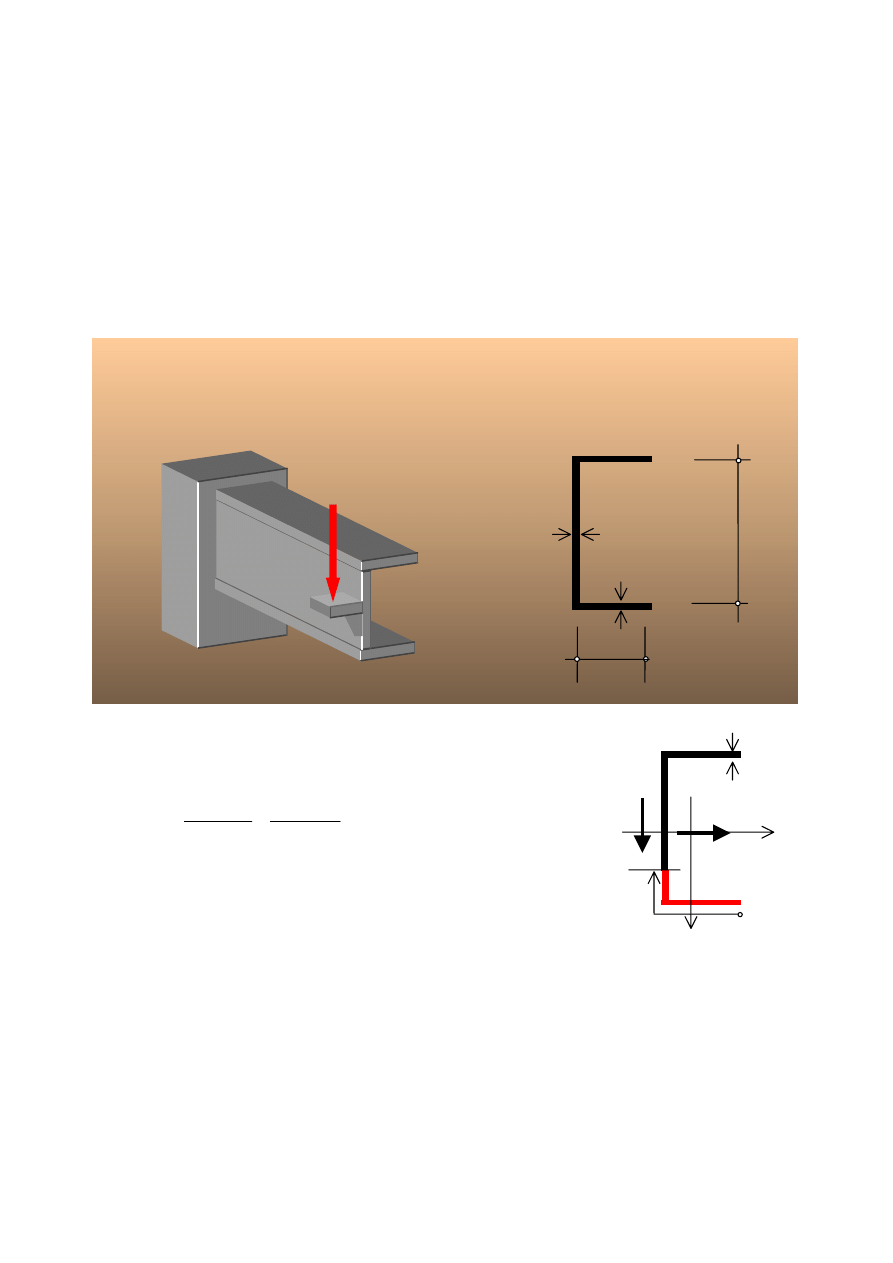
Przykład 3.7. Naprężenia styczne przy zginaniu belki cienkościennej.
Wyznacz rozkład naprężenia stycznego w przekroju podporowym belki wspornikowej
o przekroju cienkościennym obciążonej na swobodnym końcu pionową siłą P. Siła ustawiona
jest w środku sił poprzecznych.
Wyznacz położenie środka sił poprzecznych.
Wymiary przekroju poprzecznego belki podane są na rysunku zamieszczonym
poniżej.
Oblicz naprężenia przyjmując następujące wartości liczbowe:
P=20kN, a=4cm, δ=3mm
δ
δ
4a
2a
Przekrój poprzeczny
P
Rozwiązanie
Wyznaczymy rozkład naprężenia stycznego τ ze wzoru:
y
s
y
z
z
s
z
y
I
s
s
S
T
I
s
s
S
T
s
⋅
⋅
−
⋅
⋅
−
=
)
(
)
(
)
(
)
(
)
(
δ
δ
τ
, gdzie:
s- współrzędna łukowa o początku na brzegu przekroju,
T
y
– siła tnąca skierowana wzdłuż osi y,
T
z
– siła tnąca skierowana wzdłuż osi z,
s
z
S - moment statyczny względem osi centralnej z odciętej części przekroju,
T
z
T
y
y
s
δ
z
s
y
S - moment statyczny względem osi centralnej y odciętej części przekroju,
δ(s)- szerokość przekroju,
I
z
- moment bezwładności przekroju względem osi głównej centralnej z,
I
y
- moment bezwładności przekroju względem osi głównej centralnej y.
W omawianym zadaniu składowa pozioma siły tnącej równa jest zeru. Zatem wyrażenie na
naprężenie styczne upraszcza się do postaci:
z
s
z
y
I
s
s
S
T
s
⋅
⋅
−
=
)
(
)
(
)
(
δ
τ
Obliczmy poszczególne składniki powyższego wzoru.
Z treści zadania wynika, że siła tnąca T
y
jest stała i wynosi P.
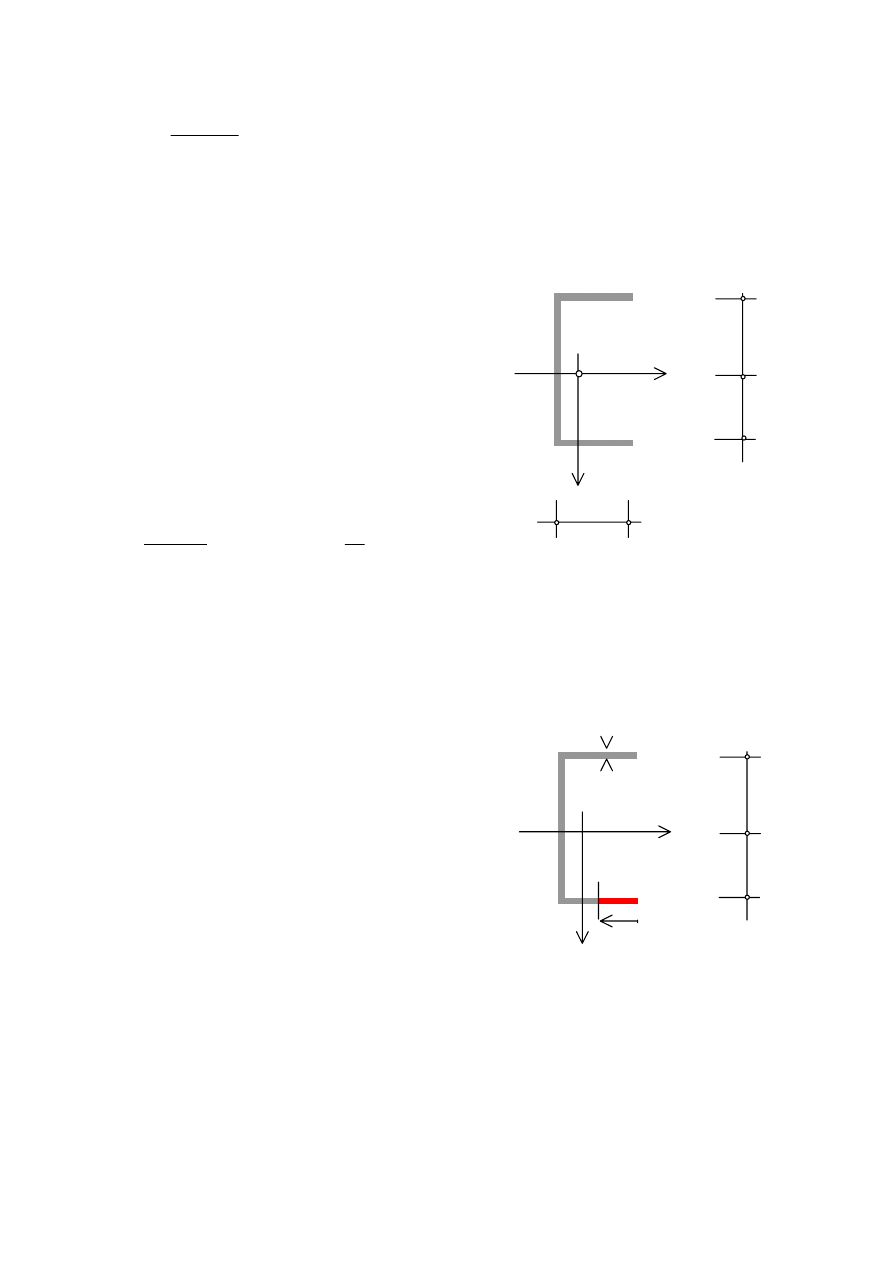
Obliczmy moment statyczny I
z
z
c
2a
2a
2a
y
δ
Do wyznaczenia momentu bezwładności
I
z
wystarczy ustalenie położenia poziomej
osi głównej centralnej. Ponieważ przekrój
poprzeczny ma poziomą oś symetrii oś ta
jest także osią główną centralną.
Moment bezwładności względem osi z
obliczymy wykorzystując wzór Steinera.
Wyrażenia, w których występuje mała
wyższego rzędu
będziemy pomijać.
3
δ
δ
δ
δ
3
2
3
3
64
2
)
2
(
2
12
)
4
(
a
a
a
a
I
z
=
⋅
⋅
+
⋅
=
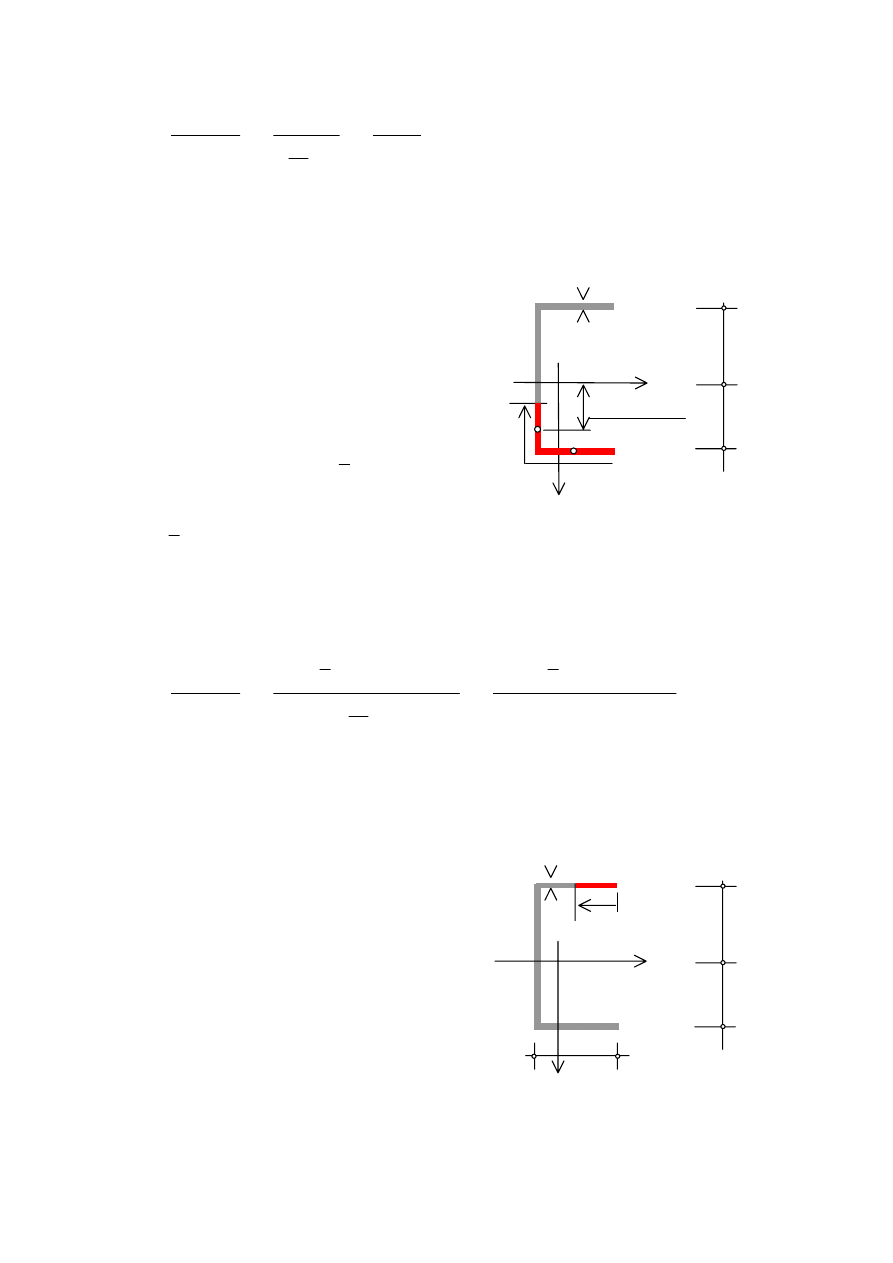
Wyznaczmy naprężenie styczne w dolnej półce przekroju dla
)
2
,
0
(
a
s
∈
z
s
2a
2a
y
δ
Obliczmy moment statyczny odciętej części przekroju
)
(
)
(
s
F
s
y
S
s
z
⋅
=
)
(s
y
- oznacza współrzędną środka ciężkości odciętej
części przekroju
)
(s
F
pole powierzchni odciętej części przekroju
Dla
)
2
,
0
(
a
s
∈
δ
s
a
s
F
s
y
S
s
z
⋅
=
⋅
=
2
)
(
)
(
Podstawiając do wzoru na naprężenie styczne obliczoną funkcję momentu statycznego
otrzymamy:
2
δ
δ
δ
δ
δ
τ
2
3
64
6
3
64
2
)
(
)
(
)
(
a
s
P
a
as
P
I
s
s
S
T
s
z
s
z
y
⋅
−
=
⋅
−
=
⋅
⋅
−
=
Znak minus oznacza , że zwrot naprężenia stycznego jest przeciwny do kierunku wzrostu
współrzędnej łukowej s.
Wyznaczmy naprężenie styczne w ściance środnika dla
)
6
,
2
(
a
a
s
∈
Obliczmy moment statyczny odciętej części przekroju
z
δ
y
s
2a-1/2 (s-2a)
2a
2a
dla
)
6
,
2
(
a
a
s ∈
)
(
)
(
s
F
s
y
S
s
z
⋅
=
δ
δ
)
2
(
)
2
(
2
1
2
4
)
(
)
(
2
a
s
a
s
a
a
s
F
s
y
S
s
z
−
⋅
−
−
+
=
⋅
=
δ
−
+
−
=
2
2
2
4
2
1
a
sa
s
S
s
z
Podstawiając do wzoru na naprężenie styczne obliczoną funkcję momentu statycznego
otrzymamy:
δ
δ
δ
δ
δ
τ
3
2
2
3
2
2
64
2
4
2
1
3
3
64
2
4
2
1
)
(
)
(
)
(
a
a
sa
s
P
a
a
sa
s
P
I
s
s
S
T
s
z
s
z
y
−
+
−
⋅
−
=
−
+
−
⋅
−
=
⋅
⋅
−
=
Znak minus oznacza , że zwrot naprężenia stycznego jest przeciwny do kierunku wzrostu
współrzędnej łukowej s
Wyznaczmy naprężenie styczne w górnej półce przekroju dla
)
8
,
6
(
a
a
s
∈
Wprowadźmy nową współrzędną łukową s’, której początek znajduje się na krawędzi górnej
półki.
Obliczmy moment statyczny odciętej części przekroju
z
δ
y
s’
2a
2a
2a
)
'
(
)
'
(
'
s
F
s
y
S
s
z
⋅
=
Dla
)
2
,
0
(
'
a
s
∈
δ
'
2
)
'
(
)
'
(
,
s
a
s
F
s
y
S
s
z
⋅
−
=
⋅
=
Podstawiając do wzoru na naprężenie styczne obliczoną funkcję momentu statycznego
otrzymamy:
3
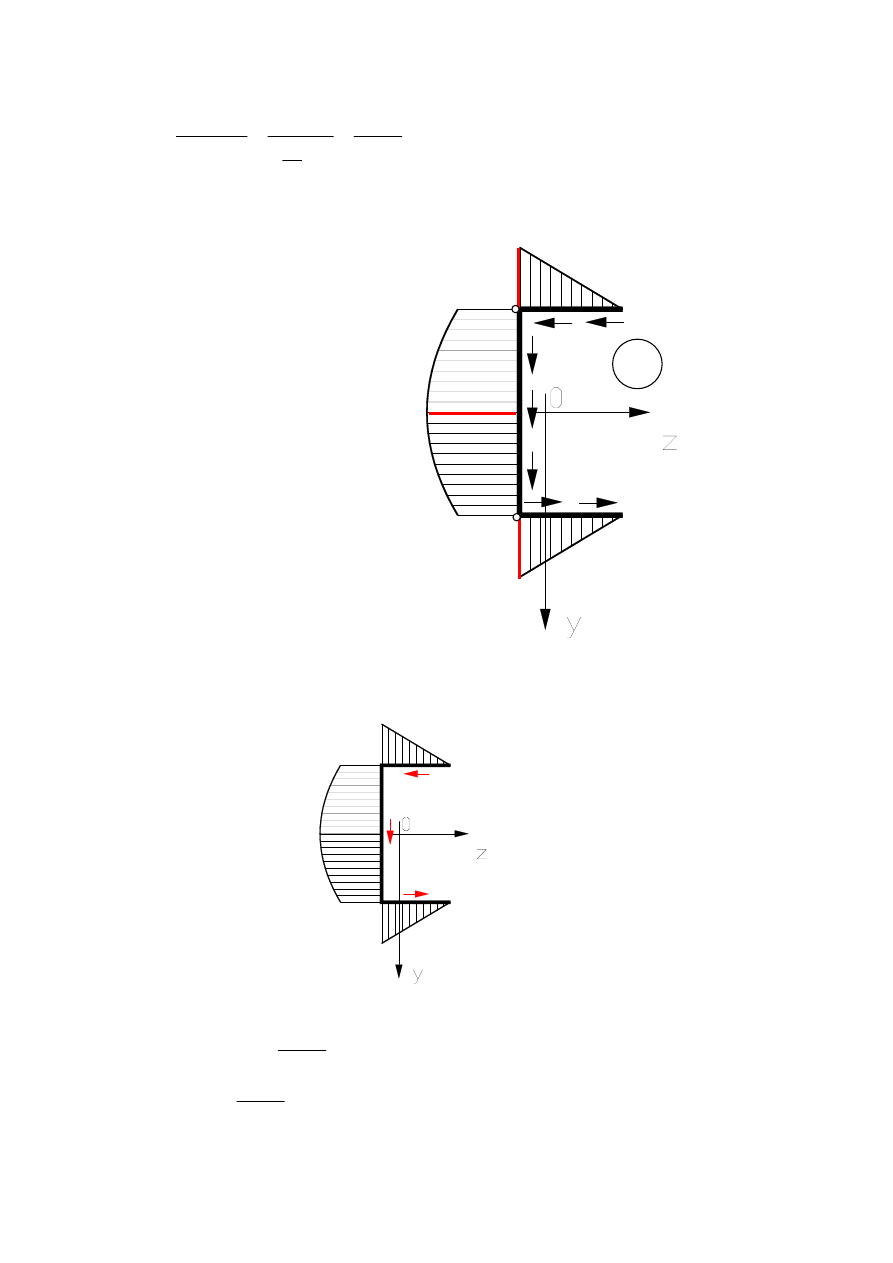
δ
δ
δ
δ
δ
τ
2
3
'
,
64
'
6
3
64
'
2
)
(
)
(
)
(
a
s
P
a
as
P
I
s
s
S
T
s
z
s
z
y
⋅
=
⋅
=
⋅
⋅
−
=
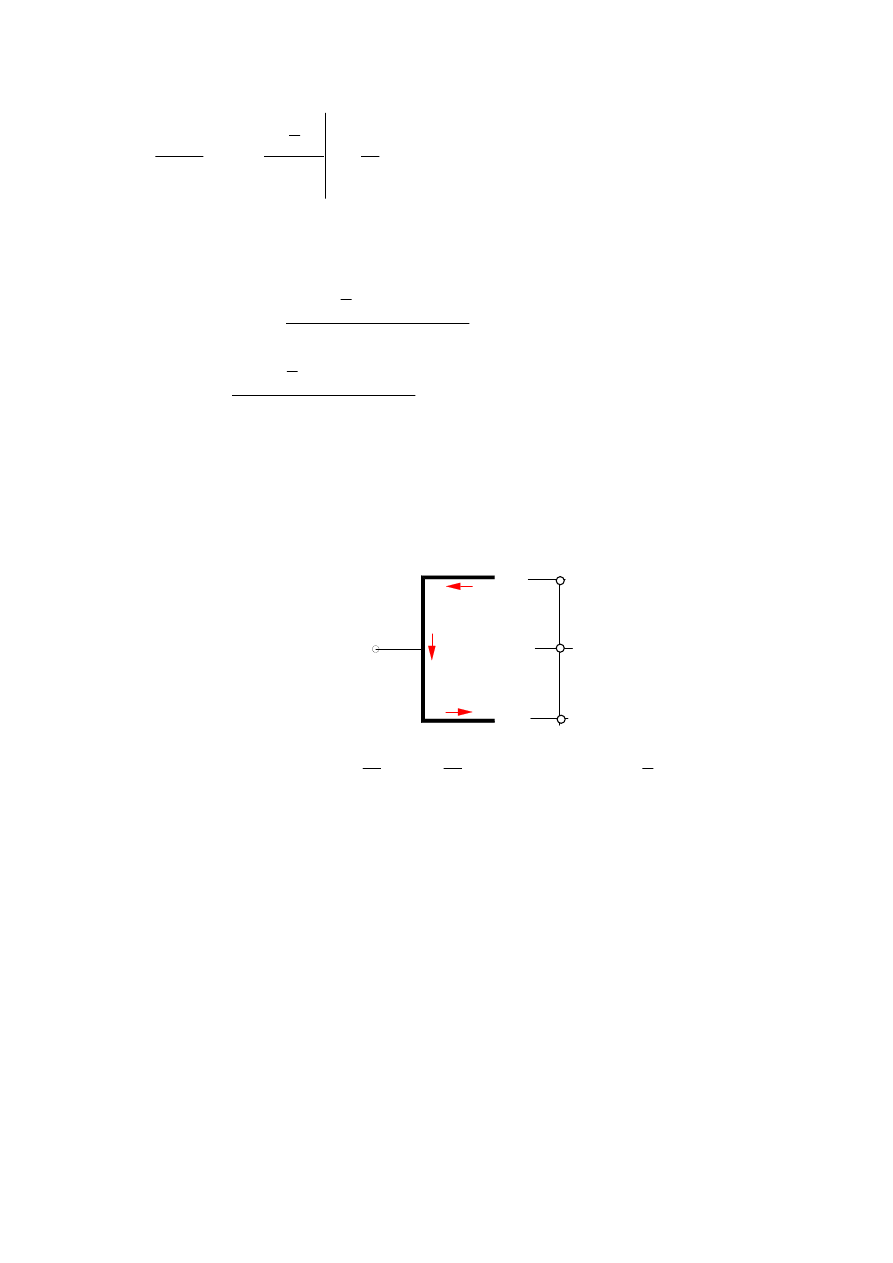
Narysujmy wykresy wyznaczonych funkcji naprężenia.
Oznaczymy zwroty naprężenia strzałkami.
τ
max
=(18/64) P/aδ=46.88 [MPa]
A
τ
A
=(12/64) P/aδ=31.25 [MPa]
τ
B
τ
B
=(12/64) P/aδ=31.25 [MPa]
Wyznaczmy położenie środka sił poprzecznych.
Policzmy sumę naprężeń stycznych działających w półkach górnej i dolnej oraz w środniku.
t
g
t
s
t
d
Sumę naprężeń
δ
τ
2
'
64
'
6
)
(
a
s
P
s
⋅
=
na górnej półce t
g
obliczymy z całki:
∫
∫
⋅
=
⋅
=
=
=
a
a
s
s
g
ds
a
Ps
ds
t
2
0
2
2
'
0
'
64
'
6
'
δ
δ
τδ
4
P
a
s
P
ds
a
Ps
t
a
a
g
16
3
64
'
2
1
6
64
'
6
2
0
2
2
2
0
2
=
=
⋅
=
∫
δ
δ
Suma naprężeń na dolnej półce t
d
jest oczywiście taka sama jak na górnej.
g
d
t
t
=
Sumę naprężeń
δ
τ
3
2
2
64
2
4
2
1
3
)
(
a
a
sa
s
P
s
−
+
−
⋅
−
=
w środniku t
s
obliczymy z całki:
∫
∫
⋅
−
+
−
⋅
=
⋅
=
=
=
a
a
a
s
a
s
s
ds
a
a
sa
s
P
ds
t
6
2
3
2
2
6
2
64
2
4
2
1
3
δ
δ
τδ
P
t
s
=
Położenie środka siłą poprzecznych obliczymy z warunku zerowania się momentów od sił w
półkach i środniku. Ponieważ środek sił poprzecznych znajduje się na osi symetrii do
wyznaczenia pozostaje tylko współrzędna pozioma.
2a
2a
t
g
ξ=?
t
s
k
t
d
0
2
2
=
−
+
=
∑
ξ
s
d
g
k
t
a
t
a
t
M
⇒
0
2
16
3
2
16
3
=
⋅
−
⋅
+
⋅
ξ
P
a
P
a
P
⇒
]
[
3
4
3
cm
a
⋅
=
=
ξ
5