Wykłady z Biofizyki dla studentów kierunku

analityka medyczna

Pomiary wielkości fizycznych,

opracowywanie wyników pomiarów;

szacowanie dokładności pomiarów

Hanna Trębacz

Katedra i Zakład Biofizyki

Uniwersytet Medyczny w Lublinie

2012/2013

Informacje wstępne

Program



15 godzin wykładów;



7 razy po dwie godziny



1raz 1 godz.



30 godzin ćwiczeń (10 razy po 3 godz.)



9 tygodni regularnych ćwiczeń



10-

ty tydzień – powtórki i odrabianie zaległości



Program wykładów – na stronie www Katedry
i na tablicy ogłoszeń

Informacje wstępne

Warunki i forma zaliczenia



Zaliczenie 9-

ciu ćwiczeń laboratoryjnych



(wg regulaminu ćwiczeń)



Zaliczenie testu końcowego z wykładów



Test wyboru oraz pytania otwarte wymagające
konkretnej, jednozdaniowej odpowiedzi



Ocena

– średnia ważona z testu i z ćwiczeń

Informacje wstępne

Literatura podstawowa:



Praca zbiorowa pod redakcją F. Jaroszyka -
„Biofizyka”



Materiały do ćwiczeń laboratoryjnych
opublikowane na stronach www Katedry
Biofizyki.

Informacje wstępne

Literatura uzupełniająca:



S. Miękisz, A. Hendrich - „Wybrane
zagadnienia z biofizyki"



M. Kapuścińska – „Fizyka. Podręcznik dla
studentów farmacji.”



W. Bulanda

– „Podstawy fizyki środowiska

przyrodniczego” (Wydawnictwo UMCS, 2007)



J.W. Kane i M.M. Sternheim

– „Fizyka dla

przyrodnikow”

Biofizyka

Interdyscyplinarna nauka, która stosuje teorie

i metody nauk fizycznych, w celu badania

systemów biologicznych na wszystkich

poziomach organizacji.

Czego dotyczy wykład – Biofizyka dla

studentów analityki medycznej

Efekty kształcenia



Po zakończeniu kursu student



rozumie fizyczne podstawy procesów
biologicznych oraz metod pomiarowych
stosowanych w diagnostyce laboratoryjnej



rozumie zasady funkcjonowania aparatury
stosowanej w medycynie laboratoryjnej



potrafi mierzyć, interpretować i opisywać
właściwości fizykochemiczne badanych
substancji

Fizyka to nauka oparta o obserwacje i
pomiary – biofizyka też

Co powtórzyć przed rozpoczęciem

kursu Biofizyki



Jednostki podstawowe i jednostki pochodne
w SI



Przedrostki stosowane do definiowania
wielokrotności i podwielokrotności jednostek



Przeliczanie jednostek



Działania na potęgach



Wektory, działania na wektorach

Siedem podstawowych jednostek SI

Nazwa

Mierzona wielkość

metr (m)

długość

kilogram (kg)

masa

sekunda (s)

czas

amper (A)

natężenie prądu elektrycznego

kelvin (K)

temperatura

mol (mol)

ilość substancji

candela (cd)

światłość

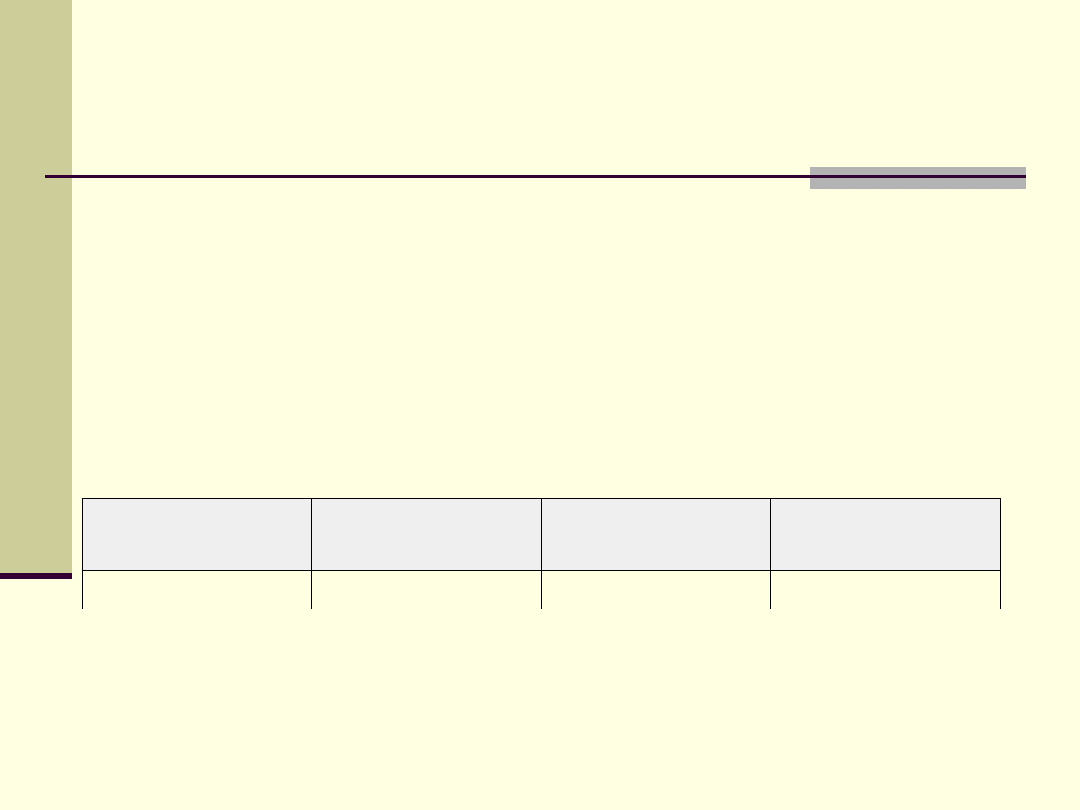
wielkość

nazwa

oznaczenie

w jednostkach
podstawowych

siła

niuton

N

kg·m·s

-2

ciśnienie

paskal

Pa

kg·m

-1

·s

-2

energia, praca

dżul

J

kg·m

2

·s

-2

Jednostki pochodne układu SI

-

jednostki utworzone w oparciu o równanie definicyjne

danej wielkości, są iloczynem jednostek podstawowych
układu SI, podniesionych do odpowiedniej potęgi.

Siła ma wartość 1 N, jeżeli nadaje ciału o masie 1 kg
przyspieszenie 1

m/s².

Np. siła

F = m·a

Jednostki, przykład



Słynne równanie Einsteina wyrażone jest jako:

E=mc

2

,



gdzie

E

to energia,

m

to masa, a

c

jest prędkością

światła.



[E] = kg·(m·s

-1

)

2

= kg·m

2

·s

-2

- Jednostka energii w

podstawowych jednostkach SI;



Inne równanie na energię to

E=mgh

,



gdzie

m

to masa,

g

to przyspieszenie grawitacyjne, a

h

to wysokość.



[E] = kg·m·s

-2

·m = kg·m

2

·s

-2

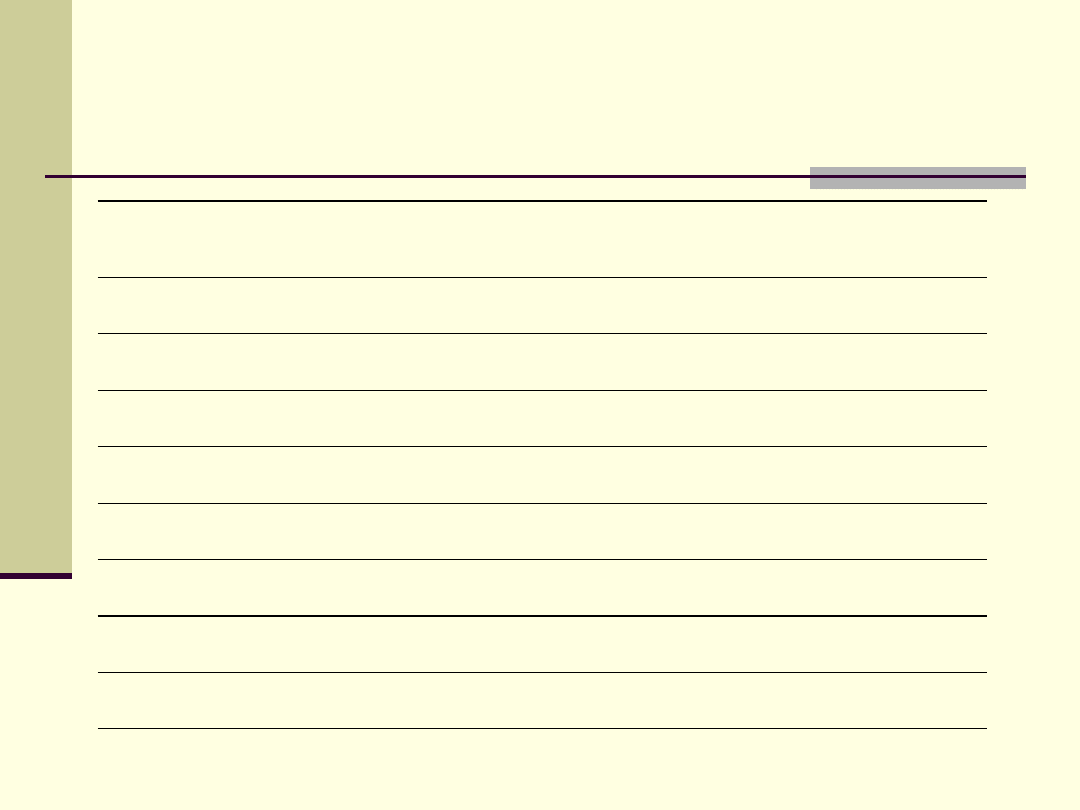
Przybliżone wartości długości różnych obiektów

Długość (m)

Odległość Ziemi od najbliższej gwiazdy

4 x 10

16

Średni promień orbity Ziemi

1.5 x 10

11

Średni promień Ziemi

6.4 x 10

6

Najwyższe góry

8.8 x 10

3

Wysokość człowieka

1.7 x 10

0

Długość muchy

5 x 10

-3

Typowy rozmiar komórki żywego organizmu

1 x 10

-5

Średnica atomu wodoru

1 x 10

-10

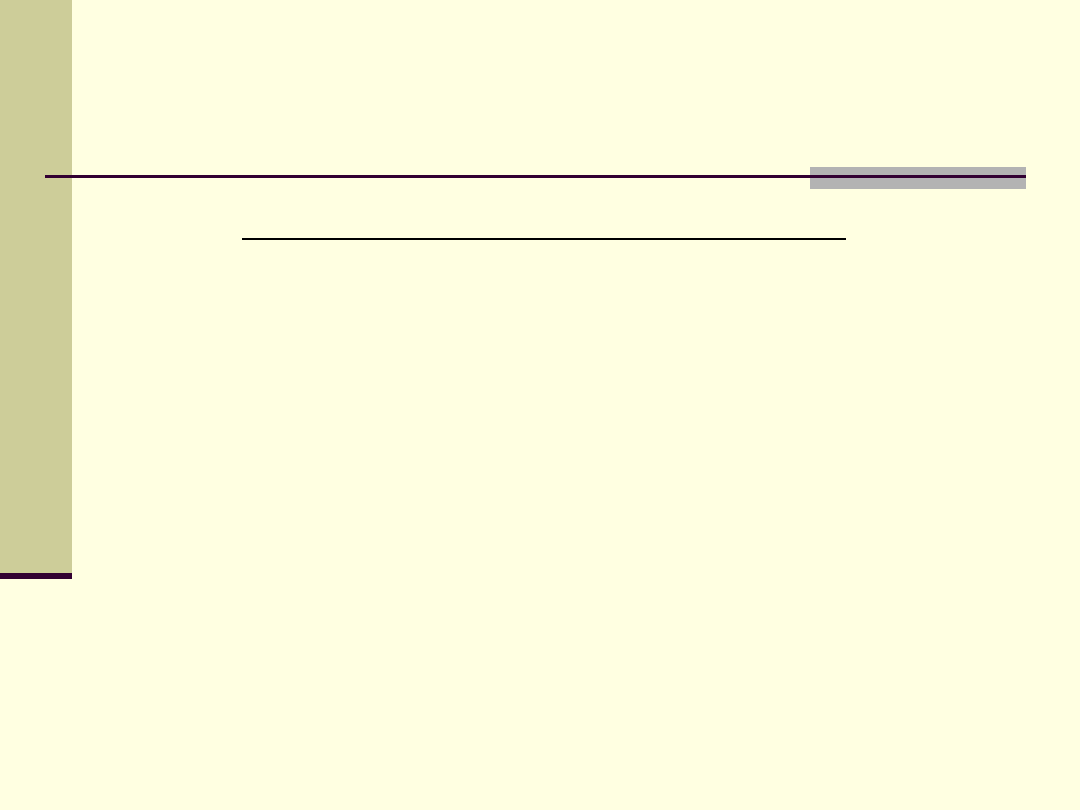
Wielokrotności i podwielokrotności

Potęga

Przedrostek

Skrót

10

-15

femto

f

10

-12

pico

p

10

-9

nano

n

10

-6

micro

μ

10

-3

milli

m

10

-2

centi

c

10

-1

deci

d

10

3

kilo

k

10

6

mega

M

10

9

giga

G

10

12

tera

T

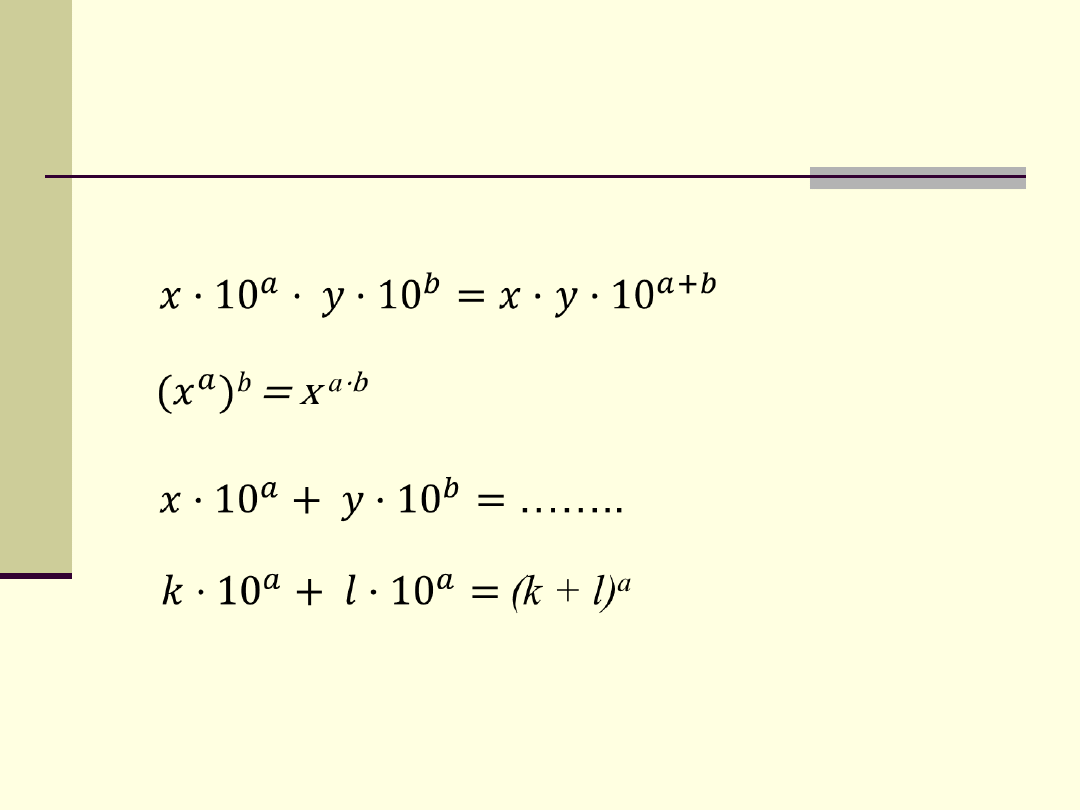
Działania na potęgach

X = 0,003; y = 1300; a = 4; b = -2

Przeliczanie jednostek - przykład



Wyraź 50 500 m w centymetrach,
milimeterach i metrach.



Objętość 1 mola gazu w warunkach
normalnych to ok. 24 L. Wyraź tę wielkość w
jednostce SI.



Gęstość krwi to ok. 1050 kg/m

3

. Oblicz masę

krwi w cm

3

.

Cyfry znaczące



Prędkość krwi w naczyniu wynosi 1.07 m/s. jak długo

krew będzie płynęła w tym naczyniu na odcinku 0.45 m?



Wynik liczenia na kalkulatorze to 0,420560747



(?)



1,07 m/s -

trzy cyfry znaczące; 0,45 m - dwie cyfry

znaczące



Poprawny wynik to 0,42 s.



Wynik obliczeń nie może być dokładniejszy niż najmniej

dokładna liczba użyta do obliczeń.

A

D

= 2 x A

D

= 3 x A

Wektory

–

Mnożenie wektorów przez liczbę

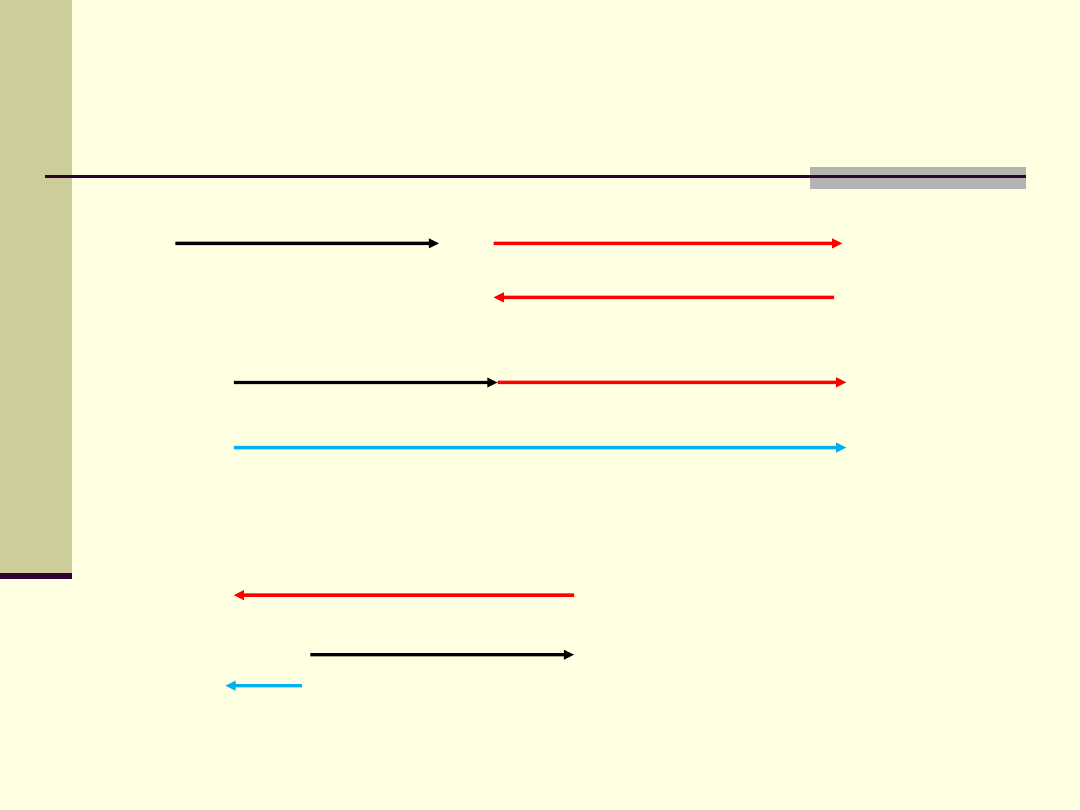
A

B

-B

B

C

= A +

B

A

A

-B

C

= A -

B

Dodawanie i odejmowanie wektorów

A

B

A

B

C =

A

+

B

A

-B

C =

A

-

B

A

B

C =

A

+

B

-B

A

C =

A

-

B

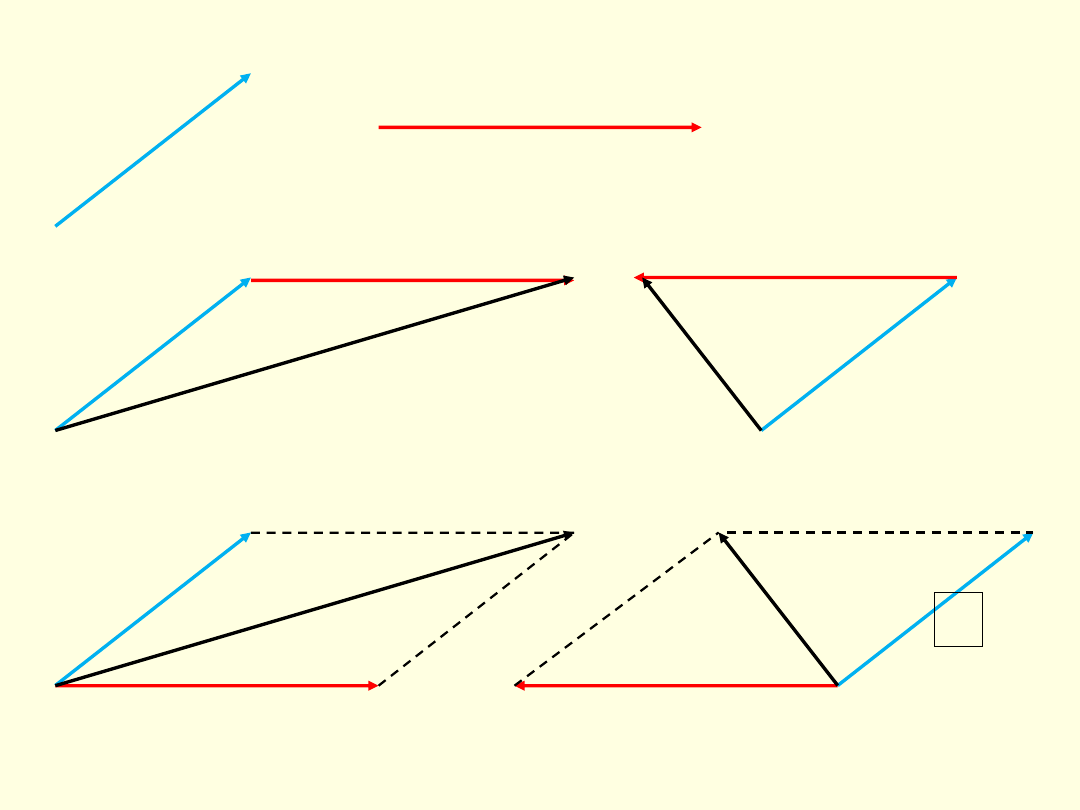
Dodawanie
wektorów

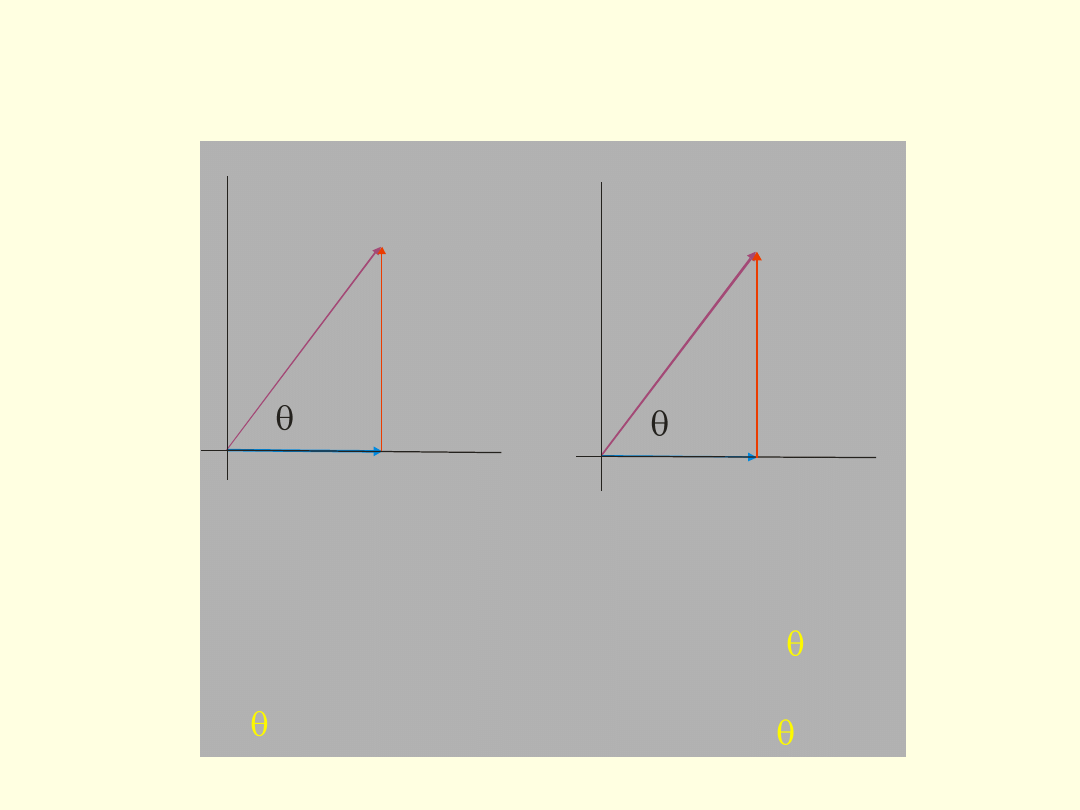
Wektory prostopadłe

y

x

C = A + B

A

B

C

C = C cos

C = C sin

x

y

C = A + B

2

2

2

= tan (A/B)

-1

y

x

C = C + C

x

y

C

x

C

y

C

Dokładność pomiaru
– podstawowe zasady oceny błędu pomiaru



Wielkość zmierzona nie jest nigdy wielkością

idealnie dokładną.



Wyniki wszystkich pomiarów obarczone są

pewnym stopniem niepewności.



Ten „stopień niepewności” można oszacować
poprzez oszacowanie

błędu pomiarowego.

Błędy grube
Błędy grube są po prostu pomyłkami.

Błędy systematyczne (niepewność pomiaru)
Przyczyny tych błędów są stałe w czasie, powtarzalne. Są
związane z narzędziem pomiarowym, ograniczoną
czułością naszych zmysłów lub ze stosowaną metodą
pomiaru.

Błędy przypadkowe (błędy losowe)
nie wynikają z czynników powtarzalnych. Wyniki kolejnych
pomiarów zmieniają się w sposób losowy, przeważnie z
powodu statystycznego charakteru mierzonej wielkości.

Przyczyna powstawania błędów pomiarowych

Definicja błędu bezwzględnego

 Otrzymana w wyniku pomiaru

wartości wielkości fizycznych A

różni się od wartości prawdziwej A

0

.



Różnicę A – A

0

= A

nazywamy rzeczywistym

błędem bezwzględnym wielkości

mierzonej i

wyrażoną w takich jednostkach jak wielkość

mierzoną.

 Wyznaczenie

błędu rzeczywistego jest rzadko możliwe; tylko

wtedy, gdy znana jest

wartość, której możemy użyć w miejsce

wartości rzeczywistej (np. z tablic). W większości przypadków
musimy

oszacować maksymalny błąd pomiaru.

0

A

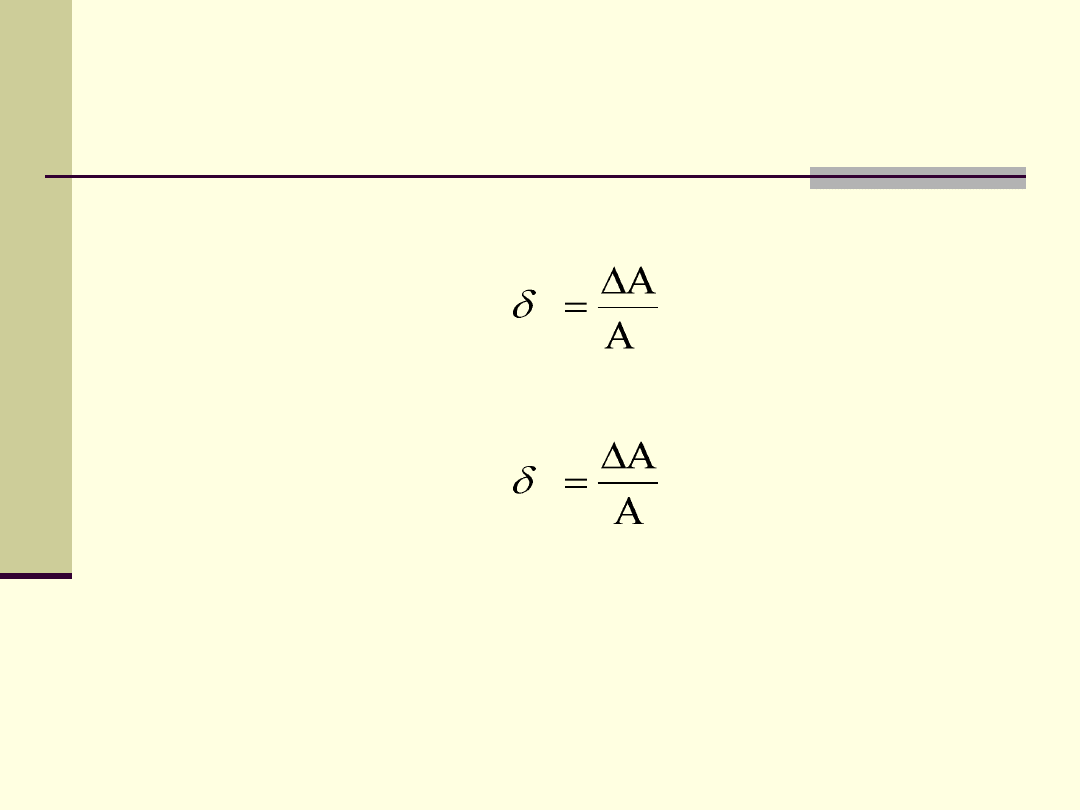
Błąd pomiaru względny możemy wyrazić w procentach:
nazywa się go wtedy błędem procentowym.

Definicja błędu względnego

A

Gdy znana jest wartość rzeczywista i rzeczywisty błąd
bezwzględny

Gdy nie jest znana wartość rzeczywista

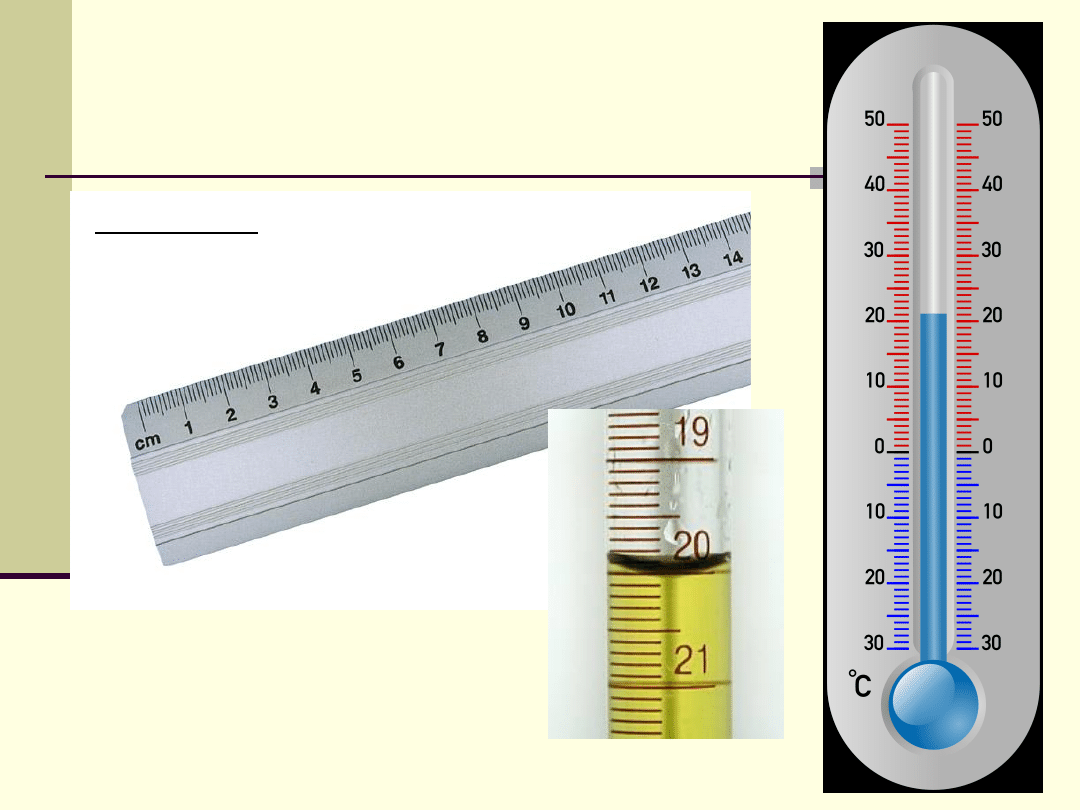
Przykład 1. Podziałka liniowa

Szacowanie błędu
systematycznego

Z reguły błąd systematyczny
szacuje się jako połowę
najmniejszej użytej działki

Przykład 2. Wyświetlacz cyfrowy

Szacowanie błędu
systematycznego

Przykład 3.

Podczas ważenia wagą laboratoryjną za błąd

pomiaru przyjmujemy masę najmniejszego odważnika w
zestawie.

Szacowanie błędu systematycznego

Przykład 4.

Odmierzając stoperem czas przyjmiemy jako

błąd pomiaru 0,2 – 0,5 s w zależności od oceny własnego
refleksu

Szacowanie błędu systematycznego

Przykład



Zmierzono temperaturę cieczy jako 46,4

o

C



Błąd pomiarowy bezwzgledny (niepewność)
pomiaru wynosił 0,1

o

C.



Wynik należy wyrazić jako t = 46,4 ± 0,1

o

C, co

oznacza, że prawdziwa wartość temperatury
była pomiędzy 46,3 a 46,5

o

C.



Błąd względny pomiaru to 0,002; czyli 0,2 %

Błędy systematyczne można minimalizować przez

stosowanie doskonalszych przyrządów i metod

pomiarowych.

Spowodowane one być mogą różnorodnymi czynnikami:

• statystycznym charakterem zjawisk fizycznych, co prowadzi
do chwilowych fluktuacji lokalnych właściwości, np. gęstości,
lepkości, wilgotności, temperatury, koncentracji jonów, itp,

• przybliżonym modelem mierzonego obiektu,

• ograniczoną zdolnością percepcji naszych zmysłów i
fluktuacji tych zdolności.

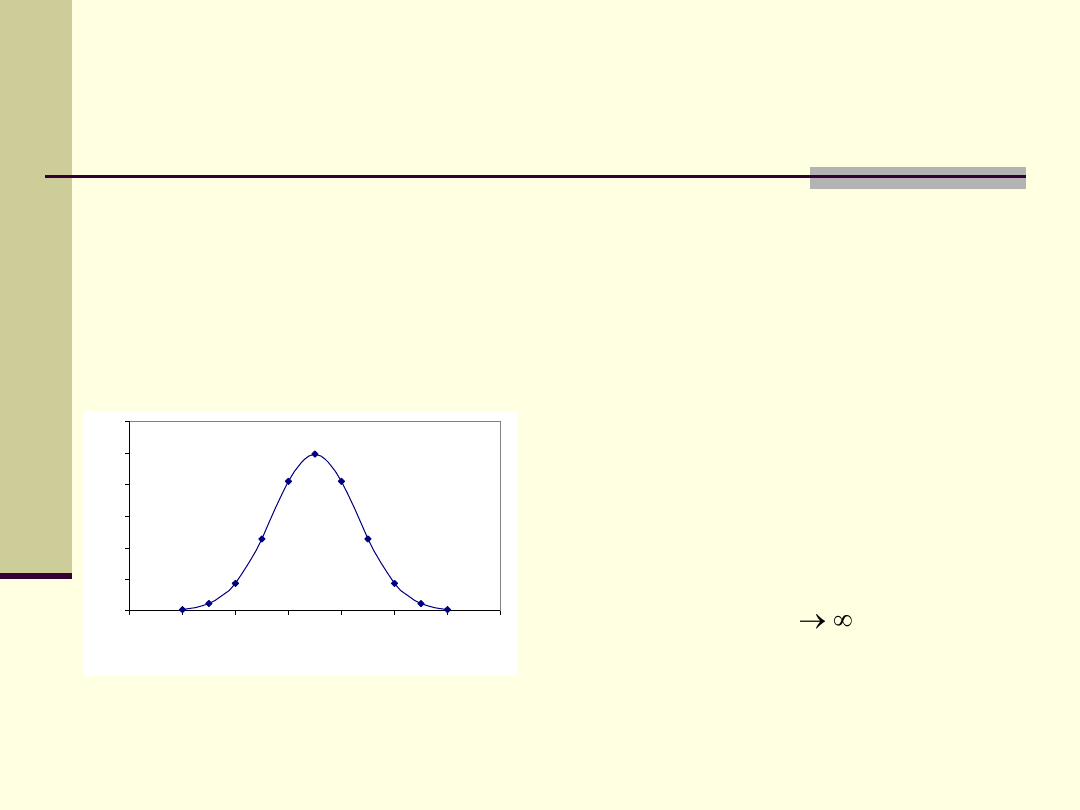
Błędy przypadkowe

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

x

N

Zauważyć można, że wyniki bardzo małe i
bardzo duże występują rzadziej, częściej
występują wyniki pośrednie. W granicy,
gdy liczba pomiarów n krzywa jest
tzw. krzywą Gaussa.

Szacowanie błędu przypadkowego

Występowanie błędów przypadkowych powoduje, że wyniki kolejnych
pomiarów zmieniają się w sposób losowy, mimo że mierzona jest ta
sama wielkość w warunkach praktycznie niezmiennych. Można je
modelować przy pomocy rozkładów statystycznych przykładowo
rozkładu normalnego (Gaussa).

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

x

N

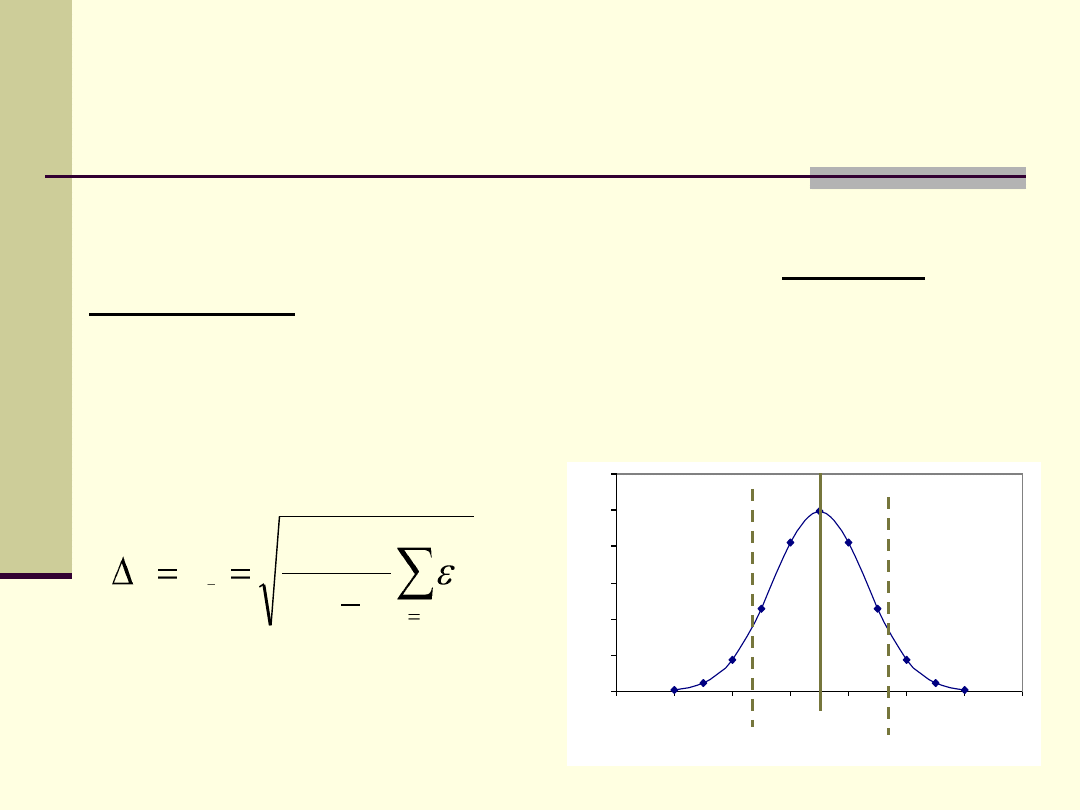
Szacowanie błędu przypadkowego

Informację na temat wielkości tego błędu można uzyskać po
wykonaniu serii pomiarów i wyliczeniu średniej oraz odchylenia
standardowego.
Wartość średnia arytmetyczna pomiarów nie jest wartością rzeczywistą
i najczęściej przyjmujemy jako błąd tej wartości tzw. średni błąd
kwadratowy średniej arytmetycznej nazywany też odchyleniem
standardowym średniej arytmetycznej

n

i

i

x

n

n

S

x

1

2

)

1

(

1



Jak była wczoraj temperatura ciała pacjenta J.K. jeśli
wyniki kolejnych sześciu pomiarów temperatury były
następujące:

38.3

o

C; 38.8

o

C; 38.5

o

C; 38.3

o

C; 38.0

o

C; 38.2

o

C;

t

śr

= 38.35

o

C = 38.4

o

C



Jaki był błąd pomiaru?



Standardowe odchylenie średniej

SD = 0.27

o

C = 0.3

o

C

Błąd przypadkowy - przykład

W praktyce laboratoryjnej dokonujemy

pomiarów kilku

wielkości prostych, z których obliczamy jakąś wielkość
złożoną.
Oznaczamy

wielkość złożoną przez f i niech będzie ona

funkcją dwóch wielkości prostych x oraz y: f = f(x,y).

Np.

prędkość przepływu cieczy (V) w przewodzie

obliczono na podstawie pomiaru czasu

przepływu przez

przewód (t) oraz długości przewodu (l)

Czyli V = f(t, l)

taką, że V= l/t

Ocena błędu wielkości złożonej

Czas

wynosił 10,3 s i zmierzono go z dokładnością do 0,1s

Długość wynosiła 27,5 cm i zmierzono ją z dokładnością do 0,1 cm.

Prędkość wynosiła więc 2,7 cm/s (0,027m/s), ale jak oszacować błąd
pomiaru

prędkości?

Błąd względny wielkości złożonej jest sumą błędów względnych
wielkości prostych (z odpowiednimi współczynnikami).

Δt/t = 0,0097; Δl/l = 0,0036
ΔV/V = Δt/t +Δl/l = 0,0097 + 0,0036 = 0,0133 = 1,3%

Ocena błędu wielkości złożonej

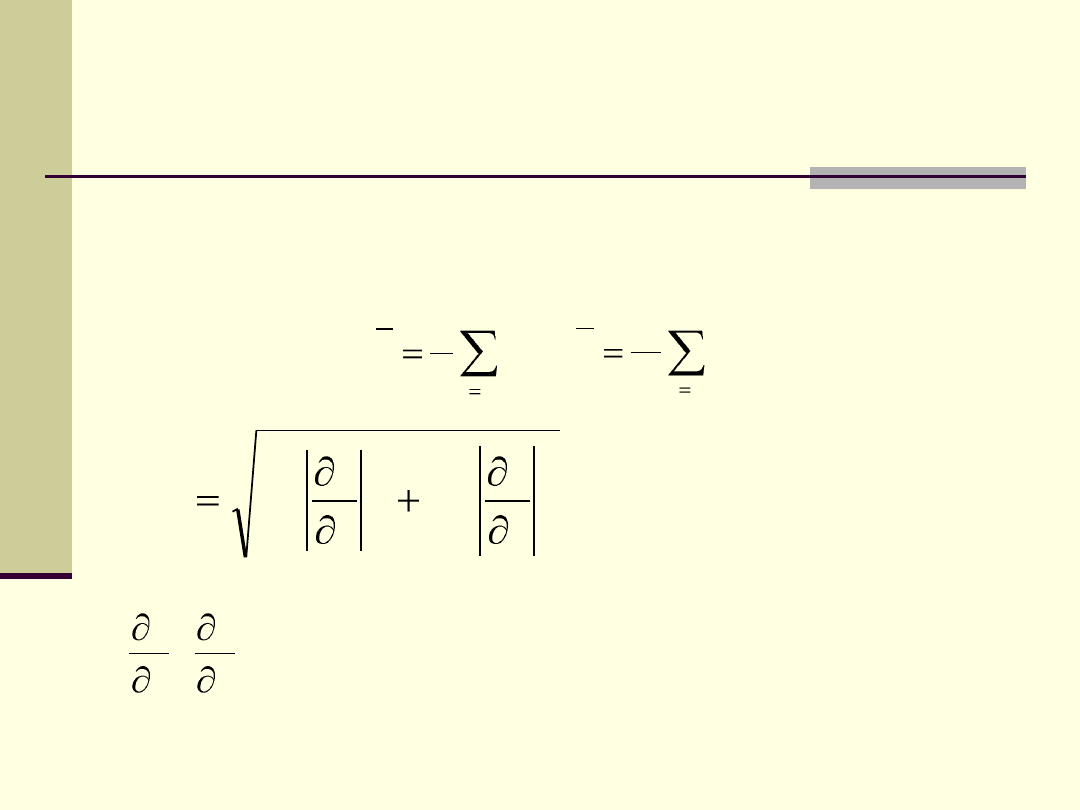
Wielkość x i y mierzono wielokrotnie otrzymując

wartości x

1

, x

2

, ... x

n

oraz y

1

, y

2

. .... y

n

.

Wielkości te mają

wartości średnie

n

n

i

i

x

n

x

1

m

i

i

y

m

y

1

1

2

2

2

2

y

f

S

x

f

S

S

y

x

f

y

f

x

f

,

oznaczają pochodne cząstkowe funkcji f po x i y
odpowiednio
S

x

, S

y

odchylenia standardowe x i y.

Ocena błędu wielkości złożonej

Dziękuję za uwagę !