
Politechnika Łódzka Rok akad. 2005/06
Wydział Budownictwa
Arch. i Inż. Środowiska
Kierunek Budownictwo
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
Kamil Jaryszek
st. zaoczne
sem. VII
KB

Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 2 -
WYKOP SZEROKOPRZESTRZENNY
Kolektor wykonany z kręgów betonowych
Dane:
D
w
– średnica wewnętrzna kręgów – 1,40 m
t – grubość ścianki – 0,14m
D
z
– średnica zewnętrzna kręgów
D
z
=D
w
+2 =1,68m
t
⋅
r – promień kręgów – 0,77m
H – wysokość nasypu ponad wierzchem rury – 3,30m
Grunt rodzimy w poziomie posadowienia:
Π – pył, I
l
=0,4
Grunt ponad rurociągiem:
P
s
- zasypka z piasku średniego, stan gruntu luźny I
d
=0,3, stan wilgotny
ρ=1,80
⎥⎦
⎤
⎢⎣
⎡
3
m
T
= 18,0
⎥⎦
⎤
⎢⎣
⎡
3
m
kN
stan wilgotny (tab. 2, PN-81/B-03020)
1. Zebranie obciążeń
a. ciężar gruntu
2
c
c
c
B
W
C
W
⋅
⋅
=
W=
ρ=1,80
⎥⎦
⎤
⎢⎣
⎡
3
m
T
B
c
=D
z
=1,68
C
c
- wsp. Marstona dla nasypów
m
B
H
c
96
,
1
68
,
1
30
,
3
=
=
r
sd
=0,8 – 0,5 dla gruntów normalnych
przyjmiemy r
sd
– 0,6 p=1
→ r
sd
p=0,6
zatem C
c
=2,83
[kN/mb]
143,77
1,68
18,0
2,83
B
W
C
W
2
2
c
c
c
=
⋅
⋅
=
⋅
⋅
=
60
,
85
68
,
1
77
,
143
'
=
=
=
z
c
c
D
W
W
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
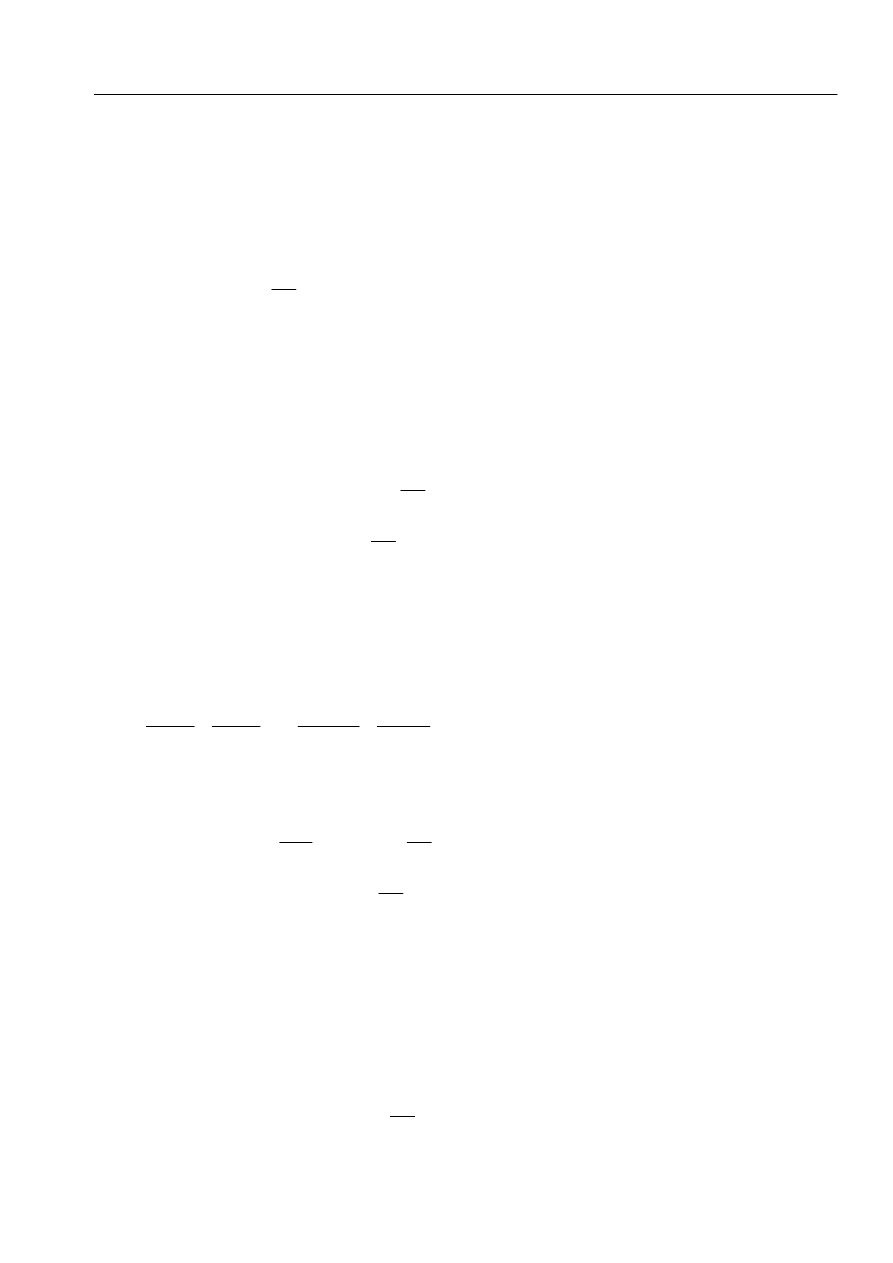
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 3 -
Obciążenie od gruntu:
γ
f
=1,2
Obciążenie zasypką obliczeniowe
ρ
0
=85,60·1,2 = 102,70
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
b. Ciężar własny obudowy, który działa na rurociąg
obciążenie własne obudowy :
γ
f
=1,1
charakterystyczne g
k
= 0,14· 24 = 3,36
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
obliczeniowe g
0
= 3,36· 1,1 = 3,70
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
c. Ciężar obudowy działający na podłoże
pole:
68
,
0
54
,
1
22
,
2
4
4
,
1
4
68
,
1
4
4
2
2
2
2
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
Π
−
⋅
Π
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
Π
−
⋅
Π
w
z
D
D
m
2
Obciążenie
obudowy oddziaływujące na podłoże:
charakterystyczne: g
rk
=
71
,
9
24
68
,
1
68
,
0
=
⋅
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
obliczeniowe: g
r0
= 9,71· 1,1 = 10,68
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
d. odpór gruntu pod rurociągiem
K= g
0
+ g
r0
= 102,70 + 10,68 = 113,38
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
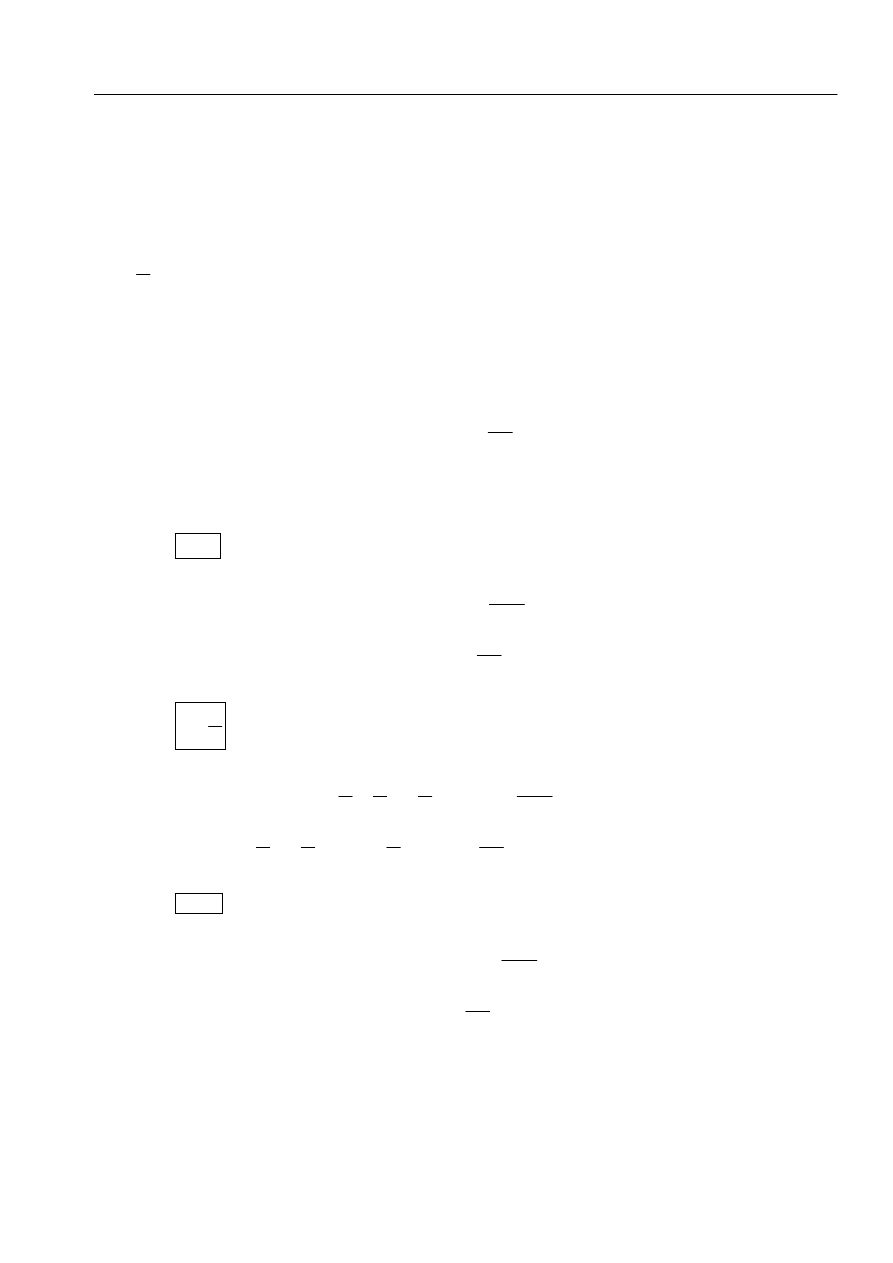
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 4 -
2. Obliczanie sił wewnętrznych w przekrojach
r = 0,77 m
⎪
⎩
⎪
⎨
⎧
=
=
=
π
ϕ
π
ϕ
ϕ
2
0
a. Od ciężaru własnego obudowy
g
0
= 3,70
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
)
cos
5
,
0
sin
(
)
sin
cos
5
,
0
1
(
2
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
⋅
=
−
−
⋅
=
r
g
N
r
g
M
0
=
ϕ
M = 3,7· 0,77
2
(1 - 0,5 cos0
° - 0 sin0°) = 1,10
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 3,7 · 0,77 (0 sin0
° - 0,5 cos0°) = - 1,43
⎥⎦
⎤
⎢⎣
⎡
m
kN
2
π
ϕ
=
M = 3,7· 0,77
2
(1 - 0,5 cos
2
π
-
2
π
sin
2
π
) = - 1,25
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 3,7· 0,77 (
2
π
sin
2
π
- 0,5 cos
2
π
) = 4,46
⎥⎦
⎤
⎢⎣
⎡
m
kN
π
ϕ
=
M = 3,7· 0,77
2
(1 - 0,5 cos
π - π sinπ ) = 3,29
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 3,7·0,77 (
π sinπ - 0,5 cosπ ) = 1,43
⎥⎦
⎤
⎢⎣
⎡
m
kN
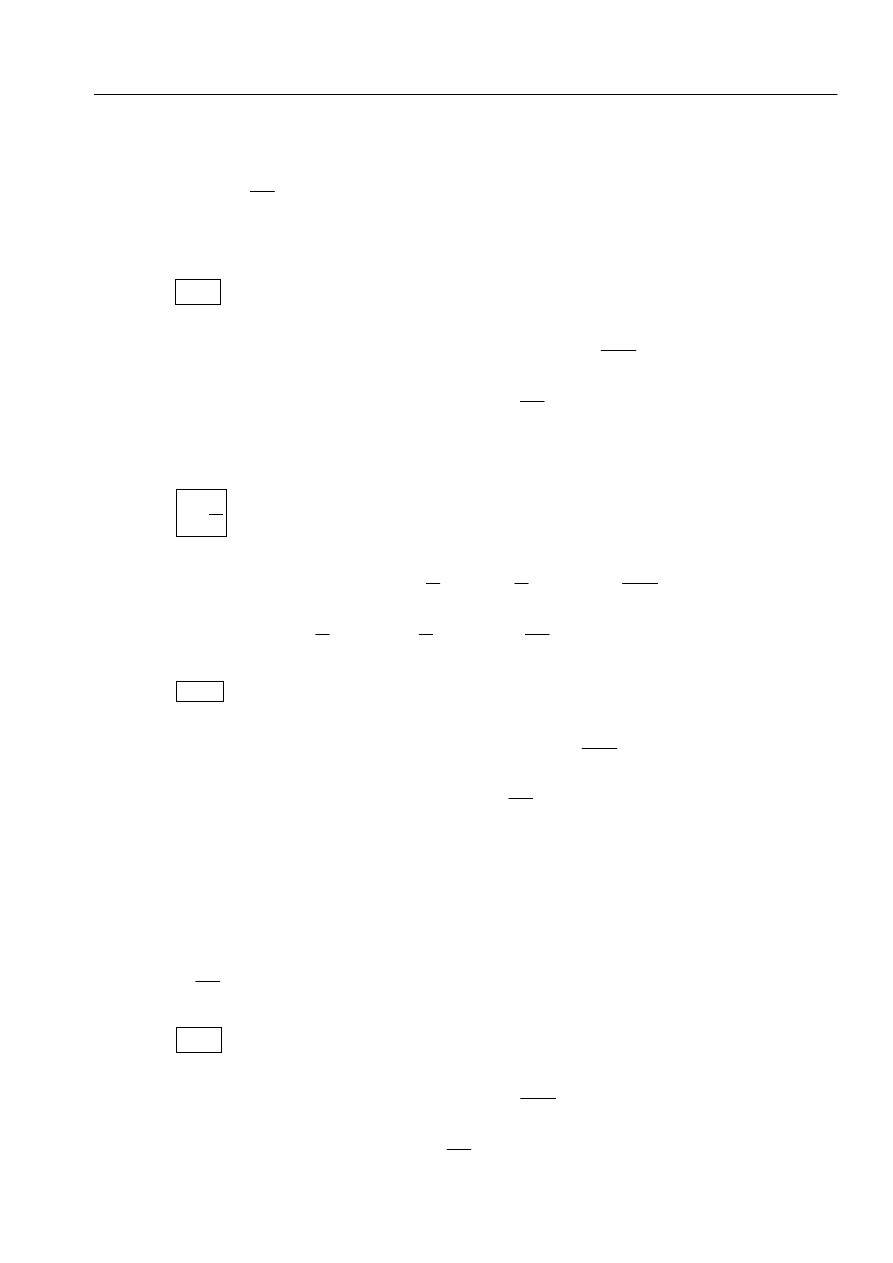
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 5 -
b. Pionowe parcie gruntu
ρ
0
= 102,70
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
0
=
ϕ
M = 102,70· 0,77
2
(0,198 + 0,106 cos0
° - 0,5 sin
2
0
°) = 18,51
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 102,70· 0,77 ( sin
2
0
° - 0,106 cos0° ) = - 8,38
⎥⎦
⎤
⎢⎣
⎡
m
kN
2
π
ϕ
=
M = 102,70· 0,77
2
(0,198 + 0,106 cos
2
π
- 0,5 sin
2
2
π
) = - 18,39
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 102,70· 0,77 ( sin
2
2
π
- 0,106 cos
2
π
) = 79,08
⎥⎦
⎤
⎢⎣
⎡
m
kN
π
ϕ
=
M = 102,70· 0,77
2
(0,693 + 0,106 cos
π - sin π ) = 35,74
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 102,70· 0,77 ( sin
π - 0,106 cos π ) = 8,38
⎥⎦
⎤
⎢⎣
⎡
m
kN
c. Odpór gruntu od dołu
K = 113,38
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
0
=
ϕ
M = 113,38· 0,77
2
(0,057 – 0,106 cos0
°) = - 3,29
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 113,38· 0,77 ( 0,106 cos0
°) = 9,25
⎥⎦
⎤
⎢⎣
⎡
m
kN
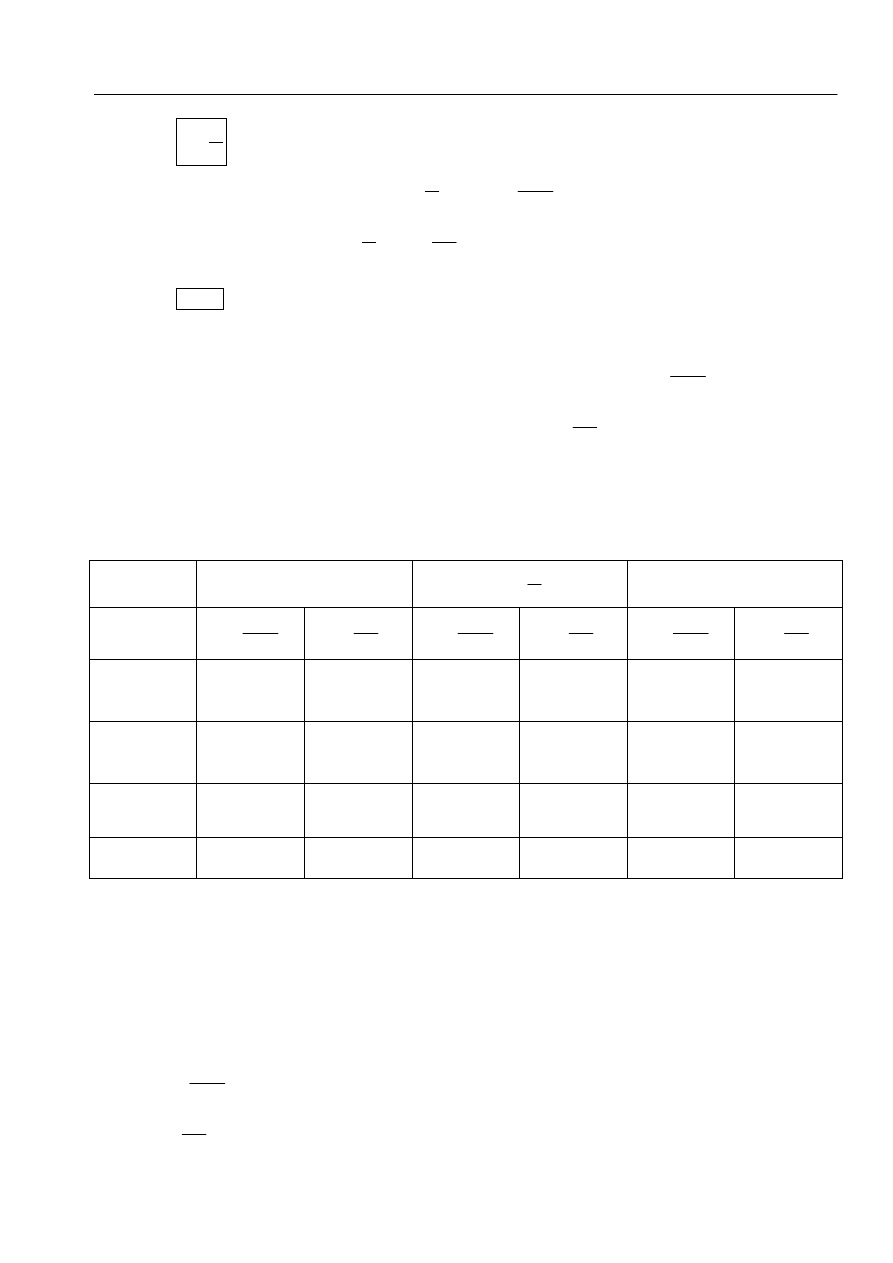
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 6 -
2
π
ϕ
=
M = 113,38· 0,77
2
(0,057 – 0,106 cos
2
π
) = 3,83
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 113,38· 0,77 ( 0,106 cos
2
π
) = 0
⎥⎦
⎤
⎢⎣
⎡
m
kN
π
ϕ
=
M = 113,38· 0,77
2
(-0,443 + sin
π - 0,106 cosπ - 0,5 sin
2
π ) = -22,65
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 113,38· 0,77 ( sin
2
π - sinπ + 0,106 cosπ ) = - 9,25
⎥⎦
⎤
⎢⎣
⎡
m
kN
ZESTAWIENIE SIŁ zasada superpozycji
przekrój
0
=
ϕ
2
π
ϕ
=
π
ϕ
=
obliczana
wielkość
M
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N ⎥
⎦
⎤
⎢⎣
⎡
m
kN
M ⎥
⎦
⎤
⎢⎣
⎡
m
kNm
N ⎥
⎦
⎤
⎢⎣
⎡
m
kN
M ⎥
⎦
⎤
⎢⎣
⎡
m
kNm
N ⎥
⎦
⎤
⎢⎣
⎡
m
kN
ciężar
własny
obudowy
1,10
- 1,43
- 1,25
4,46
3,29
1,43
pionowe
parcie gruntu
18,51
- 8,38
- 18,39
79,08
35,74
8,38
odpór gruntu
u dołu
- 3,29
9,25
3,38
0
- 22,65
- 9,25
razem
16,32
- 0,56
- 16,26
83,54
16,38
0,56
3. Sprawdzenie naprężeń w obudowie
a. przekrój dla
π
ϕ
=
M = 16,38
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 0,56
⎥⎦
⎤
⎢⎣
⎡
m
kN
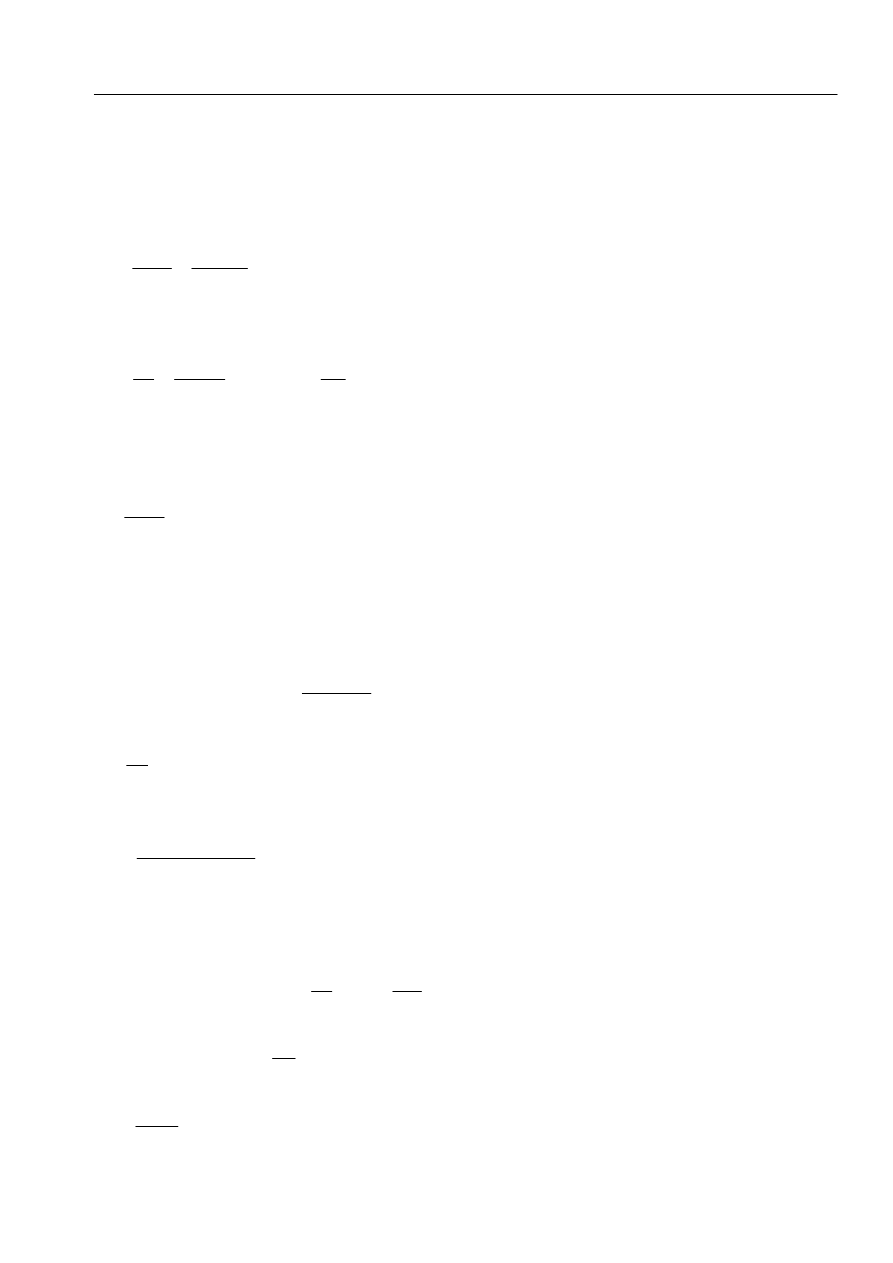
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 7 -
wymiarowanie:
h = 0,14 m
b = 1 m
a = 0,02 m h
1
= h – a = 0,14 – 0,02 = 0,12 m
0033
,
0
6
14
,
0
1
6
2
2
=
⋅
=
⋅
=
h
b
W
m
3
sprawdzenie naprężeń w betonie:
64
,
4963
0033
,
0
38
,
16
=
=
=
W
M
b
δ
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
= 4,96 Mpa
96
,
4
=
b
δ
MPa > R
dt
= 0,8 MPa
(B25)
należy zatem zaprojektować zbrojenie konstrukcyjne.
e =
25
,
29
56
,
0
38
,
16
=
m >> 10 h = 1,4 m
przekrój traktujemy jako zginany
- stal AII 18G2
→ R
a
= 295 MPa; f
yk
= 355 MPa
- beton B25
→ R
b
= 14,4 MPa; f
cm
= 1,9 Mpa
wskaźnik zbrojenia
2
1
h
b
R
M
n
W
a
z
⋅
⋅
⋅
=
E
a
= 200 000 MPa
E
b
= 30 000 MPa
20
3
67
,
6
=
⋅
≈
=
b
a
E
E
n
z uwagi na działanie obciążeń długotrwałych przyjmujemy n = 20
077
,
0
12
,
0
1
295000
38
,
16
20
2
=
⋅
⋅
⋅
=
z
W
dla W
z
= 0,077 z tablic odczytujemy n
μ = 0,087 γ = 0,511
naprężenia w betonie
54
,
7
20
295
511
,
0
0
=
=
=
n
R
a
γ
δ
MPa < R
b
= 14,4 MPa
przekrój zbrojenia
1
h
b
n
n
A
a
⋅
=
μ
000522
,
0
12
,
0
1
20
087
,
0
=
⋅
=
a
A
m
2
= 5,22 cm
2
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 8 -
sprawdzamy minimalny przekrój zbrojenia:
47
,
2
12
,
0
1
240
9
,
1
26
,
0
26
,
0
1
min
,
1
=
⋅
=
⋅
=
h
b
f
f
A
yk
ctm
s
cm
2
56
,
1
12
,
0
1
0013
,
0
0013
,
0
min
,
1
=
⋅
⋅
=
⋅
⋅
=
h
b
A
s
cm
2
min
,
1
,
1
s
reg
s
A
A
≥
5,22 > 2,47
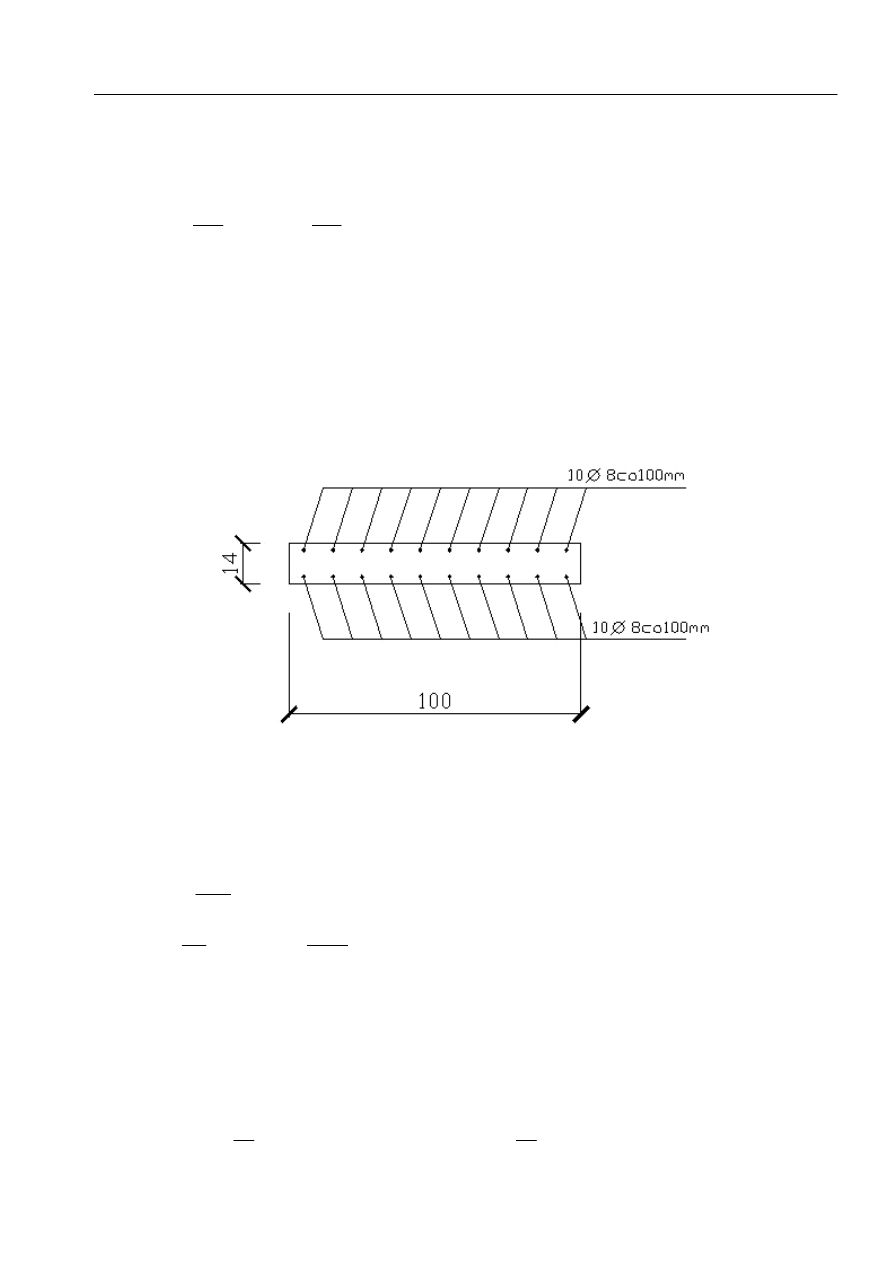
dobieramy zbrojenie
przyjęto 10
∅ 8 A
s
= 6,28 cm
2
A
si,prov
= 6,28 cm
2
>A
s.reg
= 5,22 cm
2
Sprawdzenie zbrojenia w przekroju mimośrodowo ściskanym
M = - 16,26
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 83,54
⎥⎦
⎤
⎢⎣
⎡
m
kN
19
,
0
54
,
83
26
,
16
=
=
e
m - duży mimośród
y
01
= y
02
= 0,5 0,14 = 0,07 m
A
a
= A
’
a
= 5,22 cm
2
= 0,000522 m
2
obliczenie wysokości strefy ściskanej z równania warunku równowagi:
x
3
+ 3x
2
(e – y
01
) +
b
n
6
[A
’
a
(e - y
02
+ a
’
) + A
a
(e + y
01
- a)]x-
b
n
6
[A
’
a
(e - y
02
+ a
’
) + A
a
h
1
(e + y
01
- a)]=0

Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 9 -
x
3
+3x
2
(0,19-0,07)+
1
20
6
⋅
[0,000522(0,19-0,07+0,02)+0,000522(0,19+0,07-0,02)]x-
-
1
20
6
⋅
[0,000522· 0,02(0,19-0,07+0,02)+0,000522· 0,12(0,19+0,07-0,02)]=0
x
3
+ 0,36x
2
+ 0,0237x – 0,00197 = 0
x = 0,046m = 4,6 cm
sprawdzenie warunku
δ
b
> R
b
= 14,4 MPa
)
(
2
)
(
2
2
'
1
'
2
a
a
a
a
b
A
h
a
A
n
x
A
A
n
x
b
x
N
⋅
+
⋅
−
+
+
⋅
⋅
⋅
=
δ
)
000522
,
0
12
,
0
02
,
0
000522
,
0
(
20
2
046
,
0
)
000522
,
0
000522
,
0
(
20
2
046
,
0
1
046
,
0
54
,
83
2
2
⋅
+
⋅
⋅
−
⋅
+
⋅
+
⋅
⋅
⋅
=
b
δ
41
,
6869
001118
,
0
68
,
7
=
=
b
δ
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
= 6,87 MPa
87
,
6
=
b
δ
MPa < R
b
= 14,4 MPa dla B25
naprężenia w stali:
03
,
221
87
,
6
046
,
0
046
,
0
12
,
0
20
1
=
⋅
−
⋅
=
−
=
b
a
x
x
h
n
δ
σ
MPa < R
a
= 295 MPa
66
,
77
87
,
6
046
,
0
02
,
0
046
,
0
20
'
'
=
⋅
−
⋅
=
−
=
b
x
a
x
n
a
δ
σ
MPa < R
a
= 295 MPa
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 10 -
WYKOP WĄSKOPRZESTRZENNY
Kolektor wykonany z kręgów betonowych
Dane:
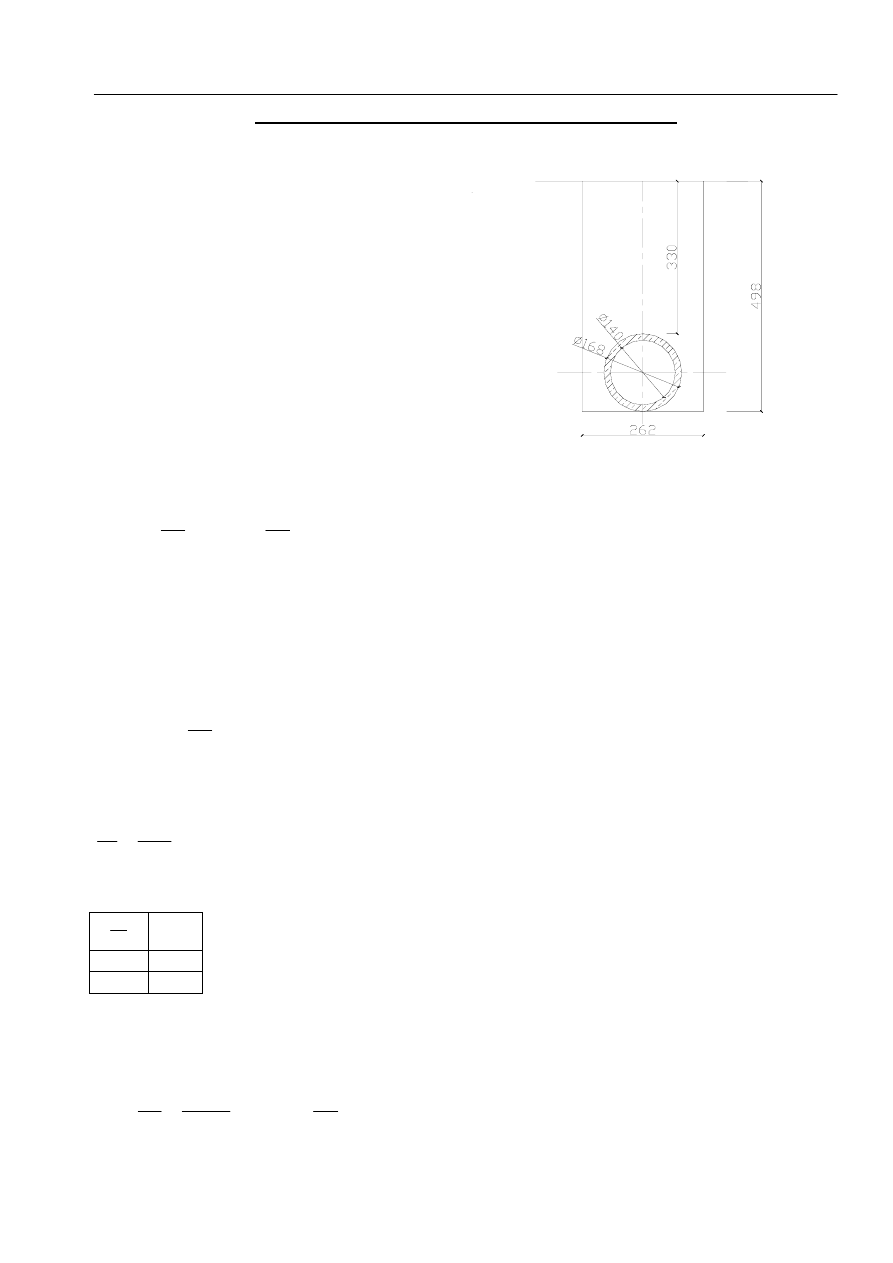
D
w
– średnica wewnętrzna kręgów – 1,40 m
t – grubość ścianki – 0,14m
D
z
– średnica zewnętrzna kręgów
D
z
=D
w
+2 =1,68m
t
⋅
r – promień kręgów – 0,77m
H – wysokość nasypu ponad wierzchem rury – 3,30m
Grunt rodzimy w poziomie posadowienia:
Π – pył, I
l
=0,4
Grunt ponad rurociągiem:
P
s
- zasypka z piasku średniego, stan gruntu luźny I
d
=0,3, stan wilgotny
ρ=1,80
⎥⎦
⎤
⎢⎣
⎡
3
m
T
= 18,0
⎥⎦
⎤
⎢⎣
⎡
3
m
kN
stan wilgotny (tab. 2, PN-81/B-03020)
4. Zebranie obciążeń
a. ciężar gruntu
2
d
d
d
B
W
C
W
⋅
⋅
=
W=
ρ=1,80
⎥⎦
⎤
⎢⎣
⎡
3
m
T
B
d
= D
z
+ 0,94 = 1,68+0,94=2,62 m
C
d
- wsp. Marstona dla nasypów
m
B
H
c
26
,
1
62
,
2
30
,
3
=
=
K
μ
=0,192
d
B
H
0,192
1,2 0,96
1,4 1,1
zatem C
d
=1,003
[kN/mb]
123,93
2,62
18,0
1,003
B
W
C
W
2
2
d
d
d
=
⋅
⋅
=
⋅
⋅
=
30
,
47
62
,
2
93
,
123
'
=
=
=
z
d
d
D
W
W
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 11 -
Obciążenie od gruntu:
γ
f
=1,2
Obciążenie zasypką obliczeniowe
ρ
0
=47,30·1,2 = 56,76
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
b. Ciężar własny obudowy, który działa na rurociąg
obciążenie własne obudowy :
γ
f
=1,1
charakterystyczne g
k
= 0,14· 24 = 3,36
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
obliczeniowe g
0
= 3,36· 1,1 = 3,70
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
c. Ciężar obudowy działający na podłoże
pole:
68
,
0
54
,
1
22
,
2
4
4
,
1
4
68
,
1
4
4
2
2
2
2
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
Π
−
⋅
Π
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
Π
−
⋅
Π
w
z
D
D
m
2
Obciążenie
obudowy oddziaływujące na podłoże:
charakterystyczne: g
rk
=
71
,
9
24
68
,
1
68
,
0
=
⋅
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
obliczeniowe: g
r0
= 9,71· 1,1 = 10,68
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
d. odpór gruntu pod rurociągiem
K= g
0
+ g
r0
= 56,76 + 10,68 = 67,44
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 12 -
5. Obliczanie sił wewnętrznych w przekrojach
r = 0,77 m
⎪
⎩
⎪
⎨
⎧
=
=
=
π
ϕ
π
ϕ
ϕ
2
0
a. Od ciężaru własnego obudowy
g
0
= 3,70
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
)
cos
5
,
0
sin
(
)
sin
cos
5
,
0
1
(
2
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
⋅
=
−
−
⋅
=
r
g
N
r
g
M
0
=
ϕ
M = 3,7· 0,77
2
(1 - 0,5 cos0
° - 0 sin0°) = 1,10
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 3,7· 0,77 (0 sin0
° - 0,5 cos0°) = - 1,43
⎥⎦
⎤
⎢⎣
⎡
m
kN
2
π
ϕ
=
M = 3,7· 0,77
2
(1 - 0,5 cos
2
π
-
2
π
sin
2
π
) = - 1,25
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 3,7· 0,77 (
2
π
sin
2
π
- 0,5 cos
2
π
) = 4,46
⎥⎦
⎤
⎢⎣
⎡
m
kN
π
ϕ
=
M = 3,7· 0,77
2
(1 - 0,5 cos
π - π sinπ ) = 3,29
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 3,7· 0,77 (
π sinπ - 0,5 cosπ ) = 1,43
⎥⎦
⎤
⎢⎣
⎡
m
kN
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 13 -
b. Pionowe parcie gruntu
ρ
0
= 56,76
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
0
=
ϕ
M = 56,76· 0,77
2
(0,198 + 0,106 cos0
° - 0,5 sin
2
0
°) = 10,23
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 56,76· 0,77 ( sin
2
0
° - 0,106 cos0° ) = - 4,64
⎥⎦
⎤
⎢⎣
⎡
m
kN
2
π
ϕ
=
M = 56,76· 0,77
2
(0,198 + 0,106 cos
2
π
- 0,5 sin
2
2
π
) = - 10,14
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 56,76· 0,77 ( sin
2
2
π
- 0,106 cos
2
π
) = 43,62
⎥⎦
⎤
⎢⎣
⎡
m
kN
π
ϕ
=
M = 56,76· 0,77
2
(0,693 + 0,106 cos
π - sin π ) = 19,71
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 56,76· 0,77 ( sin
π - 0,106 cos π ) = 4,63
⎥⎦
⎤
⎢⎣
⎡
m
kN
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 14 -
c. Odpór gruntu od dołu
K = 67,44
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
0
=
ϕ
M = 67,44· 0,77
2
(0,057 – 0,106 cos0
°) = - 1,96
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 67,44· 0,77 ( 0,106 cos0
°) = 5,51
⎥⎦
⎤
⎢⎣
⎡
m
kN
2
π
ϕ
=
M = 67,44· 0,77
2
(0,057 – 0,106 cos
2
π
) = 2,28
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 67,44· 0,77 ( 0,106 cos
2
π
) = 0
⎥⎦
⎤
⎢⎣
⎡
m
kN
π
ϕ
=
M = 67,44· 0,77
2
(-0,443 + sin
π - 0,106 cosπ - 0,5 sin
2
π ) = -13,48
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 67,44· 0,77 ( sin
2
π - sinπ + 0,106 cosπ ) = - 5,51
⎥⎦
⎤
⎢⎣
⎡
m
kN
ZESTAWIENIE SIŁ zasada superpozycji
przekrój
0
=
ϕ
2
π
ϕ
=
π
ϕ
=
obliczana
wielkość
M
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N ⎥
⎦
⎤
⎢⎣
⎡
m
kN
M ⎥
⎦
⎤
⎢⎣
⎡
m
kNm
N ⎥
⎦
⎤
⎢⎣
⎡
m
kN
M ⎥
⎦
⎤
⎢⎣
⎡
m
kNm
N ⎥
⎦
⎤
⎢⎣
⎡
m
kN
ciężar
własny
obudowy
1,10
- 1,43
- 1,25
4,46
3,29
1,43
pionowe
parcie gruntu
10,23
- 4,64
- 10,14
43,62
19,71
4,63
odpór gruntu
u dołu
- 1,96
5,51
2,28
0
- 13,48
- 5,51
razem
9,37
- 0,56
- 9,11
48,08
9,52
0,55

Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 15 -
6. Sprawdzenie naprężeń w obudowie
a. przekrój dla
π
ϕ
=
M = 9,52
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 0,55
⎥⎦
⎤
⎢⎣
⎡
m
kN
wymiarowanie:
h = 0,14 m
b = 1 m
a = 0,02 m h
1
= h – a = 0,14 – 0,02 = 0,12 m
0033
,
0
6
14
,
0
1
6
2
2
=
⋅
=
⋅
=
h
b
W
m
3
sprawdzenie naprężeń w betonie:
84
,
2884
0033
,
0
52
,
9
=
=
=
W
M
b
δ
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
= 2,88 Mpa
88
,
2
=
b
δ
MPa > R
dt
= 0,8 MPa
(B25)
należy zatem zaprojektować zbrojenie konstrukcyjne.
e =
3
,
17
55
,
0
52
,
9
=
m >> 10 h = 1,4 m
przekrój traktujemy jako zginany
- stal AII 18G2
→ R
a
= 295 MPa; f
yk
= 355 MPa
- beton B25
→ R
b
= 14,4 MPa; f
cm
= 1,9 Mpa
wskaźnik zbrojenia
2
1
h
b
R
M
n
W
a
z
⋅
⋅
⋅
=
E
a
= 200 000 MPa
E
b
= 30 000 MPa
20
3
67
,
6
=
⋅
≈
=
b
a
E
E
n
z uwagi na działanie obciążeń długotrwałych przyjmujemy n = 20
045
,
0
12
,
0
1
295000
52
,
9
20
2
=
⋅
⋅
⋅
=
z
W
dla W
z
= 0,045 z tablic odczytujemy n
μ = 0,049 γ = 0,365
Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 16 -
naprężenia w betonie
38
,
5
20
295
365
,
0
0
=
=
=
n
R
a
γ
δ
MPa < R
b
= 14,4 MPa
przekrój zbrojenia
1
h
b
n
n
A
a
⋅
=
μ
000294
,
0
12
,
0
1
20
049
,
0
=
⋅
=
a
A
m
2
= 2,94 cm
2
sprawdzamy minimalny przekrój zbrojenia
47
,
2
12
,
0
1
240
9
,
1
26
,
0
26
,
0
1
min
,
1
=
⋅
=
⋅
=
h
b
f
f
A
yk
ctm
s
cm
2
56
,
1
12
,
0
1
0013
,
0
0013
,
0
min
,
1
=
⋅
⋅
=
⋅
⋅
=
h
b
A
s
cm
2
min
,
1
,
1
s
reg
s
A
A
≥
2,94 > 2,47
dobieramy zbrojenie
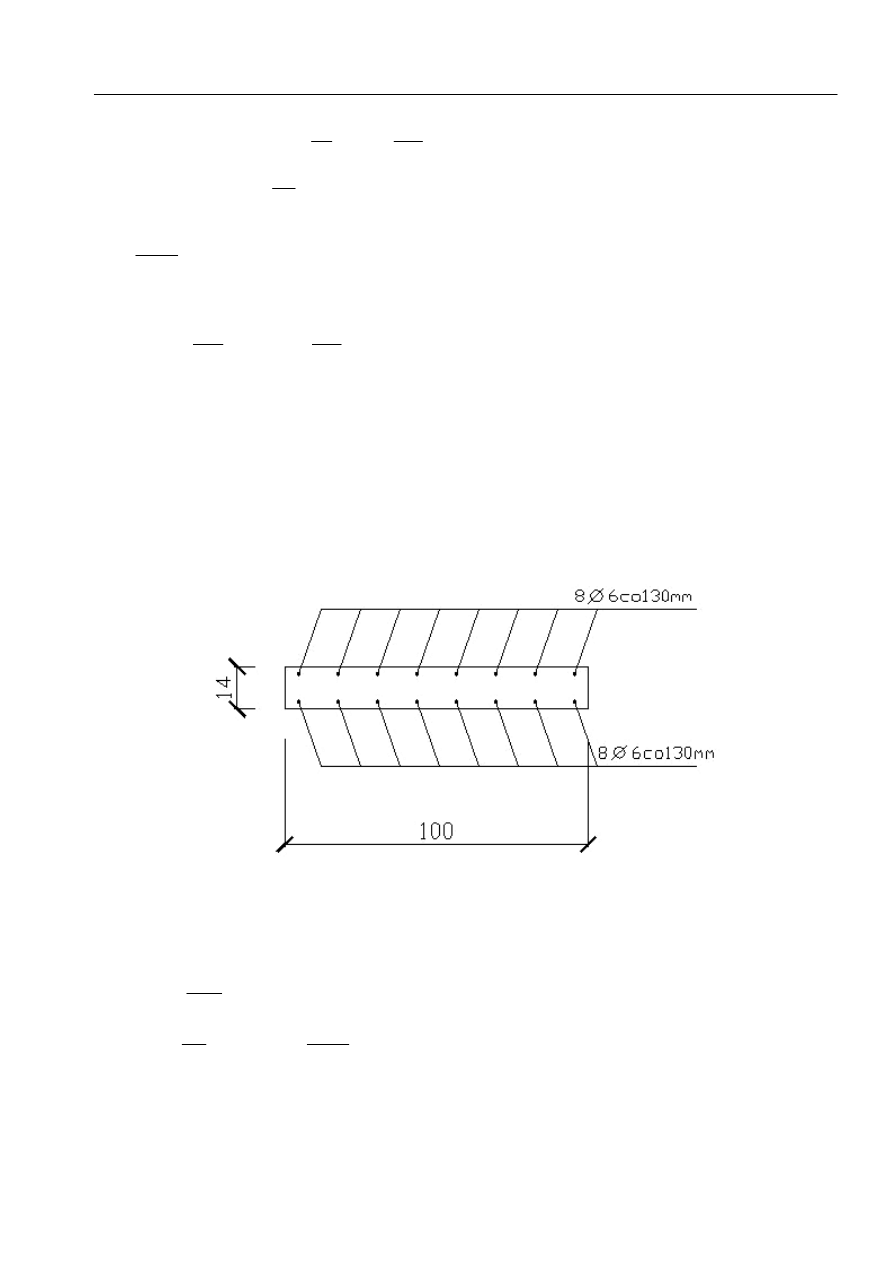
przyjęto 8
∅ 6 A
s
= 3,02 cm
2
A
si,prov
= 3,02 cm
2
>A
s.reg
= 2,94 cm
2
Sprawdzenie zbrojenia w przekroju mimośrodowo ściskanym
M = - 9,11
⎥⎦
⎤
⎢⎣
⎡
m
kNm
N = 48,08
⎥⎦
⎤
⎢⎣
⎡
m
kN
19
,
0
08
,
48
11
,
9
=
=
e
m - duży mimośród
y
01
= y
02
= 0,5 0,14 = 0,07 m
A
a
= A
’
a
= 2,4 cm
2
= 0,000294 m
2

Katedra Geotechniki i Budowli Inżynierskich
Politechniki Łódzkiej
Projekt kolektora betonowego w wykopie
- 17 -
obliczenie wysokości strefy ściskanej z równania warunku równowagi:
x
3
+ 3x
2
(e – y
01
) +
b
n
6
[A
’
a
(e - y
02
+ a
’
) + A
a
(e + y
01
- a)]x-
b
n
6
[A
’
a
(e - y
02
+ a
’
) + A
a
h
1
(e + y
01
- a)]=0
x
3
+3x
2
(0,19-0,07)+
1
20
6
⋅
[0,000294(0,19-0,07+0,02)+0,000294(0,19+0,07-0,02)]x-
-
1
20
6
⋅
[0,000294· 0,02(0,19-0,07+0,02)+0,000294· 0,12(0,19+0,07-0,02)]=0
x
3
+ 0,36x
2
+ 0,0134x – 0,0011 = 0
x = 0,038m = 3,8 cm
sprawdzenie warunku:
δ
b
> R
b
= 14,4 MPa
)
(
2
)
(
2
2
'
1
'
2
a
a
a
a
b
A
h
a
A
n
x
A
A
n
x
b
x
N
⋅
+
⋅
−
+
+
⋅
⋅
⋅
=
δ
)
0005294
,
0
12
,
0
02
,
0
000294
,
0
(
20
2
0327
,
0
)
000294
,
0
000294
,
0
(
20
2
038
,
0
1
038
,
0
08
,
8
4
2
2
⋅
+
⋅
⋅
−
⋅
+
⋅
+
⋅
⋅
⋅
=
b
δ
70
,
5018
000692
,
0
65
,
3
=
=
b
δ
⎥⎦
⎤
⎢⎣
⎡
2
m
kN
= 5,02 MPa
37
,
10
=
b
δ
MPa < R
b
= 14,4 MPa dla B25
naprężenia w stali:
65
,
216
02
,
5
038
,
0
038
,
0
12
,
0
20
1
=
⋅
−
⋅
=
−
=
b
a
x
x
h
n
δ
σ
MPa < R
a
= 295 MPa
60
,
47
02
,
5
038
,
0
02
,
0
038
,
0
20
'
'
=
⋅
−
⋅
=
−
=
b
x
a
x
n
a
δ
σ
MPa < R
a
= 295 MPa
Document Outline
Wyszukiwarka
Podobne podstrony:
projekty 3 id 400866 Nieznany
kse projekt id 252149 Nieznany
Projekt 1 Konstrukcje Betonowe
projekt inzynierski wskazowki w Nieznany
projekt29 id 400291 Nieznany
projektMOS id 400412 Nieznany
Projektowanie zwrotnic glosniko Nieznany (3)
Projekt zaliczeniowy Sprawozdan Nieznany
07 projektowanie skladuid 6941 Nieznany (2)
projektowanie 2 id 400443 Nieznany
Projekt 7 A id 398367 Nieznany
projekt0002 id 400180 Nieznany
Projekt 6 id 397770 Nieznany
Omowienie projektu id 335352 Nieznany
projekt z eksploatacji technol Nieznany
Projekt mieszanki betonowej, beton 4.1
projekt mieszalnika Politechnik Nieznany
notatek pl projekt drogi przykl Nieznany
więcej podobnych podstron