www.project-the.one.pl
Nazwa: Projekt manipulatora
Przedmiot: Podstawy Konstrukcji Maszyn
Prowadzący: -
Rok: 2
Kierunek: AiR
Autor: -
Korepetycje: -
Jeśli chcesz uzyskać wersję drukowalną, lub do
edycji, skontaktuj się z nami pod adresem
staff@project-the.one.pl
2
POLITECHNIKA ŚLĄSKA
Wydział :Mechaniczny – Technologiczny
Kierunek : Automatyka i Robotyka
Podstawy Konstrukcji Maszyn
Projekt manipulatora.
Wykonał:
3
Spis treści:
1. Założenia projektowo-konstrukcyjne. .................................................................... 4
1.1. Opis
istoty
działania.................................................................................... 4
1.2. Dane
sytuacyjne. ........................................................................................ 5
1.3. Dane
ilościowe. .......................................................................................... 5
1.4. Kryteria. ...................................................................................................... 6
1.5. Zadania
do wykonania................................................................................ 6
2. Warianty manipulatora. ......................................................................................... 7
3. Dobór wariantu manipulatora. ............................................................................... 8
4. Ruch manipulatora. ............................................................................................... 9
4.1. Ruch
poziomy............................................................................................. 9
4.2. Ruch
pionowy. .......................................................................................... 10
4.3. Obliczenia
wydajności pracy obrabiarki.................................................... 10
4.4. Wydajność czasu pracy............................................................................ 10
5. Obliczenia ramienia manipulatora. ...................................................................... 11
5.1. Obliczenia skoku siłownika;...................................................................... 11
5.2. Obliczenia reakcji podpory i siły działania siłownika : ............................... 12
5.3. Obliczenia
wytrzymałościowe ramienia . .................................................. 14
5.4. Obliczenia
ugięcia ramienia...................................................................... 16
5.5. Obliczenia
dotyczące przegubu górnego.................................................. 18
5.6. Dobór
łożyska dla przegubu. .................................................................... 19
6. Obliczenia dotyczące słupa................................................................................. 20
6.1. Wyboczenie.............................................................................................. 20
6.2. Smukłość.................................................................................................. 22
7. Dobór łożysk tocznych. ....................................................................................... 27
7.1. Łożysko górne. ......................................................................................... 28
7.2. Łożysko dolne........................................................................................... 29
8. Obliczenia przegubu siłownika. ........................................................................... 30
9. Obliczenia śrub fundamentowych. ...................................................................... 31
10. Obliczenia połączenia spawanego. ..................................................................... 35
11. Obliczenia momentu napędowego. ..................................................................... 37
4
Założenia projektowo-konstrukcyjne.
Opis istoty działania.
Przedmiotem manipulacji jest półfabrykat w postaci walca o średnicy d
i wysokości h .
Przedmiot jest obrabiany na dwóch tokarko—frezarkach o osi
pionowej sterowanych numerycznie. Jedna z nich posiada wrzeciono
dolne, a druga górne.
5
Konstruowany manipulator wykonuje następujące operacje:
1) uchwycenie walcowego półfabrykatu z palety 1 (pal.1)
2) manipulacja
przedmiotem
3) przemieszczenie obiektu przed uchwyt samo centrujący obrabiarki 1
(obr.1)
4) wprowadzenie obiektu do uchwytu samo centrującego
5) obróbka
powierzchni
przedmiotu na obrabiarce 1 (obr.1.)
6) uchwycenie obrabianego przedmiotu przez manipulator
7) zluzowanie
szczęk uchwytu samo centrującego przez obrabiarkę 1
(obr.1)
8) wysunięcie przedmiotu z uchwytu
9) manipulacja
przedmiotem
10) przemieszczenie obiektu przed uchwyt samo centrujący obrabiarki 2
(obr.2)
11) wprowadzenie obiektu do uchwytu samo centrującego
12) uchwycenie obrabianego przedmiotu przez obrabiarkę 2 (obr.2)
13) obróbka przedmiotu
14) uchwycenie obrabianego przedmiotu przez manipulator
15) zluzowanie szczęk uchwytu samo centrującego przez obrabiarkę 2
(obr.2)
16) wysunięcie przedmiotu z uchwytu
17) manipulacja przedmiotem
18) umieszczenie obrabianego przedmiotu w palecie 2 (pal.2)
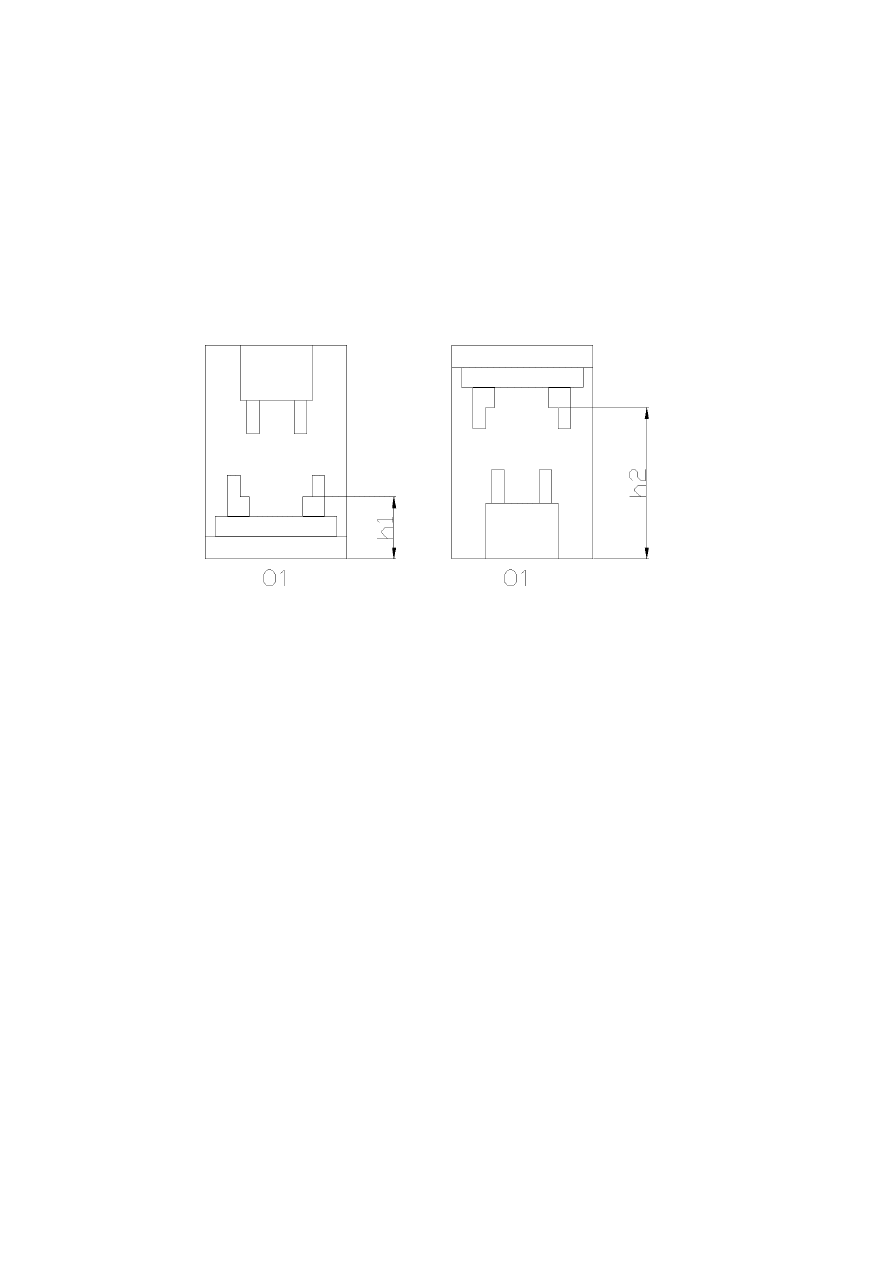
Dane sytuacyjne.
Obrabiarki mogą być usytuowane względem siebie w różny sposób.
Obrabiarka obr.1 posiada uchwyt samo centrujący dolny na wysokości h
1
obrabiarka obr.2 posiada uchwyt samo centrujący górny na wysokości h
2
Dane ilościowe.
Wymiary półfabrykatu :
h = 60 [mm]
d
=
50
[mm] t
1
=20s t
2
=36s t
3
=23s
Masa chwytaka:
m
ch
=2,9 [kg]
Średnica rozstawienia stanowisk w gnieździe:
D = 2,75 [m]
Wysokość położenia uchwytu od poziomu:
h
1
= 650 [mm]
h
2
= 900 [mm]
6
Kryteria.
K1 - minimalna masa manipulatora,
K2 - minimalna długość ruchów jałowych,
K3 – minimalny czas postoju obrabiarki
K4 - prostota działania i wykonania,
K5 – modułowość manipulatora,
K6 - błąd pozycjonowania przedmiotu,
K7 – duża sztywność,
K8 - maksymalny stopień wykorzystania elementów zmechanizowanych
Zadania do wykonania.
1) zaprojektować układ gniazda (magazyny, stanowiska reorientacji),
2) przeprowadzić analizę kinematyczną przyszłego manipulatora,
3) opracować trzy różniące się koncepcje manipulatora,
4) dokonać wyboru najlepszego wariantu struktury manipulatora,
5) dobrać cechy konstrukcyjne poszczególnych elementów manipulatora,
6) sporządzić rysunek złożeniowy manipulatora i rysunek wykonawczy
jednego elementu.
7
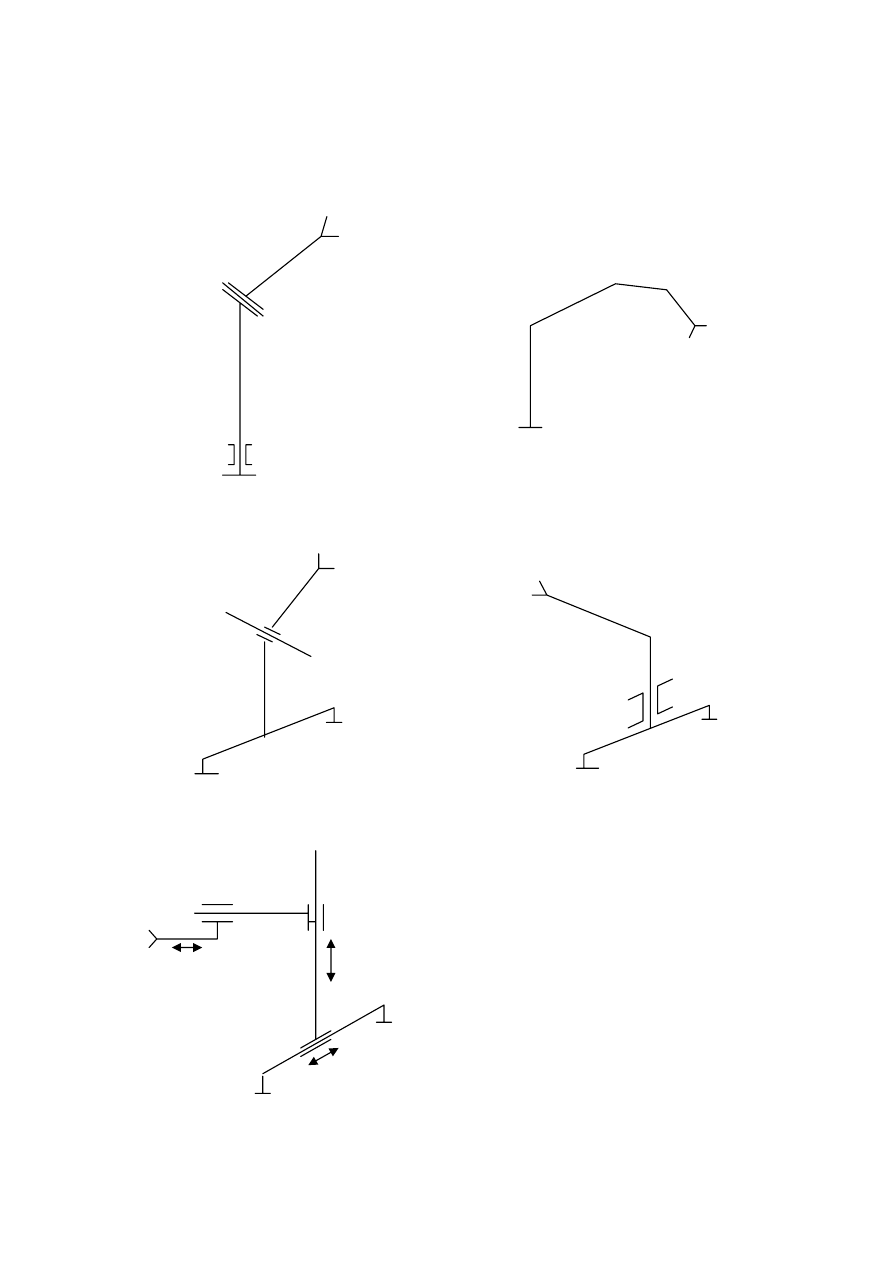
Warianty manipulatora.
1.
2.
3.
4.
5.
8
Dobór wariantu manipulatora.
Spośród pięciu koncepcji budowy manipulatora dokonuje się
wyboru najlepszej biorąc pod uwagę osiem różnych kryteriów i
przyznając im przewagę nad innymi według schematu:
1 – kryterium ważniejsze,
0 – kryterium nieważne,
0,5 – kryterium równoważne.
x K
1
K
2
K
3
K
4
K
5
K
6
K
7
K
8
ΣK
i
W
1
W
2
W
3
K
1
x 1 0,5 1 0,5 0 0 0 3 4 3 3
K
2
0 x 0,5
0,5 0 0 0 0 1 3 3 3
K
3
0,5
0,5 x 0 0,5 0 0,5 0 2 3 3 3
K
4
0 0,5 1 x 0,5 1 0,5 0,5 4 4 2 4
K
5
0,5 1 0,5 0,5 x 0.5
0,5
0,5 4 3 3 3
K
6
1 1 1 0 0.5 x 1 0.5
4,5 4 3 3
K
7
1 1 0,5
0.5
0,5
0,5 x 0,5 5 4 3 4
K
8
1 1 1 0,5
0,5
0,5 0 X 4,5 4 4 3
Następnie dokonany został wybór wariantu manipulatora:
ΣW
1
=99
ΣW
2
=84,5
ΣW
3
=83
Do dalszych obliczeń wybieram wariant 1 ponieważ najlepiej spełnia
zadane kryteria.
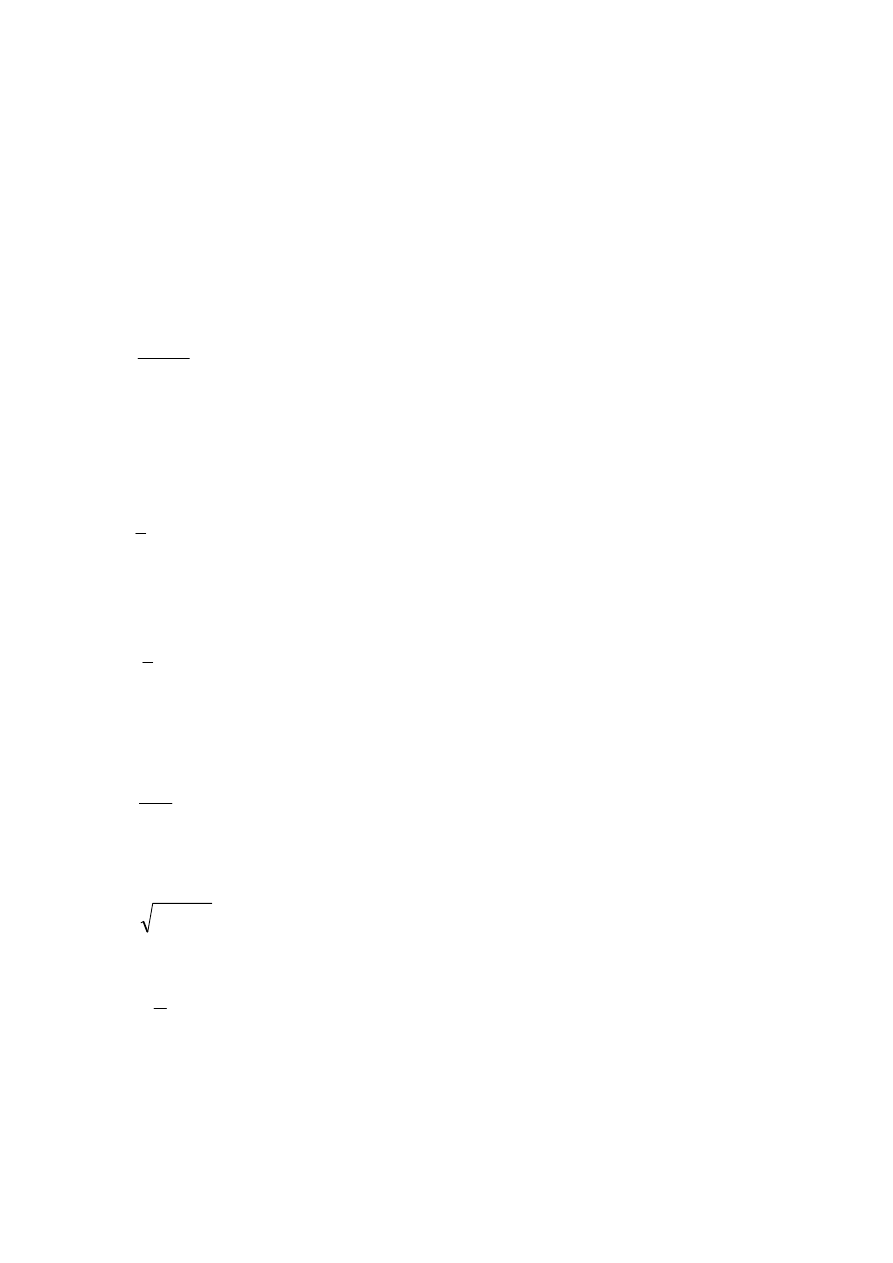
9
Ruch manipulatora.
Ruch poziomy.
v- prędkość średnia – przyjmuję 1 m/s,
r=1,375 [m],
droga:
s
start-obr.1
=0,364 [m]
s
obr.1-koniec
=0,364 [m]
Czas:
t
start-obr.1
= t
obr.1-koniec
=0,364 [s]
prędkość kątowa:
ω=1/1,375 =0,727[1/s]
prędkość obrotowa:
n=6,9 [obr/min]
przyspieszenia liniowe;
2
2
t
n
a
a
a
+
=
a=2,8 [m/s
2
]
a
n
=0,726 [m/s
2
]
a
t start-obr.1
=2,75 [m/s
2
]
a
t obr.1-koniec
=2,75 [m/s
2
]
°
Π
=
360
2
α
r
s
v
s
t
=
r
v
=
ω
Π
=
2
60
ω
n
t
v
a
r
a
t
n
=
=
2
ω
10
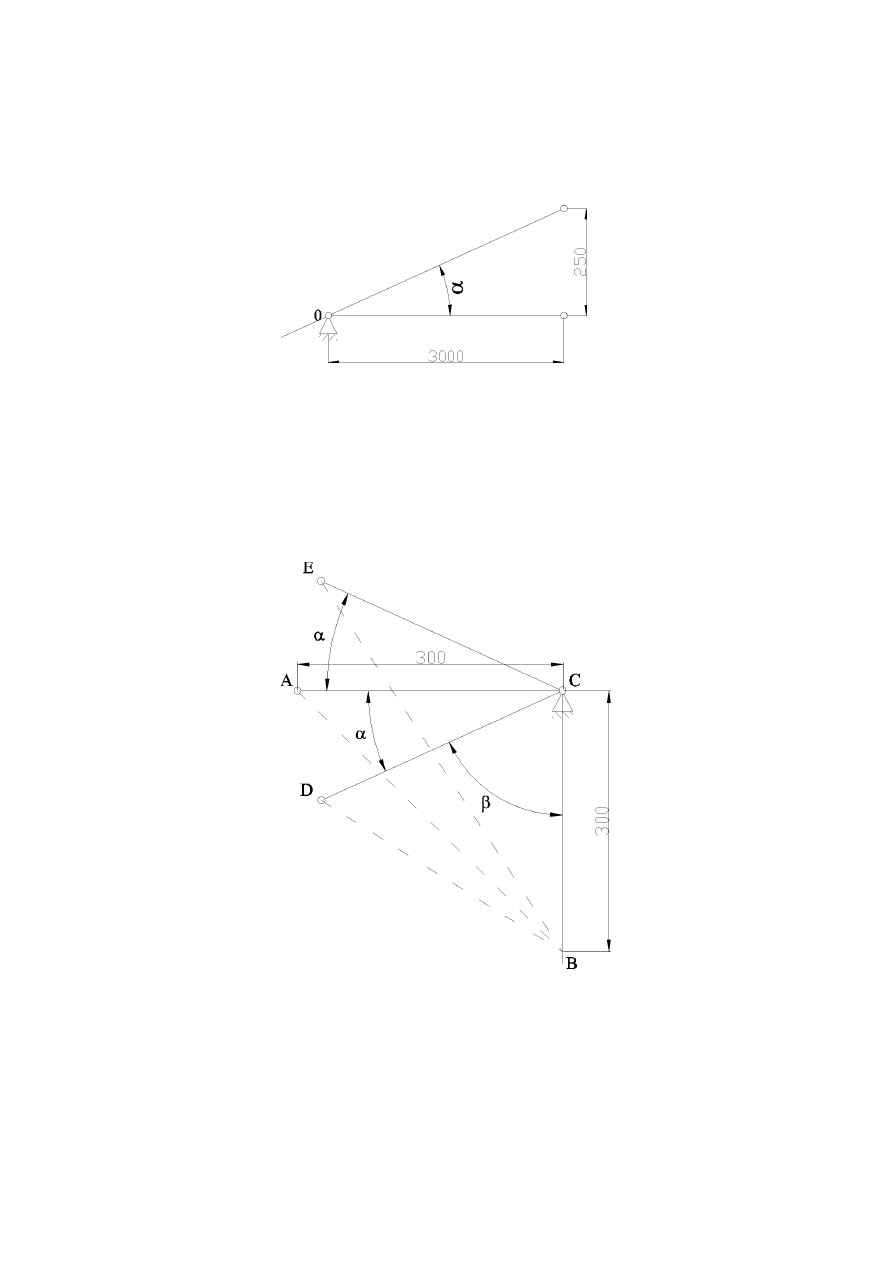
Ruch pionowy.
α=arctg125/1375=5
0
19’
2
α=10
0
38’
droga:
s
2-1
=0,125 m
s
1-3
=0,125 m
czas:
t
2-1
=0,125 [s]
t
1-3
=0,125 [s]
Obliczenia wydajności pracy obrabiarki
T=117s
W
1
= (t
3
- t
1
)/T * 100
% = 2,564
W
2
= (t
2
)/T * 100
% = 30,77
Wydajność czasu pracy
M.= (
Σk
i
/T)* 100
% = 32,48
°
Π
=
360
2
α
r
s
11
Obliczenia ramienia manipulatora.
α=5
0
19’
h=0,125 [m]
r=1,375 [m]
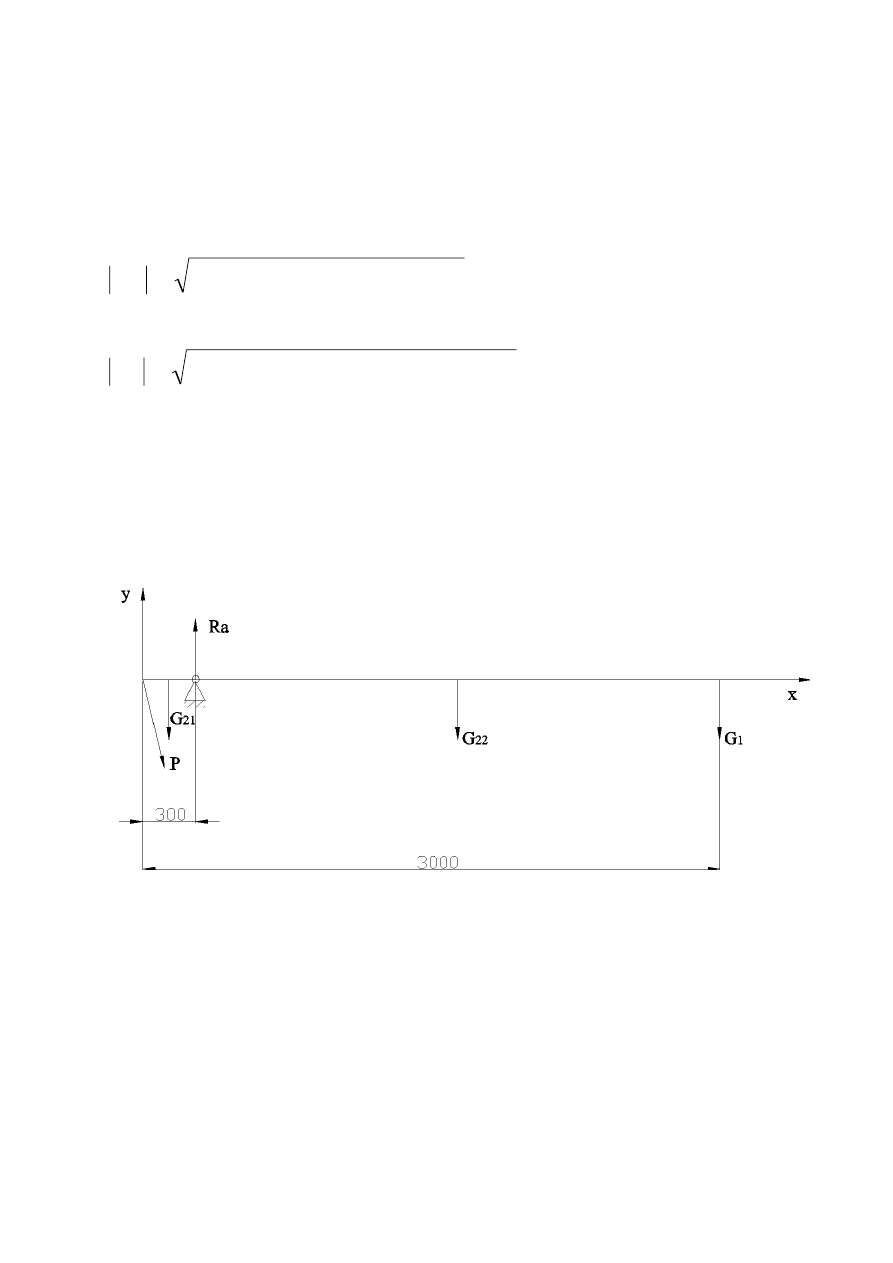
Obliczenia skoku siłownika;
12
Z twierdzenia Pitagorasa:
AB=0,566 [m]
β=90-α=84
0
81’
z twierdzenia cos.:
β
cos
2
2
2
BCDC
DC
BC
BD
−
+
=
BD=0,540 [m]
)
2
cos(
2
2
2
β
α
+
−
+
=
CECB
CB
CE
EB
EB=0,59 [m]
Skok = |EB|-|BD|=0,05 [m]
Skok siłownika wynosi =0,05 [m]
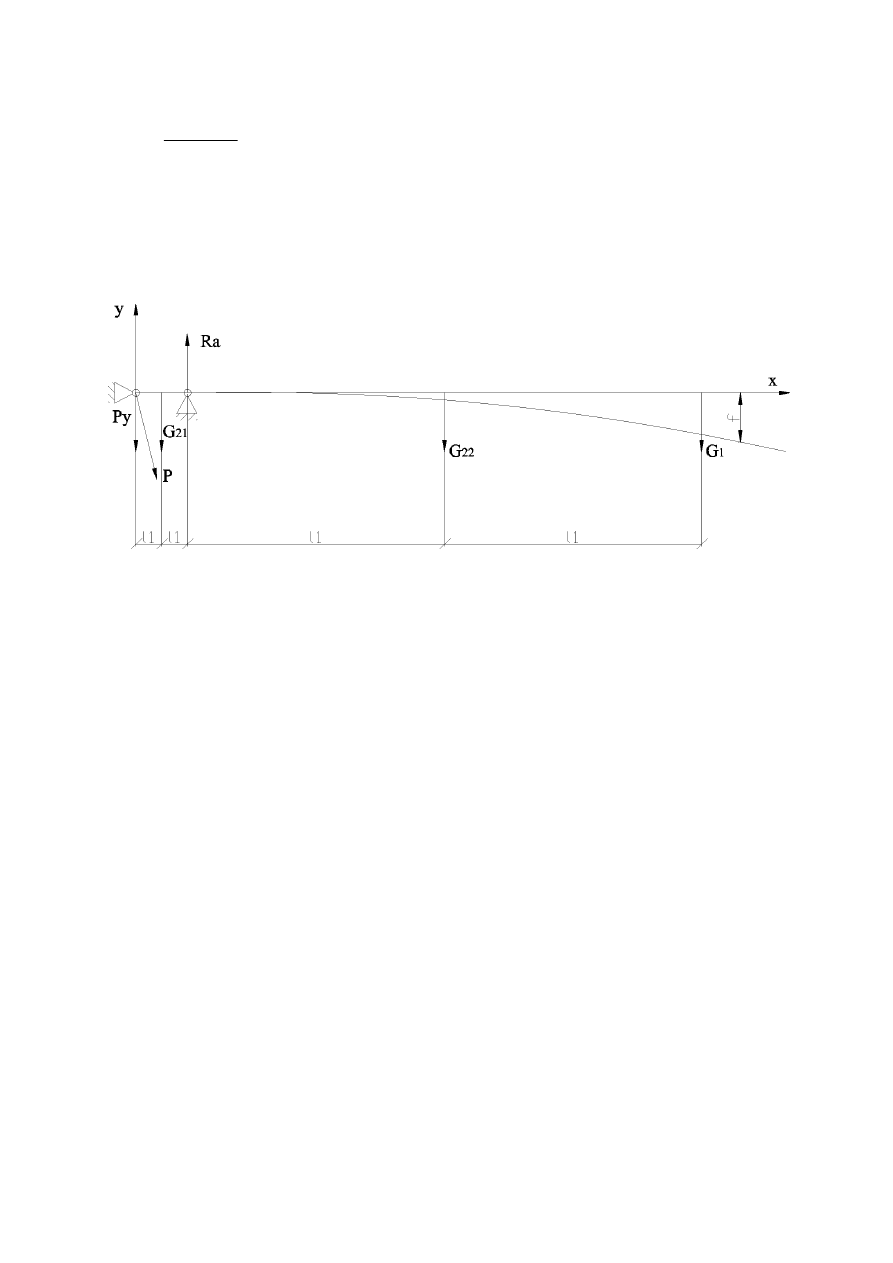
Obliczenia reakcji podpory i siły działania siłownika :
Wartość sił działających na ramię:
G
1
- składa się z ciężaru elementu i chwytaka
G
1
=(m
ch
+m
p
)g
13
Masa przedmiotu jest nieznana. Wyznaczam ją z warunków
geometrycznych przyjmując wartość maksymalną zakładając że
półfabrykat jest wykonany z aluminium AK-20 o gęstości:
ρ=2,72
[g/cm
3
]=2720 [kg/m
3
]
m
p
=0,32 [kg] ; masa chwytaka : m
ch
=2,9 [kg]
G
1
=(2,9+0,32)*9,81=31,56 [N]
G
22
– masa ramienia
Ramię wykonano z ceownika C160 PN-86/H-93403, dane:
masa:18,8 [kg/m],
wskaźniki wytrzymałości: W
x
=116 [cm
3
],
W
y
=18,3 [cm
3
],
moment bezwładności: I
x
=925 [cm
4
],
I
y
=85,3 [cm
4
].
G
2
=1,375*18,8*9,81=253,33 [N] - ciężar ramienia na długości 1,375
[m],
G
3
=0,4*18,8*9,81=73,696 [N]
- ciężar ramienia na długości 0,4 [m].
Równania równowagi:
Siłownik w stosunku do ramienia jest umieszczony pod kątem 45
0
.
Oś y:
ΣF
iy
:
-P sin(45
0
)- G
3
+ R
A
– G
2
–G
1
= 0
ΣM
iA
:
P*0,4 sin(45
0
)+ G
3
*0,2 – G
2
*0,688 – G
1
*1,375 = 0
P = 725 [N]
R
A
= 871,6 [N]
h
d
V
V
m
p
p
p
4
*
2
Π
=
=
ρ
14
Na podstawie obliczeń dobieram siłownik typu:
DNC-100-50-PPV-A, o parametrach:
- numer katalogowy: 163467, wykonanie według normy: ISO 6431,
- skok: 50 [mm],
- średnica tłoczyska 25 [mm],
- minimalne/maksymalne
ciśnienie pracy: 0,6[bar]/12[bar],
- zakres temperatur pracy: -20[
o
C]
÷80[
o
C],
- masa
całkowita: 4,653 [kg],
- efektywna
siła wyciągu: 4712 [N],
- efektywna
siła wciągu: 4418 [N],
- średnie zużycie powietrza: 2,6 [l]
Obliczenia wytrzymałościowe ramienia .
Obliczenia wytrzymałościowe momentu gnącego .
Dane:
l
1
=0,2 [m], l
2
=0,688 [m]
P
y
= 512,6 [N]
15
Dla 0<x<l
1
dla
0
dla
l
1
M
g
=-P
y
x
M
g
=0
M
g
=-P
y
l
1
= -102,5 [Nm]
Dla l
1
<x<2l
1
M
g
= - P
y
x – G
3
(x – l
1
)
dla x=l
1
dla
x=2l
1
M
g
= -102,5 [Nm]
M
g
= -219,7 [Nm]
Dla 2l
1
<x<2l
1
+l
2
M
g
= - P
y
x – G
3
(x – l
1
) + R
A
(x-2l
1
)
dla x=l
1
dla
x=2l
1
+l
2
M
g
= -219,7 [Nm]
M
g
= -23,4 [Nm]
Dla 2l
1
+l
2
<x<2l
1
+2l
2
M
g
= - P
y
x – G
3
(x – l
1
) + R
A
(x-2l
1
) – G
2
(x-2l
1
– l
2
)
dla x=2l
1
+l
2
dla
x=2l
1
+2l
2
M
g
=
-23,4
[Nm]
M
g
= 0 [Nm]
Maksymalny moment gnący wynosi
M
gmax
= - 219,7 [N]
Z norm dobieram wartość W dla zadanego ceownika :
W
x
= 1,16 * 10
-4
[m
3
]
W
y
= 1,83 * 10
-5
[m
3
]
Dla stali st7 dopuszczalne naprężenia Kg
0
=65 [MPa]
Ceownik jest dobrze dobrany , jeżeli jest spełniona nierówność:
go
x
g
x
k
W
M
<
=
max
σ
1,89 [MPa] <65 [MPa]
16
go
y
g
y
k
W
M
<
=
max
σ
12,1 [MPa] < 65 [MPa]
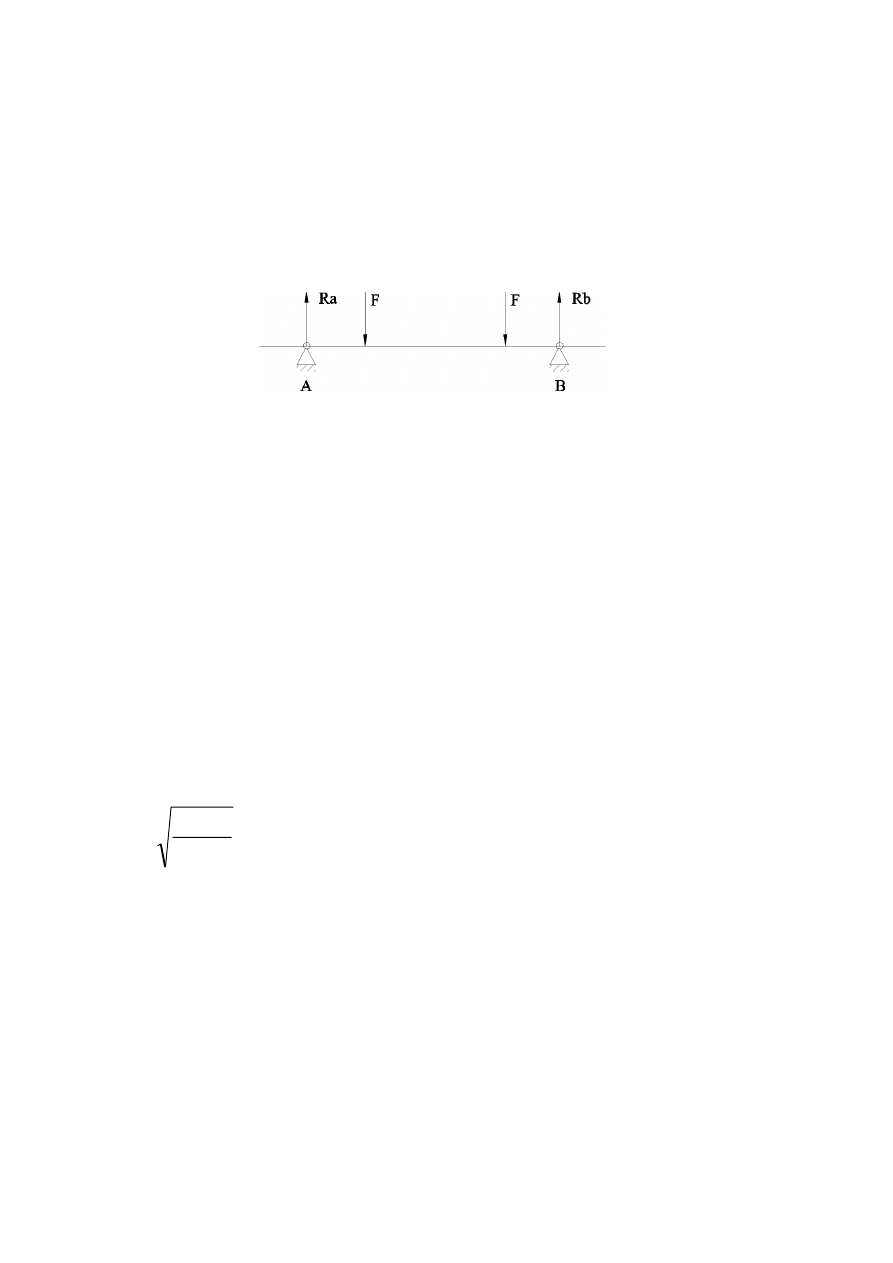
Obliczenia ugięcia ramienia.
f- strzałka ugięcia
moduł Young’a: E= 20*10
11
[N/m
2
]
osiowy moment bezwładności: I= 9,25*10
-6
[m
4
]
Py=Psin
α=512,6 [N]
M
g
= -Pyx - G
3
(x-0.2) + R
A
(x-0.4) - G
2
(x-1.0688) –G
1
(x-1.775)
EIy’’= -M
g
EIy’’= Pyx + G
3
(x-0.2) - R
A
(x-0.4) + G
2
(x-1.088) +G
1
(x-1.775)
EIy’= Py(x
2
/2) - G
3
[(x-0.2)
2
/2] + R
A
[(x-0.4)
2
/2] - G
2
[(x-1.088)
2
/2] -
G
1
[(x-1.775)
2
/2] + C
Eiy = Py(x
3
/6) - G
3
[(x-0.2)
3
/6] + R
A
[(x-0.4)
3
/6] - G
2
[(x-1.088)
3
/6] -
G
1
[(x-1.775)
3
/6] + Cx + D
17
warunki:
x=0
y’=0
x=0
y
=0
C= -131,879
D= 74,659
x = 1,775 y = 0
Obliczam ugięcie:
Y=(1/EI)*(4,976)
Y=2,69*10
-6
[m] = 0,00269 [mm]
Ramię zostało poprawnie dobrane ponieważ ugięcie mieści się w
przedziale
0< y < 0,2 [mm].
18
Obliczenia dotyczące przegubu górnego.
Ramię manipulatora będzie osadzone na osi ustalonej w łożyskach
osadzonych w uchwycie który jest przyspawany do słupa. Szerokość
ramienia jest równa szerokości ceownika i wynosi: 160 [mm].
Obliczam średnicę osi:
Fr– siła reakcji ramienia równa reakcji R
A
Fr=871,6 [N],
F=0,5*Fr=435,8 [N],
a=0,2 [m] - odległość pomiędzy łożyskami,
b=0,02 [m] - odległość pomiędzy łożyskiem a punktem podparcia
ramienia.
Maksymalny moment gnący :
Mgmax=F*b=0,5*Fr*0,02=8,7 [Nm]
Dla stali st7
kg=200 [MPa]
Obliczam średnicę;
kg
Mg
d
r
10
≥
d
r
=6,6*10
-3
przyjmuję d
r
=10 [mm]
19
Dobór łożyska dla przegubu.
P
0
=F=435,8 [N]
Dobieram współczynnik S
0
=2 odnoszący się do dużych wymagań
bezproblemowej pracy przegubu.
C
0
=P
0
*S
0
C
0
=435,8*2=871,6 [N]
C
0
– nośność spoczynkowa
Z katalogu dobieram łożysko walcowe jednorzędowe NUP2304E
gdzie:
C=4100 [N],
C
0
=4600 [N],
masa łożyska: 0,22 [kg],
wymiary: d=20 [mm], D=52 [mm], B=21 [mm]
20
Obliczenia dotyczące słupa.
Wyboczenie.
H=0,775 [m],
R
A
=F=871,6 [N]
E=2*10
5
[MPa]
Korzystając ze wzoru Eulera:
n
w
- współczynnik bezpieczeństwa (1,3
÷4) – przyjmuję n
w
= 4
Wyznaczam moment bezwładności :
I = 1,062*10
-9
[m
4
]
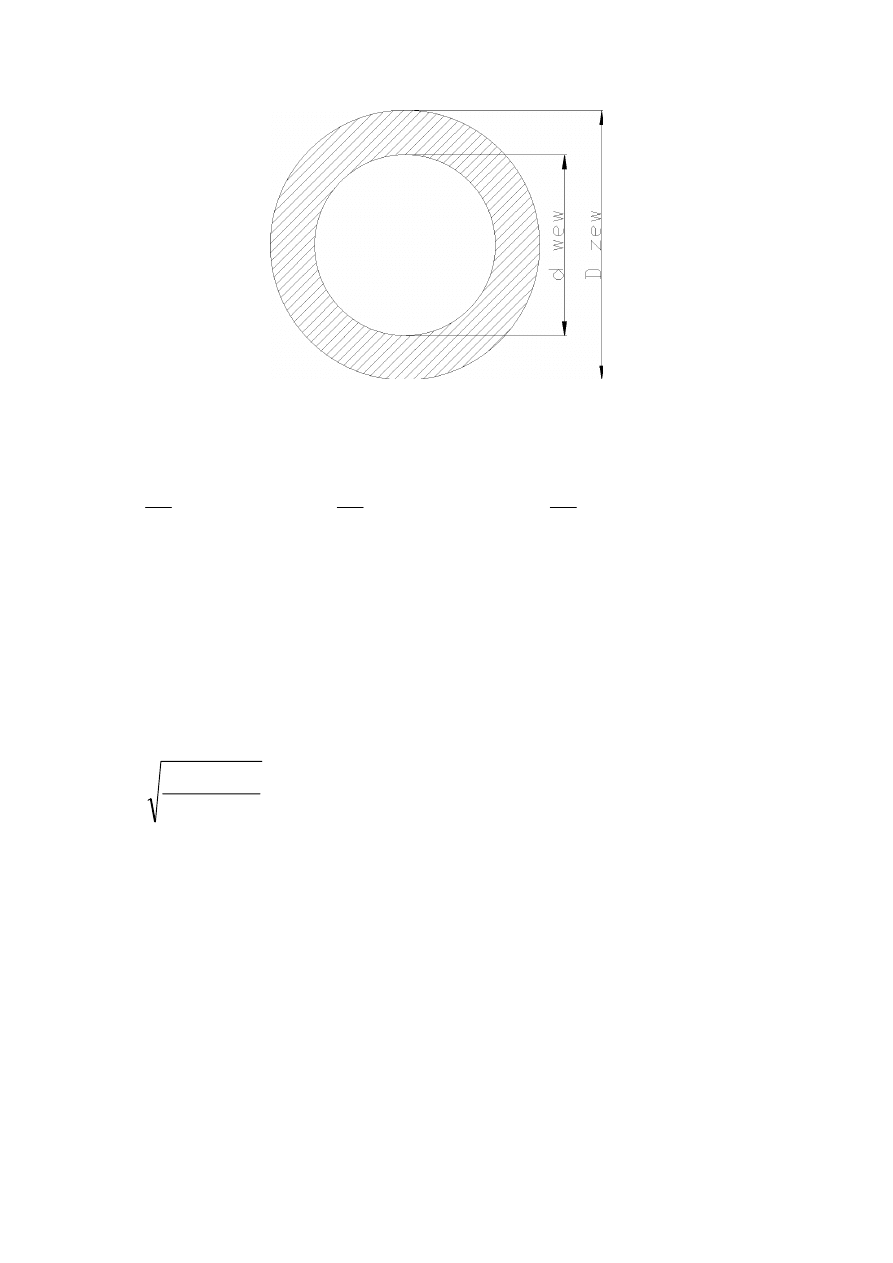
Zakładam średnicę zewnętrzną słupa D
zew
=260 [mm], średnicę
wewnętrzną d
wew
=200[mm] czyli średnica wyrażana przez grubość
ścianki wygląda następująco:
D
zew
=13*g,
d
wew
=10*g, czyli g=20 [mm]
w
n
H
EI
F
2
2
Π
=
E
n
FH
I
w
2
2
Π
=
21
Moment bezwładności:
I=290,01*
Πg
4
[m
4
]
Przyrównując oba momenty otrzymuję:
290,01*
Π*g
4
=3,94*10
-9
4
9
01
,
290
*
10
94
,
3
Π
⋅
≥
−
g
g
≥1,44 10
-3
warunek na wyboczenie jest spełniony dla g=20 [mm].
[
]
4
4
4
4
4
18561
*
64
)
10
(
)
13
(
64
)
(
64
g
g
g
d
D
I
wew
zew
Π
=
−
Π
=
−
Π
=
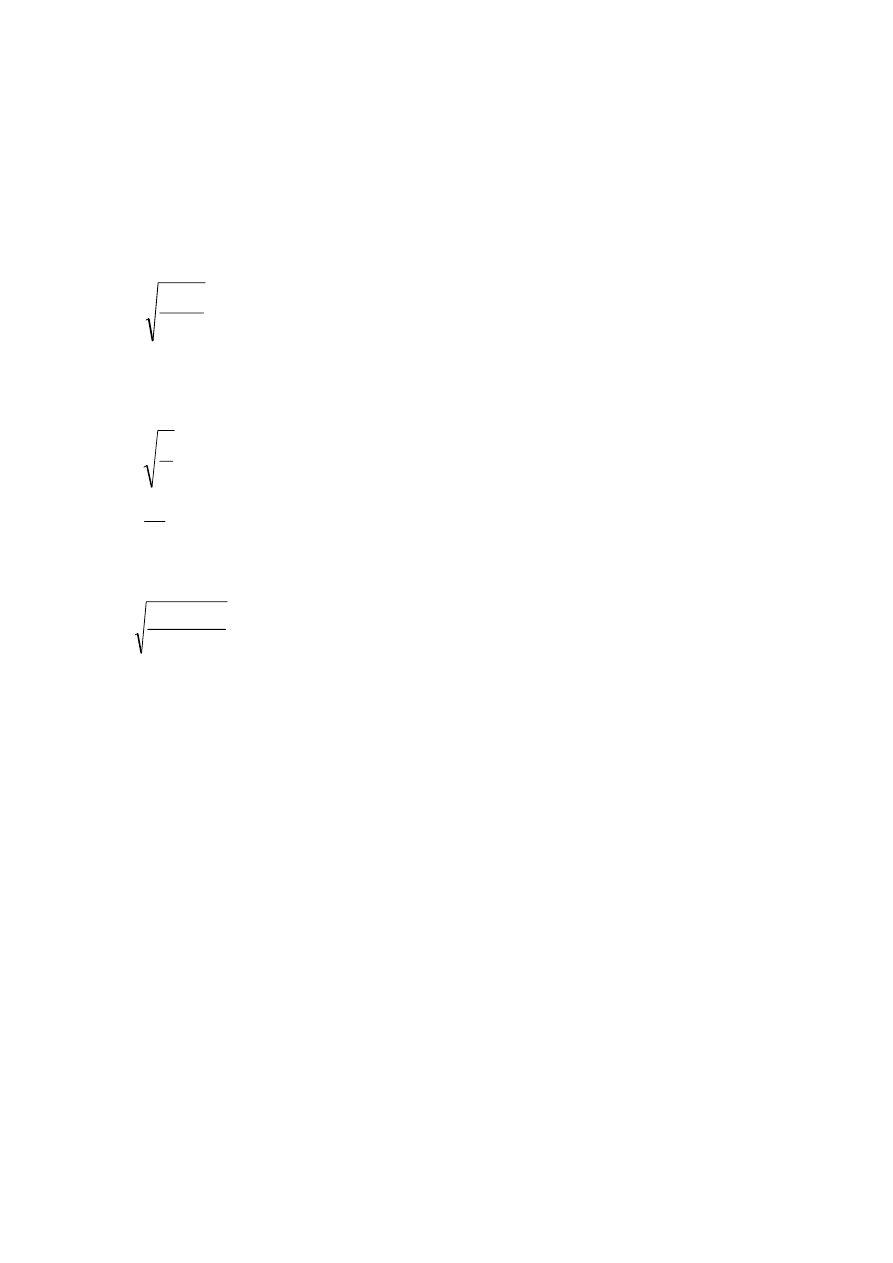
22
Smukłość.
R
w
=200 [MPa]
λ>λ
gr
λ
gr
=
w
R
E
2
Π
λ=l
r
/i
gdzie: s – pole przekroju, i – promień
bezwładności.
000426
,
0
10
26
,
4
0216
,
0
10
94
,
3
4
9
=
⋅
=
⋅
=
−
−
i
λ
gr
=99,3
λ=H/i = 1760,56
warunek
λ>λ
gr
jest spełniony.
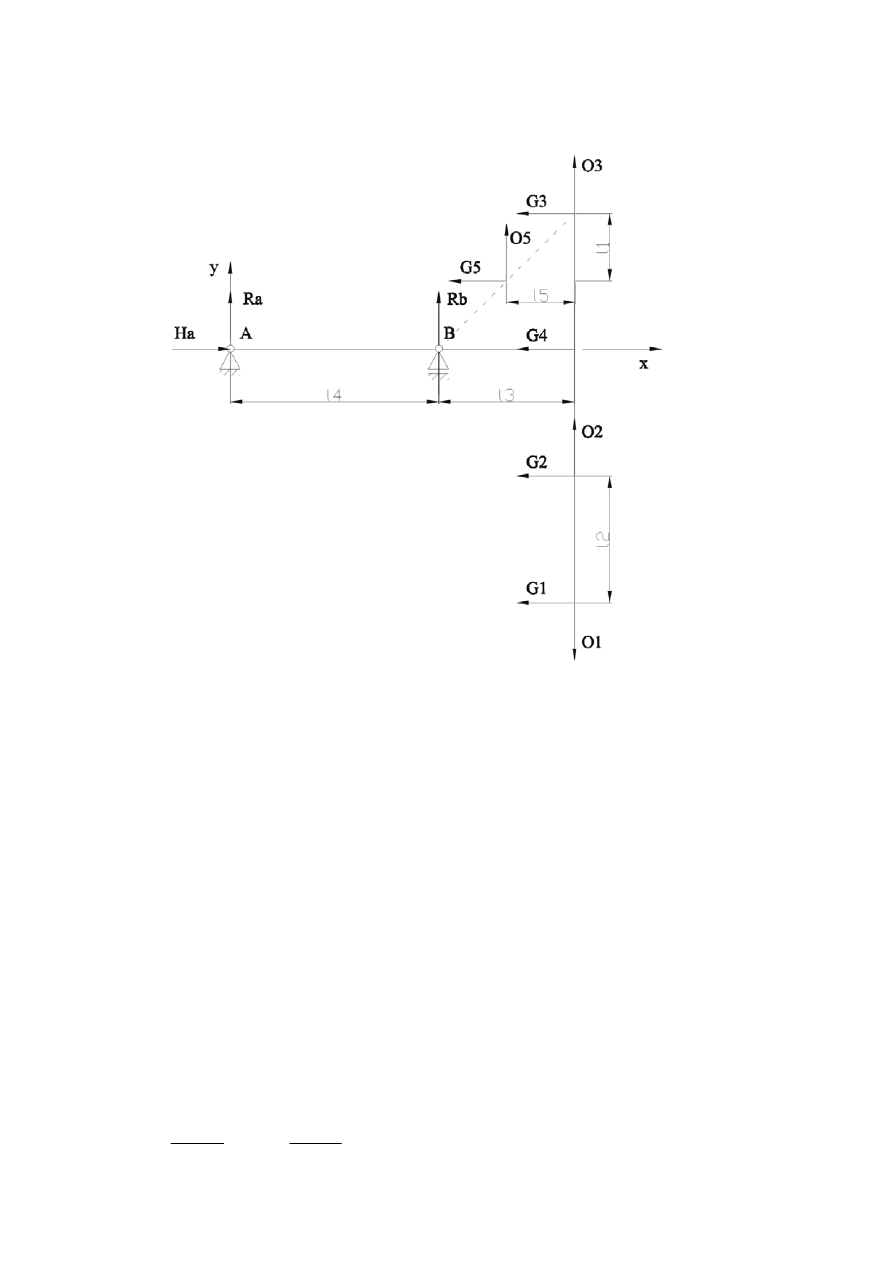
s
I
i
=
]
[
0216
,
0
)
(
*
4
2
2
2
m
d
D
s
wew
zew
=
−
Π
=
23
Zginanie.
Py=512,6 [N],
G
1
=31,56 [N],
G
2
=253,33 [N],
G
3
=73,696 [N],
l
1
=0,2 [m],
l
2
=0,688 [m],
l
3
=0,4 [m],
l
4
=0,375 [m],
l
5
=0,2 [m],
a
1
=1,375 [m/s
2
],
a
2
=0,688 [m/s
2
],
a
3
=0,4 [m/s
2
],
t=1,8 [s],
obliczam siłę G
4
G
4
=
ρ*V*g
H
d
H
D
V
wew
zew
4
4
2
2
Π
−
Π
=
24
ρ=7800 [kg/m
3
],
g=9.81 [m/s
2
],
V=0,0062 [m
3
]
G
4
=785 [N]
obliczam siłę G
5
G
5
=m
s
*g
m
s
=4,65 [kg]
G
5
=45,61 [N]
obliczam przyspieszenia punktu G
5
G
5
⇒ a
1
/2l
2
=a
5
/l
5
a
5
=0,2 [m/s
2
]
obliczam prędkości liniowe poszczególnych punktów
V
1
= a
1
t V
1
= 2,475 [m/s]
V
2
= a
2
t V
2
= 1,24 [m/s]
V
3
= a
3
t V
3
= 0,72 [m/s]
V
5
= a
5
t V
5
= 0,36 [m/s]
obliczam siły odśrodkowe
m
1
=3,22 [kg],
m
2
=25,9 [kg],
m
3
=7,52 [kg],
m
5
=4,65 [kg],
O
1
= (m
1
*V
1
2
)/2l
2
O
1
=14,36
O
2
= (m
2
*V
2
2
)/l
2
O
2
=58
O
3
= (m
3
*V
3
2
)/2l
1
O
3
=0,52
O
5
= (m
5
*V
5
2
)/l
1
O
5
=0,13
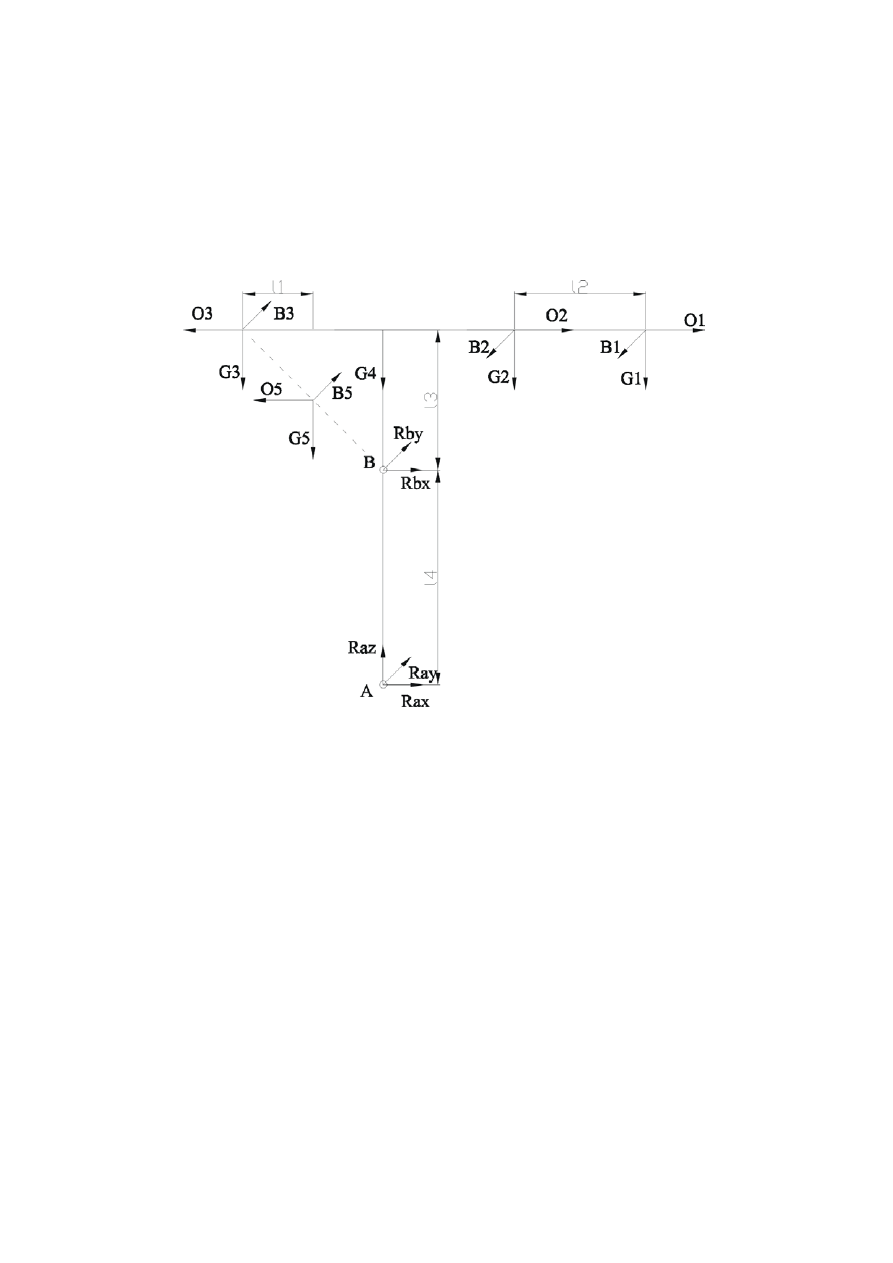
- równania
równowagi
ΣFiy: Ha – G
4
–G
3
– G
2
–G
1
–G
5
-Py= 0
ΣFix: -Ra -Rb -O
5
- O
3
+
O
1
+ O
2
= 0
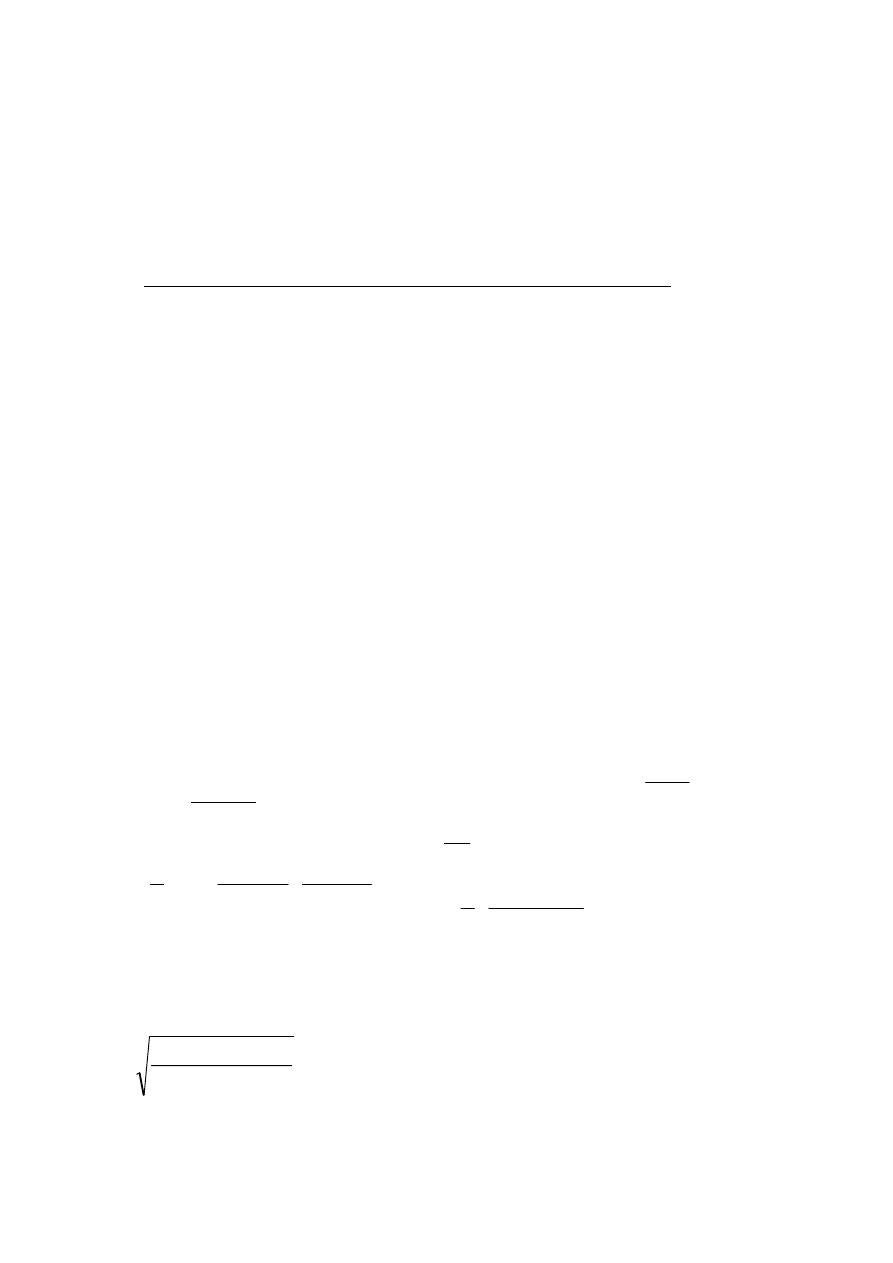
25
ΣMi
A
: R
B
l
4
+ O
5
(l
4
+l
3
*0,5)+G
5
l
1
+O
3
(l
4
+ l
3
)+Py*2l
1
–G
2
l
2
-O
2
(l
4
+ l
3
) – G
1
2l
2
- O
1
(l
4
+ l
3
)=0
−
z równań równowagi otrzymuję
Ha=G
1
+G
2
+G
3
+G
4
+Py+G
5
=1701,8 [N]
(
)
(
)
(
)
4
1
3
4
3
3
2
2
3
4
2
2
1
5
5
4
5
3
4
1
l
l
G
l
l
O
l
G
l
l
O
l
G
l
G
l
O
l
l
O
R
b
−
+
−
+
+
+
⋅
+
−
−
+
=
R
b
=587,9 [N]
R
a
=525,9 [N]
obliczam maksymalny moment gnący
Mg
1
= Ra*x
x
1
=l
4
= 197,21 [Nm]
Mg
2
= Ra * (x-l
4
) + Rb*x
x
2
=l
3
= 271,11 [Nm]
obliczenia wytrzymałościowe na zginanie
64
64
4
4
max
wew
zew
x
x
dop
d
D
I
e
I
W
W
Mg
Π
−
Π
=
=
=
≥
σ
σ
( ) (
)
[
]
3
4
4
4
4
01
,
40
5
,
6
1
,
260
1
,
260
10
13
64
5
,
6
2
10
13
g
g
g
e
I
W
g
g
g
I
g
D
e
g
d
g
D
x
zew
wew
zew
Π
=
Π
=
=
Π
=
−
Π
=
=
=
=
=
stąd
[ ]
m
g
g
027
.
0
10
100
01
,
40
11
,
271
3
6
≥
⋅
⋅
Π
≥
b
a
R
O
O
O
O
R
−
+
−
−
−
=
1
2
5
3
26
Przyjmuję więc grubość ścianki g=20 [mm]. Spełnia ona założone
wymagania wytrzymałościowe.
27
Dobór łożysk tocznych.
Na słupie osadzone będą dwa łożyska . Górne przenosi tylko obciążenia
poprzeczne , dolne przenosi obciążenia wzdłużne i poprzeczne .
G
1
=31,56 [N],
G
2
=253,33 [N],
G
3
=73,33 [N],
G
4
=786,3 [N],
G
5
=45,61 [N],
O
1
=14,36 [N],
O
2
=58 [N],
O
3
=9,8 [N],
O
5
=0,6 [N],
m
1
=3,22 [kg],
m
2
=25,9 [kg],
m
3
=7,25 [kg],
m
5
=4,65 [kg],
l
1
=0,2 [m],
l
2
=0,688 [m],
l
3
=0,4 [m],
l
4
=0,375 [m],
l
5
=0,2 [m],
28
a
1
=1,375 [m/s
2
],
a
2
=0,688 [m/s
2
],
a
3
=0,4 [m/s
2
],
a
5
=0,2 [m/s
2
],
- momenty
bezwładności
B
1
=m
1
a
1
B
1
=4,43 [N],
B
2
=m
2
a
2
B
2
=17,82 [N],
B
3
=m
3
a
3
B
3
=2,9 [N],
B
5
=m
5
a
5
B
5
=0,93 [N],
- równania
równowagi
ΣFix:
R
ax
+ R
bx
+ O
1
+ O
2
- O
3
- O
5
=0
ΣFiy:
R
ay
+ R
by
+ B
3
+ B
5
- B
2
- B
1
=0
ΣFiz:
R
az
- G
5
- G
4
- G
3
- G
2
- G
1
=0
ΣMix: R
by
l
4
+ B
2
(l
4
+l
3
) + B
1
(l
4
+l
3
) - B
3
(l
4
+l
3
) - B
5
l
4
=0
ΣMiy: R
bx
l
4
+ O
2
(l
4
+l
3
) + O
1
(l
4
+l
3
) - O
5
l
4
- O
3
(l
4
+l
3
) +G
1
2l
2
+ G
2
l
2
- G
3
l
1
+
- G
5
l
5
= 0
Z równań równowagi:
R
bx
= -645,6 [N]
R
b
= 646,78 [N]
R
by
= -39,07 [N]
R
ax
= 583,64 [N]
R
ay
= 57,5 [N]
R
a
= 584,9 [N]
R
az
= 1189,2[N]
Łożysko górne.
- obciążenie statycznie równoważne.
Fr = R
b
= 646,78 [N] P
0
= Fr
- nośność spoczynkowa:
C
0
= S
0
*P
0
gdzie:
S
0
- współczynnik zabezpieczający łożysko przed zbyt dużym
odkształceniem trwałym: S
0
=2 dla łożysk kulowych, S
0
=3,3
dla łożysk wałeczkowych.
29
Przyjmuję łożysko kulowe
C
0
=2*646,78 = 1293,56 [N]
- dobieram
łożysko kulkowe 6048 dla którego:
C
0
= 31700 [N], C=25600 [N], d=240 [mm], D=360 [mm], B=56 [mm].
Łożysko dolne.
Przyjmuję łożysko stożkowe.
- obliczam
obciążenie równoważne styczne ze wzoru:
P
0
= Fr + y
0
F
a
Fr = R
A
F
A
= R
Az
y
0
= wsp. obciążeń statycznych .= 2.1
P
o
= 646,78 + 2,1 * 1189,2 = 3539,22 [N]
- obliczam
nośność statyczna
S
0
= 3,3
dla łożysk walcowych
C
0
= 3,3*3539,22 =1268,33 [N]
- dobieram łożysko 32328 dla którego:
C
0
= 165000 [N], C = 12200 [N], d=140 [mm], D=300 [mm], H=107 [mm].
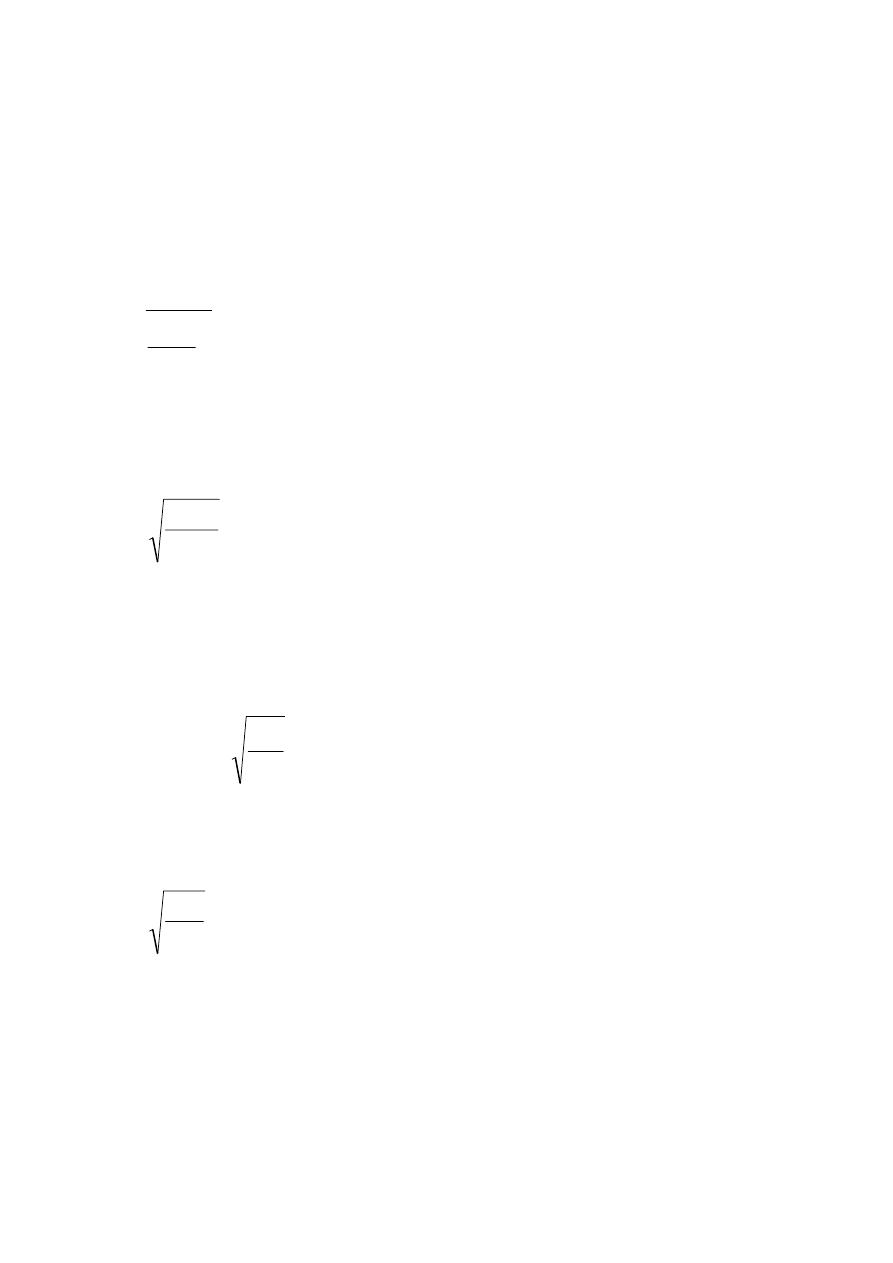
30
Obliczenia przegubu siłownika.
Do połączenia siłownika z ramieniem stosuję połączenie sworzniowe .
Sworzeń wykonany jest ze stali St6 k
s
≈ k
t
= 110 [MPa]
- warunek
wytrzymałościowy
t
k
n
d
F
≤
Π
≤
4
2
τ
- obliczam
średnicę sworznia
n = 1,
F = 4014,76 [N],
k
t
= 110 [MPa]
t
nk
F
d
Π
≥
4
d
≥6,81*10
-3
[m]
przyjmuję d = 12 [mm]
- w otworze ucha znajduje się panewka łożyska ślizgowego, obliczam
to łożysko wg PN-72/11-84020
dla st6 k
go
= 65 [MPa],
k
0
= 6 [MPa]
λ = l/d ≈
0
45
,
0
k
k
go
λ = 1,48
przyjmuję
λ = 1,5
- obliczam
średnicę czopa.
F=4014,76 [N]
λ
0
k
F
d
≥
d
≥0,021 [m]
przyjmuję d= 25 [mm]
- długość czopa
l =
λ * d
l = 1,5*25 = 38 [mm]
31
Obliczenia śrub fundamentowych.
Równania równowagi
ΣFix: O
1
+ O
2
- O
3
- O
5
= Rx
ΣFiy: B
3
- B
2
– B
1
+ B
5
= Ry
ΣFiz: - G
5
- G
4
- G
2
– G
3
– G
1
= Rz
Mx = B
1
(l
3
+l
4
) + B
2
(l
3
+l
4
) - B
3
(l
3
+l
4
)- B
5
l
4
My = O
1
(l
3
+l
4
) + O
2
(l
3
+l
4
) - O
3
(l
3
+l
4
) - O
5
l
4
+ G
1
2l
2
+ G
2
l
2
- G
3
l
1
-G
5
l
5
Mz = - B
1
2l
2
- B
2
l
2
- B
3
l
1
- B
5
l
5
Rx= 61.96 [N],
Ry= -18,42 [N],
Rz= -1189,2 [N],
Mx= 14,63 [Nm],
My= 220,4 [Nm],
Mz= -19,17 [Nm]
R
x
, R
y
, M
z
- siły przesuwające,
R
z
- siła wyrywająca,
M
z
, M
y
- siły gnące (rozciągające)
32
R
z
= Q
z
* n Q
z
= R
z
/ n
Q
z
= 297,3 [N]
Q
Mgmax
= (Mg * l
max
) /
Σ l
i
2
Q
Mgy
= (Mg
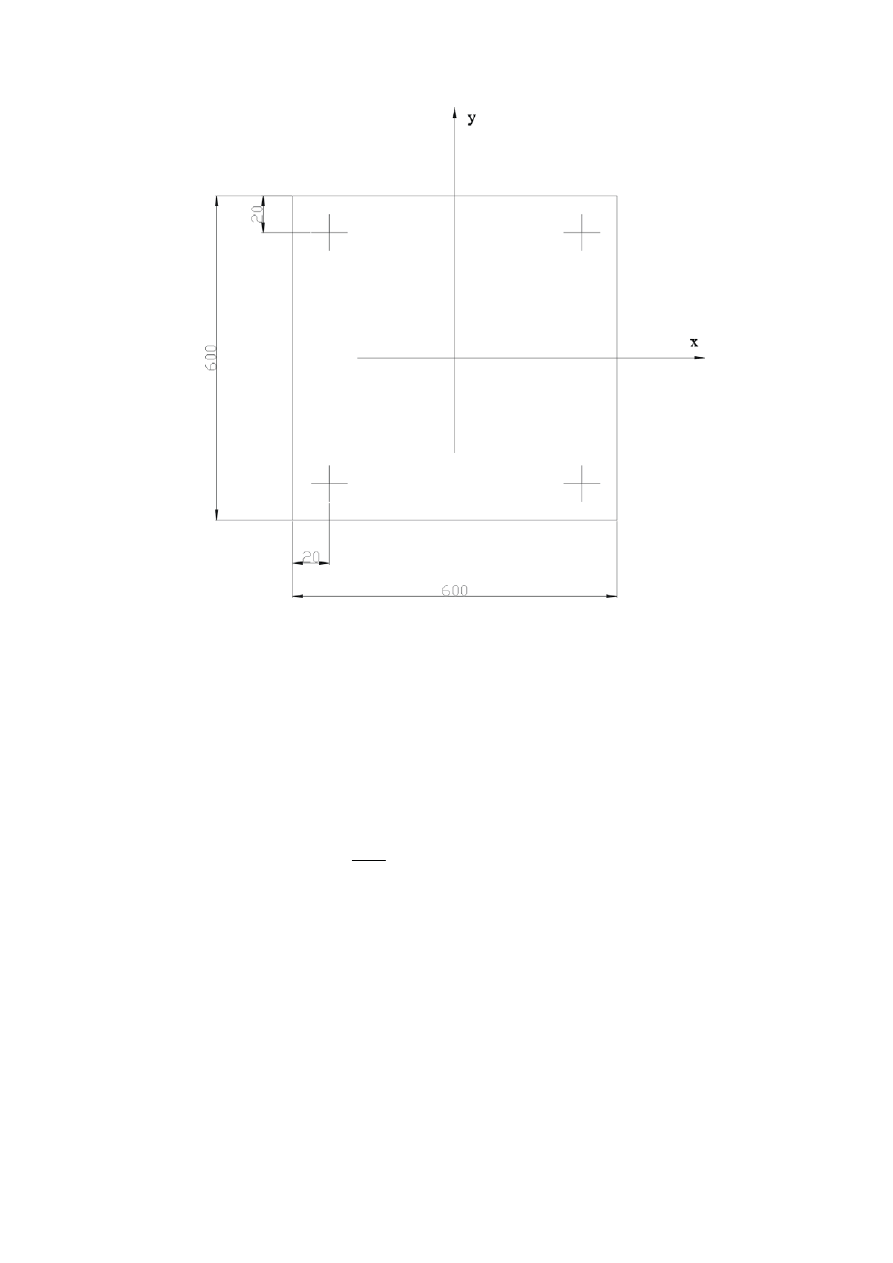
y
* 0,6) / 2*(0,02
2
+0,58
2
) = 196,5 [N]
Q
Mgx
= (Mg
x
* 0,6) / 2*(0,02
2
+0,58
2
) = 13,1 [N]
R
Q z
Q
R
z
x
x
x
x
= ⋅
⋅
⇒
=
µ
µ
µ = 0.2 dla betonu i stali
z - ilość śrub
Q
x
= R
x
/
µz = 77,45 [N]
Q
y
= R
y
/
µz = -23,03 [N]
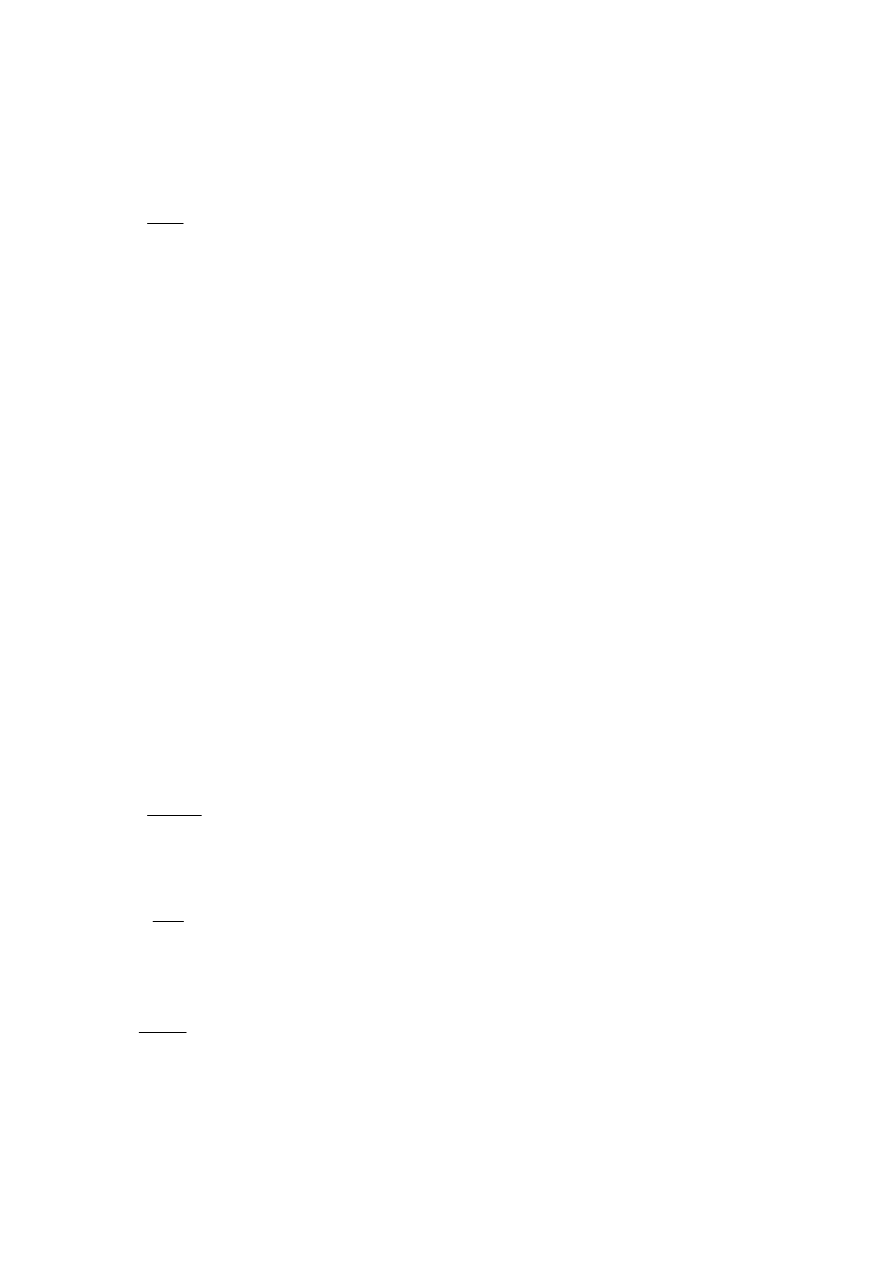
33
obliczam siłę aktywną F
F
M
l
i
z
=
l - odległość pomiędzy środkiem podstawy a śrubą
F
i
= 19,17 / 0,395 = 48,53 [N]
Q
Mz
- siła dociskająca
Q
Mz
= F
i
/
µ = 242,65 [N]
obliczam siłę wstępną w śrubie
Q
wst
=Q
x
+ Q
y
+ Q
Mz
=297,07 [N]
Siła wypadkowa wyraża się wzorem
Q
wyp
=Q
Mz
+ Q
z
+ Q
wst
= 836,37 [N]
warunek wytrzymałościowy
σ =
≤
Q
S
k
wyp
r
R
e
= 300 [MPa]
x = 2
[
]
k
R
x
MPa
r
e
=
=150
Ponieważ przekrój śruby jest kołem
S
d
=
Π
2
4
34
Przekształcając warunek wytrzymałościowy otrzymuję wzór na średnicę
rdzenia śruby:
[ ]
mm
d
k
Q
d
r
wyp
78
,
8
4
≥
Π
⋅
≥
Przyjmuję więc średnicę rdzenia 10 [mm]. Dobrałem śrubę M10 PN-
72/M-85061
35
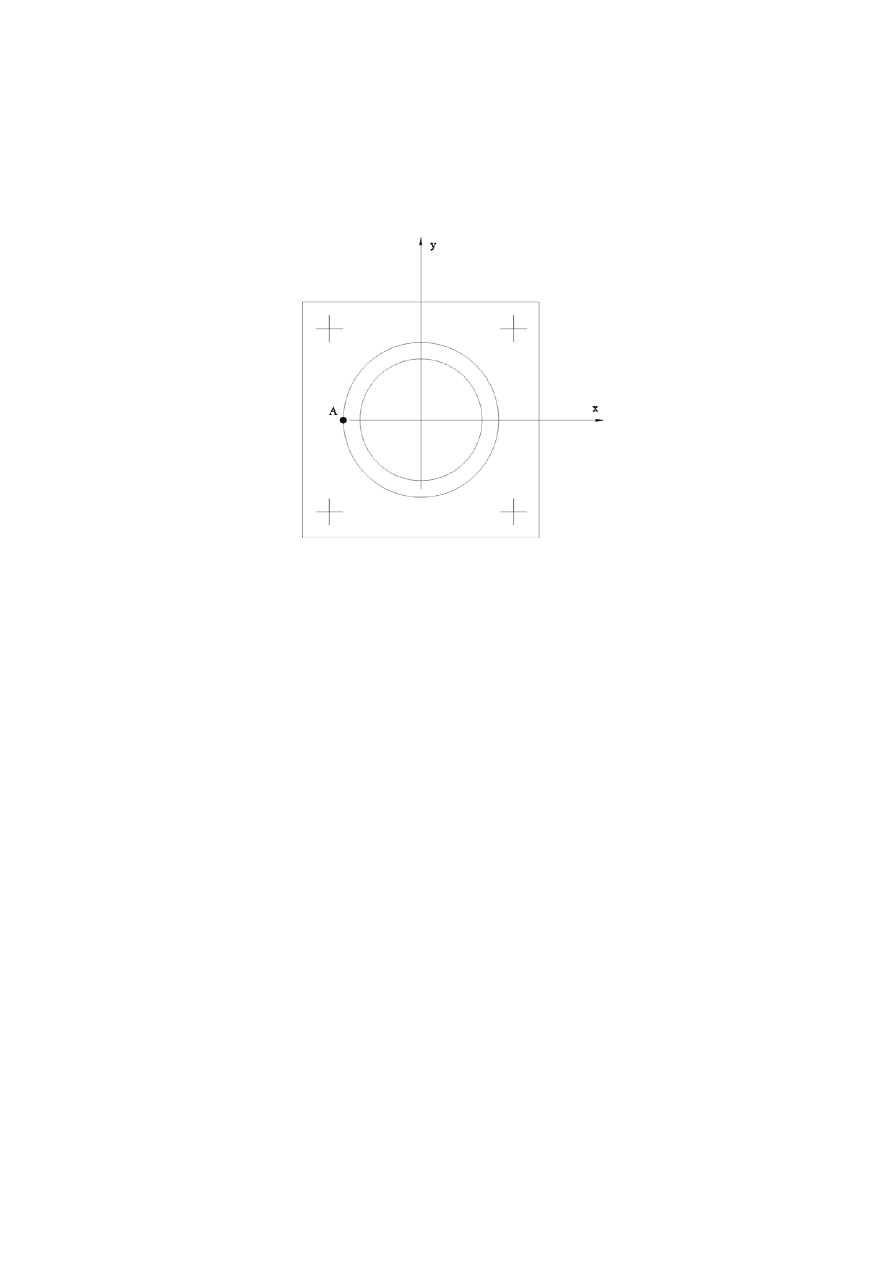
Obliczenia połączenia spawanego.
Obliczenia dotyczą spoiny pachwinowej o grubości 5 [mm].
Rx= 61.96 [N],
Ry= -18,42 [N],
Rz= -1189,2 [N],
Mx= 14,63 [Nm],
My= 220,4 [Nm],
Mz= -19,17 [Nm],
- obliczam
wskaźnik wytrzymałości
I
x
= U
y
= (
Π/64) (D
zew
4
- d
wew
4
) = 14,5*10
-5
[m
4
]
e
x
= e
y
= D
zew
/2
Wx = Wy = (
Π/32) (S
4
- d
wew
4
/D
zew
) = 3,91*10
-4
[m
3
]
36
obliczam naprężenia w spoinie
τ
x
= R
x
/P
P = (
Π/4) (0,28
2
- 0,26
2
) = 8,48*10
-3
τ
x
= 730,66
τ
y
= -217,22
τ
z
= 140235,85
τ
Mx
= Mx/Wx
τ
Mx
= 37416,9
τ
My
= 563682,9
- dla spoiny pachwinowej
τ ≤ sR*1,1
s = 0,8
R = 250 [MPa]
τ ≤1,1*sR = 220 [MPa]
Maksymalnie jest obciążony punkt A i dla niego :
2
2
2
)
(
My
Mx
z
y
x
A
τ
τ
τ
τ
τ
τ
+
+
+
+
=
τ
A
= 2,836 [MPa]
≤ 220 [MPa]
Warunek wytrzymałościowy jest spełniony – spoina wytrzyma zadane
obciążenia.
37
Obliczenia momentu napędowego.
ΣMz: M
B
- B
3
2l
1
- B
5
l
1
=B
2
l
2
+ B
1
2* l
2
- M
n
= 0
M
n
= 324,14 [Nm]
Dobieram siłownik hyrauliczny obrotowy firmy Mannesmann Rexroth
Engineering model A4F0 71 o parametrach:
budowa osiowo-tłokowa z tarczą wychylną
T
max
= 395 [Nm],
masa 34 [kg],
ciśnienie nominalne/maksymalne 350 [bar]/400[bar]