Akademia Górniczo-Hutnicza

w Krakowie

Modelowanie w Projektowaniu Maszyn

Stół wibracyjny

Projekt

Gr. I

Przywara Patryk

Śliwa Wojciech

Wełna Wojciech

Węglarz Mateusz

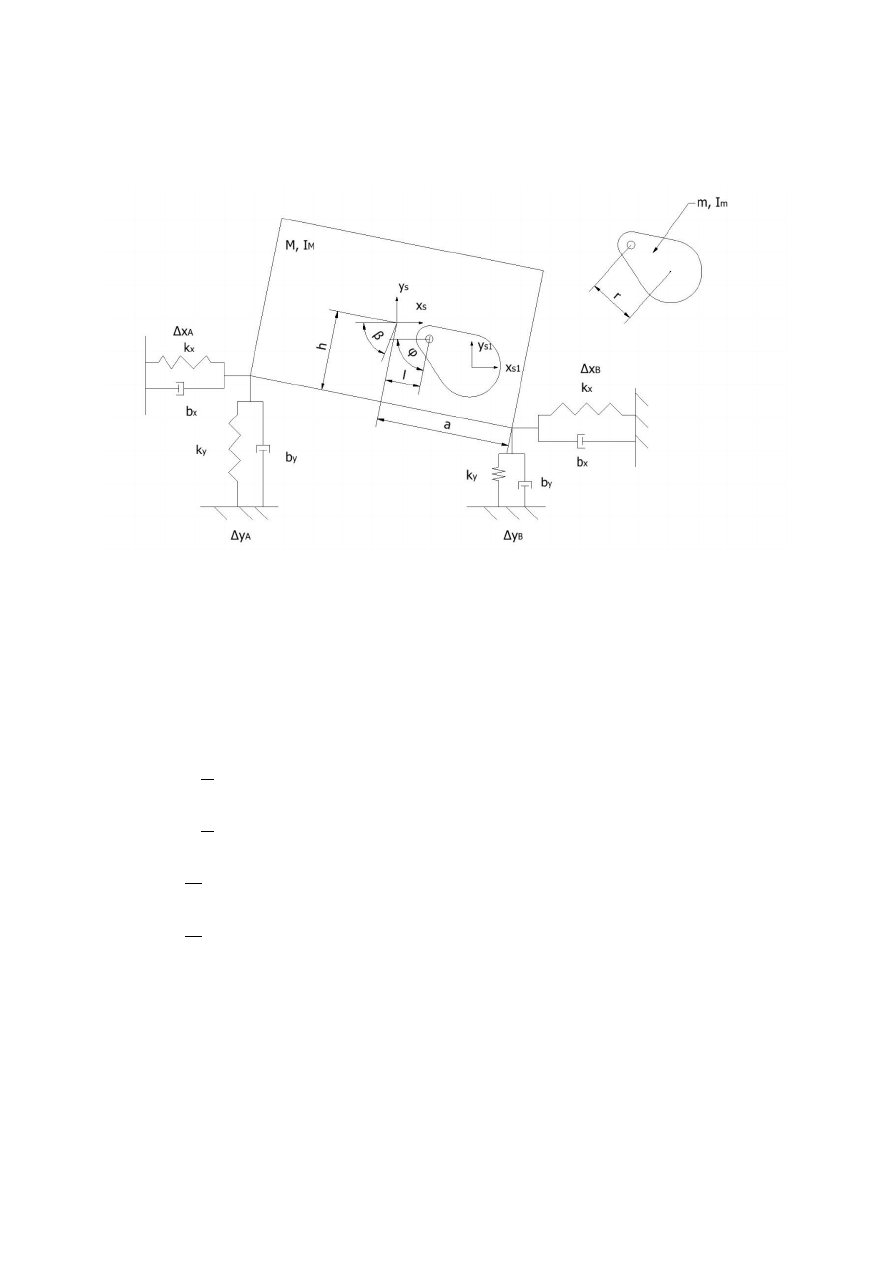
1. Rozwiązanie zagadnienia

Schemat:

Dane:

𝑀 = 90 𝑘𝑔 − 𝑚𝑎𝑠𝑎 𝑠𝑡𝑜ł𝑢

𝑚 = 7 𝑘𝑔 − 𝑚𝑎𝑠𝑎 𝑤𝑖𝑏𝑟𝑎𝑡𝑜𝑟𝑎

𝐼

𝑀

= 10,32 𝑘𝑔 ∙ 𝑚

2

− 𝑚𝑜𝑚𝑒𝑛𝑡 𝑏𝑒𝑧𝑤ł𝑎𝑑𝑛𝑜ś𝑐𝑖 𝑠𝑡𝑜ł𝑢

𝐼

𝑚

= 0,0063 𝑘𝑔 ∙ 𝑚

2

− 𝑚𝑜𝑚𝑒𝑛𝑡 𝑏𝑒𝑧𝑤ł𝑎𝑑𝑛𝑜ś𝑐𝑖 𝑤𝑖𝑏𝑟𝑎𝑡𝑜𝑟𝑎

𝑘𝑥 = 12915,9

𝑁

𝑚

− 𝑤𝑠𝑝ół𝑐𝑧𝑦𝑛𝑛𝑖𝑘 𝑠𝑝𝑟ęż𝑦𝑠𝑡𝑜ś𝑐𝑖 𝑛𝑎 𝑘𝑖𝑒𝑟𝑢𝑛𝑘𝑢 𝑋

𝑘𝑦 = 67371,1

𝑁

𝑚

− 𝑤𝑠𝑝ół𝑐𝑧𝑦𝑛𝑛𝑖𝑘 𝑠𝑝𝑟ęż𝑦𝑠𝑡𝑜ś𝑐𝑖 𝑛𝑎 𝑘𝑖𝑒𝑟𝑢𝑛𝑘𝑢 𝑌

𝑏𝑥 = 62,73

𝑘𝑔

𝑠

− 𝑤𝑠𝑝ół𝑐𝑧𝑦𝑛𝑛𝑖𝑘 𝑡ł𝑢𝑚𝑖𝑒𝑛𝑖𝑎 𝑛𝑎 𝑘𝑖𝑒𝑟𝑢𝑛𝑘𝑢 𝑋

𝑏𝑦 = 62,73

𝑘𝑔

𝑠

− 𝑤𝑠𝑝ół𝑐𝑧𝑦𝑛𝑛𝑖𝑘 𝑡ł𝑢𝑚𝑖𝑒𝑛𝑖𝑎 𝑛𝑎 𝑘𝑖𝑒𝑟𝑢𝑛𝑘𝑢 𝑌

𝑎 = 1 𝑚

ℎ = 0,2 𝑚

𝑒 = 0,03 𝑚

𝑙 = 0,5 𝑚

Współrzędne wyjściowe

𝑥

𝑠

, 𝑦

𝑠

, 𝜑, 𝛽, 𝑥

𝑠1

, 𝑦

𝑠1

Równania więzów:

{

𝑥

𝑠1

= 𝑥

𝑠

+ 𝑟 ∙ 𝑐𝑜𝑠𝜑 + 𝑙

𝑦

𝑠1

= 𝑦

𝑠

+ 𝑟 ∙ 𝑠𝑖𝑛𝜑 + 𝑙 ∙ 𝛽

{

𝑥

𝑠1

̇ = 𝑥

𝑠

̇ − 𝑟 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜑̇

𝑦

𝑠1

̇ = 𝑦̇

𝑠

+ 𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑̇ + 𝑙 ∙ 𝛽̇

Zastosowane uproszczenia:

𝑠𝑖𝑛𝛽 = 𝛽

𝑐𝑜𝑠𝛽 = 1

Założenia:

∆𝑥

𝐴

= 𝑥

𝑠

+ ℎ ∙ 𝛽

∆𝑥

𝐵

= 𝑥

𝑠

− ℎ ∙ 𝛽

∆𝑦

𝐴

= 𝑦

𝑠

− 𝑎 ∙ 𝛽

∆𝑦

𝐵

= 𝑦

𝑠

+ 𝑎 ∙ 𝛽

Energia kinetyczna układu:

𝐸

𝑘

=

1
2

∙ 𝑀 ∙ 𝑥

𝑠

̇

2

+

1
2

∙ 𝑀 ∙ 𝑦

𝑠

̇

2

+

1
2

∙ 𝐼

𝑀

∙ 𝛽̇

2

+

1
2

∙ 𝑚 ∙ 𝑥

𝑠1

̇

2

+

1
2

∙ 𝑚 ∙ 𝑦

𝑠1

̇

2

+

1
2

∙ 𝐼

𝑚

∙ 𝜑̇

2

𝐸

𝑘

=

1
2

∙ 𝑀 ∙ 𝑥

𝑠

̇

2

+

1
2

∙ 𝑀 ∙ 𝑦

𝑠

̇

2

+

1
2

∙ 𝐼

𝑀

∙ 𝛽̇

2

+

1
2

∙ 𝑚(𝑥

𝑠

̇ −

𝑟 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜑

̇

)

2

+

1
2

∙ 𝑚(𝑦

𝑠

̇ +

𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑

̇

+ 𝑙 ∙ 𝛽

̇

)

2

+

1
2

𝐼

𝑚

∙ 𝜑̇

2

𝐸

𝑘

=

1
2

∙ 𝑀 ∙ 𝑥

𝑠

̇

2

+

1
2

∙ 𝑀 ∙ 𝑦

𝑠

̇

2

+

1
2

∙ 𝐼

𝑀

∙ 𝛽̇

2

+

1
2

∙ 𝑚 ∙ (𝑥

𝑠

̇

2

− 2𝑥

𝑠

̇ ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜑̇ + 𝑟

2

∙ 𝑠𝑖𝑛

2

𝜑 ∙ 𝜑̇

2

)

+

1
2

𝑚 ∙ (𝑦

𝑠

̇

2

+ 𝑟

2

∙ 𝑐𝑜𝑠

2

𝜑 ∙ 𝜑̇

2

+ 𝑙

2

∙ 𝛽

2

+ 2𝑦

𝑠

̇ ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑̇ + 2𝑦

𝑠

̇ ∙ 𝑙 ∙ 𝛽̇ + 2 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑̇ ∙ 𝑙 ∙ 𝛽̇)

+

1
2

𝐼

𝑚

∙ 𝜑̇

2

Energia potencjalna układu:

𝐸

𝑝

=

1
2

∙ 𝑘𝑥(

∆𝑥

𝐴

+ ∆𝑥

𝐵

)

2

+

1
2

∙ 𝑘𝑦(

∆𝑦

𝐴

+ ∆𝑦

𝐵

)

2

𝐸

𝑝

=

1
2

∙ 𝑘𝑥 ((

𝑥

𝑠

+ ℎ ∙ 𝛽

)

2

+

(𝑥

𝑠

− ℎ ∙ 𝛽)

2

)

+

1
2

∙ 𝑘𝑦 ((

𝑦

𝑠

− 𝑎 ∙ 𝛽

)

2

+

(𝑦

𝑠

+ 𝑎 ∙ 𝛽)

2

)

𝐸

𝑝

=

1
2

∙ 𝑘𝑥(

𝑥

𝑠

2

+ 2 ∙ 𝑥

𝑠

∙ ℎ ∙ 𝛽 + ℎ

2

∙ 𝛽

2

+ 𝑥

𝑠

2

− 2 ∙ 𝑥

𝑠

∙ ℎ ∙ 𝛽 + ℎ

2

∙ 𝛽

2

) +

1
2

∙ 𝑘𝑦(

𝑦

𝑠

2

− 2 ∙ 𝑦

𝑠

∙ 𝑎 ∙ 𝛽

+ 𝑎

2

∙ 𝛽

2

+ 𝑦

𝑠

2

+ 2 ∙ 𝑦

𝑠

∙ 𝑎 ∙ 𝛽 + 𝑎

2

∙ 𝛽

2

)

𝐸

𝑝

= 𝑘𝑥 (

𝑥

𝑠

2

+ ℎ

2

∙ 𝛽

2

)

+ 𝑘𝑦(𝑦

𝑠

2

+ 𝑎

2

∙ 𝛽

2

)

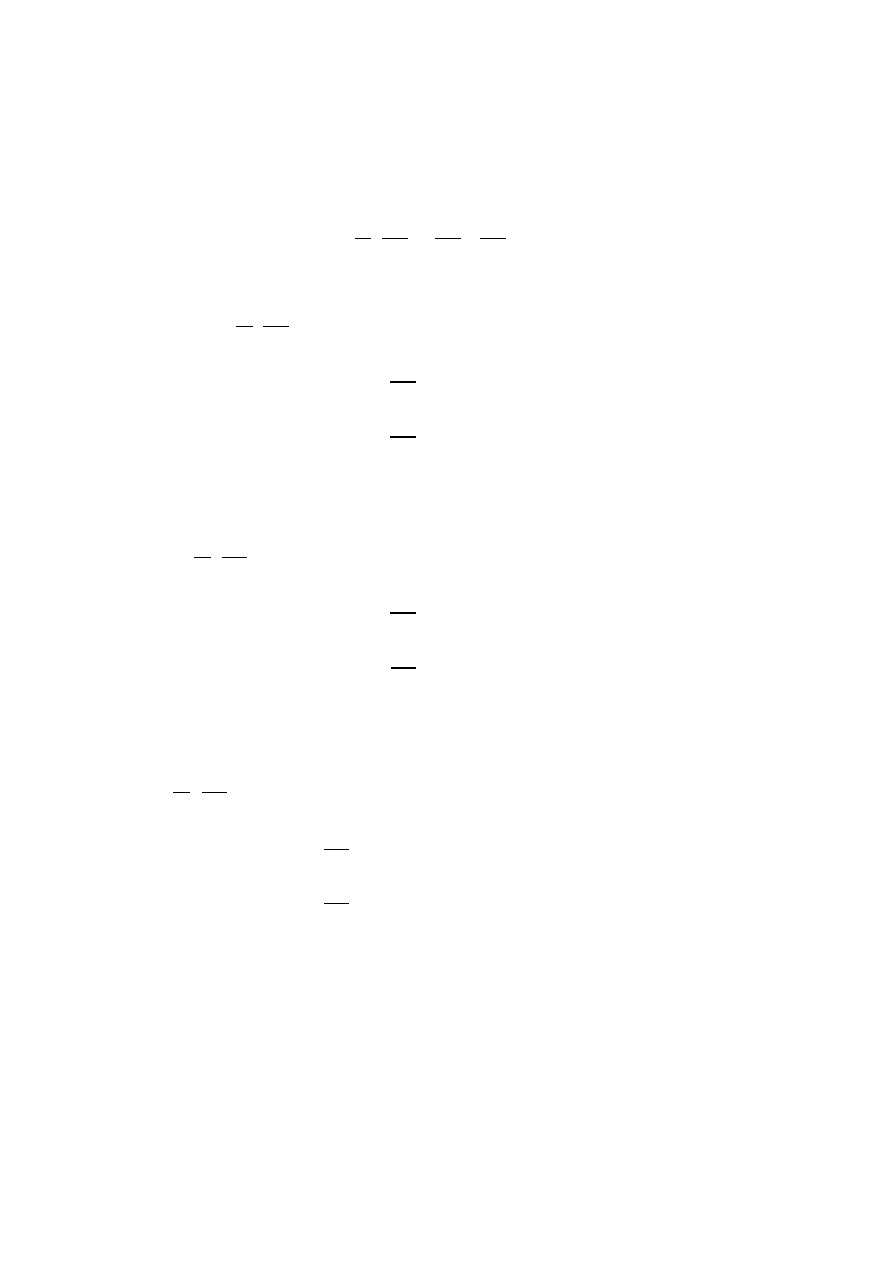
Energia strat układu:

𝐸

𝑑

= 𝑘𝑥 (

𝑥

𝑠

̇

2

+ ℎ

2

∙ 𝛽

̇

2

)

+ 𝑘𝑦(𝑦

𝑠

̇

2

+ 𝑎

2

∙ 𝛽

̇

2

)

Ogólna postać równania Lagrange’a II rodzaju:

𝑑

𝑑𝑡

(

𝛿

𝐸

𝑘

𝛿𝑞̇

) +

𝛿

𝐸

𝑝

𝛿𝑞

+

𝛿

𝐸

𝑑

𝛿𝑞̇

= 𝐹

Równanie Lagrange’a II rodzaju dla współrzędnej 𝑥

𝑠

:

𝑑

𝑑𝑡

(

𝛿

𝐸

𝑘

𝛿𝑥

𝑠

̇

) = 𝑀 ∙ 𝑥

𝑠

̈ + 𝑚 ∙ 𝑥

𝑠

̈ − 𝑚 ∙ 𝑟 ∙ (𝑐𝑜𝑠𝜑 ∙ 𝜑̇ ∙ 𝜑̇ + 𝑠𝑖𝑛𝜑 ∙ 𝜑̈)

𝛿

𝐸

𝑝

𝛿𝑥

𝑠

= 2 ∙ 𝑘𝑥 ∙ 𝑥

𝑠

𝛿

𝐸

𝑝

𝛿𝑥

𝑠

̇

= 2 ∙ 𝑏𝑥 ∙ 𝑥

𝑠

̇

𝑥

𝑠

̈ (𝑀 + 𝑚) − 𝑚 ∙ 𝑟 ∙ (𝑐𝑜𝑠𝜑 ∙ 𝜑̇ ∙ 𝜑̇ + 𝑠𝑖𝑛𝜑 ∙ 𝜑̈) + 2 ∙ 𝑘𝑥 ∙ 𝑥

𝑠

+ 2 ∙ 𝑏𝑥 ∙ 𝑥

𝑠

̇ = 0

Równanie Lagrange’a II rodzaju dla współrzędnej 𝑦

𝑠

:

𝑑

𝑑𝑡

(

𝛿

𝐸

𝑘

𝛿𝑦

𝑠

̇

) = 𝑀 ∙ 𝑦

𝑠

̈ + 𝑚 ∙ 𝑦

𝑠

̈ − 𝑚 ∙ 𝑟 ∙ (−𝑠𝑖𝑛𝜑 ∙ 𝜑̇ ∙ 𝜑̇ + 𝑐𝑜𝑠𝜑 ∙ 𝜑̈) + 𝑚 ∙ 𝑙 ∙ 𝛽̈

𝛿

𝐸

𝑝

𝛿𝑦

𝑠

= 2 ∙ 𝑘𝑦 ∙ 𝑦

𝑠

𝛿

𝐸

𝑝

𝛿𝑦

𝑠

̇

= 2 ∙ 𝑏𝑦 ∙ 𝑦

𝑠

̇

𝑦

𝑠

̈ (𝑀 + 𝑚) + 𝑚 ∙ 𝑟 ∙ (−𝑠𝑖𝑛𝜑 ∙ 𝜑̇ ∙ 𝜑̇ + 𝑐𝑜𝑠𝜑 ∙ 𝜑̈) + 𝛽̈ ∙ 𝑚 ∙ 𝑙 + 2 ∙ 𝑘𝑦 ∙ 𝑦

𝑠

+ 2 ∙ 𝑏𝑦 ∙ 𝑦

𝑠

̇ = 0

Równanie Lagrange’a II rodzaju dla współrzędnej 𝛽:

𝑑

𝑑𝑡

(

𝛿

𝐸

𝑘

𝛿𝛽̇

) = 𝐼

𝑀

∙ 𝛽̈ + 𝑚 ∙ 𝑙

2

∙ 𝛽̈ + 𝑚 ∙ 𝑙 ∙ 𝑦

𝑠

̈ + 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ (−𝑠𝑖𝑛𝜑 ∙ 𝜑̇ ∙ 𝜑̇ + 𝑐𝑜𝑠𝜑 ∙ 𝜑̈)

𝛿

𝐸

𝑝

𝛿𝛽

= 2 ∙ 𝑘𝑥 ∙ ℎ

2

∙ 𝛽 + 2 ∙ 𝑘𝑦 ∙ 𝑎

2

∙ 𝛽

𝛿

𝐸

𝑝

𝛿𝛽̇

= 2 ∙ 𝑏𝑥 ∙ ℎ

2

∙ 𝛽̇ + 2 ∙ 𝑏𝑦 ∙ 𝑎

2

∙ 𝛽̇

𝛽̈(𝐼

𝑀

+ 𝑚 ∙ 𝑙

2

) + 𝑦

𝑠

̈ ∙ 𝑚 ∙ 𝑙 + 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ (−𝑠𝑖𝑛𝜑 ∙ 𝜑 ∙̇ 𝜑̇ + 𝑐𝑜𝑠𝜑 ∙ 𝜑̈) + 𝛽 ∙ (2 ∙ 𝑘𝑥 ∙ ℎ

2

+ 2 ∙ 𝑘𝑦 ∙ 𝑎

2

)

+ 𝛽̇ ∙ (2 ∙ 𝑘𝑥 ∙ ℎ

2

+ 2 ∙ 𝑘𝑦 ∙ 𝑎

2

) = 0

Równanie Lagrange’a II rodzaju dla współrzędnej 𝜑:

𝑑

𝑑𝑡

(

𝛿

𝐸

𝑘

𝛿𝜑̇

) = −𝑚 ∙ 𝑟 ∙ (𝑥

𝑠

̈ ∙ 𝑠𝑖𝑛𝜑 + 𝑥

𝑠

̇ ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑̇) + 𝑚 ∙ 𝑟

2

∙ [(2 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑̇) ∙ 𝜑̇ + 𝑠𝑖𝑛

2

𝜑 ∙ 𝜑̈]

+ 𝑚 ∙ 𝑟

2

∙ [(2 ∙ 𝑐𝑜𝑠𝜑 ∙ (−𝑠𝑖𝑛𝜑) ∙ 𝜑̇) ∙ 𝜑̇ + 𝑐𝑜𝑠

2

𝜑 ∙ 𝜑̈]

+ 𝑚 ∙ 𝑟 ∙ (𝑦

𝑠

̈ ∙ 𝑐𝑜𝑠𝜑 + 𝑦

𝑠

̇ ∙ (−𝑠𝑖𝑛𝜑) ∙ 𝜑̇)

+ 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ (−𝑠𝑖𝑛𝜑 ∙ 𝜑 ∙̇ 𝛽̇ + 𝑐𝑜𝑠𝜑 ∙ 𝛽̈) + 𝐼

𝑚

∙ 𝜑̈

𝛿

𝐸

𝑝

𝛿𝜑

= 0

𝛿

𝐸

𝑝

𝛿𝜑̇

= 0

𝑚 ∙ 𝑟 ∙ [𝑦

𝑠

̈ ∙ 𝑐𝑜𝑠𝜑 − 𝑥

𝑠

̈ ∙ 𝑠𝑖𝑛𝜑 − 𝜑̇ ∙ (𝑦

𝑠

̇ ∙ 𝑠𝑖𝑛𝜑 + 𝑥

𝑠

̇ ∙ 𝑐𝑜𝑠𝜑)] + 𝜑̈ ∙ (𝐼

𝑚

+ 𝑚 ∙ 𝑟

2

)

+ 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ (𝑐𝑜𝑠𝜑 ∙ 𝛽̈ − 𝑠𝑖𝑛𝜑 ∙ 𝜑̇ ∙ 𝛽̇) = 𝑀

𝑒𝑙

Równania ruchu:

a) dla współrzędnej 𝑥

𝑠

:

𝑥

𝑠

̈ (𝑀 + 𝑚) − 𝜑̈ ∙ 𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 = 𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜑̇

2

− 2 ∙ 𝑘𝑥 ∙ 𝑥

𝑠

− 2 ∙ 𝑏𝑥 ∙ 𝑥

𝑠

̇

b) dla współrzędnej 𝑦

𝑠

:

𝑦

𝑠

̈ (𝑀 + 𝑚) + 𝜑̈ ∙ 𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 + +𝛽̈ ∙ 𝑚 ∙ 𝑙 = 𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜑̇

2

− 2 ∙ 𝑘𝑦 ∙ 𝑦

𝑠

− 2 ∙ 𝑏𝑦 ∙ 𝑦

𝑠

̇

c) dla współrzędnej 𝛽:

𝛽̈(𝐼

𝑀

+ 𝑚 ∙ 𝑙

2

) + 𝑦

𝑠

̈ ∙ 𝑚 ∙ 𝑙 + 𝜑̈ ∙ 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑐𝑜𝑠𝜑 = 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜑̇

2

− 2 ∙ 𝛽 ∙ 𝑘𝑥 ∙ ℎ

2

− 2 ∙ 𝛽 ∙ 𝑘𝑦 ∙ 𝑎

2

− 2 ∙ 𝛽̇ ∙ 𝑏𝑥 ∙ ℎ

2

− 2 ∙ 𝛽̇ ∙ 𝑏𝑦 ∙ 𝑎

2

d) dla współrzędnej 𝜑:

𝑦

𝑠

̈ ∙ 𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 − 𝑥

𝑠

̈ ∙ 𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 + 𝜑̈ ∙ (𝐼

𝑚

+ 𝑚 ∙ 𝑟

2

) + 𝛽̈ ∙ 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑐𝑜𝑠𝜑

= 𝜑̇ ∙ 𝑦

𝑠

̇ ∙ 𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 + 𝜑̇ ∙ 𝑥

𝑠

̇ ∙ 𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 + 𝛽̇ ∙ 𝜑̇ ∙ 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑠𝑖𝑛𝜑

Podstawienia:

𝑥

𝑠

̇ = 𝑉

𝑥

𝑦

𝑠

̇ = 𝑉

𝑦

𝛽̇ = 𝜔

𝛽

𝜑̇ = 𝜔

𝜑

𝑀

𝑒𝑙

=

3147,488 ∙ (157 − 𝜑̇)

2686,98 + (157 − 𝜑̇)

2

Równania ruchu w postaci macierzowej:

[

1 0 0 0

0

0

0

0

0 1 0 0

0

0

0

0

0 0 1 0

0

0

0

0

0 0 0 1

0

0

0

0

0 0 0 0

𝑀 + 𝑚

0

0

−𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑

0 0 0 0

0

𝑀 + 𝑚

𝑚 ∙ 𝑙

𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑

0 0 0 0

0

𝑚 ∙ 𝑙

𝐼

𝑀

+ 𝑚 ∙ 𝑙

2

𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑐𝑜𝑠𝜑

0 0 0 0 −𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑐𝑜𝑠𝜑

𝐼

𝑚

+ 𝑚 ∙ 𝑟

2

]

∙

𝑑

𝑑𝑡

[

𝑥

𝑠

𝑦

𝑠

𝛽

𝜑

𝑣

𝑥

𝑣

𝑦

𝜔

𝛽

𝜔

𝜑

]

=

=

[

𝑣

𝑥

𝑣

𝑦

𝜔

𝛽

𝜔

𝜑

𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜔

𝜑

2

− 2 ∙ 𝑘𝑥 ∙ 𝑥

𝑠

− 2 ∙ 𝑏𝑥 ∙ 𝑣

𝑥

𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜔

𝜑

2

− 2 ∙ 𝑘𝑦 ∙ 𝑦

𝑠

− 2 ∙ 𝑏𝑦 ∙ 𝑣

𝑦

𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜔

𝜑

2

− 2 ∙ 𝑘𝑥 ∙ ℎ

2

∙ 𝛽 − 2 ∙ 𝑘𝑦 ∙ 𝑎

2

∙ 𝛽 − 2 ∙ 𝑏𝑥 ∙ ℎ

2

∙ 𝜔

𝛽

− 2 ∙ 𝑏𝑦 ∙ 𝑎

2

∙ 𝜔

𝛽

𝑚 ∙ 𝑟 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜔

𝜑

∙ 𝑣

𝑦

+ 𝑚 ∙ 𝑟 ∙ 𝑐𝑜𝑠𝜑 ∙ 𝜔

𝜑

∙ 𝑣

𝑥

+ 𝑚 ∙ 𝑟 ∙ 𝑙 ∙ 𝑠𝑖𝑛𝜑 ∙ 𝜔

𝜑

∙ 𝜔

𝛽

+ 𝑀

𝑒𝑙

]

Rozwiązanie zagadnienia:

[𝑀]

𝑑

𝑑𝑡

[𝑋̅] = [𝑄̅]

𝑑

𝑑𝑡

[𝑋̅] = [𝑀]

−1

∙ [𝑄̅]