WYKŁAD 1

Sterowanie-
Oddziaływanie za pomocą urządzenia sterującego na proces fizyczny (obiekt sterowania)
tak, aby został osiągnięty zamierzony cel.

Układ sterowania-
Zespół współpracujących urządzeń, realizujących zadany proces fizyczny lub
technologiczny i jego sterowanie. W skład układu sterowania wchodzi zawsze obiekt
sterowany (obiekt regulacji) oraz urządzenie sterujące (regulator).

Sterowanie w układzie otwartym -
Proces sterowania przebiega bez śledzenia stanu wielkości sterowanej i bez
przekazywania informacji o stanie wielkości sterowanej do urządzenia sterującego.

Sterowanie w układzie zamkniętym -
Proces sterowania zwany w tym przypadku procesem automatycznej regulacji, przebiega
w wyniku śledzenia (pomiaru) stanu wielkości sterowanej (regulowanej) i przekazywaniu
tej informacji poprzez układ sprzężenia zwrotnego do urządzenia sterującego (regulatora).

Regulacja automatyczna -
Jest to proces kompensacji wpływu wielkości zakłócających na przebieg realizowanego
procesu fizykalnego (technologicznego) w taki sposób, aby wartości wielkości
regulowanych jak najmniej różniły się od wartości pożądanych tych wielkości, czyli od
wartości wielkości zadanych.

Obiekt regulacji –
Podukład układu regulacji, w którym dokonuje się regulacji jednej lub wielu wielkości
fizykalnych.

Regulator –
Podukład układy regulacji, który dokonuje pomiaru wartości wielkości regulowanej,
porównania tej wartości z wartością wielkości zadanej, przetworzenia sygnału różnicy
wielkości zadanej i wielkości regulowanej na sygnał nastawczy wywołujący taki skutek, ze
wartość wielkości regulowanej jest (z założonym odchyleniem) równa wartości wielkości
zadanej.

Wartość zadana wielkości regulowanej –
To wartość wielkości regulowanej, która ma być uzyskana w wyniku procesu regulacji.

Błąd (uchyb, odchyłka) regulacji –
Jest to różnica pomiędzy bieżącą wartością wielkości zadanej w, a bieżącą rzeczywistą
wartością wielkości regulowanej y

e=w-y

Æ

e(t)=w(t)-y(t)

w- wartość zadana
y- bieżąca rzeczywista wartość wielkości regulowanej
e – błąd regulacji

Sygnał –
To dowolna wielkość fizyczna, występująca w procesie sterowania za pomocą której są
przekazywane informacje. Sygnał charakteryzuje się treścią fizyczną sygnału oraz
parametrem informacji.

Informacja –
To każdy czynnik zmniejszający naszą niewiedzę na temat otaczającej nas rzeczywistości,
zmniejszający naszą niepewność

Treść fizyczna sygnału –
Wielkość fizyczna, która jest nośnikiem informacji (np. ciśnienie cieczy, bądź gazu,
natężenie przepływu gazu, prądu). Podczas przesyłania sygnału treść fizyczna sygnału
może wielokrotnie ulegać przetwarzaniu.

Parametr informacji –
To wartość wielkości fizycznej, podlegającej obserwacji bądź sterowaniu. Podczas
przesyłania sygnału parametr informacji może być wielokrotnie transformowany, lecz nie
może ulegać zmianie.

Sygnał analogowy (ciągły) –
Taki sygnał, którego wartość wielkości fizykalnej są jednoznacznie i w sposób ciągły
odwzorowywane poprzez nieskończenie liczny zbiór parametrów informacji.

Sygnał dyskretny –
Taki sygnał, który charakteryzuje się określoną liczbą skończonych wartości parametru
informacji. Sygnały dyskretne można dzielić na: próbkowane, kwantowane i kodowane
(cyfrowe)

Sygnał próbkowany –
Powstaje przez pobranie parametru informacji w określonej chwili czasu i przyjęciu
założenia, że pobrana wartość wielkości fizykalnej reprezentuje sygnał próbkowany w
zadanym przedziale, wynikającym z narzuconej częstotliwości (gęstości) próbkowania.

Sygnał kwantowany –
Powstaje poprzez pomiar przyrostu parametru informacji w określonej chwili czasu i
przyjęciu założenia o przyrostowej reprezentacji sygnału kwantowanego w zadanym
przedziale wynikającym z narzuconej częstotliwości (gęstości) kwantowania sygnału.

WYKŁAD 2

Sterowanie ręczne –
Ma miejsce wtedy, gdy sygnały sterujące procesem zachodzącym w obiekcie sterowania
(procesem technologicznym) są wytwarzane przez urządzenie sterujące w wyniku
oddziaływania wymuszeń wywołanych bezpośrednio aktywnością człowieka (gdy sygnały
sterujące procesem są wywoływane w wyniku bezpośredniej aktywności człowieka).

Sterowanie automatyczne –
Ma miejsce wtedy, gdy sygnały sterujące procesem zachodzącym w obiekcie sterowania
(procesem technologicznym) są wytwarzane przez urządzenie sterujące w wyniku
oddziaływania wymuszeń wywołanych przez celowo dobrane środki techniczne
wchodzące w skład urządzenia sterującego.

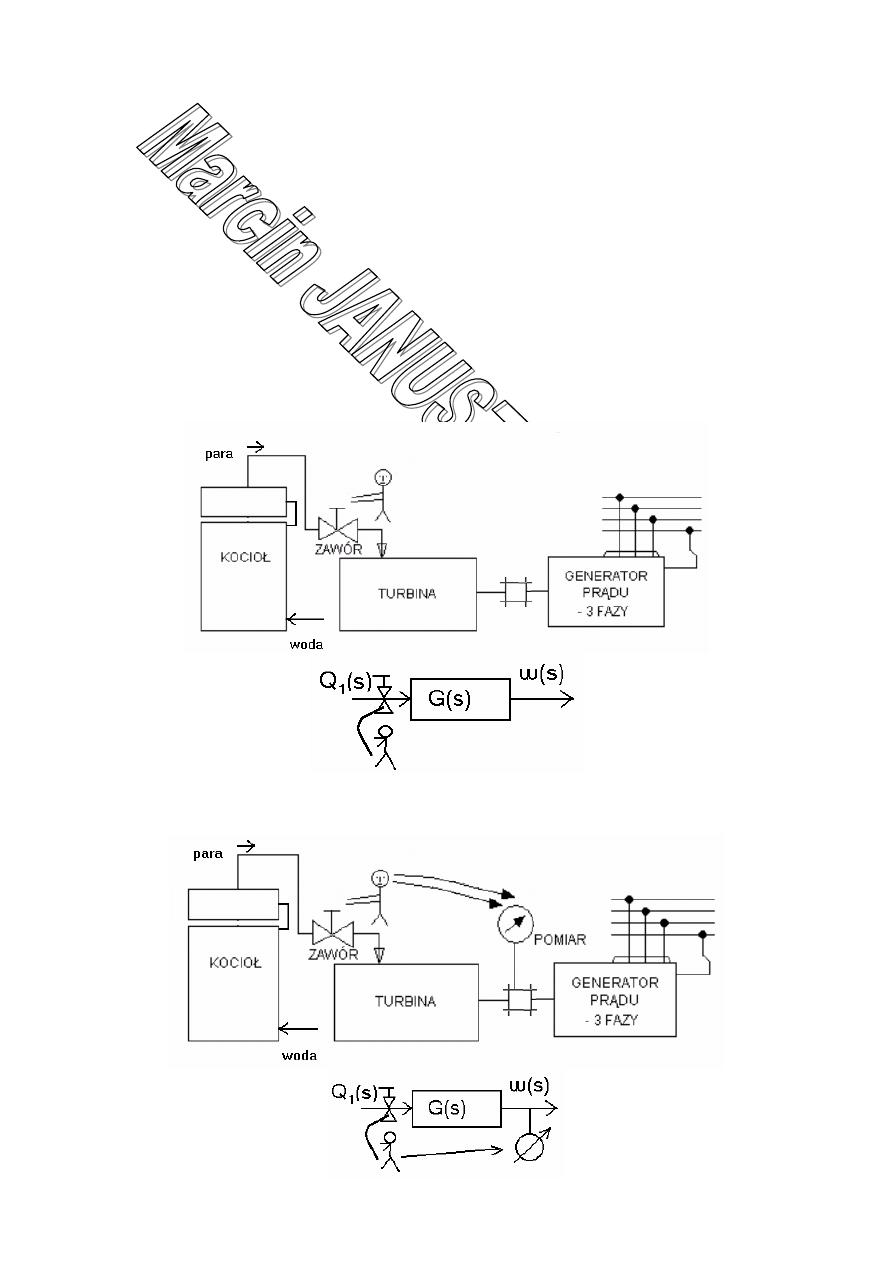
Sterowanie ręczne w układzie otwartym:

Sterowanie ręczne w układzie zamkniętym:

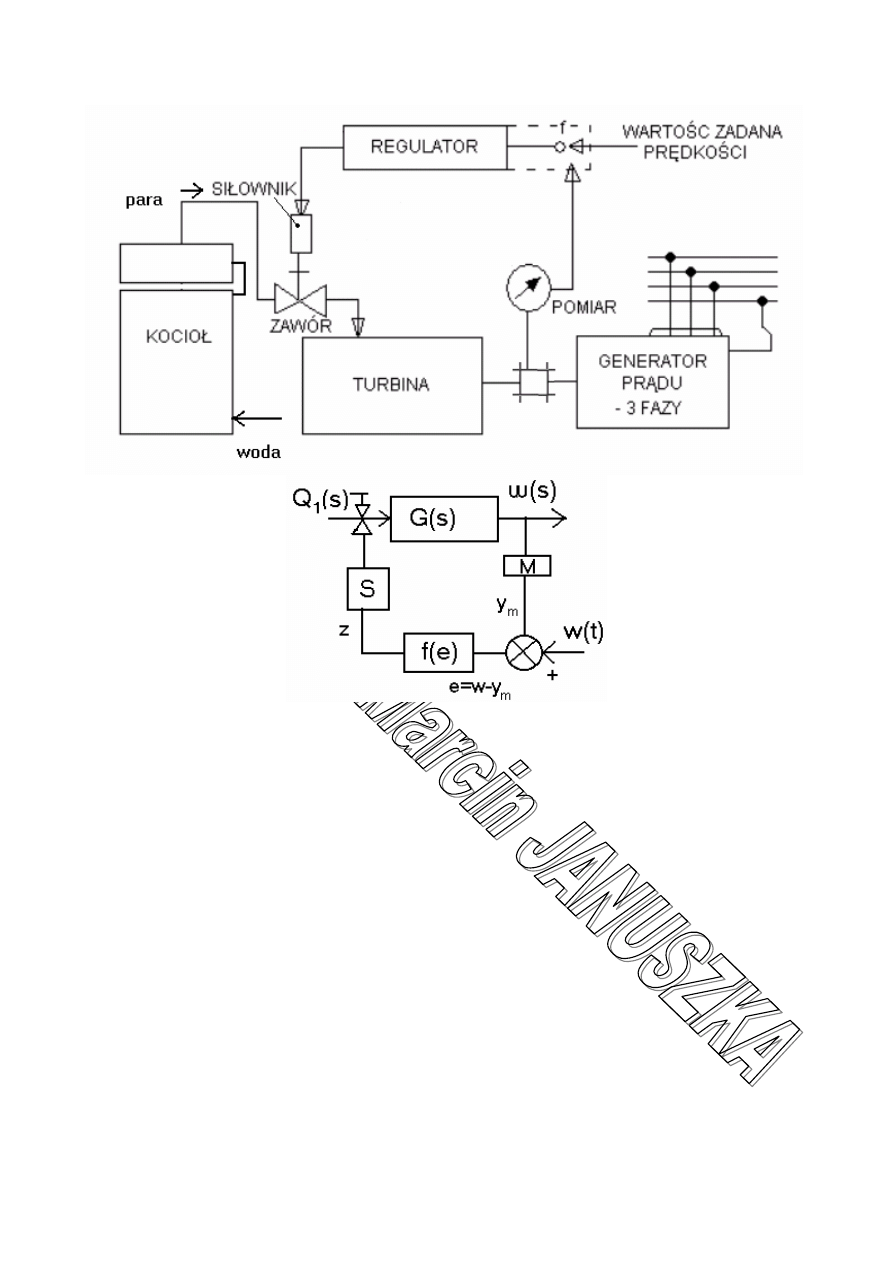
Sterowanie automatyczne w układzie zamkniętym:

z(t)=f [e(t)]

e(t)=w(t)·y

m

(t)

o

Element układu automatyki

o

Człon układu automatyki

Blok układu automatyki –
Schemat w postaci prostokąta, w którym za pomocą odcinków ze strzałkami oznaczono
wejście i wyjście oraz tor i kierunek przekazywania sygnału.

o

Prosty człon układu automatyki

o

Złożony człon układu automatyki –
To człon, który obejmuje kilka członów prostych, a przetwarzanie sygnału
wejściowego na sygnał wyjściowy następuje wielokrotnie. Człony proste i złożone
dzieli się na urządzenia: pomiarowe, wzmacniające, sumacyjne i nastawcze.

Tor oddziaływań –
To tor przepływu sygnału w układzie schematu blokowego układu automatyki,
przedstawionego poprzez bloki członów prostych układu połączonych zgodnie ze strukturą
modelowanego układu automatyki.

o

Łącza –
Elementy łączące, nie przekazują sygnału o zmienionej wartości np. przewody
elektryczne, rury, złączki.

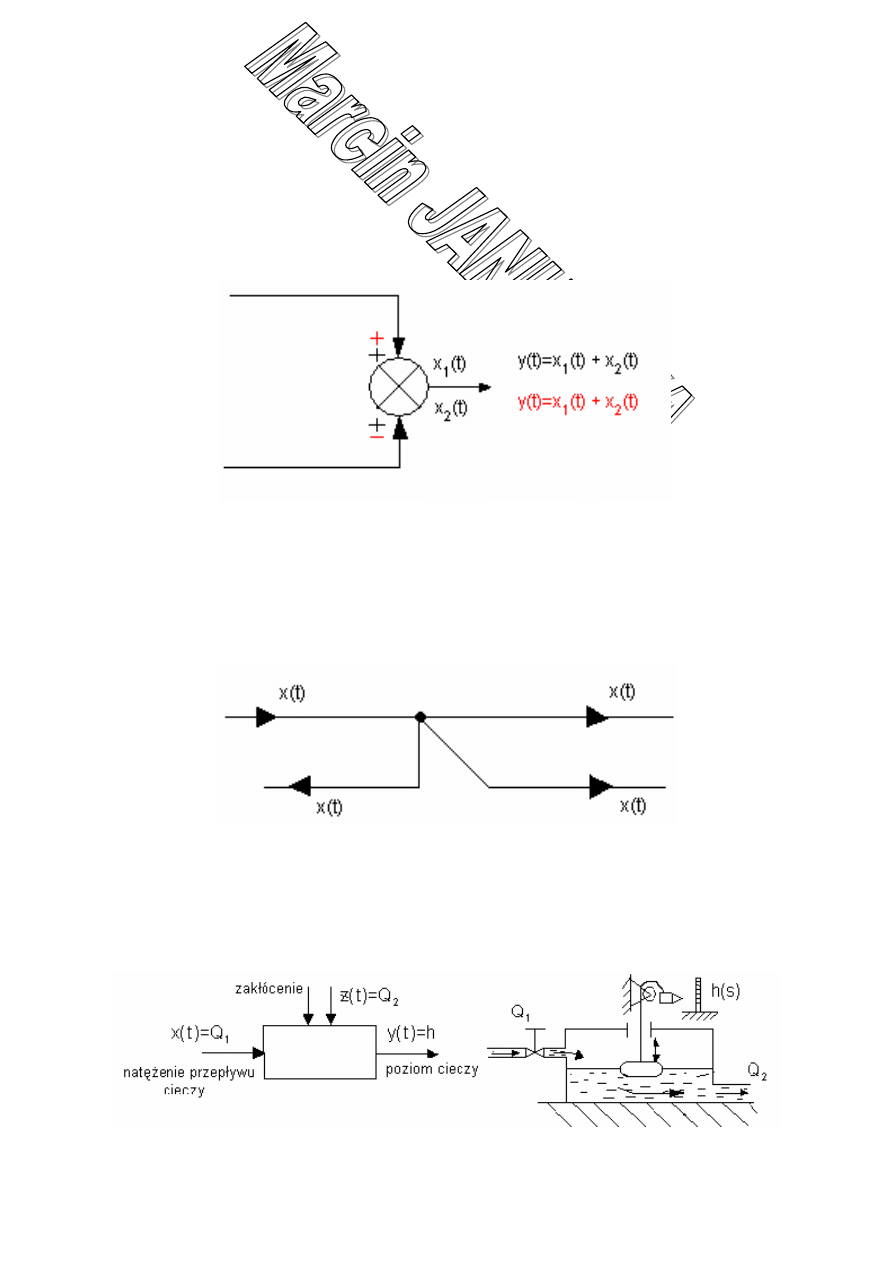
Węzeł sumujący (sumacyjny)–
To węzeł układy automatyki, utworzony przez człon sumujący, posiadający co najmniej
dwa wejścia i jedno wyjście, przy czym wielkości wejściowe nie ulegają zmianie, jedynie
dodają się do siebie algebraicznie.

)

(

)

(

1

t

x

t

y

n

i

i

i

∑

=

=

=

Węzeł zaczepowy (rozgałęziony) –
Jest to takie rozgałęzienie w torze oddziaływań (torze przepływu sygnału), do którego nie
stosuje się reguł dodawania lub odejmowania

Sprzężenie zwrotne –
To połączenie w torze oddziaływań, umożliwiające przepływ sygnału reprezentacyjnego
wielkość wyjściową y (wielkość regulowaną) do węzła sumacyjnego celem porównania jej
z sygnałem reprezentującym wartość wielkości zadanej w i wywołanie oddziaływania na
urządzenie nastawcze na drodze sygnału wejściowego x do obiektu.

Układ bez sprzężenia zwrotnego

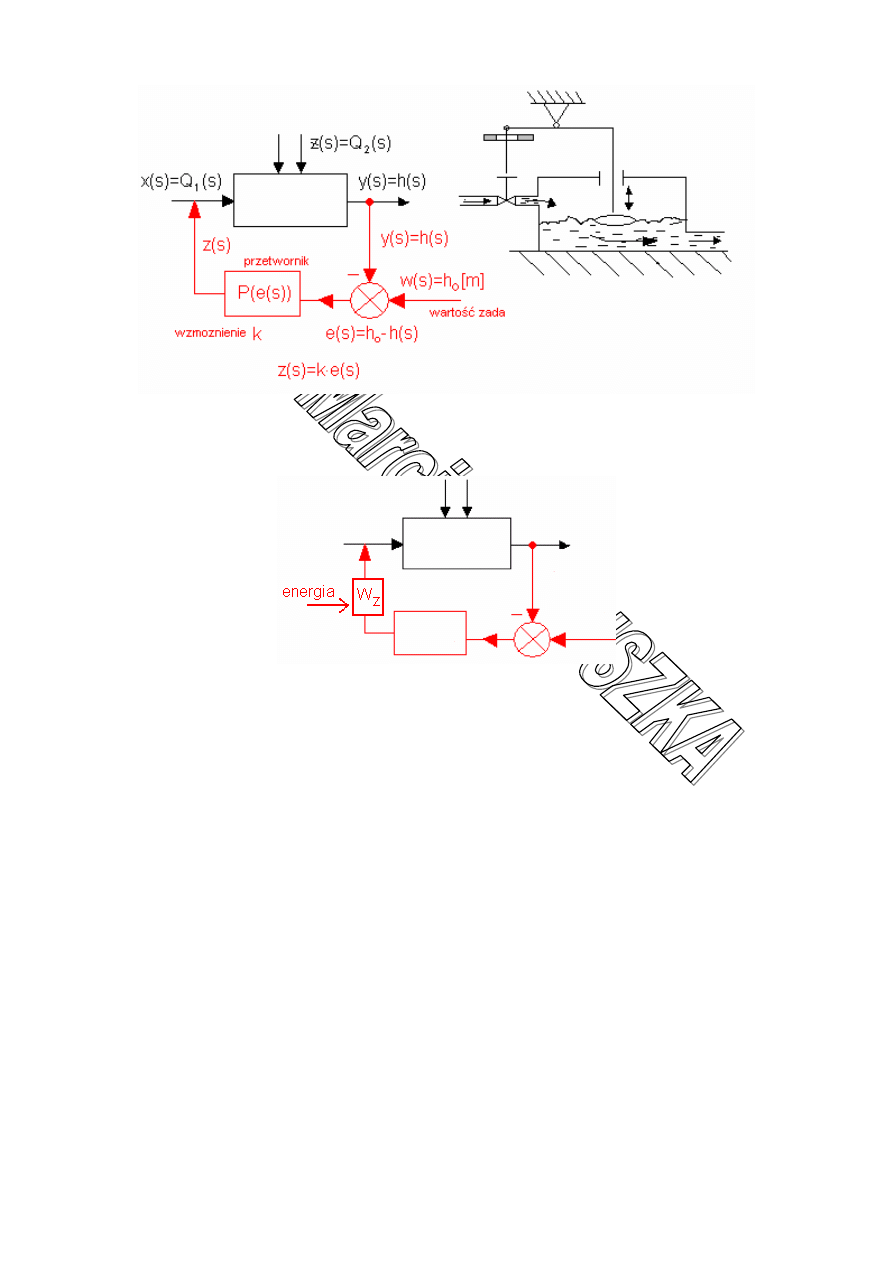
Układ ze sprzężeniem zwrotnym

Czasem należy dodać energię z zewnątrz bo siła tarcia w zaworze w powyższym
przypadku może być większa od siły wyporu suwaka:

Sprzężenie zwrotne ujemne –
To takie sprzężenie zwrotne, w którym węzeł sumujący dokonuje odejmowania wartości
sygnału wielkości regulowanej od wartości sygnału wielkości zadanej.

Sprzężenie zwrotne dodatnie –
To takie sprzężenie zwrotne, w którym węzeł sumujący dokonuje dodawania wartości
sygnału wielkości regulowanej od wartości sygnału wielkości zadanej.

WYKŁAD 3

Podział układów automatycznej regulacji:

a) ze względu na tor oddziaływań:

• otwarte

• zamknięte

b) ze względu na charakter wielkości zadanej:

• układ regulacji stałowartościowej

• układ regulacji programowej

• układ regulacji nadążnej (śledzący)

• układ regulacji ekstremalnej

• układ regulacji adaptacyjnej

• układy rozgrywające

c) ze względu na model rzeczywistości:

• liniowe

• nieliniowe

• dyskretne

• ciągłe

• dyskretno-ciągłe

• stacjonarne

• niestacjonarne

• o parametrach skupionych

• o parametrach rozłożonych w sposób ciągły

• zdeterminowane

• stochastyczne

d) ze względu na rodzaj układów sterowania

• mechaniczne

• hydrauliczne

• pneumatyczne

• elektryczne

• elektroniczne

• mieszane

e) ze względu na znajomość modelu obiektu i zależność jego parametrów od

zakłóceń:

• serwomechanizmy

• układy regulacji przemysłowej

f) ze względu na liczbę zmiennych regulowanych

• układy o jednej zmiennej regulowanej

• układy o wielu zmiennych regulacji

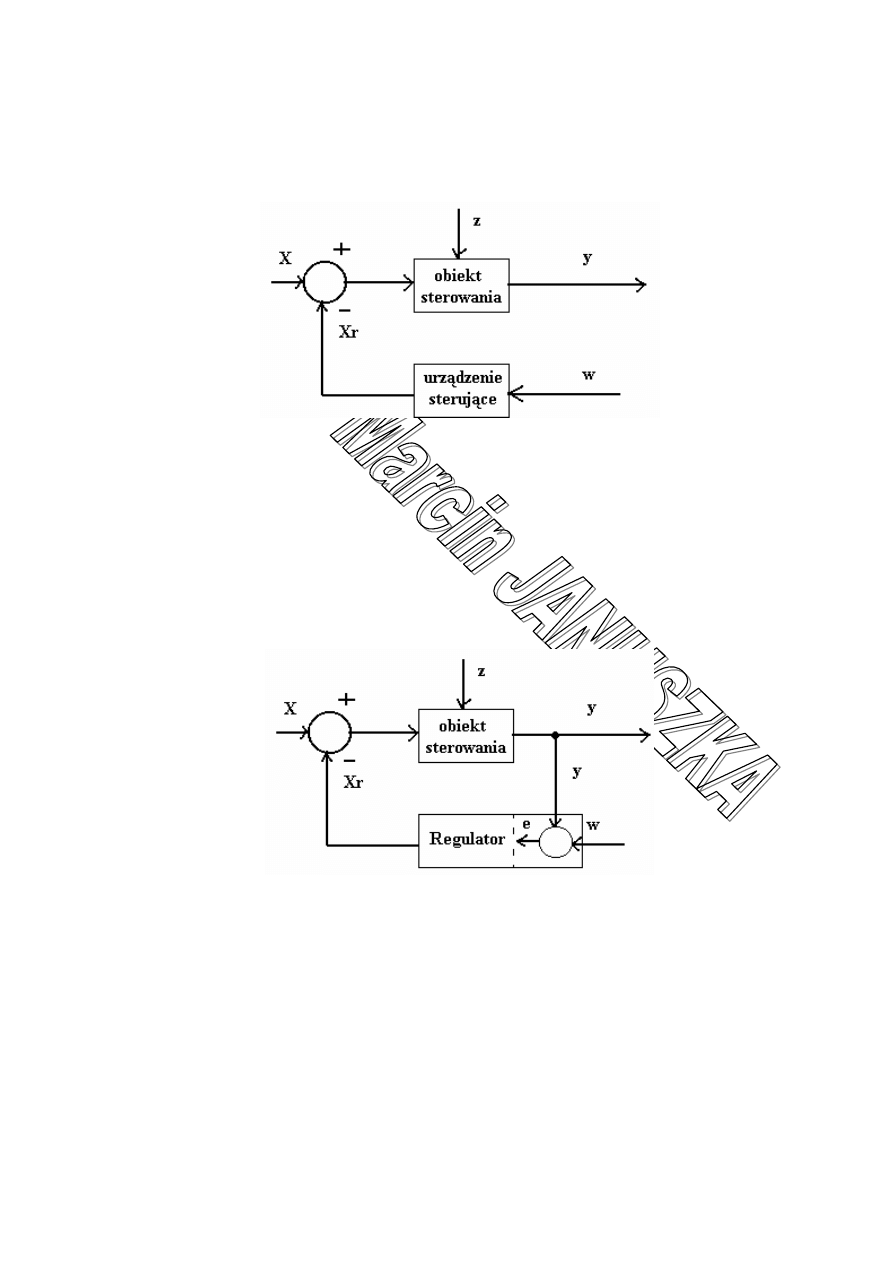
ad a) ze względu na tor oddziaływań

•

Otwarty układ sterowania –

To taki układ, w którym urządzenie sterujące nie oddziaływuje na wielkości sterowane
w obiekcie (brak sprzężenia zwrotnego)

x - sygnał wejściowy
y - sygnał wyjściowy
w - wartość zadana wielkości sterowanej
X

r

- sygnał sterujący

Z - zakłócenia

•

Zamknięty układ sterowania (układ automatycznej regulacji) –

To taki układ, w którym na urządzenie sterujące oddziałują wielkości sterowane w
obiekcie (występuje sprzężenie zwrotne- warunek stabilności). W takim przypadku
urządzenie sterujące nazywa się regulatorem.

e – błąd regulacji (e=w-y)

Cechy układu automatycznej regulacji:

• zamknięta pętla (obwód) oddziaływań elementów tworzących układ

• jednobieżność przepływu sygnału w torze oddziaływań

• ujemne

sprzężenie zwrotne w torze oddziaływań

• stała gotowość układu do działania

ad b) ze względu na charakter wielkości zadanej:

•

Układ regulacji stałowartościowej

To taki układ gdzie wartość sygnału zadanego w(t) jest stała

•

Układ regulacji programowej

z góry znany przebieg wartości zadanej wielkości regulowanej (wprowadzamy program
zmian wartości zadanej np.: w przypadku klimatyzacji możemy ustawić inną
temperaturę w domu w momencie gdy jesteśmy w nim, inną gdy śpimy i inną gdy nas
nie ma- „programujemy klimatyzator”)

•

Układ regulacji nadążnej (śledzący)

Gdy wartość nie jest stała, zmienia się w sposób nieznany z góry, a jej przebieg
powstaje w wyniku pomiaru przebiegu innego sygnału, pochodzącego spoza układu

•

Układ regulacji ekstremalnej

Taki układ, który realizuje stale ekstremalny poziom wielkości regulowanej (tak
prowadzić proces, aby funkcja podlegająca regulacji osiągała maksimum lub minimum
np. minimalne zanieczyszczenie, maksymalna moc)

•

Układ regulacji adaptacyjnej

Taki układ, w którym algorytm sterowania ulega zmianie, realizując pożądane działanie
układu, mimo zmian własności obiektu sterowania oraz zmian oddziaływań
zewnętrznych.

ad c) ze względu na model rzeczywistości:

•

Liniowy układ sterowania

Układ, którego model matematyczny ma postać liniowych równań różniczkowych,
całkowych, różniczkowo-różnicowych bądź operatorowych.

•

Nieliniowy układ sterowania

Układ, którego model matematyczny ma postać nieliniowych równań różniczkowych,
całkowych, różniczkowo-różnicowych bądź operatorowych.

•

Dyskretny układ sterowania

Taki układ sterowania, który można opisać równaniami różniczkowo-róznicowymi.

•

Ciągły układ sterowania

Taki układ sterowania, który można opisać równaniami różniczkowymi.

•

Dyskretno-ciągły układ sterowania

Taki układ sterowania, który można opisać równaniami różniczkowymi oraz
różniczkowo-różnicowymi

•

Stacjonarny układ sterowania

Taki układ sterowania, którego parametry można przedstawić w postaci stałych
wielkości fizykalnych niezmiennych w czasie

(parametry układu nie zależą od czasu).

•

Niestacjonarny układ sterowania

Taki układ sterowania, którego parametry można przedstawić w postaci wielkości
fizykalnych zmiennych w czasie

(parametry układu zależą od czasu).

•

Układy sterowania o parametrach skupionych

Taki układ sterowania, którego parametry są stałe lub zmienne w czasie, lecz nie są
funkcjami współrzędnych przestrzennych układu.

•

Układy sterowania o parametrach rozłożonych w sposób ciągły

Taki układ sterowania, którego parametry są stałe lub zmienne w czasie, i są funkcjami
współrzędnych przestrzennych układu.

•

Zdeterminowany układ sterowania

Taki układ sterowania, którego parametry fizykalne oraz wymuszenia są funkcjami
stałymi lub zdeterminowanymi funkcjami czasu i zmiennej stanu układu.

•

Stochastyczny układ sterowania

Taki układ sterowania, którego parametry fizykalne oraz wymuszenia są funkcjami
losowymi o znanych, bądź zadanych charakterystykach probabilistycznych.

ad e) ze względu na znajomość modelu obiektu i zależność jego param. od zakłóceń:

•

Serwomechanizm

Urządzenia mechaniczne, które śledzą pewną wielkość np. prędkość obrotową i
przekazują w postaci innych wielkości.

Opis analityczny członów i układów:

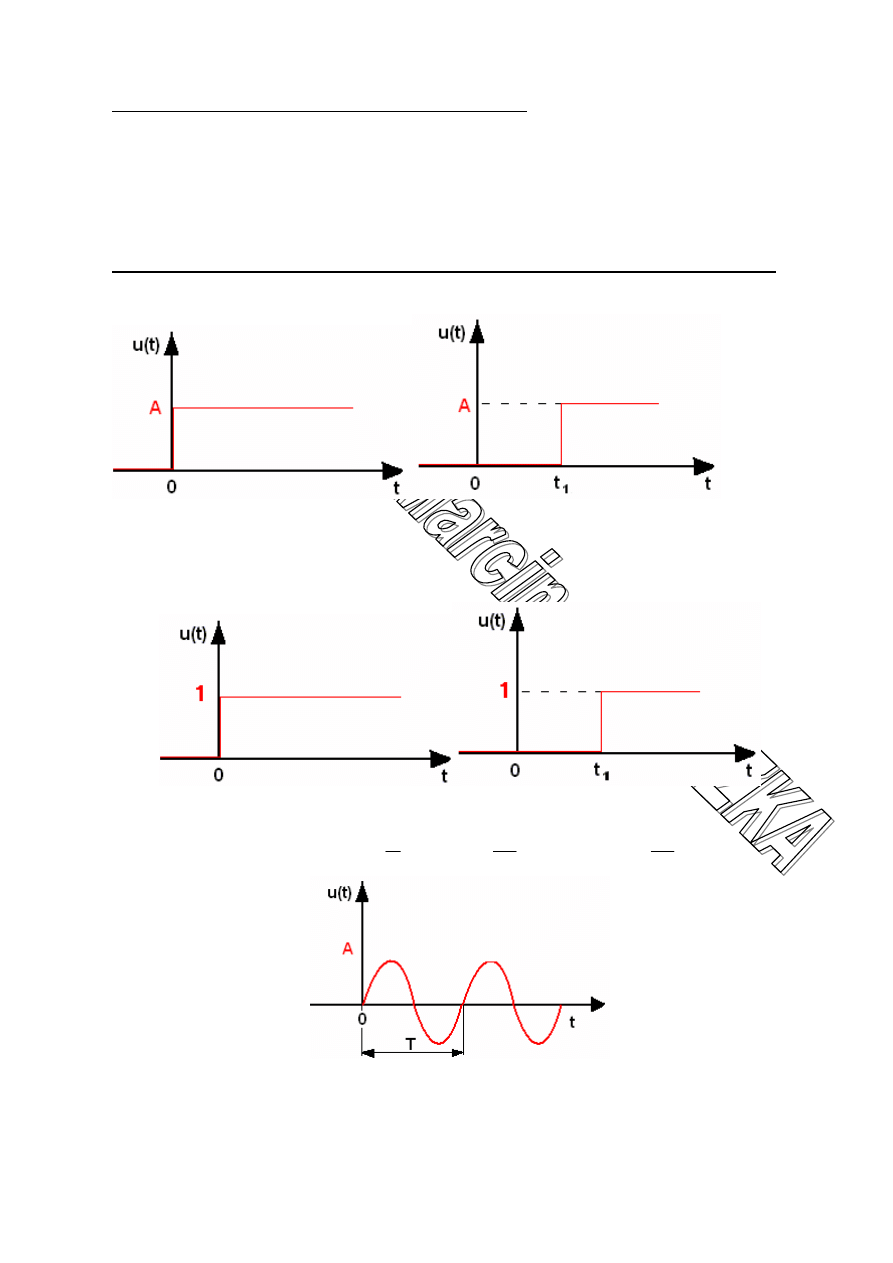
Klasyfikacja wymuszeń:
Wymuszenia – sygnały wejściowe doprowadzane do obiektu; Zarówno w badaniach
teoretycznych modeli układów automatycznej regulacji, jak i w badaniach
doświadczalnych rzeczywistych układów stosuje się powszechnie standardowe funkcje
wymuszające.

Do podstawowych funkcji standardowych stosowanych jako wymuszenia używa się:

Wymuszenia skokowe

u(t)=0 przy t<0

u(t- t

1

)=0 przy t<t

1

u(t)=A przy t≥0 u(t-

t

1

)=A przy t≥t

1

Wymuszenia skokowe jednostkowe (funkcja Heaviside’a) –
(skok jednostkowy) to wymuszenie skokowe przy A=1, może być przesunięta do t

1

.

Wymuszenie harmoniczne zmienne –

)

sin(

)

(

t

A

t

u

⋅

⋅

=

ω

]

[

1

s

f

T

=

]

[

2

Hz

f

π

ω

=

Æ

]

/

[

2

sek

rad

T

ω

π

=

Może być przesunięta w czasie

u(t)=w(t-t

1

) A·sinω(t- t

1

)

1

1

1

1

t

t

1

)

t

(

0

)

t

(

{

≥

<

=

−

=

−

t

t

przy

przy

t

w

t

w

Jeżeli A=1 to harmonicznie zmienna jednostkowa

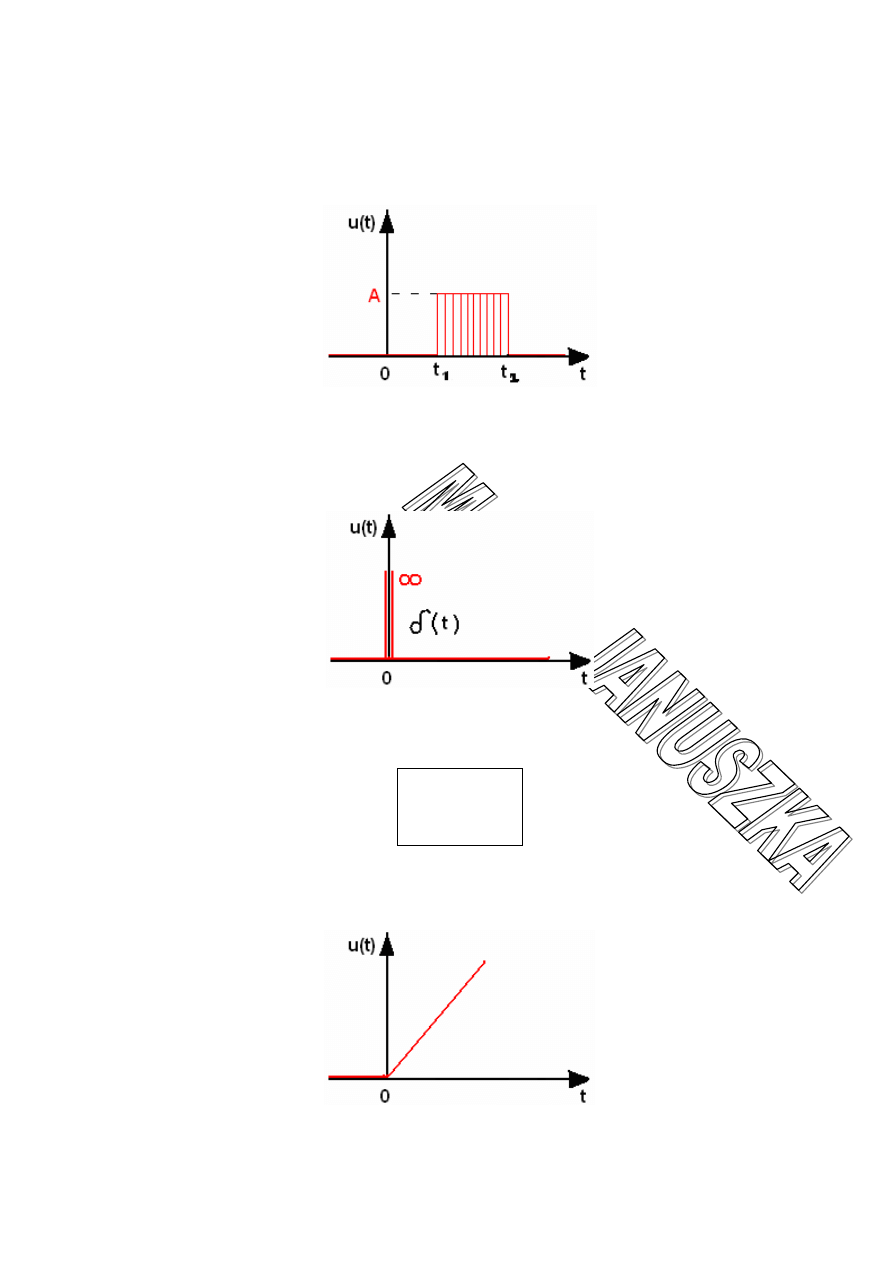
WYKŁAD 4

Impuls prostokątny –
Jest to różnica dwóch wymuszeń skokowych o równych wartościach skoku A

t

2

- t

1

= ∆t

Impuls prostokątny jednostkowy –
gdy A=1

Impuls jednostkowy (funkcja Diraca) –

0

0

)

(

0

)

(

{

=

≠

∞

→

=

t

t

przy

przy

t

t

δ

δ

Przy czym pole impulsu jest stałe równe 1

∫

+∞

=

−∞

=

=

t

t

dt

t

1

)

(

δ

Wymuszenie może mieć postać:

• funkcji

liniowej:

• może być paraboliczne:

Wymuszenie przypadkowe (losowe) –
Jest to wymuszenie szumem o zadanych charakterystykach losowych

Do celów analizy członów i układów dynamicznych najczęściej stosuje się wymuszenia:
skokowe jednostkowe, harmonicznie zmienne i w postaci impulsu jednostkowego.

ZASADY MODELOWANIA MATEMATYCZNEGO

Bardzo często zamiast badać rzeczywisty układ, bada się jego model

matematyczny. Model matematyczny buduje się poprzez opis analityczny tzw. modelu
fenomenologicznego (zjawiskowego), czyli modelu uzyskanego poprzez maksymalne
możliwe uproszczenie obiektu modelowania z uwagi na klasę zjawisk, które mają
podlegać obserwacji. Jeśli to tylko możliwe należy dokonać redukcji stopni swobody
układu, linearyzacji jego parametrów, przyjęcia założeń o stacjonarności układu i jego
ciągłości.

Najczęstszym sposobem budowania modelu matematycznego jest opis zjawisk

fizykalnych w układzie albo zastosowanie któregoś z narzędzi analitycznych np. równań
Lagrangea II rodzaju. Najczęściej używanym modelem matematycznym jest model w
postaci równań różniczkowych zwyczajnych. Można je uzyskać poprzez stosowanie praw
fizyki odpowiednich w danej klasie zjawisk.

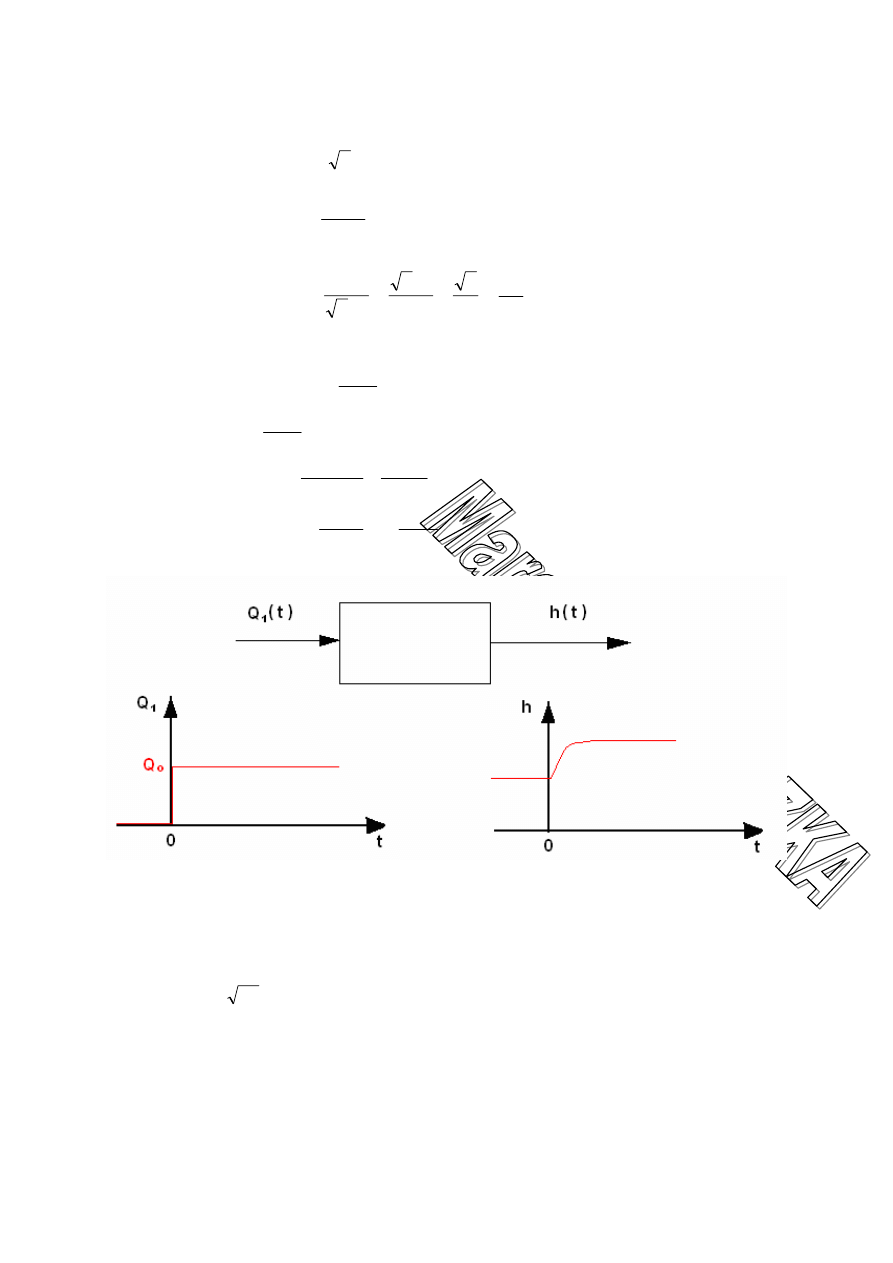
Przykład:

)

(

1

t

Q

]

[

3

s

m

- natężenie przepływu cieczy na wlocie do zbiornika

(wielkość wejściowa x(t)) Q

1

(t)>0

)

(

2

t

Q

]

[

3

s

m

-

natężenie przepływu cieczy na wypływie ze zbiornika

)

(t

h

- wysokość poziomu cieczy w zbiorniku

]

[m

(wielkość wyjściowa, odpowiedź układu y(t)) h(t)<0

s

-

stałe, niezależne od wysokości h, pole powierzchni zwierciadła

cieczy

]

[

2

m

)

(t

v

-

objętość cieczy w zbiorniku, przy czym

]

[

3

m

∆v(t)=s∆h(t), a przy ∆tÆdt

∆v(t)=dv(t), oraz ∆h(t)=dh(t), można wtedy zapisać:

dv=SD,

natomiast:

h

a

t

Q

=

)

(

2

(wynika z prawa swobodnego wypływu) lub

)

(

)

(

2

h

R

h

t

Q

h

=

, gdzie:

a

h

a

h

h

h

a

h

h

h

R

h

=

⋅

⋅

=

⋅

=

)

(

]

[

2

m

s

a – opór wypływu

Z bilansów przepływów wynika:

dt

t

dv

Q

Q

)

(

2

1

+

=

, gdzie:

dt

t

dv )

(

- natężenie przyrostu objętości cieczy w zbiorniku, zatem:

dt

t

sdh

t

h

R

h

Q

h

)

(

))

(

(

1

+

=

dt

t

dh

s

h

R

t

h

t

Q

h

)

(

)

(

)

(

)

(

1

⋅

+

=

Równanie różniczkowe przepływu cieczy przez zbiornik ze swobodnym wypływem.

Przekształcenia Laplace’a

Opisuje związek między funkcją czasu f(t), zwaną oryginałem, a odpowiadającą jej funkcją
zmiennej zespolonej F(s), zwanej transformatą zmiennej zespolonej s, przy czym s=a+jb,
gdzie a,b

∈

R,

1

−

=

j

. Funkcję F(s) nazywa się także obrazem funkcji f(t).

Zachodzi związek:

∫

∞

−

=

=

0

)

(

)

(

)]

(

[

dt

e

t

f

s

F

t

f

L

st

, gdzie:

e- jest podstawą logarytmu naturalnego


Warunki istnienia transformaty Laplace’a:

1. f(t)=o przy t<0
2. f(t) jest określona, jednowartościowa i posiada pochodną przy t>0
3. istnieje taka liczba rzeczywista c, że spełniona jest nierówność:

∫

∞

−

∞

<

0

)

(

dt

e

t

f

ct

Aby transformata funkcji f(t) była określona wystarczy żeby całka w postaci:

∫

∞

−

0

)

(

dt

e

t

f

st

istniała dla pewnego zbioru wartości s, przy czym dla pozostałych pozostałych całka może
nie istnieć. Jeżeli ta całka nie istnieje dla żadnej wartości s przekształcenie Laplace’a jest
niemożliwe.

Tablice transformat Laplace’a – literatura

Podstawowe twierdzenia:

1. transformata iloczynu stałej a przez funkcję f(t)

)

(

)

(

s

aF

t

af

⇔

2. transformata sumy funkcji:

∑

∑

=

=

⇔

n

i

n

i

i

i

s

F

t

f

1

1

)

(

)

(

3. transformata pochodnej funkcji f(t)

dt

t

df

t

)

(

)

(

=

ψ

•

∫

∫

∞

∞

−

−

=

=

=

0

0

)

(

)

(

)]

(

[

dt

dt

df

e

dt

t

e

s

t

L

st

st

ψ

ψ

ψ

całkując przez części zakładając fizykalną realizowalność funkcji ψ(t), uzyskuje
się:

)

0

(

)

(

)

(

f

s

sF

s

−

=

ψ

, gdzie:

F(0) – jest tak zwaną wartością początkową funkcji f(t), a ściślej jest

prawostronną granicą funkcji f(t) przy tÆ0

+

• uogólnienie:

n

n

dt

t

f

d

t

)

(

)

(

=

ψ

)

0

(

...

)

0

(

'

)

0

(

)

(

)

(

)

1

(

2

1

−

−

−

−

−

−

−

=

n

n

n

n

f

f

s

f

s

s

F

s

s

ψ

4. Transformata całki funkcji:

∫

=

t

dt

t

f

t

0

)

(

)

(

ϕ

dt

t

d

t

f

)

(

)

(

ϕ

=

,

0

)

0

(

=

ϕ

)

(

)

(

s

s

s

F

φ

=

)

(

1

)

(

s

F

s

s

=

φ

4.1 Transformata całki funkcji jest równa transformacie tej funkcji podzielonej przez
operator s.

WYKŁAD 5

ZASTOSOWANIE PRZEKSZTAŁCEŃ LAPLACE’A DO ROZWIĄZYWANIA

RÓWNAŃ RÓŻNICZKOWYCH