1

Podstawy sztucznej inteligencji - PROJEKT - Rok akad. 2014/2015

Konrad Rugała

Krzysztof Sobieraj

Temat:

Działanie pojedynczego neuronu

13.11.2014

Grupa ćwiczeniowa: 3

Zadanie 1.

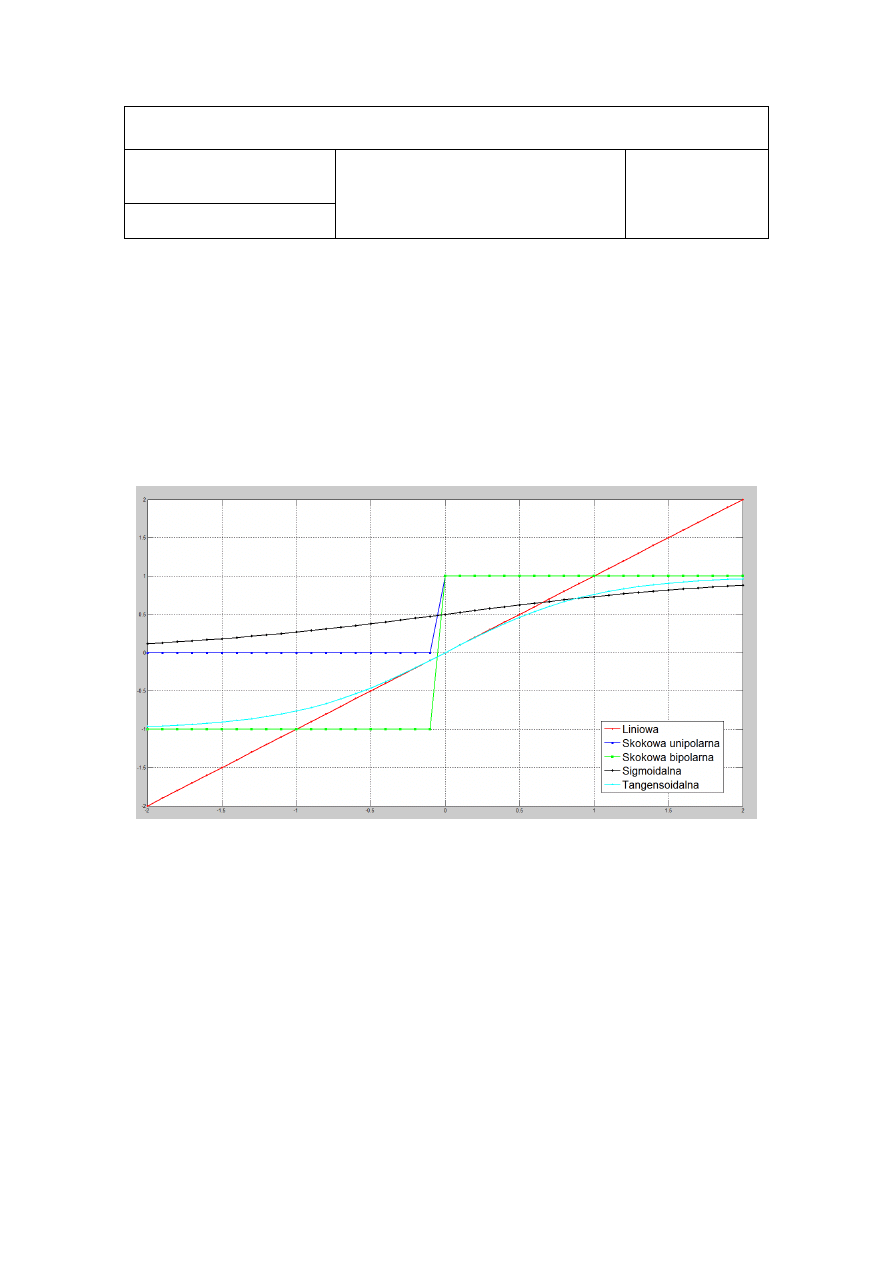
Celem zadania pierwszego było zapoznanie się z funkcjakmi aktywacji sztucznego neuronu. Przy
użyciu oprogramowania MatLab należało narysować popularne funkcje aktywacji:



Liniowa



Progowa (unipolarna)



Znaku (signum, bipolarna)



Sigmoidalna



Tangensoidalna

Wykres powyżej przedstawia wszystkie wymienione funkcje narysowane na podstawie ich wartości
dla argumentów z przedziału <-2, 2> przy kroku 0.1.

2

Zadanie 2.

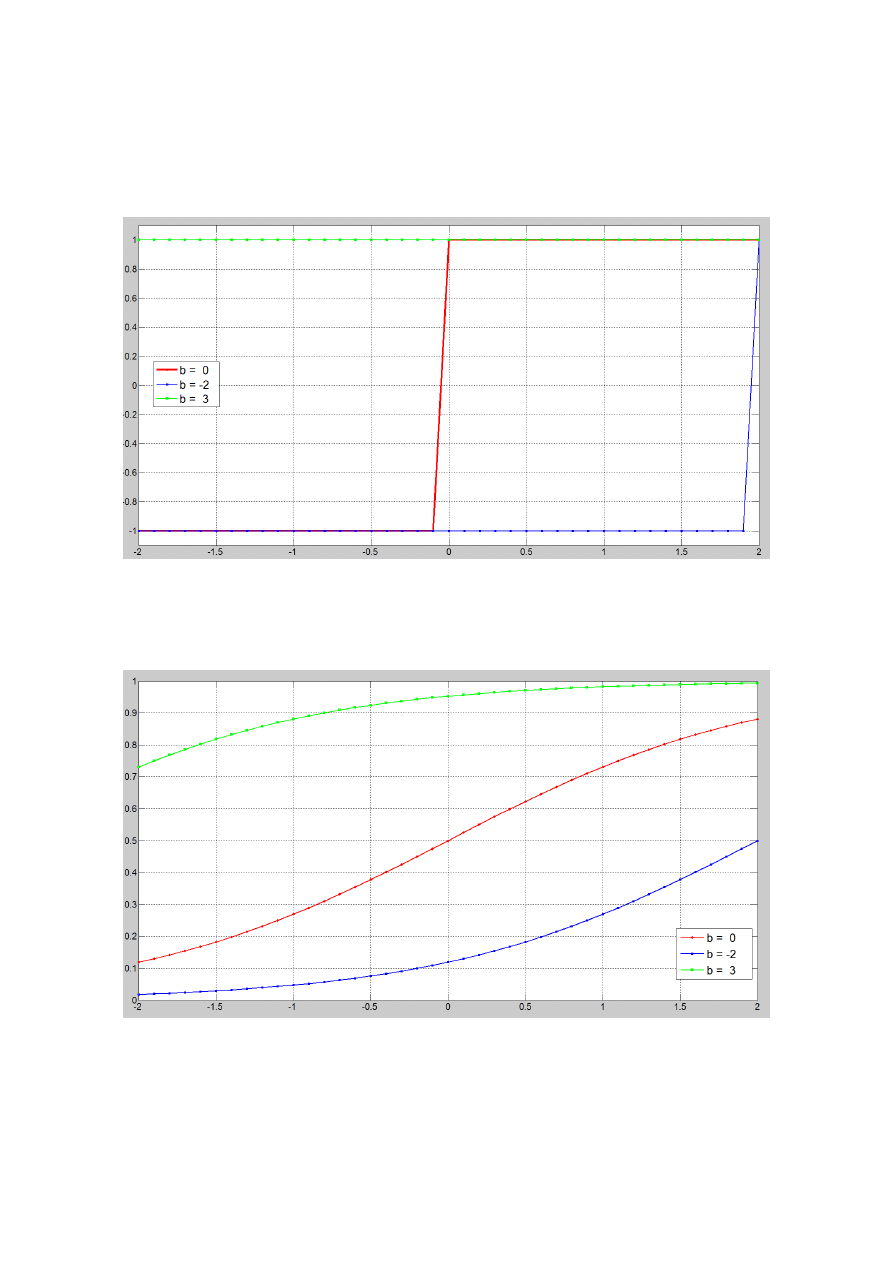
W tym zadaniu należało zapoznać się z wpływem sygnału progowego (bias) na przebieg funkcji
aktywacji ciągłej i nieciągłej. Dla każdej z funkcji należało wykonać trzy wykresy z wartościami bias
odpowiednio -2, 0, 3.

Na wykresie przedstawiliśmy funkcję skokową bipolarną. Skok funkcji oznaczonej kolorem zielonym
znalazł się poza przedziałem. Jak łatwo zobaczyć na przedstawionym wykresie współczynnik bias
przesuwa funkcję skokową wzdłuż osi OX. Dodatnie wartości przesuwają w lewa, natomiast ujemne
w prawo.

Podobnie jak w przypadku funkcji nieciągłej, zmiana biasu powoduje przesunięcie funkcji
sigmoidalnej. Nie jest to najlepiej widoczne na powyższym wykresie dlatego wykonaliśmy wykres
dodatkowy, który lepiej obrazuje przebieg funkcji.

3

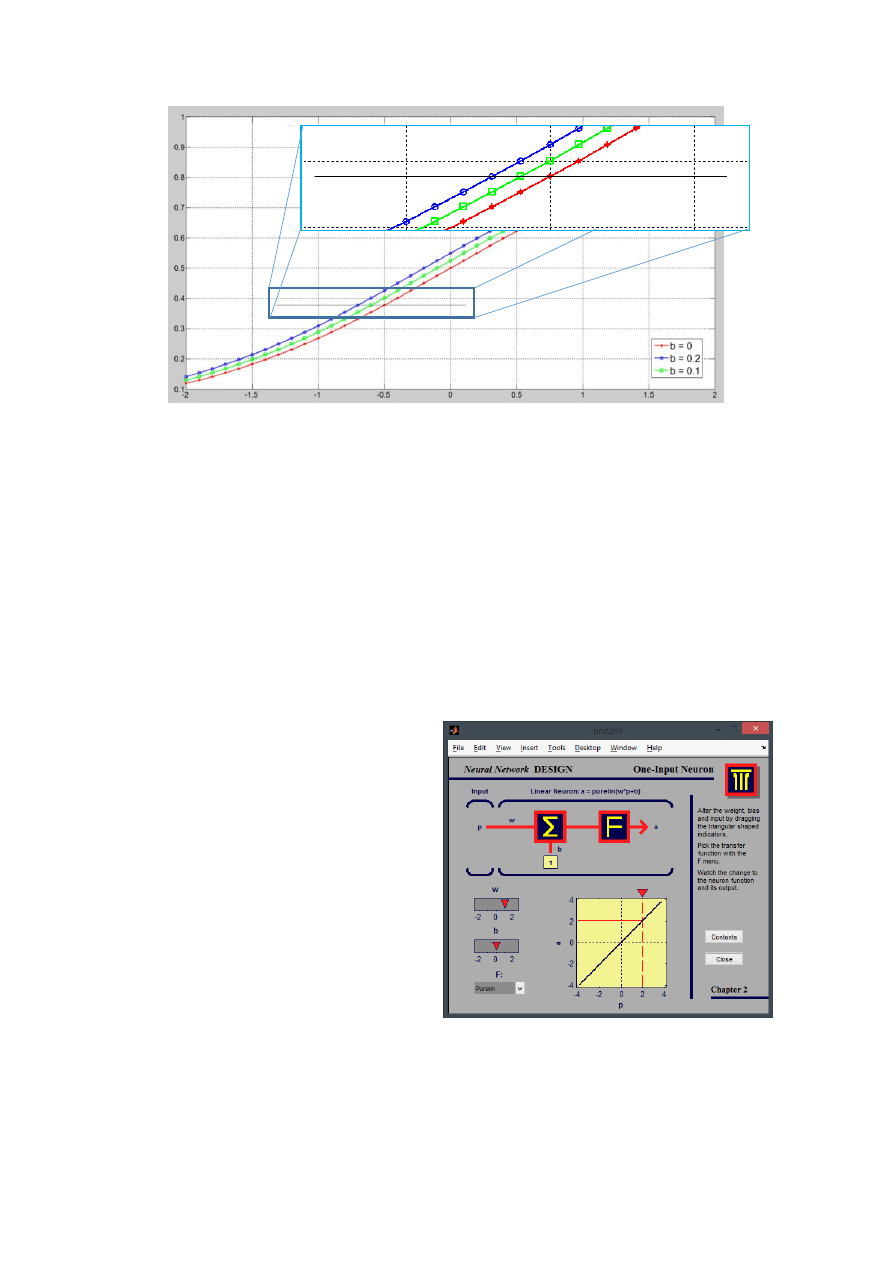
Na powyższym wykresie zmniejszyliśmy bias na małą wartość. Punkty o takiej samej wartości zostały
przecięte czarną linią żeby zobrazować przesunięcie wykresu.

Zadanie 3.

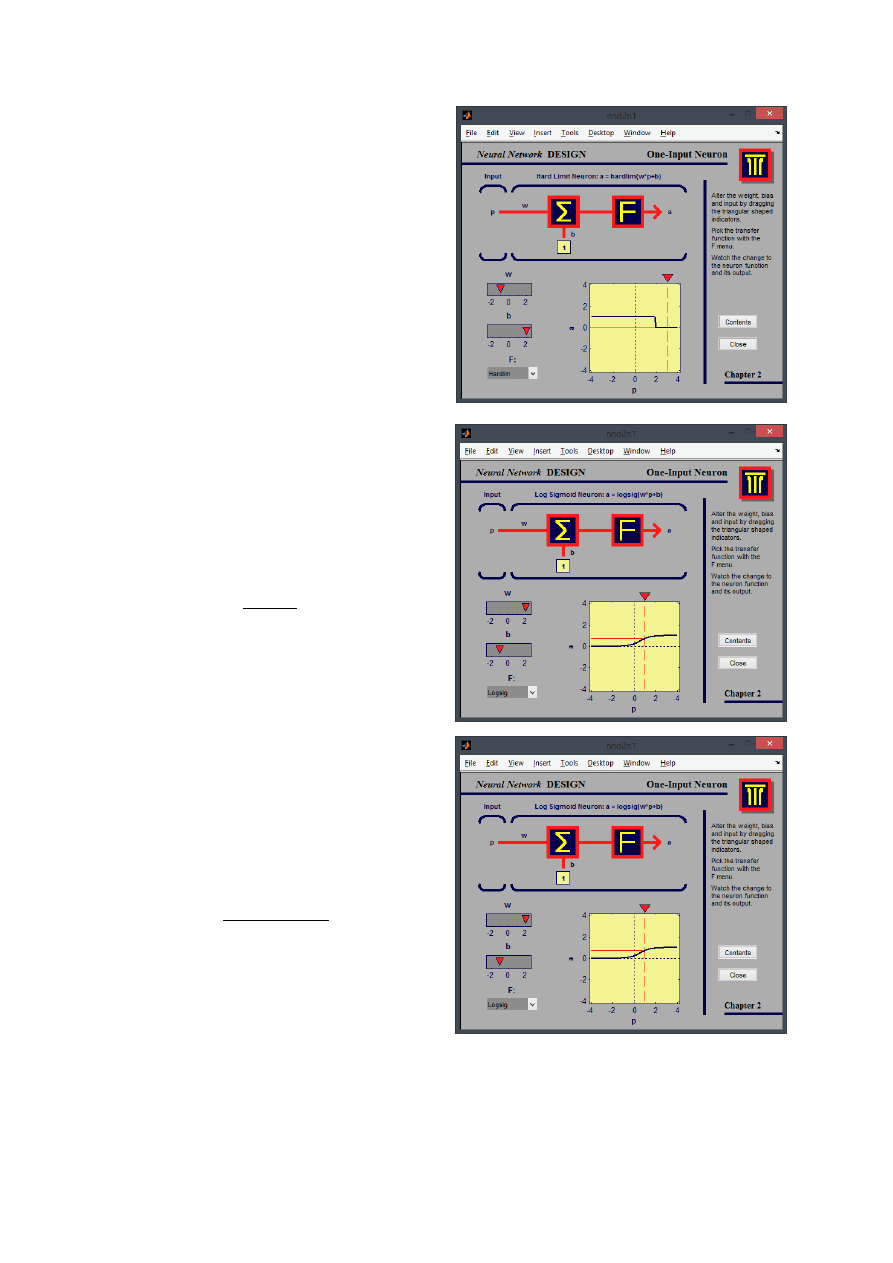
W zadaniu trzecim należało użyć programiku nnd2n1. Program ten obrazuje działanie pojedynczego
neuronu. Po krótkiej analizie działania programu doszliśmy do następującyhc wniosków:



Waga zmienia kierunek dla funkcji liniowej



Duże wagi zwiększają odległości między kolejnymi wartościami funkcji



Funkcje przejścia nieciągłe mają bardzo mały zbiór wartości



Wartość progowa przesuwa wykres funkcji wzdłuż osi OX.

Kolejnymi etapami zadania było ustawienie wykresu na podane parametry, zrobienie zrzutu ekranu
oraz obliczenie wartości na wyjściu neuronu. Poniżej prezentujemy zebrane wyniki:

Funkcja: liniowa
w = 1
b = 0

Przykład obliczeń dla p = 2, a = 1:

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) = 𝑓(1 ∗ 2) = 2

4

Funkcja: skokowa unipolarna
w = -1
b = 2

Przykład obliczeń dla p = 3:

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) = 𝑓(−1 ∗ 3 + 1) = 0

Funkcja: sigmoidalna
w = 2
b = -1

Przykład obliczeń dla p = 1:

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) = 𝑓(2 ∗ 1 − 1) =

= 𝑓(1) =

1

1 + 𝑒

−𝟏

≈ 0,26894

Funkcja: tangensoidalna
w = -2
b = 1

Przykład obliczeń dla p = 1:

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) = 𝑓(−2 ∗ 1 + 1) =

= 𝑓(−1) =

2

1 + 𝑒

((−2)∗(−𝟏))

≈ 0,96403

Wyniki odczytane z wykresu nie są dość dokładne ze względu na nie precyzyjną skalę, pomimo to
wyniki te są bardzo zbliżone do wyników otrzymanych metodą analityczną.

5

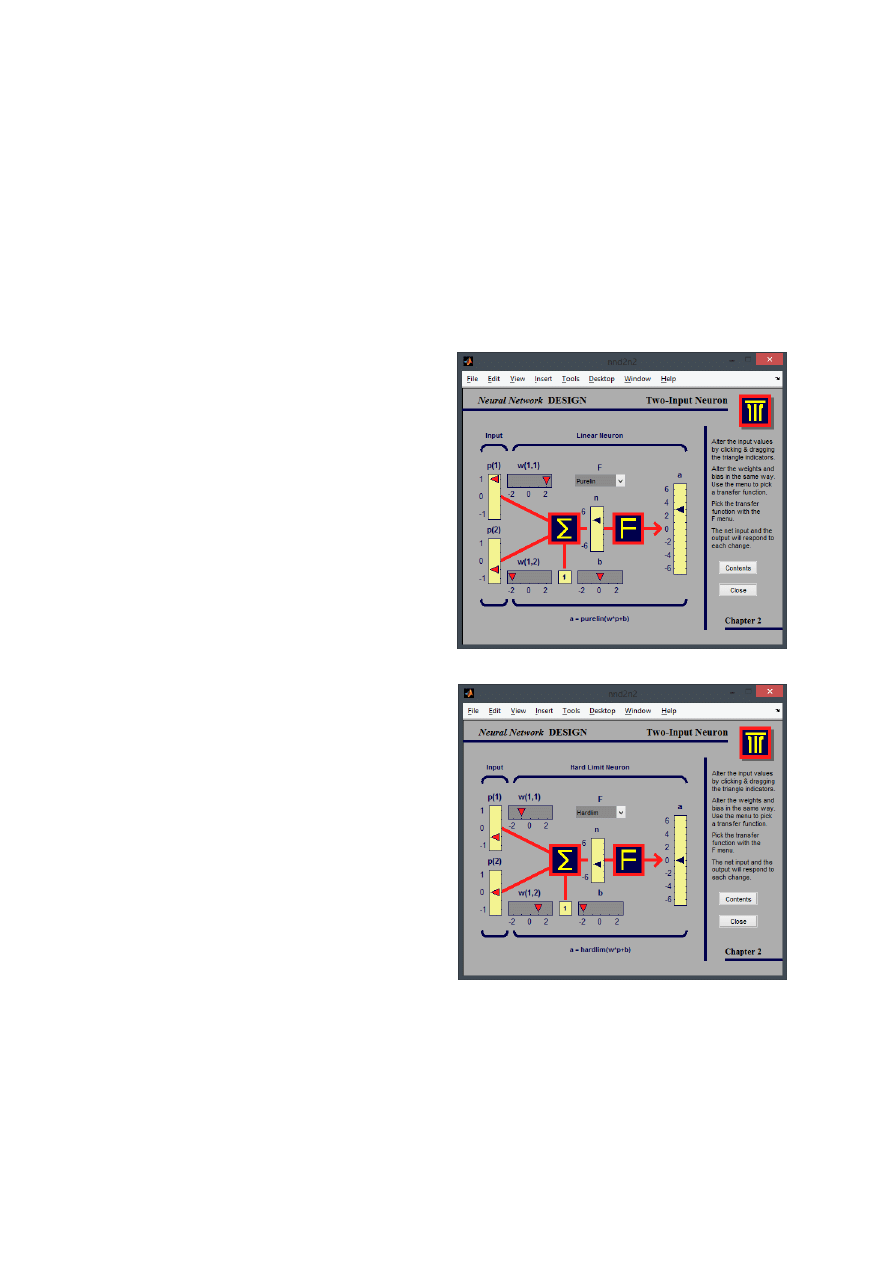
Zadanie 4.

W zadaniu trzecim należało użyć programiku nnd2n1. Program ten obrazuje działanie pojedynczego
neuronu. Po krótkiej analizie działania programu doszliśmy do następującyhc wniosków:



Jeżeli ustawimy wagę na wartość zero to dana wejściowa nie wpływa na wynik końcowy



Jeżeli wagi są przeciwne, a p(1) = p(2) to wynik jest zależny tylko od biasu

Podobnie jak w zadaniu trzecim należało ustawić neuron na podane parametry, zrobić zrzuty ekranu
oraz obliczyć wartości na wyjściu neuronu. Poniżej prezentujemy zebrane wyniki:

Funkcja: liniowa
w

1

= 2, w

2

= -2

b = 0
p

1

= 1, p

2

= -0,5

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) =

= 𝑓(2 ∗ 1 + (−2) ∗ (−0,5)) = 3

Funkcja: skokowa unipolarna
w

1

= -1, w

2

= 1

b = -2
p

1

= -0.5, p

2

= 0

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) =

= 𝑓(−1 ∗ (−0,5) + 1 ∗ 0 − 2) = 𝑓(−1,5) = 0

6

Funkcja: sigmoidalna
w

1

= 1, w

2

= 0

b = 1
p

1

= 0,5, p

2

= 1

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) =

= 𝑓(1 ∗ 0,5 + 0 ∗ 1 − 1) =

= 𝑓(−0,5) =

1

1 + 𝑒

𝟎,𝟓

≈ 0,92553

Funkcja: tangensoidalna
w

1

= 1, w

2

= -1

b = -2
p

1

= -0.5, p

2

= 0,5

𝑎 = 𝑓 (∑ 𝑤

𝑖

𝑝

𝑖

+ 𝑏

𝑛

𝑖=1

) =

= 𝑓(1 ∗ (−0,5) + (−1) ∗ 0,5 − 2) =

= 𝑓(−3) =

2

1 + 𝑒

((−2)∗(−𝟑))

≈ −0,99505

Wyniki uzyskane po przez symulacje są porównywalne z wynikami uzyskanymi metodą analityczną.
Wykonane przez nas obliczenia są dokładniejsze niż wyniki odczytywane z wykresu.