
KRZYWE STOPNIA DRUGIEGO
Zad 1. Sklasyfikować krzywe:
a)
0
3
12
16
17
12
8
2
2
=
+
−
+
+
−
y
x
y
xy
x
, elipsa
b)
0
7
18
34
7
18
17
2
2
=
+
−
+
−
−
y
x
y
xy
x
, hiperbola,
c)
0
2
2
4
5
2
2
=
−
+
+
+
−
y
x
y
xy
x
, proste przec,
d)
0
2
2
2
2
2
3
2
3
2
2
=
+
−
+
+
+
y
x
y
xy
x
, punkt,
e)
0
54
44
12
11
6
19
2
2
=
+
+
−
+
−
y
x
y
xy
x
,pusty,
f)
0
6
2
2
2
2
2
=
−
−
+
+
y
x
y
x
, okrąg,
g)
0
2
6
7
4
2
=
+
−
+
y
x
x
, parabola,
h)
0
29
14
6
2
2
2
=
+
−
+
+
−
y
x
y
xy
x
, parabola,
i)
0
11
30
20
9
12
4
2
2
=
−
−
+
+
−
y
x
y
xy
x
, pr. równ. j)
0
4
12
4
9
6
2
2
=
+
−
+
+
−
y
x
y
xy
x
, prosta,
k)
0
3
2
4
4
4
2
2
=
+
+
+
+
+
y
x
y
xy
x
, pusty.
Zad 2. Sprowadzić do postaci kanonicznej
a)
0
80
56
32
8
4
5
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
36
9
4
2
2
=
′′
+
′′
y
x
b)
0
4
4
2
4
2
2
2
=
+
+
−
+
+
y
x
y
xy
x
,
)
0
,
0
(
c)
0
175
24
38
24
7
2
=
+
+
−
−
y
x
xy
x
,
1
9
16
2
2
=
′′
−
′′
x
y
d)
0
2
2
4
5
2
2
=
−
+
+
+
−
y
x
y
xy
x
,
0
)
5
34
(
)
34
5
(
2
2
=
′′
−
−
′′
+
y
x
, poste nierównoległe
e)
0
30
40
16
24
9
2
2
=
+
−
+
+
y
x
y
xy
x
,
x
y
′′
−
=
′′
2
2
f)
0
5
6
12
4
4
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
3
4
2
=
′
y
Zad 3. Dana jest krzywa
0
80
56
32
8
4
5
2
2
=
+
−
−
+
+
y
x
y
xy
x
. Znaleźć współrzędne wierzchołków i
ognisk, równania osi i kierownic oraz narysować krzywą w układzie OXY.
Zad 4. Dana jest parabola
0
29
14
6
2
2
2
=
+
−
+
+
−
y
x
y
xy
x
. Znaleźć współrzędne wierzchołka i ogniska,
równanie osi oraz narysować tę parabolę w układzie OXY.
Zad 5. Nie korzystając z teorii niezmienników sprowadzić następujące równania do postaci kanonicznej:
a)
0
1
4
4
2
2
2
=
+
−
+
−
y
x
y
x
,
1
15
64
15
32
2
2
=
′
−
′
y
x
,
b)
0
5
7
2
4
2
=
+
+
−
y
x
y
,
x
y
′
=
′
2
1
2
,
c)
0
13
14
2
3
10
3
2
2
=
−
−
−
+
+
y
x
y
xy
x
,
0
8
2
8
2
2
=
−
′′
−
′′
y
x
.
Zad 6. W układzie OXY znaleźć współrzędne wierzchołków, współrzędne ognisk oraz równania osi,
kierownic i asymptot hiperboli
0
19
16
2
4
2
2
=
−
+
+
−
y
x
y
x
.
Zad 7. W zależności od wartości parametru k sklasyfikować krzywe:
a)
0
1
2
2
6
2
4
2
2
=
+
+
+
+
+
ky
x
y
kxy
x
,
b)
0
4
2
9
12
4
2
2
=
+
+
+
+
−
k
ky
x
y
xy
x
.
Zad 8. Wykazać, że równanie
0
2
2
2
33
23
13
2
22
12
2
11
=
+
⋅
+
⋅
+
⋅
+
⋅
⋅
+
⋅
a
y
a
x
a
y
a
y
x
a
x
a
, gdzie
0
2
22
2
12
2
11
>
+
+
a
a
a
określa okrąg wtedy i tylko wtedy, gdy
0
4
2
<
=
pW
i
w
p
.
Zad 9. Sklasyfikować krzywe
a)
0
5
2
3
3
2
2
=
−
+
−
+
y
x
y
x
,
okrąg
b)
0
4
4
2
2
2
=
−
+
+
y
x
y
x
,
elipsa
c)
0
4
6
8
4
2
2
=
−
−
−
−
y
x
y
x
,
hiperbola
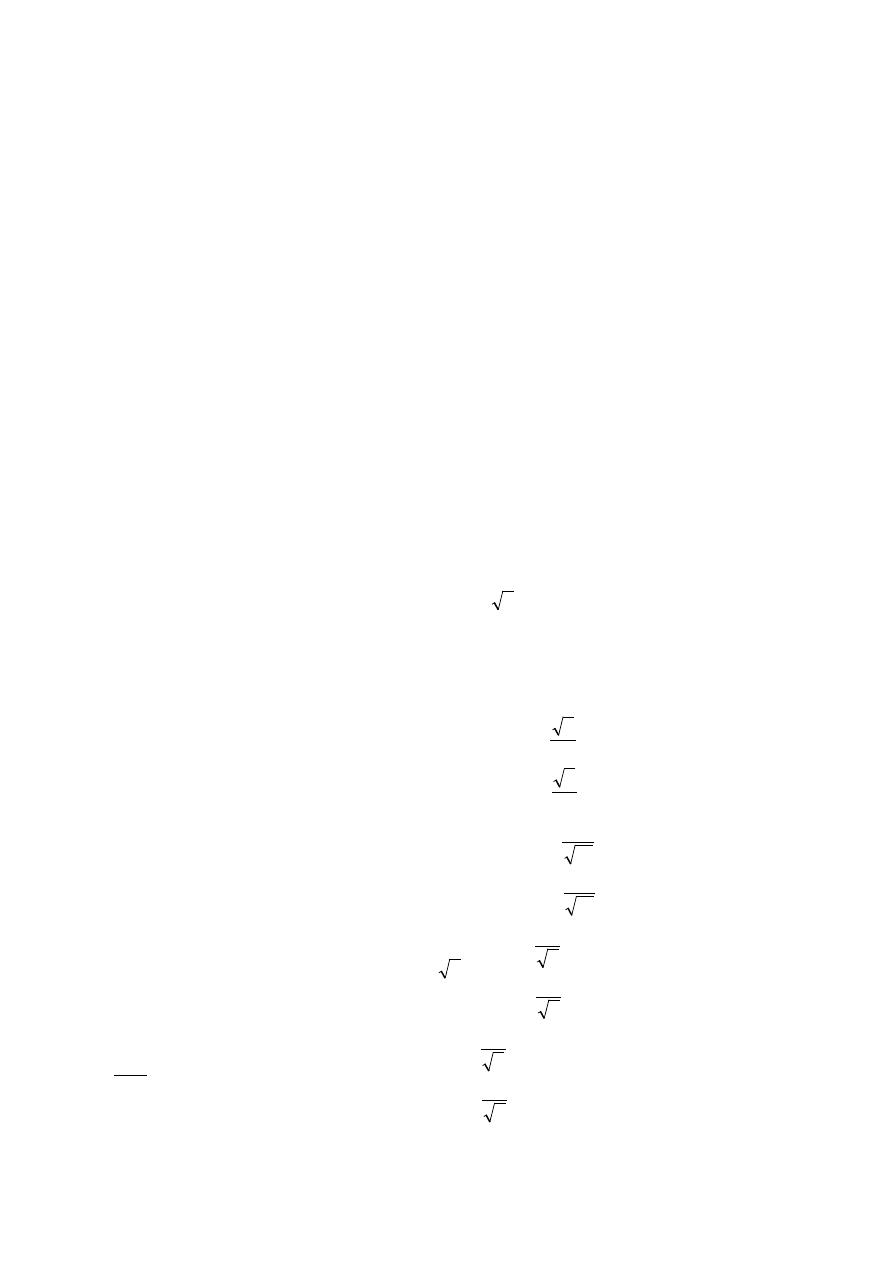
d)
0
1
4
3
8
6
2
2
=
+
−
+
+
y
x
y
x
,
zbiór pusty eliptyczny
e)
0
1
4
6
2
3
2
2
=
+
−
+
−
y
x
y
x
,
dwie proste równoległe
f)
0
6
3
6
2
2
=
+
+
+
y
x
x
,
parabola
g)
0
10
6
2
=
+
+
y
y
,
zbiór pusty paraboliczny
h)
0
1
2
5
4
3
2
2
2
=
−
+
−
+
+
y
x
y
xy
x
,
elipsa
i)
0
2
6
8
4
4
2
2
=
−
+
−
+
−
y
x
y
xy
x
,
parabola
j)
0
9
6
2
2
2
=
+
+
+
+
y
y
xy
x
,
parabola
k)
0
1
6
6
4
2
2
=
+
+
+
−
y
x
y
xy
,
hiperbola
l)
0
9
12
6
3
4
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
dwie proste nierównoległe
ł)
0
67
8
100
35
8
50
2
2
=
+
−
+
+
−
y
x
y
xy
x
,
zbiór pusty eliptyczny
m)
0
3
16
24
4
12
9
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
dwie proste równoległe
n)
0
425
120
160
9
24
16
2
2
=
+
+
−
+
−
y
x
y
xy
x
,
zbiór pusty paraboliczny
o)
0
1
6
4
9
12
4
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
prosta podwójna.
Zad 10. Następujące równania sprowadzić do postaci kanonicznej
a)
0
36
18
24
9
24
41
2
2
=
−
+
+
+
+
y
x
y
xy
x
,
9
9
2
2
=
′′
+
′′
y
x
b)
0
129
112
34
34
24
41
2
2
=
+
−
+
+
+
y
x
y
xy
x
,
0
2
2
2
=
′′
+
′′
y
x
c)
0
67
8
100
35
8
50
2
2
=
+
−
+
+
−
y
x
y
xy
x
,
1
3
2
2
2
−
=
′′
+
′′
y
x
d)
0
23
30
10
7
6
2
2
=
+
−
+
−
−
y
x
y
xy
x
,
1
4
2
2
=
′′
−
′′
y
x
e)
0
7
60
14
32
60
7
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
0
4
2
2
=
′′
−
′′
y
x
f)
0
25
6
10
2
2
2
=
+
−
−
+
−
y
x
y
xy
x
,
x
y
′′
=
′′
2
4
2
g)
0
1
6
4
9
12
4
2
2
=
+
−
−
+
+
y
x
y
xy
x
,
0
2
=
′′
y
h)
0
7
6
6
2
2
2
=
+
+
−
+
−
y
x
y
xy
x
,
1
2
=
′′
y
Zad 11. Następujące równania sprowadzić do postaci kanonicznej i wskazać zamianę zmiennych
a)
0
16
16
16
5
6
5
2
2
=
−
−
−
+
+
y
x
y
xy
x
,
16
4
2
2
=
′′
+
′′
y
x
,
+
−
−
=
′′
−
−
=
′′
)
2
(
2
2
)
(
2
2
y
x
y
y
x
x
b)
0
19
12
22
12
5
2
=
−
−
−
+
y
x
xy
x
,
36
4
9
2
2
=
′′
−
′′
y
x
,
−
+
−
=
′′
−
+
=
′′
)
1
3
2
(
13
1
)
5
2
3
(
13
1
y
x
y
y
x
x
c)
0
25
6
10
2
2
2
=
+
−
−
+
−
y
x
y
xy
x
,
x
y
′′
=
′′
2
4
2
,
+
+
−
=
′′
−
+
=
′′
)
1
(
2
1
)
3
(
2
1
y
x
y
y
x
x
d)
1
1
−
=
x
y
,
2
2
2
=
′′
−
′′
y
x
,
+
+
−
=
′′
−
+
=
′′
)
1
(
2
1
)
1
(
2
1
y
x
y
y
x
x
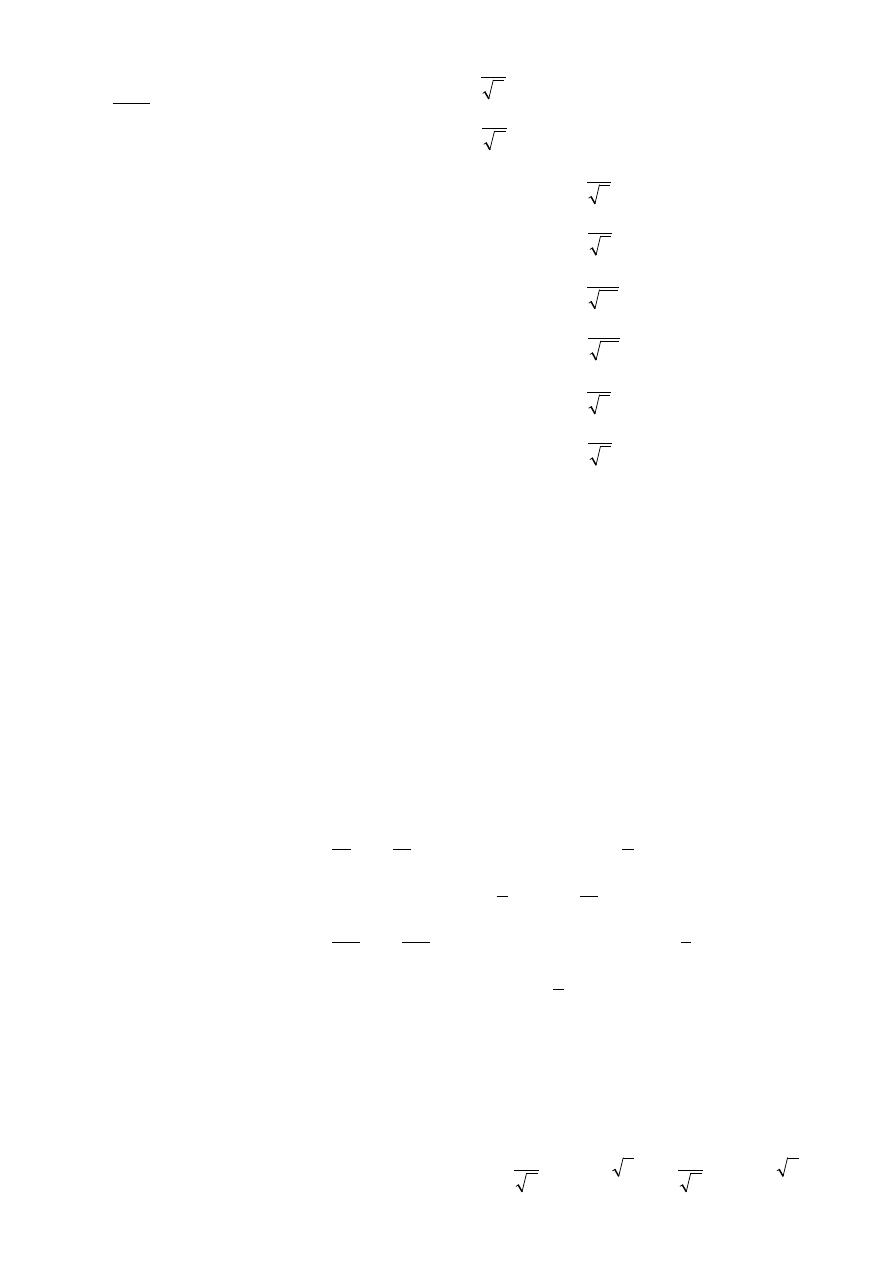
e)
1
2
+
−
=
x
x
y
,
6
2
2
=
′′
−
′′
y
x
,
−
+
−
=
′′
+
=
′′
)
2
(
2
1
)
(
2
1
y
x
y
y
x
x
f)
0
7
12
14
2
12
7
2
2
=
+
+
−
−
−
y
x
y
xy
x
,
0
2
2
2
=
′′
−
′′
y
x
,
+
+
−
=
′′
−
+
=
′′
)
2
2
(
5
1
)
1
2
(
5
1
y
x
y
y
x
x
g)
0
54
44
12
11
6
19
2
2
=
+
+
−
+
−
y
x
y
xy
x
,
1
2
2
2
−
=
′′
+
′′
y
x
,
+
+
−
=
′′
+
+
=
′′
)
2
3
(
10
1
)
6
3
(
10
1
y
x
y
y
x
x
h)
0
11
6
12
4
4
2
2
=
−
+
+
+
+
y
x
y
xy
x
,
4
2
=
′′
x
,
−
+
−
=
′′
+
+
=
′′
)
4
2
(
5
1
)
3
2
(
5
1
y
x
y
y
x
x
Zad 12. W układzie OXY znaleźć równania osi krzywych
a)
0
28
4
16
5
4
8
2
2
=
−
+
+
+
+
y
x
y
xy
x
,
0
2
2
,
0
1
2
=
+
+
=
+
−
y
x
y
x
b)
0
3
2
4
2
=
−
+
−
y
x
xy
,
0
3
,
0
1
=
+
−
=
−
+
y
x
y
x
c)
0
2
5
2
3
2
2
2
=
−
+
−
+
y
y
xy
x
,
0
3
3
,
0
1
3
=
+
−
=
+
+
y
x
y
x
.
Zad 13. Sprawdzić, że krzywa
0
11
26
12
8
6
2
=
+
−
−
+
y
x
y
xy
jest hiperbolą, oraz w układzie OXY
znaleźć jej wierzchołki, ogniska, równania osi, równania kierownic i równania asymptot.
Zad 14. Sprawdzić, że krzywa
0
9
18
18
5
8
5
2
2
=
+
−
−
+
+
y
x
y
xy
x
jest elipsą, oraz w układzie OXY
znaleźć jej wierzchołki, ogniska, równania osi, równania kierownic.
Zad 15. Sprawdzić, że krzywa
0
2
2
4
4
2
2
=
+
−
−
+
−
y
x
y
xy
x
jest parabolą, oraz w układzie OXY znaleźć
jej wierzchołek, ognisko, równanie osi, równanie kierownicy.
Zad 16. Sprowadzić do postaci kanonicznej i podać postać zamiany zmiennych
a)
0
1
2
4
4
2
2
=
−
−
+
−
y
x
y
x
,
1
19
16
19
4
2
2
=
′′
−
′′
y
x
,
4
1
,
2
−
′′
=
−
′′
=
y
y
x
x
,
b)
0
3
4
6
2
2
=
−
−
+
y
x
x
,
y
x
′′
=
′′
2
2
,
8
15
,
2
3
−
′′
=
−
′′
=
y
y
x
x
,
c)
0
1
6
4
2
2
=
+
−
+
+
y
x
y
x
,
1
129
64
129
16
2
2
=
′′
+
′′
y
x
,
8
1
,
3
+
′′
=
−
′′
=
y
y
x
x
,
d)
0
33
24
4
4
4
2
2
=
+
+
−
+
y
x
y
x
,
1
2
2
=
′′
+
′′
y
x
,
3
,
2
1
−
′′
=
+
′′
=
y
y
x
x
,
e)
0
7
6
2
=
+
+
y
y
,
2
2
=
′′
y
,
3
,
−
′′
=
′′
=
y
y
x
x
,
f)
0
3
2
2
=
+
−
x
x
,
2
2
−
=
′′
y
,
y
y
x
x
′′
=
+
′′
=
,
1
,
g)
0
9
6
2
=
+
+
x
x
,
0
2
=
′′
x
,
y
y
x
x
′′
=
−
′′
=
,
3
,
h)
0
1
2
2
2
=
+
+
+
x
y
x
,
0
2
2
=
′′
+
′′
y
x
,
y
y
x
x
′′
=
−
′′
=
,
1
,
i)
0
2
4
4
2
2
2
=
−
+
+
−
y
x
y
x
,
0
2
2
2
=
′′
−
′′
y
x
,
2
,
1
+
′′
=
−
′′
=
y
y
x
x
,
j)
0
16
16
16
5
6
5
2
2
=
−
−
−
+
+
y
x
y
xy
x
,
16
4
2
2
=
′′
+
′′
y
x
,
)
2
(
2
1
),
2
(
2
1
+
′′
+
′′
=
+
′′
−
′′
=
y
x
y
y
x
x
,

k)
0
5
6
15
24
8
2
2
=
−
−
+
+
y
y
xy
x
,
2
24
2
2
=
′′
−
′′
y
x
,
)
5
3
4
(
5
1
),
15
8
6
(
10
1
−
′′
+
′′
=
+
′′
−
′′
=
y
x
y
y
x
x
,
l)
0
6
2
12
2
4
2
2
2
=
−
+
−
+
+
y
x
y
xy
x
,
y
x
′′
−
=
′′
8
2
,
)
8
9
(
2
1
),
8
23
(
2
1
−
′′
+
′′
=
−
′′
−
′′
=
y
x
y
y
x
x
,
Zad 17. Sprawdzić, że krzywa
0
384
32
25
16
2
2
=
−
−
+
x
y
x
jest elipsą oraz w układzie OXY znaleźć jej
ś
rodek, ogniska, równania osi oraz równanie kierownicy.
Zad 18. Sprawdzić, że krzywa
0
5
2
2
2
=
−
+
+
y
x
x
jest parabolą oraz w układzie OXY znaleźć jej
wierzchołek, ognisko, równanie osi oraz równanie kierownicy.
Zad 19. Dla jakich wartości parametru k równanie
0
2
6
6
2
2
=
+
+
+
+
+
k
y
x
y
xy
x
przedstawia dwie
proste równoległe?
Zad 20. Dla jakich wartości parametru k równanie
0
2
2
3
2
3
2
2
=
+
+
−
+
−
k
y
x
y
xy
x
przedstawia punkt?
Zad 21. Dla jakich wartości parametrów k i r równanie
0
3
7
2
2
2
2
=
+
+
−
+
+
ry
x
y
kxy
x
przedstawia dwie
proste równoległe?
Zad 22. Sklasyfikować następujące krzywe w zależności od wartości parametru k:
a)
0
1
2
)
1
(
)
1
(
2
2
=
+
+
−
+
+
x
y
k
x
k
, b)
0
4
4
2
2
2
=
+
+
−
+
−
k
y
x
y
xy
x
, c)
0
1
4
2
2
2
=
+
−
+
−
x
ky
kxy
x
.
Zad 23. Wykazać, że równanie
0
2
2
2
33
23
13
2
22
12
2
11
=
+
⋅
+
⋅
+
⋅
+
⋅
⋅
+
⋅
a
y
a
x
a
y
a
y
x
a
x
a
, gdzie
0
2
22
2
12
2
11
>
+
+
a
a
a
typu parabolicznego (w=0) można zawsze przedstawić w postaci
0
2
2
)
(
33
23
13
2
2
1
=
+
+
+
+
a
y
a
x
a
y
k
x
k
.
Zad 24. Wykazać, że równanie
0
0
,
≠
≠
+
+
=
d
c
b
a
i
c
gdzie
d
cx
b
ax
y
przedstawia zawsze hiperbolę.
Zad 25. Wykazać, że równanie
1
)
(
)
(
2
2
2
2
2
1
1
1
=
+
+
+
+
+
c
y
b
x
a
c
y
b
x
a
, gdzie
0
1
2
1
2
1
2
2
1
1
=
+
=
b
b
a
a
i
b
a
b
a
określa elipsę. Znaleźć jej równanie kanoniczne i równania osi.
Zad 26. Dla jakich krzywych stopnia drugiego spełnione są warunki
0
0
22
11
≠
=
+
=
W
i
a
a
p
?
Zad 27. Wykazać, że równanie paraboli
0
2
2
2
33
23
13
2
22
12
2
11
=
+
⋅
+
⋅
+
⋅
+
⋅
⋅
+
⋅
a
y
a
x
a
y
a
y
x
a
x
a
(
0
,
0
≠
=
W
w
) można zawsze przedstawić w postaci
y
a
a
W
x
a
a
′′
+
−
±
=
′′
+
22
11
2
22
11
2
)
(
, gdzie
Y
X
O
′′
′′
′′
jest
nowym układem współrzędnych.
Wyszukiwarka
Podobne podstrony:
Krzywe stopnia drugiego -zadania
39 Klasyfikacja krzywych algebraicznych stopnia drugiego i ich postacie kanoniczne (Susińska)x
09 7 Powierzchnie stopnia drugiego rysunki
termodynamika zadania dla I stopnia, Wybrane zadania z te
Sprawozdanie z drugiego zadania, WAT, SEMESTR I, PKC
01 3 Stopnie utlenienia zadania do lekcji nr 1
Matematyka I (Ćw), Lista 09. Krzywe drugiego stopnia
18 Krzywe drugiego stopnia
5 Krzywe 2 ego stopnia
Zadania bilanse, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia,
Wyniki.I-KolokwiumB.2008, Nieorganiczna, chemia2, Arkusze powtórzeniowe, Pobieranie1, studia 1.2, za
APROKSYMACJA CHARAKTERYSTYK WIELOMIANEM DRUGIEGO STOPNIA
mater. - zadania z rozpuszczalności, Karta pracy - krzywe rozpuszczalności zadania
więcej podobnych podstron