
Analiza nakładów i wyników - model Leontiewa
Przedmiotem takiej analizy są przepływy międzygałęziowe w złożo-
nych układach gospodarczych.
Wartości przepływów międzygałęziowych ustalane są w oparciu o
statystyczne obserwacje działalności produkcyjnej poszczególnych
gałęzi rozpatrywanego układu w ustalonym okresie.
Zebrane w ten sposób dane, wyrażone w jednostkach pieniężnych,
przedstawione są w postaci tablicy przepływów międzygałęziowych.
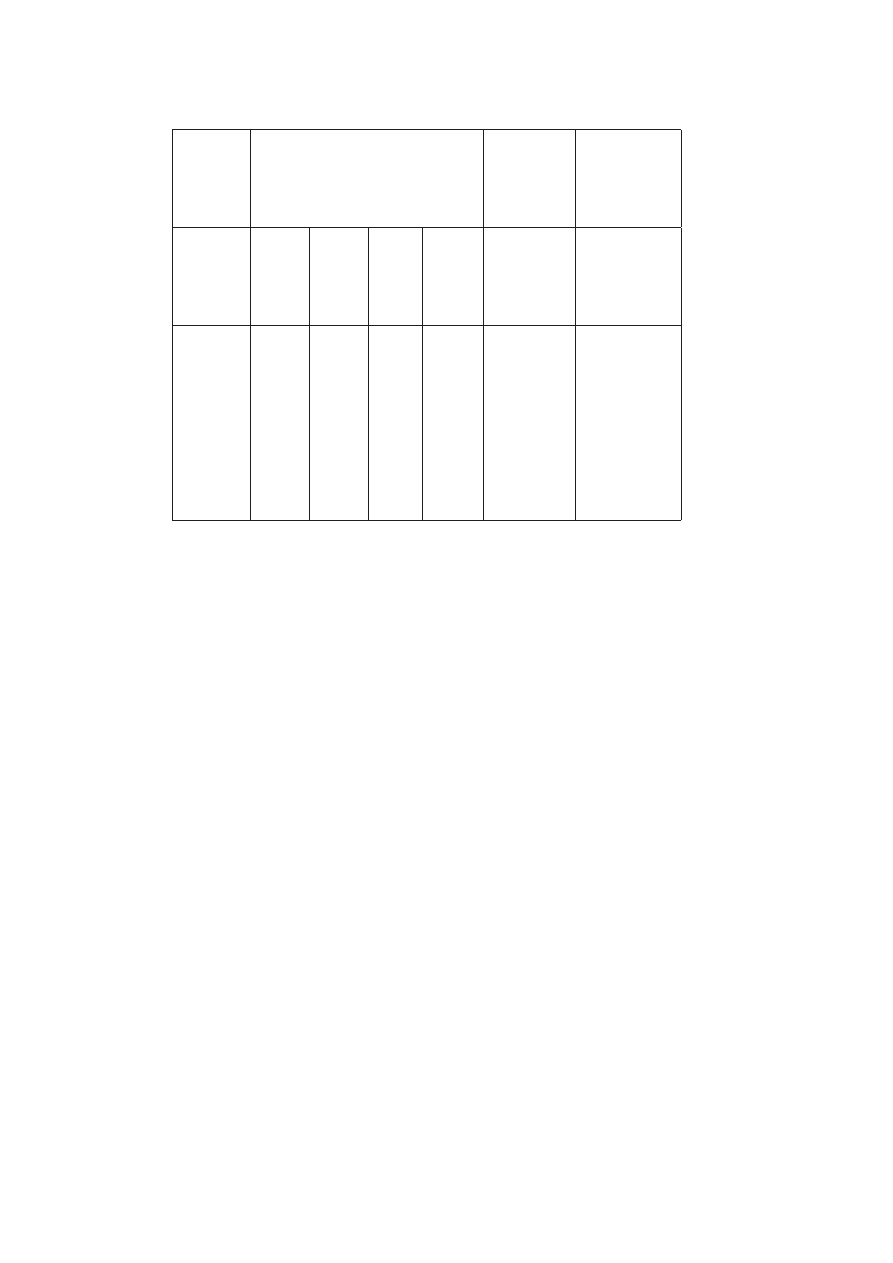
Tablica przepływów międzygałęziowych
Numer
Przepływ
x
ij
Produkt Produkcja
gałęzi
z gałęzi
i do gałęzi j
końcowy
globalna
j
1
2
· · ·
n
d
i
x
i
i
1
x
11
x
12
· · · x
1
n
d
1
X
1
2
x
21
x
22
· · · x
2
n
d
2
X
2
...
...
...
...
...
...
...
n
x
n1
x
n2
· · · x
nn
d
1
X
1

Macierz współczynników kosztów (współczynników technicznych):
A =
a
11
a
12
. . . a
1
n
a
21
a
22
. . . a
2
n
. . . . . . . . . . . .
a
n1
a
n2
. . . a
nn
.
Współczynnik a
ij
=
x
ij
X
i
oznacza wartość towaru i niezbędnego do
wyprodukowania towaru j o wartości 1 jednostki pieniężnej.

Oznaczenia:
~
d - wektor konsumpcji (produktu końcowego);
~x - wektor produkcji globalnej;
A~x - wektor nakładów w procesie produkcyjnym niezbędny do uzy-
skania wyników określonych przez wektor ~x.
Aby zaspokoić ustalony popyt ~
d należy tak dobrać wektor ~x aby
było spełnione równanie:
~x = A~x + ~
d.
Lewa strona wyraża całkowitą podaż, a prawa - całkowity popyt. Na
popyt składa się nie tylko wektor pożądanej konsumpcji ~
d, lecz także
wielkość A~x potrzebna jako nakłady w procesie produkcyjnym.

Aby obliczyć wektor wyników ~x przy założonym poziomie konsump-
cji ~
d należy rozwiązać równanie macierzowe
(I − A)~x = ~
d.
Macierz I−A nazywamy macierzą Leontiewa. Jeśli macierz Leontie-
wa posiada macierz odwrotną to równanie ma rozwiązanie postaci
~x = (I − A)
−
1
~
d.
Tw. Jeśli suma wyrazów w każdej kolumnie macierzy A jest mniej-
sza niż jeden, to macierz Leontiewa posiada macierz odwrotną.

Przykład:
Pewnien fikcyjny system gospodarczy składa się z trzech gałęzi (np.:
energetyki, hutnictwa, i budownictwa). Poniższa tablica jest tablicą
przepływów międzygałęziowych w tym systemie.
Numer
Przepływ
x
ij
Produkt
Produkcja
gałęzi
z gałęzi
i do gałęzi j końcowy
globalna
j 1
2
3
d
i
x
i
i
1
24 9
20
67
120
2
48 27
10
5
90
3
12 18
30
40
100

Z pierwszego wiersza tej tabeli wynika, że na produkcję globalną
pierwszej gałęzi równą 120 składa sie produkt końcowy (konsump-
cja) o wartości 76 oraz produkty zużyte do produkcji w pierwszej,
drugiej i trzeciej gałęzi o wartościach równych odpowiednio 24, 9,
20. Podobne informacje zawiera wiersz drugi i trzeci. Współczynnik
a
ij
= x
ij
/x
j
oznacza wartość towaru i niezbędnego do wyprodu-
kowania towaru j o wartości 1 jednostki pieniężnej.

Numer
Przepływ
x
ij
Produkt
Produkcja
gałęzi
z gałęzi
i do gałęzi j końcowy
globalna
j 1
2
3
d
i
x
i
i
1
24 9
20
67
120
2
48 27
10
5
90
3
12 18
30
40
100
Przedstawmy produkcję globalną i produkt końcowy w postaci wek-
torów i obliczmy macierz kosztów:
~x =
120
90
100
~
d =
67
5
40
A =
24
120
9
90
20
100
48
120
27
90
10
100
12
120
18
90
30
100

A =
24
120
9
90
20
100
48
120
27
90
10
100
12
120
18
90
30
100
=
0, 2 0, 1 0, 2
0, 4 0, 3 0, 1
0, 1 0, 2 0, 3
Macierz Leontiewa :
I − A =
0, 8 −0, 1 −0, 2
−0, 4
0, 7 −0, 1
−0, 1 −0, 2
0, 7

Macierz odwrotna do macierzy Leontiewa
(I − A)
−
1
=
1, 48 0, 35 0, 47
0, 91 1, 70 0, 50
0, 47 0, 54 1, 64

Łatwo sprawdzić, że zachodzą następujące równości:
120
90
100
=
0, 2 0, 1 0, 2
0, 4 0, 3 0, 1
0, 1 0, 2 0, 3
·
120
90
100
+
67
5
40

oraz
120
90
100
=
0, 8 −0, 1 −0, 2
−0, 4 0, 7 −0, 1
−0, 1 −0, 2 0, 7
−
1
·
67
5
40
=
1, 48 0, 35 0, 47
0, 91 1, 70 0, 50
0, 47 0, 54 1, 64
·
67
5
40
Wyszukiwarka
Podobne podstrony:
ANALIZA PRZEPŁYWÓW MIĘDZYGAŁĘZIOWYCH, studia, pomoce naukowe - repetytoria, ekonomia
Analiza przepływu wody przez przekrój mostowy (FM)
analiza przeplywow, BANKOWOŚĆ, Bankowość i Finanse
Analiza regresji między dwiema zmiennymi, Płyta farmacja Bydgoszcz, statystyka, pozostałe
imw w02 strukturysp analiza przeplywow
Analiza regresji między dwiema zmiennymi, Statystyka, statystyka(3)
Ściągi mikro, Ściąga wykład 9, Teoria produkcji- zajmuje się rzeczową stroną procesów wytwórczych, a
Analiza przeplywu przez przepus Nieznany (2)
Analiza regresji między dwiema zmiennymi, statystyka matematyczna(1)
Przepływy międzygałęziowe (15 stron), Przepływy międzygałęziowe
przepływy międzygałęziowe(11 str), Ekonomia
Przeplywy miedzygaleziowe
więcej podobnych podstron