1

Ćwiczenia rachunkowe z Fizyki do wykładu prof. T. Stobieckiego, I rok Elektronika, studia stacjonarne.

Zestaw 8. Pole elektrostatyczne.

Obowiązujący zakres materiału: Prawo Coulomba. Natężenie pola elektrycznego. Strumień pola elektrycznego.

Prawo Gaussa. Potencjał elektryczny. Pojemność elektryczna. (źródło: wykład , D.Halliday, R.Resnick,

J.Walker "Podstawy Fizyki", t.III , str. 1-127 (dla wydania z roku 2003)

Zad. 1.
Na ciało o masie m poruszające się prostoliniowo z prędkością początkową V

0

działa siła hamująca

ruch, proporcjonalna do prędkości: F = -b·V gdzie b jest stałe.

1. Znaleźć zależność prędkości ciała od czasu.

2.

Obliczyć całkowitą drogę przebytą przez to ciało.

Zad. 2.

Dane jest pole sił

(

)

N

j

x

i

y

F

ˆ

ˆ

2

2

⋅

−

⋅

=

r

. Oblicz pracę pola sił przy przesuwaniu cząstki od położenia

I (0,1) [m] do położenia II (1,0) [m], jeżeli praca jest wykonywana:

1. po linii prostej y=1-x,
2. po

okręgu x

2

+y

2

=1

3. po osiach współrzędnych x=0, y=0.

Czy to pole jest potencjalne?

Zad. 3.

Czy siła

(

)

N

y

z

x

yz

x

y

xz

F

2

2

2

3

2

,

6

2

,

2

2

−

−

−

−

=

r

jest siłą zachowawczą? Jeśli tak to wyznacz

odpowiadającą jej energię potencjalną E

p

.

Zad. 4.
Znależć zależność energii potencjalnej od odległości od centrum w polu sił dla:

r

r

k

F

ˆ

4

−

=

r

,

r

kr

F

ˆ

2

−

=

r

,

r

r

k

F

ˆ

2

=

r

gdzie k jest stałą a

rˆ

wektorem jednostkowym wzdłuż promienia wodzącego.

Zad. 5.
Sprawdzić czy pole wektorowe o składowych F

x

= 6xy, F

y

= 3x

2

– 3y

2

, F

z

= 0 jest zachowawcze licząc

całkę po konturze będącym prostokątem o wierzchołkach w punktach: A(0,0); B(0,y

0

); C(x

0

,y

0

);

D(x

0

,0).

Zad. 6.

W wierzchołkach trójkąta równoramiennego o boku a = 5 cm znajdują się ładunki rozmieszczone jak
na rysunku, gdzie q = 1x10

-8

C. Ile wynosi natężenie pola elektrycznego i potencjał elektryczny w

punkcie P.

2

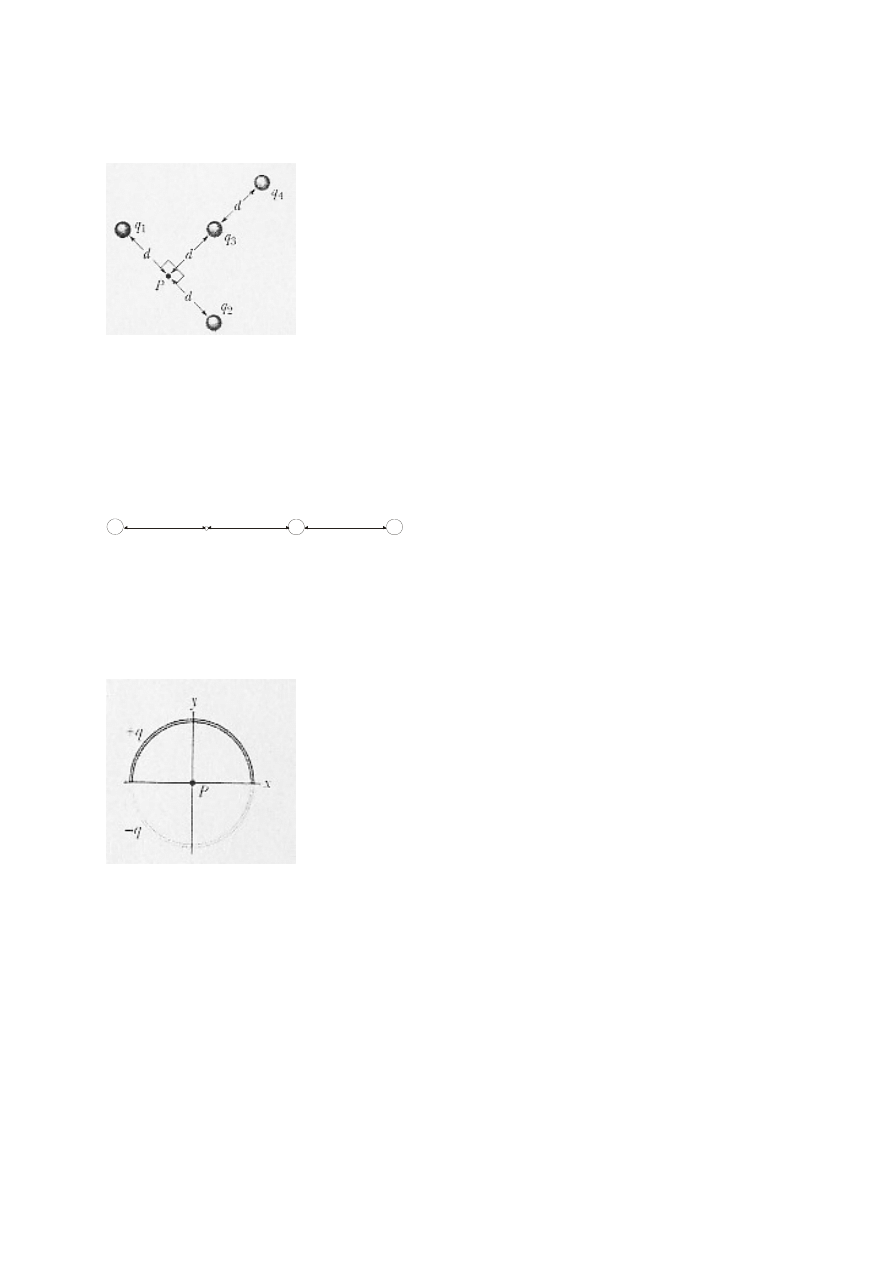
Zad. 7.
Wyznacz natężenie pola elektrycznego i potencjał elektryczny w punkcie P wytworzony przez cztery
ładunki punktowe przedstawione na rysunku.

Zad. 8.

Ładunki Q

1

, Q

2

, Q

3

rozmieszczone są jak na rysunku, przy czym Q

2

=2Q

1

=4C. Potencjał elektryczny w

punkcie A jest równy zero.
Wyznacz:

1. ładunek Q

3

,

2. wypadkowe

natężenie pola elektrycznego w punkcie A (narysuj wektory natężenia

pola

pochodzące od ładunków składowych)

Zad. 9.

Dwa zakrzywione pręty plastikowe jeden o ładunku +q, drugi o ładunku –q tworzą w płaszczyźnie XY
okrąg o promieniu R. Oś x przechodzi przez punkty łączące pręty. Na obydwu prętach ładunek jest
rozłożony równomiernie. Jaką wartość i kierunek ma natężenie pola elektrycznego wytworzonego w
środku okręgu P?

Zad. 10.

W jednorodnym polu elektrostatycznym o natężeniu pola E=500V/m umieszczono sześcian boku
15cm.
1. Ile wynosi największy i najmniejszy strumień elektryczny przenikający przez powierzchnie

poszczególnych ścian sześcianu i przy jakim usytuowaniu sześcianu względem wektora natężenia
pola elektrycznego?

2. Ile wynosi sumaryczny strumień elektryczny przezechodzący przez całą powierzchnię sześcianu?

Zad. 11.
Obliczyć strumień pola elektrycznego

Ψ przechodzący przez powierzchnię kuli o promieniu R ,

wewnątrz której znajduje się:
1. naładowany kondensator
2. dipol
3. metalowa kulka naładowana ładunkiem Q

A

q

1

q

2

q

3

d

d

d

3

Zad. 12.

Wyznacz natężenie i potencjał pola elektrostatycznego w odległości r od ładunku punktowego q

Zad. 13.

Dana jest jednorodnie naładowana sfera kulista o promieniu R.

1. Wyznacz natężenie pola elektrycznego w odległości

r

R

≥ i

R

r

≥

2.

Wyznacz potencjał pola elektrostatycznego

w odległości

r

R

≥ i

R

r

≥

Zad. 14.

Dana jest pełna metalowa kula o promieniu R i ładunku Q rozłożonym równomiernie wzdłuż
promienia kuli.

1. Wyznacz natężenie pola elektrycznego w odległości

r

R

≥ i

R

r

≥

2.

Wyznacz potencjał pola elektrostatycznego

w odległości

r

R

≥ i

R

r

≥

Zad. 15.

Dana jest jednorodnie naładowana kula ( z izolatora) o promieniu R.

1. Wyznacz natężenie pola elektrycznego w odległości

r

R

≥ i

R

r

≥

2.

Wyznacz potencjał pola elektrostatycznego

w odległości

r

R

≥ i

R

r

≥

Zad. 16.

Wyznacz natężenie i potencjał pola elektrostatycznego w odległości r od jednorodnie naładowanego
długiego, cienkiego pręta

Zad. 17.
Wyznacz natężenie i potencjał pola elektrostatycznego w odległości r od jednorodnie naładowanej
nieskończonej płaszczyzny,

Zad. 18.

Wyznacz natężenie i potencjał pola elektrostatycznego w odległości r pomiędzy dwoma jednorodnie
naładowanymi j płaszczyznami.

Zad. 19.

Korzystając z prawa Gaussa, wyprowadź wzór na pojemność:

1. kondensatora płaskiego powietrznego,
2. kondensatora płaskiego z dielektrykiem,
3. kondensatora walcowego,
4. kondensatora kulistego,
5. izolowanej kuli.

Zad. 20.

Małą kulkę o masie m i ładunku q zawieszono na nici o długości l i wprawiono w ruch po
kole. W środku koła znajduje się drugi identyczny, ale nieruchomy ładunek q . Nić opisuje
powierzchnię stożka i tworzy z pionem kąt

α. Z jaką prędkością kątową wiruje kulka i ile

wynosi naciąg nici?

B.Dziurdzia, 30.11.2012