1

Funkcje popytu skompensowanego

oraz efekt substytucyjny i dochodowy

1. Funkcja skompensowanego popytu

2. Efekty: substytucyjny i dochodowy

3. Problem minimalizacji wydatków

4. Wyprowadzenie funkcji skompensowanego popytu

i funkcji wydatków: przykład

5. Matematyczne wyprowadzenie efektu

substytucyjnego i dochodowego

6. Równanie Słuckiego

7. Elastyczność substytucji i wielkość efektu

substytucyjnego

8. Analiza nadwyżki konsumenta

2

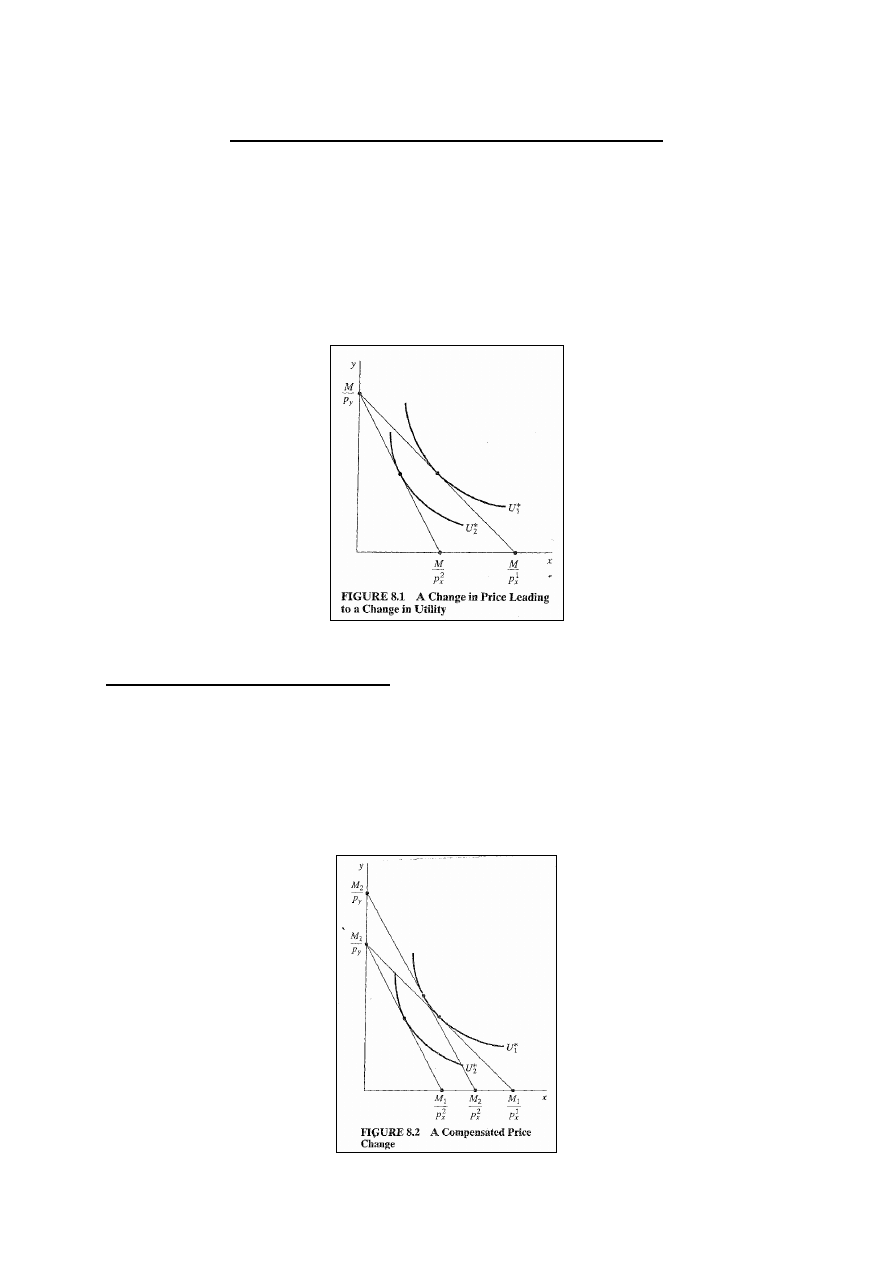
Funkcja skompensowanego popytu

Wyprowadziliśmy wielkość popytu na dane dobro jako
funkcję jego ceny przy stałym dochodzie i stałych cenach
pozostałych dóbr, ale pozwalając użyteczności zmieniać się.
Konsument w końcu znajduje się na innej krzywej
obojętności dla każdej zmiany ceny. (rys.8.1).

Kompensacja zmiany ceny
Przyjmijmy teraz, że po każdej zmianie ceny dochód
konsumenta jest dostosowywany w taki sposób aby utrzymać
go na tej samej krzywej obojętności, na jakiej znajdował się
przed zmianą ceny. (rys. 8.2). Ta zmiana dochodu określana
jest mianem kompensacji wywołanej zmianą ceny.

3

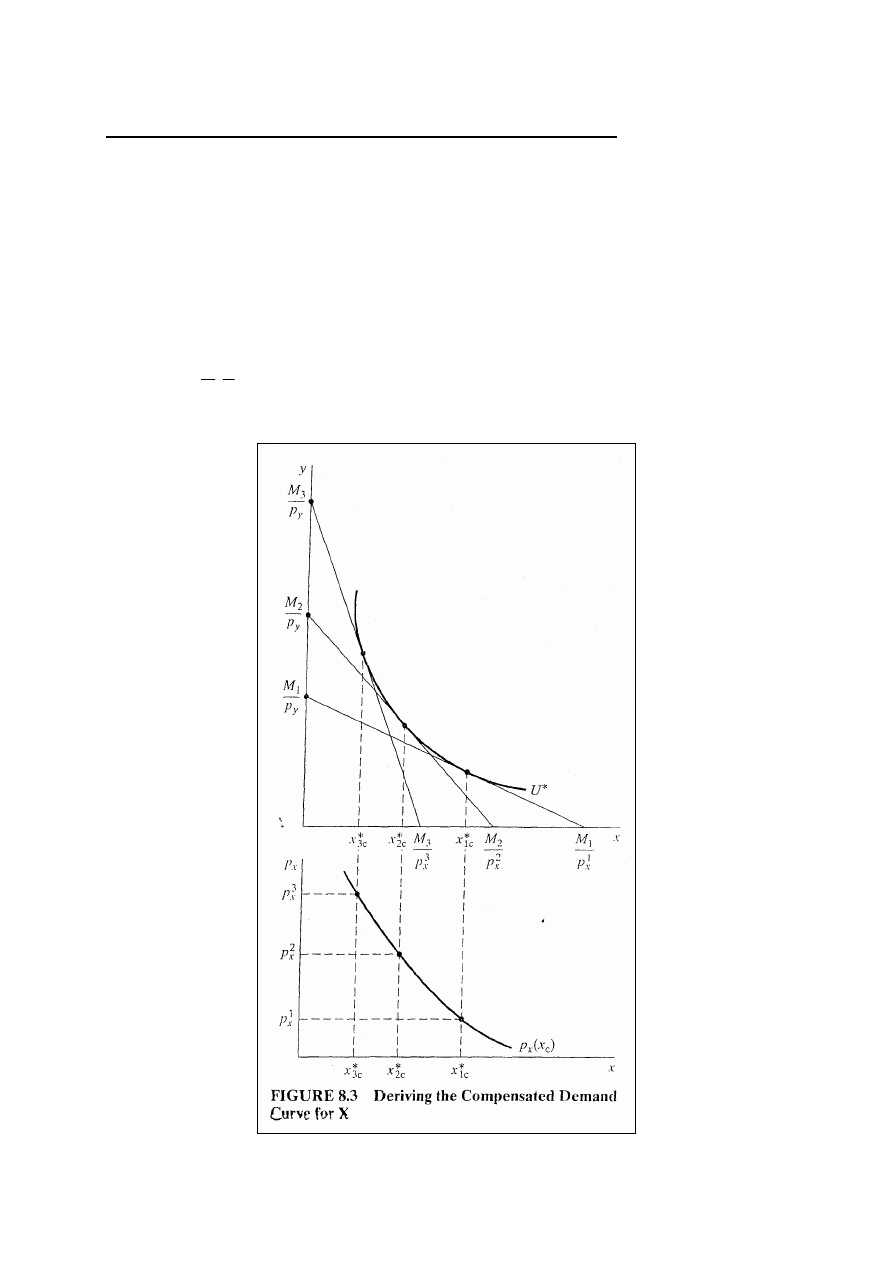
Optymalne wybory konsumpcji po kompensacji
Jeżeli wyznaczymy ścieżkę optymalnych wyborów x po
kompensacji (x

c

) na wykresie ilustrującym problem

maksymalizacji użyteczności, przy x

c

na osi poziomej i p

x

na

osi pionowej, to możemy wyprowadzić odwrotny wykres
wielkości popytu na X jako funkcję p

x

utrzymując

użyteczność i p

y

jako stałe i pozwalamy dochodowi zmieniać

się.

(

)

y

x

c

c

p

U

p

x

x

,

;

*

*

=

.

Jest to funkcja popytu skompensowanego na X (rys.8.3).

4

Krzywe popytu skompensowanego zawsze mają nachylenie
ujemne
Ponieważ optymalna wartość x

c

musi znajdować się na

krzywej obojętności, która jest wypukła względem początku
układu współrzędnych, to wielkość popytu na X po
kompensacji musi maleć przy wzroście p

x

(i musi rosnąć gdy

p

x

maleje). Wynika z tego, że krzywa skompensowanego

popytu zawsze ma nachylenie ujemne.
Zawsze się tak dzieje, gdy cena rośnie i krzywa obojętności
spełnia warunek malejącej MRS, gdyż krzywa obojętności
musi mieć nachylenie ujemne i być wypukła względem
początku układu współrzędnych. Jeżeli więc linia
ograniczenia budżetowego zwiększa nachylenie (p

x

rośnie),

to punkty styczności wymuszają wzrost y i malenie x.

Efekty: substytucyjny i dochodowy

Krzywa skompensowanego popytu ilustruje wpływ zmiany cen
względnych na wielkość popytu, przy stałym poziomie
użyteczności. Podczas analizy ekonomicznej korzystniej jest
podzielić ruch wzdłuż zwykłej krzywej popytu na dwa
oddzielne efekty:

-

jeden wywołany zmianą cen względnych

-

drugi spowodowany zmianą dostępnego zbioru koszyków
dóbr konsumpcyjnych wywołaną zmianą ceny danego
dobra.

Ten podział jest ważny ze względu na to, że dwie różne
rzeczy dzieją się przy wzroście ceny dobra. Po pierwsze,
stosunek cen X i Y zmienia się prowadząc do zmiany
nachylenia linii ograniczenia budżetowego. Po drugie,

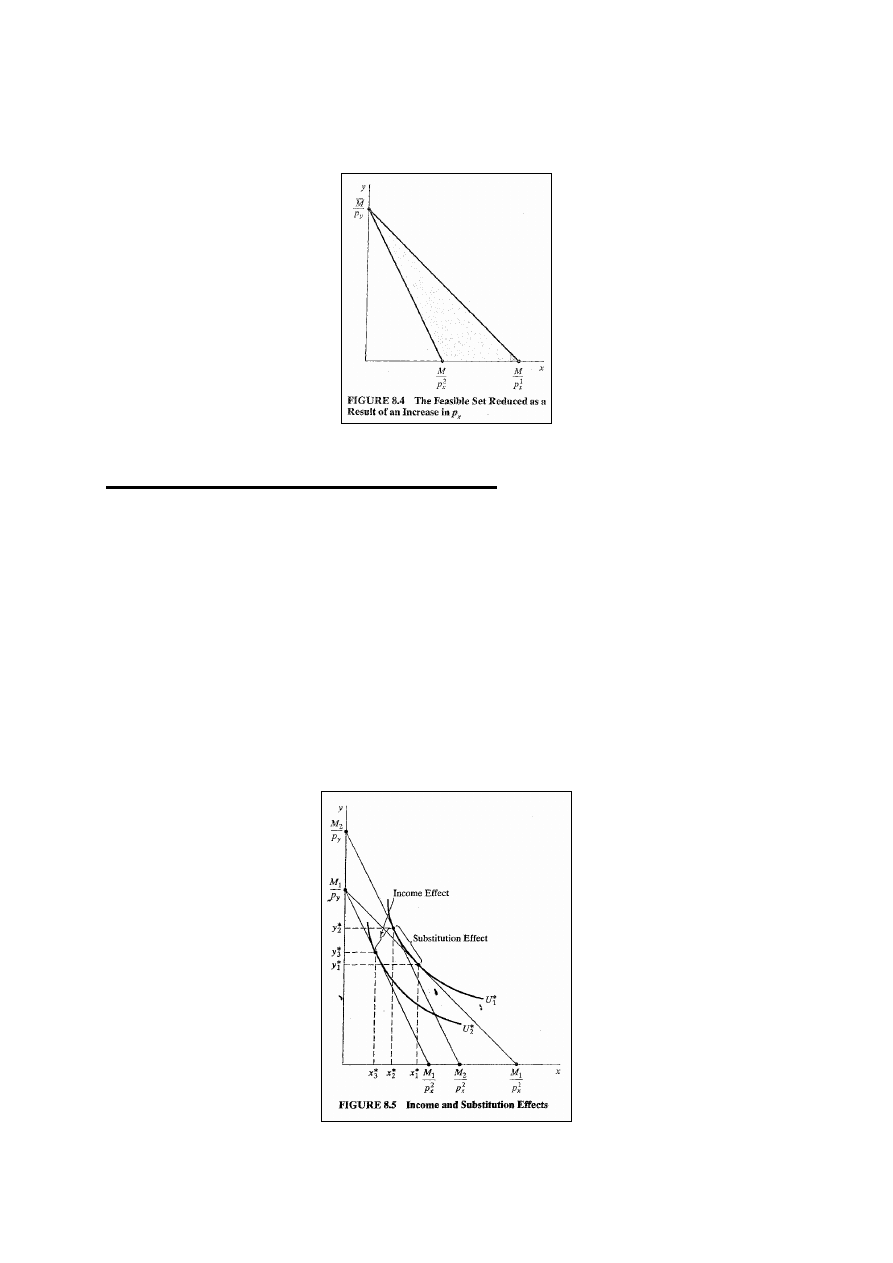
5

dostępny zbiór koszyków maleje, co oznacza zmniejszenie
się realnego dochodu konsumenta (rys. 8.4).

Efekty: substytucyjny i dochodowy
Te dwie zmiany oddziałujące na wybór konsumenta nazywane
są:

1. efekt substytucyjny: efekt wpływający na wybór

konsumenta wywołany zmianą stosunku cen przy
niezmienionej użyteczności;

2. efekt dochodowy: efekt wpływający na wybór

konsumenta wywołany zmianą zbioru dostępnych
koszyków przy niezmienionym stosunku cen.

Rys.8.5

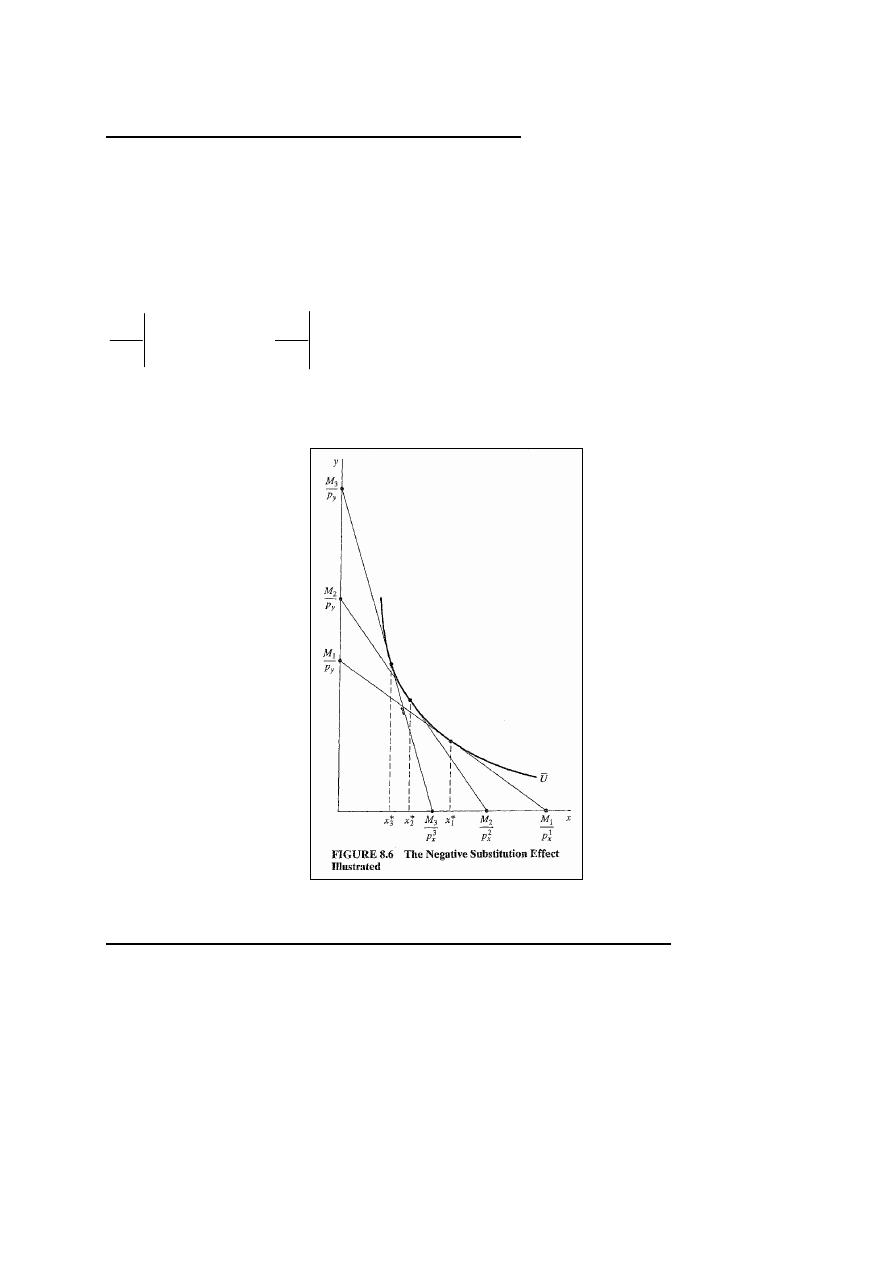
6

Ujemny znak efektu substytucyjnego
Co możemy powiedzieć o zwykłych funkcjach popytu patrząc
na ES i ED? Po pierwsze, wiemy, że wzrost p

x

zmniejsza x

poprzez działanie ES przy ruchu wzdłuż krzywej obojętności,
która obrysowuje ściśle wypukły zbiór. (rys. 8.5)
Matematycznie:

0

*

0

0

<

=

=

y

dp

dU

x

dp

dx

i

0

*

0

0

<

=

=

x

dp

dU

y

dp

dy

.

Ponieważ pochodne cząstkowe są ujemne, to mówimy, że ES
zawsze musi być ujemny (rys. 8.6).

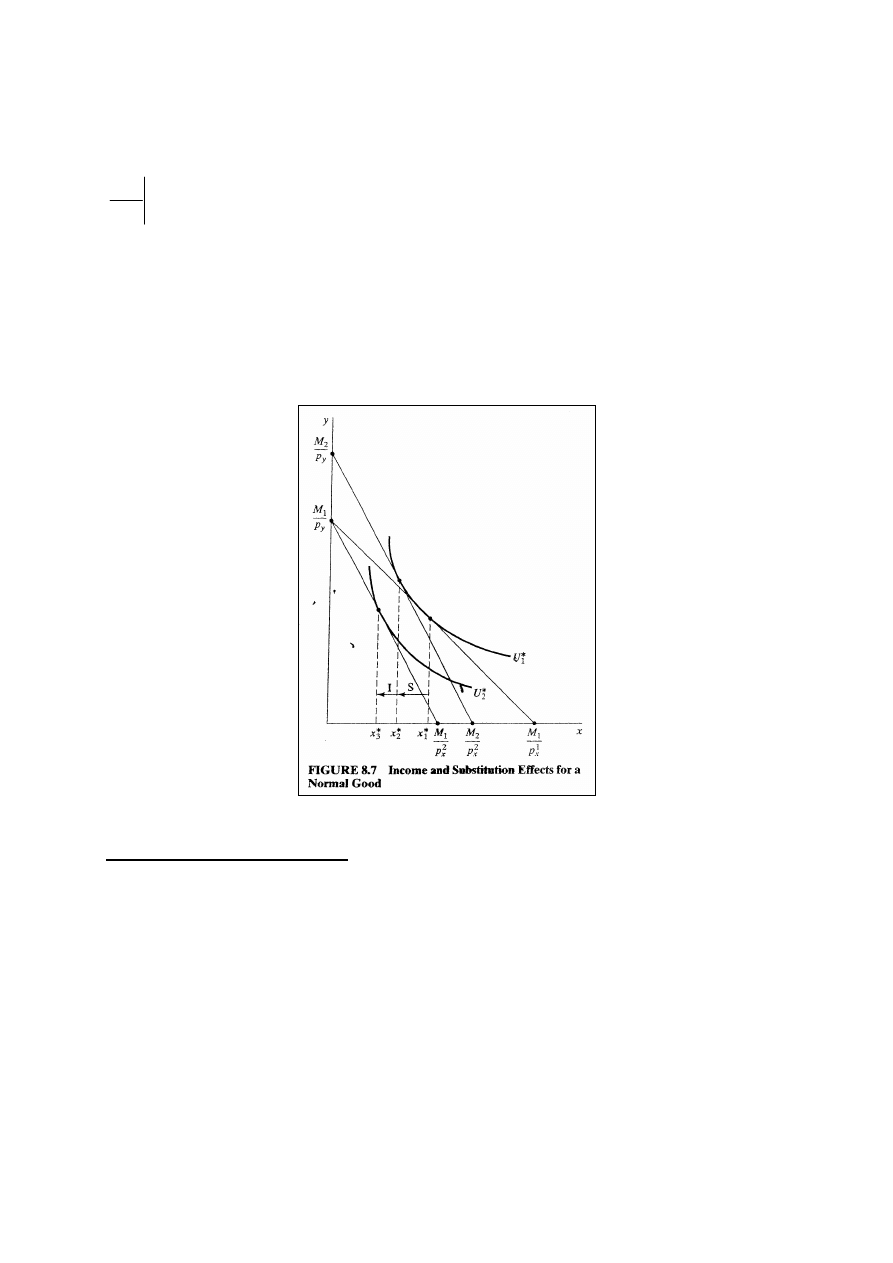
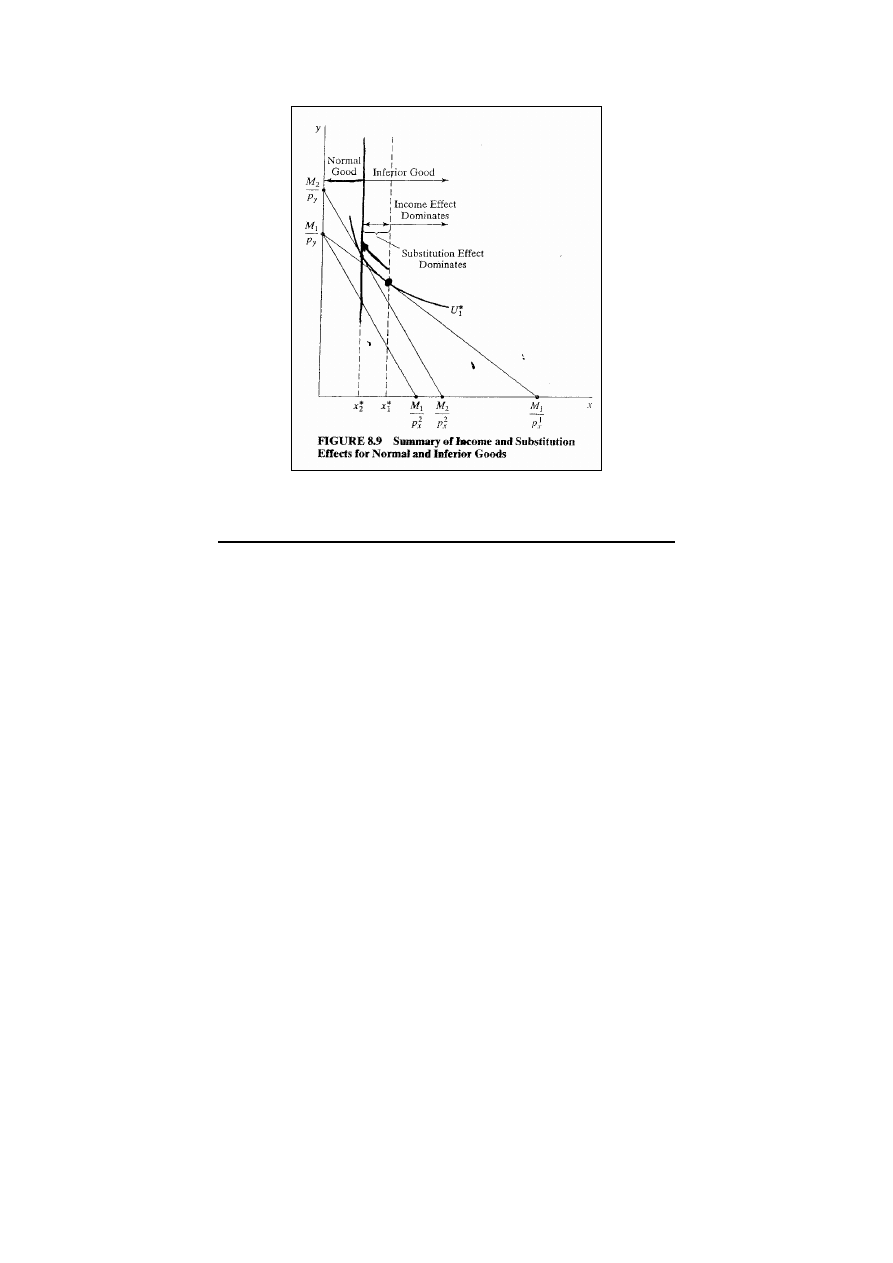
Dobra normalne i ujemnie nachylona krzywa popytu
ES musi być ujemny, ale ED może być zarówno dodatni, jak i
ujemny w zależności od tego, czy dobro jest normalne, czy
też niższego rzędu. Jeżeli dobro jest normalne, przy
zmniejszeniu się zbioru dostępnych koszyków na skutek
wzrostu ceny, to wielkość popytu maleje na skutek działania
ED. Dzieje się tak gdyż zmniejszenia się dochodu oznacza

7

zmniejszenie wielkości popytu na dobro normalne, co możemy
przedstawić w formie matematycznej:

0

*

0

0

>

=

=

y

x

dp

dp

dM

dx

dla dobra normalnego.

W przypadku dobra normalnego, kiedy cena rośnie, wielkość
popytu maleje na skutek działania ES wzmocnionego ED.
Dlatego połączony wpływ na wielkość popytu wzdłuż krzywej
zwykłego popytu musi być taki, że wielkość popytu maleje
przy wzroście ceny dobra. (rys. 8.7)

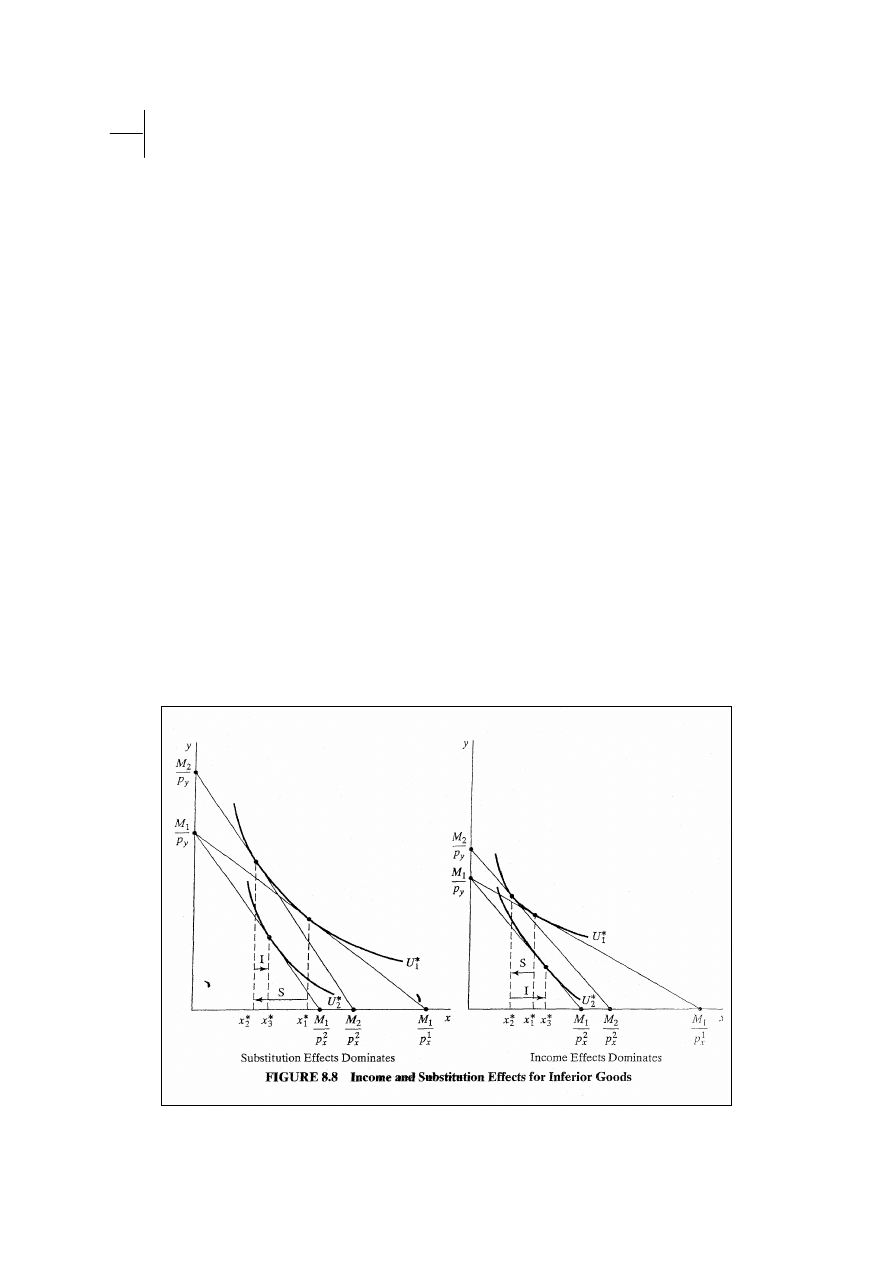
Dobra niższego rzędu
Jeżeli mamy do czynienia z dobrem niższego rzędu, to
wielkość popytu rośnie przy zmniejszeniu się dochodu. Z
tego wynika, że zmniejszenie dostępnego zbioru koszyków
spowodowane wzrostem ceny, prowadzi do zwiększenia
wielkości popytu w wyniku działania ED. Zwiększenie się
dostępnego zbioru prowadzi do przeciwnego rezultatu.
Matematycznie możemy zapisać to:

8

0

*

0

0

<

=

=

y

x

dp

dp

dM

dx

dla dobra niższego rzędu.

Jeżeli cena rośnie, ES zawsze zmniejsza wielkość popytu z
powodu malejącej MRS. Ale w przypadku dobra niższego
rzędu, zbiór dostępnych koszyków ulega zmniejszeniu przy
wzroście ceny i ED prowadzi do wzrostu wielkości popytu.
Całkowity efekt nieskompensowany może oznaczać wzrost
lub zmniejszenie się wielkości popytu w zależności od tego,
który efekt, ED czy ES, jest silniejszy. Rys. 8.8: lewa część:
SE przeważa DE; prawa część: jeżeli mamy do czynienia z
dobrem niższego rzędu i jeżeli ED jest silniejszy od ES, to
efekt całkowity może oznaczać wzrost x* z x

1

* do x

3

*.

Jeżeli więc ED przeważa ES w przypadku dobra niższego
rzędu, to zwykła krzywa popytu będzie miała nachylenie
dodatnie, nawet przy spełnieniu wszystkich założeń modelu
preferencji konsumenta. Dobra, które mają dodatnio
nachyloną krzywą popytu nazywamy dobrami Giffena.

9

Problem minimalizacji wydatków

Rozwiązaliśmy problem maksymalizacji konsumenta i
wyprowadziliśmy uogólnione funkcje popytu:

U*

=

U*

(

x*

,

y*

).

Ponieważ U* zmienia się przy każdej zmianie ceni dochodu,
to możemy myśleć o U* jako funkcji cen i dochodu. Sposób
skonstruowania funkcji U* polega na tym, że wykorzystujemy
uogólnione funkcje popytu będące funkcjami od cen i
dochodu do przedstawienia optymalnych wyborów x i y.
Następnie formułujemy U* jako funkcję x* i y*, gdzie x* i y*
są uogólnionymi funkcjami popytu na X i Y. W przypadku
dwóch dóbr konsumpcyjnych problem możemy przedstawić
następująco:
max

U

(

x

,

y

)

p.w.

p

x

x

+

p

y

y

=

M

Uogólnione funkcje popytu:

x*

=

x*

(

p

x

,

p

y

,

M

) i

y*

=

y*

(

p

x

,

p

y

,

M

)

Optymalne rozwiązanie:

U*

=

U*

(

x*

(

p

x

,

p

y

,

M

),

y*

(

p

x

,

p

y

,

M

))

10

Tą ostatnią funkcję, U*, można zapisać prościej jako funkcję
od wszystkich cen i dochodu. W tej postaci nosi ona nazwę
pośredniej funkcji użyteczności (ponieważ wybory x* i y*
zostały „schowane”)

U*

=

U*

(

p

x

,

p

y

,

M

)

Problem dualny konsumenta
Problemem dualnym do maksymalizacji użyteczności jest
minimalizacja wydatków. Konstruując problem dualny,
minimalizujemy ograniczenie budżetowe problemu
pierwotnego przy ograniczeniu jakim jest teraz optymalne
rozwiązanie funkcji celu z problemu wyjściowego.
Problem wyjściowy: maksymalizacja funkcji celu zadanej
przez

U

=

U

(

x

,

y

) przy ograniczeniu:

p

x

x

+

p

y

y

=

M

.

Rozwiązaniem jest U*. Zgodnie z zasadami konstruowania
problemów dualnych przyjmujemy, że funkcją celu jest teraz
minimalizacja wyjściowego ograniczenia budżetowego.
Minimalizujemy więc funkcję celu w postaci:

M =p

x

x

+

p

y

y

przy ograniczeniu jakim jest wyjściowa funkcja

celu:

U

=

U

(

x

,

y

).

Rozwiązaniem jest M*. Co więcej, dla każdego U* przy
ograniczeniu budżetowym

M

w problemie wyjściowym mamy

odpowiadające M* przy ograniczeniu użyteczności

U

w

problemie dualnym.

U*

w pierwotnym =

U

w dualnym

M*

w dualnym =

M

w pierwotnym.

Analogicznie jak w problemie pierwotnym (maksymalizacji
użyteczności), rozwiązanie problemu dualnego (minimalizacji
wydatków) związane jest z wyznaczeniem zbioru funkcji
popytu. Ponieważ użyteczność jest utrzymywana na stałym

11

poziomie, a zmienia się dochód, to funkcje popytu są
funkcjami skompensowanego popytu.
Aby uzyskać

M*

potrzebujemy funkcje popytu

skompensowanego w postaci ogólnej (analogicznie, jak
potrzebowaliśmy normalne funkcje popytu w postaci ogólnej
do wyznaczenia

U*

).

Uogólnione postacie funkcji popytu skompensowanego można
zapisać:

(

)

U

p

p

x

x

y

x

c

c

;

;

*

*

=

i

(

)

U

p

p

y

y

y

x

c

c

;

;

*

*

=

.

Podobnie do problemu pierwotnego, optymalne rozwiązanie
problemu dualnego można wyrazić jako uogólnione funkcje
popytu:

(

)

(

)

U

p

p

y

p

U

p

p

x

p

y

p

x

p

M

y

x

c

y

y

x

c

x

c

y

c

x

;

;

;

;

*

*

*

*

*

+

=

+

=

Funkcja

M*

nazywa się funkcją wydatków. I ponownie po

opuszczeniu

*

c

x

i

*

c

y

można ją zapisać jako funkcję od cen i

użyteczności:

M*

=

M*

(

p

x

,

p

y

,

U

).

Porównanie problemu wyjściowego i dualnego
Okazuje się więc, że:

(

)

(

)

(

)

(

)

M

p

p

U

p

p

x

U

p

p

M

p

p

x

y

x

y

x

c

y

x

y

x

;

;

*

;

;

;

;

*

;

;

*

*

=

i:

(

)

(

)

(

)

(

)

M

p

p

U

p

p

y

U

p

p

M

p

p

y

y

x

y

x

c

y

x

y

x

;

;

*

;

;

;

;

*

;

;

*

*

=

gdzie:

U*

=

U

M*

=

M

.

Rysunek 8.10 przedstawia to zagadnienie graficznie.

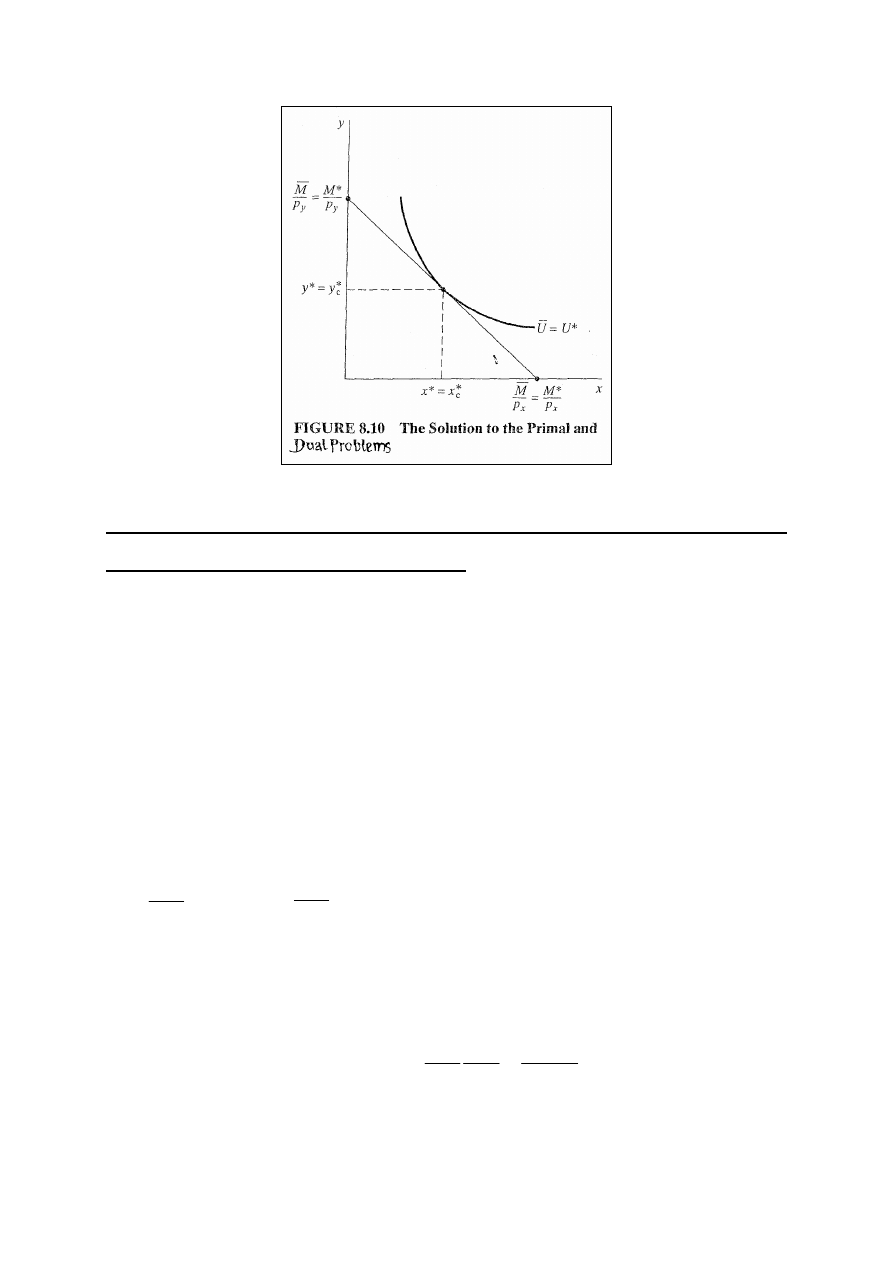
12

Wyprowadzenie funkcji skompensowanego popytu i
funkcji wydatków: przykład

Możemy przejść do wyprowadzenia funkcji
skompensowanego popytu i funkcji wydatków. Wykorzystamy
funkcję użyteczności postaci Cobb – Douglas’a:

U

=

xy

(α =

β

= 1).

Problem maksymalizacji użyteczności:
max

U

=

xy

p.w.:

p

x

x

+

p

y

y

=

M

.

Dla α = β = 1 otrzymujemy uogólnione funkcje popytu
nieskompensowanego:

x

p

M

x

2

*

=

i

y

p

M

y

2

*

=

Jeśli otrzymane funkcje popytu wstawimy do funkcji
użyteczności,

U

=

xy

, to otrzymamy pośrednią funkcję

użyteczności dla optymalnych wartości

x*

i

y*

:

y

x

y

x

p

p

M

p

M

p

M

y

x

U

4

2

2

*

*

*

2

=

=

=

13

Budujemy problem dualny:
min

M

=

p

x

x

+

p

y

y

p.w.:

xy

=

U

.

Lagrangian przyjmuje postać:

L

=

p

x

x

+

p

y

y

+ λ(

U

–

xy

)

Warunki pierwszego rzędu są następujące:

y

p

y

p

x

L

x

x

=

⇒

=

−

=

∂

∂

λ

λ

0

x

p

x

p

y

L

y

y

=

⇒

=

−

=

∂

∂

λ

λ

0

0

=

−

=

∂

∂

xy

U

L

λ

Rozwiązując dla λ:

x

p

p

y

x

p

y

p

y

x

y

x

=

⇒

=

=

λ

Dlatego:

2

1

*

2

0













=

⇒

=

⇒

=















−

U

p

p

x

U

p

p

x

x

p

p

x

U

x

y

c

y

x

y

x

2

1

*













=

U

p

p

x

x

y

c

: uogólniona funkcja skompensowanego popytu na

X

.

Wstawiając

2

1

*













=

U

p

p

x

x

y

c

do

x

p

p

y

y

x

=

otrzymujemy:

2

1

2

1

*















=













=

U

p

p

U

p

p

p

p

y

y

x

x

y

y

x

c

2

1

*















=

U

p

p

y

y

x

c

: uogólniona funkcja skompensowanego popytu na

Y

.

14

Rozwiązując problem dualny wstawiamy optymalne wybory
zdefiniowane w oparciu o funkcje skompensowanego popytu
do funkcji celu:

(

) (

)

(

)

2

1

2

1

2

1

2

1

2

1

2

*

*

*

U

p

p

U

p

p

U

p

p

U

p

p

p

U

p

p

p

y

p

x

p

M

y

x

y

x

y

x

y

x

y

x

y

x

y

x

=

+

=















+













=

+

=

(

)

2

1

2

*

U

p

p

M

y

x

=

: funkcja wydatków.

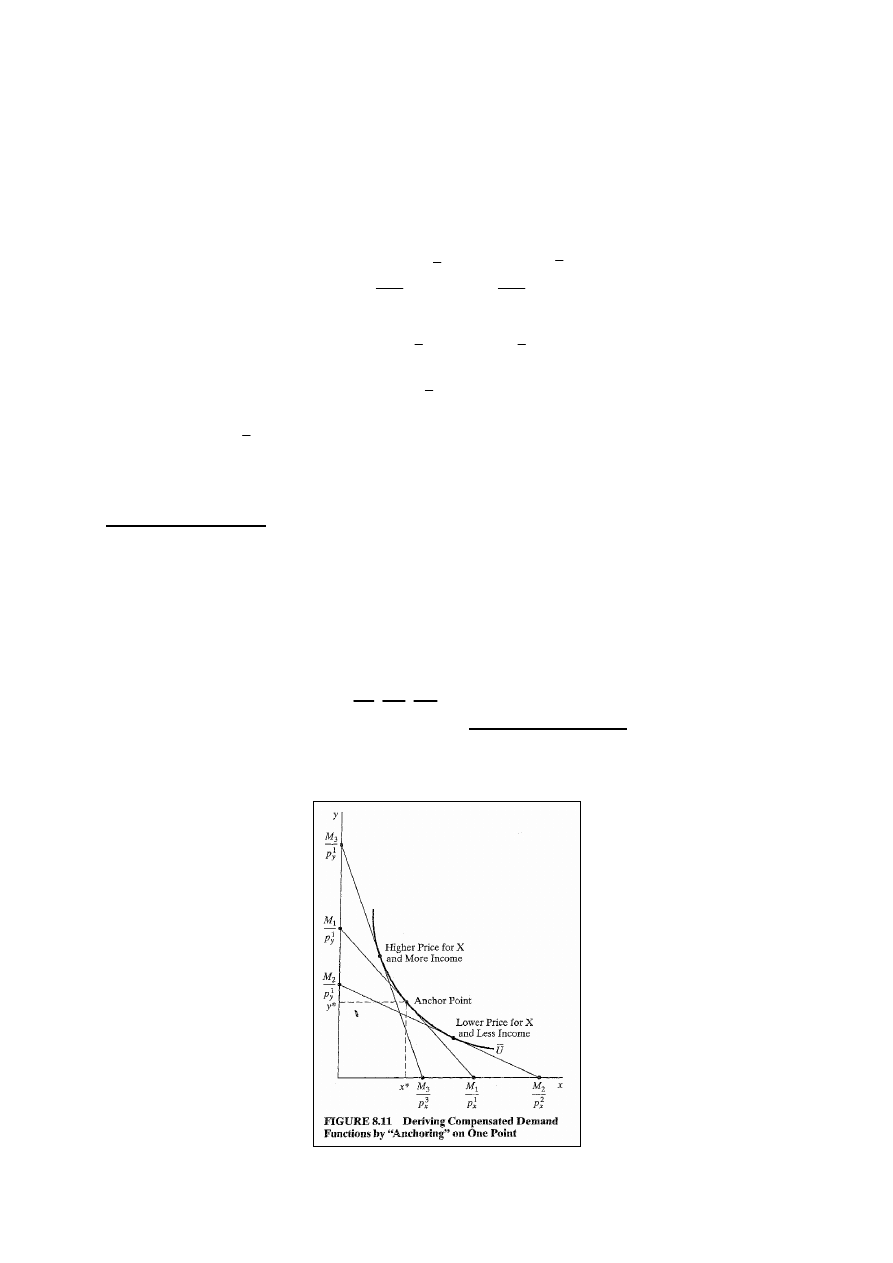
Zakotwiczenie
Aby wyprowadzić funkcje skompensowanego popytu musimy
utrzymać użyteczność na stałym poziomie (dążymy do
znalezienia punktów styczności wzdłuż jednej krzywej
użyteczności).
Możemy zacząć od punktu wyboru optymalnego przy danym
dochodzie i cenach (

y

x

p

p

M

;

;

).

Zakotwiczamy

więc funkcje

skompensowanego popytu w tym punkcie (technikę tę
pokazuje rys. 8.11).

15

Stały poziom użyteczności (

U

) związany jest z wyborem

x*

i

y*

przy cenach i dochodzie:

1

1

1

;

;

M

p

p

y

x

. Aby utrzymać ten

poziom użyteczności przy zmianie

p

x

a utrzymaniu

niezmienionej

p

y

, konsument musi otrzymać

M

2

.

Wyprowadzenie zakotwiczonych funkcji skompensowanego
popytu
Wykorzystując nasz przykład możemy określić użyteczność
dla (

y

x

p

p

M

;

;

) dzięki przekształceniu pośredniej funkcji

użyteczności:

y

x

p

p

M

U

4

2

=

Możemy teraz zakotwiczyć funkcje skompensowanego

popytu na wartości:

y

x

p

p

M

4

2

wyznaczającej ograniczenie

użyteczności (

U

). Posługując się tą metodą możemy

wyprowadzić funkcje skompensowanego popytu, które nie
zależą bezpośrednio od użyteczności. Jest to szczególnie
ważne przy estymowaniu popytu, gdyż użyteczność nie jest
zmienną obserwowalną.

Wyprowadzając funkcje skompensowanego popytu dla punktu
zakotwiczenia musimy dokonać rozróżnienia między
dochodem i cenami wykorzystanymi do obliczenia
ograniczenia użyteczności (

y

x

p

p

M

;

;

) i zmiennymi cenami i

dochodem wykorzystanymi do skonstruowania funkcji
skompensowanych popytów. W przykładzie utrzymamy

p

y

na

stałym poziomie (

y

p

) i pozwolimy

p

x

zmieniać się względem

(

x

p

). Za każdym razem kiedy zmieni się

p

x

znajdziemy

M*

,

czyli minimalny dochód niezbędny do utrzymania

U

.

16

Utrzymując użyteczność i

p

y

na stałym poziomie (

U

,

y

p

)

możemy wyprowadzić funkcję skompensowanego popytu na
dobro

X

jako funkcję od

p

x

wstawiając

U

i

y

p

do

uogólnionej funkcji skompensowanego popytu na dobro

X

. Po

zrobieniu tego musimy utrzymać parametr

x

p

wykorzystany

do zakotwiczenia ograniczenia użyteczności, gdyż to była
cena dobra

X

wykorzystana do obliczenia

U

. Funkcja jest

więc wyprowadzona względem tego punktu. Postać funkcyjna
będzie więc zawierać zarówno

x

p

, jak i

p

x

.

Wstawiając

y

x

p

p

M

U

4

2

=

i

y

p

do

2

1

*













=

U

p

p

x

x

y

c

otrzymujemy:

.

1

2

4

2

1

2

1

2

2

1

*















=















=















=

x

x

y

x

x

y

x

y

c

p

p

M

p

p

M

p

p

U

p

p

x

Analogicznie otrzymujemy skompensowany popyt na dobro

Y

:

.

2

4

2

1

2

1

2

2

1

*















=















=















=

x

x

y

y

x

y

x

y

x

c

p

p

p

M

p

p

M

p

p

U

p

p

y

Możemy wyznaczyć

M*

, minimalny dochód niezbędny do

utrzymania użyteczności

U

, wstawiając

.

1

2

2

1

*















=

x

x

c

p

p

M

x

i

.

2

2

1

*















=

x

x

y

c

p

p

p

M

y

do funkcji celu problemu dualnego,

M

=

p

x

x

+

p

y

y

, utrzymując

p

y

na poziomie

y

p

:

x

p

M

=

*

2

1

1

2















x

x

p

p

M

2

1

2

1

2















=















+

x

x

x

x

y

y

p

p

M

p

p

p

M

p

.

2

1

*















=

x

x

p

p

M

M

: minimalny dochód.

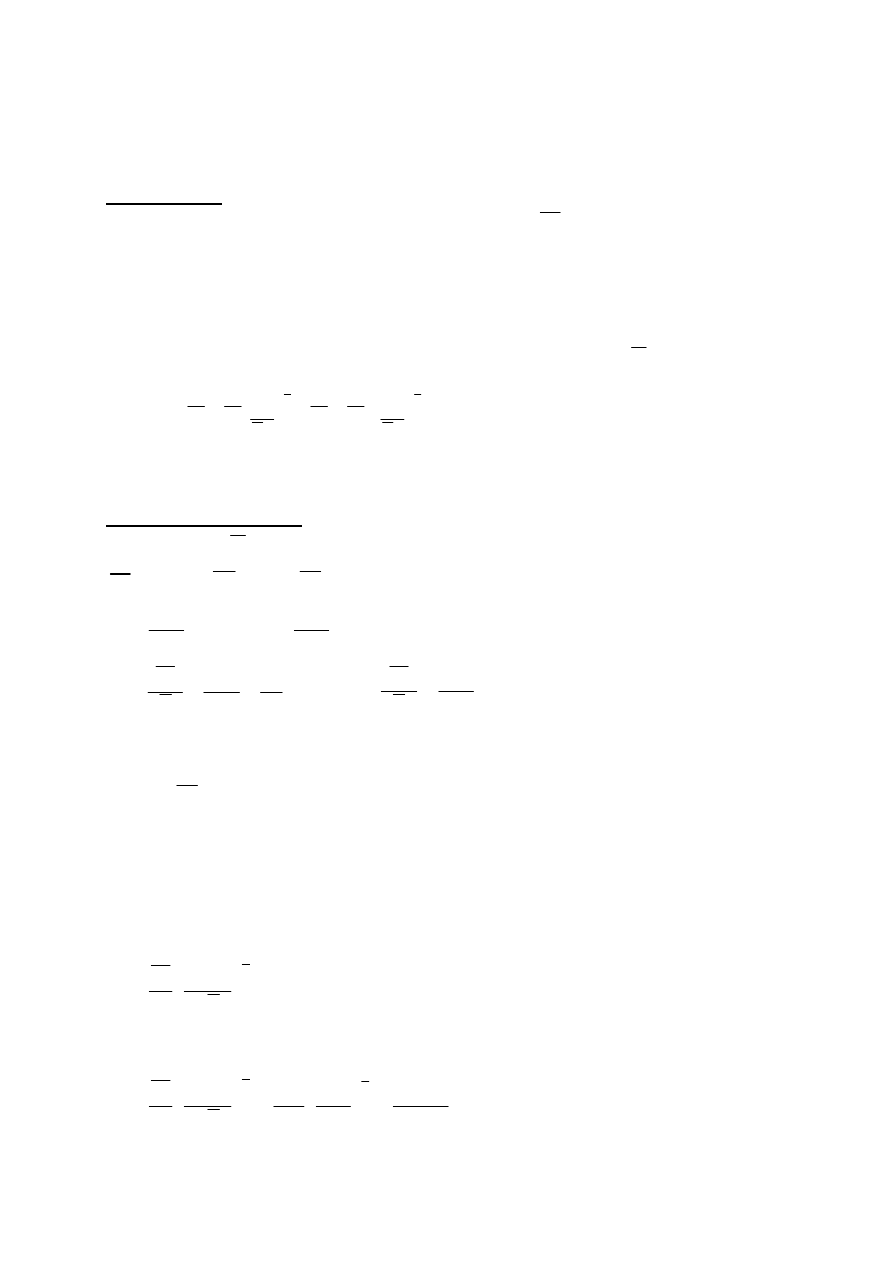
17

Aby osiągnąć minimalny dochód niezbędny do utrzymania
danego poziomu użyteczności konsumentowi trzeba dać
subwencję równą różnicy między hipotetycznym, minimalnym
dochodem i rzeczywistym dochodem,

M

. Aby wyznaczyć tą

minimalną subwencję niezbędną do osiągnięcia minimalnego,
skompensowanego dochodu odejmujemy rzeczywisty dochód
od minimalnego dochodu skompensowanego. Jeżeli

S*

to

minimalna subwencja potrzebna do utrzymania

U

, to:





















−















=

−















=

−

=

1

*

*

2

1

2

1

x

x

x

x

p

P

M

M

p

P

M

M

M

S

Przykład liczbowy
Określimy

U

dla początkowego dochodu i zbioru cen:

M

= 100;

y

p

= 5;

x

p

= 4. Wstawimy te wielkości do

x

p

M

x

2

*

=

i

y

p

M

y

2

*

=

otrzymując:

2

25

)

4

(

2

100

2

*

=

=

=

x

p

M

x

i

10

)

5

(

2

100

2

*

=

=

=

y

p

M

y

Taki wybór generuje użyteczność:

125

2

25

10

*

=













=

U

.

Jeżeli utrzymamy użyteczność na poziomie 125 i

p

y

= 5, to

możemy wyznaczyć funkcje skompensowanego popytu na

X

i

Y

jako funkcje

p

x

wstawiając przyjęte wielkości liczbowe do

x

c

*:

.

1

2

2

1

*















=

x

x

c

p

p

M

x

Obliczamy więc

*

c

x

:

( )

2

/

1

2

1

2

1

*

25

4

1

2

100

1

2

x

x

x

x

c

p

p

p

p

M

x

=













=















=

.

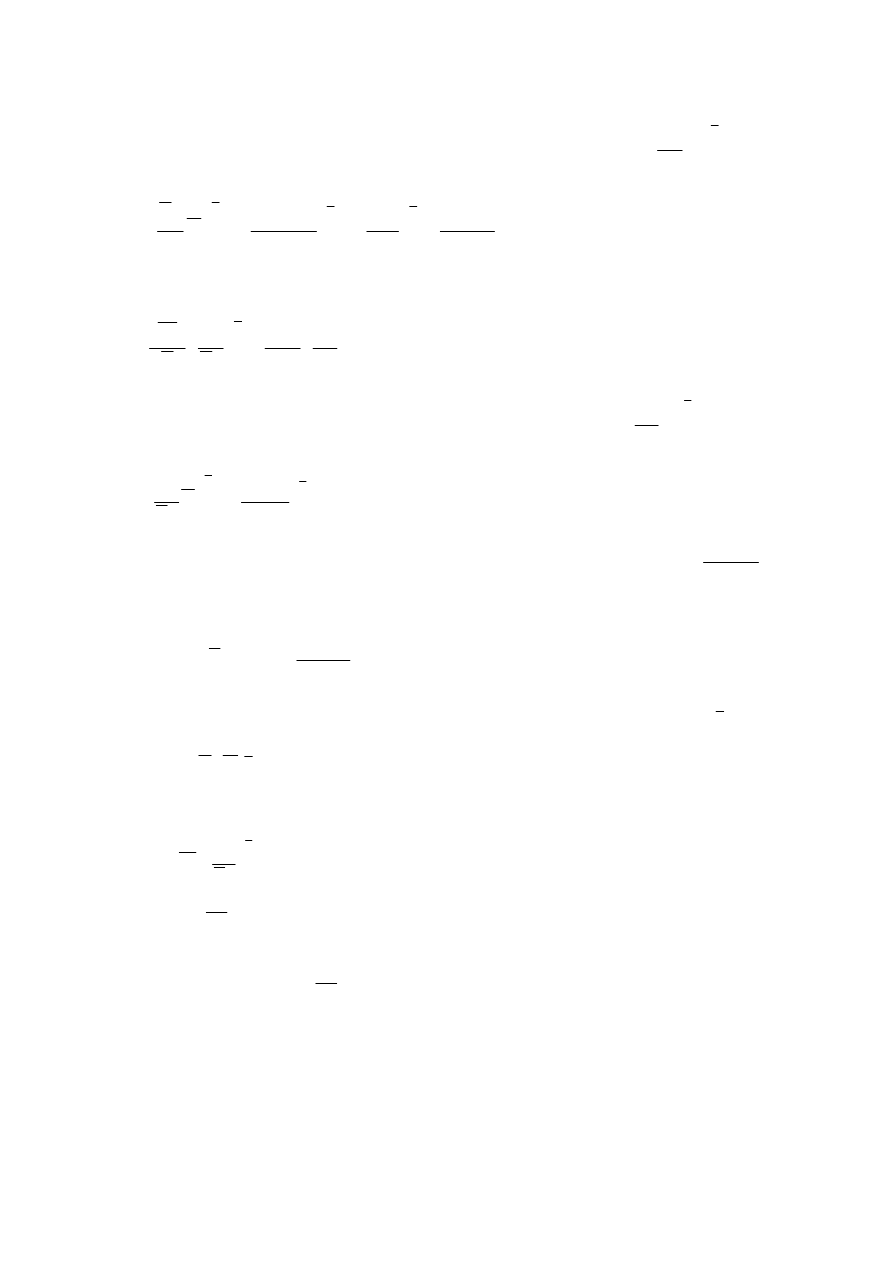
18

Alternatywnie możemy wstawić:

U*

= 125 do

2

1

*













=

U

p

p

x

x

y

c

( )

2

/

1

2

1

2

1

2

1

*

25

625

)

125

)(

5

(

x

x

x

x

y

c

p

p

p

U

p

p

x

=













=













=















=

Aby znaleźć

*

c

y

:

2

/

1

2

/

1

2

1

*

)

(

5

4

)

5

(

2

100

2

x

x

x

x

y

c

p

p

p

p

p

M

y

=













=















=

Alternatywnie można wstawić:

U*

= 125 do

2

1

*















=

U

p

p

y

y

x

c

:

(

)

( )

2

/

1

5

25

5

125

2

/

1

2

1

2

1

*

x

x

x

y

x

c

p

p

p

U

p

p

y

=

=













=















=

.

Aby wyznaczyć minimalny dochód wstawiamy

( )

2

/

1

*

25

x

c

p

x

=

i

( )

2

/

1

5

*

x

c

p

y

=

do funkcji celu:

( )

( )

[

]

( )

( )

( )

2

/

1

2

/

1

2

/

1

2

/

1

2

/

1

*

*

50

25

25

5

5

25

*

x

x

x

x

x

x

c

y

c

x

p

p

p

p

p

p

y

p

x

p

M

=

+

=

+

















=

+

=

.

Alternatywnie można wstawić

U*

= 125 do

(

)

2

1

2

*

U

p

p

M

y

x

=

:

(

)

[

]

( )

2

/

1

2

/

1

2

1

50

)

125

)(

5

(

2

2

*

x

x

y

x

p

p

U

p

p

M

=

=

=

.

Aby wyznaczyć optymalną subwencję wstawiamy

( )

2

/

1

50

*

x

p

M

=

do





















−















=

1

*

2

1

x

x

p

P

M

S

:

100

)

(

50

*

*

2

/

1

−

=

−

=

x

p

M

M

S

.

Pamiętamy, że „zakotwiczyliśmy” krzywą skompensowanego
popytu określając

x

p

= 4. Jeśli więc

p

x

zwiększy się ponad 4,

to optymalna subwencja będzie dodatnia. Jeśli natomiast

p

x

zmniejszy się poniżej 4, to optymalna subwencja będzie
ujemna. Jeżeli

p

x

pozostanie na poziomie 4, to optymalna

19

subwencja wyniesie 0. (Informacja ta jest zawarta w
równaniu:

100

)

(

50

*

*

2

/

1

−

=

−

=

x

p

M

M

S

.)

0

100

)

4

(

50

2

/

1

=

−

: niezmieniona cena

50

100

)

9

(

50

2

/

1

=

−

: wyższa cena

50

100

)

1

(

50

2

/

1

−

=

−

: niższa cena.

Matematyczne wyprowadzenie efektu

substytucyjnego i dochodowego

Nasz przykład możemy teraz rozszerzyć do obliczenia ES i
ED związanych ze zmianą ceny dobra X. Jak pamiętamy
początkowe parametry zostały określone w sposób
następujący:

M

= 100;

y

p

= 5;

x

p

= 4.

Przy tych parametrach początkowy wybór x i y wyniósł:
x* = 25/2 = 12.5 i y* = 10.
Przyjmijmy teraz, że p

x

rośnie do 5. Możemy teraz określić

x

c

* i y

c

* przy nowej cenie na X:

( )

( )

( )

18

,

11

)

24

,

2

(

5

5

5

5

25

25

2

/

1

2

/

1

2

/

1

*

=

≈

=

=

=

x

c

p

x

( )

( )

18

,

11

)

24

,

2

(

5

5

5

5

2

/

1

2

/

1

*

=

≈

=

=

x

c

p

y

Tak więc ES wynosi:
(x*, y*)

→

(x

c

*, y

c

*) = (12,5; 10)

→

(11,18; 11,18)

Ponownie skoncentrujemy się wyłącznie na X. ES wywołany
wzrostem ceny p

x

z 4 na 5 prowadzi do zmniejszenia

wielkości popytu wzdłuż krzywej skompensowanego popytu z
12,5 jednostek do 11,18 jednostek.
Aby utrzymać początkowy poziom użyteczności konsument
potrzebuję wyższego dochodu niż przed wzrostem ceny.
Można go obliczyć wstawiając p

x

= 5 do

( )

2

/

1

50

*

x

p

M

=

:

( )

112

)

24

,

2

(

50

)

5

(

50

50

*

2

/

1

2

/

1

=

≈

=

=

x

p

M

.

20

Subwencja potrzebna do utrzymania konsumenta na poziomie
użyteczności

U

po wzroście ceny wynosi:

12

100

112

*

*

=

−

=

−

=

M

M

S

.

Przy p

x

= 5, jeżeli byśmy zabrali konsumentowi subwencję w

wysokości 12, to nowy nieskompensowany popyt wyniósłby:

10

)

5

(

2

100

2

*

=

=

=

x

u

p

M

x

i

10

)

5

(

2

100

2

*

=

=

=

y

u

p

M

y

.

Tak więc IE wynosi:
(x

c

*, y

c

*)

→

(x

u

*, y

u

*) = (11,18; 11,18)

→

(10; 10)

Ponownie koncentrując się na dobrze X, możemy stwierdzić,
że ED wywołany wzrostem ceny p

x

z 4 do 5 wzmacnia

zmniejszenie wielkości popytu wzdłuż krzywej Engla przy p

x

= 5 z około 11,18 jednostek do 10 jednostek.

Równanie Słuckiego

Jak już zobaczyliśmy ES i ED mogą być wykorzystywane do
badania zależności między dobrami normalnymi i opadającą
krzywą popytu. Pokazaliśmy, że jeden z dwóch warunków
wystarcza aby zagwarantować ujemne nachylenie zwykłej
krzywej popytu:

1. analizowane dobro jest dobrem normalnym lub
2. w przypadku dobra niższego rzędu ES jest silniejszy od

ED.

Te wnioski dotyczące nachylenia krzywej popytu można
przedstawić za pomocą równania zawierającego nachylenia
odpowiednich krzywych popytu, a zwanego równaniem
Słuckiego. Zaczniemy od zapisania równania i zastanowimy
się, w jaki sposób ilustruje ono to, co przed chwilą
stwierdziliśmy. Następnie zobaczymy, jak to równanie można
wyprowadzić z rozwiązania problemu minimalizacji wydatków.

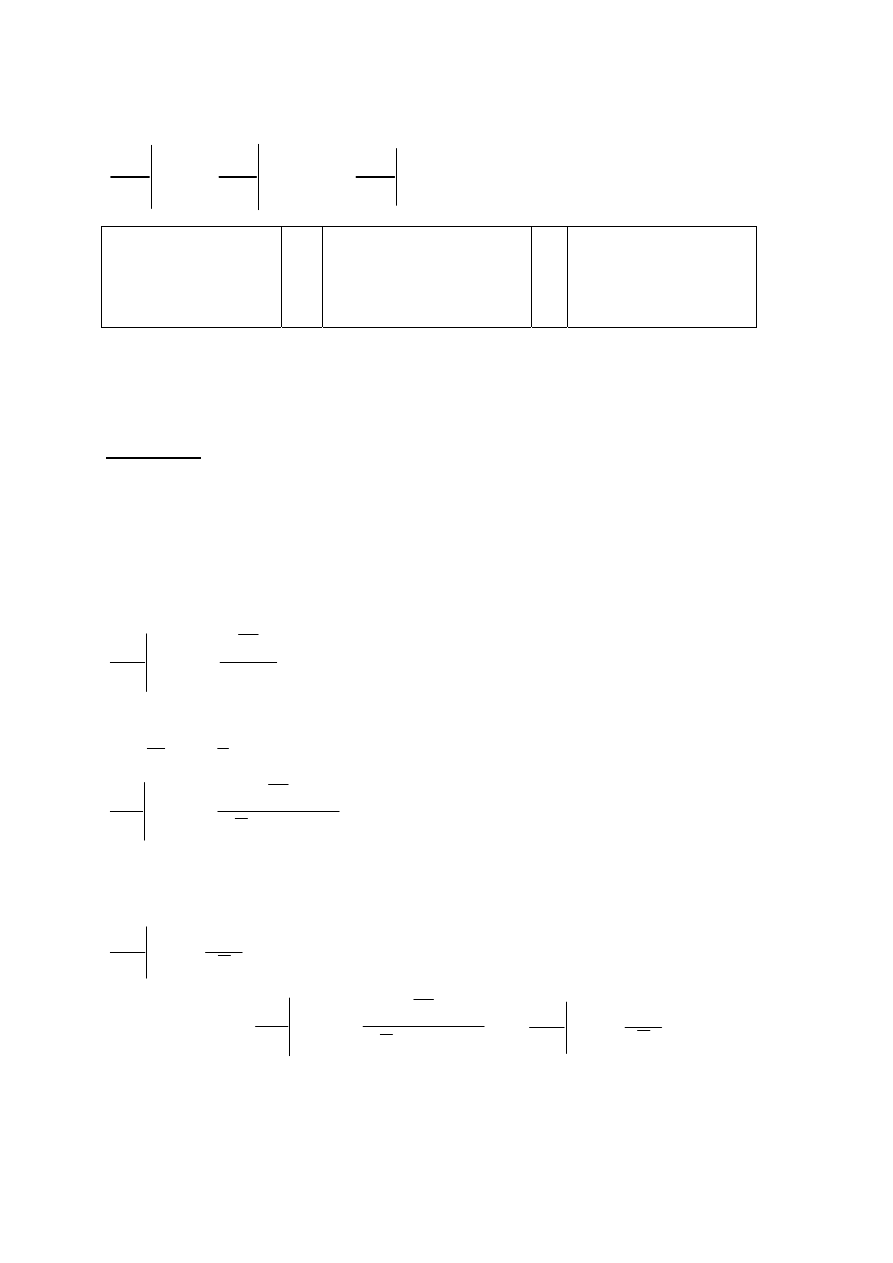
21

Równanie Słuckiego:

0

0

0

0

*

0

0

*

*

*

=

=

=

=

=

=

−

=

y

x

y

y

dp

dp

dp

dU

x

c

dp

dM

x

dM

dx

x

dp

dx

dp

dx

Nachylenie
normalnej
funkcji popytu

=

Nachylenie
funkcji popytu
skompensowanego

-

x*

(nachylenie

krzywej Engla)

Lub:
Całkowity efekt = efekt substytucyjny – efekt dochodowy

Przykład
Możemy zilustrować równanie Słuckiego wstawiając
nachylenia funkcji popytu wyprowadzonych z funkcji
użyteczności: U = xy do równania Słuckiego. Wiemy, że
zwyczajną funkcję (nieskompensowanego) popytu na X
opisuje wzór: x* = M/2p

x

. Czyli:

( )

2

0

0

2

*

x

dp

dM

x

p

M

dp

dx

y

−

=

=

=

.

Zakotwiczona funkcja skompensowanego popytu:

(

)

2

/

1

*

,

2

/

y

x

c

p

p

M

x

=

. Czyli:

( )

( )

2

/

3

2

/

1

0

0

*

4

x

x

dp

dM

x

c

p

p

M

dp

dx

y

−

=

=

=

.

Można wyprowadzić krzywą Engla z równania : x* = M/2p

x

.

Czyli:

x

dp

dp

p

dM

dx

y

x

2

1

*

0

0

=

=

=

.

Wstawiając

( )

( )

2

/

3

2

/

1

0

0

*

4

x

x

dp

dM

x

c

p

p

M

dp

dx

y

−

=

=

=

i

x

dp

dp

p

dM

dx

y

x

2

1

*

0

0

=

=

=

, równanie

Słuckiego przyjmuje postać:

22

( )

( )

x

x

x

dp

dM

x

p

x

p

p

M

dp

dx

y

2

1

*

4

*

2

/

3

2

/

1

0

0

−

−

=

=

=

.

Wstawiając zwyczajną funkcję popytu na x* do ostatniego
równania i pozwalając aby

x

x

p

p

=

, (gdyż została wyznaczona

dla nieskończenie małej zmiany p

x

)

( )

( )

( )

( )

2

2

2

2

0

0

2

4

4

2

1

2

4

*

x

x

x

x

x

x

dp

dM

x

p

M

p

M

p

M

p

p

M

p

M

dp

dx

y

−

=

−

−

=

−

−

=

=

=

,

co jest wynikiem, jaki uzyskaliśmy:

( )

2

0

0

2

*

x

dp

dM

x

p

M

dp

dx

y

−

=

=

=

przy

różniczkowaniu zwyczajnej funkcji popytu względem p

x

.

Funkcje popytu o nachyleniu ujemnym i dodatnim
Znak nachylenia zwyczajnej funkcji popytu można wyznaczyć
dzięki określeniu znaków każdego z komponentów równania
Słuckiego i porównując ED i ES, gdy dobro jest niższego
rzędu. Po pierwsze, określamy znak każdego komponentu:

1. Nachylenie funkcji skompensowanego popytu jest

ujemne ze względu na malejącą MRS.

2. x* jest dodatnie, gdyż X jest dobrem konsumpcyjnym.
3. Nachylenie krzywej Engla jest dodatnie, gdy X jest

dobrem normalnym I ujemne, gdy X jest dobrem
niższego rzędu.

23

Możemy streścić znaki nachyleń funkcji popytu w
następujący sposób:
Dobro normalne:

Nieskompensowany
(-)

=
skompensowany
= (-)

-x*(krzywa
Engla)
-(+) (+)

Ujemne
nachylenie

Dobro niższego rzędu:

Nieskompensowany
(-)

=
skompensowany
= (-)

-x*(krzywa
Engla)
-(+) (-)

Ujemne
nachylenie

SE jest silniejszy od DE

(+)

= (-)

-(+) (-)

Upward sloping

DE jest silniejszy od DE

Wyprowadzenie równania Słuckiego
Aby wyprowadzić równanie Słuckiego zaczniemy od
rozwiązania problemu minimalizacji wydatków:

(

)

*

*

;

;

*

c

y

c

x

y

x

y

p

x

p

U

p

p

M

+

=

=

Wiemy, że optymalne rozwiązania problemy pierwotnego i
dualnego mają te same rozwiązania x* i y* przy tej samej
krzywej obojętności i linii ograniczenia budżetowego. Dla

U*

=

U

i

M*

=

M

, funkcje popytu skompensowanego I

nieskompensowanego muszą dać te same wartości x i y. Dla
tych równości możemy przekształcić równania

(

)

(

)

(

)

(

)

M

p

p

U

p

p

x

U

p

p

M

p

p

x

y

x

y

x

c

y

x

y

x

;

;

*

;

;

;

;

*

;

;

*

*

=

do postaci:

(

)

(

)

(

)

U

p

p

M

p

p

x

U

p

p

x

y

x

y

x

y

x

c

;

;

*

;

;

*

;

;

*

=

Różniczkując obie strony ostatniego równania względem p

x

:

x

x

x

c

p

M

M

x

p

x

p

x

∂

∂

∂

∂

+

∂

∂

=

∂

∂

*

*

*

*

,

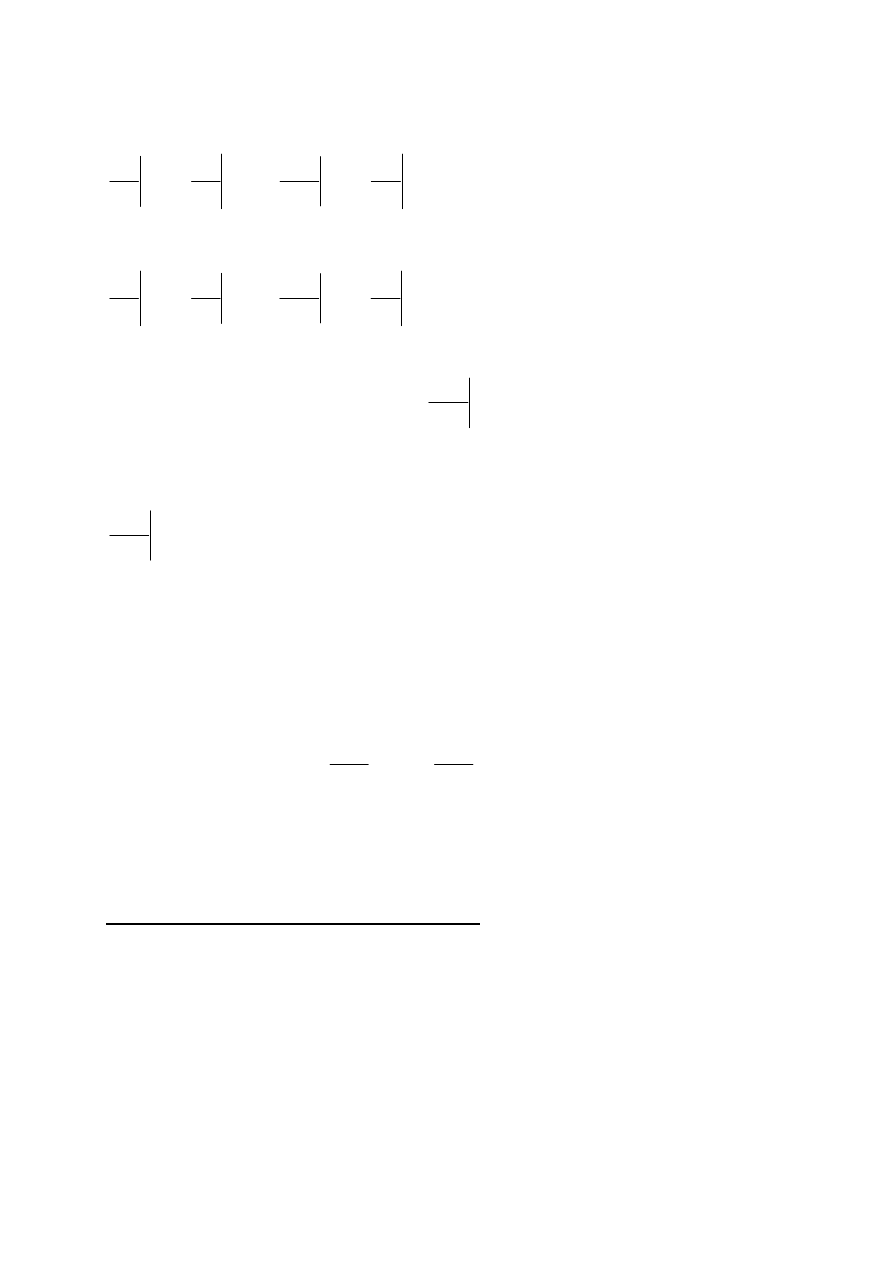
24

co przekształcamy do postaci:









































+

=

=

=

=

=

=

=

=

=

0

0

*

0

0

0

0

*

0

0

*

*

y

x

y

y

y

dp

dp

dp

dU

x

dp

dM

x

dp

dU

x

c

dM

dx

dp

dM

dp

dx

dp

dx

.

Przekształcamy wyrażenia w ostatnim równaniu:









































−

=

=

=

=

=

=

=

=

=

0

0

*

0

0

0

0

*

0

0

*

*

y

x

y

y

y

dp

dp

dp

dU

x

dp

dU

x

c

dp

dM

x

dM

dx

dp

dM

dp

dx

dp

dx

.

Widzimy, że ostatnie równanie jest takie samo, jak równanie
Słuckiego oprócz wyrażenia:

0

0

*

=

=

y

dp

dU

x

dp

dM

.

W równaniu Słuckiego wyrażenie to jest po prostu x*. Jeżeli
możemy wykazać, że:

*

*

0

0

x

dp

dM

y

dp

dU

x

=

=

=

,

to wykażemy, że równanie Słuckiego jest poprawne. Aby to
zrobić odwołamy się do twierdzenia o obwiedni. Wiemy, że
pochodna funkcji celu względem jednego z parametrów jest
pochodną cząstkową, pomijając drugorzędne zmiany
parametru. Innymi słowy jeżeli:

*

*

*

y

p

x

p

M

y

x

+

=

, to

*

*

x

p

M

x

=

∂

∂

i

*

*

y

p

M

y

=

∂

∂

.

Ten wniosek nosi nazwę lematy Hotellinga I pokazuje, że
równanie Słuckiego jest prawdziwe.

Interpretacja równania Słuckiego
Interpretacja równania Słuckiego sprowadza się do
stwierdzenia, że nieskończenie mała zmiana wzdłuż zwykłej
krzywej popytu może być podzielona na dwie części. Zmiana
wzdłuż krzywej popytu skompensowanego to SE. Zmiana
wzdłuż krzywej Engla ważona wielkością dobra w
rzeczywistości nabywaną to DE. W przypadku dóbr niższego

25

rzędu, DE może być silniejszy od SE i zwykła krzywa popytu
może mieć nachylenie dodatnie.

Elastyczność substytucji

i wielkość efektu substytucyjnego

Konsumenci z krzywymi obojętności o różnych kształtach
będą mieli różne efekty substytucyjne dla danej zmiany
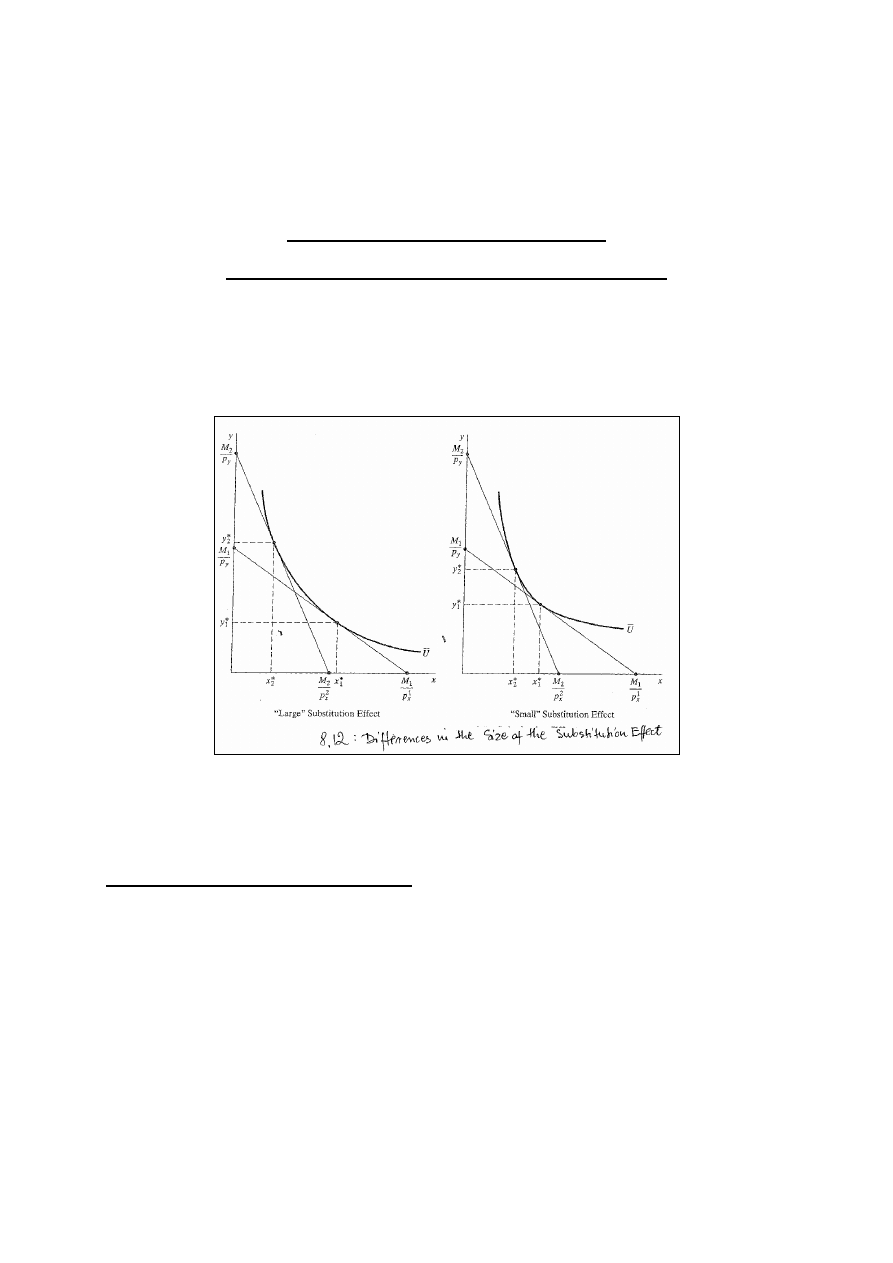
ceny. Siłę substytucji pokazuje rys. 8.12.

Do porównywania efektów substytucyjnych u poszczególnych
konsumentów wykorzystujemy miernik określany mianem:
elastyczności substytucji. (W lewej części rysunku
elastyczność substytucji jest względnie duża.)

26

Elastyczność substytucji mierzy procentową zmianę

stosunku y/x spowodowaną procentową zmianą stosunku cen.

Przyjmijmy oznaczenia:

=

yx

σ

elastyczność substytucji Y na miejsce X

=

x

y

stosunek wielkości zakupu Y do X

=

y

x

p

p

stosunek cen

Dla ułatwienia załóżmy:

x

y

≡

Ψ

i

y

x

p

p

≡

Ρ

.

Mamy więc:

Ψ

∆Ρ

Ρ

∆Ψ

=

Ρ

∆Ρ

Ψ

∆Ψ

=

=

/

/

/

/

/

_

_

/

_

_

y

x

yx

p

p

zmiana

procentowa

x

y

zmiana

procentowa

σ

.

Czyli:

(

)

(

)

x

y

p

p

p

p

d

x

y

d

y

x

y

x

yx

/

/

/

/

/

/

=

Ψ

∆Ρ

Ρ

∆Ψ

=

σ

.

Wyprowadzając krzywą popytu skompensowanego dla funkcji

U

=

xy

stwierdziliśmy, że

y

x

p

p

x

y =

(krzywa konsumpcji

dochodowej). Dlatego dla tej funkcji użyteczności:

1

1

1

=

Ρ

Ρ

=

Ψ

Ρ

=

⇒

=

Ρ

Ψ

⇒

Ρ

=

Ψ

yx

d

d

σ

.

Warunek:

1

=

yx

σ

charakteryzuje funkcje użyteczności typu

Cobb – Douglas’a, np.

U

=

x

α

y

β

dla

x

,

y

> 0. Aby to wykazać

posługujemy się krzywą konsumpcji dochodowej:

x

p

p

y

y

x

α

β

=

.

Po przekształceniu otrzymujemy:

y

x

p

p

x

y

α

β

=

,

lub:

(

)

1

/

=

Ρ

Ρ

=

Ψ

Ρ

Ρ

Ψ

⇒

Ρ

=

Ψ

α

β

α

β

α

β

d

d

27

Inne funkcje użyteczności mają inne elastyczności
substytucji, np. dla

y

x

xy

U

+

=

wyznaczamy:

(

)

(

)

(

)

(

)

y

x

y

x

p

p

x

y

y

x

xy

y

x

x

y

x

xy

y

x

y

MU

MU

MRS

=

=

+

−

+

+

−

+

=

=

2

2

2

2

i po obliczeniu pierwiastków kwadratowych otrzymujemy:

2

1

2

1

2

/

1

2

/

1

2

/

1

2

/

1

=

Ρ

Ρ

Ρ

=

Ψ

Ρ

Ρ

Ψ

=

Ρ

=

Ψ

⇒















=

−

d

d

p

p

x

y

yx

y

x

σ

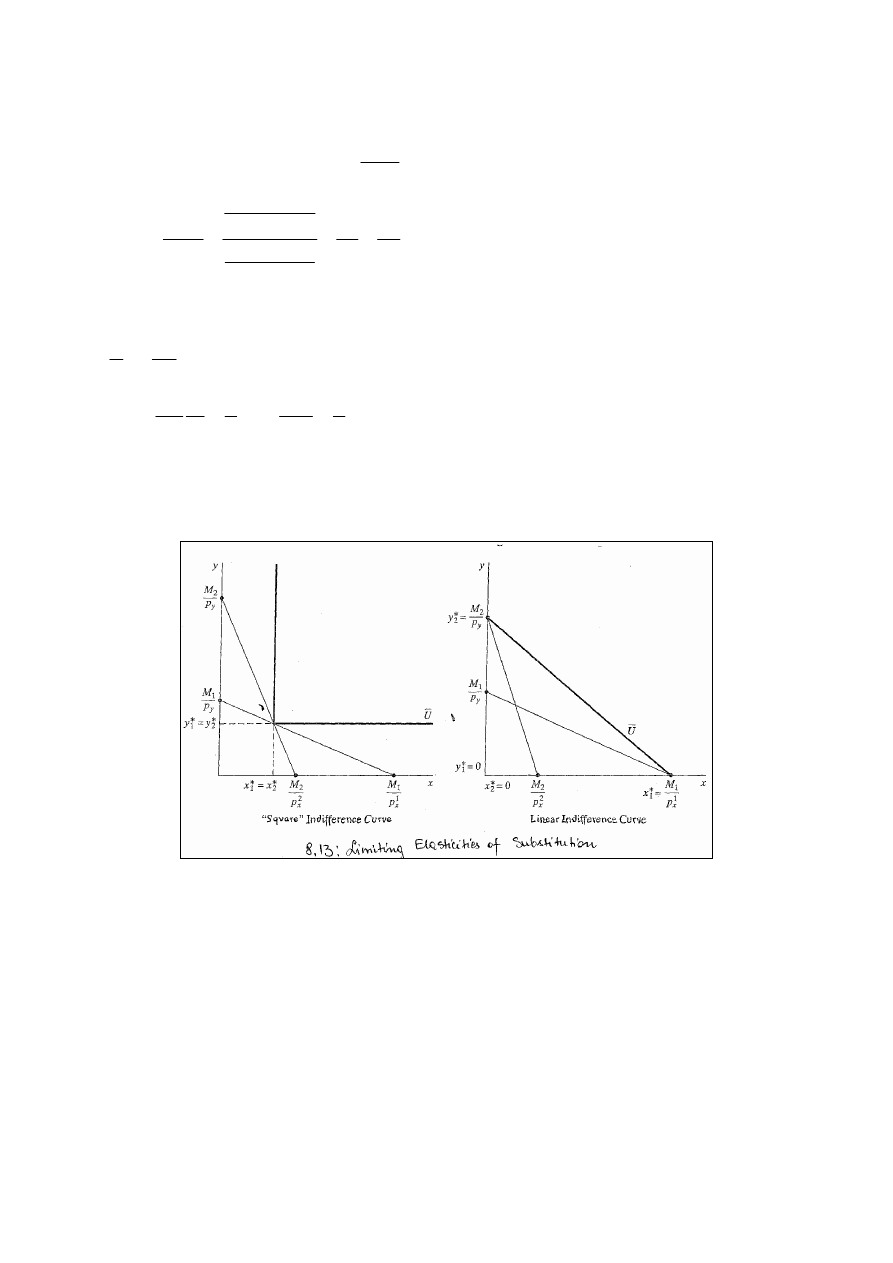
Skrajne przypadki elastyczności substytucji pokazuje rys.
8.13.