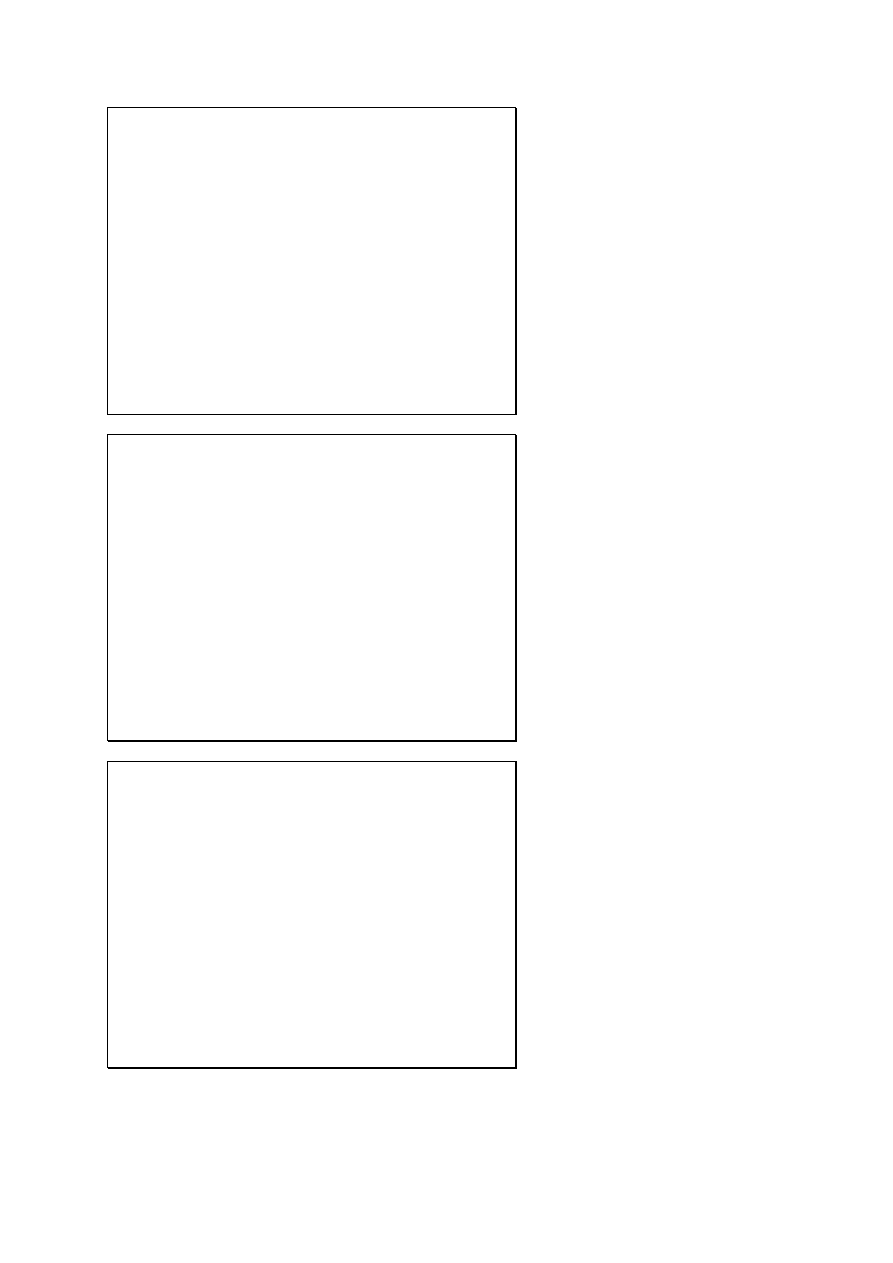
Fizyka kwantowa

dotyczy świata mikroskopowego

wiele wielkości jest skwantowanych,

tzn. występuje w całkowitych

wielokrotnościach pewnych minimalnych

porcji zwanych kwantami

 

Foton, kwant światła

Zjawiska świadczące o kwantowej naturze

światła:
zjawisko fotoelektryczne – energia

kwantów - równanie Einsteina
efekt Comptona - pęd fotonów
widma emisyjne atomów
prawidłowy opis promieniowania

termicznego z postulatem kwantyzacji

energii świetlnej - prawo Plancka

„

„

„

„

 

Zjawisko fotoelektryczne

Wiązka światła wybija elektrony z powierzchni metalu
z falowej teorii wynika:

elektron nie opuści metalu dopóki amplituda fali E

o

nie

przekroczy określonej wartości krytycznej
energia emitowanych elektronów wzrasta proporcjonalnie

do E

o

2

liczba emitowanych elektronów powinna zmniejszyć się ze

wzrostem częstotliwość światła

wyniki eksperymentalne:

progowego natężenia nie zaobserwowano
energia elektronów okazała się niezależna od wielkości E

o

zauważono zależność energii elektronów od częstotliwości

„

„

„

„

„

„

„

„

„

 

Teoria Einsteina

światło o częstości

ν

stanowi zbiór pakietów

energii zwanych fotonami lub kwantami z

których każdy posiada energię h

ν

h to uniwersalna stała Plancka = 6.626×10

–34

Js

kwanty światła (fotony) zachowują się podobnie

do cząstek materialnych (przy zderzeniu foton

może być pochłonięty, a cała jego energia

przekazana jest elektronowi).
maksymalna energia kinetyczna elektronu

opuszczającego metal o pracy wyjścia W

o

wynosi

o

W

h

K

−

ν

=

max

„

„

„

„

 

Doświadczenia

fotoelektryczne

j

A

U

j

U

U

h

I

o

2I

o

liczba emitowanych elektronów

(prąd j) rośnie ze wzrostem

natężenia światła I

o

maksymalna energia elektronów

K

max

=U

h

nie zależy od natężenia

światła I

o

, rośnie ze wzrostem

częstotliwości ν

o

W

h

K

−

ν

=

max

o

o

W

h

=

ν

max

K

ν

o

ν

częstość progowa

0

K

T

materiał

tarczy:

 

Pęd fotonu

Foton, oprócz energii E=h

ν, posiada również pęd p

Zgodnie z teorią relatywistyczną wszystkie cząstki

które posiadają energię muszą posiadać pęd,

nawet jeśli nie mają masy spoczynkowej

λ

ν

h

c

h

c

E

p

=

=

=

pc

E =

( )

(

)

2

2

2

2

c

m

pc

E

o

+

=

0

=

o

m

Kierunek pędu fotonu jest zgodny z kierunkiem

rozchodzenia się fali elektromagnetycznej

Foton nie ma ładunku elektrycznego ani momentu

magnetycznego, ale może oddziaływać z innymi cząstkami

 

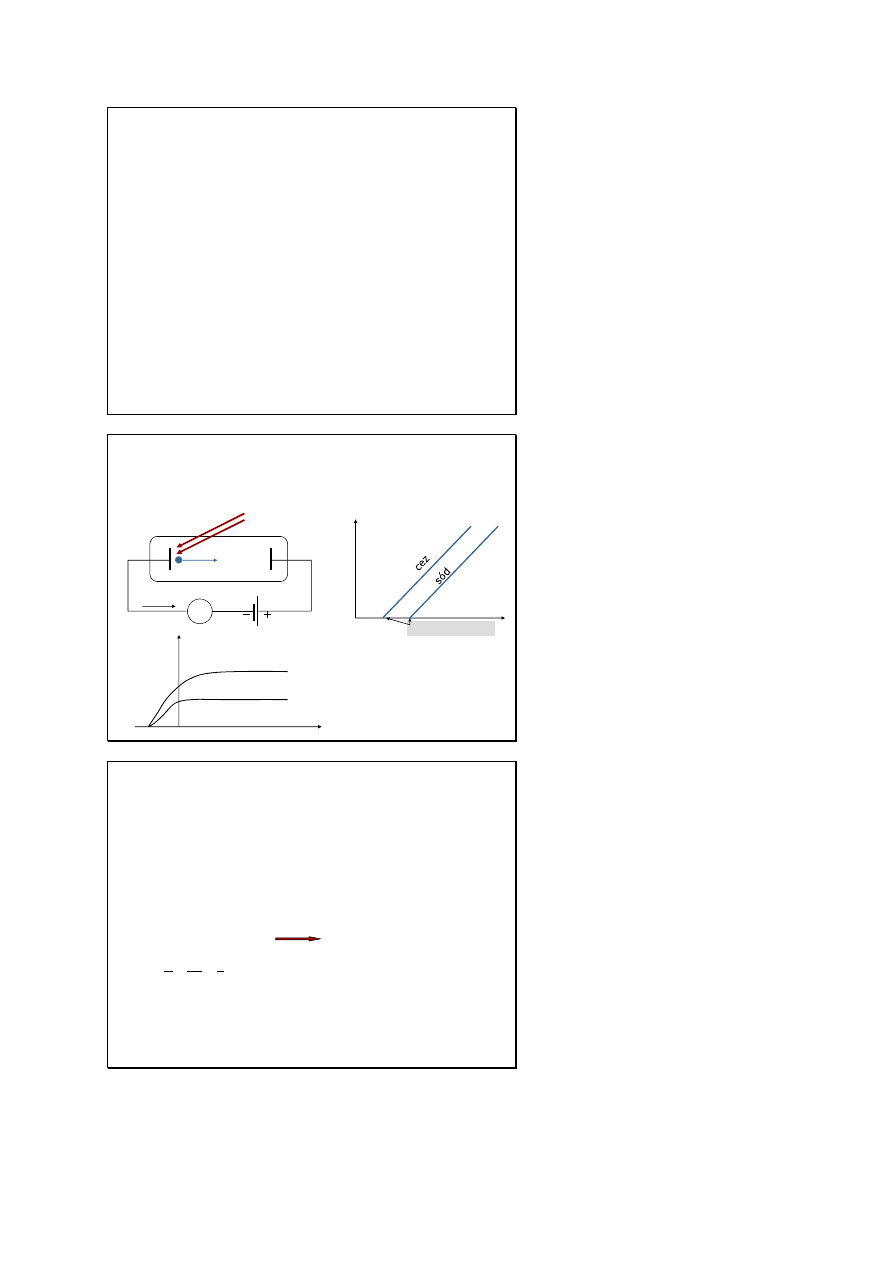
Efekt Comptona

Rozpraszanie fotonów na swobodnych elektronach:

wiązka promieniowania rentgenowskiego o długości

fali

λ rozpraszana przez grafitową tarczę zmieniała

swą długość w zależności od kąta rozpraszania

θ .

W klasycznym podejściu długość fali wiązki

rozproszonej powinna być taka sama jak padającej.

θ

detektor

szczeliny

kolimujące

λ

'

λ

tarcza

grafitowa

wiązka

rozproszona

promieniowanie

rentgenowskie

pr

hν

'

pr

e

p'

r

θ

przed zderzeniem

po

e

e

z prawa zachowania energii

i pędu przed i po zderzeniu

e

E

h

h

'

'

+

=

ν

ν

e

p

p

p

'

' r

r

r

+

=

(

)

θ

−

=

λ

−

λ

cos

'

1

mc

h

λ

ν

h

c

h

p

=

=

pc

E

=

 

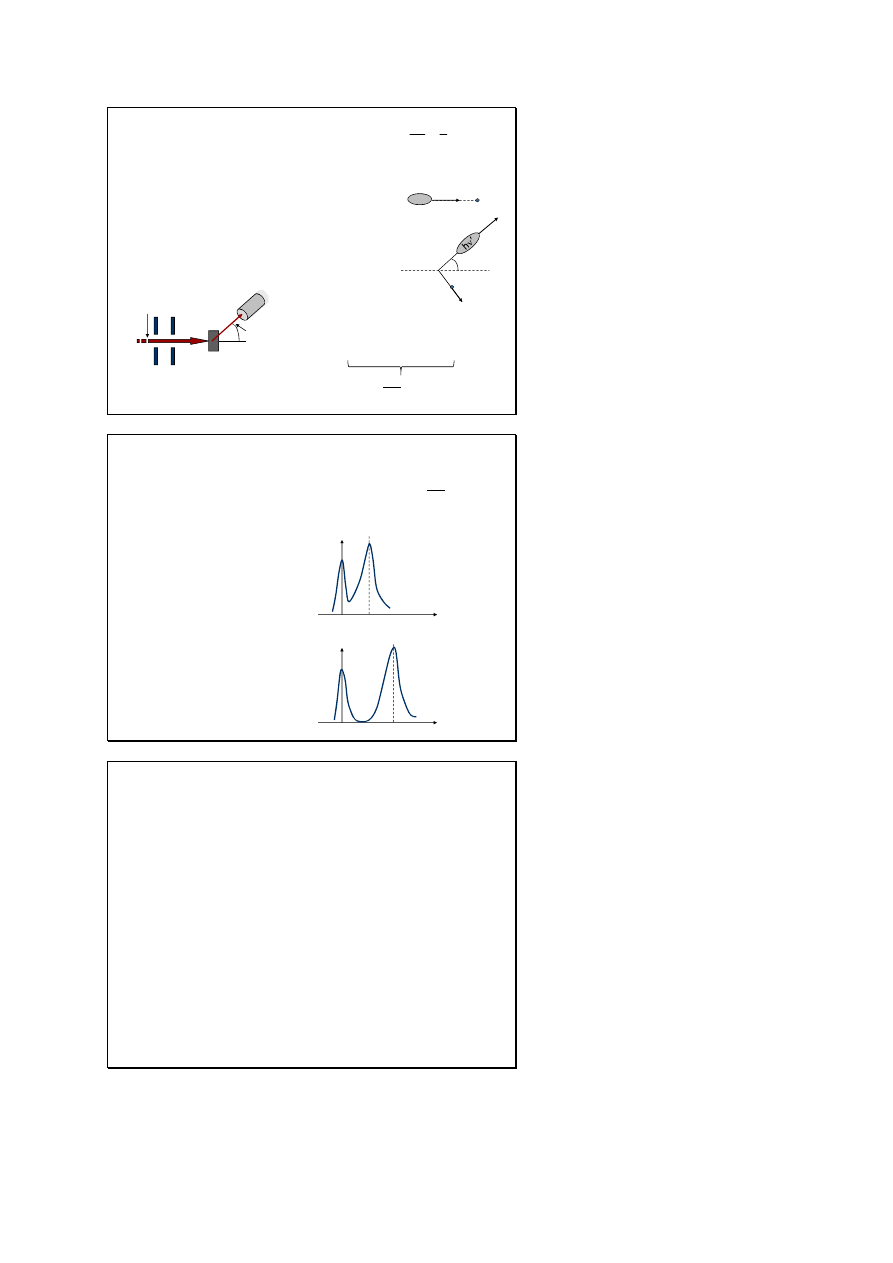
Wyniki doświadczenia

Comptona

przesunięcie comptonowskie

Δλ=λ’-λ zwiększa się wraz ze

wzrostem kąta rozpraszania
obecność wiązki o nie

zmienionej długości fali

wynika z rozproszenia na

elektronach związanych
im większa masa cząstki tym

mniejsze przesunięcie Δλ

efekt Comptona potwierdza

korpuskularny charakter

światła – fotony obdarzone

energią i pędem

„

„

„

„

λ

λ’

I

o

długość fali

ϕ=90°

λ

λ’

I

o

długość fali

ϕ=135°

(

)

θ

−

=

λ

−

λ

cos

'

1

mc

h

 

Widma emisyjne atomów

pochodzenie dyskretnych linii

spektralnych można wyjaśnić w

oparciu o dwa założenia:

pojęcie fotonu
istnienie poziomów energetycznych

atomu

„

„

„

 

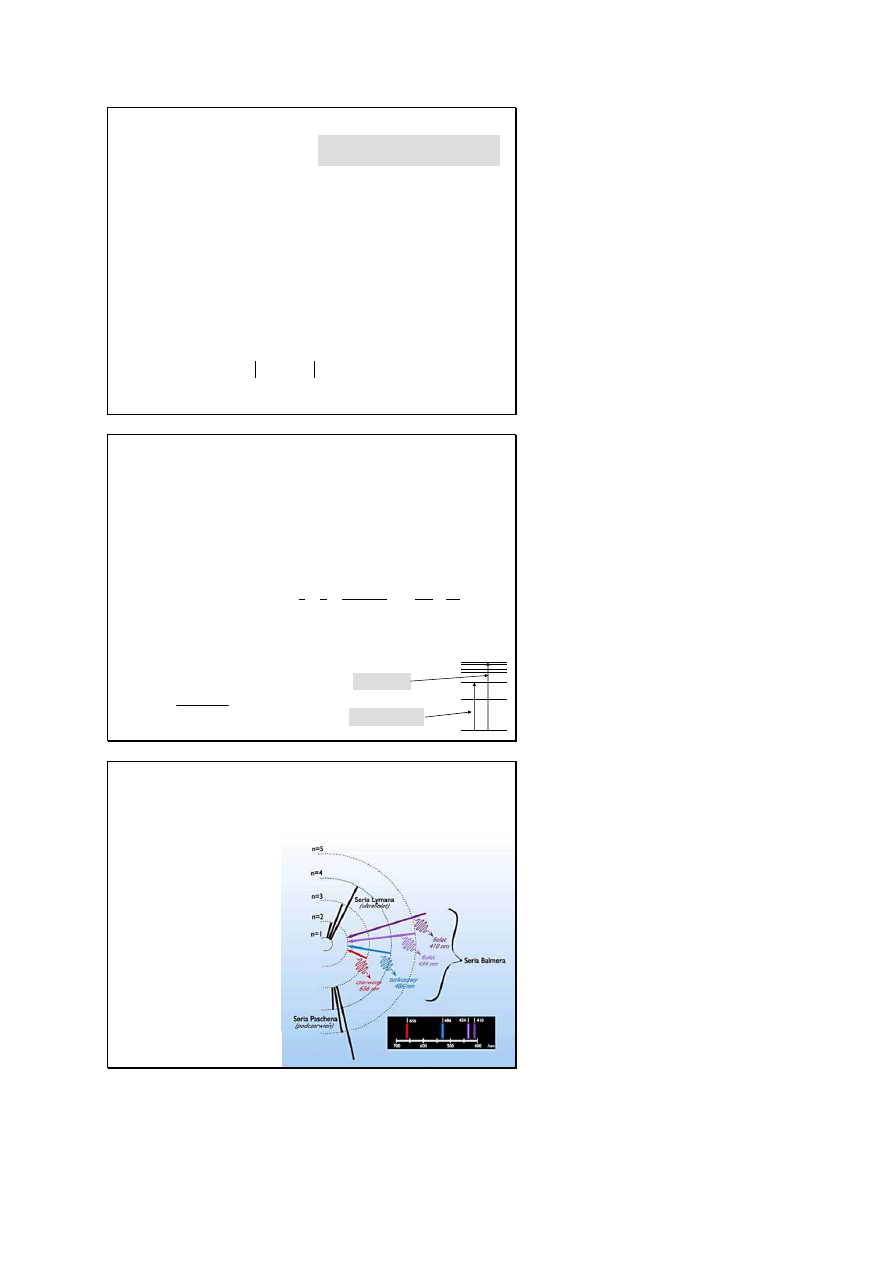
Model Bohra

elektrony poruszają się w atomach nie

promieniując energii, po takich orbitach

kołowych, że moment pędu elektronu jest równy

całkowitej wielokrotności stałej

przejścia elektronu z orbity o energii E

n

na

orbitę, gdzie energia wynosi E

m

, towarzyszy

emisja lub absorpcja fotonu o częstości

określonej wzorem

h

n

mv

„

„

r =

ν

=

−

h

E

E

m

n

n = 1, 2, 3..

h

1913r. – 13 lat przed sformułowaniem
równania Schrodingera

 

Widmo atomu wodoru

wzbudzenie atomu – przejście elektronu na

wyższy poziom energetyczny
po czasie 10

-8

s samorzutny powrót do stanu o

niższej energii i emisja fotonu o długości λ

jonizacja atomu – przejście elektronu na

najwyższy poziom energetyczny o zerowej

energii (elektron swobodny)

(energia jonizacji = E

0

)

„

„

„

⎟

⎠

⎞

⎜

⎝

⎛

−

=

−

=

ν

=

λ

2

2

1

1

1

n

m

R

hc

E

E

c

m

n

R – stała Rydberga

c

me

R

o

3

2

3

4

64

h

ε

π

=

E

1

E

2

E

3

E

∞

jonizacja

wzbudzenie

 

Serie widmowe

seria Lymana
seria Balmera
seria Paschena
seria Bracketta
seria Pfunda

„

„

„

„

„

BohrModel.swf

 

Promieniowanie termiczne

model ciała doskonale czarnego
prawa promieniowania termicznego

prawo Kirchhoffa
prawo Stefana-Boltzmanna
prawo przesunięć Wiena

prawo Rayleigha-Jeansa - klasyczne
prawo Plancka - kwantowe

„

„

„

„

„

„

„

Jak teoria fotonów wyjaśnia ciągłe widmo

promieniowania emitowanego przez gorące,

nieprzezroczyste ciała?

 

Podstawowe definicje

Promieniowaniem termicznym

(zwanym też cieplnym lub

temperaturowym) nazywamy promieniowanie wysyłane przez

ciała ogrzane do pewnej temperatury - jest wynikiem drgań

ładunków elektrycznych

Zdolność emisyjna

ciała e(ν,T)dν definiujemy jako energią

promieniowania wysyłanego w jednostce czasu z jednostki

powierzchni o temperaturze T, w postaci fal elektromagne-

tycznych o częstościach zawartych w przedziale od ν do ν + dν.

Zdolność absorpcyjna

, a, określa jaki

ułamek energii padającej na

powierzchnię zostanie pochłonięty.

Zdolność odbicia

, r, określa jaki ułamek

energii padającej zostanie odbity.

(

) (

)

1

=

ν

+

ν

T

r

T

a

,

,

 

Ciało doskonale czarne

Promień

świetlny

Powierzchnia

o dużej zdolności

absorpcyjnej

Ciało doskonale czarne

(c.d.cz.) całkowicie

absorbuje promieniowanie termiczne.

a =1 i r =0

Stosunek zdolności emisyjnej do

zdolności absorpcyjnej jest dla

wszystkich powierzchni jednakowy i

równy zdolności emisyjnej c.d.cz.

Prawo Kirchhoffa

:

(

)

(

)

(

)

T

T

a

T

e

,

,

,

ν

ε

=

ν

ν

Ponieważ zawsze a≤1, więc i e(ν,T) ≤ ε(ν,T), tzn.

zdolność emisyjna każdej powierzchni nie jest większa

od zdolności emisyjnej ciała doskonale czarnego.

 

Prawa promieniowania

c.d.cz.

ν

max

1

ν

max

2

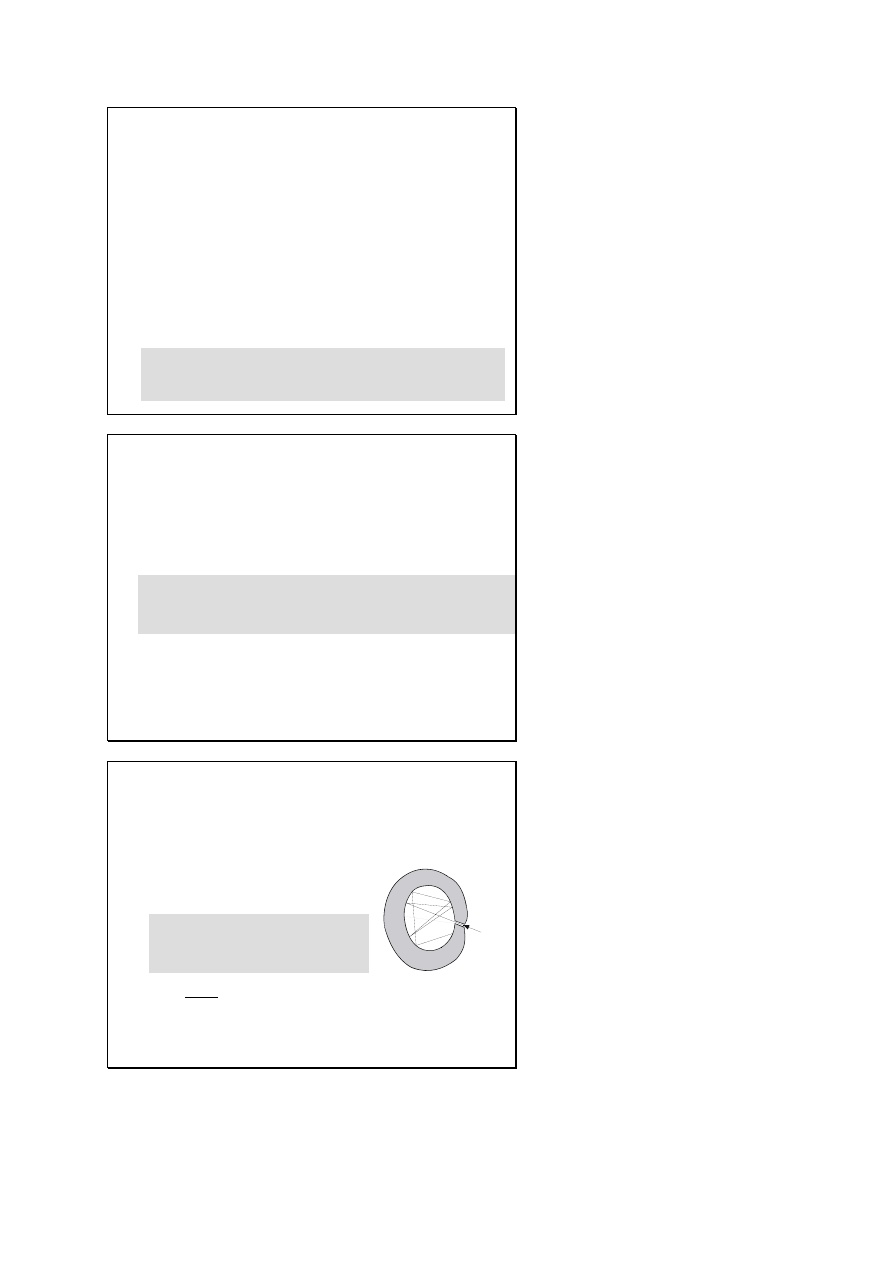
Prawo Stefana-Boltzmanna

4

T

E

σ

=

T

b ⋅

=

ν

max

Prawo przesunięć Wiena

(

)

kT

c

T

2

2

2

πν

=

ν

ε ,

Prawo Rayleigha-Jeansa

Stała Stefana-Boltzmanna

σ = 5.67×10

–8

Wm

–2

K

–4

Stała Wiena

b = 5.877×10

10

s

–1

K

–1

katastrofa

nadfioletowa

 

Prawo Plancka

Hipoteza Plancka: elektryczny oscylator harmoniczny

stanowiący model elementarnego źródła promieniowania, w

procesie emisji promieniowania może tracić energię tylko

porcjami, czyli kwantami ΔE, o wartości proporcjonalnej do

częstości ν jego drgań własnych.

ν

=

Δ

h

E

gdzie stała Plancka h = 6.626×10

–34

Js

zdolność emisyjna c.d.cz. jest funkcją częstości i temperatury

(

)

(

)

1

1

2

2

3

−

ν

ν

π

=

ν

ε

kT

h

c

h

T

/

exp

,

i pozostaje w bardzo dobrej zgodności z doświadczeniem

 

Wnioski

Postulat

Plancka

(energia

nie

może

być

wypromieniowana w sposób ciągły), doprowadził

do teoretycznego wyjaśnienia promieniowania

ciała doskonale czarnego.
Z

prawa

Plancka

wynika

prawo

Stefana-

Boltzmanna i prawo przesunięć Wiena.
Porcje energii promienistej emitowanej przez

ciało wynoszące h

ν

zostały nazwane kwantami

lub fotonami.
Hipoteza

Plancka

dała

początek

fizyce

kwantowej, a stała h występuje obecnie w wielu

równaniach fizyki atomowej, jądrowej i ciała

stałego.

(

)

ν

ν

ε

d

T

E

∫

∞

=

0

,

„

„

„

„

(

)

0

=

∂

∂

ν

ν

ε

T

,

 

Jak światło może być

jednocześnie falą i cząstką

opisy światła: falowy i korpuskularny

są uzupełniające się
potrzeba obu tych opisów do

pełnego modelu świata, ale do

określenia konkretnego zjawiska

wystarczy tylko jeden z tych modeli
dlatego mówimy o dualizmie

korpuskularno-falowym światła

„

„

„

 

Falowa natura cząstek

Promień świetlny jest falą,

ale energię i pęd przekazuje

materii w postaci fotonów.

Dlaczego innych cząstek np.

elektronów nie traktować jako

fal materii ?

 

Hipoteza de Broglie’a

W 1924 r. Louis de Broglie przypisał elektronom o pędzie p

długość fali λ

– długość fali de Broglie’a

p

h

=

λ

Słuszność hipotezy de Broglie’a została potwierdzona w 1927 r.

przez Davissona i Germera, którzy wykazali, że wiązka

elektronów ulega dyfrakcji tworząc typowy obraz interferencyjny

Promieniowanie i materia wykazują dwoistą falowo-korpuskularną

naturę – nazywamy to dualizmem korpuskularno-falowym

m

s

m

kg

s

J

p

h

27

6

34

10

6

6

1

10

1

0

10

63

6

−

−

−

⋅

=

⋅

⋅

⋅

⋅

=

=

,

,

,

λ

dla pyłku unoszonego

przez wiatr

 

Dyfrakcja elektronów

mK

h

p

h

2

=

=

λ

Dla elektronów o K=1000eV

λ=4×10

–11

m

θ

= sin

d

p

h

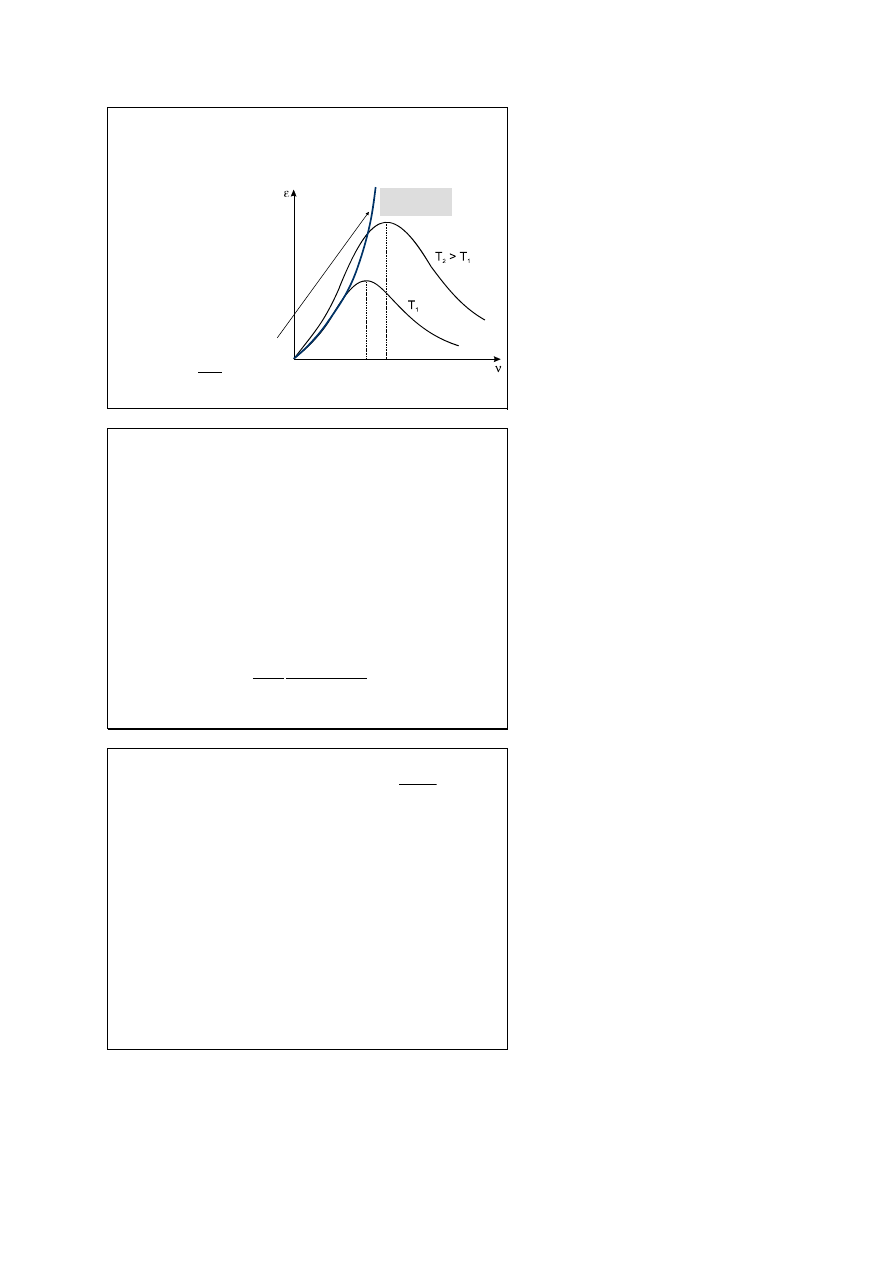
Znając kąt θ przy którym

obserwuje się pierwsze

maksimum można określić

stałą Plancka

ΔD = d sinθ

ΔD =λ

θ

=

sin

pd

h

Doświadczenie Davissona - Germera

(dyfrakcja elektronów)

 

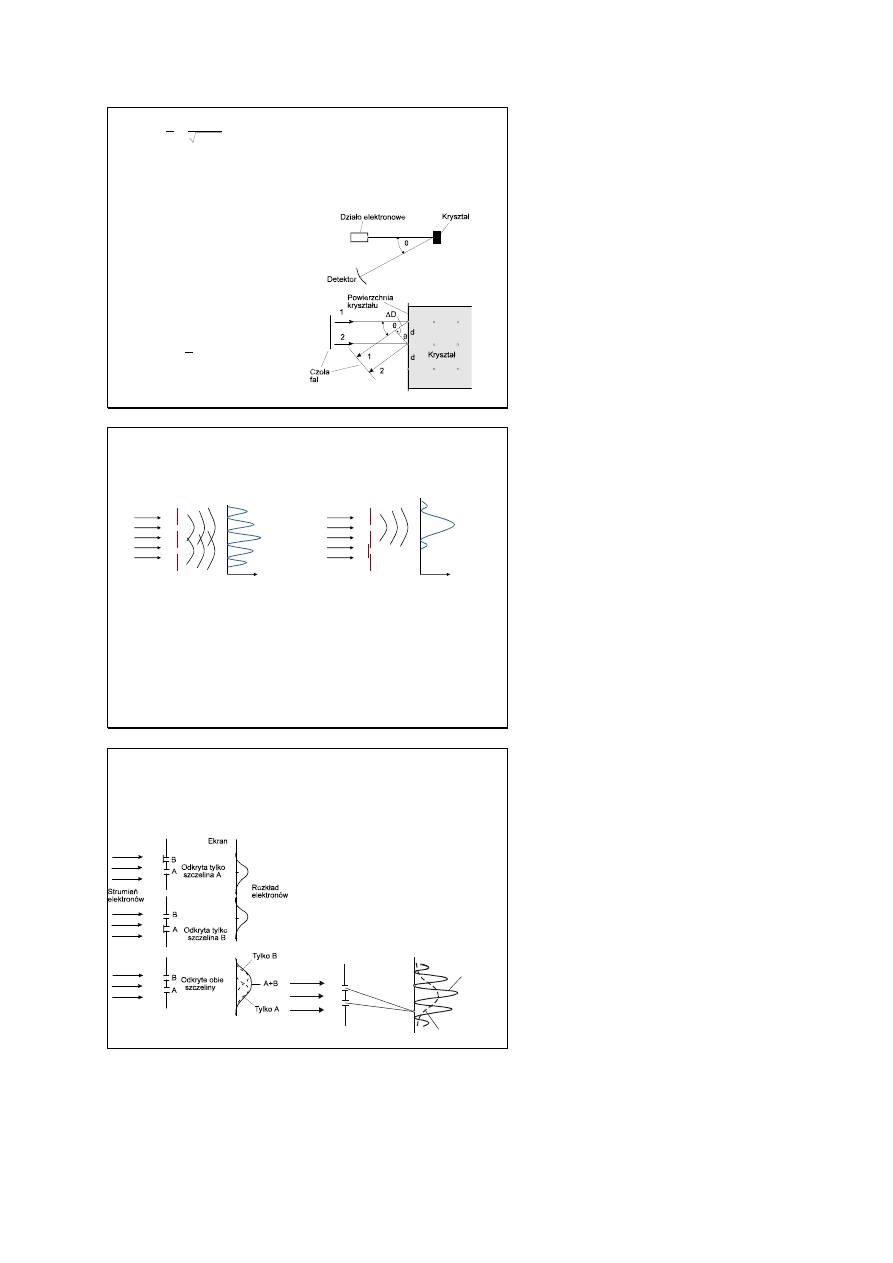
Jak elektron przechodzi

przez szczelinę?

• Pojedyncze elektrony padające na dwie szczeliny

dają obraz dyfrakcyjny w postaci szeregu prążków

• zasłonięcie jednej szczeliny (B) powoduje zmianę

obrazu dyfrakcyjnego

• skąd elektron wie, że szczelina B jest zasłonięta?
• fakt, że obraz dyfrakcyjny może zostać utworzony

przez różne nieoddziałujące ze sobą elektrony

świadczy o tym, że każdy elektron przechodzi

przez obie szczeliny i interferuje sam ze sobą

A

B

wiązka

elektronów

A

B

wiązka

elektronów

 

Fale prawdopodobieństwa

r

1

r

2

A

B

P

1

P

2

Rozkład

klasyczny

Rozkład

obserwowany

Rozkład elektronów na ekranie powinien być

sumą rozkładów dla każdej szczeliny oddzielnie

- obserwujemy obraz interferencyjny dla

dwóch szczelin

Do wyjaśnienia tego paradoksu musimy

stworzyć nowy formalizm matematyczny:

fale materii traktować jako fale

prawdopodobieństwa wytwarzającą na ekranie

obraz „prążków prawdopodobieństwa”

klasycznie

 

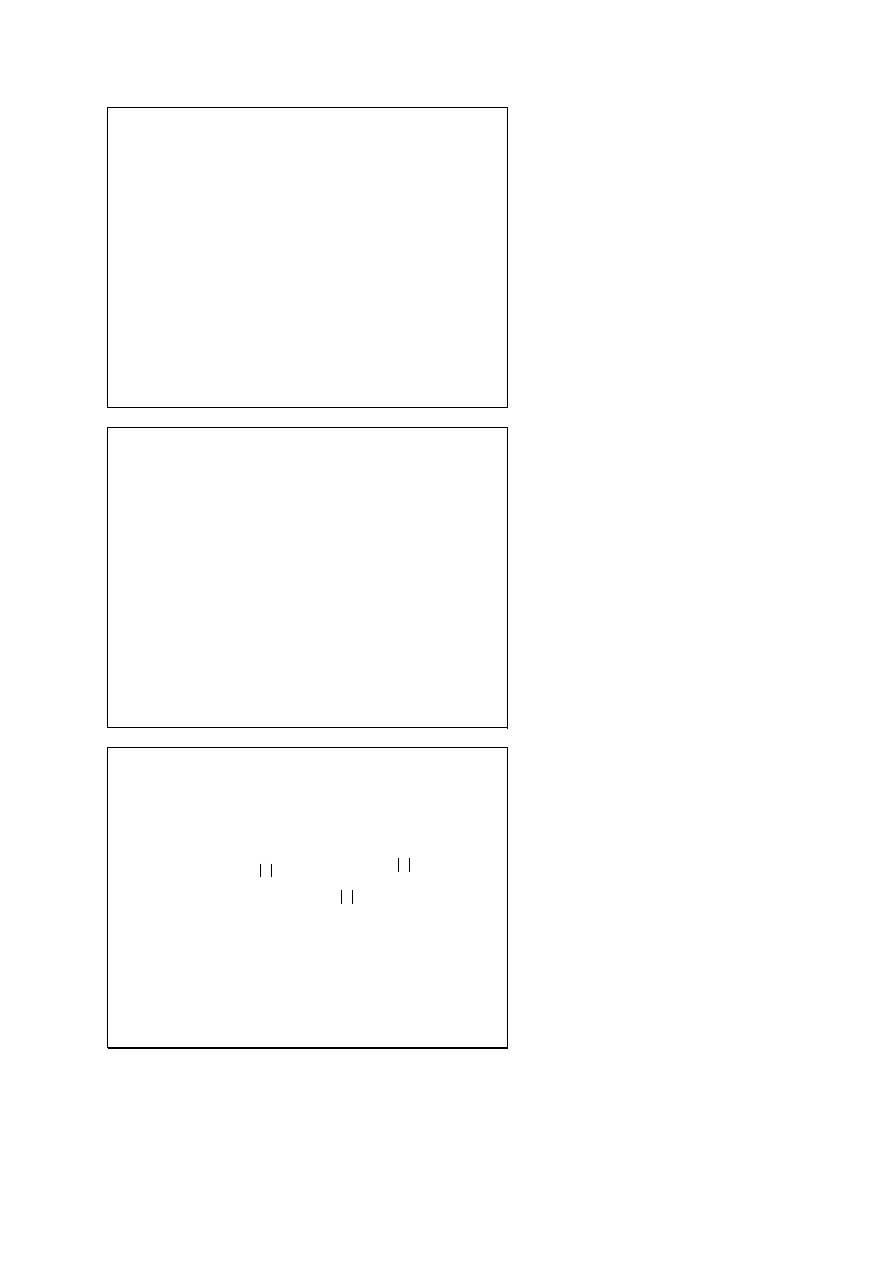
Mechanika kwantowa

dział mechaniki zajmujący się

ruchem mikrocząstek, których

stan opisany jest funkcją falową

będącą rozwiązaniem równania

Schrodingera

 

Funkcja falowa

Formalizm matematyczny za pomocą którego usuwa się te

paradoksy, przypisuje każdej cząstce materialnej funkcję

falową

Ψ (x,y,z,t) będącą funkcją współrzędnych i czasu

Znajdując rozkład natężenia w obrazie dyfrakcyjnym

można określić prawdopodobieństwo, że elektron padnie w

określonym miejscu ekranu

Kwadrat amplitudy funkcji falowej jest proporcjonalny do

gęstości prawdopodobieństwa znalezienia elektronu w

danym elemencie obszaru

„

„

„

 

Właściwości funkcji falowej

Prawdopodobieństwo znalezienia się elektronu

w objętości dV=dxdydz wynosi

gdzie

warunek unormowania

funkcji falowej

zasada superpozycji Ψ = Ψ

1

+ Ψ

2

funkcja falowa powinna być ograniczona |Ψ|<∞

funkcja falowa Ψ nie stanowi bezpośrednio obserwowanej

wielkości. Fale klasyczne i fale odpowiadające cząstkom

podlegają równaniom matematycznym tego samego typu.

Lecz w przypadku klasycznym amplituda fali jest

bezpośrednio obserwowana, a dla funkcji falowej Ψ– nie.

„

„

„

„

„

1

2

=

Ψ

∫

dV

V

dxdydz

PdV

2

Ψ

=

∗

Ψ

⋅

Ψ

=

Ψ

2

 

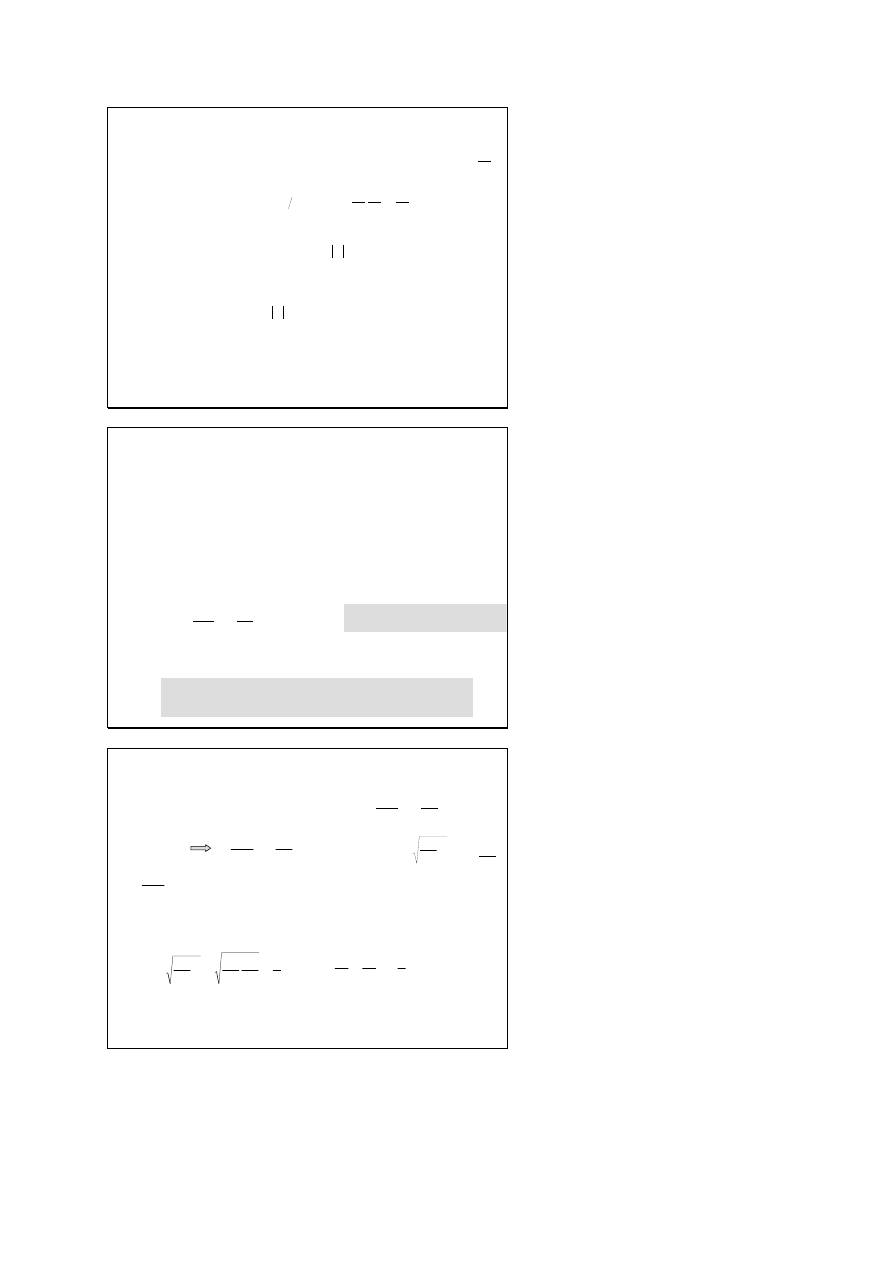
Postać funkcji falowej

o

o

o

k

h

h

p

π

λ

π

π

2

2

2

=

=

o

o

h

p

λ

=

o

o

k

p

h

=

π

2

o

o

h

=

h

Funkcja falowa cząstki o pędzie p

o

poruszającej się wzdłuż osi x,

odpowiada równaniu fali o długości λ

o

i wektorze falowym k

o

(

)

t

x

k

A

o

ω

−

=

Ψ

cos

Rzeczywista postać funkcji falowej jest niewłaściwa bo istniałyby

punkty, gdzie nie można cząstki zaobserwować. Lepsza zespolona

(

)

t

x

o

k

i

Ae

ω

−

=

Ψ

(

)

(

)

(

)

(

)

2

2

A

Ae

Ae

t

x

k

i

t

x

k

i

o

o

=

=

Ψ

Ψ

=

Ψ

−

−

−

∗

ω

ω

(

)

t

x

k

A

o

ω

−

=

Ψ

2

2

2

cos

Pokazaliśmy, że jeżeli pęd cząstki posiada określoną wartość, to

cząstkę można znaleźć z jednakowym prawdopodobieństwem w

dowolnym punkcie przestrzeni. Inaczej mówiąc,

Z hipotezy de Broglie’a:

jeżeli pęd cząstki

jest dokładnie znany, to nic nie wiemy o jej miejscu położenia.

 

Równanie Schrodingera

( )

[

]

Ψ

−

−

=

Ψ

x

U

E

m

dx

d

2

2

2

2

h

stacjonarne, jednowymiarowe

równanie Schrödingera

W sytuacjach stacjonarnych, gdy potencjał nie zmienia się w czasie,

zmienne przestrzenne i czas można rozseparować i zapisać funkcję

falową w postaci:

(

)

(

)

t

i

e

z

y

x

t

z

y

x

ω

−

Ψ

=

Ψ

,

,

,

,

,

Postać przestrzennej funkcji falowej, dla przypadku jednowymia-

rowego, wyznaczamy z równania Schrödingera:

gdzie: m – masa cząstki, E – całkowita energia mechaniczna cząstki,

U(x) – energia potencjalna w danym obszarze

równania Newtona – fale dźwiękowe i fale w strunach

równania Maxwella – fale świetlne

równanie Schrödingera – fale materii (funkcja falowa)

 

Równanie Schrodingera dla

cząstki swobodnej

( )

[

]

Ψ

−

−

=

Ψ

x

U

E

m

dx

d

2

2

2

2

h

Ψ

−

=

Ψ

E

m

dx

d

2

2

2

2

h

E

m

k

2

2

h

=

( )

0

=

x

U

Ψ

−

=

Ψ

2

2

2

k

dx

d

( )

ikx

ikx

Be

Ae

x

−

+

=

Ψ

oznaczając

którego rozwiązaniem jest

przyjmując B=0 (cząstka porusza się w kierunku dodatnich x)

(

)

( )

(

)

t

kx

i

t

i

Ae

e

x

t

x

ω

ω

−

−

=

Ψ

=

Ψ ,

funkcją falową cząstki swobodnej jest fala płaska o długości λ

określonej zależnością de Broglie’a

p

h

p

k

=

=

=

h

π

π

λ

2

2

m

p

E

2

2

=

tylko

kinetyczna

h

h

h

p

m

p

m

E

m

k

=

=

=

2

2

2

2

2

2

 

Paczki falowe materii

Dla cząstki znajdującej się w t=0 w

określonym obszarze przestrzeni

kwadrat modułu funkcji falowej

przyjmuje postać funkcji Gaussa

( )

(

)

x

ik

x

A

x

o

x

exp

exp

,

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

σ

−

=

Ψ

2

2

4

0

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

σ

−

=

Ψ

2

2

2

2

2

x

x

A exp

Ψ

2

Tak zlokalizowana funkcja

nazywana jest paczką falową

Elektron jako paczka falowa

przechodzi przez obie szczeliny

 

Superpozycja fal

monochromatycznych

(

)

( )

( )

∫

∞

∞

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

Ψ

dk

ikx

k

B

x

ik

x

o

x

exp

exp

exp

2

2

4

σ

Paczka falowa powstaje w wyniku superpozycji fal o różnych

długościach, którym odpowiadają różne wartości pędu

współczynniki Fouriera

Amplitudy tych fal B(k), zwane

współczynnikami Fouriera,

posiadają również postać funkcji

Gaussa wokół wartości k

o

Pomiędzy funkcją falową Ψ(x),

a współczynnikami Fouriera B(k)

istnieje ścisły związek

k

B(k)

k

o

 

Δk

niemożliwe jest jednoczesne dokładne określenie wartości
współrzędnej i pędu cząstki

Zasada nieoznaczoności

czym szerszy zakres k odpowiadający większemu rozrzutowi

Δp

x

, tym

paczka falowa jest przestrzennie węższa (mniejsze

Δx)

x

p

x

Δ

=

Δ

h

k

x

Δ

=

Δ

1

h

≥

Δ

Δ

x

p

x

B(k)

k

k

o

Re (Ψ)

x

B(k)

k

k

o

Re (Ψ)

x

k

p

x

Δ

=

Δ

h

Δk

Δx

Δx

gdy

Δ p

x

=0,

to

Δ x = ∞

cząstka
swobodna

 

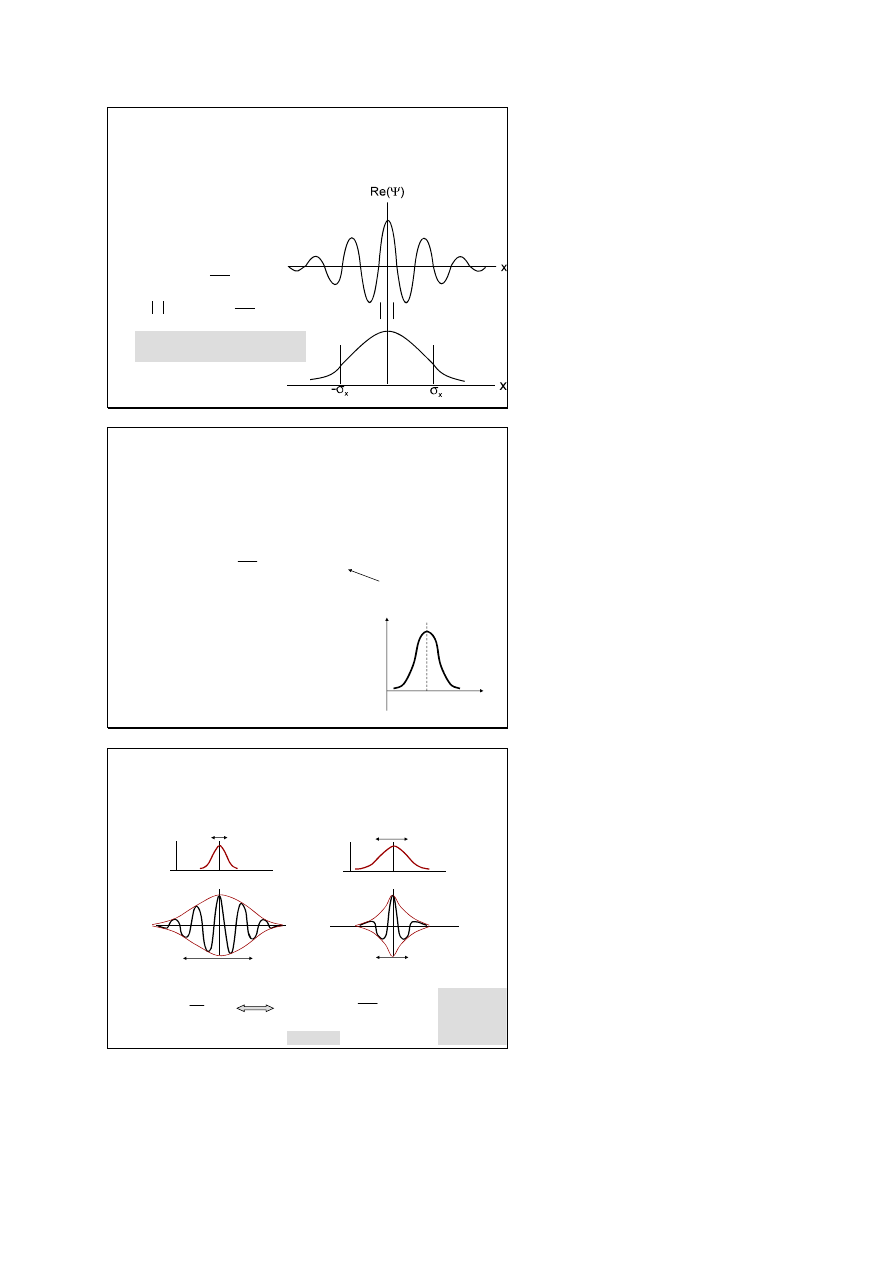
Zasada nieoznaczoności w pociągu

2

λ

=

Δl

t

n

t

l

v

λ

=

=

λ

n

l =

n

v

t

t

l

v

2

2

=

=

Δ

=

Δ

λ

2

2

λ

n

l

x

=

=

Δ

4

λ

v

v

x

=

Δ

⋅

Δ

4

λ

p

p

x

=

Δ

⋅

Δ

chcemy zmierzyć prędkość pociągu wiedząc, że każdy wagon ma długość λ

minęło nas n wagonów w ciągu czasu t

pokonana przez pociąg droga wynosi

średnia prędkość

pociągu wynosi

im większy przedział czasu tym pomiar prędkości dokładniejszy, ale maleje

dokładność położenia pociągu w chwili pomiaru

w mechanice kwantowej pociąg to paczka falowa o długości fali λ

rozciągająca się na obszar l = n

λ

p

h

=

λ

h

≈

=

Δ

⋅

Δ

4

h

p

x

λ

 

Znaczenie zasady

nieoznaczoności Heisenberga

Δt=1/Δω

Δx=1/Δk

szerokość

paczki

falowej

k

p

h

=

h

=

Δ

⋅

Δ

p

x

ω

h

=

E

h

=

Δ

⋅

Δ

t

E

Działanie S można określić z dokładnością stałej Plancka
Zasada nieoznaczoności określa granice możliwości naszych

pomiarów.

Jest jednym z fundamentalnych twierdzeń mechaniki kwantowej:
• wyjaśnia dyfrakcję na szczelinie
• energie cząstek są zawsze większe od zera
• elektron nie spada na jądro atomowe

h

h

=

ΔS

 

Prędkość grupowa paczki

dk

d

v

g

ω

=

E

=

ω

h

p

k =

h

( )

m

k

2

2

h

h =

ω

m

p

E

2

2

=

m

k

dk

d

h

=

ω

v

m

p

m

k

dk

d

v

g

=

=

=

=

h

ω

v

v

g

=

Paczka falowa przemieszcza się z prędkością równą
prędkości cząstki

klasycznie

relatywistycznie

2

2

2

2

c

p

E

E

o

+

=

dp

pc

dE

E

2

2

2

=

v

mc

mv

c

E

p

c

dp

dE

dk

d

v

g

=

=

=

=

=

2

2

2

ω

 

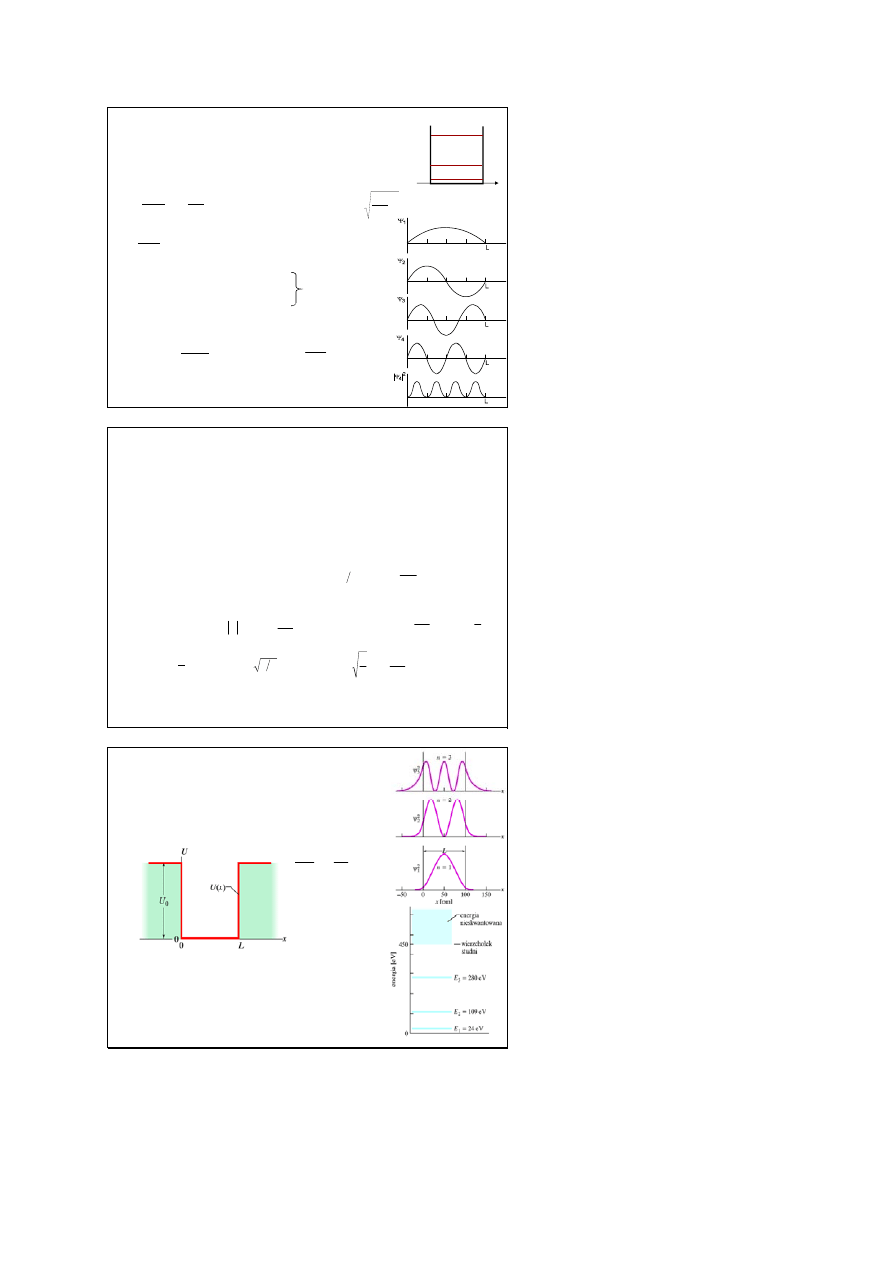
Równanie Schrodingera dla

nieskończonej jamy potencjału

„

„

wartości energii E

n

nazywamy wartościami własnymi

odpowiadające im funkcje falowe Ψ

n

– funkcjami

własnymi

( )

[

]

Ψ

−

−

=

Ψ

x

U

E

m

dx

d

2

2

2

2

h

E

m

k

2

2

h

=

( )

0

=

x

U

Ψ

−

=

Ψ

2

2

2

k

dx

d

( )

ikx

ikx

Be

Ae

x

−

+

=

Ψ

( )

( )

0

0

=

Ψ

=

Ψ

L

0

=

+ B

A

0

=

+

−ikL

ikL

Be

Ae

(

)

0

=

−

−ikL

ikL

e

e

A

( )

0

=

kL

sin

π

= n

kL

2

2

2

2

2mL

n

E

n

h

π

=

( )

⎟

⎠

⎞

⎜

⎝

⎛

=

Ψ

L

x

n

C

x

n

π

sin

0

L

U=0

U=∞

warunki brzegowe

E

1

E

2

E

3

U=∞

n=1,2,3...

Ai

C

2

=

 

Wnioski

energia jest skwantowana, występują dyskretne wartości

(poziomy) energii (n – liczba kwantowa)
cząstka nie może posiadać energii zerowej – wynika z

zasady nieoznaczoności

stałą C wyznaczamy z warunku unormowania

dla obiektów klasycznych poszczególne poziomy są tak

bliskie, że nierozróżnialne

L

„

„

„

„

x =

Δ

L

p h

≥

Δ

0

2

2

>

=

m

p

E

h

≥

Δ

Δ

p

x

1

0

0

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

=

Ψ

⋅

Ψ

∫

∫

dx

x

L

n

C

dx

L

L

π

sin

*

2

0

2

L

dx

x

L

n

L

=

⎟

⎠

⎞

⎜

⎝

⎛

∫

π

sin

1

2

2

=

L

C

L

C

2

=

( )

⎟

⎠

⎞

⎜

⎝

⎛

=

Ψ

x

L

n

L

x

n

π

sin

2

 

Elektron w skończonej

studni potencjału

studnia potencjału o głębokości U

o

( )

[

]

Ψ

−

−

=

Ψ

x

U

E

m

dx

d

2

2

2

2

h

równanie

Schrodingera

rozwiązujemy dla

trzech obszarów

wyniki zbliżone jak dla nieskończonej studni, lecz:
•fale materii wnikają w ściany studni
•energie dla każdego stanu są mniejsze niż w ∞
•elektron o energii większej od U

0

nie jest

zlokalizowany, jego energia nie jest skwantowana

 

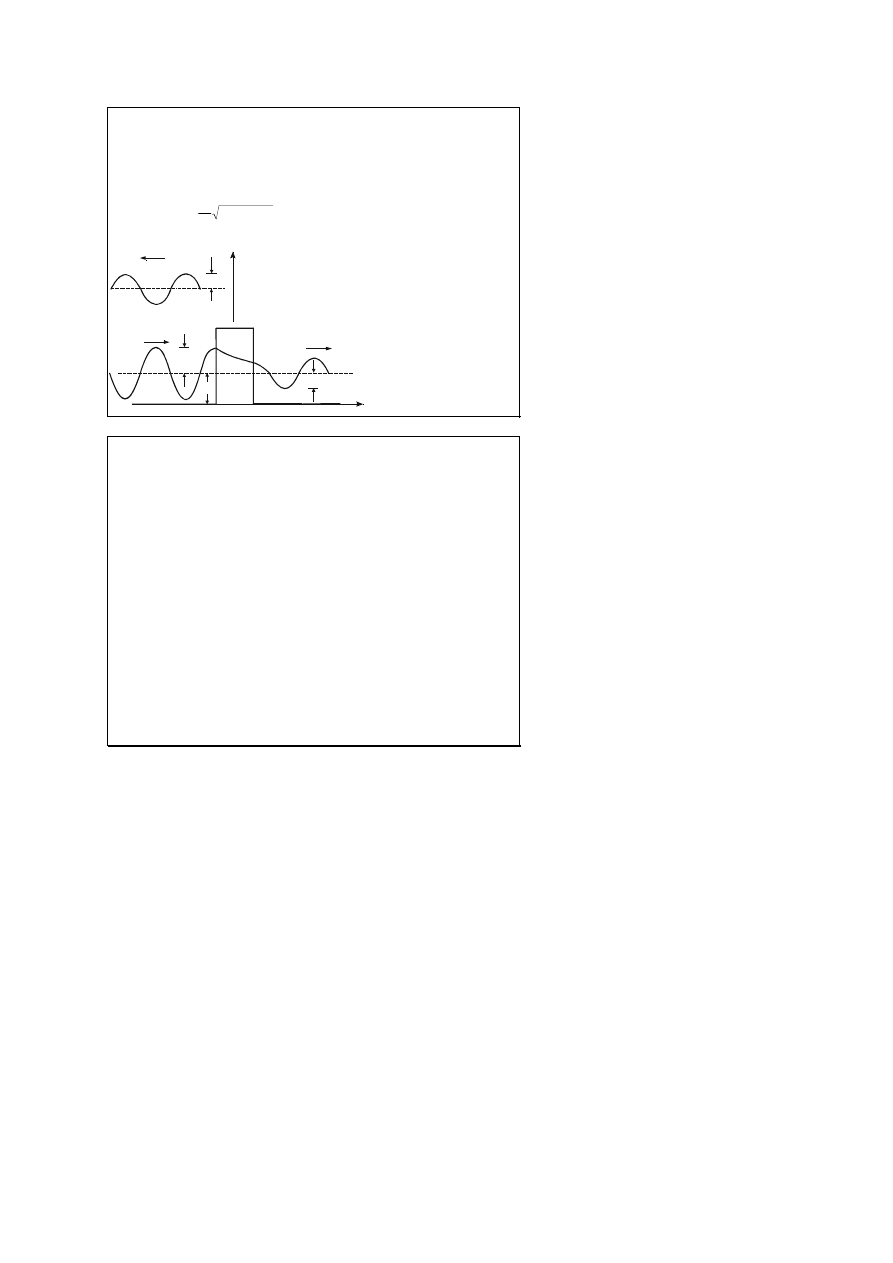
Efekt tunelowy - przenikanie

cząstki przez barierę potencjału

E

A

1

B

1

A

3

U >E

o

0 l

Ψ(x)

x

„

„

„

„

prawdopodobieństwo

przejścia przez barierę

potencjału zależy od L i U

o

szybko maleje ze

wzrostem jej szerokości i

wysokości
wg. mechaniki klasycznej

przenikanie przez barierę

jest niemożliwe
energia cząstki, w

odróżnieniu od jamy

potencjału nie jest

skwantowana

(

)

E

U

m

L

o

e

T

−

−

≈

2

2

h

 

Przykłady efektu

tunelowego

Dioda tunelowa (efekt tunelowy w złączu

p-n) Nagroda Nobla 1973r

Esaki - tunelowanie w półprzewodnikach

np. diody tunelowe
Giaever - tunelowanie w nadprzewodnikach
Josephson – złącze Josephsona, szybki

przełącznik kwantowy

Skaningowy Mikroskop Tunelowy

Binning i Rohrer Nagroda Nobla 1986r

„

„

„

„

„

„