Ruch harmoniczny tłumiony

Wyznaczanie logarytmicznego dekrementu drgań

tłumionych

Ćw.4

Cel ćwiczenia

Zapoznanie się ze zjawiskiem ruchu harmonicznego tłumionego oraz wielkościami charakteryzującymi ten

ruch. Przypomnienie zasad dynamiki.

Zakres obowiązującego materiału teoretycznego

Dynamika ruchu obrotowego. Ruch harmoniczny nietłumiony i wielkości charakteryzujące ten ruch: okres,

amplituda, częstotliwość, częstość kołowa. Ruch harmoniczny tłumiony i wielkości charakteryzujące ten ruch:

dekrement logarytmiczny tłumienia, współczynnik tłumienia, czas relaksacji.

Przyrządy i materiały użyte w doświadczeniu

Naczynia z cieczami, skala wychyleń, dysk ze wskazówką zawieszony na drucie stalowym (wahadło

torsyjne).

Wprowadzenie

Zgodnie z II zasada dynamiki dla ruchu obrotowego równanie ruchu walca umocowanego na sprężystym

drucie może być przedstawione w postaci:

ε

= J

M

(1)

gdzie: M - wypadkowy moment sił działających na walec;

J - moment bezwładności walca;

ε - przyspieszenie kątowe.

Jeżeli założyć, że moment sił działających na walec wynika ze sprężystości drutu, to jest on proporcjonalny do

kąta wychylenia walca z położenia równowagi:

φ

−

= k

M

(2)

gdzie k - oznacza współczynnik sprężystości drutu, stąd:

φ

−

=

ε

k

J

0

k

dt

d

J

2

2

=

φ

+

φ

(3)

1

Jest to równanie ruchu harmonicznego nietłumionego. Rozwiązaniem jest funkcja:

(

)

0

0

0

t

sin

θ

+

ω

φ

=

φ

(4)

gdzie: ω

0

- częstość kołowa drgań nietłumionych;

θ

0

- faza początkowa drgań;

φ

0

- amplituda drgań.

Z równania (4) wynika, że walec będzie wykonywał drgania wokół położenia równowagi ze stałą amplitudą

φ

0

(maksymalnym wychyleniem z położenia równowagi) oraz ze stałą częstością kołową ω

0

.

W przypadku gdy ruch jest tłumiony przez moment sił hamujących wypadkowy moment sił działających na

walec wynosi:

2

1

M

M

M

+

=

(5)

gdzie: M

1

- jest momentem siły harmonicznej;

M

2

- jest momentem siły hamującej.

Moment sił hamujących (np. sił oporu ze strony cieczy) dla niewielkich prędkości jest proporcjonalny do

prędkości kątowej stąd:

dt

d

b

M

2

φ

−

=

(6)

gdzie b - współczynnik oporu.

Równanie ruchu przybiera postać:

dt

d

b

k

dt

d

J

φ

φ

φ

−

−

=

2

2

(7)

0

k

dt

d

b

dt

d

J

2

2

=

φ

+

φ

+

φ

(8)

Jest to równanie drgań harmonicznych tłumionych, którego rozwiązanie można przedstawić w postaci:

(

)

θ

+

ω

φ

=

φ

β

−

t

cos

e

t

0

(9)

gdzie: ω - częstość drgań tłumionych;

β - współczynnik tłumienia drgań.

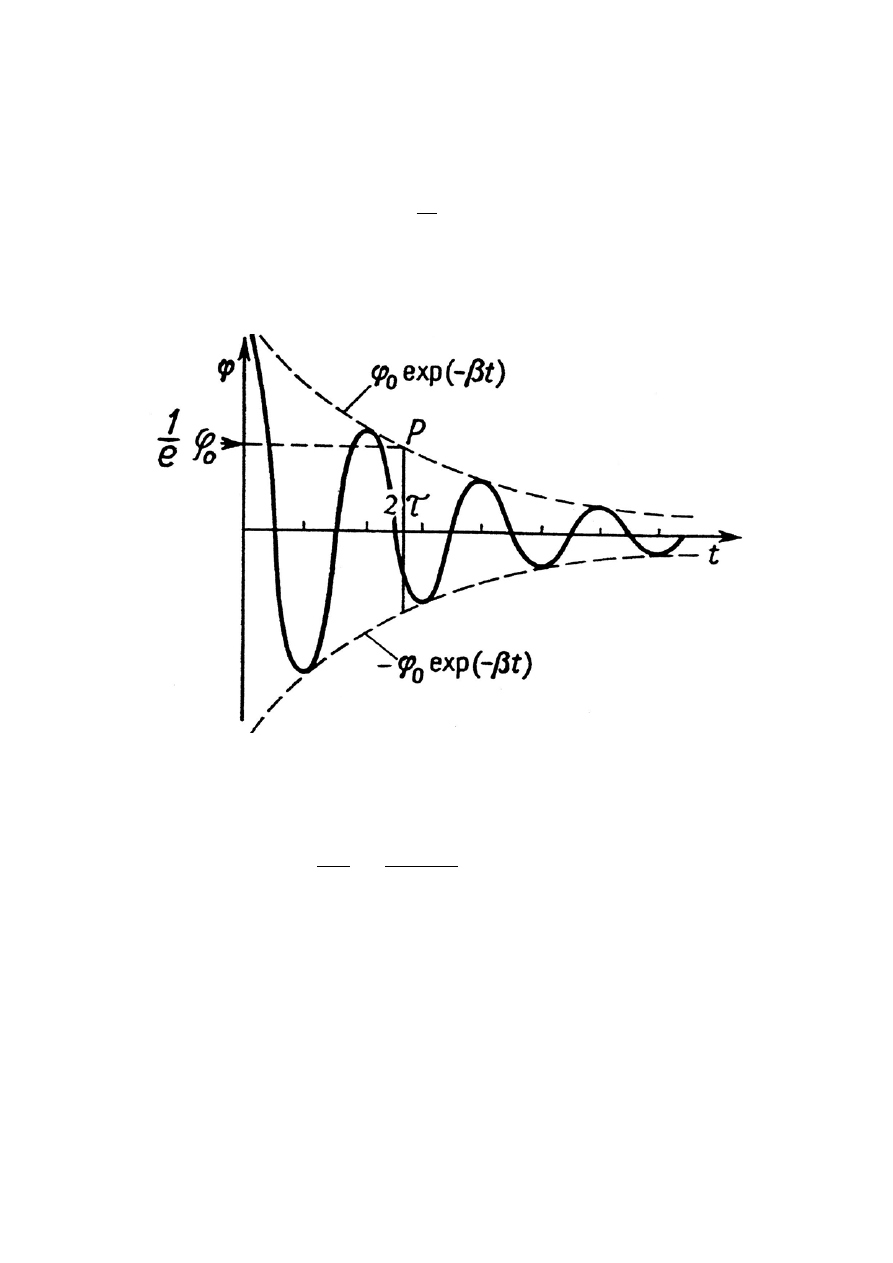
Amplituda w przeciwieństwie do ruchu nietłumionego jest malejącą w czasie:

t

0

t

e

β

−

φ

=

φ

(10)

Częstość drgań tłumionych ω jest mniejsza niż w przypadku drgań nietłumionych i wynosi:

2

2

2

0

2

β

−

ω

=

ω

(11)

Wielkość:

β

=

τ

2

1

(12)

nazywana jest czasem relaksacji oscylatora. Wyznacza on czas t=2

τ, po którym amplituda drgań maleje

e-krotnie.

Rys.1 Zależność wychylenia z położenia równowagi od czasu dla drgań harmonicznych tłumionych.

Logarytm naturalny stosunku dwóch kolejnych amplitud następujących po czasie równym okresowi drgań T

nazywa się dekrementem logarytmicznym drgań tłumionych

λ:

(

)

T

e

ln

e

e

ln

ln

t

T

t

0

t

0

T

t

t

β

=

=

φ

φ

=

φ

φ

=

λ

β

+

β

−

β

−

+

(13)

3

Część doświadczalna

Zasada pomiaru

Pomiar dekrementu logarytmicznego drgań tłumionych polega na mierzeniu kolejnych maksymalnych wychyleń

(amplitud) φ

t

walca zanurzonego w dwu różnych cieczach oraz obliczeniu szeregu wartości

λ

k

jako logarytmu

naturalnego stosunku kolejnych, następujących po czasie T, maksymalnych wychyleń.

Po wyznaczeniu wartości φ

t

i okresu T drgań harmonicznych tłumionych oraz obliczeniu średniej wartości λ

należy wyznaczyć wartości częstości drgań tłumionych ω i nietłumionych ω

o

oraz współczynnika tłumienia β.

Wykonanie ćwiczenia

1. Zanurzyć dysk całkowicie w wodzie tak, aby nie opierał się o dno naczynia; skalę obrócić tak, aby

wskazówka pokrywała się z podziałką zerową skali.

2. Wprawić wahadło obrotowe w ruch drgający odchylając palcem wskazówkę do podziałki 40

o

, uważając aby

zachowany był pion wahadła a następnie usunąć palec.

3. Po wykonaniu przez wahadło pierwszego pełnego drgnięcia, zacząć odczytywać wartości kolejnych,

maksymalnych wychyleń w lewo i w prawo. Pomiary prowadzić dla kolejnych 15 pełnych drgań. Zmierzyć

stoperem czas trwanie tych 15 pełnych drgań.

4. Wyniki pomiaru zapisać w tabelce.

Wychylenie w lewo

Wychylenie w prawo

λ

k

φ

k

[deg]

k

φ

p

[deg]

λ

k

1

2

...

5. Następnie wyjąć dysk z wody wysuszyć go za pomocą ściereczki i wstawić do drugiego naczynia z cieczą

(roztwór gliceryny).

6. Wykonać pomiary jak w przypadku wody, ale prowadzić je tylko dla kolejnych 7 pełnych drgań. Wyniki

zapisać w tabelce. Po wykonaniu pomiaru NIE WYLEWAĆ ROZTWORU GLICERYNY!!!!

Wykonać obliczeń dla wody i dla drugiego ośrodka tłumiącego

1. Obliczyć okres drgań dzieląc czas trwania t pomiaru n okresów przez ich liczbę.

n

t

T

=

Przyjmując błąd pomiaru czasu ∆t=0,4s należy obliczyć błąd pomiaru okresu metodą różniczki zupełnej

(instrukcja nr 17).

n

t

T

∆

=

∆

4

2. Obliczyć częstość drgań tłumionych ω

T

π

ω

2

=

oraz jej błąd bezwzględny (

∆ω) i względny (∆

ω)

. Błąd względny częstości równa się błędowi względnemu

okresu:

∆

ω

=

T

T

∆

=

∆

ω

ω

3. Obliczyć logarytmiczny dekrement tłumienia drgań λ

k

dla kolejnych amplitud (osobno dla wychyleń w prawo i

w lewo). Umieścić w sprawozdaniu przykład obliczeń. Wszystkie wyniki umieścić w tabeli.

1

k

k

k

ln

+

φ

φ

=

λ

Następnie obliczyć wartość średnią λ

k

(do obliczeń należy wykorzystać wszystkie wyliczone wartości λ

k

,

zarówno dla wychyleń w lewo jak i w prawo dla danego roztworu), oraz metodą Studenta-Fishera

(instrukcja nr 17) błąd bezwzględny i względny pomiaru.

Przykład obliczenia błędu dla wielkości x (x reprezentuje λ

k

):

błąd pomiaru wielkości x

1

n

S

t

x

−

=

∆

α

gdzie: t

α

- współczynnik Studenta odczytany z tablic (instrukcja Nr 17) dla r = n-1 stopni swobody i poziomie

istotności α = 0,05;

n - liczba pomiarów (nie mylić z liczbą okresów);

S - odchylenie standardowe wyrażone wzorem:

(

)

n

x

x

S

n

1

i

2

i

∑

=

−

=

gdzie: x

i

- i-ty pomiar wielkości x;

x

- wartość średnia wielkości x wyliczona ze wzoru:

n

x

x

n

1

i

i

∑

=

=

Wynik pomiaru wynosi:

x

x

x

∆

±

=

Błąd względny pomiaru wynosi:

5

%

100

x

x

x

∆

=

∆

4. Na podstawie równania (13) obliczyć współczynnik tłumienia drgań β, oraz metodą różniczki

zupełnej (instrukcja nr 17) wyznaczyć jego błąd względny (

∆

β

) i bezwzględny (∆β).

∆

β

=

T

T

∆

+

λ

λ

∆

=

β

β

∆

5. Mając wyznaczony współczynnik tłumienia drgań β, oraz częstość drgań tłumionych ω, obliczyć na

podstawie równania (11) częstość drgań nietłumionych ω

o

, oraz jej błąd bezwzględny (

∆ω

o

) metodą różniczki

zupełnej (instrukcja nr 17)

β

∆

ω

β

+

ω

∆

ω

ω

=

ω

∆

0

0

0

Błąd względny (

∆

ωo

) wynosi:

0

0

ω

ω

∆

=

∆

ω

o

Opracowanie sprawozdania

Sprawozdanie powinno zawierać:

-

wstęp teoretyczny z podkreśleniem celu i zakresu wykonanych pomiarów;

-

tabele pomiarowe podpisane przez prowadzącego bezpośrednio po wykonaniu ćwiczenia;

-

obliczenia wielkości wymaganych w ćwiczeniu oraz ich błędów bezwzględnych i względnych;

-

zestawienie na osobnej stronie oddzielnie dla dwu ośrodków tłumiących końcowych wyników obliczeń z

uwzględnieniem ich błędów: okresu (T ±

∆T), logarytmicznego dekrementu tłumienia drgań (λ ± ∆λ, ∆

λ

),

współczynnika tłumienia drgań (

β ± ∆β, ∆

β

), częstości drgań nietłumionych (ω

o

±

∆ω

o

,

∆

ωο

) i tłumionych

(ω ±

∆ω, ∆

ω

);

-

dyskusję wyników.

Proszę nie zapomnieć o wpisaniu jednostek przy wielkościach mianowanych oraz o prawidłowym

zaokrągleniu błędów!

6