4. DYNAMIKA: Tarcie. Praca, moc, energia

Tarcie

4.1. Wagon kolejowy o masie m = 2·10

4

kg porusza się z prędkością v

1

= 30 km/h. Znaleźć średnią wartość siły

działającej na wagon dla następujących przypadków zatrzymania wagonu:

a)

przy hamowaniu trwającym t

1

= 10 s;

b)

pod wpływem siły tarcia w czasie t

2

= 10 min.

4.2. Na stole leży deska o masie M = 3 kg, a na niej wiaderko z wodą o masie m = 9 kg. Jaką minimalną siłą
należy zadziałać na deskę, by wysunąć ją spod wiadra. Współczynniki tarcia wynoszą odpowiednio: między deską
a stołem - µ

DS

= 0,5, zaś między deską a wiadrem µ

DW

= 0,25.

4.3. Samochód przejeżdża nachylony zakręt o promieniu krzywizny R. Jaki powinien być kąt nachylenia zakrętu,
aby bezpiecznie przejechać po nim samochodem z prędkością v (tarcie pominąć)? Jaki musiałby być
współczynnik tarcia, gdyby zakręt był płaski?

4.4. Aby ruszyć z miejsca sanie o masie m = 100 kg potrzebna jest siła F

S

= 500 N, podczas gdy siła F

K

= 150 N

wystarczy na to, żeby sanie znajdowały się w ruchu po ruszeniu z miejsca. Znaleźć współczynniki tarcia
spoczynkowego i tarcia poślizgowego.

4.5. Samochód porusza się z prędkością v

0

= 50 km/h. Współczynnik tarcia pomiędzy oponami i drogą równa się

µ = 0,75. Znaleźć minimalną odległość na jakiej samochód może się zatrzymać.

4.6. Sanie o masie m = 200 kg poruszają się ruchem jednostajnie przyspieszonym w kierunku poziomym.
Działająca siła F = 1000 N przyłożona jest pod kątem

α

= 30

o

do poziomu. Współczynnik tarcia µ = 0,05.

Znaleźć przyspieszenie sań.

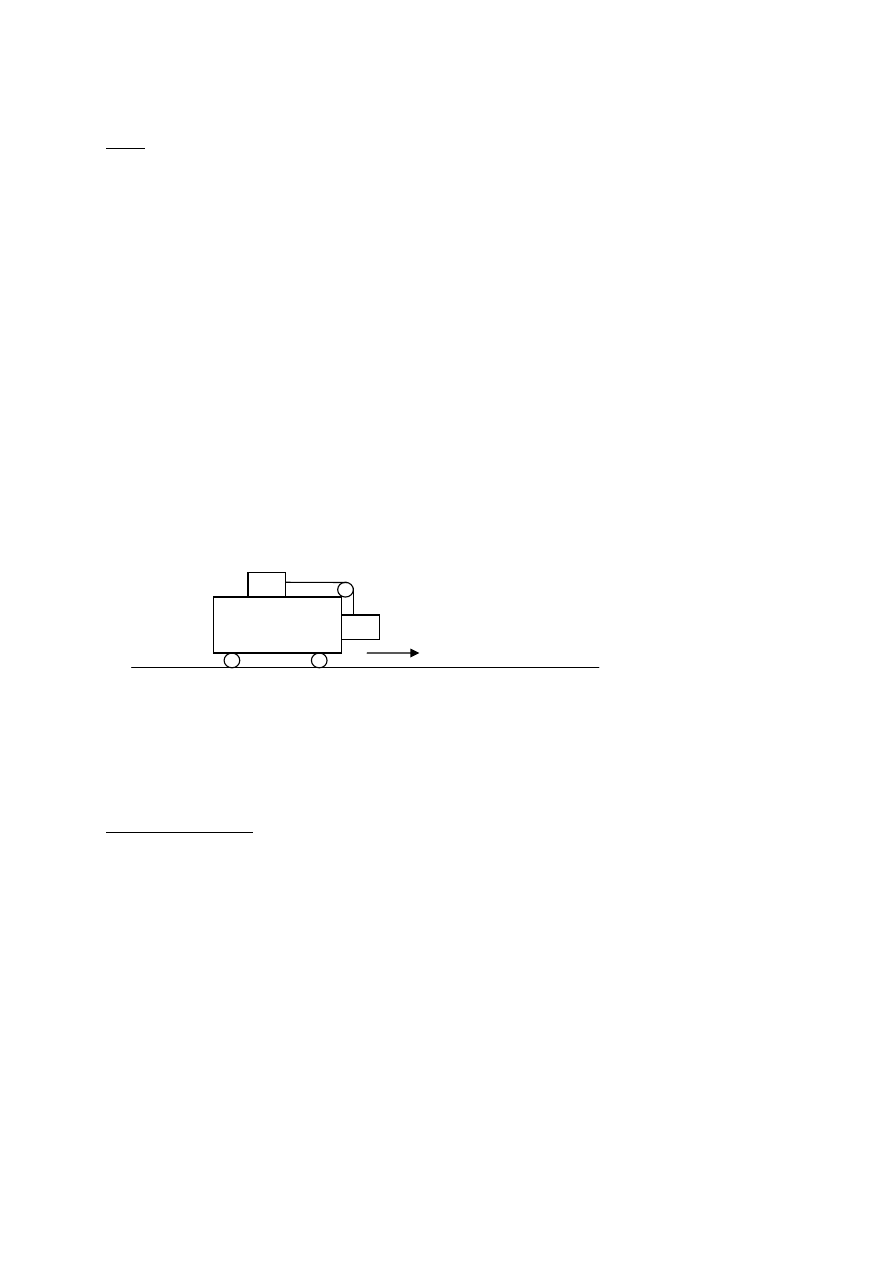
4.7. Z jakim przyspieszeniem a powinien poruszać się wózek, aby położenie mas m

1

i m

2

pozostawało bez

zmian? Współczynnik tarcia między masami a wózkiem – µ.

4.8. Znaleźć prędkość z jaką poruszał się samochód, jeżeli długość drogi hamowania kół równa się l = 25 m.
Współczynnik tarcia opon o nawierzchnię drogi µ = 0,3.

4.9. Pociąg o masie M i drezyna o masie m poruszają się z jednakowymi prędkościami v po równoległych,
poziomych szynach. Udowodnić, że zarówno pociąg, jak i drezyna zatrzymają się w jednej i tej samej chwili, po
przejściu jednakowych odległości s, jeżeli współczynnik tarcia µ kół o szyny w obydwu przypadkach jest
jednakowy. Siły ciągu przestają działać w tej samej chwili zarówno w przypadku pociągu jak i drezyny.

Obliczanie pracy i mocy

4.10. Oblicz, jaką masę ma kula karabinowa, jeśli wiadomo, że należy wykonać pracę W, by wyleciała ona z lufy
o długości l z prędkością v. Siły oporu zaniedbać. Założyć, że lufa skierowana jest równolegle do powierzchni
ziemi.

4.11. Bramkarz rzuca piłkę ręką działając na nią stałą siłą przez czas ∆t = 0,1 s. Ręka jego porusza się do przodu
na odległość l = 1 m. Masa piłki m = 600 g. Znaleźć przyspieszenie piłki. Jaka jest wartość siły działającej na
piłkę? Znaleźć średnią moc bramkarza.

4.12. Samochód przy holowaniu ciągnie poziomo inny samochód ze stałą prędkością v = 5 m/s. Napięcie liny
holowniczej równa się F = 600 N. Jaka praca jest wykonywana przy przesunięciu samochodu na odległość
1,5 km? Znaleźć moc rozwijaną przez samochód przy holowaniu.

4.13. Przy ładowaniu węgla do wagonów stosuje się transportery taśmowe, które podnoszą węgiel do góry
ukośnie na wysokość h = 5 m. W ciągu 1 minuty transporter przenosi m = 12 ton węgla. Jaką pracę wykonuje
transporter w ciągu 5 minut?

4.14. Transporter taśmowy o mocy P = 10 kW rozładowuje barkę z węglem przesypując go na przystań. Średnia
wysokość przystani h = 2,5 m. Zakładając, że sprawność transportera równa się η = 75%, znaleźć ile ton węgla
może rozładować transporter w ciągu ∆t = 20 minut.

m

1

m

2

4.15.* Siła napędzająca samochód zmienia się wraz z przesunięciem według prawa: F = D + Bs + Cs

2

. Znaleźć

pracę wykonaną przez tę siłę na odcinku drogi (s

1

, s

2

).

4.16.* Jaką pracę należy wykonać, aby wyciągnąć korek z rurki, jeżeli długość korka wynosi l

0

, a siła tarcia

między całym korkiem a rurką równa się F. Ściany rurki ściskają korek na całej jego długości równomiernie.

4.17.* Sanki poruszające się po lodzie z v = 8 m/s wjeżdżają na asfalt. Długość płóz sanek L = 1 m,
współczynnik tarcia o asfalt µ = 0,8. Jaką drogę przebędzie na asfalcie początkowy punkt płóz do momentu
całkowitego zatrzymania się sanek? Założyć, że masa jest równomiernie rozłożona na całej długości sanek.
Współczynnik tarcia o lód jest znacznie mniejszy niż µ.

4.18.* Na podłodze leży łańcuch o masie m i długości l. Jeden z jego końców podnosimy do góry dopóki
łańcuch nie oderwie się od Ziemi. Wyznacz minimalną pracę jaką należy wykonać, aby podnieść łańcuch w polu
grawitacyjnym Ziemi. Załóż, że łańcuch jest jednorodny.

4.19.* Wiatr wiejący z v

o

=20 m/s działa na żagiel o powierzchni S =25 m

2

siłą F = aS

ρ

(v

o

-v)

2

/2, gdzie a –

niemianowany współczynnik,

ρ

– gęstość powietrza, v – prędkość łodzi. Znaleźć warunki, przy których moc

wiatru będzie maksymalna. Znaleźć pracę wykonaną przez wiatr w czasie t = 60 s, jeśli a = 1, v = 15 m/s,

ρ

= 1,2 kg/m

3

.