07 Momenty, hipoteza

98

MOMENTY BEZWŁADNOŚCI

FIGUR PŁASKICH

Przekroje poprzeczne prętów, wałów i belek – figury płaskie,
charakteryzujące się następującymi parametrami:

– polem powierzchni przekroju

[mm

2

, cm

2

, m

2

],

–

położeniem środka ciężkości przekroju,

– momentami statycznymi

[cm

3

, m

3

],

–

momentami bezwładności

[cm

4

, m

4

].

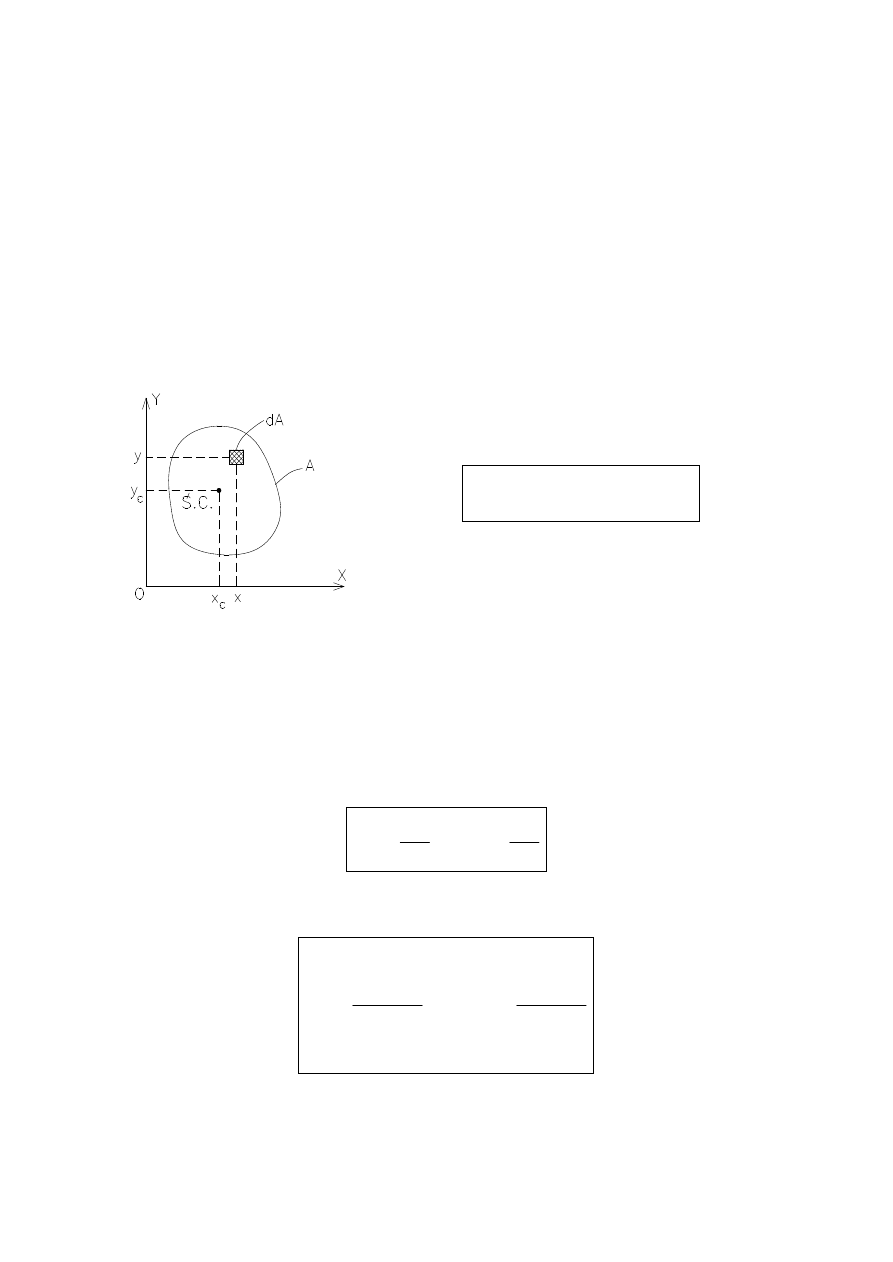
Definicja momentu statycznego w w
układzie osi X i Y:









A

A

y

x

xdA

S

,

ydA

S

W zależności od położenia przekro-

ju względem osi układu współrzęd-
nych

mogą przyjmować wartości

dodatnie i ujemne.

Wykorzystując znane ze statyki pojęcie środka sił, dla środka

ciężkości można napisać:

.

A

x

S

,

A

y

S

c

y

c

x





Korzystając z tych zależności, współrzędne środka ciężkości

figury płaskiej można obliczyć ze wzoru:

.

A

S

y

,

A

S

x

x

c

y

c





Środek ciężkości przekrojów złożonych –podział przekroju na

figury proste.

,

A

y

A

y

,

A

x

A

x

n

1

i

i

n

1

i

i

i

c

n

1

i

i

n

1

i

i

i

c





















A

i

– pola powierzchni figur prostych, x

i

, y

i

–

współrzędne środ-

ków ciężkości poszczególnych figur prostych.

Definicja momentu statycznego

07 Momenty, hipoteza

99

P

RZYKŁAD

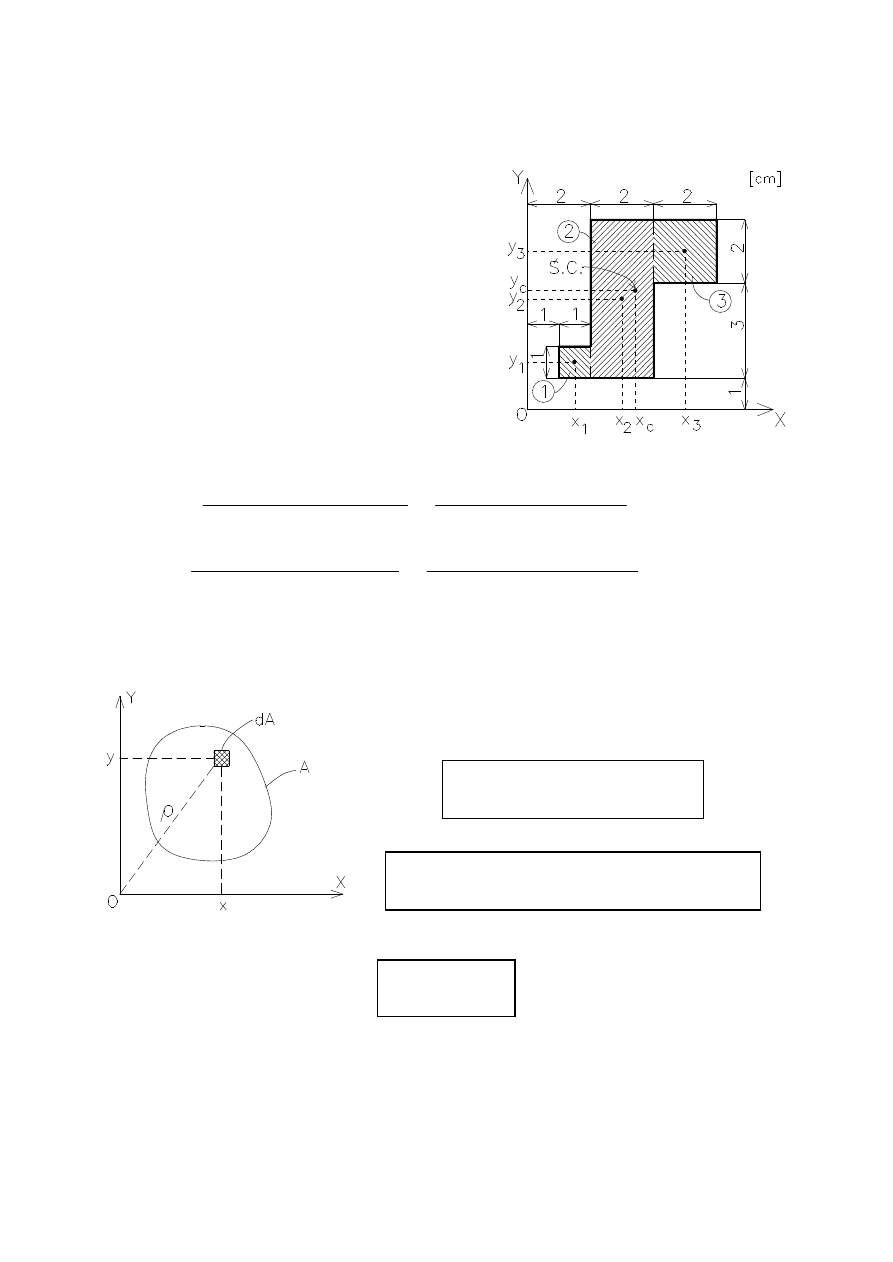
Określić położenie środka ciężkości fi-

gury przedstawionej na rysunku.

Przekrój po

dzielono na trzy prostokąty

o następujących polach powierzchni:
A

1

= 1  1 = 1 cm

2

,

A

2

= 2  5 = 10 cm

2

,

A

3

= 2  2 = 4 cm

2

.

Współrzędne środka ciężkości całej figu-
ry wyno

szą

,

cm

43

,

3

4

10

1

5

4

3

10

5

,

1

1

A

A

A

x

A

x

A

x

A

x

3

2

1

3

3

2

2

1

1

c





























.

cm

77

,

3

4

10

1

5

4

5

,

3

10

5

,

1

1

A

A

A

y

A

y

A

y

A

y

3

2

1

3

3

2

2

1

1

c





























Momenty bezwładności

Definicja

momentów bezwładności:

–

osiowe momenty bezwładności









A

2

y

A

2

x

,

dA

x

J

,

dA

y

J

–

biegunowy moment bezwładności





,

J

J

dA

y

x

dA

J

y

x

A

A

2

2

2

0

















–

moment dewiacyjny (zboczenia, odśrodkowy)





A

xy

.

xydA

J

Momenty osiowe oraz m

oment biegunowy są

zawsze dodatnie, natomiast

moment dewiacyjny może być dodatni lub ujemny.

07 Momenty, hipoteza

100

Momenty bezwładności figur złożonych są sumą momentów

bezwładności prostych figur składowych. Figura złożona może
składać się z figur „pełnych” oraz „pustych”. Przy sumowaniu
momentów bezwładności figury „puste” uważa się za figury z
ujemnymi polami powierzchni.

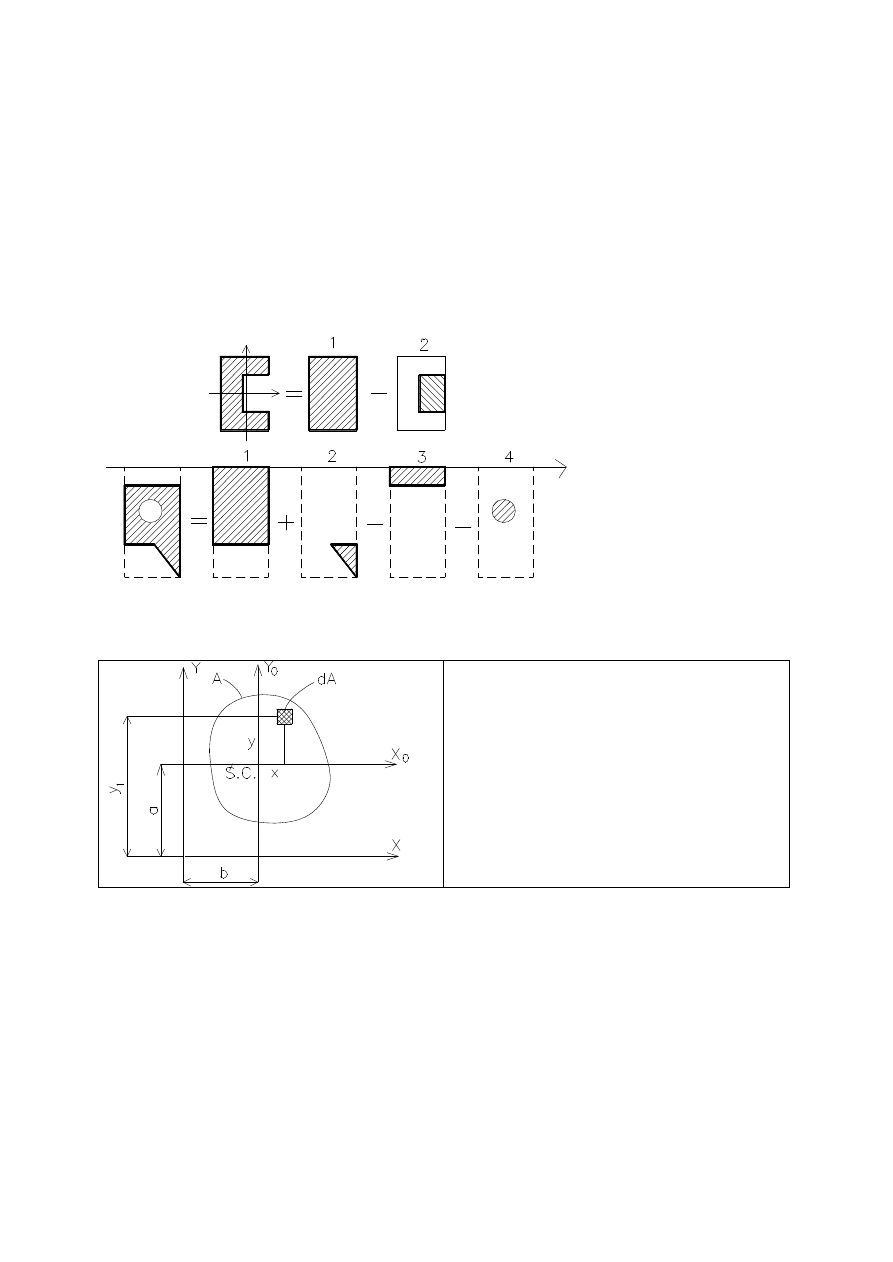
P

RZYKŁAD

Figury złożone przedstawione na rysunku podzielić na figury proste.

Podział

figury złożonej

na figury proste

(

jeden z możliwych

do zastosowania

podziałów figury).

Twierdzenie Steinera

Twierdzenie Steinera umożli-
wia obliczanie momentów bez-
władności

figur

płaskich

względem

osi

równolegle

przesuni

ętych w stosunku do

osi centralnych (osi przecho-
dzących przez środek ciężko-
ści przekroju).

Dla figury

płaskiej o powierzchni A, obliczyć momenty bez-

władności względem osi X–Y, równolegle przesuniętych w sto-
sunku do osi centralnych (środkowych) X

0

–Y

0

o odcinki a i b.

Na podstawie definicji momentu bezwładności moment osio-

wy względem osi X dla y

1

= y + a wyraża wzór:































A

A

A

A

2

x

A

2

2

2

1

x

.

Aa

J

dA

a

ydA

a

2

dA

y

dA

a

y

dA

y

J

0

07 Momenty, hipoteza

101

W powyższym równaniu całka



A

ydA

opisuje moment statycz-

ny, który względem osi centralnych jest równy zeru. W podobny
sposób określa się moment względem osi Y oraz moment de-
wiacyjny

































A

y

x

xy

A

2

x

2

y

.

Aab

J

dA

b

x

a

x

J

,

Ab

J

dA

b

x

J

0

0

0

Wyprowadzone wyżej zależności noszą nazwę twierdzenia

Steinera.

Osiowy moment bezwładności figury płaskiej względem osi

równoległej odległej od środka ciężkości o określoną wartość
jest równy momentowi względem osi równoległej przechodzą-
cej przez środek ciężkości figury, powiększonemu o iloczyn
powierzchni figury i kwadratu odległości między osiami.

Moment dewiacyjny figury płaskiej względem osi równolegle

przesuniętych jest równy momentowi dewiacyjnemu wzglę-
dem osi centralnych, powiększonemu o iloczyn powierzchni i
obu składowych równoległego przesunięcia.

Twierdzenie Steinera ma następująca postać matematyczną:

.

Aab

J

J

,

Ab

J

J

,

Aa

J

J

0

0

0

0

y

x

xy

2

y

y

2

x

x













07 Momenty, hipoteza

102

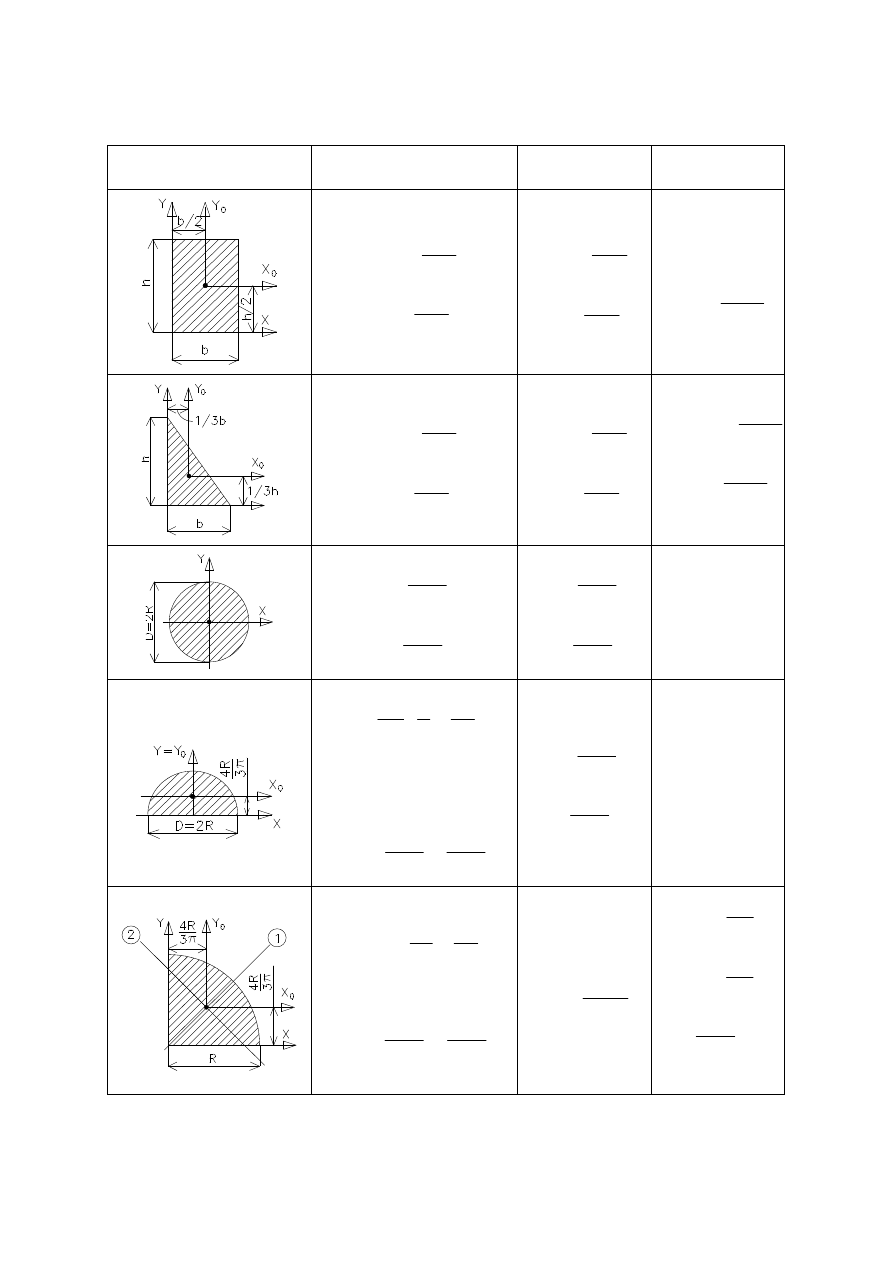
Momenty bezwładności figur prostych

Figura

J

x

J

y

J

xy

3

bh

J

12

bh

J

3

x

3

x

o





3

hb

J

12

hb

J

3

y

3

y

o





4

h

b

J

0

J

2

2

xy

y

x

o

o





12

bh

J

36

bh

J

3

x

3

x

o





12

hb

J

36

hb

J

3

x

3

x

o





24

h

b

J

72

h

b

J

2

2

xy

2

2

y

x

o

o







4

R

64

D

J

4

4

x











4

R

64

D

J

4

4

y











0

J

xy



8

R

128

D

J

R

1098

,

0

D

00686

,

0

9

8

8

16

D

J

4

4

x

4

4

4

x

o





































8

R

128

D

J

4

4

y











0

J

0

J

o

o

y

x

xy





16

R

256

D

J

R

0549

,

0

9

4

16

R

J

4

4

x

4

4

x

o

































16

R

J

4

x





4

4

4

y

x

4

xy

R

0165

,

0

9

R

4

8

R

J

8

R

J

0

o

















07 Momenty, hipoteza

103

P

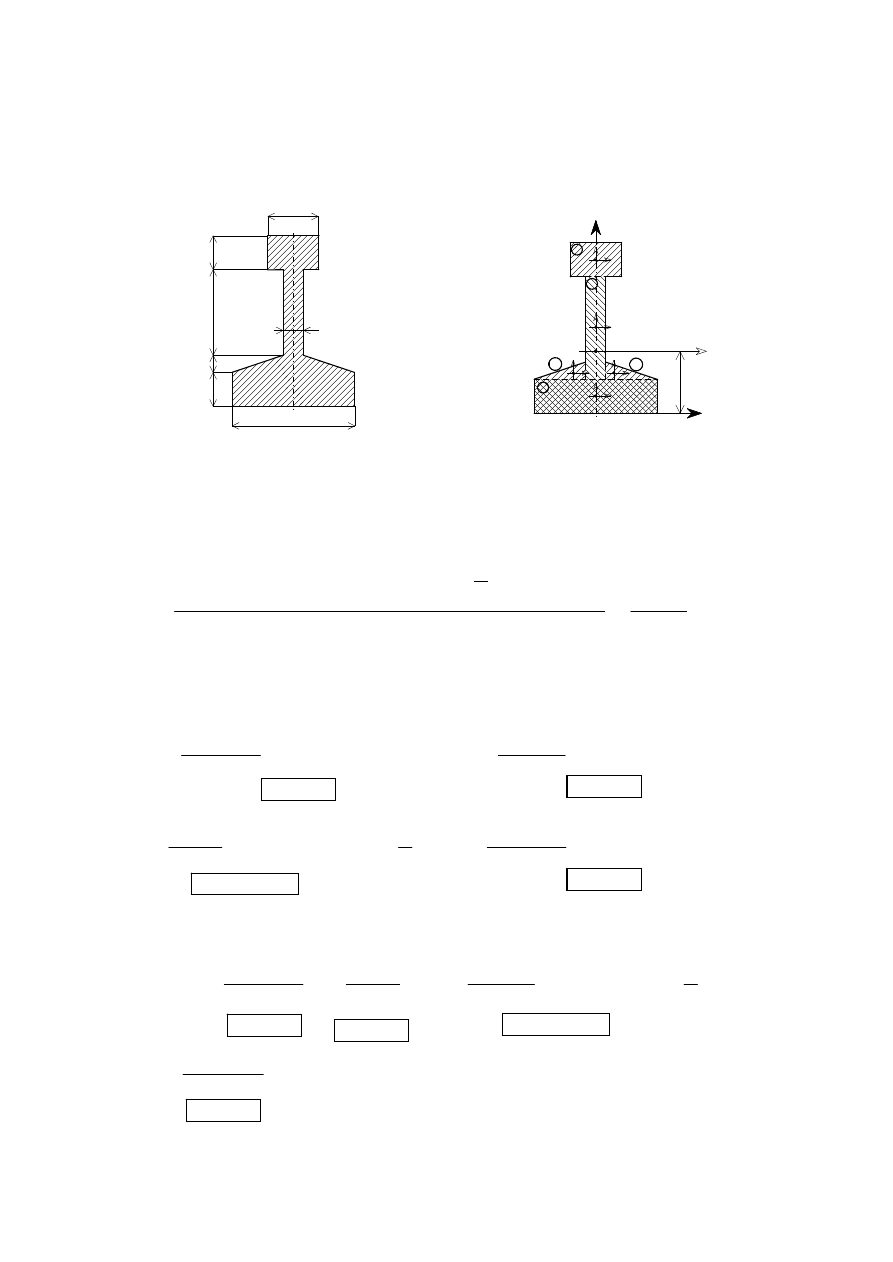
RZYKŁAD

Dla figury płaskiej pokazanej wyznaczyć wartości centralnych momen-

tów bez

władności.

2

t

5

t

7t

2

t

t

t

3t

1

2

4

3"

3'

X

X

X

X

X

X

Y

Y

Y

Y

Y

C

2

1

C

X

s

4

C

3

C'

3

C"

x

s

C

Y

Y

s

=

Figura złożona zostaje podzielona na figury proste. Korzystając ze

wzorów na wy

znaczanie środka ciężkości względem osi X-Y otrzymuje

się

 

 

 

 

 

 

 

   

   

.

0

x

,

t

62

,

3

t

29

t

105

t

14

t

5

,

1

2

t

6

t

6

t

t

14

t

3

1

2

t

5

,

1

2

t

5

t

6

t

9

t

6

y

s

2

3

2

2

2

2

2

2

2

2

s





































Osiowe momenty bezwładności wynoszą

 

 





 

 





 

 

 





,

t

57

,

381

t

77

,

100

t

57

,

2

2

t

43

,

29

t

23

,

246

t

t

62

,

3

t

14

12

t

2

t

7

t

3

1

2

t

62

,

3

t

5

,

1

36

t

t

3

2

t

62

,

3

t

5

t

6

12

t

6

t

t

62

,

3

t

10

t

6

12

t

2

t

6

J

2

2

2

2

2

2

t

62

,

2

2

3

2

t

287

,

1

2

3

2

t

38

,

1

2

2

t

38

,

6

2

2

3

x

s





































































































































 

 

 

.

t

42

,

70

t

17

,

57

t

125

,

4

2

t

5

,

0

t

5

,

4

12

)

t

7

(

t

2

t

3

3

1

t

5

,

0

t

5

,

1

36

t

3

t

2

12

t

t

6

12

t

3

t

2

J

J

4

4

4

4

4

3

2

t

5

,

1

2

3

3

3

y

y

s

















































































































Figura 1

Figura 3’ i 3”

Figura 4

Figura 1

Figura 2

Figura 2

Figura 3’ i 3”

Figura 4

07 Momenty, hipoteza

104

HIPOTEZY WYTRZYMAŁOŚCIOWE

W praktyce inżynierskiej występują złożone stany naprężenia,
będące kombinacją naprężeń normalnych i stycznych. Przyjęcie
hipotezy wytrzymałościowej umożliwia znalezienie matema-
tycznej funkcji pozwalającej na zastąpienie złożonego, prze-
strzennego stanu naprężenia przez stan jednoosiowego rozcią-
gania, dokładnie opisany przez statyczną próbę rozciągania.
Dzięki temu w obliczeniach wytrzymałościowych można wyko-
rzystać warunek wytrzymałościowy:

.

n

nieb

dop

red











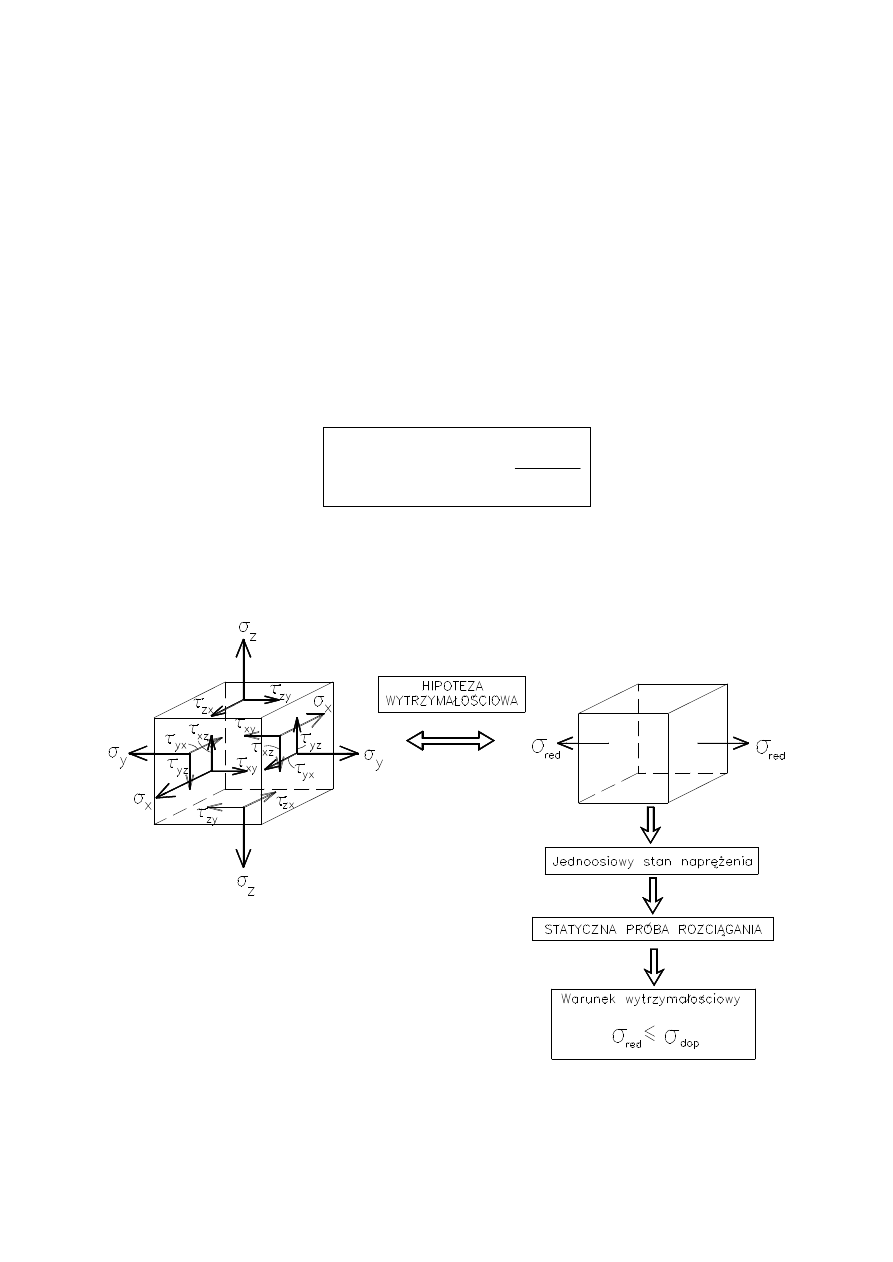
Ideę obliczeń wytrzymałościowych opartą na

naprężeniach zredukowanych pokazano na rysunku.

07 Momenty, hipoteza

105

Obecnie znanych jest kilkadziesiąt hipotez wytrzymałościo-

wych. Niektóre z nich mają już tylko znaczenie historyczne, inne
nie są dostatecznie potwierdzone przez doświadczenie, jeszcze
inne są bardzo wyspecjalizowane i przeznaczone do wąskiej
klasy zagadnień wytrzymałościowych.

Spośród hipotez ogólnych, dających wyniki zgodne z do-

świadczeniem, należy wymienić hipotezę energii odkształce-
nia postaciowego (hipo

tezę Hubera).

Maksymilian Tytus Huber (1872-1950) polski uczony,

wspó

łtwórca współczesnej mechaniki teoretycznej,

profesor Politechniki Lwowskiej, Politechnika Warszawskiej

i po II Wojnie Światowej Politechniki Gdańskiej.

Hipoteza

ta należy do licznej grupy tzw. hipotez energetycz-

nych. Twórcy hipotezy (Huber 1904, Mises 1913, Hencky 1925)
przyjęli, że miarą wytężenia materiału jest wartość energii
sprężystej odkształcenia postaciowego.

Dla przypadku jednoczesnego występowania naprężeń nor-

malnych i stycznych (zginanie belek), naprężenia zredukowane
zastępujące ten złożony stan naprężenia oblicza się z zależno-
ści:

.

3

2

2

red











Hipoteza Hubera (Hubera – Misesa – Hencky’go) jest po-

twierdzona doświadczalnie i jest obecnie bardzo szeroko sto-
sowana w praktyce inżynierskiej.