
Janusz Kacerka
Podstawy Informatyki
————————————————————————————————————————
Semestr 1 AiR
Przetwarzanie informacji

Spis treści
2
Podstawy Informatyki

Przetwarzanie informacji
1. Przetwarzanie informacji
1.2. Elektroniczne elementy cyfrowe
Podstawowymi elementami urządzeń zwanych urządzeniami cyfrowymi, takich jak
- sterowniki PLC (Programmable Logic Controller),
- mikrokomputery,
- przemysłowe regulatory cyfrowe,
są elektroniczne elementy logiczne. Działanie ich sprowadza się do przyjmowania
dwóch stanów 0 lub 1. Wartości te umownie oznaczają określone poziomy napięć,
zależne od realizacji wybranych elementów. Na przykład w technice TTL
(Transistor - Transistor Logic) przy zasilaniu elementów napięciem +5V
3
Podstawy Informatyki

Przetwarzanie informacji
- sygnał 0 odpowiada przedziałowi napięć 0,2
÷
0,4 V,
- sygnał 1 odpowiada przedziałowi napięć 2,4
÷
3,3 V.
Z podstawowych elementów logicznych buduje się większe moduły wchodzące w
skład urządzeń cyfrowych, stosując coraz większą skalę integracji, to znaczy
wytwarzając coraz większą ilość bramek na płytce krzemu.
Zasady realizacji operacji logicznych określone są w algebrze Boole’a.
1.1 Algebra Boole’a
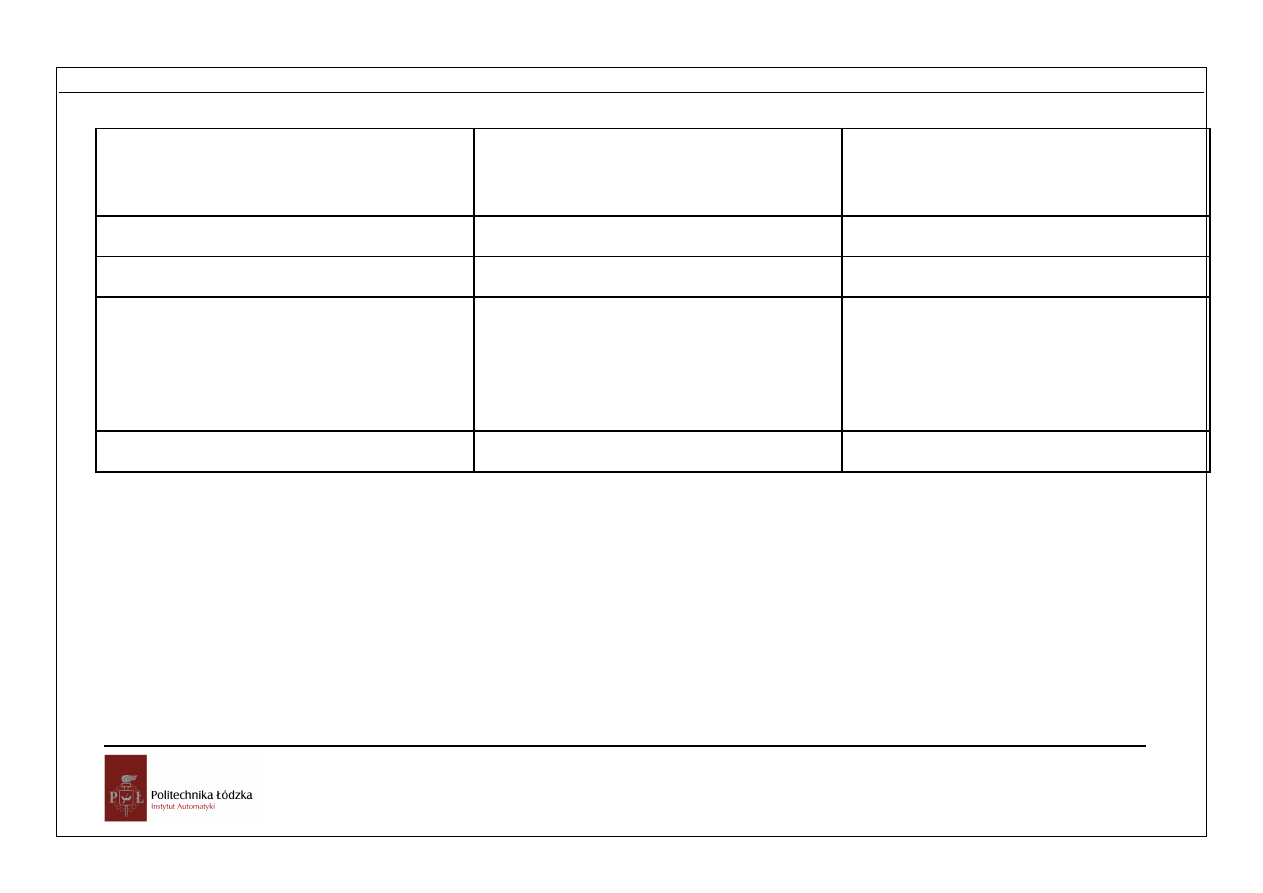
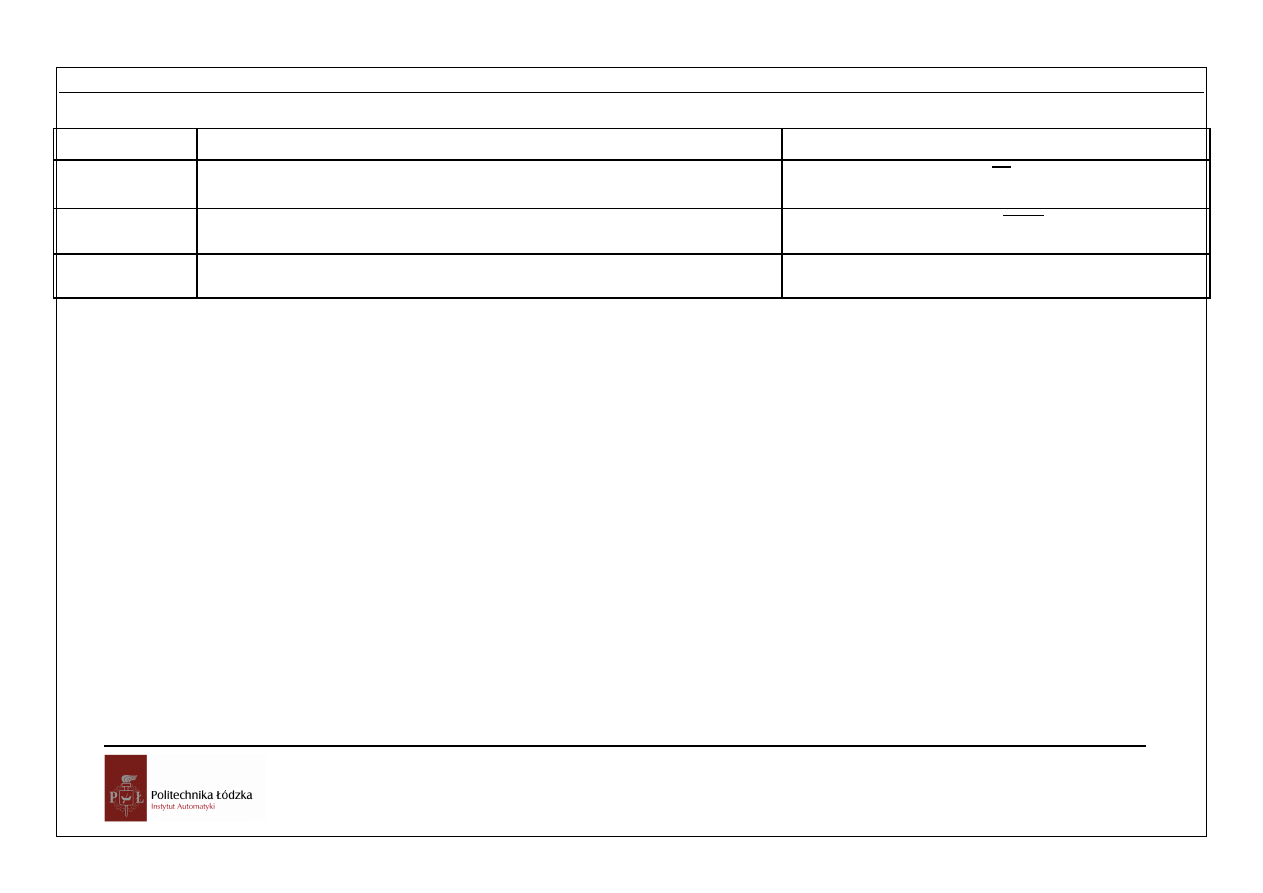
Aksjomaty, czyli pewniki algebry Boole’a przedstawiono w tabeli
Nazwa
Aksjomaty dotyczące
operacji dodawania
Aksjomaty dotyczące
operacji mnożenia
Prawo łączności
(A + B) + C = A + (B + C)
(A B) C= A (B C)
4
Podstawy Informatyki
Przetwarzanie informacji
Nazwa
Aksjomaty dotyczące
operacji dodawania
Aksjomaty dotyczące
operacji mnożenia
Prawo przemienności
A + B = B + A
A B = B A
Prawo rozdzielności
A + BC = (A + B) (A + C)
A (B + C)= A B + A C
Prawo istnienia jedynego
elementu
identycznościowego
A + 0 = A
A
×
1 = A
Prawo dopełnienia
A + Ā = 1
A Ā = 0
Z treści aksjomatu w kolumnie drugiej tabeli można otrzymać postać w kolumnie
trzeciej zastępując znak dodawania znakiem mnożenia i znak mnożenia znakiem
dodawania. Odpowiednio z zależności w kolumnie trzeciej otrzyma się zależności w
kolumnie drugiej postępując podobnie. Jest do właściwość dualności algebry Boole’a.
5
Podstawy Informatyki

Przetwarzanie informacji
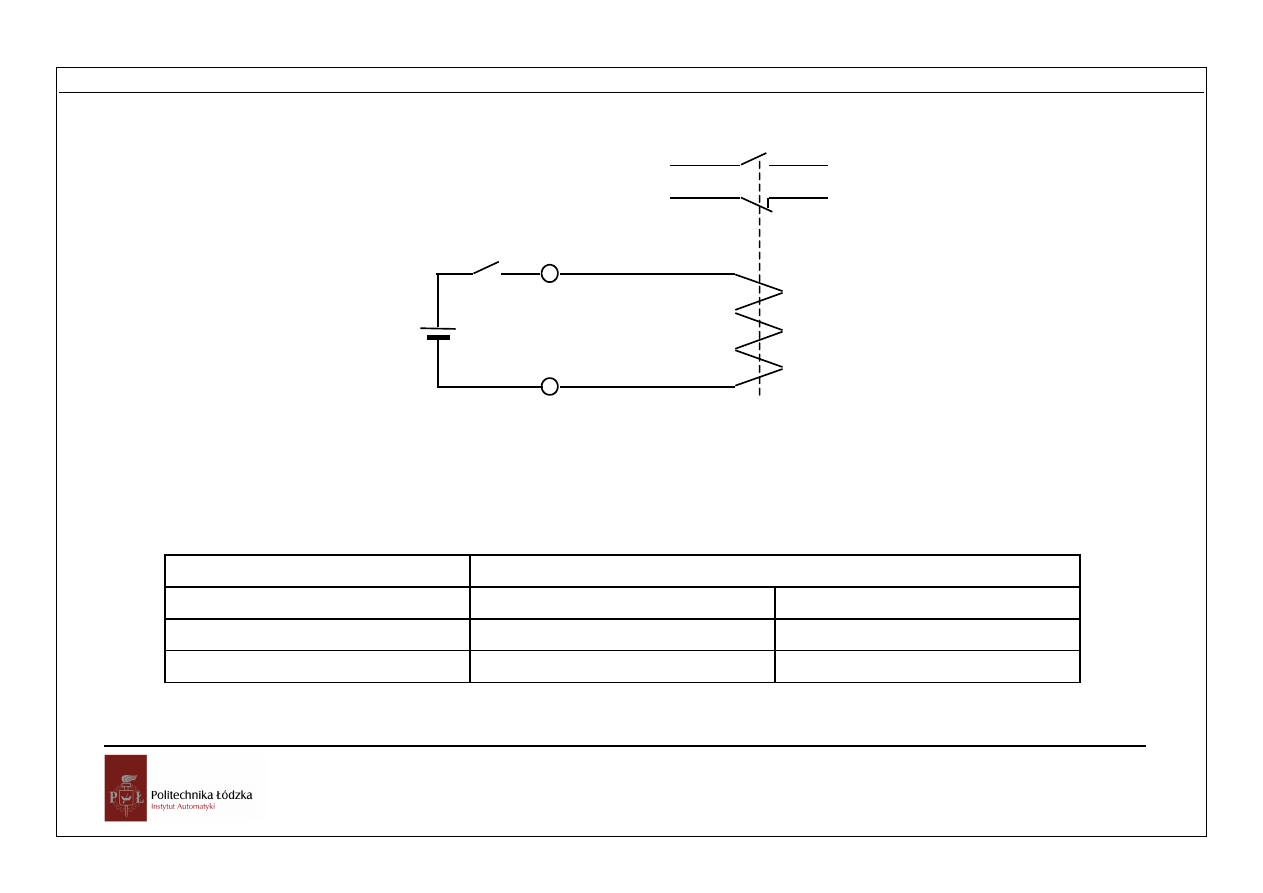
Znaczenie podanych aksjomatów można przeanalizować na przykładzie przekaźnika
elektromechanicznego (Rys. 2.1). Cewka przekaźnika może być w jednym z dwóch
stanów. Może przez nią płynąć prąd w wyniku przyłożenia do jej zacisków napięcia z
zewnętrznego źródła lub prąd nie będzie płynął. Zestyki przekaźnika przyjmują
położenie zależne od stanu cewki. Zestyki normalnie otwarte, to znaczy otwarte, gdy
cewka nie jest wzbudzona, są zamknięte, gdy cewka jest wzbudzona. Odwrotnie jest z
zestykami normalnie zamkniętymi. Stanowi wzbudzenia cewki przypisuje się stan 0
(cewka nie jest wzbudzona) lub 1, gdy cewka jest wzbudzona. Z kolei zestyki otwarte
określa się jako stan 0 a zamknięte jako 1.
6
Podstawy Informatyki
Przetwarzanie informacji
a
ā
A
Rys. 1.1 Przekaźnik jako element dwustanowy
Tabela 1.1 Stany zestyków przekaźnika
Stan cewki
Stan zestyków
A
a
ā
0
0
1
1
1
0
7
Podstawy Informatyki
Przetwarzanie informacji
a
ā
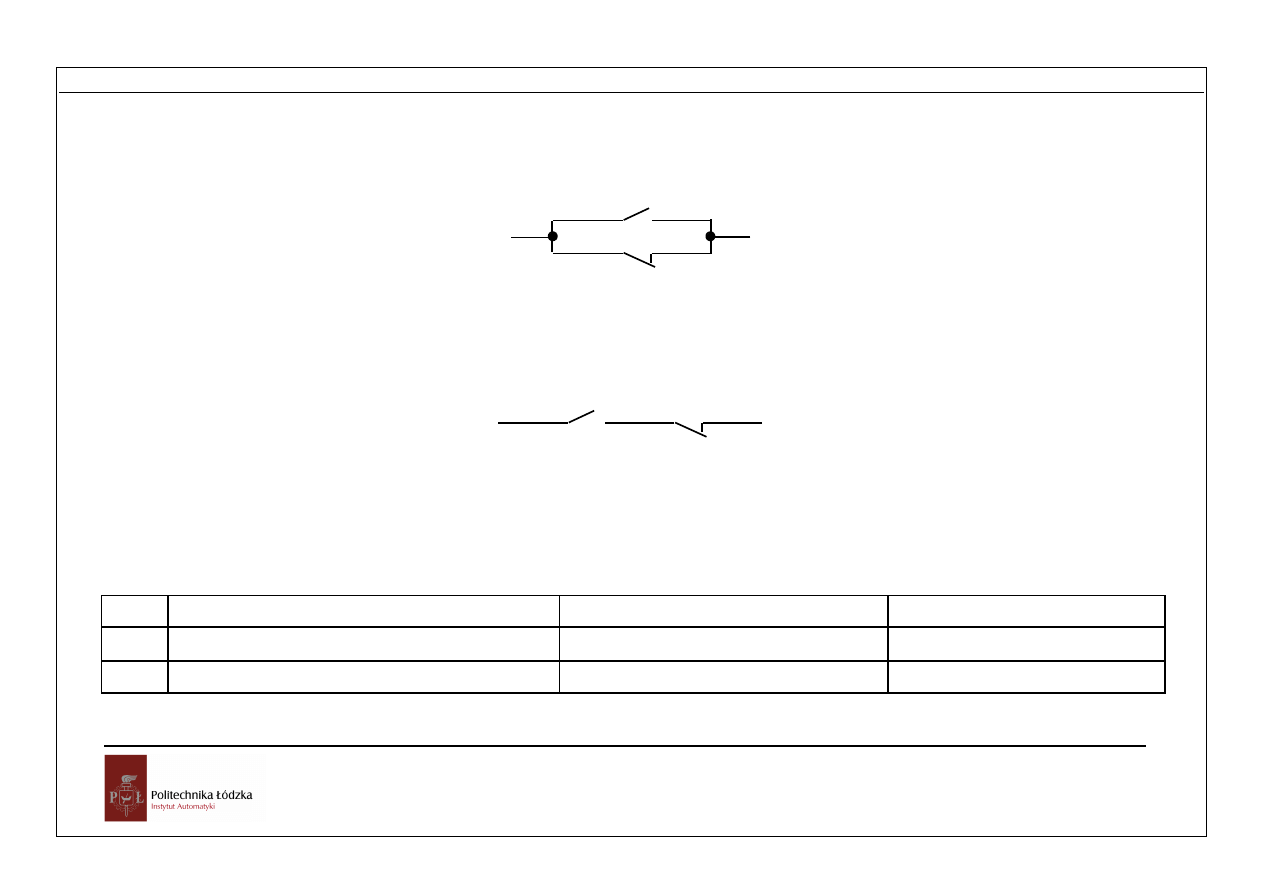
Rys. 1.2 Prawo dopełnienia
a + ā = 1
a
ā
Rys. 1.3 Prawo dopełnienia
a ā = 0
Nr
Nazwa twierdzenia
Dodawanie
Mnożenie
1
Prawo stałych elementów
A+1=1
A
×
0=0
2
Prawo powtórzenia
A+A=A
AA=A
8
Podstawy Informatyki

Przetwarzanie informacji
Nr
Nazwa twierdzenia
Dodawanie
Mnożenie
3
Prawo podwójnej negacji
A
A
=
4
Prawo de Morgana
B
A
B
A
=
+
B
A
AB
+
=
5
Uogólnione prawo de Morgana
(
)
(
)
+
×
=
×
+
,
,...
C
,
B
,
A
,
,...
C
B,
A,
f
f
6
Reguła pochłaniania 1
A+AB=A
A(A+B)=A
7
Reguła pochłaniania 2
A+ĀB=A+B
A(Ā+B)=AB
8
Uogólniona reguła 6 i 7
(
)
(
)
,...
C
B,
0,1,
A
,...
C
B,
,
A
A,
A
f
f
+
=
=
+
(
)
(
)
,...
C
B,
1,0,
A
,...
C
B,
,
A
A,
A
f
f
=
=
9
Reguła sklejania
A
B
A
AB
=
+
(
)
(
)
A
B
A
B
A
=
+
+
1.2 Funkcje logiczne dwóch zmiennych
Tabela 1.2 Nazwy funkcji dwóch zmiennych
9
Podstawy Informatyki
Przetwarzanie informacji
L.p.
Nazwa
Postać
0
Stała zero
f
0
= 0
1
Koniunkcja (AND)
f
1
= XY
2
Zakaz przez Y
Y
X
f
2
=
3
Zmienna X
X
f
3
=
4
Zakaz przez X
Y
X
f
4
=
5
Zmienna Y
Y
f
5
=
6
ALBO, Suma modulo 2, różnica
Y
X
Y
X
f
6
+
=
7
LUB, dysjunkcja, alternatywa, OR
Y
X
f
7
+
=
8
NOR, funkcja Peirce’a
Y
X
f
8
+
=
9
Równoważność
Y
X
XY
f
9
+
=
10
Negacja Y
Y
f
10
=
11
Implikacja X przez Y
Y
X
f
11
+
=
12
Negacja X
X
f
12
=
10
Podstawy Informatyki
Przetwarzanie informacji
L.p.
Nazwa
Postać
13
Implikacja Y przez X
Y
+
=
X
f
13
14
NAND
XY
f
14
=
15
Stała 1
1
f
15
=
1.3 Tablice stanów
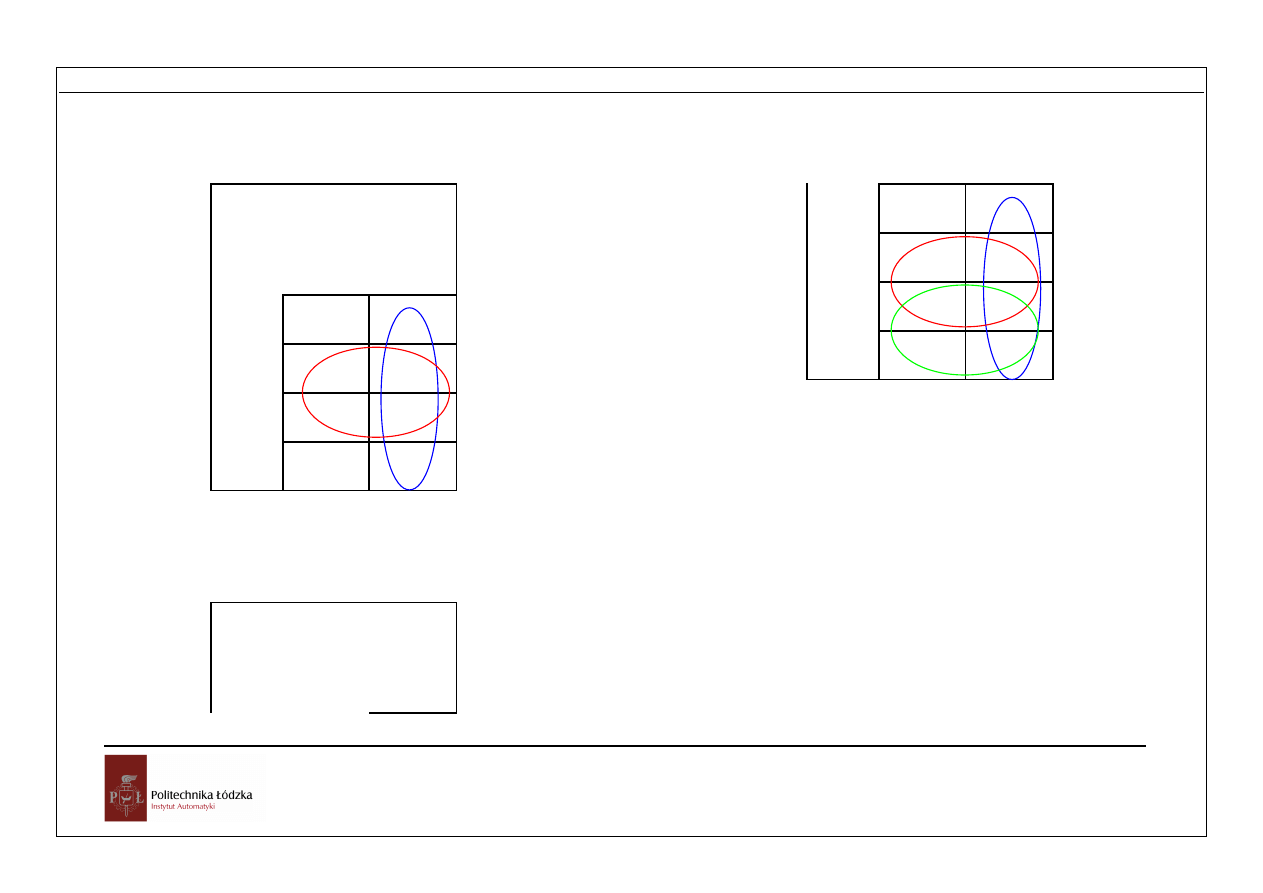
Tablice stanów tworzy się, wpisując w odpowiednich polach wartości funkcji
logicznej. Na rysunku 2.4 pokazano prostą tablicę stanów zwaną tablicą Karnaugh (czyt.
Karno) dla dwóch zmiennych X i Y
11
Podstawy Informatyki

Przetwarzanie informacji
0
1
0
0
1
1
1
1
Rys. 1.4 Tablica Karnaugh funkcji f(X,Y)=X+Y
12
Podstawy Informatyki
X Y
Przetwarzanie informacji
0
1
0 0
0
1
0 1
1
1
1 1
1
1
1 0
0
1
F(A,B,C)=AB+B(~C)+C
Wynik minimalizacji B+C
0
1
0 0
0
1
0 1
1
1
1 1
1
1
1 0
1
1
F(A,B,C)=A+B(~C)+C
Wynik minimalizacji A+B+C
13
Podstawy Informatyki
C
AB
C
Przetwarzanie informacji
Y
X
XY
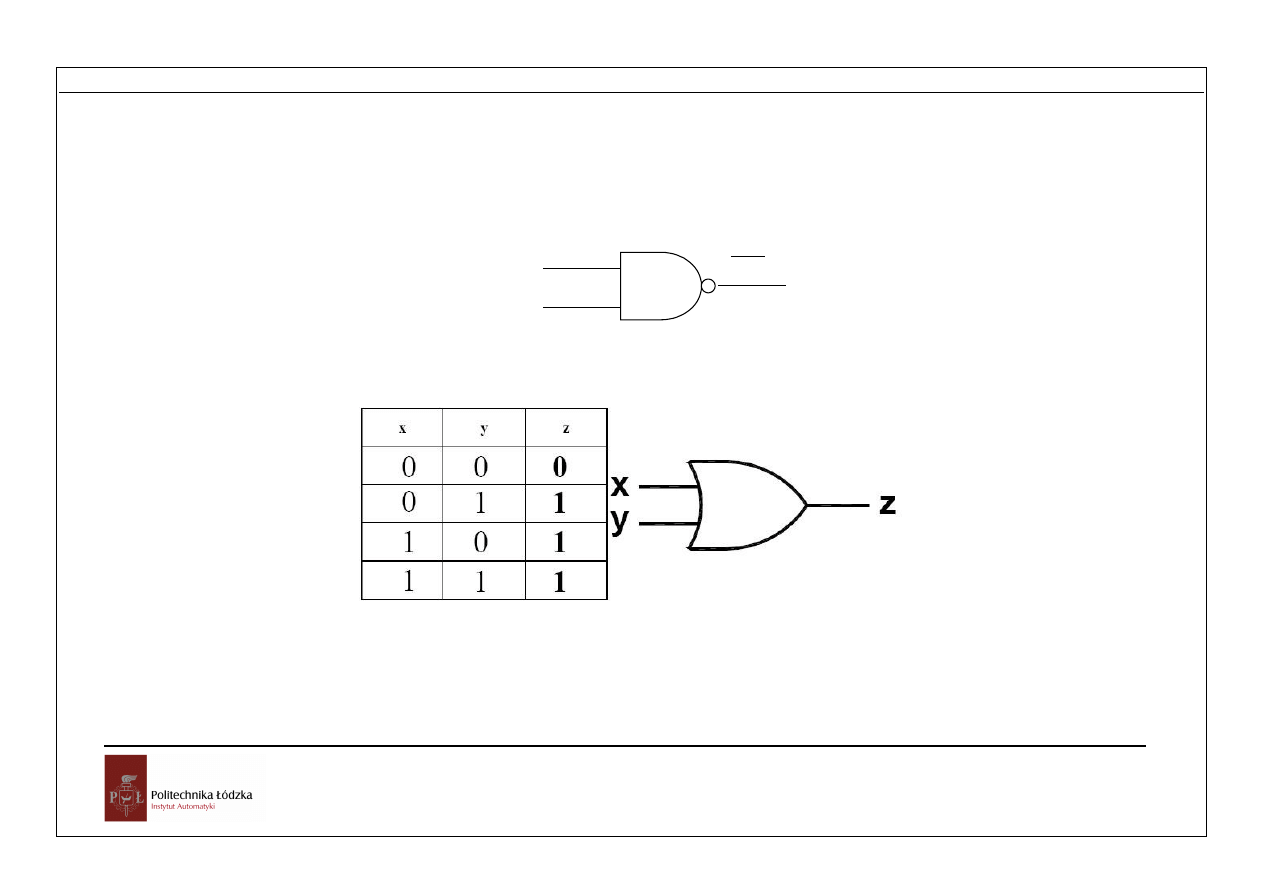
Rys. 1.5 Element NAND (TTL)
Rys. 1.6 Suma logiczna
14
Podstawy Informatyki
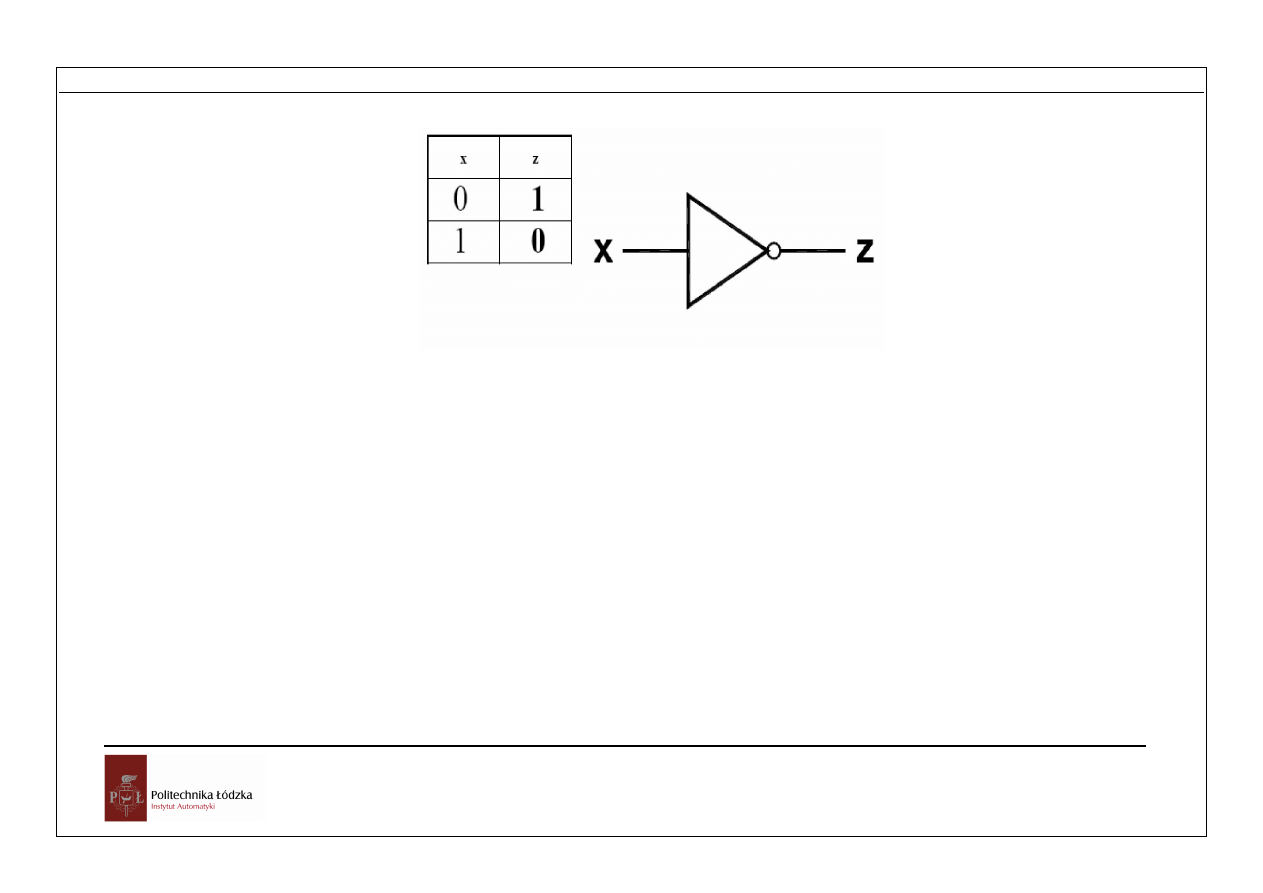
Przetwarzanie informacji
Rys. 1.7 Element NOT
15
Podstawy Informatyki
Przetwarzanie informacji
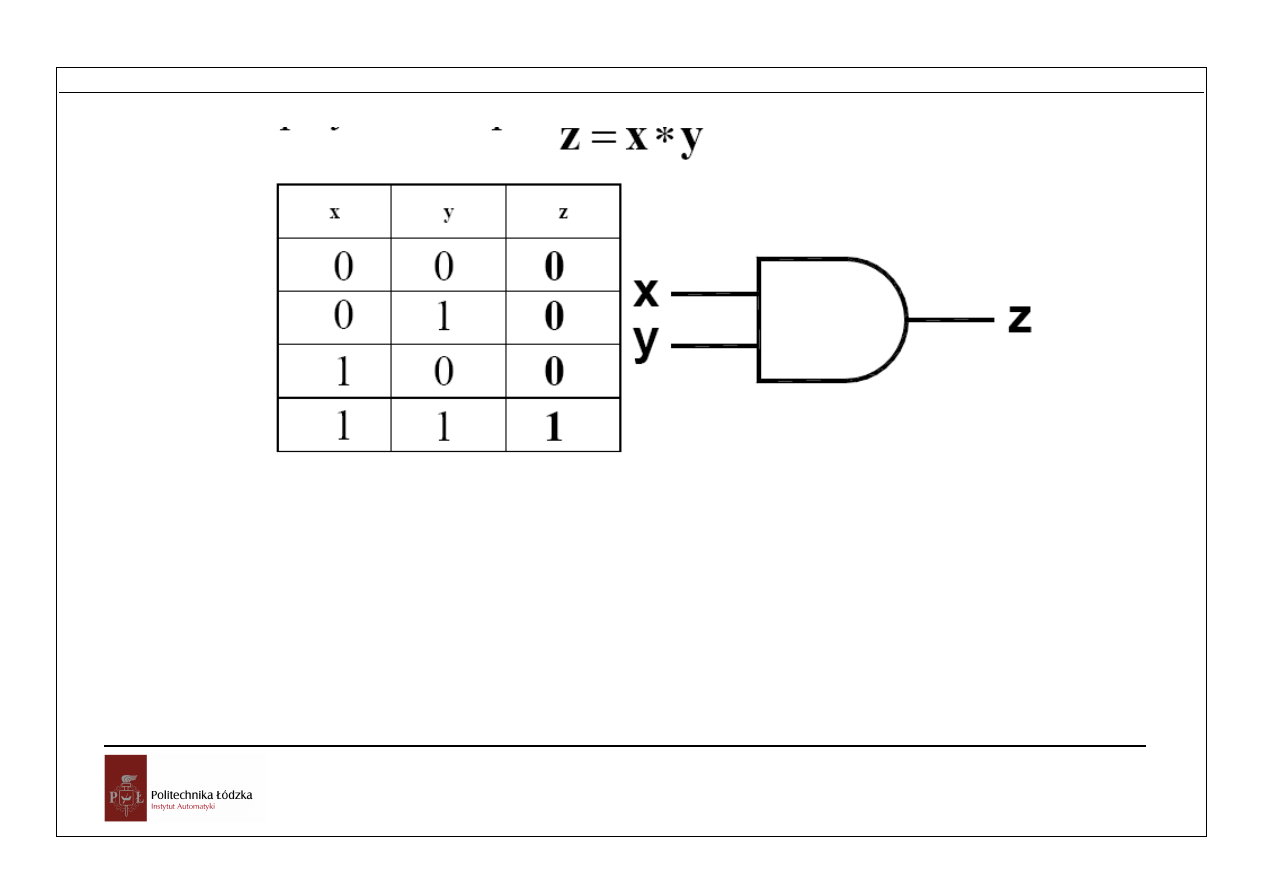
Rys.1.8 Iloczyn logiczny
16
Podstawy Informatyki
Przetwarzanie informacji
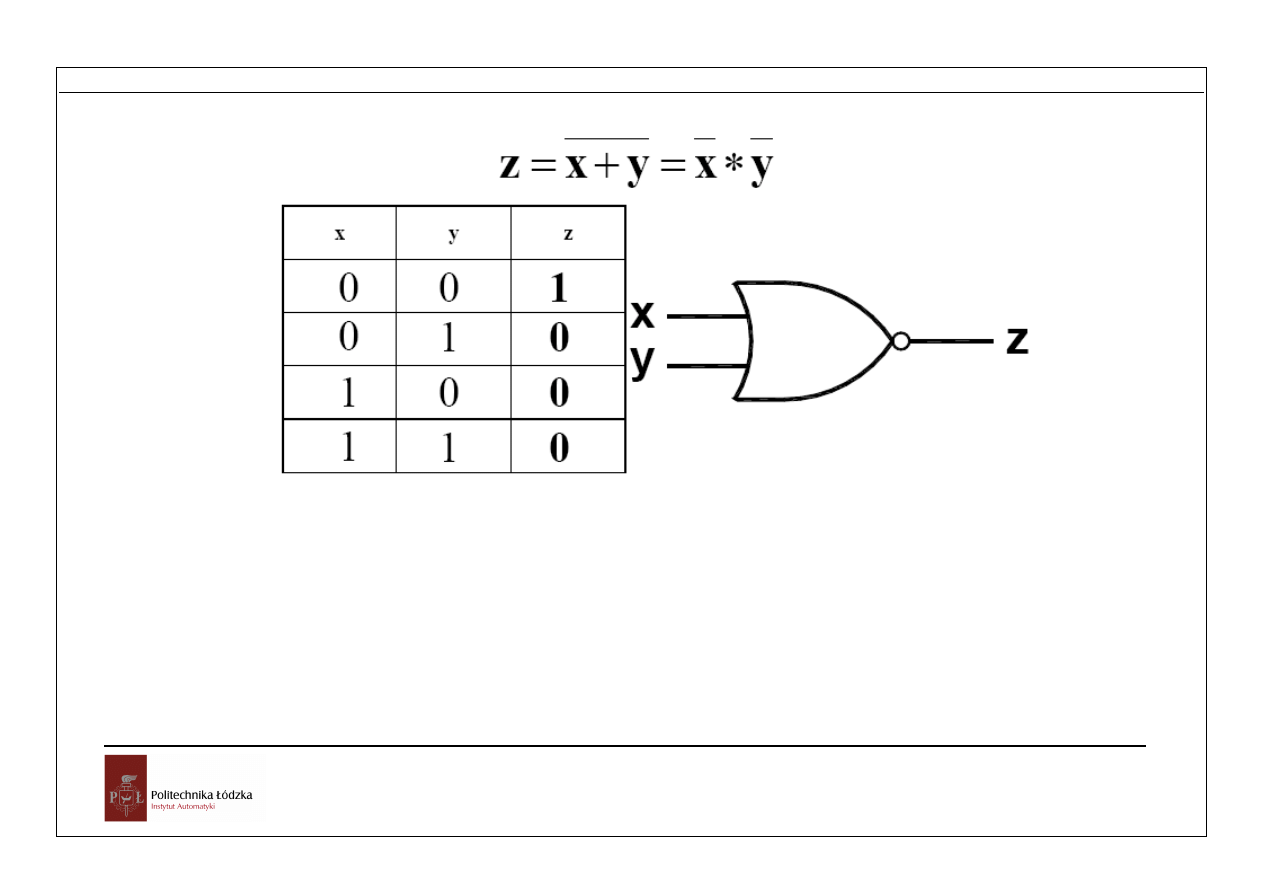
Rys. 1.9 Element NOR
Z elementów tego typu tworzy się układy kombinacyjne.
17
Podstawy Informatyki
Przetwarzanie informacji
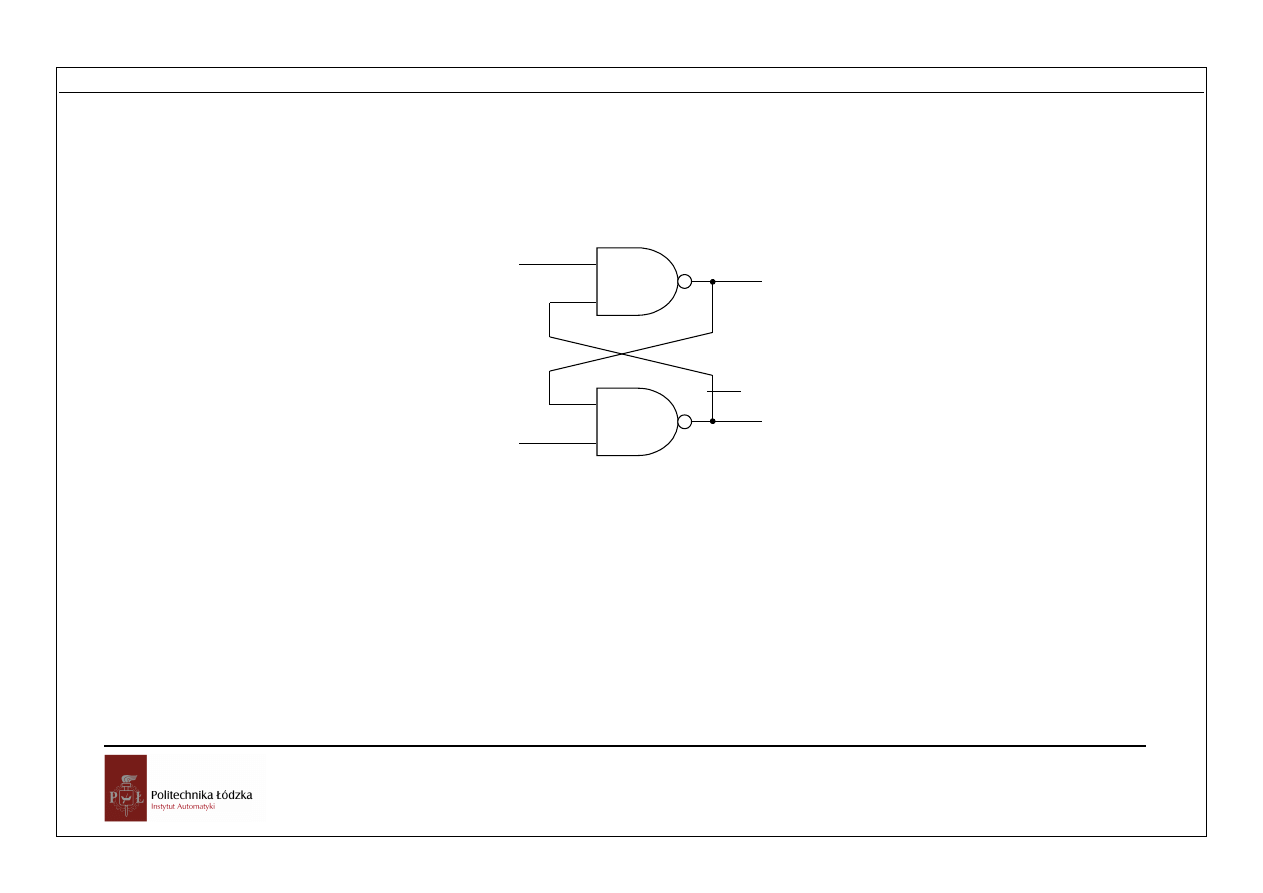
1.4 Elementy pamięciowe
Przerzutnik R-S
S
Q
R
Q
101011
111110
011110
100001
Rys. 1.6. Przerzutnik R-S i jego stany
W przerzutnikach tego typu jest zapamiętywana informacja o stanie wejść. Element
taki i inne przerzutniki umożliwiają tworzenie układów sekwencyjnych, to znaczy takich,
w których występuje pamięć poprzednich sygnałów. W przerzutniku RS stany wejść
powodują zmiany wyjść w następujący sposób:
18
Podstawy Informatyki
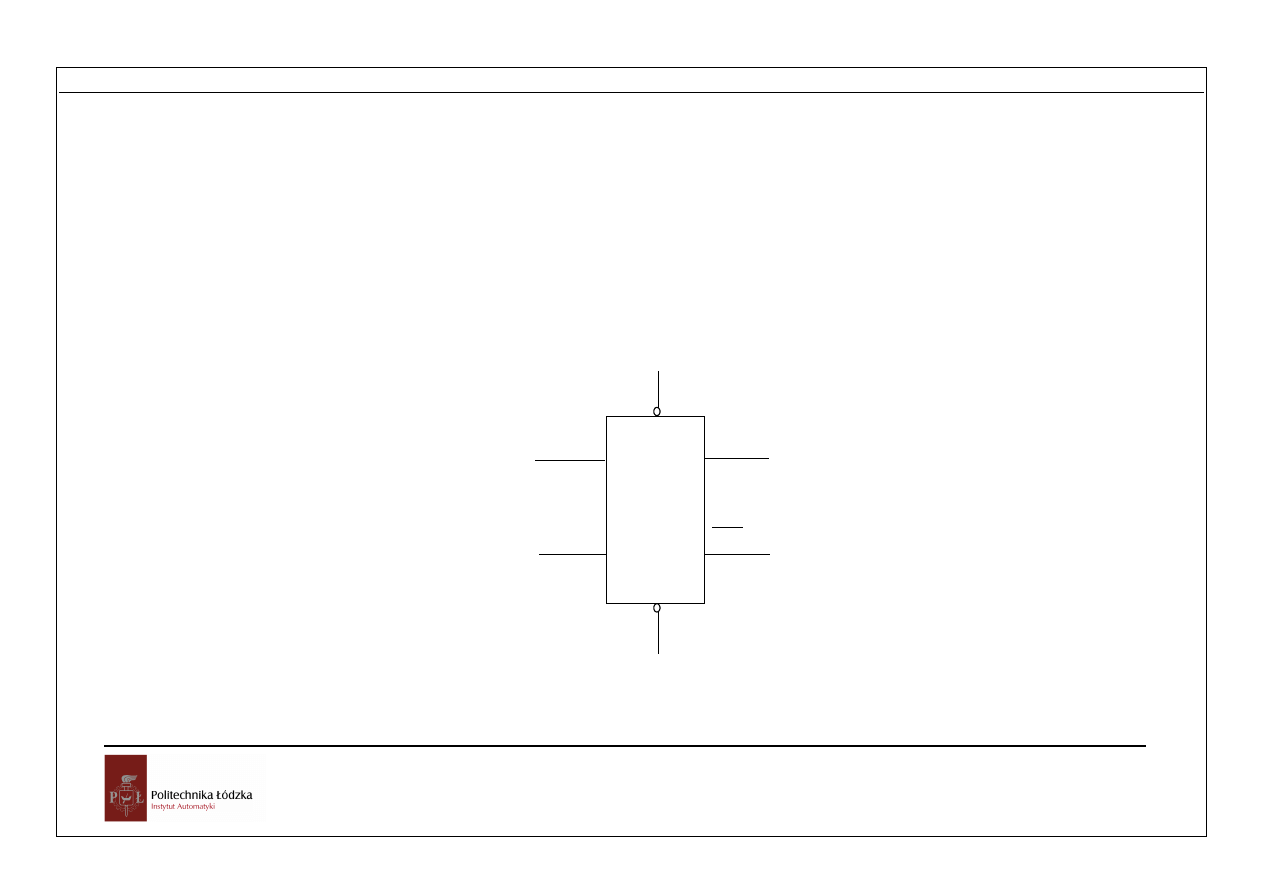
Przetwarzanie informacji
S=1 R=1 Q=0
S=0 R=1 Q=1
Powrót S do 1 nie zmieni stanu,
Zmiana R na 0 spowoduje zmianę Q =0
Stan S=0, R = 0 nie jest dopuszczalny.
r
Q
s
Q
D
C
Rys. 1.7 Przerzutnik typu D
19
Podstawy Informatyki
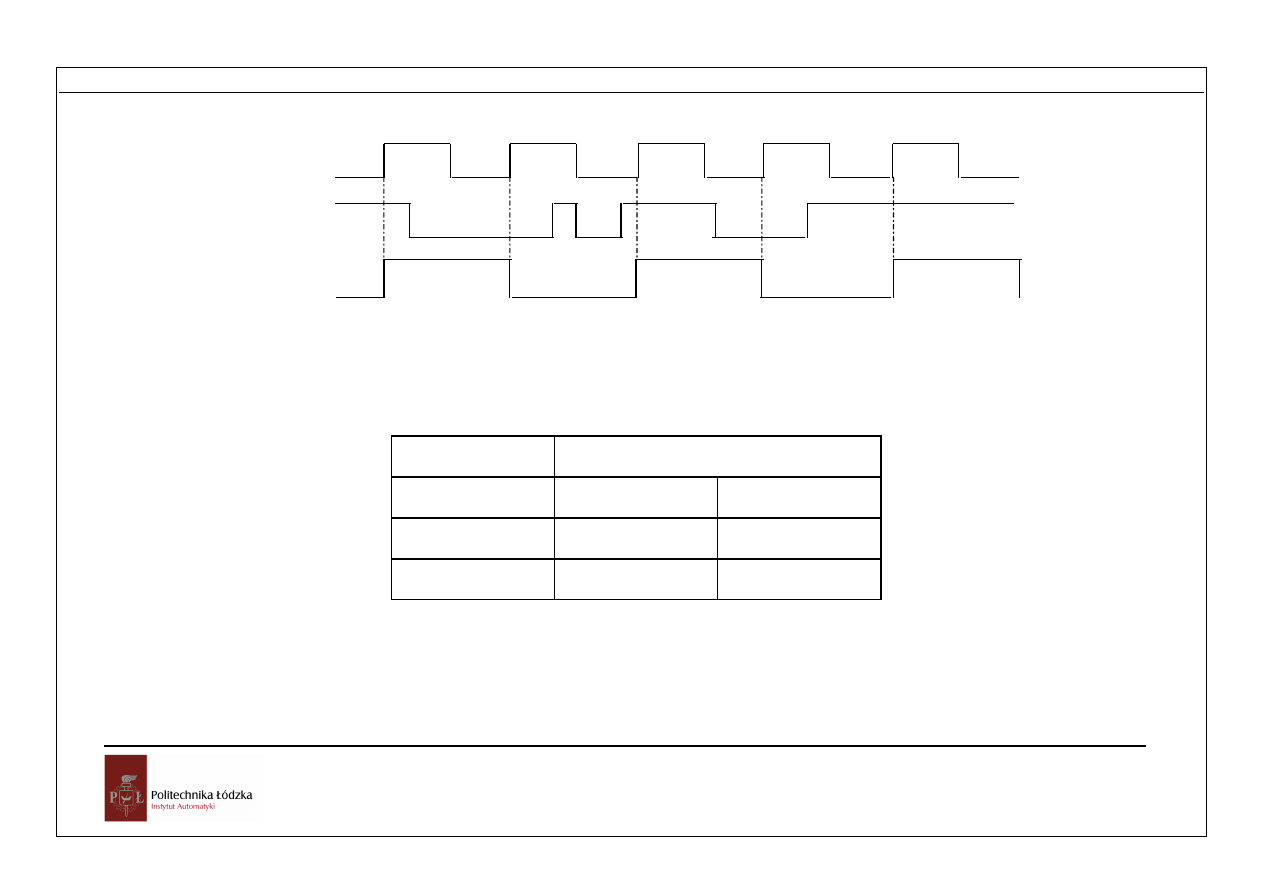
Przetwarzanie informacji
C
Q
D
Rys. 1.8. Przebiegi sygnałów przerzutnika typu D
Tabela 1.3 Stany przerzutnika D
t
n
t
n+1
D
Q
!Q
0
0
1
1
1
0
Tabela zawiera stany wejścia informacyjnego D występujące przed pojawieniem się
20
Podstawy Informatyki

Przetwarzanie informacji
zbocza wyzwalającego impulsu C ( impulsu zegarowego) oraz stany wyjść następujące
zaraz po nim.
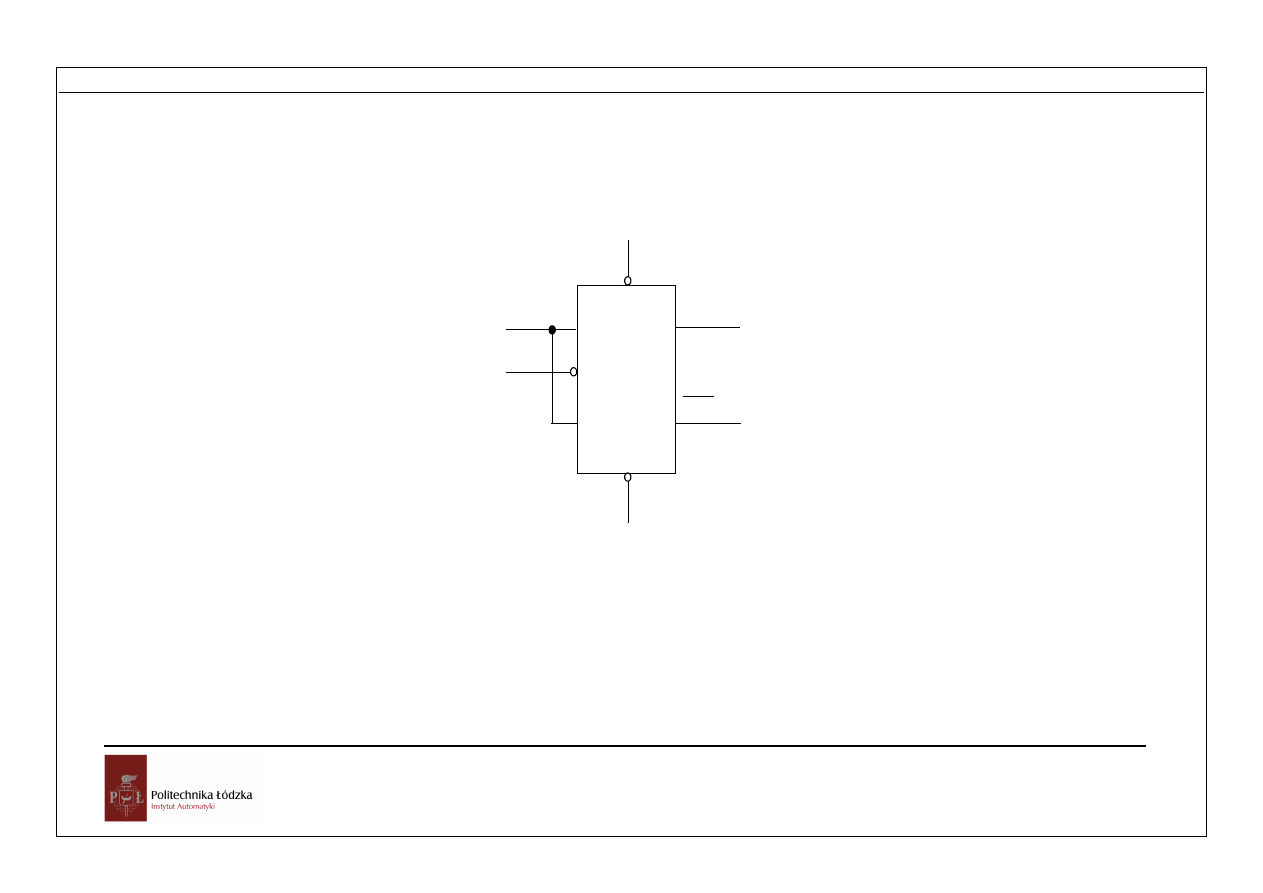
Rys. 1.9 Przerzutnik typu J-K
21
Podstawy Informatyki

Przetwarzanie informacji
C
K
J
Q
Rys. 1.10. Przebiegi sygnałów przerzutnika typu J-K
Stan następny przerzutnika zależy od stanu wejść J K i stanu aktualnego według
zasady:
J=0 i K= 0 brak zmiany stanu
J=1 i K=0 stan następny Q=1
J=0 i K=1 stan następny Q=0
22
Podstawy Informatyki
Przetwarzanie informacji
J=1 i K=1 zmiana stanu na przeciwny
Przerzutnik typu T ma postać
Wejście ustawiające
Q
Q
J
K
C
Wejście zerujące
T
Rys. 1.9 Przerzutnik typu T
23
Podstawy Informatyki
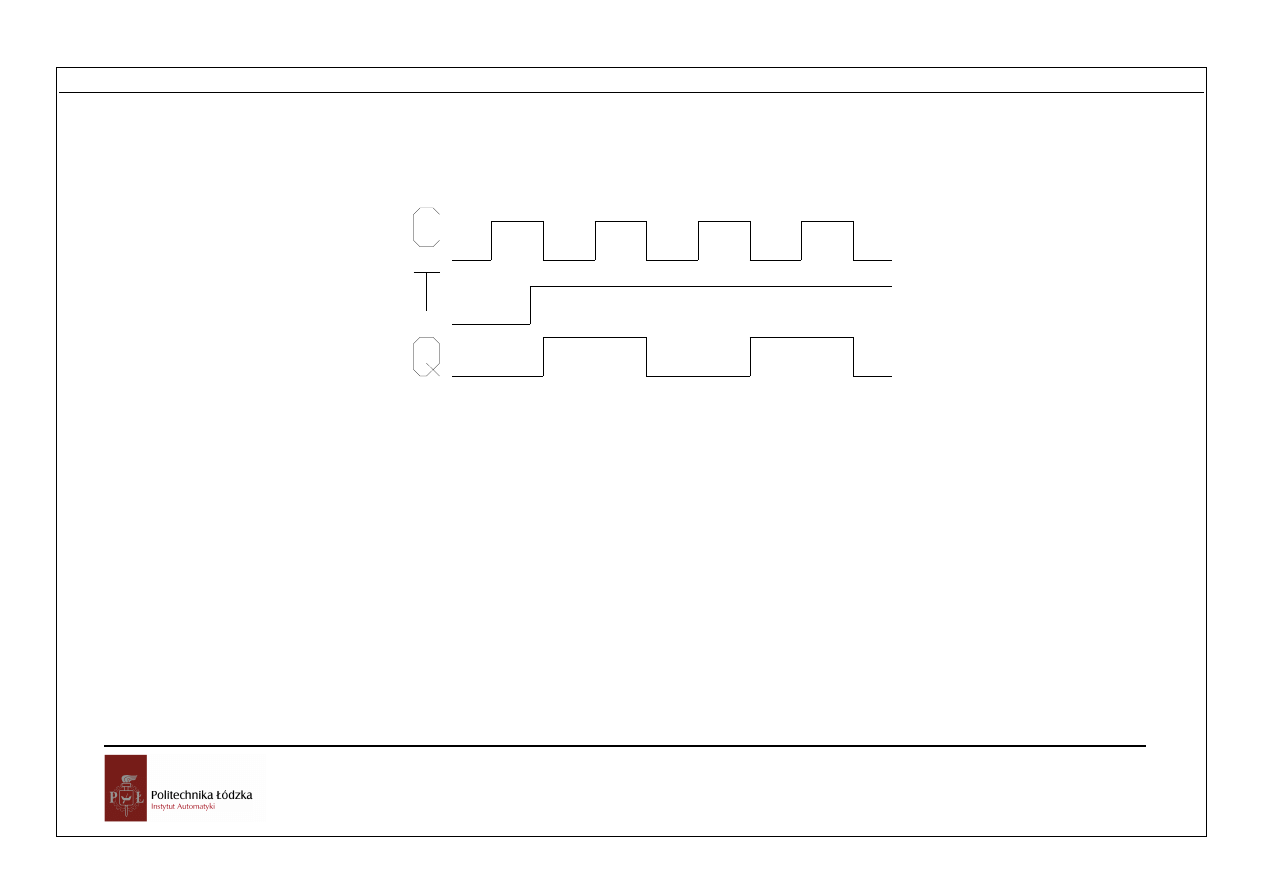
Przetwarzanie informacji
Rys.1.10 Przebiegi sygnałów przerzutnika T
24
Podstawy Informatyki
Przetwarzanie informacji
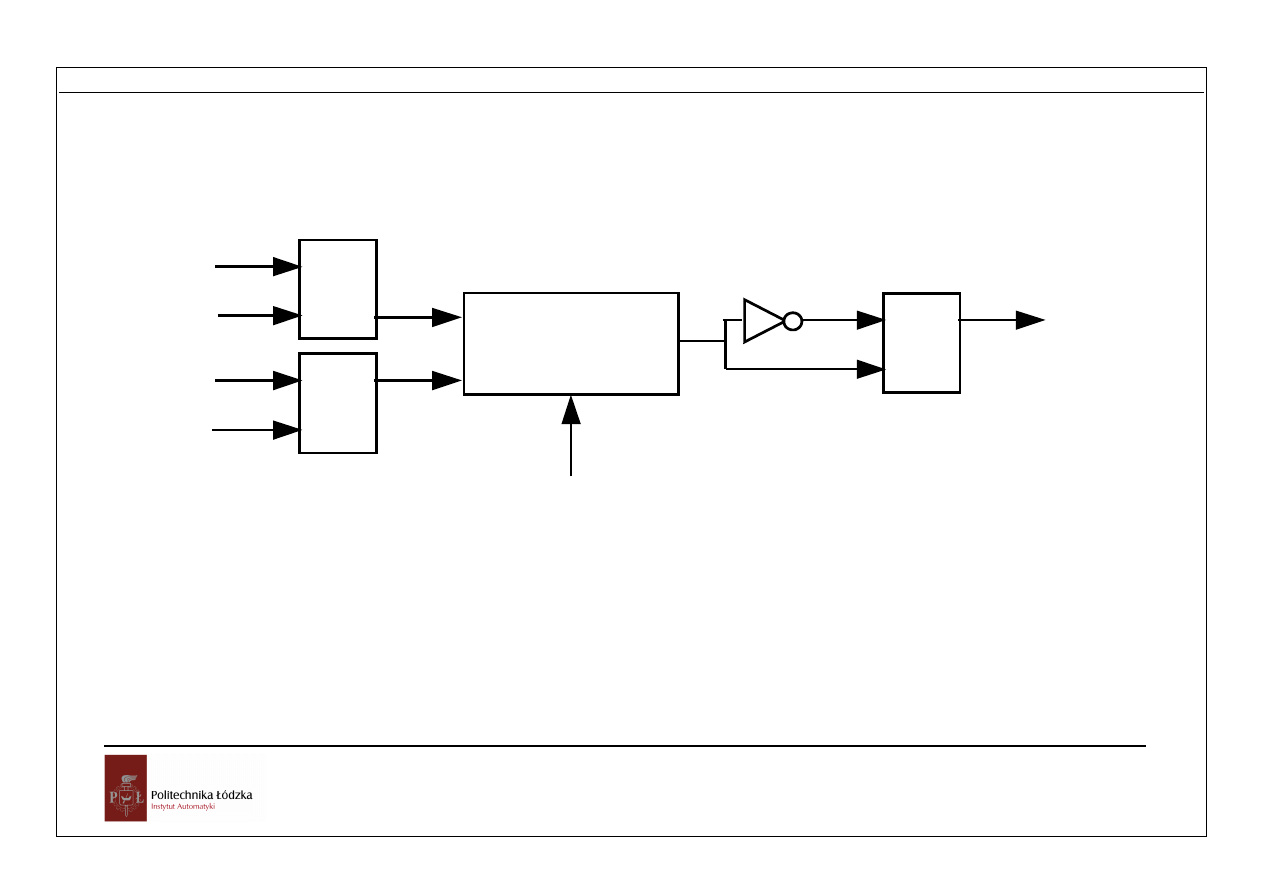
1.5 Operacje elementarne
Obwód
elementarny
Sterowanie
Q
R
S
Q
R
S
Q
R
S
R1
R2
Akumulator
(rejestr
wynikowy)
Rys. Operacje elementarne na bitach
25
Podstawy Informatyki

Przetwarzanie informacji
1
1
1
1
1
1
1
1
0
1
0
1
1
1
|
1
1
0
1
1
0
1
−
−
−
−
−
−
−
Bitowy operator logiczny OR
26
Podstawy Informatyki

Przetwarzanie informacji
1
0
0
0
1
0
1
1
0
1
0
1
1
1
&
1
1
0
1
1
0
1
−
−
−
−
−
−
−
Bitowy operator logiczny AND
27
Podstawy Informatyki

Przetwarzanie informacji
0
1
1
1
0
1
0
1
0
1
0
1
1
1
^
1
1
0
1
1
0
1
−
−
−
−
−
−
−
Bitowy operator logiczny EX-OR
28
Podstawy Informatyki

Przetwarzanie informacji
1
0
1
1
0
0
0
1
0
0
1
1
~
−
−
−
−
−
−
Negacja bitowa
1.5.1 Sumator
Sumowanie liczb binarnych
29
Podstawy Informatyki

Przetwarzanie informacji
0
0
0
0
1
0
0
1
1
0
1
0
1
1
1
1
0
1
1
0
1
−
−
−
−
−
−
−
−
+
Rys. Dodawanie liczb binarnych 91+53=144
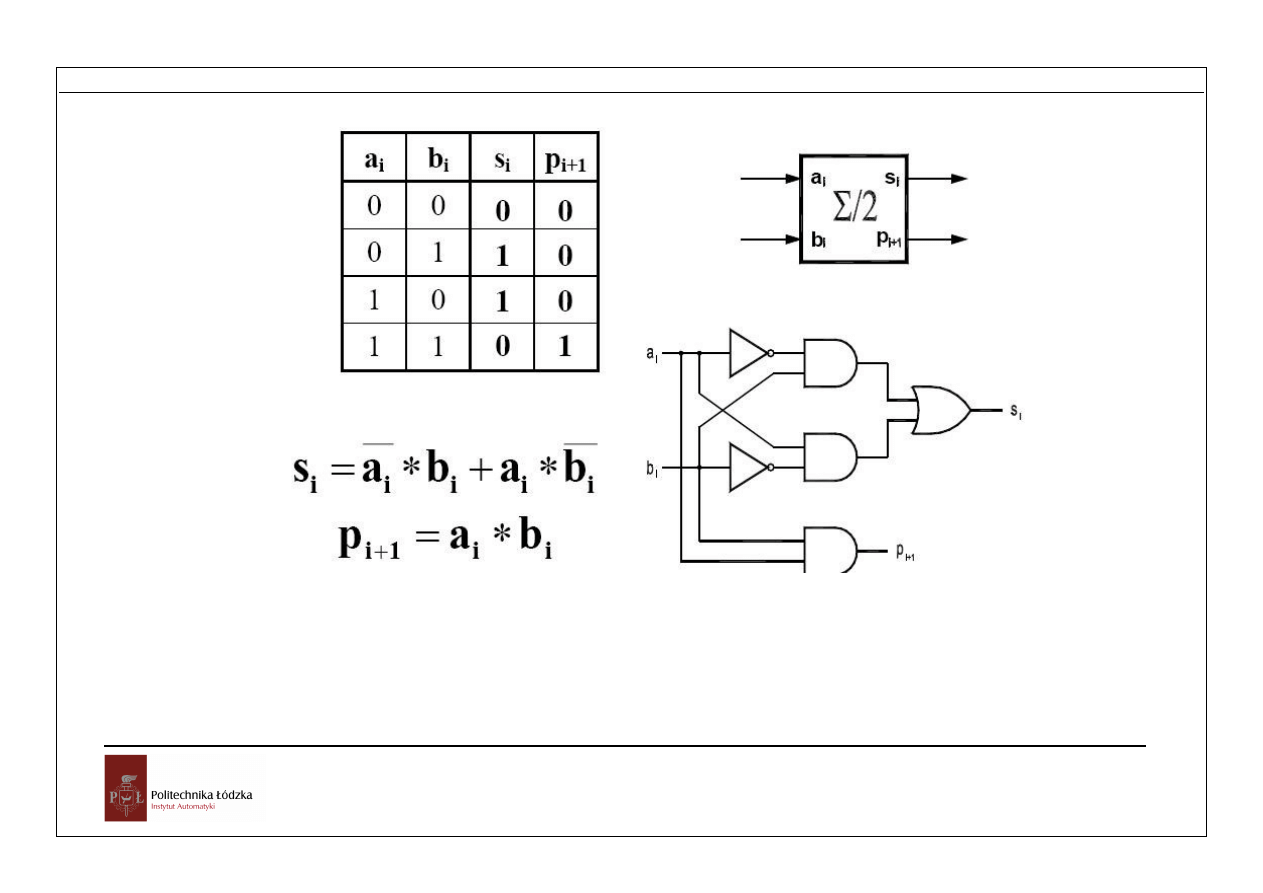
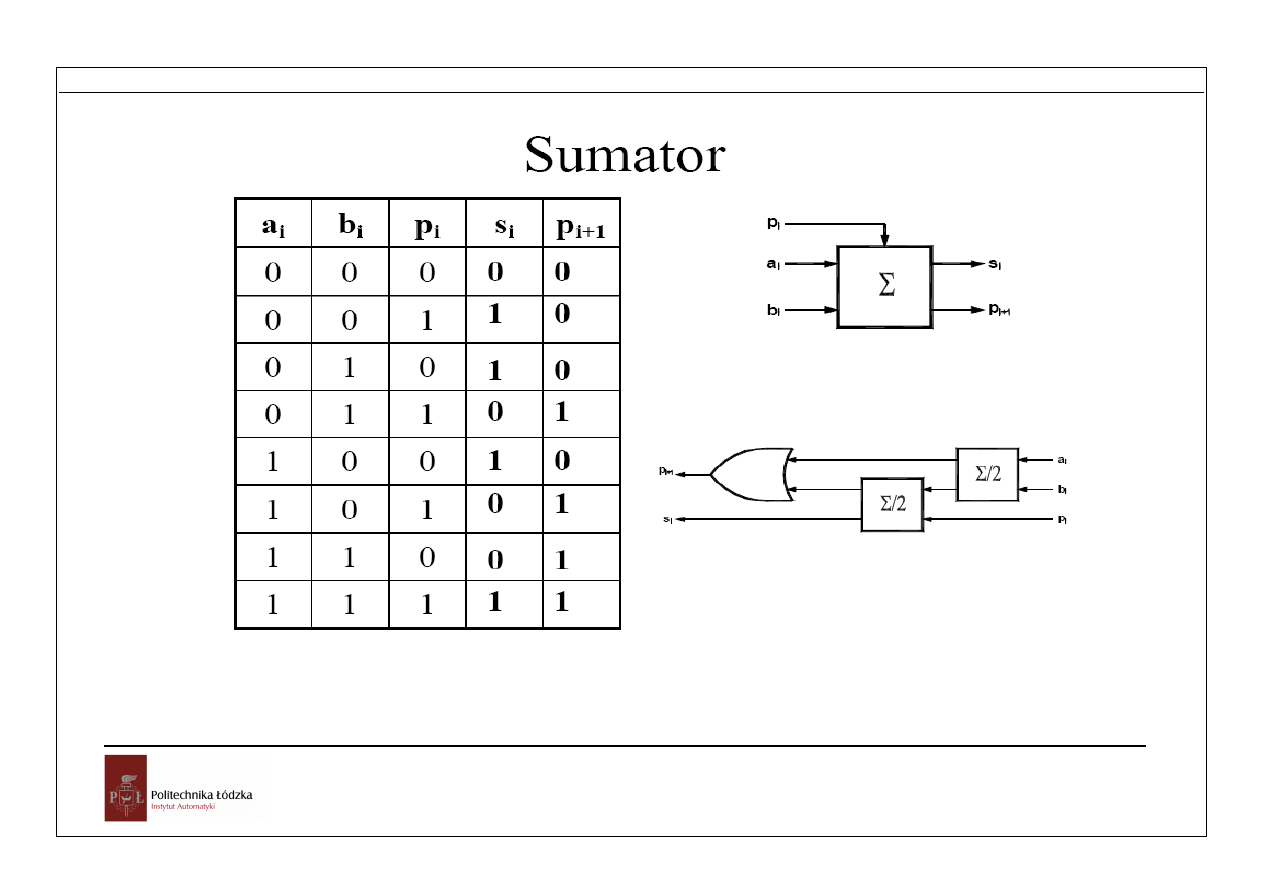
Sumowanie odbywa się w układach kombinacyjnych wyznaczających kolejno dla par
bitów dodawanych liczb ich sumę modulo 2 s
i
oraz przeniesienie p
i
. Półsumator
wyznacza s
i
oraz przeniesienie p
i
dla dwóch bitów a
i
oraz b
i
, natomiast sumator
uwzględnia również przeniesienie z poprzedniej operacji.
30
Podstawy Informatyki
Przetwarzanie informacji
Rys. Półsumator
31
Podstawy Informatyki
Przetwarzanie informacji
Rys. Budowa sumatora
32
Podstawy Informatyki

Przetwarzanie informacji
1.6 Kodery, dekodery i konwertery
W przesyłaniu sygnałów cyfrowych istnieje zwykle potrzeba przetwarzania informacji
z jednej zakodowanej postaci w drugą. Do tego celu służą specjalne układy cyfrowe
zwane konwerterami kodów lub translatorami, czy też przetwornikami kodów. W
szczególności układy służące do przetwarzania kodu "1 z n" na dowolny inny kod
dwójkowy przyjęto nazywać koderami, natomiast układy wykonujące operację odwrotną
- dekoderami. W związku z tym pozostałe układy, tj. układy przetwarzające dowolny kod
dwójkowy na inny, lecz nie "1 z n" nazywa się ogólnie konwerterami. Układy logiczne
koderów, dekoderów i konwerterów są układami kombinacyjnymi.
Kodowaniem nazywa się sposób odwzorowania informacji w zbiór słów, to jest
ciągów określonych symboli. W urządzeniach cyfrowych zawsze stosuje się kodowanie
binarne, tj. przetwarzanie informacji na ciąg 0 i 1. Jeśli zmienna X reprezentuje
33
Podstawy Informatyki

Przetwarzanie informacji
informację nieliczbową, to jedynym sposobem określenia kodu jest podanie w tabeli
wszystkich słów kodowych, jakie może przyjmować zmienna.
Kod nazywa się zupełnym, jeżeli zbiór słów kodowych jest zbiorem wszystkich słów
o podanej długości. Jeśli na przykład X może przyjmować n różnych wartości i jest
kodowana słowami binarnymi o długości m, to dla
n = 2
m
jest kod zupełny,
n
<
2
m
jest kod niezupełny.
Tabela barw sygnalizatora (n=3, m=2)
X
0
X
1
X
0
0
0
1
Czerwona
1
0
Żółta
34
Podstawy Informatyki
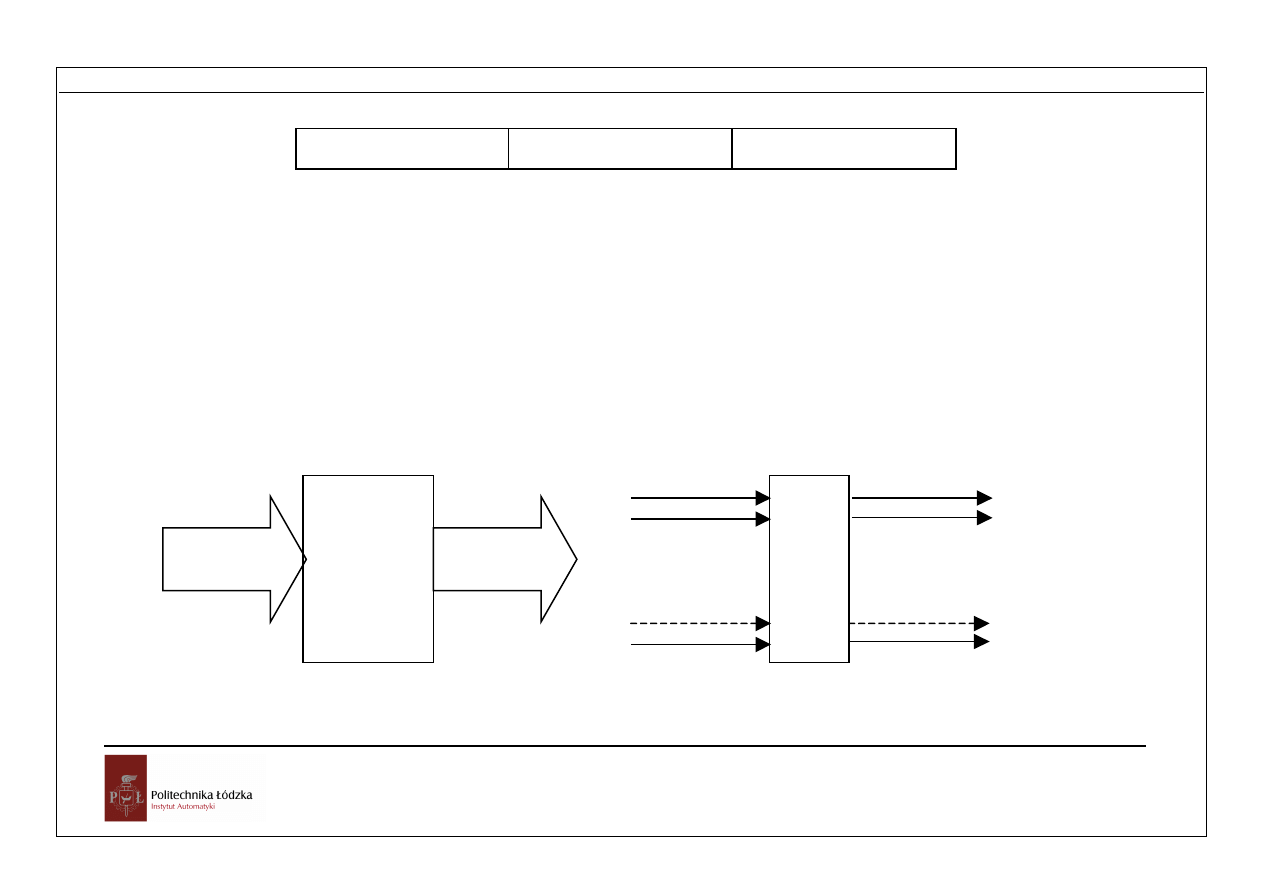
Przetwarzanie informacji
1
1
Zielona
Kody niezupełne mogą służyć do wykrywania błędów. Kody mogą być tak
zbudowane, aby zawsze słowo kodowe zawierało parzysta liczbę jedynek, co umożliwia
wykrycie przekłamania pojedynczego bitu
Koderami są nazywane układy służące do przetworzenia kodu "1 z n" podanego na
wejście układu w określony dwójkowy kod wyjściowy:
Koder
Kod 1 z n
Kod n z m
Koder
1
2
1
Kod 1 z n
2
n
2
0
2
m-1
Kod n z m
Rys. Symbol kodera 1 z n
35
Podstawy Informatyki

Przetwarzanie informacji
Kodery są stosowane głównie do wprowadzania informacji w postaci liczb
dziesiętnych (np. z przełączników 10-pozycyjnych) do systemów cyfrowych. Na wyjściu
kodera pojawia się stan odpowiadający "numerowi" wyróżnionego wejścia,
przedstawiony w żądanym kodzie dwójkowym. Przykładem scalonego układu kodera
może być układ UCY74147 o schemacie logicznym przedstawionym na rysunku
poniżej. Służy on do zamiany kodu "1 z 10" (z negacją) na kod BCD 8421. Kody BCD,
to zapis dwójkowy liczb dziesiętnych (binary coded decimal).
Kod 8421 nosi nazwę z tego powodu, że wagi kolejnych bitów X
3
, X
2
, X
1
, X
0
wynoszą
odpowiednio 8 4 2 i 1. Postać liczby jest
X=8 X
3
+ 4X
2
+ 2X
1
+ X
0
Wejścia
Wyjścia
Kod 1 z 10
36
Podstawy Informatyki

Przetwarzanie informacji
0
1
2
3
4
5
6
7
8
9
D C B A
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
9
8
7
6
5
4
3
2
1
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
0
0
0
1
0
1
1
0
0
0
1
0
0
1
0
0
0
0
0
0
0
Tabela kodów enkodera zwykłego
37
Podstawy Informatyki
Przetwarzanie informacji
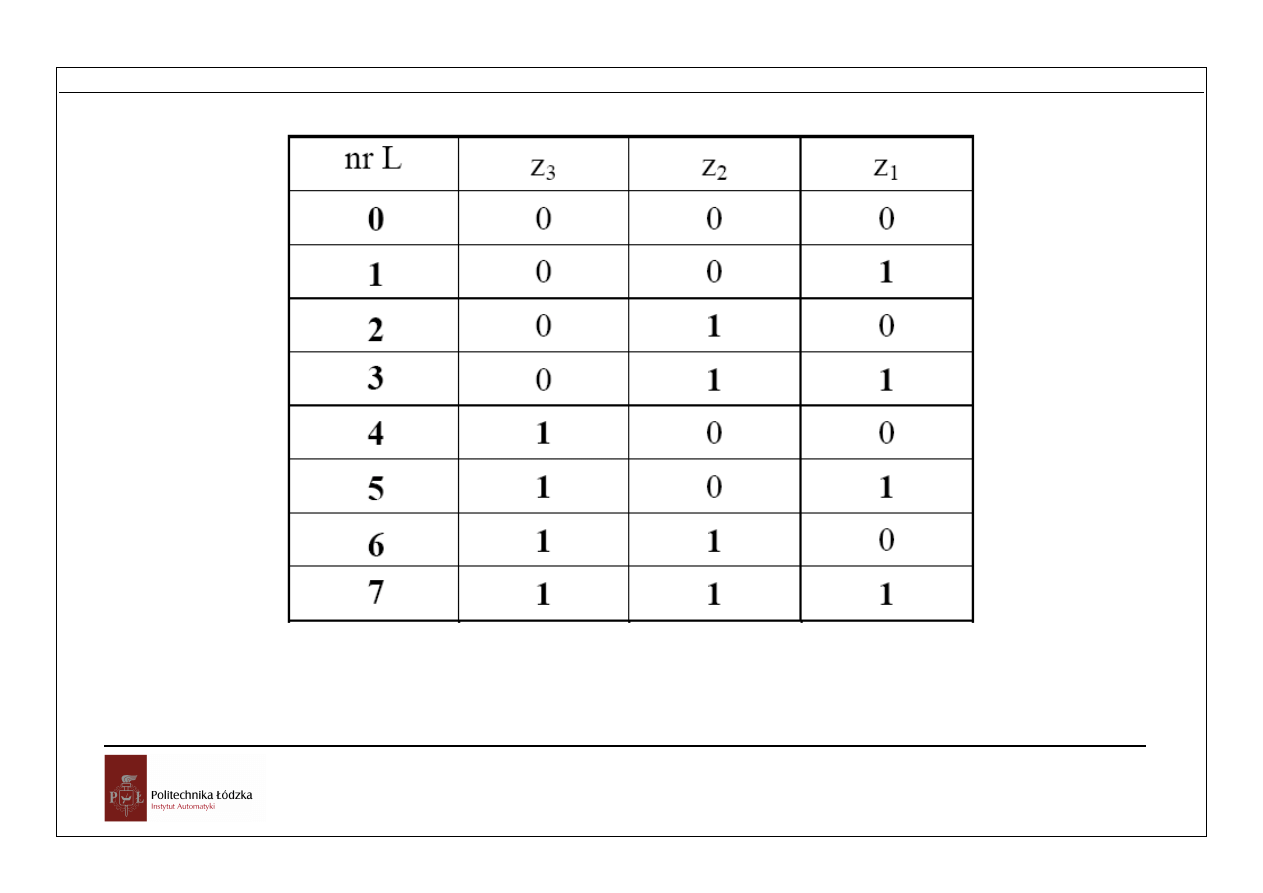
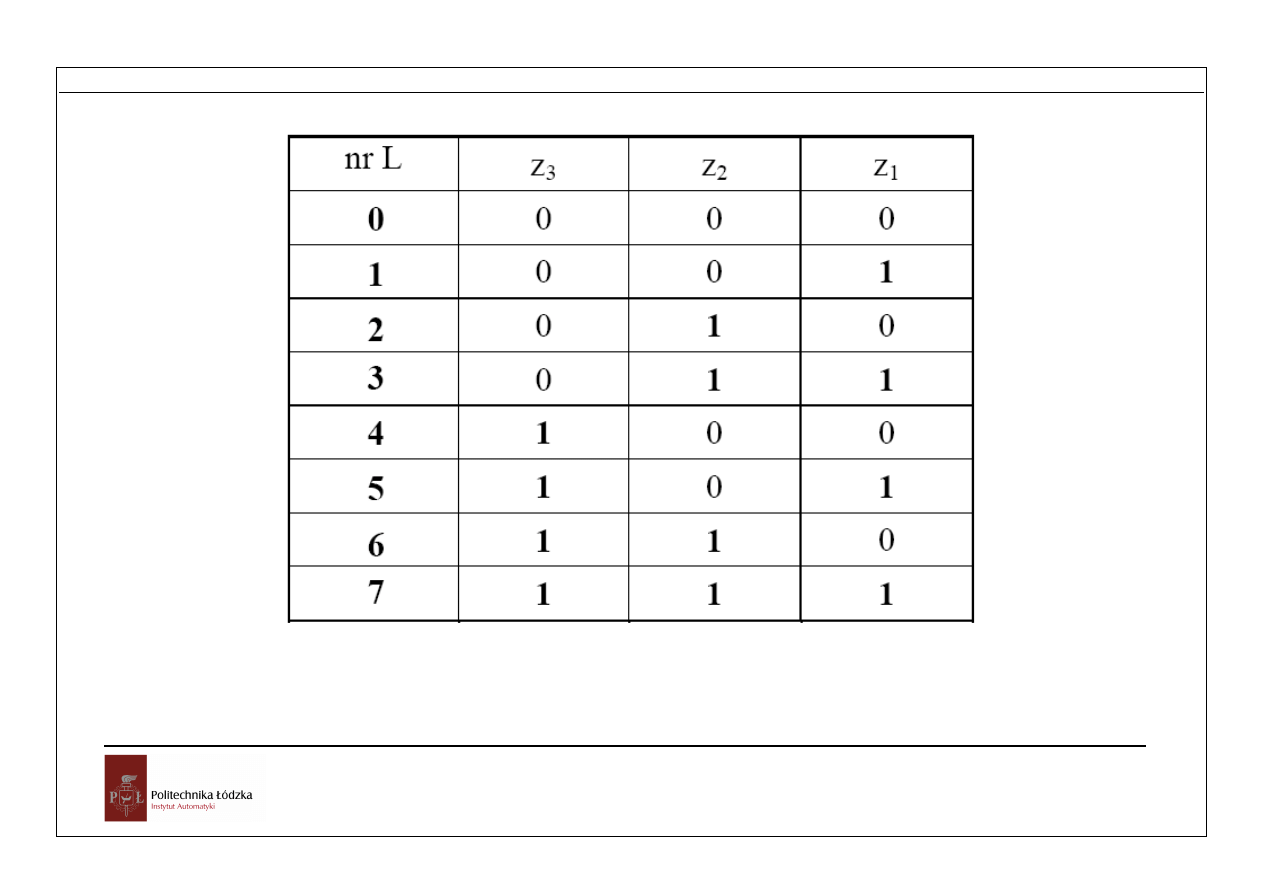
Rys. Tablica kodowa kodera 1 z 8. Wyjścia z
1
,z
2
,z
3
38
Podstawy Informatyki
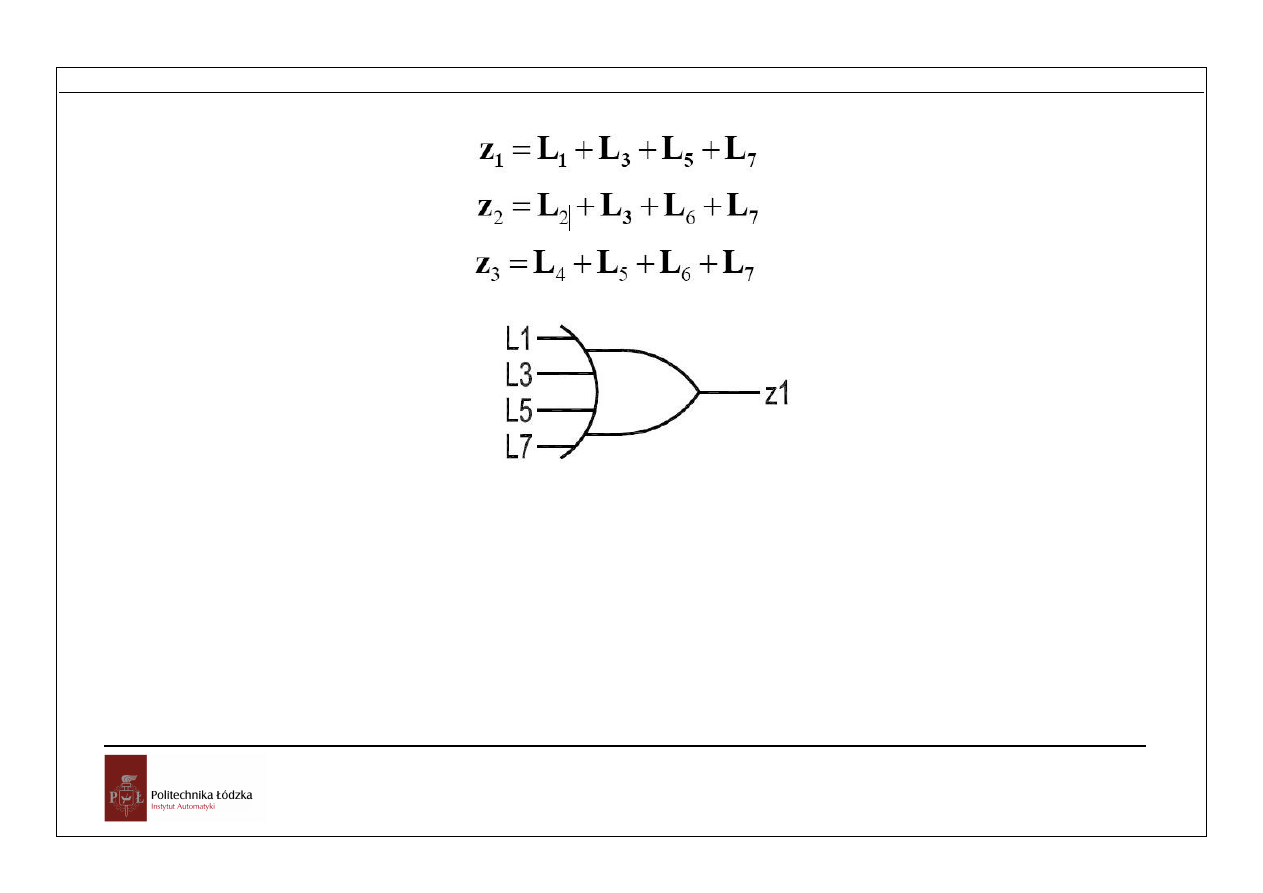
Przetwarzanie informacji
Rys. Kodowanie pozycji z1
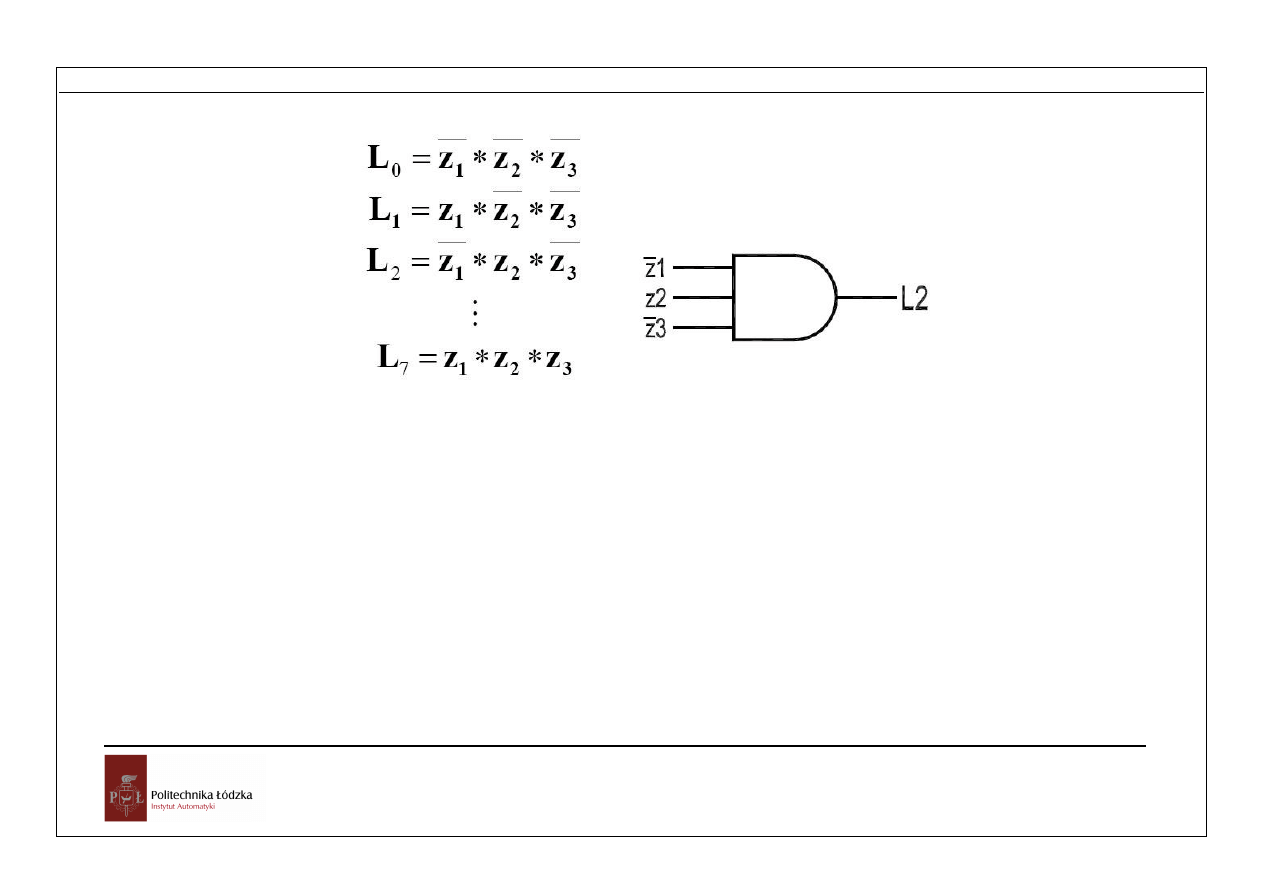
Dekoderem jest nazywany układ realizujący zamianę dowolnego kodu dwójkowego
na kod "1 z n”., zatem zadanie dekodera jest odwrotne niż kodera. Ważne znaczenie
mają dekodery dwójkowo-dziesiętne, służące do konwersji 4-bitowego kodu BCD na
39
Podstawy Informatyki
Przetwarzanie informacji
kod "1 z 10" oraz dekodery służące do konwersji naturalnego kodu dwójkowego o
określonej długości N słowa kodowego na kod "1 z n", przy czym n=2
N
.
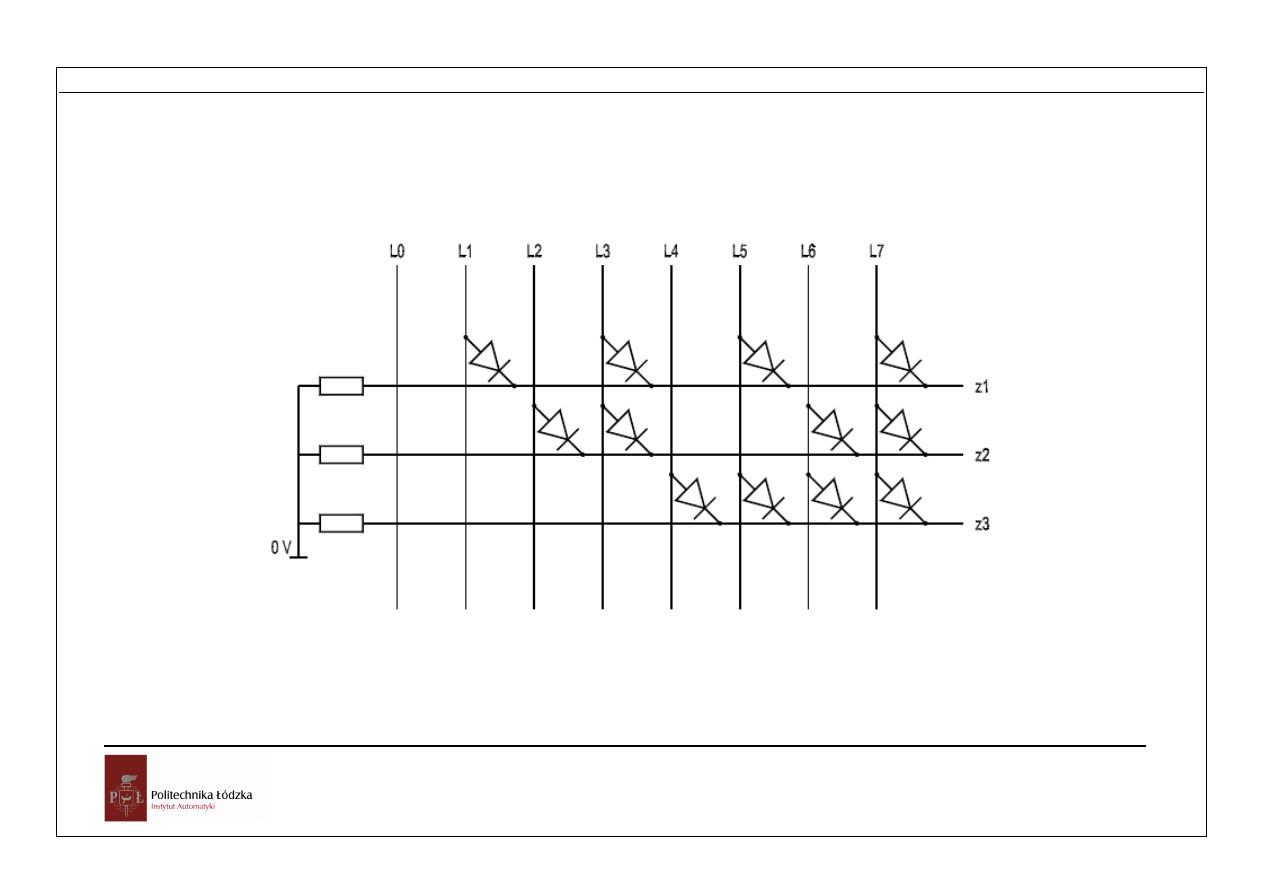
Matryca diodowa kodera dla kodu 1 z 8
Dekoder może mieć ogólnie m wejść i n wyjść, przy czym n<=2
m
. Dla każdej
40
Podstawy Informatyki

Przetwarzanie informacji
kombinacji wejściowej zer i jedynek istnieje jedno i tylko jedno wyjście wyróżnione, tzn.
przyjmujące wartość 1. Niekiedy w celu dogodniejszego sterowania działaniem układu
dekodera jest w nim wyprowadzone wejście uaktywniające. Gdy na tym wejściu jest
stan 0, wówczas na wszystkich wyjściach jest również 0. Jeśli na wejściu
uaktywniającym jest stan logiczny 1, to układ działa jak konwencjonalny dekoder.
41
Podstawy Informatyki
Przetwarzanie informacji
Rys. Tablica kodowa (powtórzenie dla dekodera)
42
Podstawy Informatyki
Przetwarzanie informacji
Rys. Dekodowanie liczby L2
43
Podstawy Informatyki
Przetwarzanie informacji
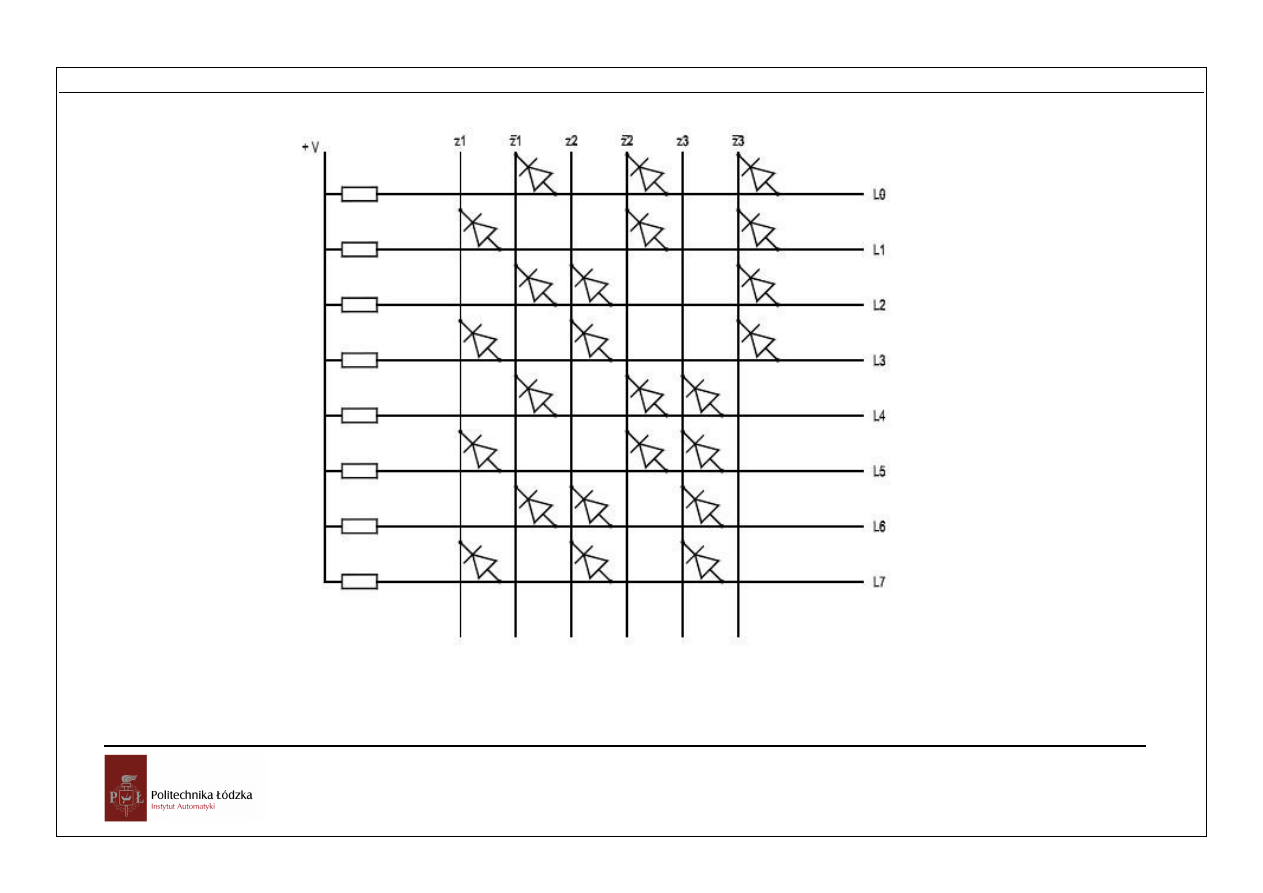
Rys. Matryca diodowa dekodera
44
Podstawy Informatyki

Przetwarzanie informacji
Transkoder przetwarza jeden określony kod dwójkowy na inny kod dwójkowy, ale nie
"1 z n". Transkodery mogą być budowane przez połączenie wyjść odpowiedniego
dekodera z wejściami kodera:
Kod Gray’a
Zasada konwersji kodu naturalnego w kod Gray’a
G
n
=B
n
; G
n-1
=B
n
⊕
B
n-1
; G
n-2
=B
n-1
⊕
B
n-2
; G
n-3
=B
n-2
⊕
B
n-3
;
Przykład X
10
= 11; X
B
= B
3
B
2
B
1
B
0
= 1 0 1 1; X
G
= G
3
G
2
G
1
G
0
= 1 1 1 0,
G
3
=B
3
= 1; G
2
=B
3
⊕
B
2
=1
⊕
0=1; G
1
=B
2
⊕
B
1
=1; G
0
=B
1
⊕
B
0
=1
⊕
1=0;
45
Podstawy Informatyki

Przetwarzanie informacji
Liczba dziesiętna
Kod naturalny
Kod Gray’a
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
1
1
1
0
1
1
1
1
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
0
0
0
1
0
1
1
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
1
1
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
0
0
1
0
0
1
1
0
0
1
0
0
0
0
0
0
0
46
Podstawy Informatyki

Przetwarzanie informacji
1.7 Rejestry
Rejestry służą do przechowywania informacji, na przykład słów maszynowych i
stanowią zespół przerzutników..
Rejestry mogą być:
- równoległe,
- szeregowe.
Zasadniczą mikrooperacją wykonywaną w rejestrze jest operacja wpisywania do
rejestru R := X,
gdzie R – stan rejestru,
X zapisywane słowo.
47
Podstawy Informatyki
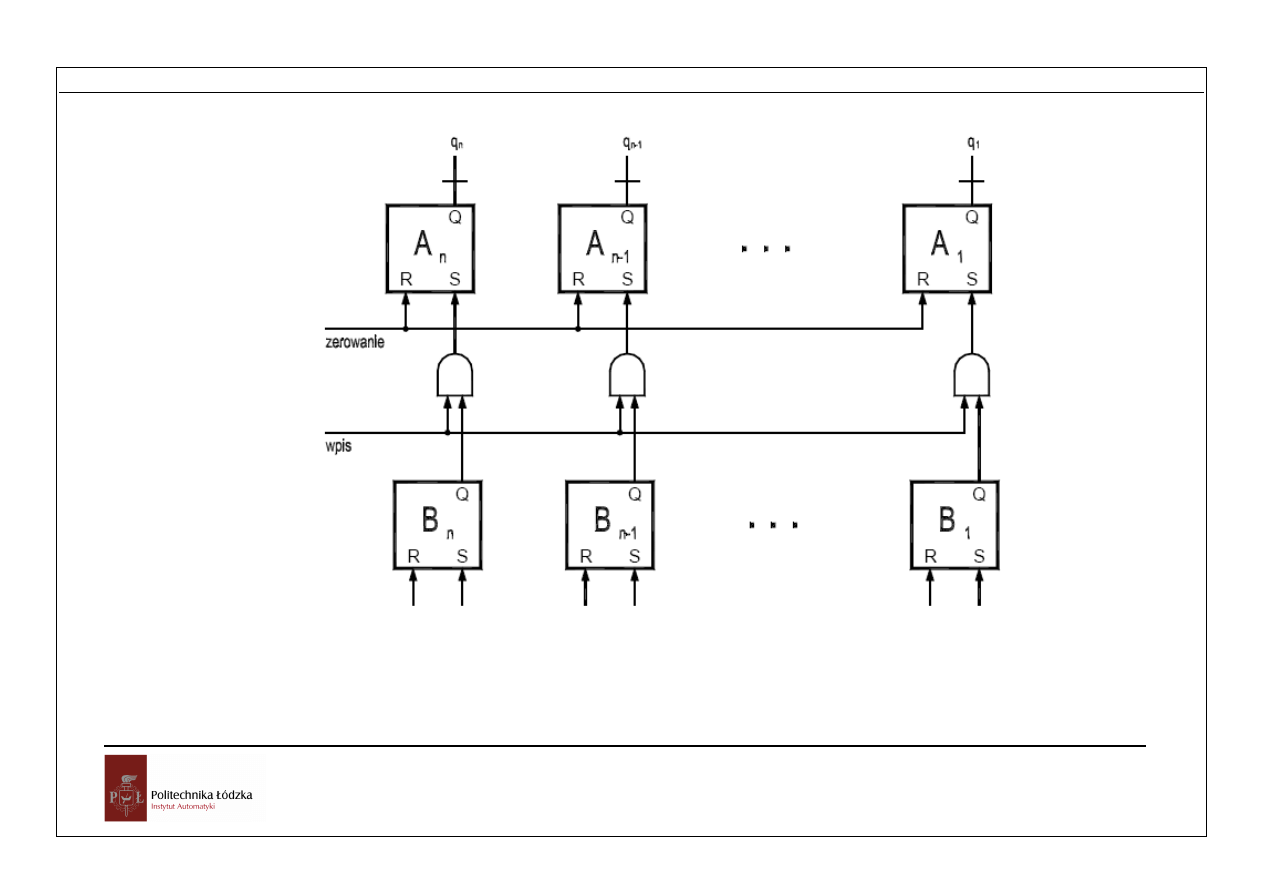
Przetwarzanie informacji
Rys. Rejestr równoległy z zerowaniem
48
Podstawy Informatyki
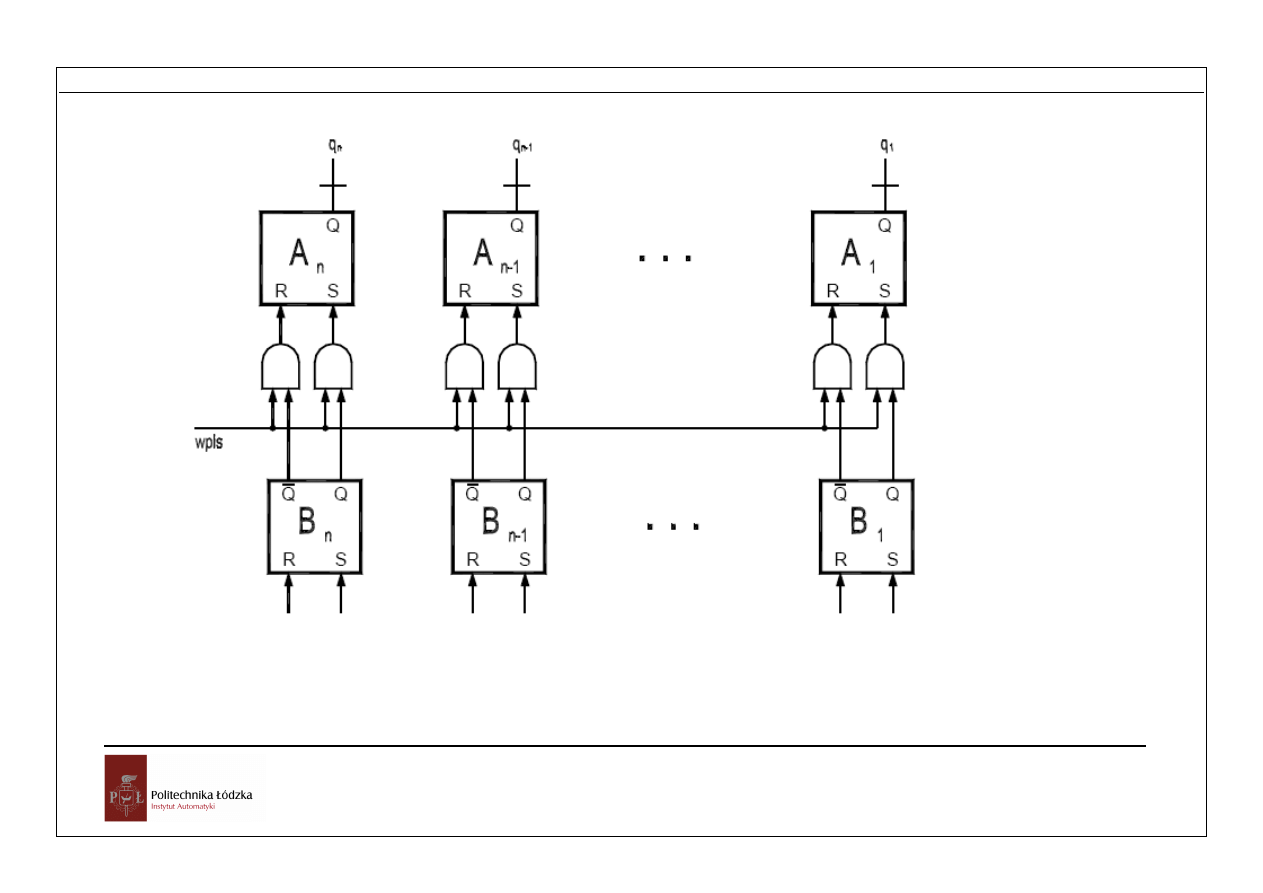
Przetwarzanie informacji
Rys. Rejestr równoległy z forsowaniem
49
Podstawy Informatyki

Przetwarzanie informacji
Rejestry szeregowe (przesuwające) [4] mogą realizować kilka funkcji:
- w przypadku informacji liczbowej mnożenie lub dzielenie liczby zapisanej w
rejestrze przez 2
- zmiana postaci informacji szeregowej na równoległą,
- wybieranie kolejnych bitów słowa zapisanego w rejestrze.
50
Podstawy Informatyki
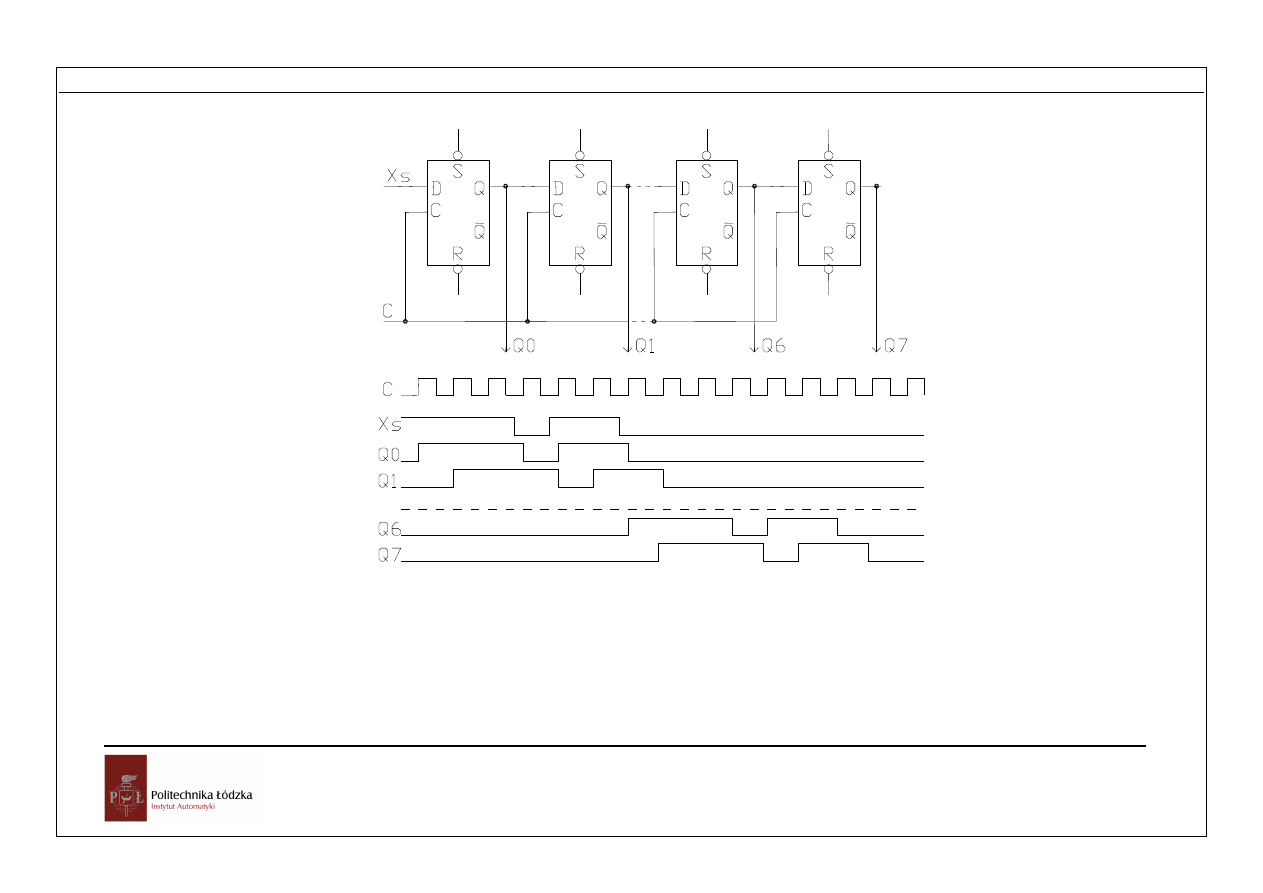
Przetwarzanie informacji
Rys. Rejestr przesuwający (szeregowy)
51
Podstawy Informatyki

Przetwarzanie informacji
1.8 Pamięć operacyjna
Pamięć operacyjna jest urządzeniem technicznym, które pozwala zapisać i
przechowywać dane a następnie wprowadzać je do systemu.
Na pamięć operacyjną składają się punkty pamięci, przechowujące informacje
jednobitowe.
Uporządkowany zbiór punktów nazywa się komórką pamięci zawierający słowo
maszynowe.
52
Podstawy Informatyki
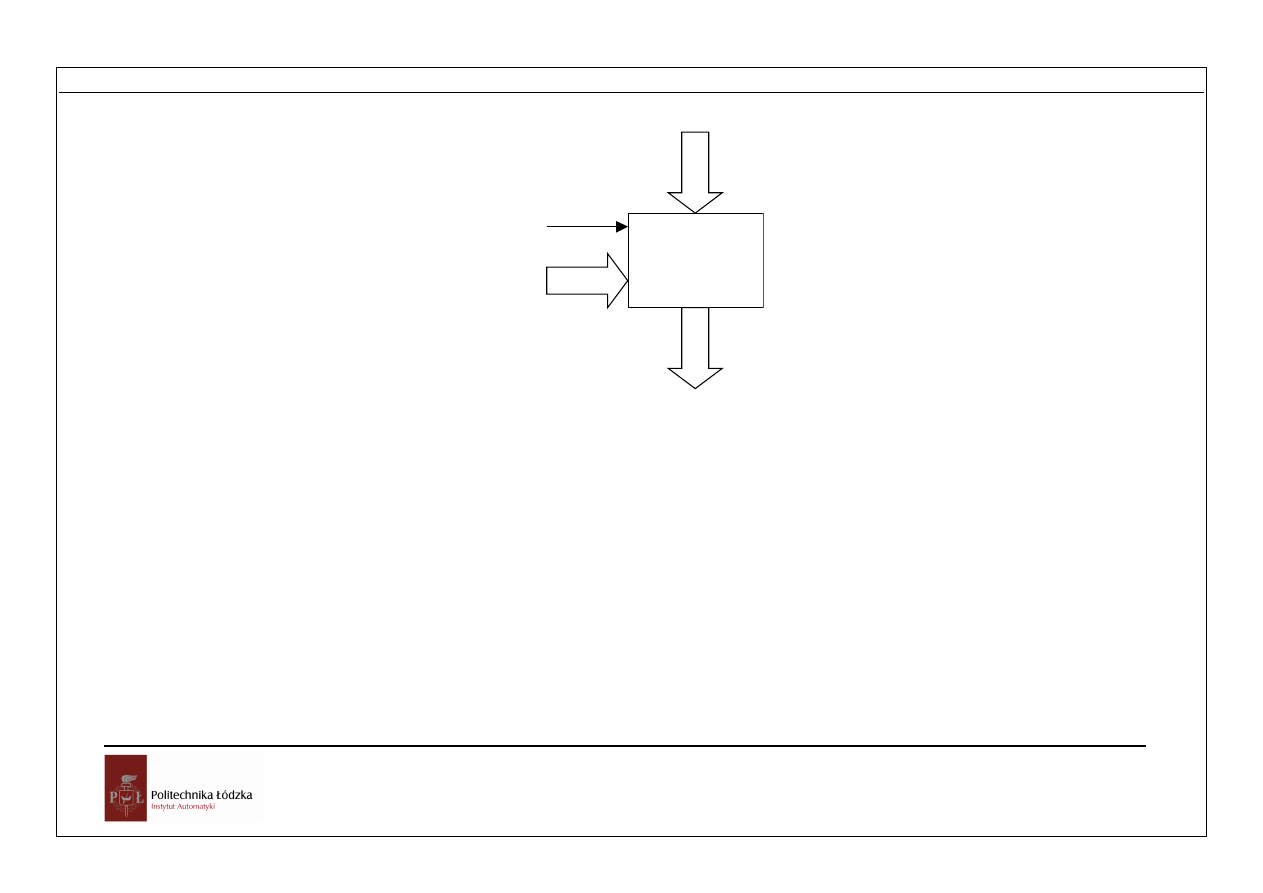
Przetwarzanie informacji
X
A
W
Y
RAM
Rys. Symbol pamięci zapisywalnej
Oznaczenia:
X – wejście informacyjne,
Y – wyjście informacyjne,
53
Podstawy Informatyki

Przetwarzanie informacji
A – wejście adresowe,
W – sterowanie zapisem.
54
Podstawy Informatyki
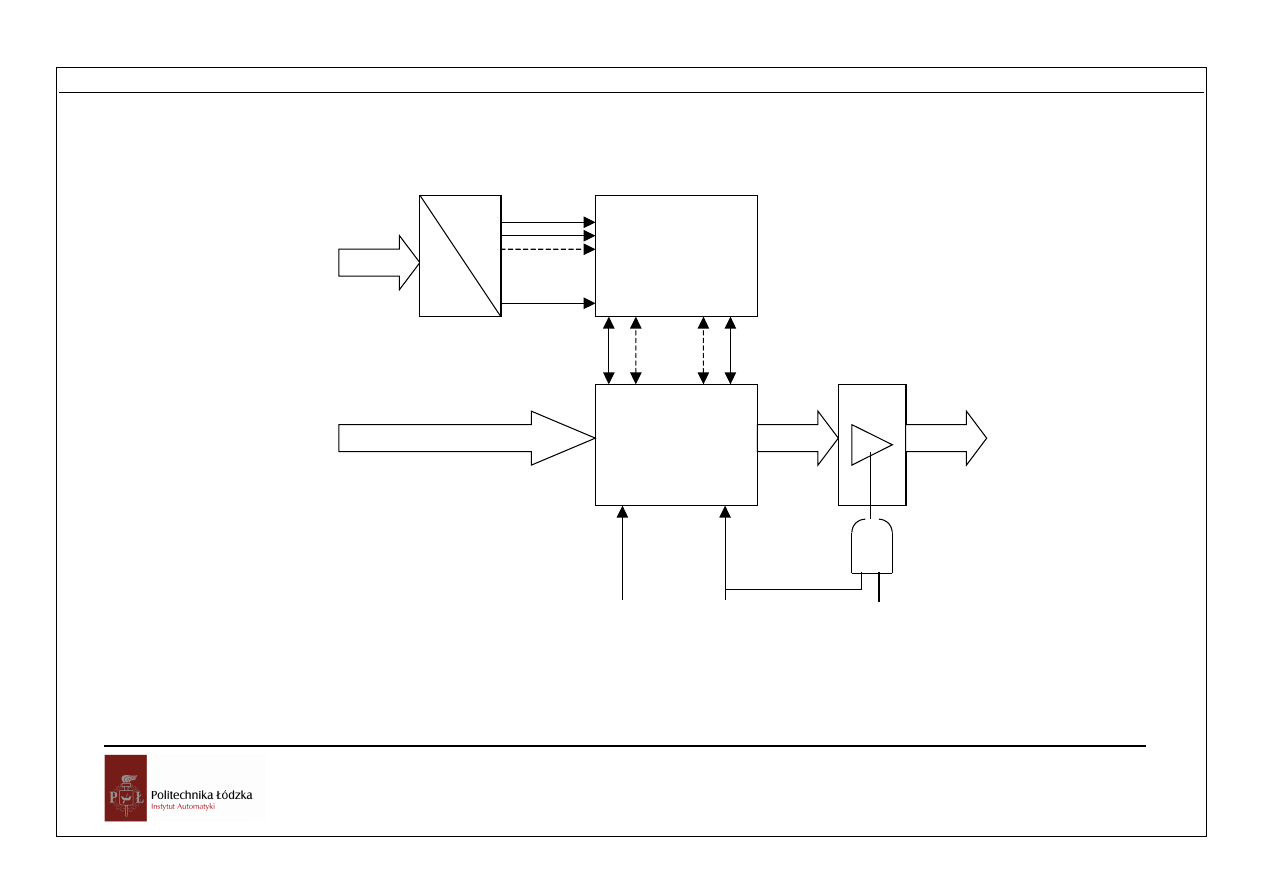
Przetwarzanie informacji
A
W
Dekoder
adresu
Matryca
pamięciowa
X
Układ zapisu/
odczytu
S
R
Y
Rys. Schemat funkcjonalny pamięci RAM
55
Podstawy Informatyki

Przetwarzanie informacji
S – sygnał wybierania pamięci,
R – sygnał odczytu.
Bramka trójstanowa umożliwia dołączenie do magistrali. R = 1 spowoduje przesłanie
zaadresowanej komórki do wyjścia Y. Przy S= 1 (pamięć wybrana) podanie sygnału
zapisu W =1 powoduje wpisanie słowa wejściowego X do zaadresowanej komórki. S =
0 wyjście pamięci jest w stanie zwiększonej impedancji a zapis zablokowany.
56
Podstawy Informatyki

Przetwarzanie informacji
57
Podstawy Informatyki

Literatura
Literatura
Małecki R., Arendt D., Bryszewski A., Krasiukianis R.: Wstęp do Informatyki. Skrypt P.Ł. Łódź, 1997
Kisielewicz A.: Wprowadzenie do informatyki. Helion, Gliwice 2002
Biernat J.: Architektura komputerów. Politechnika Wrocławska, Wrocław 2002
Misiurewicz P.: Układy automatyki cyfrowej. WSiP, Warszawa 1978
Document Outline
Wyszukiwarka
Podobne podstrony:
Pod Inf Pamięc Student, Podstawy Informatyki
Podstawy informatyki, Podstawy Informatyki, Przetwarzanie informacji
Zagadnienia egzamin Podstawy Inf egzamin, PŁ, Podstawy Informatyki
podst inf v101 166, Studia, Informatyka, Podstawy Informatyki
Sem II Transport, Podstawy Informatyki Wykład XXI Object Pascal Komponenty
Podstawy Informatyki Wykład XIX Bazy danych
Podstawy Informatyki Wykład V Struktury systemów komputerowych
1 Epidemiologia i podstawowe informacje o NSid 8500 ppt
Dydaktyka jako nauka podstawowe informacje
Podstawowe informacje o planowa Nieznany (4)
Podstawowe informacje na temat zasad przylaczenia farm wiatrowych
praca dyplomowa 1 strona wzor, Szkoła, prywatne, Podstawy informatyki
Podstawowe informacje
Witaminy - zestawienie podstawowych informacji, administracja, Reszta, Promocja zdrowia
podstawowe informacje o ochronie prawnej wzorów przemysłowych, Studia - Politechnika Śląska, Zarządz
wstęp i podstawowe informacje, Automatyka i Robotyka, Semestr II, Ekologia i zarządzanie środowiskie
Podstawowe informacje o rynkach nieruchomości w UE, Nieruchomości, Nieruchomości - pośrednik
więcej podobnych podstron