1

IV.2. BADANIE I WZORCOWANIE CZUJNIKÓW PRZEPŁYWU

GAZU.

2.1. WPROWADZENIE.

Pomiar przepływu gazu polega na wyznaczeniu ilości gazu przemieszczającego się

w określonej przestrzeni w określonym czasie np. w czasie 1s; 1min; 1h; 1doby itd. Ilość
przepływającego gazu zwykle określa się w jednostkach objętości np. w molach, litrach,
metrach sześciennych albo w jednostkach masy np. w kilogramach. Ilość przepływającego
gazu przypadająca na jednostkę czasu nazywa się natężeniem przepływu albo wprost
przepływem. Wartości przepływu mogą być wyrażane w różnych jednostkach np. w [l/s]; [m

3

/h]; [kg/min], [mol/s] itp. Istotnym parametrem przepływu jest jego prędkość. W przypadku
przepływu gazu w otwartej przestrzeni (np. wiatr) trudno określić objętość albomasę
poruszającego się (przepływającego) gazu, można natomiast określić prękość jego przepływu.

Znając prędkość przepływu gazu w rurociągu, kształt i wymiary geometryczne przekroju

rurociągu oraz parametry fizykochemiczne gazu można wyznaczyć jego przepływ
objętościowy lub masowy. W przypadku rurociągu o przekroju okrągłym można napisać dla
przeływu:



4

2

D

t

V

Q

V







- przepływ objętościowy (2.1);





4

2

D

t

m

Q

m







- przepływ masowy (2.2)

gdzie: D – średnica wewnętrzna rurociągu,
 – gęstość właściwa gazu (płynu)
 – prędkość średnia gazu (płyny) w kierunku przepływu.

Należy zauważyć że, prawe strony zależności (2.1) i (2.2) nie określają ilości substancji

przepływającego gazu. Zwykle w praktyce dokonuje się pomiaru przepływu gazu w celu
wyznaczenia ilości substancji gazowej.

1mol gazu doskonałego, którego zachowanie się opisuje równanie Clapeyrona:

T

R

pV

mol



(2.3)

gdzie R

mol

- uniwersalna stała gazowa

















K

mol

J

8,313

mol

R

w warunkach normalnych (p = p

0

1013,3hPa; T = T

0

= 273,15K) zajmuje objętość

V = V

0

 22,4dm

3

(22,4 l) i zawiera N

A

 6,022 10

23

cząstek.

Biorąc pod uwagę zależności (2.1), (2.2) oraz (2.3) można stwierdzić że, przy tej samej

prędkości przepływu gazu  może być jego różna ilość. Istotny jest stan w jakim gaz się
znajduje (ciśnienie – p; objętość – V oraz jego temperatura bezwzględna – T).

Tylko niektóre gazy rzeczywiste (gazy jednoatomowe) spełniają w przybliżeniu równanie

(2.3) spełniane przez gaz doskonały.

W przypadku gazów rzeczywistych jest:





wew

cz

mol

E

m

T

p

f

R

T

pV

;

;

;

;





(2.4).

2

Zawsze jednak spełnione jest prawo Avogadra, w myśl którego 1mol gazu zawiera liczbę

cząstek lub atomów równą liczbie atomów w masie 12g izotopu węgla

12

C

t.j. N

A

 6,02210

23

.

W procesie pomiaru przepływu gazów rzeczywistych wykorzystuje się różne zjawiska

zachodzące w tych gazach. Zjawiska te powodują określone zmiany stanu fizycznego
czujnika pomiarowego (np. powstanie napięcia na czujniku, zmiana jego rezystancji, zmiana
stanu jego ruchu itp.). Znajomość składu chemicznego, budowy cząsteczkowej gazu
rzeczywistego oraz warunków fizycznych, w których się znajduje (p;V;T,

) oraz parametrów

drogi przepływu gazu (np.średnicy rurociągu, materiału z którego jest zbudowany itd.) jest
konieczna dla właściwego doboru rodzaju i parametrów czujnika do pomiaru przepływu.

W praktyce w procesie projektowania czujników i układów do pomiaru przepływu zwykle

wykorzystuje się empiryczne i przybliżone zależności opisujące zachowanie się badanego
płynu (gazu; cieczy względnie cieczy nieniutonowskiej). Różne rodzaje i konstrukcje
przepływomierzy (przyrządów do pomiaru przepływu zawierających określony rodzaj
czujnika oraz współpracujący z nim układ przetwarzania sygnału z czujnika pomiarowego)
mają różne zależności sygnału wyjściowego Y od mierzonego przepływu Q – np. Y(Q

V

),

Y(Q

m

), Y(

). W praktyce dokonuje się wzorcowania przepływomierzy, w wyniku tego

przypisuje się wzorcowanemu przepływomierzowi wartości na jego skali tak aby spełniał on
wymaganą dokładność (wzorcowanie powinno spełniać odpowiednie normy metrologiczne).

W ćwiczeniu laboratoryjnym bada się czujniki przepływu powietrza w rurociągu na

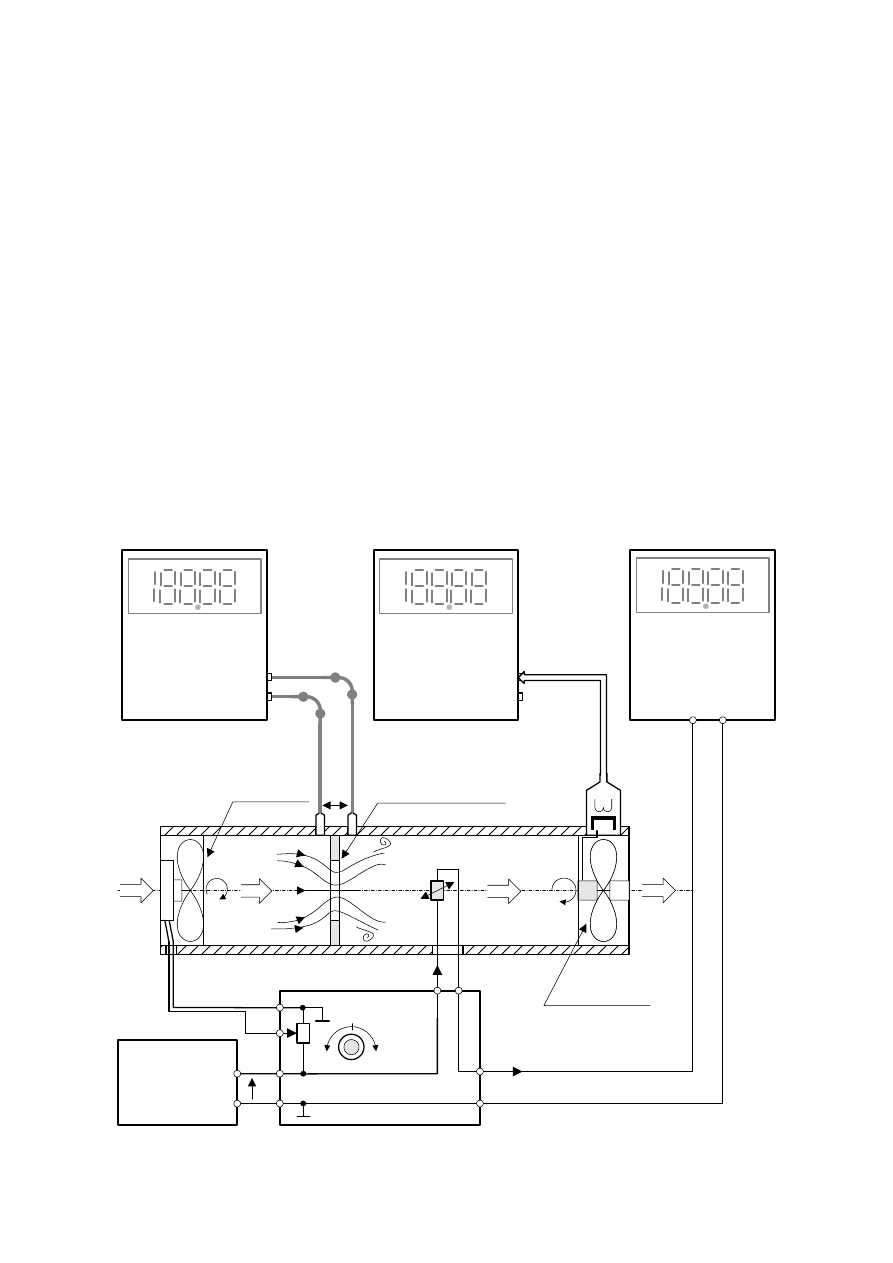
stanowisku laboratoryjnym pokazanym na rys.2.1.

Mikromanometr

Cyfrowy

Anemometr

Cyfrowy

Multimetr

Cyfrowy

p

I

T

R

T

Turbinka

pomiarowa

Kryza pomiarowa

n

Wentylator



p

1

p

2



G



T

[mA]

[m/s]

[kPa]

Zasilacz

stabilizowany

U

z

I

T

Regulator przepływu



r

Rys.2.1. Schemat funkcjonalny stanowiska do badania czujnikow przepływu gazu.

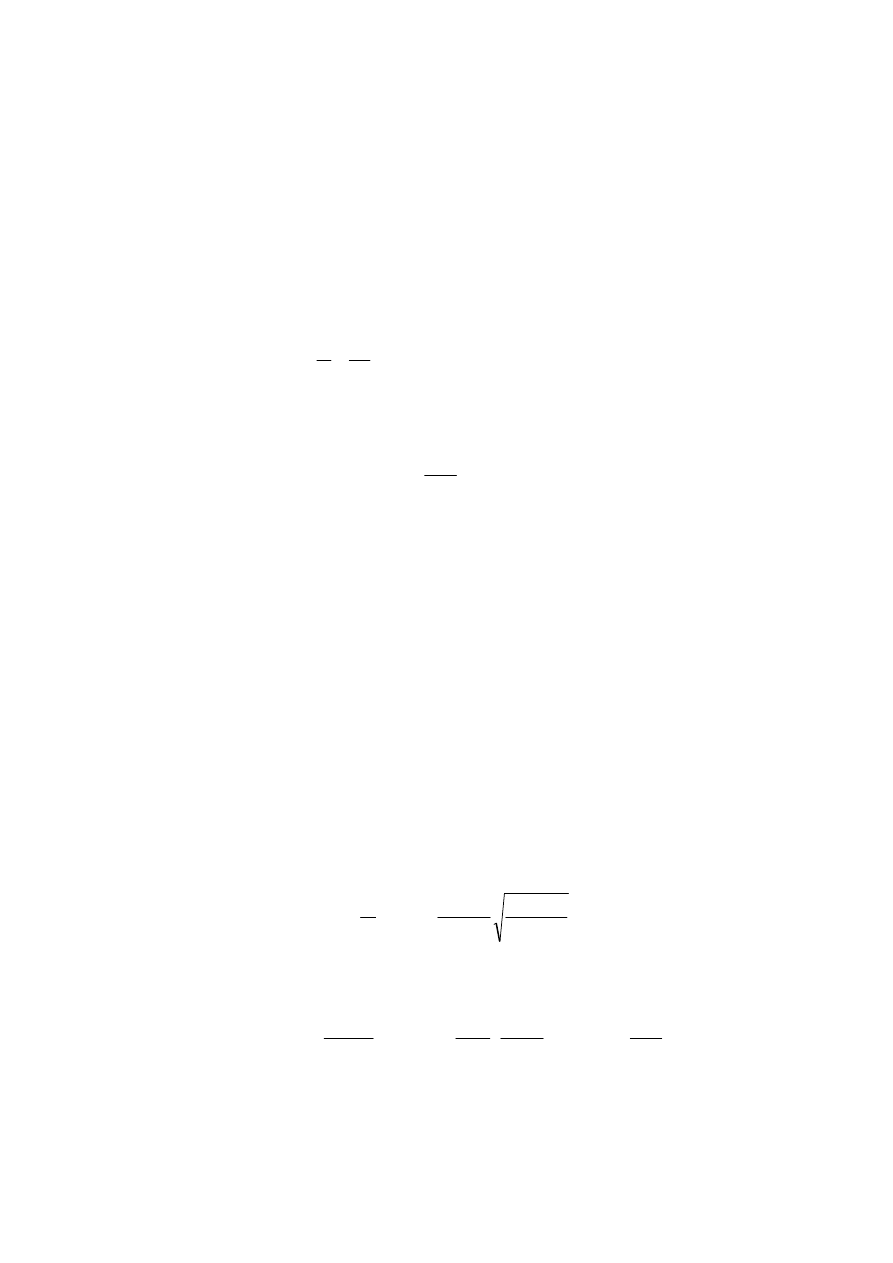
3

Na stanowisku laboratoryjnym pokazanym na rys.2.1 znajduje się kryza pomiarowa

współpracująca z mikromanometrem cyfrowym, termoanemometr, którego grzejnikiem a
zarazem czujnikiem temperatury jest półprzewodnikowy termorezystor typu KTY84-130
zasilany stabilizowanym napięciem U

Z

. Prąd przepływający przez termorezystor mierzony

jest za pomocą miliamperomierza (multimetr cyfrowy) oraz anemometr z czujnikiem
turbinkowym, który w ćwiczeniu jest przyrządem wzorcowym.

2.2. KRYZA POMIAROWA

Na podstawie prawa przepływu Bernouliego:

const

C

p







2

2





(2.5)

dla kryzy pomiarowej umieszczonej w rurociągu (rys.2.1) można napisać:

C

p

p

p

2

2

2

1













(2.6).

Na stanowisku laboratoryjnym mierzy się bezpośrednio charakterystykę

 







f

p

za

pomocą kryzy pomiarowej - różnicę ciśnień p

1

i p

2

jako funkcja średniej prędkości przepływu

gazu przez rurociąg

. Jeśli kryza pomiarowa będzie przy tej charakterystyce wywzorcowana

to będzie mogła służyć jako przepływomierz przy czym zwykle wystąpi konieczność
wyznaczenia jej charakterystyk pośrednich:





V

Q

f

p 



lub





m

Q

f

p 



.

Z zależności (2.6) wynika że, w wyniku przepływu płynu o gęstości właściwej  przez

przewężenie (kryza) powstaje różnica ciśnień p proporcjonalna do kwadratu prędkości
przepływu płynu. Jest to zależność dla idealnego przepływu. W rzeczywistości kryza
pomiarowa zmienia charakter przepływu (przed kryzą następuje spiętrzenie płynu i wzrost
ciśnienia (p

1

> p) a za kryzą spadek ciśnienia (p

2

< p). Ponadto za kryzą powstają zawirowania

przepływu. Przepływ za kryzą nie jest laminarny ale burzliwy (turbulentny). W przypadku
rzeczywistym wartość C = C

R

jak w zależności (2.6) nie jest stała. Zależy ona od prędkości

przepływu

, charakteru przepływu (liczby Reynoldsa Re – dla przepływu burzliwwego Re

>2000) współczynnika przewężenia kryzy  = d/D a także od stopnia rozprężenia płynu za
kryzą – liczba ekspansji .

Przepływ masowy Q

m

mierzony za pomocą kryzy w warunkach rzeczywistych opisuje

zależność:





2

2

2

1

2

4



















p

D

C

t

m

Q

R

m

(2.7)

przy czym:

 

4

0337

,

0

1

4

09

,

0

Re

58

,

431

2

3

4

4

2

75

,

0

5

,

2

d

D

f

C

R







































(2.8);

 

3

1

,

2

184

,

0

0312

,

0

5959

,

0













f

;

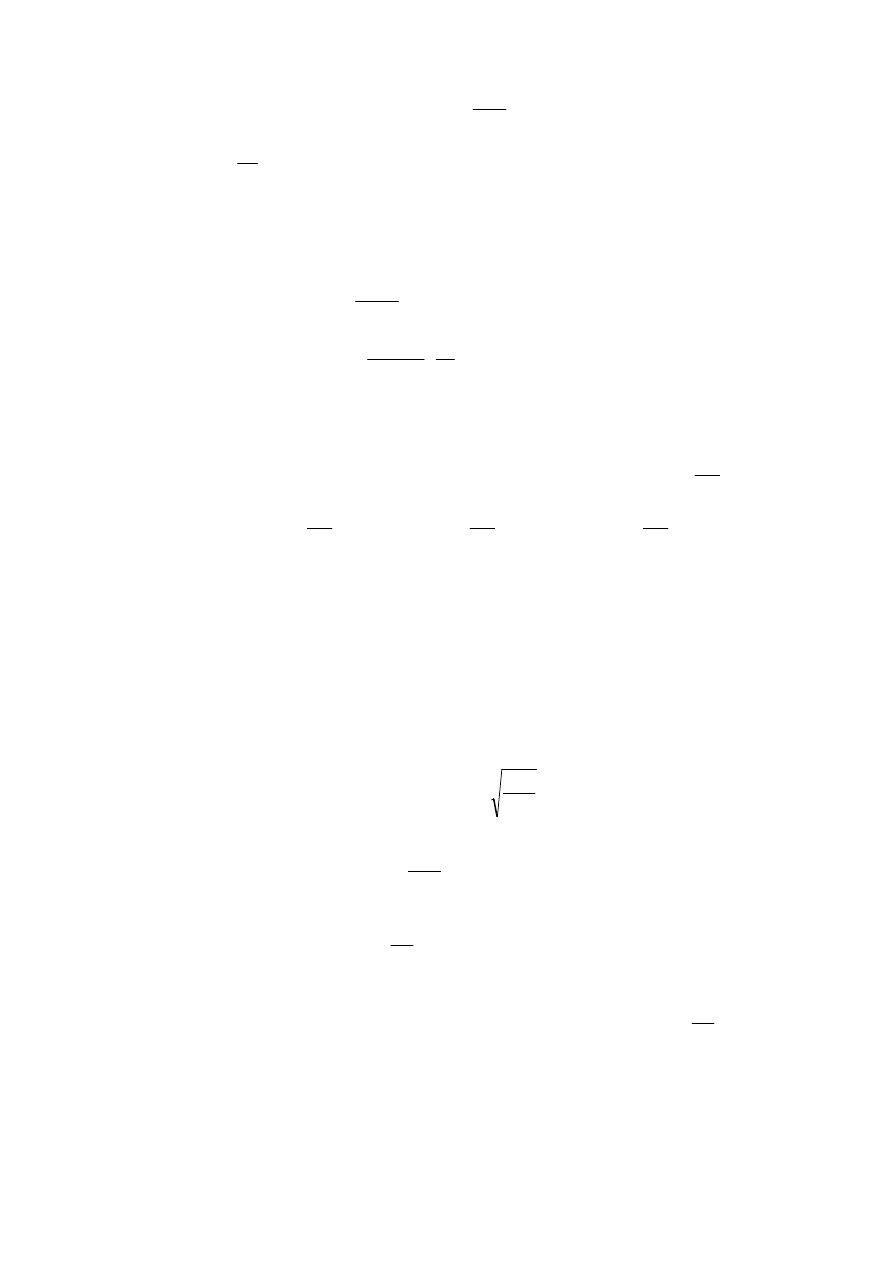
4





1

4

35

,

0

41

,

0

1

p

p















- liczba ekspansji (2.9);

V

p

c

c





- wykładnik adiabaty (dla powietrza  = 1,4)

-

 = f (; p/ p

1

) – wartość można odczytać z wykresu dla określonej

zwężki np. kryzy o danej wartości ;

N

q

- liczba przepływu;









D

Q

V

4

Re

- liczba Reynoldsa (2.10);

5

,

1

0

0

























T

T

C

T

C

T

S

S

n

- lepkość dynamiczna gazu (2.11).

w warunkach normalnych (p

0

=101,33kPa; T

0

=273,15K) dla powietrza można przyjąć:

 = 1,4; C

S

= 113K- stała Sutherlanda;



n

 17,0810

-6

[Pas];















3

m

kg

1,293

n



















3

m

kg

1,206

C

20



,

















3

m

kg

0,945

C

100



,





























3

m

kg

0,277

C

1000



.

Kryza pomiarowa wykorzystywana w ćwiczeniu laboratoryjnym (rys.2.1) ma parametry:

D = 78mm; d = 50mm    0,64, f()  0,56.

Dla stanowiska laboratoryjnego (rys.2.1) i warunków przyjętych w ćwiczeniu

laboratoryjnym (małe przepływy powietrza o temperaturze pokojowej w otwartym rurociągu
– kanale przelotowym) zależności (2.7)  (2.11) po uwzględnieniu parametrów stanowiska
przyjmują postaci szczegółowe:





kg/s





p

C

Q

R

m













2

10

547

,

2

3

(2.12);

75

,

0

Re

5

,

97

56

,

0

















R

C

(2.13);





















2

333

,

0

1

p

p

(2.14)

Uwaga! Zależność (2.14) wyprowadzona na podstawie wykresu

const

p

p

f























1

2

dla

kryzy o wartości  = 0,64 przy  = 1,4 – jest to przybliżona zależność słuszna tylko dla
konstrukcji stanowiska o podanych wyżej parametrach! W cwiczeniu laboratoryjnym można
orientacyjnie przyjąć do obliczeń wartość

85

,

0





;

5







V

Q

32

,

16

Re

(2.15)

albo















3

10

98

,

77

Re

(2.16);





Pa.s

113K









T

T

5

,

1

6

10

28

,

18



(2.17).

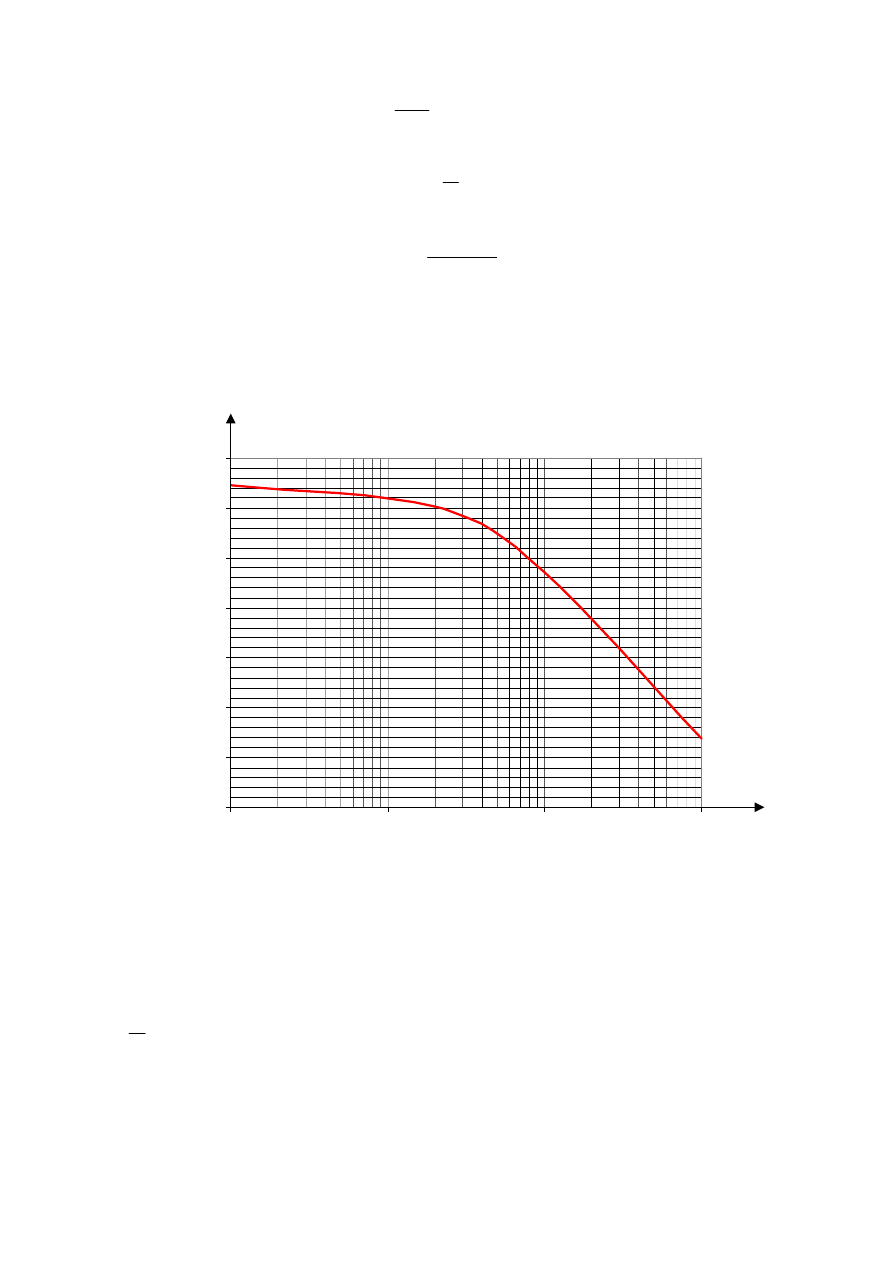
Zależności (2.12)  (2.16) odnoszą się do warunków opisanego wyżej stanowiska

laboratoryjnego. Mogą być wykorzystane w opracowaniu wyników pomiarów na tym
stanowisku. Na rys.2.2 przedstawiono wykres gęstości powietrza w funkcji temperatury

 







f

pod ciśnieniem normalnym (101,33kPa).

0,000

0,200

0,400

0,600

0,800

1,000

1,200

1,400

1

10

100

1000



f 

[

o

C]



[kg/m

3

]

Rys.2.2.

2.3. TERMOANEMOMETR.

Na stanowisku laboratoryjnym jak na rys.2.1 oprócz badanej kryzy pomiarowej znajduje

się przyrząd wzorcowy - anemometr turbinkowy mierzący średnią prędkość przepływu













s

m



oraz badany termoanemometr w postaci termorezystora półprzewodnikowego typu

KTY84-130. Termorezystor ten jest jednocześnie źródłem ciepła dostarczanego do
przepływającego gazu (powietrza) i czujnikiem temperatury. Jest on zasilany z zasilacza
stabilizowanego - źródła napięciowego o napięciu U

Z

= 25V. Prąd płynący przez

termorezystor jest mierzony za pomocą miliamperomierza cyfrowego. Prąd płynący przez
termorezystor jest równy:

6

T

A

T

Z

A

T

Z

T

R

R

R

U

R

R

U

I









;

(2.18).

Bezpośrednio mierzy się za pomocą termoanamometru na opisywanym stanowisku

laboratoryjnym charakterystykę

 



 f

I

T

. Podobnie jak w przypadku kryzy pomiarowej

można

przeprowadzić

wzorcowanie

termoanemometru,

także

można

wyznaczyć

charakterystyki pośrednie:





V

T

Q

f

I 

lub





m

T

Q

f

I 

.

W przypadku termorezystora wykorzystywanego na stanowisku laboratoryjnym jako

termoanemometru należy brać pod uwagą zależność jego rezystancji od temperatury

 



f

R

T

-

charakterystykę statyczną termorezystora oraz zmianę jego temperatury w wyniku przepływu
prądu I

T

(wydzielania się ciepła w wynika mocy traconej w termorezystorze) oraz

przejmowania od niego ciepła przez opływający go gaz poruszający się w rurociągu
z prędkością  .

W warunkach ustalonej wymiany ciepła pomiędzy ośrodkiem (powietrzem w rurociągu

o temperaturze 

G

) a termorezystorem ustala się temperatura termorezystora

G

T







.

W tych warunkach strumień wymienianego ciepła

0



TG

q

, rezystancja termorezystora

jest równa





G

T

f

R





zgodnie z jego charakterystyką statyczną

 



f

R

T

. Przepływ prądu

przez termorezystor powoduje wydzielanie się w nim ciepła Joule’a i jego przepływ do
otoczenia – gazu (jeśli

T

G







). Można dla tego stanu napisać dla strumienia wymienianego

ciepła:









G

T

q

G

T

T

q

T

dl

A

q























(2.19)

gdzie:

t

Q

q

T



- strumień cieplny [W];



q

– współczynnik wymiany ciepła













K

m

W

2

dl

A

T





- powierzchnia termorezystora wymieniająca ciepło [m

2

]

(d – średnica termorezystora [m], l – długość termorezystora [m]);
Przyjmując że, źródłem ciepła jest termorezystor, na kktórym wydziela się moc

elektryczna:

T

Z

T

T

T

I

U

R

I

P





2

(2.20),

można dla układu termoanemometru jak na rys.2.1 napisać:





G

T

q

T

Z

dl

I

U













(2.21).

Stąd otrzymuje się:





G

T

Z

q

T

U

dl

I













(2.22).

Zależność (2.22) opisuje charakterystykę cieplną termoanemometru. W rzeczywistości

prąd I

T

termoanemometru zależy od przepływu gazu. Zależność ta uwzględniona jest poprzez

współczynnik wymiany ciepła pomiędzy termorezystorem i przepływającym w rurociągu
gazem (powietrzem).

Zależność (2.22) można zapisać w postaci:

7







k

p

Z

T

c

U

l

I









Re

Pr

Nu

(2.23).

Stąd charakterystyka termoanemometru:

 

T

T

k

p

Z

I

f

I

c

l

U

















Nu

Re

Pr

(2.24)

gdzie: c

p

– ciepło właściwe gazu (powietrza) przy stałym ciśnieniu;



k

– lepkość kinetyczna gazu;

 – gęstość gazu;

Nu – liczba Nusselta;





d

q





Nu

;  - przewodność cieplna gazu;

Pr – liczba Prandtla;







p

c

Pr

; - lepkość dynamiczna gazu;

Re – liczba Reynoldsa;









Re

;  - prędkość średnia gazu.

Po uwzględnieniu w zależności (2.23) powierzchni przekroju rurociągu

4

2

1

D

A





oraz

gęstości gazu  uzyskuje się podobnie jak w przypadku kryzy pomiarowej charakterystyki
pośrednie:

 

T

V

T

k

p

Z

V

I

f

I

c

l

U

D

Q











Nu

4

Re

Pr

2

(2.25)

albo

 

T

m

T

k

p

Z

m

I

f

I

c

l

U

D

Q









Nu

4

Re

Pr

2

(2.26).

Analizując zależności (2.22)  (2.26) można zauważyć że, w układzie termoanemometru

jak na rys.2.1 zależność prądu I

T

od prędkości przepływu gazu  jest funkcję rosnącą. Wynika

to stąd że, ze wzrostem prędkości przepływu gazu zwiększa się w bilansie cieplnym udział
ubytku ciepła w wyniku jego unoszenia przez masę poruszającego się gazu. W pobliże
termorezystora napływa stale gaz o niższej temperaturze niż ta jaka ustaliłaby się przy
nieruchomej masie gazu ( = 0). Wskutek tego obniża się temperatura 

T

termorezystora

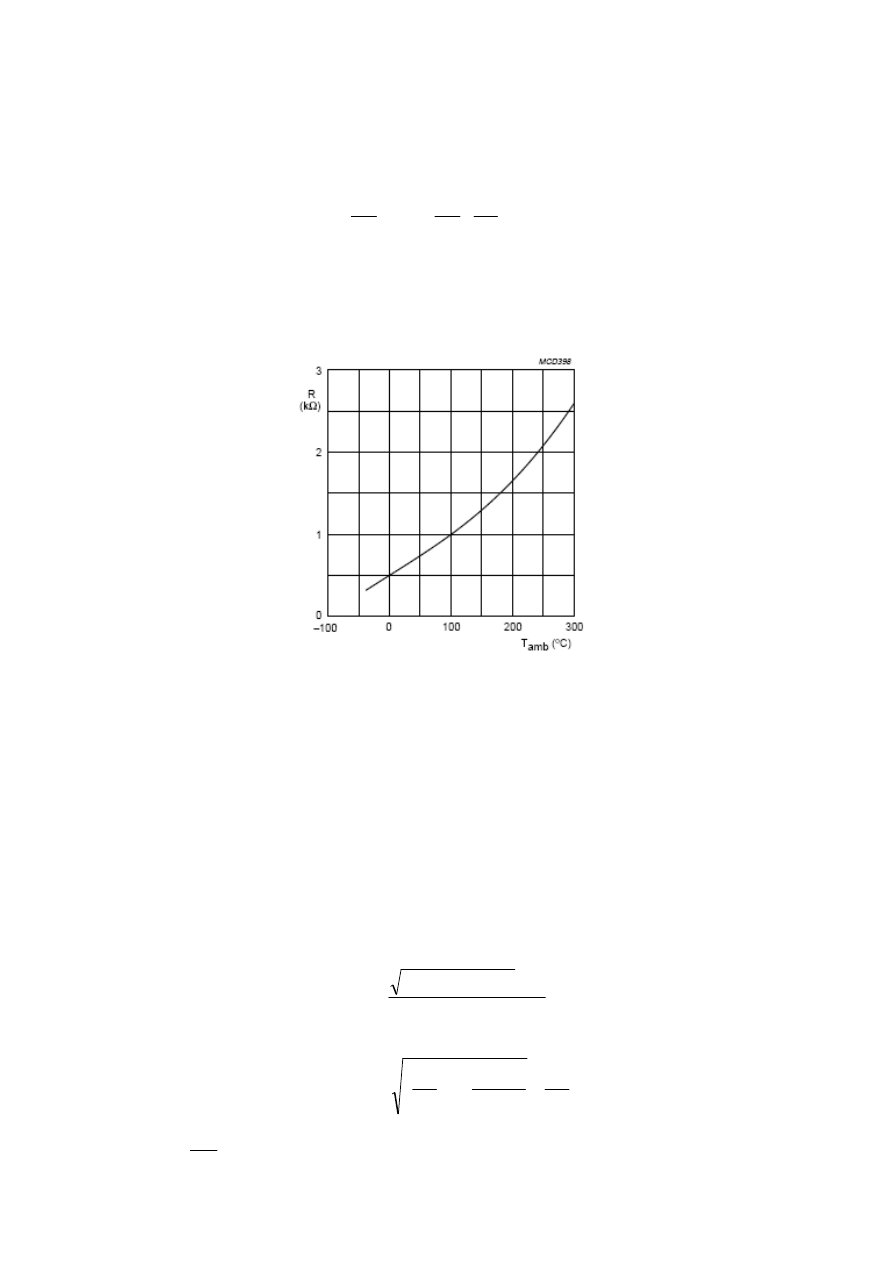
a tym samym jak wynika z charakterystyki R

T

= f(

T

) termorezystora (rys.2.3). W wyniku

obniżenia się temperatury termorezystora maleje jego rezystancja R

T

i rośnie prąd

przepływający przez termorezystor:

T

Z

T

R

U

I 

(2.27).

W myśl przeprowadzonego rozumowania jest również:





T

T

T

T

Z

T

T

Z

T

Z

T

R

R

R

R

U

R

R

U

R

U

I





















(2.28).

8

Z zależności (2.28) wynika że, jeśli R

T

< 0 to I

T

>0 - odpowiada to przyrostowi

prędkości przepływu gazu  > 0.

Rezystancję R

T

termorezystora w nieznanej temperaturze wyznacza się n a podstawie

pomiaru prądy I

T

(zależność 2.27):

1

;









T

A

T

Z

A

T

Z

T

R

R

I

U

R

I

U

R

(2.29).

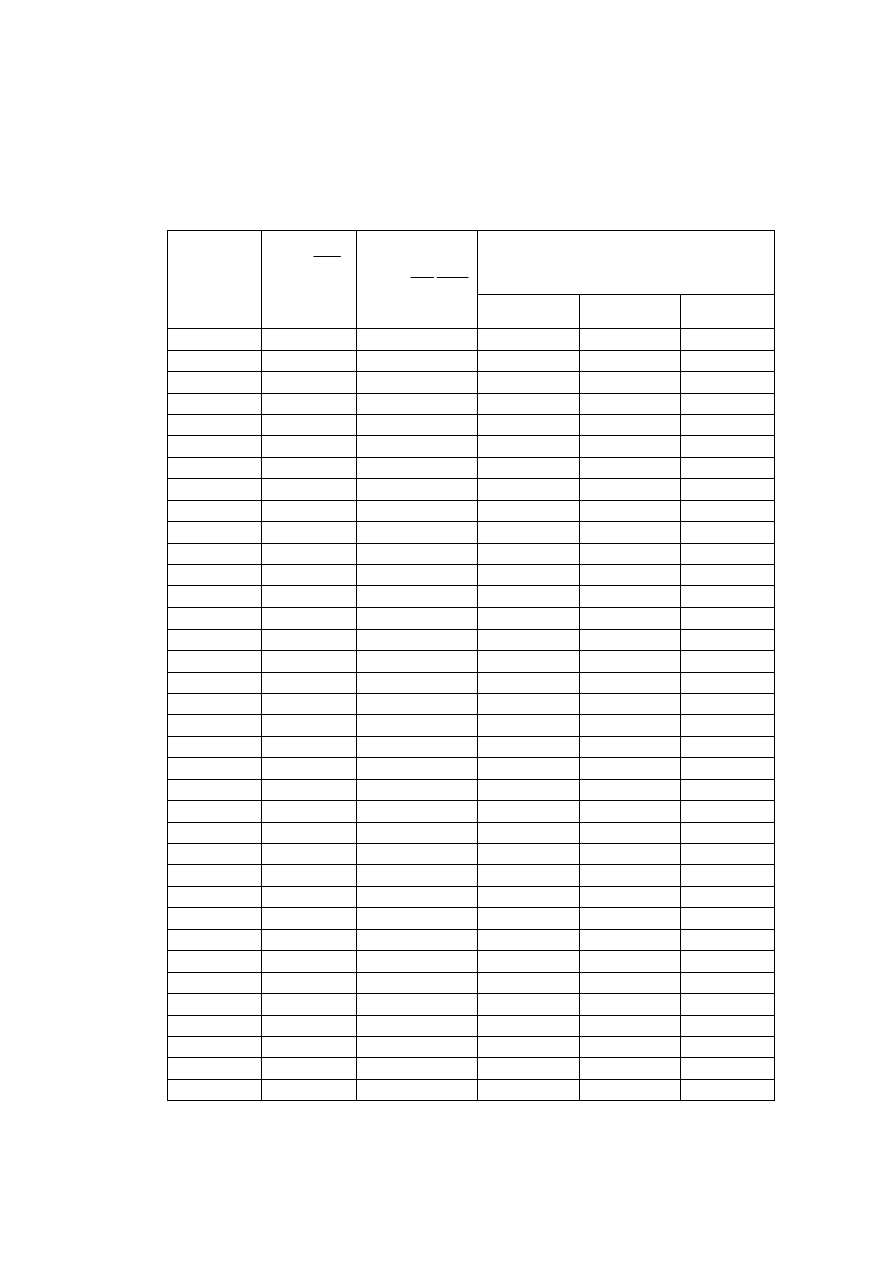
W ćwiczeniu laboratoryjnych używany jest termorezystor typu KTY84-130 o wymiarach

geometrycznych: d =1.6mm; l = 3,04mm. Wymiary te występują w zależnościach (2.22)
,...(2.26). Podstawowe parametry tego termorezystora podano niżej w tablicy 2.1 oraz na
(rys.2.3).

Rys.2.3. Orientacyjna charakterystyka termorezystora typu KTY84-130.

W zakresie temperatur otoczenia czujnika





C

a













130

30

charakterystykę statyczną

 

a

T

f

R





termorezystorów serii KTY można opisać przybliżoną zależnością:

 









2

25

1

a

a

a

T

R

f

R























(2.30)

gdzie:

 

1

K









3

10

88

,

7



;





2

K









5

10

937

,

1



;

0

a

a

a













;

(298K)

C

25



0

a



.

Jeśli znana jest wartść rezystancji R

25

w temperaturze 

a0

= 25C

oraz wartść R

T

w dowolnej temperaturze 

a

= ; -30C <  < +130C albo ( 243K < T < 403K) to można

wyznaczać temperaturę 

T

termorezystora z przybliżonej zależności:





 

C







































2

1

4

25

2

T

T

k

(2.31)

albo





 

C





















































2

1

2

25

2

T

T

k

gdzie

25

R

R

k

T

T



.

9

Wyznaczając temperaturę termorezystora z zależności (2.31) bądź z jego charakterystyki

(tablica 2.1) należy liczyć się z błędem wynikającym z rozrzutu charakterystyk różnych
egzemplarzy termorezystorów a także z błędem wynikającym z zależności współczynnika k

T

termorezystora od

prądu I

T

przepływającegopo przez termorezystor.

Tablica 2.1.



a

[C]

25

R

R

k

T

T



a

T

T

T

d

dR

R

Tk





1

[%K

-1

]

KTY84-130 (I

T

= 2mA)

R

T

[]

Min.

Typ.

Max.

-40

0,595

0,84

340

359

379

-30

0,648

0,83

370

391

411

-20

0,703

0,82

403

424

446

-10

0,723

0,80

437

460

483

0

0,826

0,79

474

498

522

10

0,892

0,77

514

538

563

20

0,954

0,75

555

581

607

25

1

0,74

577

603

629

30

1,038

0,73

599

626

752

40

1,114

0,71

645

672

700

50

1,197

0,70

694

722

750

60

1,282

0,68

744

773

801

70

1,370

0.66

797

826

855

80

1,463

0,64

852

882

912

90

1,559

0,63

910

940

970

100

1,658

0,61

970

1000

1030

110

1,761

0,60

1029

1062

1096

120

1,869

0,58

1089

1127

1164

130

1,980

0,57

1152

1194

1235

140

2,093

0,55

1216

1262

1309

150

2,212

0,54

1282

1334

1385

160

2,333

0,53

1350

1407

1463

170

2,458

0,52

1420

1482

1544

180

2,587

0,51

1492

1560

1628

190

2,720

0,49

1566

1640

1714

200

2,856

0,48

1641

1722

1803

210

2,997

0,47

1719

1807

1894

220

3,139

0,46

1798

1893

1988

230

3,287

0,45

1879

1982

2085

240

3,438

0,44

1962

2073

2184

250

3,592

0,44

2046

2166

2286

260

3,750

0,42

2132

2261

2286

270

3,909

0,41

2219

2357

2496

280

4,066

0,38

2304

2452

2600

290

4,216

0,34

2384

2542

2700

300

4,405

0,29

2456

2624

2791

10

2.3. PROGRAM ĆWICZENIA.

1. Przeprowadzić identyfikację układu pomiarowego na stanowisku laboratoryjnym
2. Sprawdzić i zanotować wskazania przyrządów pomiarowych przy wyłączonum

zasilaczu stabilizowanym (U

Z

= 0)

3. Włączyć zasilacz i w razie potrzeby ustawić wartość napięcia U

Z

= 25V

4. Nastawić pokrętłem regulatora prędkości przepływu maksymalny przepływ
5. Dokonać odczytu wskazań przyrządów pomiarowych na stanowisku
6. Dokonać pomiaru charakterystyki kryzy oraz termoanemometru (charakterystyki

wzorcowania) nastawiając kolejne wartości prędkości przepływu  - Uwaga! należy
dokonywać odczytów wskazań przyrządów wtedy gdy ustalą się wskazania.

7. Sporządzić wykresy zmierzonych charakterystyk wzorcowania:

 







f

p

dla kryzy

pomiarowej oraz

 



 f

I

T

dla termoanemometru.

8. Na podstawie zmierzonych charakterystyk i podanych w opracowaniu zależności

wyznaczyć charakterystyki:

 

p

f 







;

 

p

f

Q

V

V





;

 

p

f

Q

m

m





dla kryzy

pomiarowej oraz charakterystyki:

 

T

I

f







;

 

Z

V

V

I

f

Q 

;

 

T

m

m

I

f

Q 

9. Sporządzić wykresy charakerystyk czułości dla zmierzonych charakterystyk kryzy

oraz termoanemomtru.

10. Wyznaczyć charakterystykę termiczną termoanemometru:

 







f

T

.

11. Wnioski.

Opracował: Jan Leks