Zakład Inżynierii i Sterowania Procesami Chemicznymi
POMIAR NATĘŻENIA PRZEPŁYWU GAZU ZA POMOCĄ ZWĘŻKI POMIAROWEJ ORAZ RURKI PRANDTLA
Data wykonania:		Ocena:		Data:	Podpis:
Data oddania:

POMIAR NATĘŻENIA PRZEPŁYWU GAZU ZA POMOCĄ ZWĘŻKI POMIAROWEJ (1)

Przyrządy służące do określania natężenia przepływu różnego rodzaju płynów, noszą nazwę przepływomierzy. Taki przepływomierz zwężkowy składa się:

- ze zwężki pomiarowej (element dławiący z obudową posiadającą otwory impulsowe) wbudowanej w prosty odcinek rurociągu

- z manometru różnicowego

- z przewodów impulsowych wraz z armaturą

Jedną z wielkości charakteryzujących zwężkę jest jej moduł. Jest to stosunek pola powierzchni otworu przepływowego zwężki do pola powierzchni przekroju rurociągu w temp. przepływającego płynu przez odcinek pomiarowy:

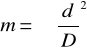
gdzie: m - moduł zwężki

d - średnica otworu zwężki [m]

D - średnica rurociągu [m]

Pomiar natężenia przepływu płynu za pomocą zwężki opiera się na pomiarze różnicy ciśnień statycznych przed i za zwężką, wywołanych przewężeniem strumienia płynu na skutek umieszczenia w przewodzie elementu dławiącego. Schemat takiego pomiaru wygląda następująco:

Przepływ płynu przez odcinek pomiarowy z wbudowaną zwężką

Rozkład przyściennego ciśnienia statycznego w kierunku przepływu

Powstała różnica ciśnień ∆p = p₂ - p₁, zwana ciśnieniem różnicowym, jest zależna od średniej prędkości przepływu płynu w przewodzie i dla zwężek wyraża się zależnością:

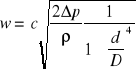
gdzie: w - średnia prędkość przepływu płynu [m/s]

∆p - różnica ciśnień statycznych przed i za zwężką (ciśnienie różnicowe) [N/m²]

ρ - gęstość płyn

c - stała

Przyjmując, że: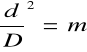
oraz

gdzie: α - współczynnik poprawkowy zwany liczbą przepływu

otrzymujemy:

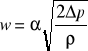
Liczba przepływu α jest wielkością wyznaczoną doświadczalnie i zależy od rodzaju zwężki, jej modułu, liczby Reynoldsa, chropowatości rurociągu i nieostrości krawędzi wlotowej zwężki. Występowanie jej w równaniu jest skutkiem różnicy prędkości przepływu w przepływie teoretycznym i przepływie rzeczywistym.

POMIAR NATĘŻENIA PRZEPŁYWU GAZU ZA POMOCĄ RURKI PRANDTLA (2)

Rurką Prandtla mierzymy różnicą ciśnienia całkowitego p_c i statycznego p_s, czyli ciśnienie dynamiczne p_d : p_d = p_c - p_s. Czoło rurki odbiera impuls ciśnienia całkowitego, zaś otworki na obwodzie rurki odbierają impuls ciśnienia statycznego (co widać na poniższym rysunku). Ciśnienie dynamiczne wyrażone jest zależnością:

skąd: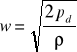

gdzie: w - miejscowa prędkość przepływu płynu

p_d - zmierzone ciśnienie dynamiczne

ρ - gęstość płynu

Aby wyznaczyć rozkład prędkości w rurociągu, należy kołowy przekrój pomiarowy podzielić na 5-16 pierścieni o równej powierzchni. Pomiary prędkości należy wykonać, przez ustawienie równoległe do kierunku przepływu czynnika rurki Prandtla, w środkach ciężkości tych pierścieni. Położenie środków ciężkości w zależności od liczby pierścieni można wyznaczyć z następującego wzoru:

gdzie: D - średnica przekroju pomiarowego

i - kolejny numer pierścienia, licząc od środka

m - liczba pierścieni, na które podzielono powierzchnię koła

Zasada pomiaru rurką Prandtla

POMIARY I OBLICZENIA

• dane wykorzystane do obydwu pomiarów:

wyszczególnienie	oznaczenie	oznaczenie i jednostki w układzie SI
temperatura otoczenia	to = 24 °C	to = 297,15 K
temperatura przepływającego płynu	t = 24 °C	t = 297,15 K
ciśnienie barometryczne	pb = 750 mmHg	pb = 99991,78 Pa
średnica wewnętrzna rurociągu	D = 100 mm	D = 0,1 m
średnica otworu zwężki	d = 0,445 mm	d = 4,45∙10^-2 m

• Wzory stosowane w poniższych obliczeniach zaczerpnięte są z normy PN-93 M - 53950/01 Pomiar strumienia masy i strumienia objętości płynów za pomocą zwężek pomiarowych.

• Obliczamy przewężenie kryzy β:

β = 0,445

• Do obliczenia gęstości powietrza w warunkach pomiaru wykorzystujemy wzór z podanej powyżej normy:

gdzie: K₁ - względny współczynnik ściśliwości, przyjmujemy K₁ = 1

ρ_n - gęstoś powietrza w temperaturze 293,15 K równa 1,00 kg/m³

T_n - temperatura odniesienia równa 293,15 K

p_n - ciśnienie odniesienia równe 101325 Pa

ρ₁, T₁, p₁ - odpowiednio: gęstość, temperatura i ciśnienie w warunkach pomiaru

ρ₁ = 0,907 kg/m³

• Do obliczenia lepkości powietrza w warunkach pomiaru wykorzystujemy wzór z normy:

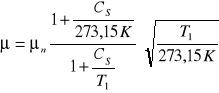
gdzie: T₁ - temperatura w warunkach roboczych

C_S - stała Sutherlanda, dla powietrza wynosi 113

μ_n - lepkość dynamiczna w warunkach normalnych, dla powietrza wynosi 17,08∙10^-6 Pa∙s

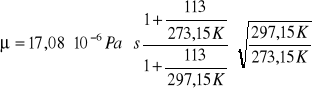
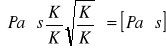
μ = 18,25∙10^-6 Pa∙s

WYNIKI POMIARÓW NATĘŻENIA PRZEPŁYWU ZA POMOCĄ ZWĘŻKI POMIAROWEJ

ciśnienie odczytane z (1) manometru h1 [mH2O]	ciśnienie różnicowe na zwężce p [Pa]	ciśnienie odczytane z (3) manometru h3 [mH2O]	nadciśnienie przed zwężką p1 [Pa]	ciśnienie za zwężką p = p1 - p [Pa]
0,023	225	0,020	100186	99961
0,043	420	0,037	100351	99931
0,097	948	0,077	100740	99791
0,158	1545	0,125	101206	99661
0,233	2278	0,183	101769	99491
0,273	2669	0,218	102109	99440
0,315	3080	0,249	102410	99331
0,362	3539	0,286	102770	99231

• W celu wyznaczenia gęstości cieczy znajdującej się w manometrze w warunkach pomiaru wykorzystałyśmy następujący wzór:

gdzie: ρ₀ - gęstość cieczy w temperaturze t₀

β_t - współczynnik rozszerzalności cieplnej w zakresie temperatur od t do t₀

Dla wody w temperaturze t₀ = 20°C dane te odpowiednio wynoszą:

ρ₀ = 999,2 kg/m³

β_t = 0,00018 1/°C

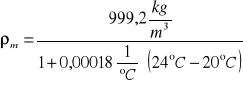
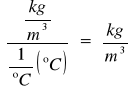
ρ_m = 997,48 kg/m³

• Do przeliczenia ciśnień odczytanych z manometru (1) h₁ na p wykorzystałyśmy wzór

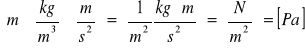
gdzie: ρ_m - gęstość cieczy w manometrze

ρ - gęstość powietrza

• Do przeliczenia nadciśnienia przed zwężką wykorzystałyśmy wzór:

• Iteracyjnie obliczamy masowe i objętościowe natężenie przepływu:

• do pierwszego pomiaru zakładamy liczbę Reynoldsa równą Re = 1∙10⁶

• obliczamy współczynnik przepływu C (z wzoru Stolza):

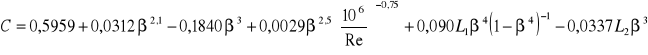
zakładając, że L₁, L₂ są równe 0, powyższy wzór upraszcza się do postaci:

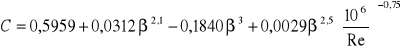
i w tej formie wykorzystujemy do dalszych obliczeń.

• chcąc skorzystać z wzoru na liczbę ekspansji musimy poznać wartości następującej zależności:

Pa

lp
1.	100186	0,965
2.	100351	0,965
3.	100740	0,965
4.	101206	0,965
5.	101769	0,965
6.	102109	0,965
7.	102410	0,965
8.	102770	0,966

• obliczamy liczbę ekspansji ε wykorzystując doświadczalny wzór:

do obliczeń przyjmujemy wykładnik izentropy κ = 1,42

• wyznaczamy tymczasowe przybliżone wartości masowego i objętościowego natężenia przepływu (q_m i q_V) i wszystkie obliczenia powtarzamy do momentu, kiedy błąd względny pomiędzy wartościami liczby Reynoldsa założonej i obliczonej jest nie większy niż 5%. Do obliczenia masowego i objętościowego natężenia przepływu wykorzystujemy następujące wzory:

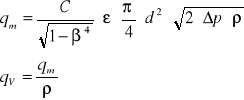
gdzie: q_m - masowe natężenie przepływu (strumień masy)

q_V - objętościowe natężenie przepływu (strumień objętości)

ρ - gęstość płynu (tu powietrza) w warunkach pomiaru

wyniki dla pomiaru 1

1.	2.	3.	4.	5.	6.	7.	8.	9.
p1 [Pa]	Δp [Pa]	założona do obliczeń liczba Re [-]	współczynnik przepływu C [-]	liczba ekspansji ε [-]	strumień masy qm [kg/s]	strumień objętości qv [m^3/s]	obliczona liczba Re [-]	błąd [%]
100186	225	1E+06	0,5858	0,9993	0,0949	0,1046	6,6214E+06	562,14
100186	225	6,6214E+06	0,5870	0,9993	0,0951	0,1049	6,6349E+06	0,20

wyniki dla pomiaru 2

1.	2.	3.	4.	5.	6.	7.	8.	9.
100351	420	1E+06	0,5858	0,9987	0,1296	0,1429	9,0438E+06	804,38
100351	420	9,0438E+06	0,5874	0,9987	0,1300	0,1433	9,0688E+06	0,28

wyniki dla pomiaru 3

1.	2.	3.	4.	5.	6.	7.	8.	9.
100740	948	1E+06	0,5858	0,9972	0,1945	0,2144	1,3567E+07	1256,7
100740	948	1,3567E+07	0,5881	0,9972	0,1952	0,2153	1,3621E+07	0,40

wyniki dla pomiaru 4

1.	2.	3.	4.	5.	6.	7.	8.	9.
101206	1545	1E+06	0,5858	0,9954	0,2478	0,2732	1,7288E+07	1628,8
101206	1545	1,7288E+07	0,5886	0,9954	0,2490	0,2745	1,7373E+07	0,49

wyniki dla pomiaru 5

1.	2.	3.	4.	5.	6.	7.	8.	9.
101769	2278	1E+06	0,5858	0,9933	0,3003	0,3311	2,0948E+07	1994,8
101769	2278	2,0948E+07	0,5891	0,9933	0,3020	0,3330	2,1069E+07	0,58

wyniki dla pomiaru 6

1.	2.	3.	4.	5.	6.	7.	8.	9.
102109	2669	1E+06	0,5858	0,9921	0,3246	0,3579	2,2648E+07	2164,8
102109	2669	2,2648E+07	0,5894	0,9921	0,3266	0,3601	2,2787E+07	0,61

wyniki dla pomiaru 7

1.	2.	3.	4.	5.	6.	7.	8.	9.
102410	3080	1E+06	0,5858	0,9910	0,3483	0,3840	2,4302E+07	2330,2
102410	3080	2,4302E+07	0,5896	0,9910	0,3506	0,3865	2,4460E+07	0,65

wyniki dla pomiaru 8

1.	2.	3.	4.	5.	6.	7.	8.	9.
102770	3539	1E+06	0,5858	0,9897	0,3729	0,4111	2,6016E+07	2501,6
102770	3539	2,6016E+07	0,5898	0,9897	0,3755	0,4140	2,6195E+07	0,69

ZESTAWIENIE WYNIKÓW DLA POMIARU NATĘŻENIA PRZEPŁYWU ZA POMOCĄ ZWĘŻKI POMIAROWEJ:

lp	ciśnienie różnicowe p [Pa]	nadciśnienie przed zwężką p1 [Pa]	współczynnik przepływu C [-]	liczba ekspansji ε [-]	strumień masy qm [kg/s]	strumień objętości qv [m^3/s]	liczba Reynoldsa Re [-]
1.	225	100186	0,5870	0,9993	0,0951	0,1049	6,6349E+06
2.	420	100351	0,5874	0,9987	0,1300	0,1433	9,0688E+06
3.	948	100740	0,5881	0,9972	0,1952	0,2153	1,3621E+07
4.	1545	101206	0,5886	0,9954	0,2490	0,2745	1,7373E+07
5.	2278	101769	0,5891	0,9933	0,3020	0,3330	2,1069E+07
6.	2669	102109	0,5894	0,9921	0,3266	0,3601	2,2787E+07
7.	3080	102410	0,5896	0,9910	0,3506	0,3865	2,4460E+07
8.	3539	102770	0,5898	0,9897	0,3755	0,4140	2,6195E+07

WNIOSKI:

Jak widać z obliczeń gęstość powietrza w 24°C jest mniejsza niż dla temperatury 20 °C. Lepkość natomiast powietrza zwiększa się ze wzrostem temperatury, co jest cechą charakterystyczną dla gazów.

W miarę zwiększania się natężenia przepływu powietrza nadciśnienie przed zwężką powinno wzrastać, zatem różnica ciśnień przed i za zwężką p również musi ulec zwiększeniu. Wzrost wartości liczby Reynoldsa świadczy o zwiększaniu się natężenia przepływu powietrza (wartości te informują nas również, że jest to przepływ burzliwy) co pociąga za sobą wzrost nadciśnienia przed zwężką i większy spadek ciśnienia za nią. Różnica ciśnień również uległa zwiększeniu. Zależność ta w naszym doświadczeniu jest zachowana co widoczne jest w obliczeniach i przedstawiamy to na załączonych wykresach.

Jak widać pomiary są łatwe i szybkie do wykonania, ale obliczenia zajmują dużo czasu.

WYNIKI POMIARÓW NATĘŻĘNIA PRZEPŁYWU ZA POMOCĄ RURKI PRANDTLA

lp.	h [mmHg]	h [mHg]	ciśnienie dynamiczne pd [Pa]	miejscowa prędkość w [m/s]
1.	4,14	4,14E-03	5,46E+02	34,70
2.	5,81	5,81E-03	7,66E+02	41,11
3.	5,94	5,94E-03	7,84E+02	41,57
4.	6,04	6,04E-03	7,97E+02	41,92
5.	5,95	5,95E-03	7,85E+02	41,60
6.	5,79	5,79E-03	7,64E+02	41,04
7.	5,33	5,33E-03	7,03E+02	39,38
8.	5,33	5,33E-03	7,03E+02	39,38
9.	5,07	5,07E-03	6,69E+02	38,40
10.	4,70	4,70E-03	6,20E+02	36,98
11.	4,39	4,39E-03	5,79E+02	35,74

• w celu wyznaczenia gęstość rtęci w warunkach pomiaru, wykorzystałyśmy wzór:

Dla rtęci w temperaturze t₀ = 20°C dane te odpowiednio wynoszą:

ρ₀ = 13 546 kg/m³

β_t = 0,000181 1/°C

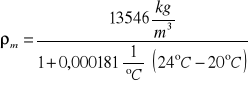
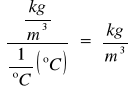
ρ_m = 13 448,6 kg/m³

• do przeliczenia ciśnienia z [mmHg] na [Pa] skorzystałyśmy z następującego wzoru:

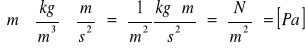
gdzie: ρ_m - gęstość rtęci

ρ - gęstość powietrza

• do obliczenia prędkości wykorzystujemy wzór:

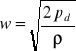
gdzie: w - miejscowa prędkość przepływu

p_d - odczytane przy pomocy rurki Prandtla ciśnienie dynamiczne

ρ - gęstość płynu, tu: powietrza w 24°C

• określamy prędkość średnią i obliczamy objętościowe natężenie przepływu gazu wykorzystując następujące wzory:

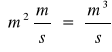
gdzie: w - miejscowa prędkość

n - liczba pomiarów

w_śr - średnia prędkość przepływu gazu w przekroju pomiarowym

A - pole powierzchni przekroju pomiarowego

D - średnica rurociągu

prędkość średnia wśr [m/s]	objętościowe natężenie przepływu qV [m^3/s]
39,256	0,3083

• podczas pomiaru średnich prędkości przepływu gazu za pomocą rurki Prandtla, na zwężce odczytaliśmy następujące wartości ciśnień:

ciśnienie odczytane z (1) manometru h1 [mH2O]	ciśnienie różnicowe na zwężce p [Pa]	ciśnienie odczytane z (3) manometru h3 [mH2O]	nadciśnienie przed zwężką p1 [Pa]
0,285	2786	0,224	100168

• na podstawie powyższych pomiarów obliczamy objętościowe natężenie przepływu postępując tak, jak wykonaliśmy to poprzednio:

p1 [Pa]	Δp [Pa]	założona liczba Re [-]	współczynnik przepływu C [-]	liczba ekspansji ε [-]	strumień masy qm [kg/s]	strumień objętości qv [m^3/s]	obliczona liczba Re [-]	błąd [%]
100168	2786	1E+06	0,5858	0,9918	0,3316	0,3656	2,3132E+07	2213,2
100168	2786	2,3132E+07	0,5928	0,9918	0,3336	0,3678	2,3276E+07	0,62

• objętościowe natężenie przepływu wynosi zatem:

• z obliczeń przy pomiarze rurką Prandtla: q_V = 0,3083 m³/s

• z obliczeń przy pomiarze za pomocą zwężki: q_V = 0,3678 m³/s

WNIOSKI:

Z powyższych obliczeń możemy zauważyć, że pomiary wykonane za pomocą rurki Prandtla i zwężką pomiarową dają nieco odmienne wyniki. Wartości są jednak do siebie zbliżone a różnica mogą być spowodowana złym odczytem z manometrów (niewielkie wahania słupa cieczy) co miało wpływ na przeprowadzone obliczenia.

Możemy również zaobserwować, że w zależności od położenia rurki w rurociągu prędkości lokalne mają różne wartości (wartość największa odpowiada najmiększemu ciśnieniu dynamicznemu - prawdopodobnie rurka przy pomiarze 4 znalazła się po środku rurociągu).

Przy pomiarach rurką Prandtla obliczamy prędkości lokalne i na podstawie tych pomiarów wyznaczamy prędkość średnią w rurociągu a przy pomiarze zwężką, nie mamy możliwości poznania natężenia przepływu w poszczególnych wysokościach rurociągu. Zatem pomiar rurką Prandtla daje nam dokładniejsze wyniki, dlatego też występuje różnica pomiędzy tymi dwoma wynikami.

Pomiary za pomocą rurki Prandtla są pracochłonne (aby wyznaczyć prędkość średnią należy wykonać kilka do kilkunastu pomiarów) ale obliczenia są prostsze (co widać powyżej) w porównaniu z doświadczeniem poprzednim. Zwężkę natomiast jest łatwiej zamontować, do określenia prędkości wystarczy jeden pomiar ale musimy liczyć się z większym błędem tego pomiaru.

1

---