Metody opracowania danych

Sprawozdanie z zadania domowego

Tomasz Serwa

Tomasz Bojarski

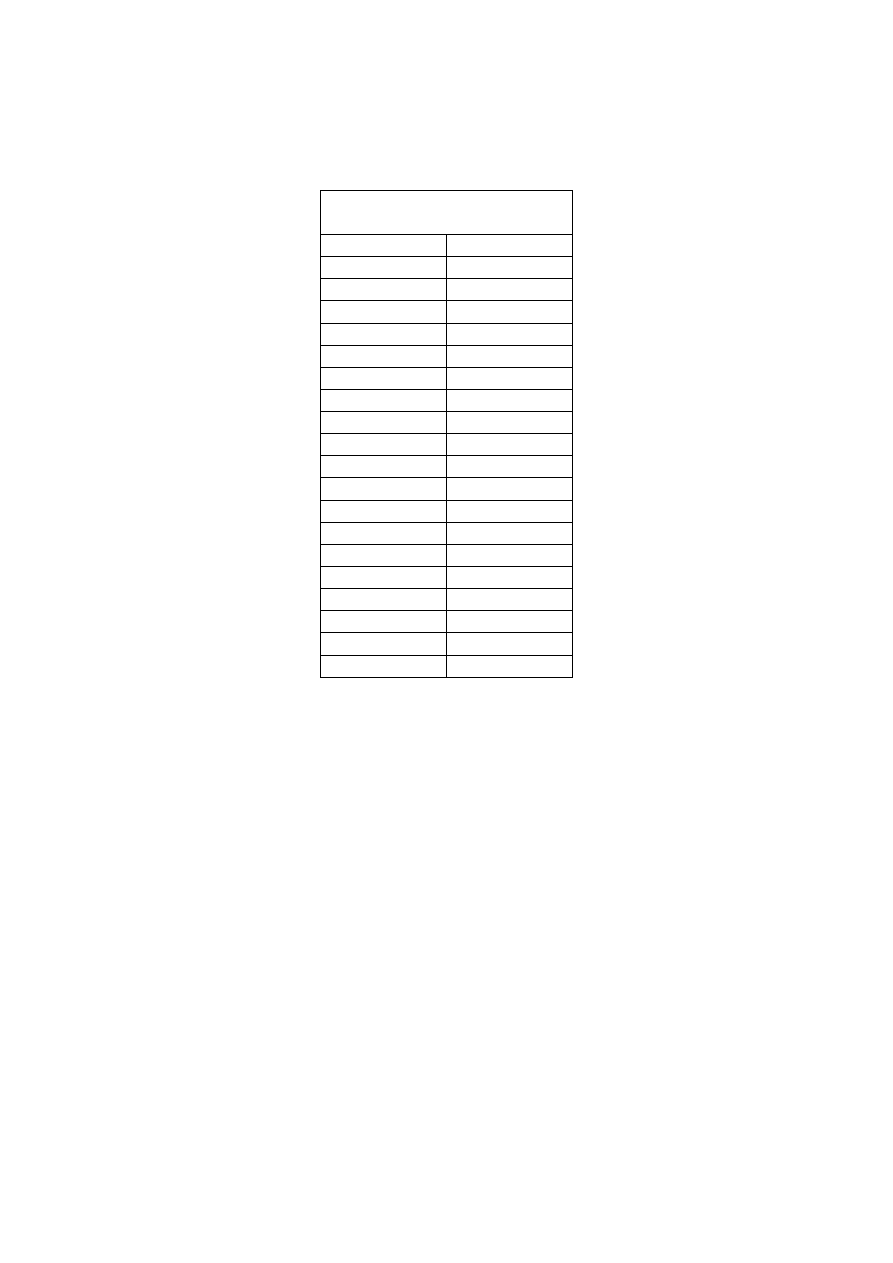
Dane:

Zestaw VII - Bierzemy pod uwagę tylko po 20 rekordów z każdej próby.

Zestaw VII

140,0566381

139,7396642

155,3835788

147,1591231

150,4254576

143,335536

149,8817265

157,4528268

146,1154445

142,2276423

146,2669442

146,3767614

141,1000029

152,0204944

143,7592555

139,1919666

156,198041

156,8113754

139,7264997

159,8951388

153,6021043

146,9131223

147,2266258

146,1618707

146,5666963

154,2979078

147,1911003

147,1888451

151,9193562

149,314915

152,0476147

148,6115681

149,1666863

154,9105305

151,3050653

150,702037

149,4339349

157,2096045

148,1426994

150,9595392

1. Sprawdzić, czy obie próby pochodzą z jednej populacji.
2. Zbadać losowość próby (pojedynczej czy połączonej – w zależności od wyniku

zadania 1).

3. W zależności od wyników zadania 1, znaleźć podstawowe charakterystyki liczbowe z

próby (średnia, odchylenie standardowe).

4. Przedziałowo oszacować średnią i wariancję dla poziomu ufności 0,95.
5. zweryfikować hipotezę, że dane są opisane rozkładem normalnym N(150,5), przy

poziomie istotności 0,05

6. Znaleźć prostoliniową funkcję regresji (przyjmując x

i

=1 do 40, y

i

– wartości w próby).

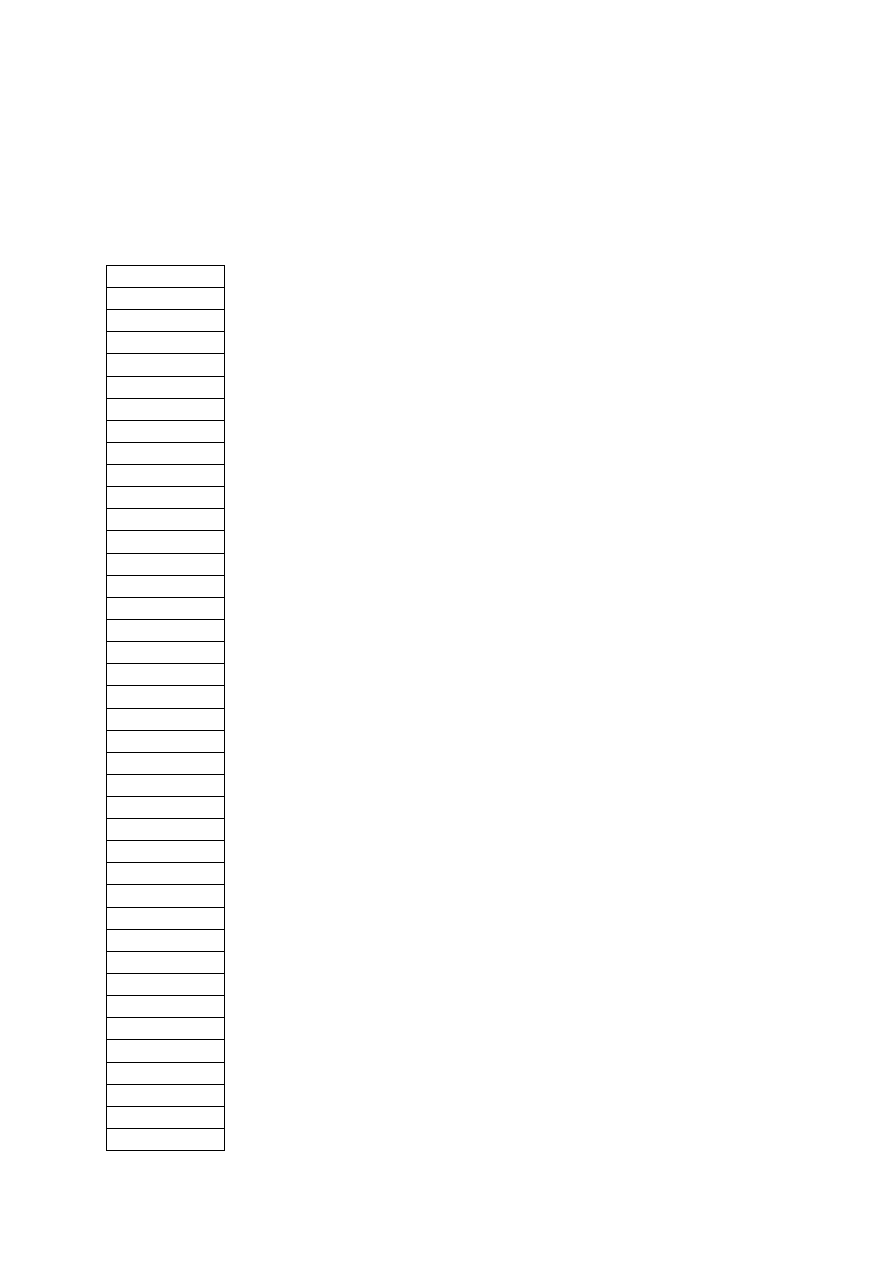
1. Sprawdzić czy obie próby należą do tej samej populacji.

Korzystamy z testu serii:

A – Liczby z pierwszej próby

B – Liczby z drugiej próby

139,1919666

B

139,7264997

A

139,7396642

B

140,0566381

A

141,1000029

A

142,2276423

B

143,335536

B

143,7592555

A

146,1154445

A

146,1618707

B

146,2669442

A

146,3767614

B

146,5666963

A

146,9131223

B

147,1591231

B

147,1888451

B

147,1911003

A

147,2266258

A

148,1426994

A

148,6115681

B

149,1666863

A

149,314915

B

149,4339349

A

149,8817265

A

150,4254576

A

150,702037

B

150,9595392

B

151,3050653

A

151,9193562

A

152,0204944

B

152,0476147

A

153,6021043

A

154,2979078

B

154,9105305

B

155,3835788

A

156,198041

A

156,8113754

B

157,2096045

B

157,4528268

B

159,8951388

B

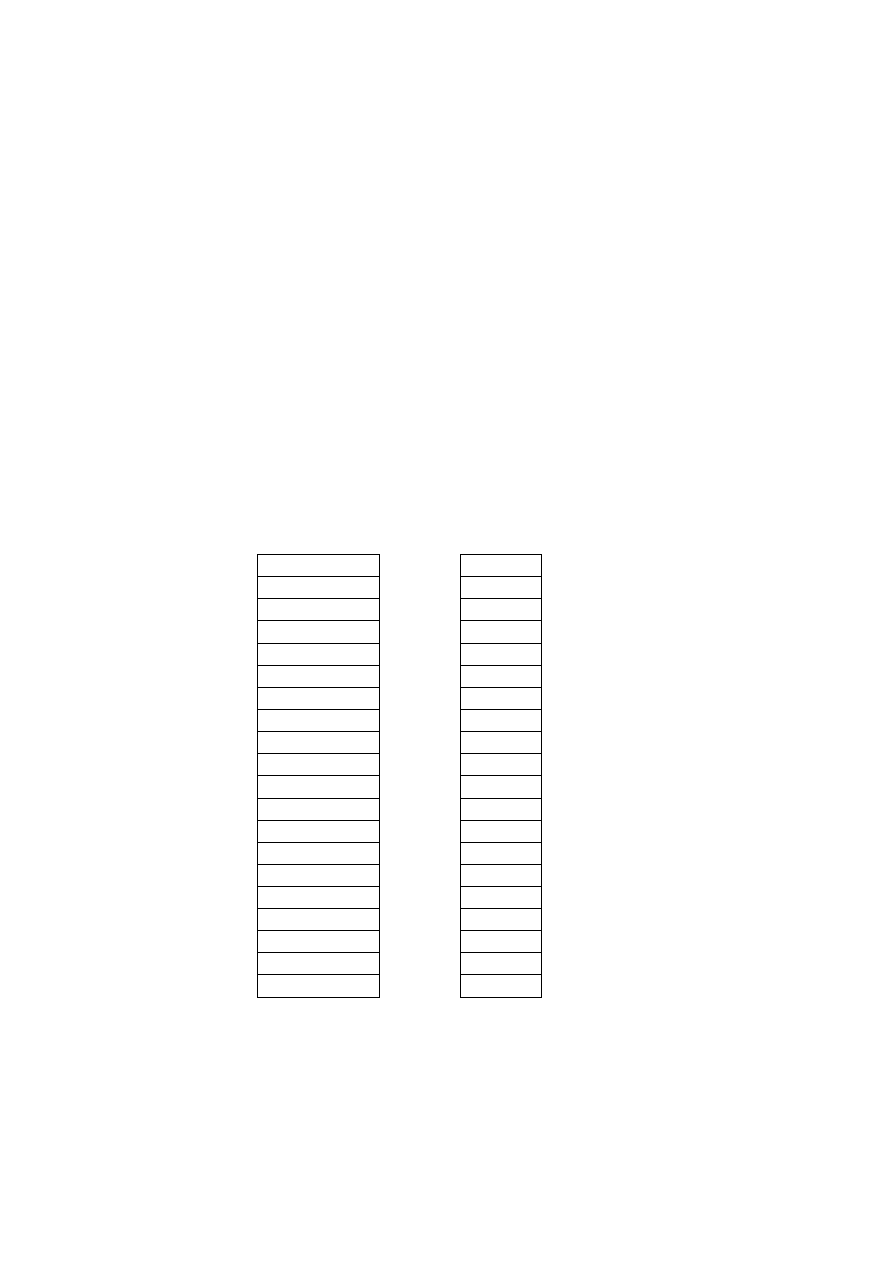
K- liczba serii = 23

Korzystamy z tabeli „Wartości krytyczne rozkładu serii”

Szukamy K

α

Próby po 20 więc z serii prób wynika, że dla poziomu ufności α= 0,05 k

α

=15

K= 23 > K

α

= 15

Nie ma podstaw do odrzucenia hipotezy H0. Stwierdzamy, że obie próby pochodzą z tej
samej populacji.

2. Zbadać losowość próby.

Do wykonania tego zadania wykorzystamy test serii. Wiemy już, że próby są z jednej

populacji. Więc, wykorzystamy Model I. Stawiamy hipotezę, że obie próby są losowe.

Mediana wynosi: 148,8891272. W poniższej tabeli, każdej wartości mniejszej od mediany

przypisujemy symbol A, a każdej wartości większej symbol B.

140,0566381

A

139,7397

A

155,3835788

B

147,1591

A

150,4254576

B

143,3355

A

149,8817265

B

157,4528

B

146,1154445

A

142,2276

A

146,2669442

A

146,3768

A

141,1000029

A

152,0205

B

143,7592555

A

139,192

A

156,198041

B

156,8114

B

139,7264997

A

159,8951

B

153,6021043

B

146,9131

A

147,2266258

A

146,1619

A

146,5666963

A

154,2979

B

147,1911003

A

147,1888

A

151,9193562

B

149,3149

B

152,0476147

B

148,6116

A

149,1666863

B

154,9105

B

151,3050653

B

150,702

B

149,4339349

B

157,2096

B

148,1426994

A

150,9595

B

Ilość serii K=20, α=0,05

Korzystając z tablic:

„Wartości krytyczne rozkładu serii” odczytujemy:

K

1

= 14

K

2

= 27

WNIOSEK:

Sprawdzamy hipotezę:

K

1

< K < K

2

14<20<27

Jako, że k zawiera się w powyższym przedziale nie mamy podstaw do odrzucenia naszej

hipotezy i tym samym stwierdzamy, że próba jest losowa.

3. Znaleźć podstawowe charakterystyki liczbowe z próby.

Parametr

Wartość

Średnia arytmetyczna

148,9

Mediana

148,889

Odchylenie

standardowe

5,33

Wariancja

28,404

4. Przedziałowo oszacować średnią i wariancję dla poziomu ufności

0,95.

W tym zadaniu zastosujemy przedział ufności dla średniej - MODEL III.

Dzielimy próby na przedziały

n

j

– liczba prób

x

j

– wartości prób

x

jsr

– wartośd środkowa przedziału

x

śr

– średnia

h – wielkośd przedziałów: 2

x

j

n

j

x

jsr

x

jsr

* n

j

(x

jsr

-x

śr

)

2

n

j

* (x

jsr

-x

śr

)

2

x

śr

139 - 141

4

140

560

80,77515625

323,100625

148,9875

141 - 143

2

142

284

48,82515625

97,6503125

148,9875

143 - 145

2

144

288

24,87515625

49,7503125

148,9875

145 - 147

6

146

876

8,92515625

53,5509375

148,9875

147 - 149

6

148

888

0,97515625

5,8509375

148,9875

149 - 151

7

150

1050

1,02515625

7,17609375

148,9875

151 - 153

4

152

608

9,07515625

36,300625

148,9875

153 - 155

3

154

462

25,12515625

75,37546875

148,9875

155 - 157

3

156

468

49,17515625

147,5254688

148,9875

157 - 160

3

158,5

475,5

90,48765625

271,4629687

148,9875

Σ

40

5959,5

1067,74375

Obliczenia:

x

śr

= ẋ

j

n

j

/n

j

= 148,9875

s

2

= (ẋ

j

-x

śr

)

2

nj /nj =26,6936

pop do s

2

: h^2/12= 0,3333

s

2

pop

= s

2

-pop= 26,3603

s= pierwiastek(s

2

pop

)= 5,1342

Z tablicy Funkcji Laplace'a dla 1-α=0,95; u

α

=1,96

Podstawiając do wzoru:



































1

n

s

u

x

m

n

s

u

x

P

Otrzymujemy: 147,396 < m < 150,579


WNIOSEK: Przedział liczbowy o końcach 147,396 i 150,579 obejmuje z ufnością 0,95

prawdziwą średnią m w populacji.

Zastosujemy przedział ufności dla wariancji - MODEL II.

Dane z poprzedniego podpunktu.

Podstawiając do wzoru:

P

s

u

n

s

u

n

1

2

1

2

1



 



























 









Otrzymujemy : 4,2114 < σ < 6,575

WNIOSEK:
Z ufnością α=0,95 przedział liczbowy o końcach 4,2114 i 6,575 obejmuje odchylenie

standardowe σ.

5. Zweryfikować hipotezę, że dane są opisane rozkładem normalnym

N(150,5), przy poziomie istotności 0,05.

Zastosujemy test dla wartości średniej populacji- MODEL III.

Dane z poprzedniego zadania. u

α

=1,96

Hipoteza: H

0

: m

0

=150;

H

1

: m

0

<150.

Podstawiamy do wzoru :

n

s

m

x

u

0





Otrzymujemy: u = -1,244 < u

α

= 1,96

WNIOSEK:

Wartość u znalazła się w obszarze krytycznym, więc hipotezę H

0

należy odrzucić na korzyść

alternatywnej H

1

. Oznacza to, że z prawdopodobieństwem błędu mniejszym niż 0,05 możemy

twierdzić, że m

0

jest niższe.

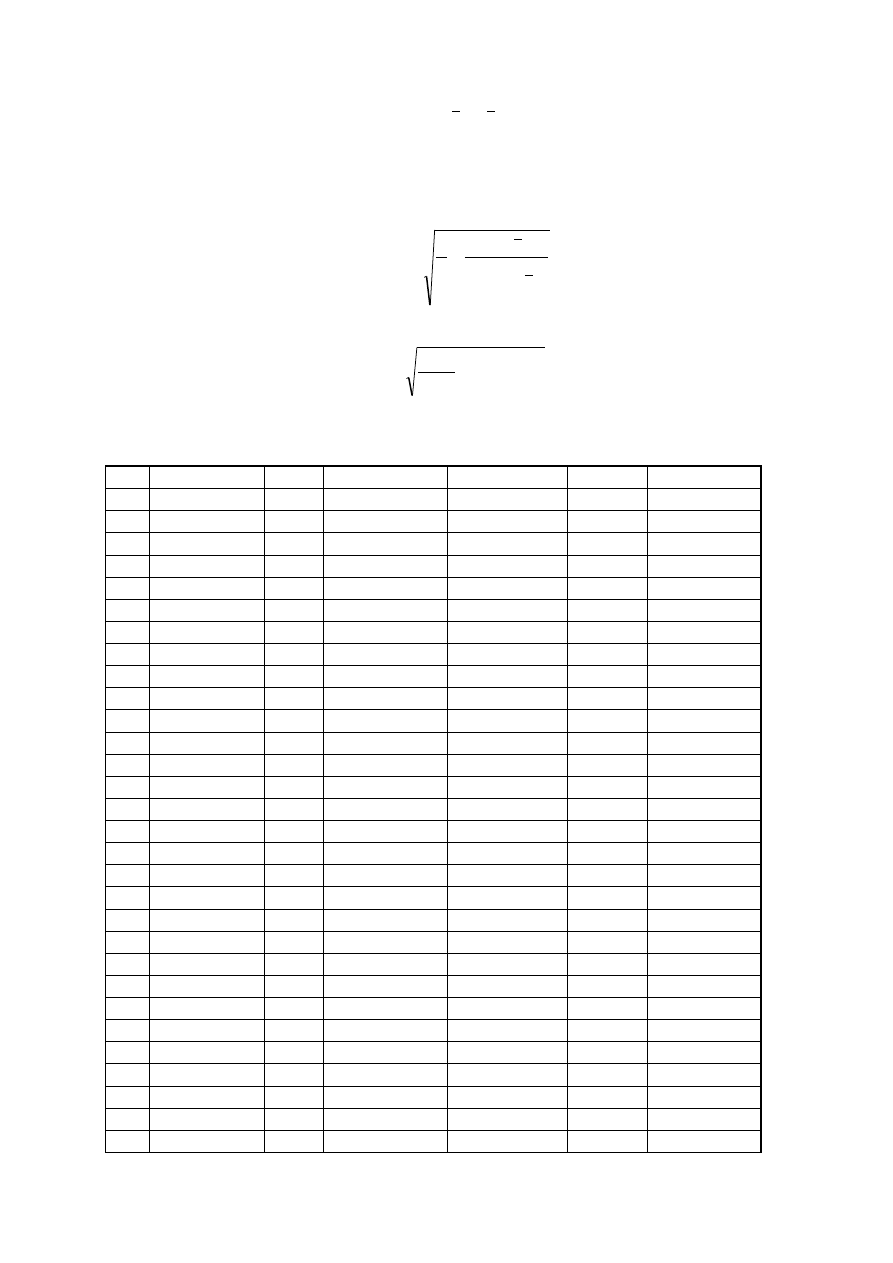
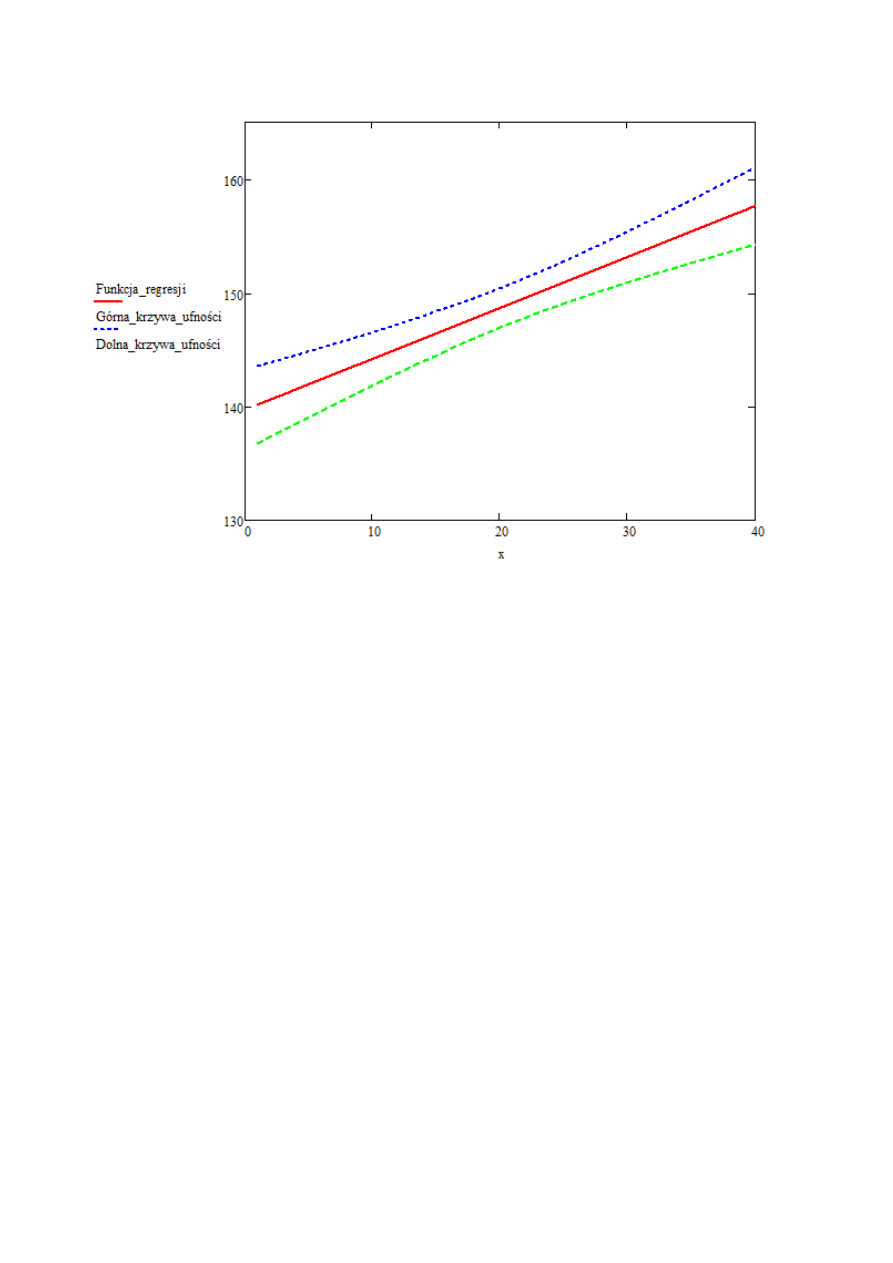
6. Znaleźć prostoliniową funkcję regresji (przyjmując xi=1 do 40, yi –

wartości w próbie).









































n

i

i

n

i

i

i

n

i

i

n

i

i

i

x

n

x

y

x

n

y

x

x

x

y

y

x

x

a

1

2

2

1

2

1

1

x

a

y

b



























1

ˆ

~

ˆ

ˆ

ˆ

i

i

y

i

y

i

s

t

y

y

s

t

y

P





















n

i

i

i

r

y

x

x

x

x

n

s

s

i

1

2

2

ˆ

1















n

i

i

i

r

y

y

n

s

1

2

ˆ

2

1

x

i

y

i

x

i

- x

śr

y

i

- y

śr

(x

i

-x

śr

)(y

i

-y

śr

)

(x

i

-x

sr

)

2

(yi - yśr)

2

1

139,1919666

-19,5

-9,707931878

189,3046716

380,25

94,24394135

2

139,7264997

-18,5

-9,173398816

169,7078781

342,25

84,15124584

3

139,7396642

-17,5

-9,160234313

160,3041005

306,25

83,90989267

4

140,0566381

-16,5

-8,843260362

145,913796

272,25

78,20325383

5

141,1000029

-15,5

-7,79989565

120,8983826

240,25

60,83837215

6

142,2276423

-14,5

-6,672256229

96,74771532

210,25

44,51900319

7

143,335536

-13,5

-5,564362536

75,11889424

182,25

30,96213043

8

143,7592555

-12,5

-5,140643013

64,25803766

156,25

26,42621059

9

146,1154445

-11,5

-2,784454027

32,02122131

132,25

7,753184228

10

146,1618707

-10,5

-2,738027794

28,74929184

110,25

7,496796201

11

146,2669442

-9,5

-2,632954349

25,01306632

90,25

6,932448604

12

146,3767614

-8,5

-2,523137079

21,44666517

72,25

6,366220719

13

146,5666963

-7,5

-2,333202165

17,49901624

56,25

5,443832343

14

146,9131223

-6,5

-1,986776203

12,91404532

42,25

3,947279681

15

147,1591231

-5,5

-1,740775438

9,574264909

30,25

3,030299126

16

147,1888451

-4,5

-1,711053396

7,699740282

20,25

2,927703724

17

147,1911003

-3,5

-1,708798191

5,980793669

12,25

2,919991258

18

147,2266258

-2,5

-1,673272723

4,183181807

6,25

2,799841606

19

148,1426994

-1,5

-0,757199091

1,135798637

2,25

0,573350463

20

148,6115681

-0,5

-0,288330391

0,144165196

0,25

0,083134414

21

149,1666863

0,5

0,266787793

0,133393896

0,25

0,071175726

22

149,314915

1,5

0,415016469

0,622524703

2,25

0,17223867

23

149,4339349

2,5

0,534036379

1,335090947

6,25

0,285194854

24

149,8817265

3,5

0,981828039

3,436398136

12,25

0,963986298

25

150,4254576

4,5

1,525559055

6,865015748

20,25

2,32733043

26

150,702037

5,5

1,802138541

9,911761976

30,25

3,247703321

27

150,9595392

6,5

2,059640664

13,38766432

42,25

4,242119665

28

151,3050653

7,5

2,405166834

18,03875126

56,25

5,784827499

29

151,9193562

8,5

3,019457673

25,66539022

72,25

9,117124639

30

152,0204944

9,5

3,120595887

29,64566093

90,25

9,73811869

31

152,0476147

10,5

3,147716245

33,05102057

110,25

9,908117559

32

153,6021043

11,5

4,702205804

54,07536675

132,25

22,11073942

33

154,2979078

12,5

5,398009336

67,4751167

156,25

29,13850479

34

154,9105305

13,5

6,010631984

81,14353178

182,25

36,12769685

35

155,3835788

14,5

6,483680278

94,01336403

210,25

42,03810995

36

156,198041

15,5

7,298142488

113,1212086

240,25

53,26288378

37

156,8113754

16,5

7,911476866

130,5393683

272,25

62,5914662

38

157,2096045

17,5

8,309705996

145,4198549

306,25

69,05121374

39

157,4528268

18,5

8,552928251

158,2291726

342,25

73,15258167

40

159,8951388

19,5

10,9952403

214,4071858

380,25

120,8953092

820

5955,995941

2389,131569

5330

1107,754575

x

śr

= 20,5

y

śr

= 148,8998985

a= 0,44824

b= 139,71098

y=0,44824x + 139,71098

s

r

2

= 29,15144

s

r

= 5,39921

α= 0,05

t

γ

=2,026

1/n= 0,025

Podstawiając do wzoru (model II ) :

































































1

1

2

1

2

n

i

i

r

n

i

i

r

x

x

s

t

a

x

x

s

t

a

P

Otrzymujemy :

0,44619 <



< 0,45029