Z

ada

ni

e

5.

Kr

ato

w

ni

ca

st

at

ycz

nie

w

yz

nac

za

ln

a.

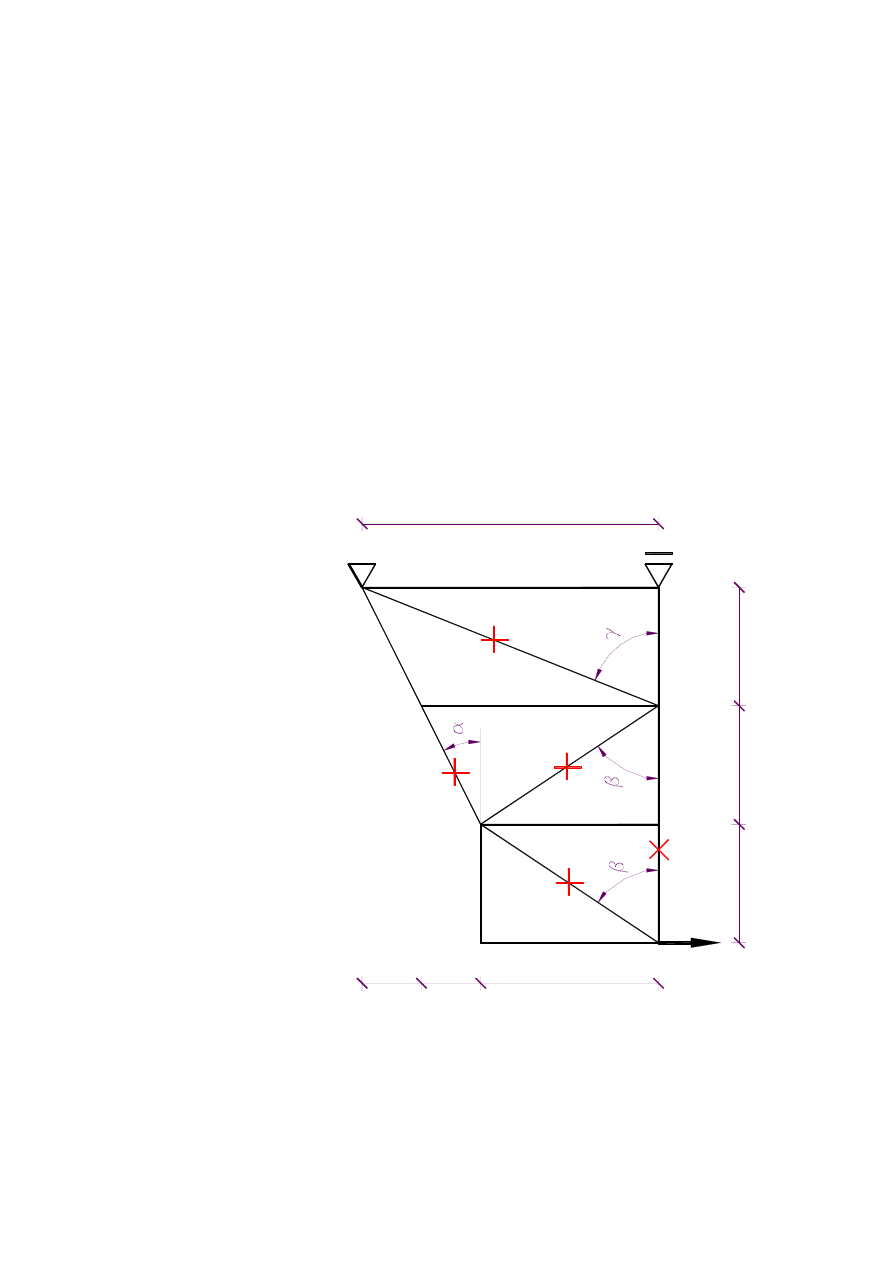
Wyznaczy

�

w

ar

to

�c

i s

i�

w

pr

�t

ac

h

krat

ow

ni

cy

s

ta

ty

cz

ni

e

wy

znacz

al

nej

pr

zeds

tawi

one

j na

Rys.1

:

a)

.

met

od

�

an

al

it

yc

zn

eg

o

równ

owa

�e

ni

a

w

�z

�ó

w

,

b)

.

m

et

od

�

graf

icz

neg

o

równo

wa

�e

ni

a

w

�z

�ó

w

; p

la

n

si

� C

re

m

on

y

,

c)

.

met

od

� pr

zek

ro

jów

– Ri

tt

era

w za

zn

ac

zon

ych

pr

�t

ac

h.

2.

0

2.

0

2.

0

3.0

1.0

1.0

5.0

20

KN

Ry

s.1

tg

�

= 0.5

sin

� = 0.4472 c

os

�

= 0

.8

944

tg

�

=

1.5

s

in

� = 0.8320 cos

� =

0

.5

547

tg

�

=

2.

5 si

n

� =

0.9

285

cos

� = 0.37

14

____________________________________________________________________________________________________________________________

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

1/11

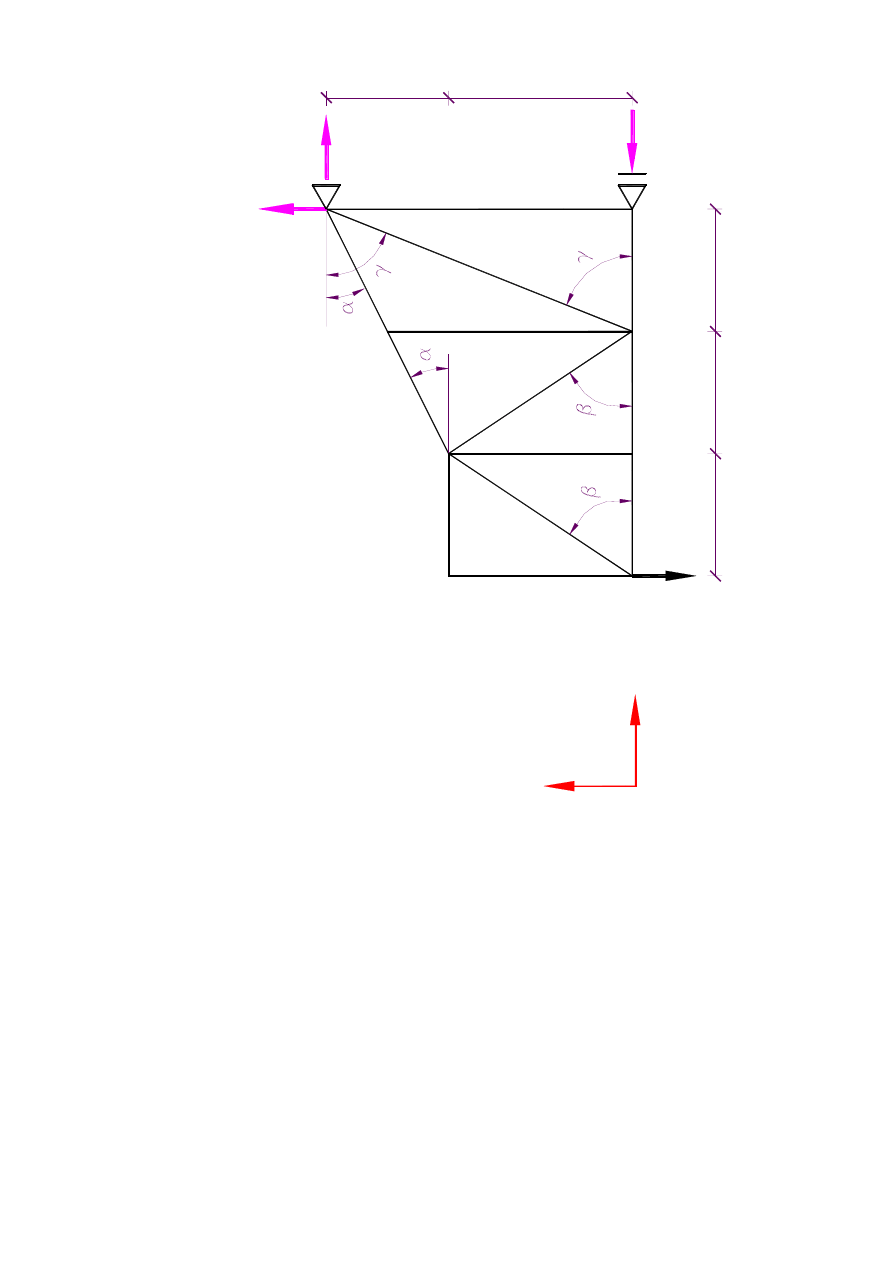
1.

Wy

zn

ac

ze

ni

e

re

ak

cji

–

R

ys

.2

Z

azn

acz

am

y w

�z

�y

kr

atownicy

: A

, B,

C,

D,

E, F, G, H.

Usuwa

m

y

my

�lo

wo po

dpo

ry, z

ast

�p

uj

em

y i

ch

d

zi

a�

ani

e posz

uki

wanym

i

re

ak

cj

am

i

p

rz

yj

m

uj

�c

d

owo

ln

ie

ic

h

zwr

oty

.

U

k�

ad

aj

�c

ró

wna

nia

ró

wn

owag

i

przy

jm

uje

si

�

zwy

kle

jak

o

dod

at

nie

s

i�y

pozi

om

e

zwróc

one

w

prawo

,

si

�y

pi

on

ow

e

zw

róc

on

e

w

gó

r�

,

a

m

om

en

ty

si

�

zw

róc

one

zgo

dni

e z

ruc

he

m

wsk

az

ówe

k

ze

ga

ra

.

Je

�e

li

p

rz

yj

�t

y

zwr

ot

r

ea

kc

ji

j

est

z

god

ny

z

rzeczywis

tym

, to

w

wyniku

ob

licze

�

ot

rz

ym

uj

em

y

do

da

tn

i�

w

art

o�

�

te

j

si

�y

. J

e�

el

i

przyj

�t

y

zw

ro

t

re

ak

cj

i

je

st

ni

ezgo

dn

y

z

rz

ecz

ywi

st

ym

, to w

wy

ni

ku

ob

li

cz

e�

o

trz

ym

uj

em

y u

jem

n�

wa

rto

��

te

j s

i�

y.

Ust

awia

m

y

odp

ow

ie

dni

e

tr

zy

równ

an

ia

ró

wno

wa

gi

z

któr

yc

h

wy

zna

cz

am

y ni

ewi

ado

m

e r

ea

kc

je

:

1.

�

Z = 0 –

20 + V

A

=

0

st

�d

:

V

A

=

2

0 K

N

2.

�

M

A

= 0

–20

•

6

+ R

B

• 5 =

0

st

�d

:

R

B

= 2

4 KN

3.

�

X

=

0

–

R

B

+

H

A

=

0

st

�d

:

R

B

=

H

A

=

2

4 K

N

Sp

ra

wdz

en

ie

:

�

M

E

= 0

H

A

• 5 – V

A

• 6 = 0

20 KN

2.

0

E

D

F

G

2.

0

C

2.

0

3.0

H

2.0

V

A

=20 KN

A

H

A

=

24

KN

B

R

B

=

24

KN

Ry

s.2

X

Z

____________________________________________________________________________________________________________________________

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

2/11

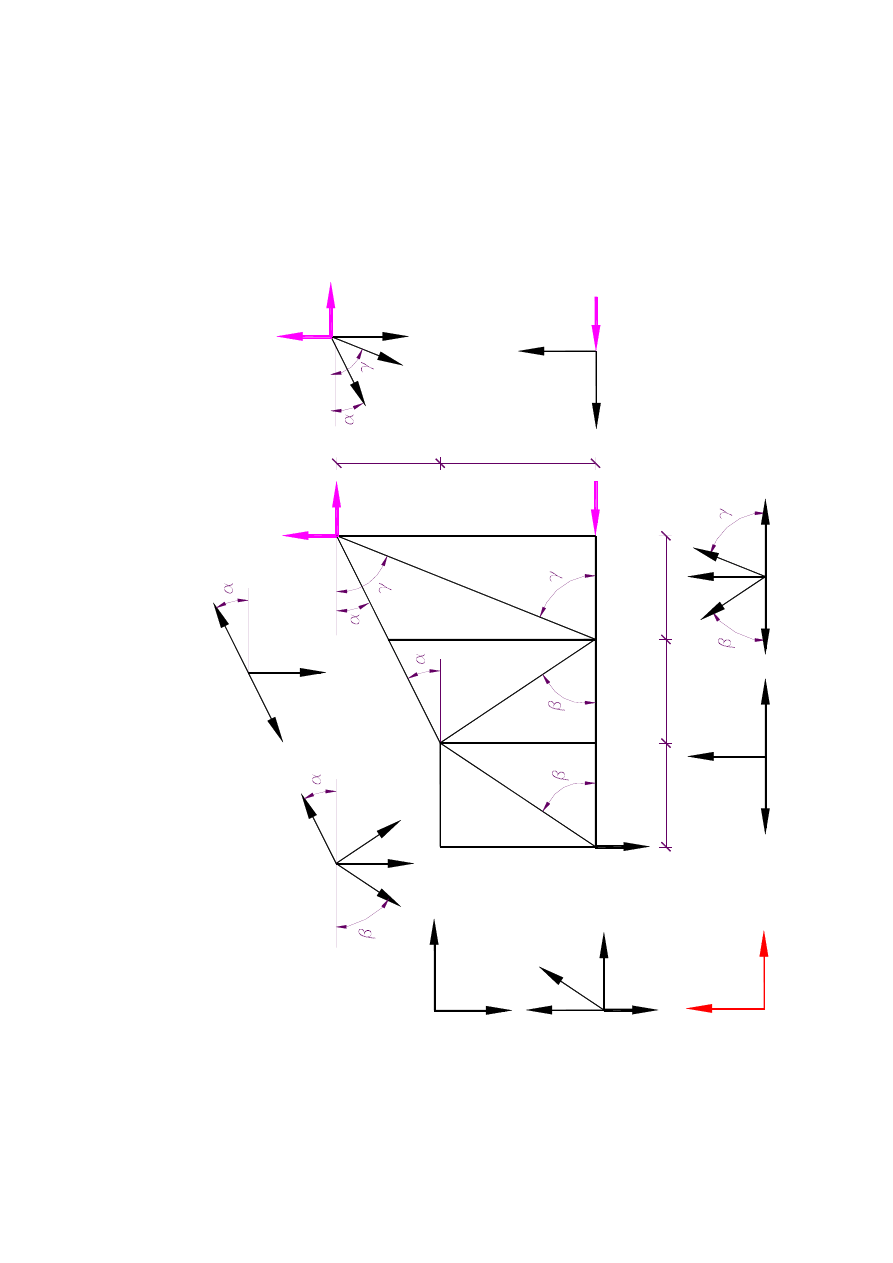
2.

Meto

da an

alityc

znego

rów

now

a�

en

ia

w

�z

�ów

kratownicy.

W

yc

in

am

y

m

y�

lo

wo

p

os

zc

zeg

ól

ne

w

�z

�y

A

,

B

,

C

,

D

,

E,

F

,

G

,

H

–

Ry

s.3

.

Na

rys

unk

ach

wyc

i�

ty

ch

w

�z

�ów

,

zwro

ty

si

�

w

p

r�

tach

odpo

wiad

aj

�

ro

zc

i�

gan

iu

. Ob

liczanie

warto

�c

i

si

�

w

p

r�

tach

roz

poczyn

am

y

od

w

�z

�a

w

k

tó

ry

m

z

bi

ega

j�

s

i�

ty

lko

dw

a

pr

�ty,

w

naszy

m

zada

niu

jest

to

w

�z

e�

B

i

F

,

a

na

st

�pn

ie

prz

ech

od

zim

y

do

w

�z

�a

,

w

k

tó

ry

m

b

�d

�

tylko

dwie

niez

nane

si

�y.

Usta

wiam

y

dwa

równani

a

równowa

gi:

�

X

=

0

i

�

Z

=

0.

Pr

zyj

m

uj

em

y z

nak

ow

ani

e:

pr

�t

r

oz

ci

�ga

ny

- w

ar

to

��

si

�y w

p

r�

ci

e m

a

zna

k d

od

at

ni

,

pr

�t

�

ci

sk

an

y

-

w

ar

to

��

s

i�

y w

p

r�

ci

e

m

a

zn

ak

uje

mny

.

20

K

N

2.0

2.

0

2.

0

3.0

24

K

N

24 KN

20 KN

2.0

24

KN

20

KN

24

KN

20

KN

A

B

F

H

C

D

E

G

F

G

H

A

B

C

D

E

Ry

s.3

X

Z

____________________________________________________________________________________________________________________________

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

3/11

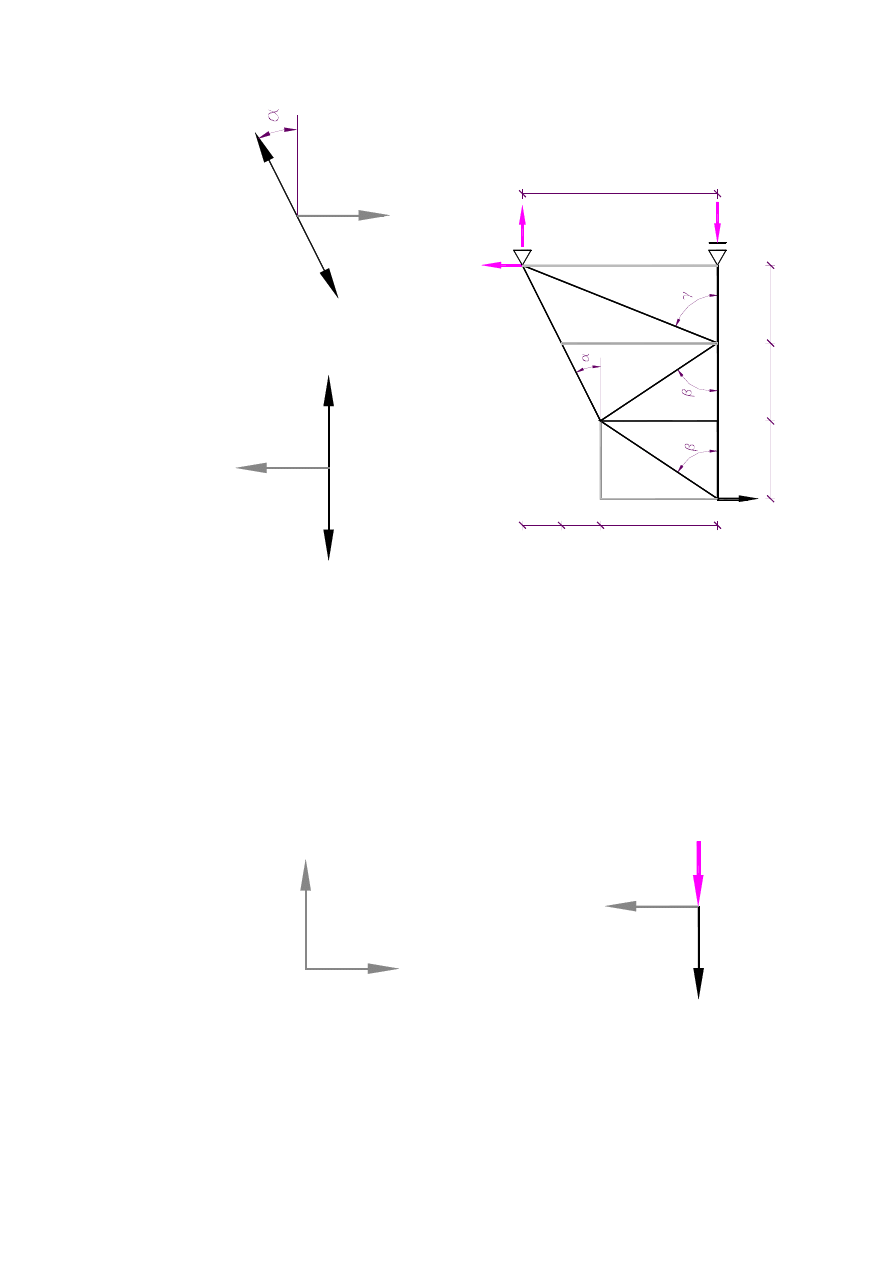
2.

1.

Wyzn

aczeni

e

pr

�tów

zerow

ych

–

R

ys

.4

,

Ry

s.

5

,

R

ys

.6

,

R

ys

.7

.

Ni

ektór

e pr

�ty pr

zy ok

re

�lo

ny

m

ob

ci

��

eni

u k

ra

to

w

ni

cy n

ie

p

ra

cu

j�

. W

ar

to

�c

i s

i�

w t

yc

h p

r�

ta

ch

s

�

rów

ne

zeru

i dlatego

naz

w

ano

je

pr

�t

am

i z

er

ow

ym

i.

Pr

ze

d p

rz

ys

t�

pi

eni

em

d

o o

bl

ic

ze

ni

a k

ra

tow

ni

cy

, wsk

az

an

e

jest

wys

zu

ka

ni

e

pr

�tów zerowych, co zna

cznie u

�atw

i wy

zna

czan

ie s

i�

w

p

r�

ta

ch.

P

r�

ty z

erowe s

�

oz

na

cz

one

k

ol

ore

m

p

op

ie

la

ty

m

–

Rys.7

1.

Je

�eli w

w

��

le

nie

obc

i��

ony

m

sc

ho

dz

� s

i�

tyl

ko

dwa

pr

�t

y

o

ró

�n

ych

ki

erun

ka

ch

, to

si

�y

w

n

ic

h s

� ró

wn

e z

eru

–

Rys

.4

N

F

G

=

0

F

N

FE

=

0

�

X =

0 ,

�

Z = 0

Rys

.4

2.

Je

�eli

w

w

��

le

s

cho

dz

�

si

�

dwa

pr

�ty

o

ró

�nyc

h

kier

unk

ac

h,

a

w

�z

e�

jes

t

ob

ci

��

on

y

si

��

o

kier

un

ku

pok

ryw

aj

�cy

m

si

�

z

ki

eru

nk

iem

j

edn

ego

z pr

�t

ów,

to

drugi

pr

�t je

st pr

�t

em

z

er

ow

ym

. –

R

ys.

5

B

24

KN

N

B

A

=

0

N

BC

�

X

=

0

N

B

C

=

–

24 KN

Rys

.5

3.

Je

�e

li

w

w

��

le

ni

eo

bc

i��

onym

scho

dz

�

si

�

tr

zy

pr

�t

y,

z

kt

ór

yc

h

dw

a

le

��

na

jedn

ej

proste

j,

to

trz

eci

pr

�t

j

es

t p

r�

te

m

z

er

ow

ym

. –

Ry

s.6

H

N

H

A

N

H

G

N

H

C

=

0

D

N

D

E

N

D

C

N

D

G

=

0

N

D

E

=

N

D

C

N

H

G

= N

H

A

Rys.6

20

KN

3.0

1.0

1.0

2.

0

2.

0

2.0

R

B

=

24

KN

B

5.0

V

A

=

20

K

N

H

A

=

24

KN

A

H

G

F

E

D

C

Rys.7

____________________________________________________________________________________________________________________________

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

4/11

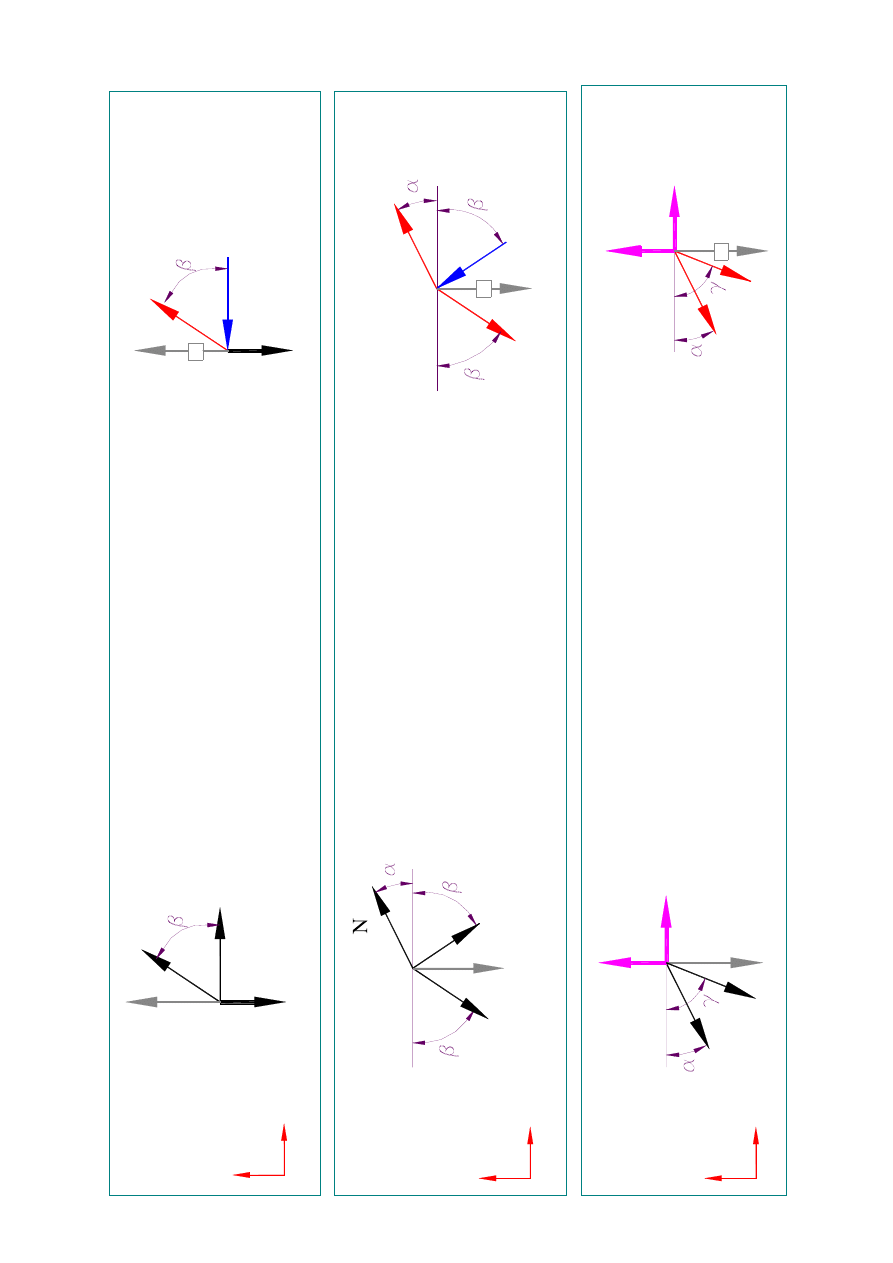
2.

2.

Wyzn

aczeni

e

w

arto

�c

i s

i�

w

p

ozos

ta

�y

ch

pr

�t

ach

krat

own

icy

kor

zys

taj

�c

z

r

ów

na

�

ró

wn

ow

ag

i:

�

X = 0 i

�

Z

=

0

W

�z

e�

E

20

K

N

E

N

ED

N

EF

N

EG

Rys

.8

1.

�

X =

0

N

E

D

+

N

E

G

• c

os

� = 0

2.

�

Z = 0

–20 + N

E

G

• si

n

� = 0

N

E

D

=

– 13

.3

33

N

E

G

=

24

.0

37

N

EG

= 24

.037

20 K

N

E

N

ED

=

13

.3

33

0

Rys.9

X

Z

X

Z

24

.0

37

X

Z

W

�z

e�

G

G

G

H

N

G

C

N

G

D

N

G

E

=

Rys

.10

N

E

G

=

N

GE

=

24.037

1.

�

X =

0

–

24.037

• c

os

� +

N

G

C

• c

os

�

+

N

G

H

• c

os

� = 0

2.

�

Z = 0

–

24.037

•

si

n

� – N

G

C

• s

in

�

+

N

G

H

• si

n

� = 0

N

G

C

=

– 12

.0

18

N

G

H

=

22

.3

62

N

G

H

=

22.

36

2

G

N

G

E

=

2

4.

03

7

N

G

C

=

1

2.

01

8

0

Rys

.11

W

�z

e�

A

24 KN

20

K

N

A

N

A

B

N

A

C

N

A

H

Rys

.12

1.

�

X =

0

– N

A

H

• c

os

� – N

A

C

• c

os

�

+ 2

4 =

0

2.

�

Z = 0

– N

A

H

• si

n

� – N

A

C

• si

n

�

+

20

= 0

N

A

C

=

10

,7

7

N

A

H

=

22

.3

62

20

KN

24

KN

N

A

C

=

10

.77

N

A

H

=

22.

36

2

A

0

Rys

.13

____________________________________________________________________________________________________________________________

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

5/11

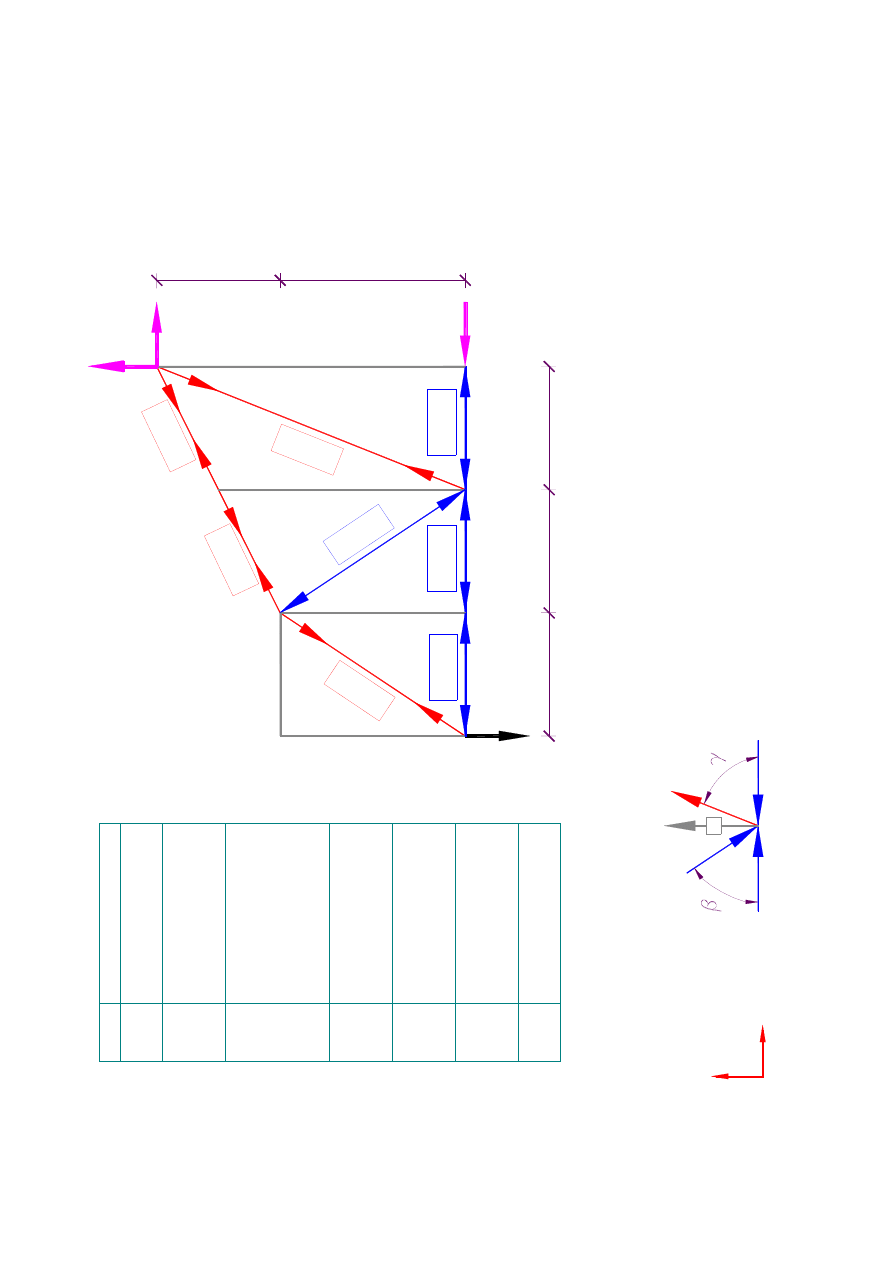
Obl

ic

zo

ne

wa

rt

o�

ci

s

i�

w

p

r�

ta

ch zest

awiam

y w tabe

lce

i na poni

�szy

m

ry

sunk

u –

Rys

.14

W

�z

e�

W

ar

to

�c

i s

i�

y w

p

r�

ci

e

F

N

FG

= 0

N

F

E

= 0

E

N

E

F

= 0

N

E

G

=

24

.0

37

N

E

D

=

-

13

.3

33

G

N

G

E

=

24

.0

37

N

GF

= 0

N

G

H

=

22

.3

62

N

G

C

= -

12

.01

8

N

GD

= 0

D

N

D

E

=

-

13

.33

3

N

D

G

= 0

N

DC

= -

13

.33

3

H

N

H

G

=

22

.3

62

N

H

A

=

22

.3

62

N

H

C

= 0

A

N

AH

=

22

.3

62

N

A

B

= 0

N

AC

= 10

.77

B

N

B

A

= 0

N

B

C

= -

24

.00

-2

4.

00

20 KN

C

D

20

K

N

2.0

2.

0

2.0

E

22

.3

6

-1

3.

33

24

.04

-1

3.

33

F

G

-12

.02

10.

77

H

22

.3

6

B

24 KN

3.0

A

24

K

N

2.0

Rys

.14

Sprawdz

enie

poprawno

�c

i ob

li

cz

e�

–

Rys

.15

:

W

w

��

le C

zb

ie

ga

j�

si

�

pr

�ty w

który

ch obliczo

ne s

� wsz

ys

tk

ie

wa

rto

�c

i s

i�

. Z

d

w

óc

h ró

w

na

� równ

owa

gi s

pra

wdza

m

y p

opr

awno

��

o

bl

ic

ze

�.

____________________________________________________________________________________________________________________________

W

�z

e�

C

N

C

A

=10.77

N

C

D

=13.333

C

N

C

G

=

12

.01

8

N

C

B

=24.00

0

Rys

.15

1.

�

X =

0

13.

333 + 1

2.018

• c

os

� + 1

0.7

7

• c

os

� – 2

4 = 0

2.

�

Z = 0

–

12

.01

8•

s

in

�

+ 1

0.7

7

• s

in

� =

0

X

Z

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

6/11

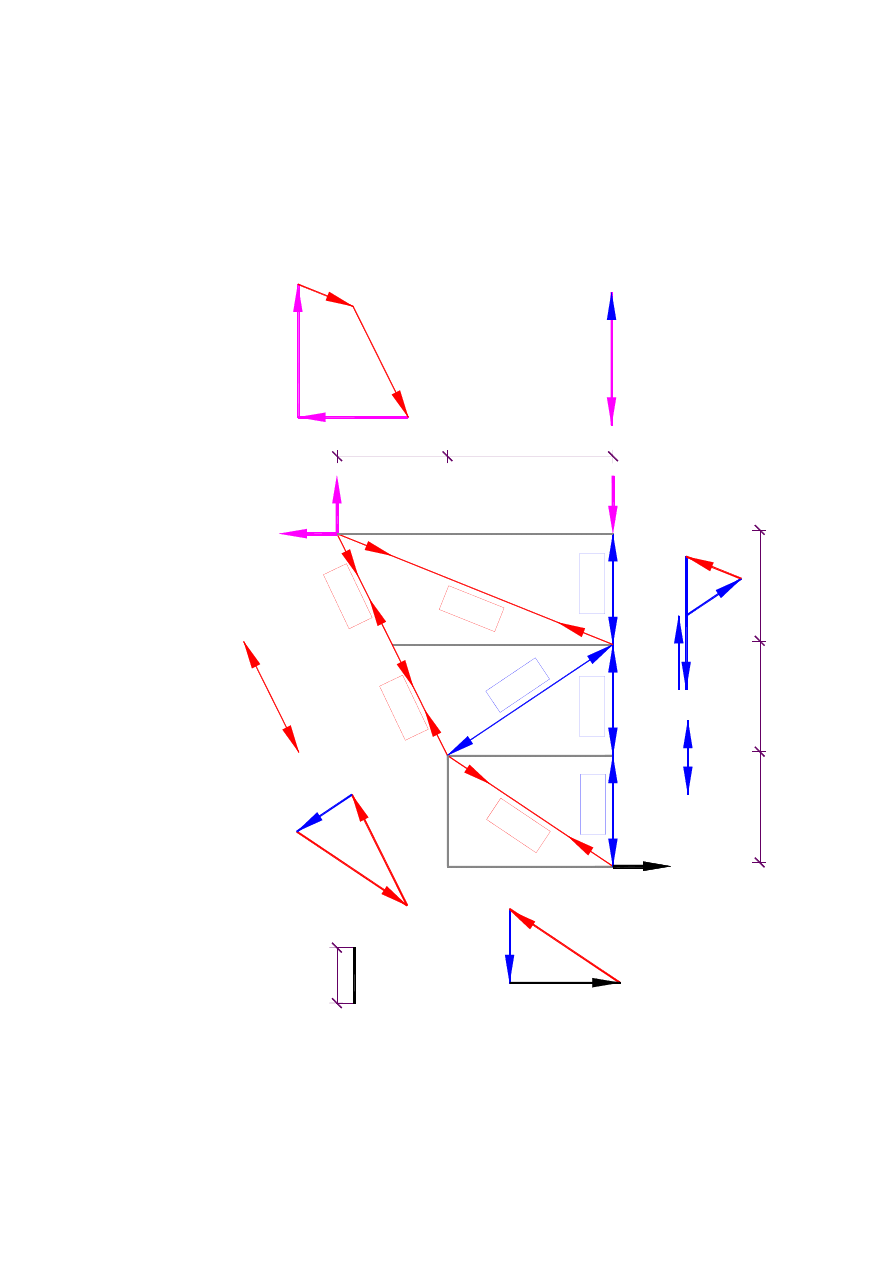
3. M

etoda gr

aficzneg

o rów

nowa

�e

nia

w

�z

�ów

kratown

icy

–

R

ys

.1

6

.

Met

oda

gra

fic

zne

go

równowa

�e

ni

a

w

�z

�ów

kratownic

y

jest

odpow

iednikiem

m

eto

dy

a

nal

it

ycz

ne

go

ró

wn

owa

�e

ni

a w

�z

�ó

w

.

Gra

ficz

ny wa

rune

k równo

wagi

si

� w dowolnym

w

��

le kratown

ic

y j

es

t spe

�ni

ony

, g

dy w

iel

obo

k s

i�

dzia

�a

j�

cyc

h na

ten w

�z

e�

jes

t zamkn

i�

ty

.

Sporz

�d

za

j�

c

w

od

powie

dnie

j

ska

li

wiel

oboki

si

�

kol

ejn

o

dla

k

a�

dego

z

wyci

�t

yc

h

w

�z

�ów,

okre

�l

am

y

si

�y

we

wsz

yst

ki

ch

pr

�t

ac

h

kr

at

ow

ni

cy

.

Z

ac

zyn

am

y

ry

so

wa

� wielobok si

� o

d

w

�z

�a

gdzie

zbiegaj

� s

i�

d

w

a

pr

�ty

.

A

E

20

K

N

2.

0

D

2.

0

2.0

C

F

G

H

24

K

N

B

3.0

24

K

N

2.0

20

K

N

A

-12

.02

-1

3.

33

-1

3.

33

-2

4.

00

22.

36

10.

77

24

.04

22.

36

22

.36

22.

36

10.

77

24

.0

0

20.00

20.00

24

.04

13

.3

3

E

G

24

.04

12

.02

12

.02

13

.3

3

C

24

.0

0

sk

al

a

si

�

10

K

N

H

22

.36

13

.3

3

D

24

.0

0

24

.0

0

B

Rys

.16

____________________________________________________________________________________________________________________________

htt

p://

riad.usk.

pk.edu.p

l/~iwro

blew/dy

daktyka

7/11