f + s = n + 1

suma maksymalnej liczby faz f , jakie mog wspó

ł

istnie w stanie równowagi,

oraz liczby stopni swobody s jest równa liczbie sk

ł

adników n plus jeden (izobaryczne).

Wykresy równowagi fazowej

Reguła faz Gibbsa

o budowie fazowej stopów (jakie i ile faz współistnieje) w stanie równowagi decyduj trzy

parametry: temperatura, ci nienie oraz st enie poszczególnych składników (skład chemiczny),

- ograniczamy si do układów (stopów) dwuskładnikowych oraz warunków izobarycznych,

s = n – f + 1

lub

f

max

= n + 1

gdy:

s = 0

układ – zbiór faz w stanie stałym, ciekłym lub gazowym zajmuj cy, przy okre lonej temperaturze

i ci nieniu, stał obj to ,

stopnie swobody (s) – liczba parametrów okre laj cych stan termodynamiczny układu (temperatura,

ci nienie, st enie składników), które niezale nie mog ulec zmianie nie wytr caj c

układu ze stanu równowagi,

układ jest niezmienny, gdy współistnieje ze sob maksymalna liczba faz (s = 0)

(zmiana dowolnego parametru bez zmniejszenia liczby faz wytr ci układ ze stanu równowagi)

(+)

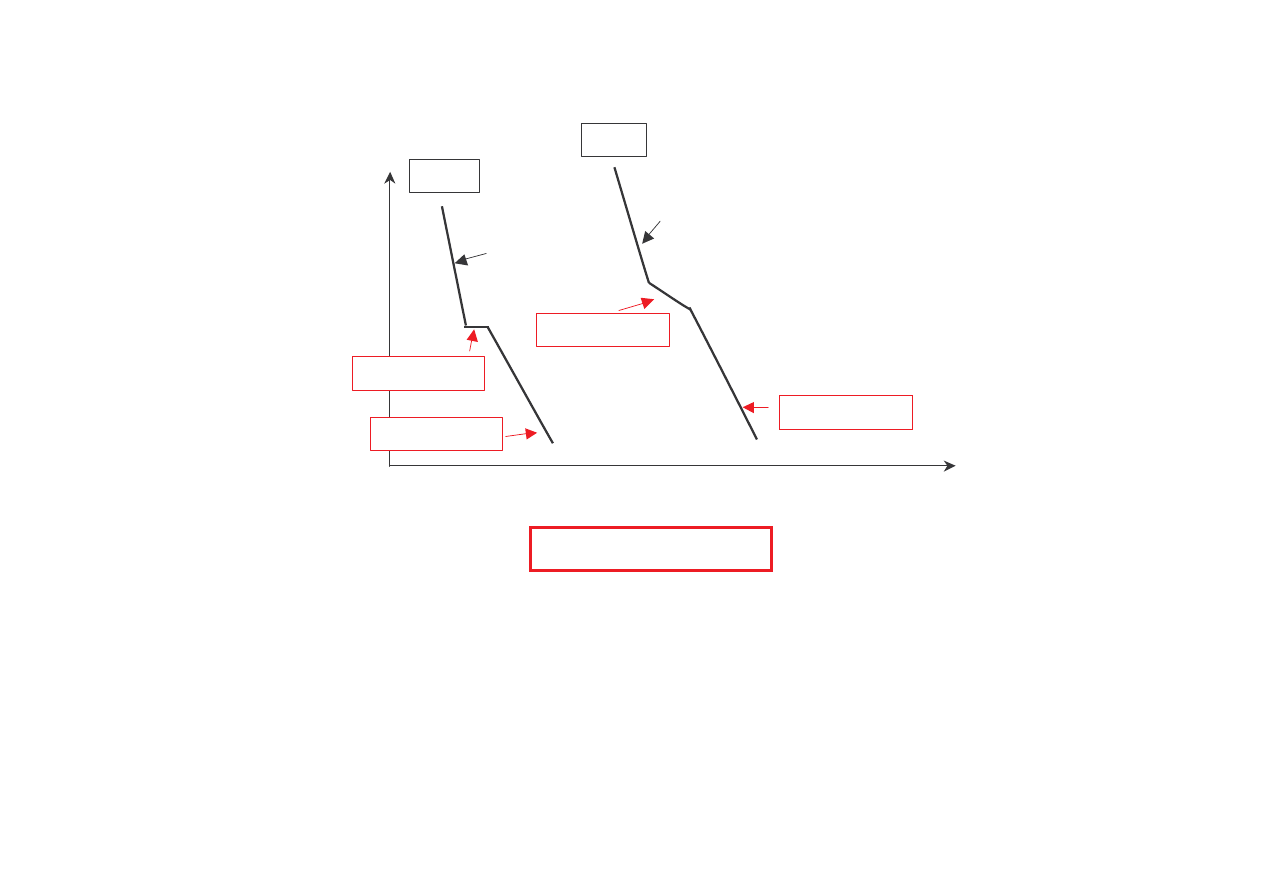
Krzywe chłodzenia dla czystego pierwiastka A oraz stopu dwuskładnikowego A-B

Czas

Te

m

pe

ra

tu

ra

stop pierwiastków A i B

pierwiastek A

T

tA

T

L

T

S

f = 1

s = 1

f = 2

s = 0

f = 2

s = 1

n = 1

n = 2

s = - f + n + 1

f = 2

s = 2

(za B. Ku nick )

••••

dla uk

ł

adu dwusk

ł

adnikowego:

- gdy w stanie równowagi

f = 1

s = 2

(temperatura i st enie mog ulega zmianie)

- gdy w stanie równowagi

f = 2

s = 1

(temperatura lub st enie mo e ulega zmianie)

- gdy w stanie równowagi

f = 3

s = 0

(temperatura = const, st enie = const)

- stan równowagi w przypadku

f > 3

jest niemo liwy.

(+)

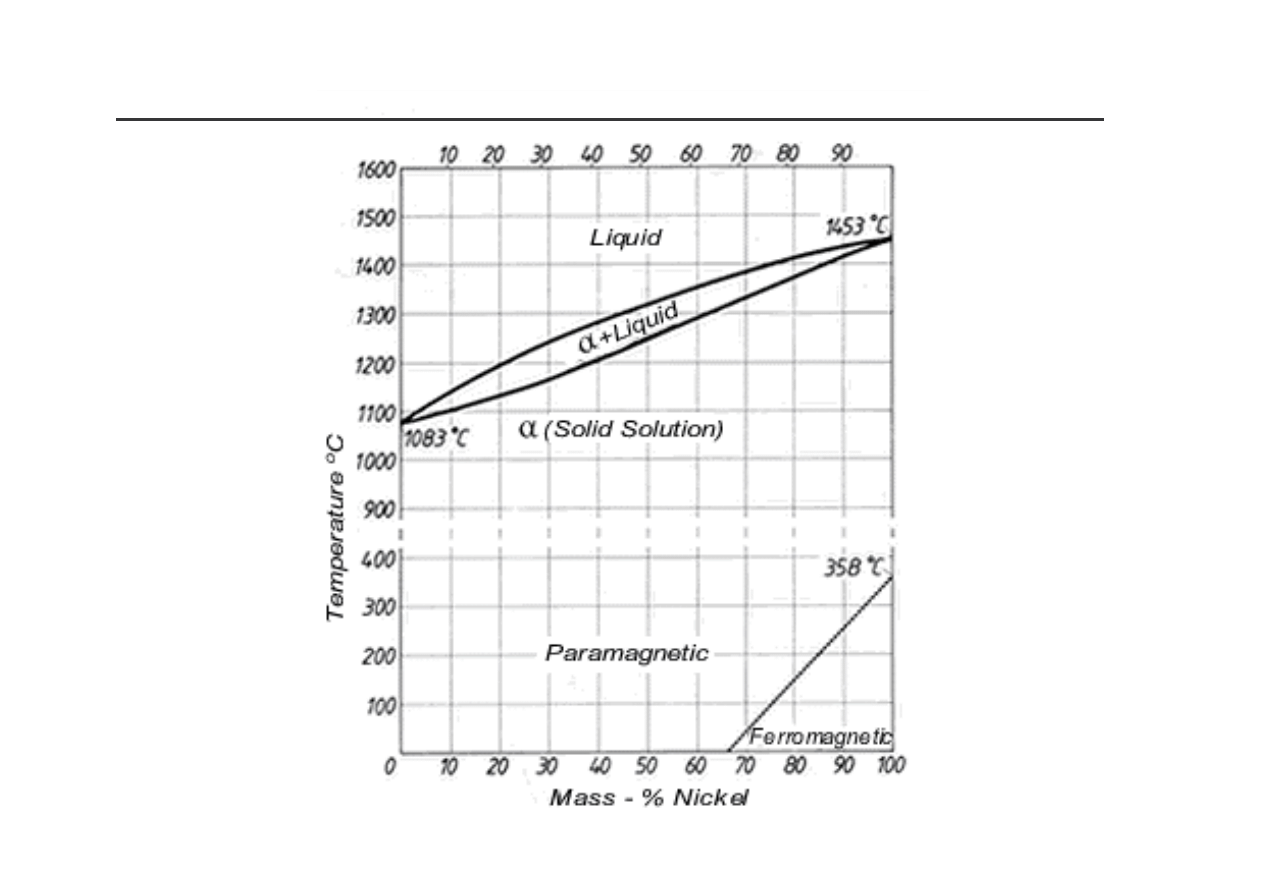
Wykres równowagi fazowej układu dwuskładnikowego:

całkowita rozpuszczalno

składników w stanie ciekłym oraz w stanie stałym

(

L

)

αααα

- roztwór stały ci gły

Cu

Ni

przykładowo:

układ Cu-Ni

(www.copper.org/applications/cuni/txt_DKI.html)

(+-)

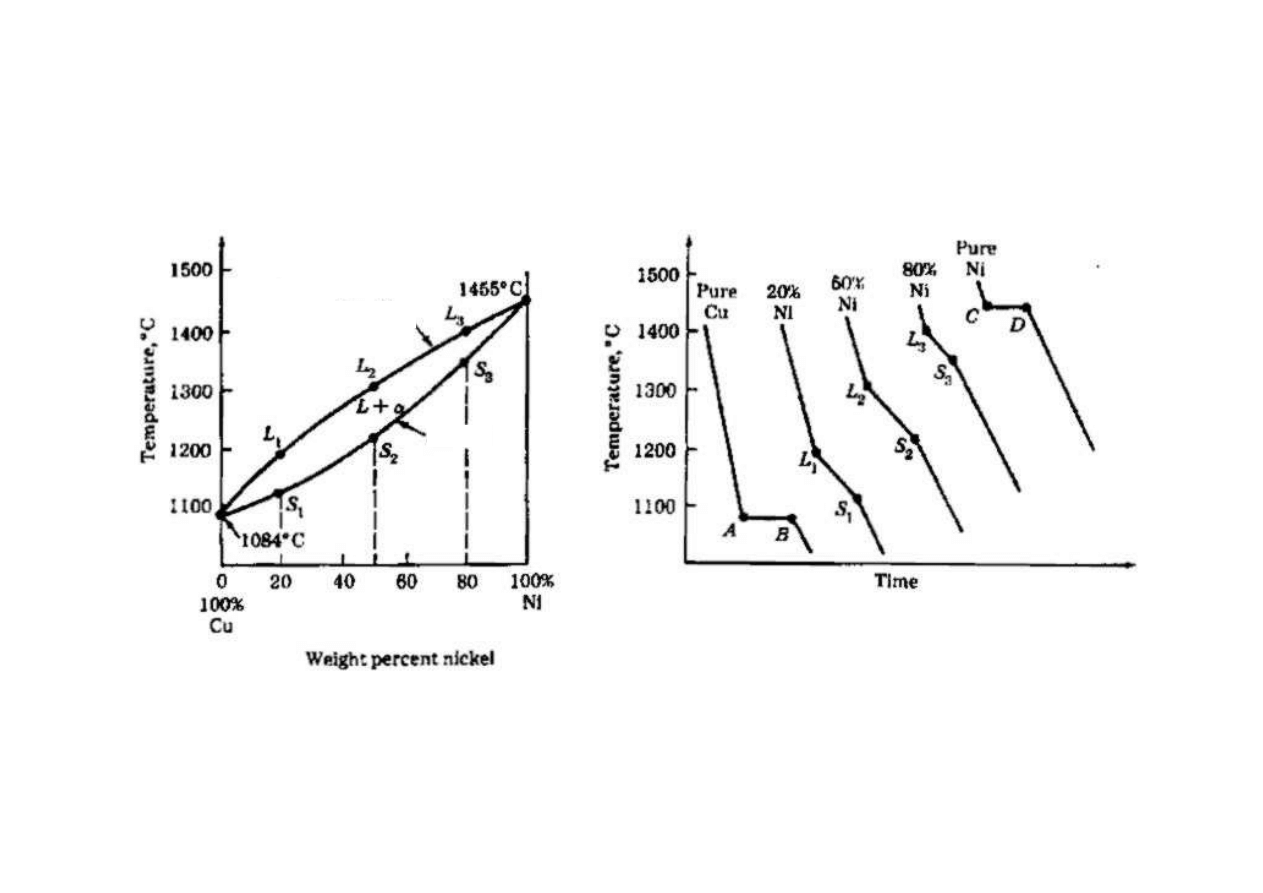
Otrzymywanie wykresu na podstawie krzywych chłodzenia

αααα

L

likwidus

solidus

(www.ce.berkeley.edu/~paulmont/CE60/alloys/sld005.htm)

(+-)

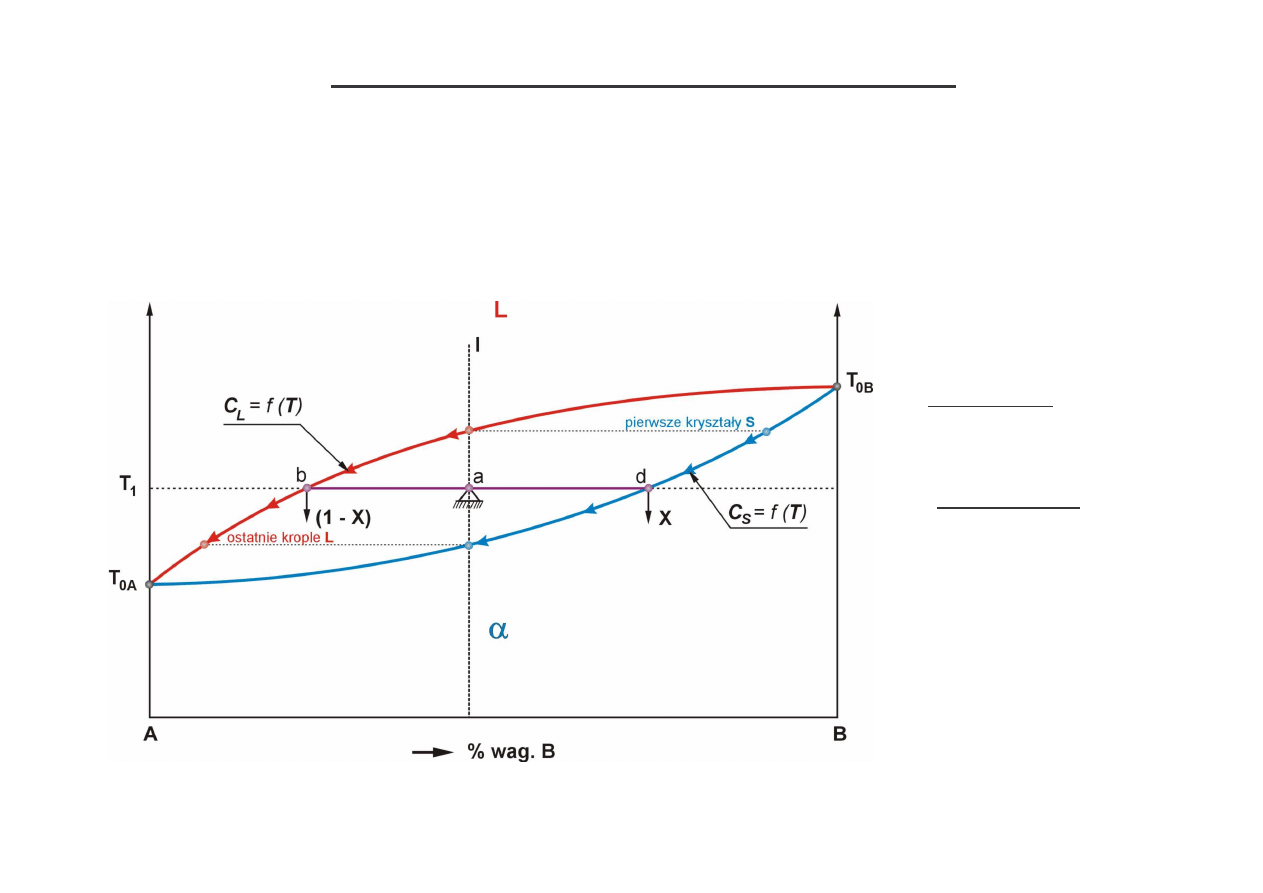
Wła ciwo ci konody – stwierdzenia reguły d wigni

konoda

– odcinek izotermy (bd) zawarty w obszarze dwufazowym,

1) ko ce konody wskazuj jakie fazy współistniej oraz jaki jest ich skład chemiczny,

2) rozpatrywany stop dzieli konod na odcinki proporcjonalne do udziału faz w stopie,

traktuj c konod jak mechaniczn d wigni podpart st eniem naszego stopu:

X – udział fazy stałej (

αααα

), (1 – X) – udział fazy ciekłej (L), gdzie „1”- ci ar całego stopu,

równanie momentów (udziały traktujemy jak siły): X · ad = (1 – X) · ab

X = ab/bd

oraz

wi c:

(1 – X) = ad/bd

udział fazy

αααα

:

%

αααα

= (c

a

– c

b

)/(c

d

– c

b

) · 100%

udział cieczy L:

%L = (c

d

– c

a

)/(c

d

– c

b

) · 100%

k = c

S

/

c

L

zwykle

<

4

równowagowy współczynnik segregacji:

dla stopu (I) w temp. T

1

:

(+!)

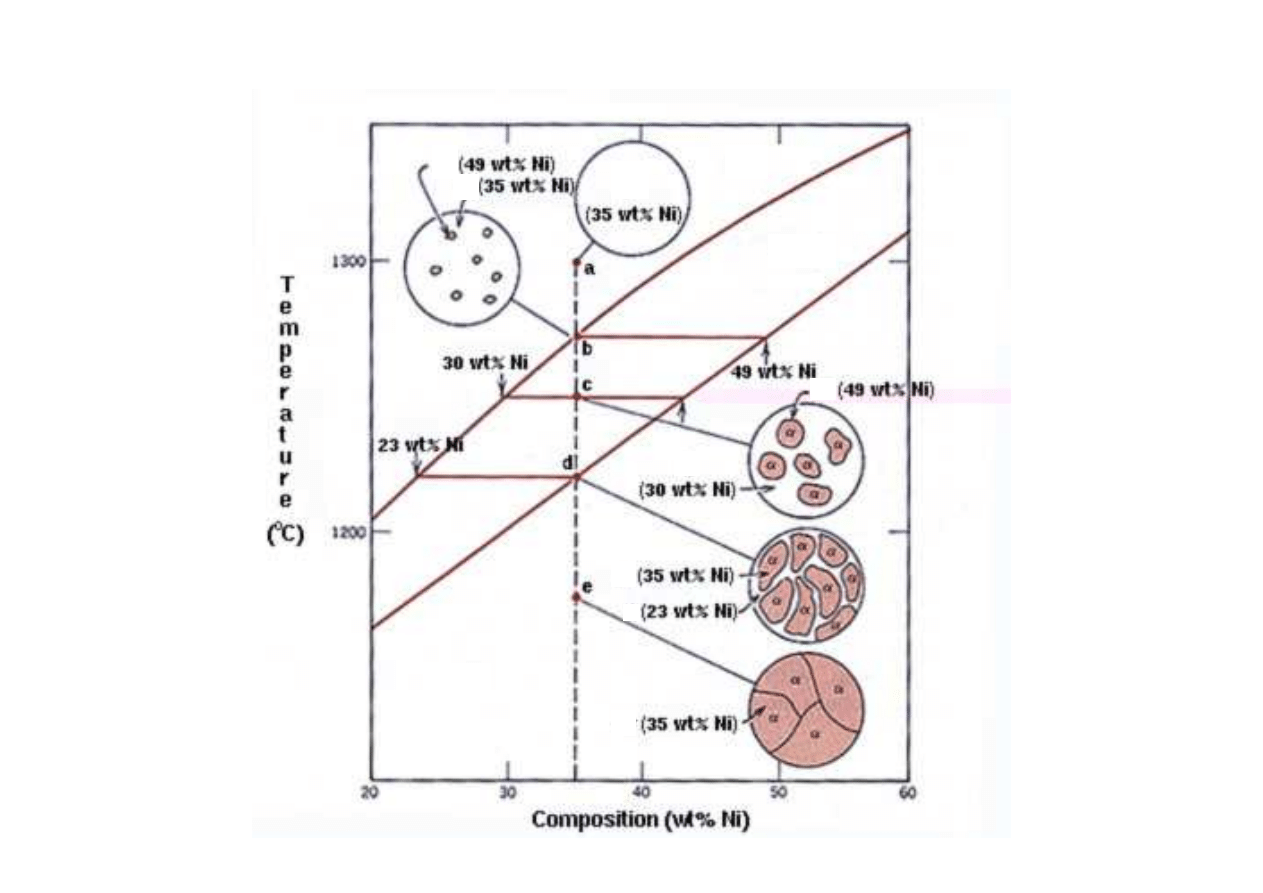
Kolejne fazy krzepni cia przykładowego stopu

(www.sv.vt.edu/classes/MSE2094)

(+-)

L

L

αααα

+

L

αααα

αααα

L

αααα

L

αααα

L

αααα

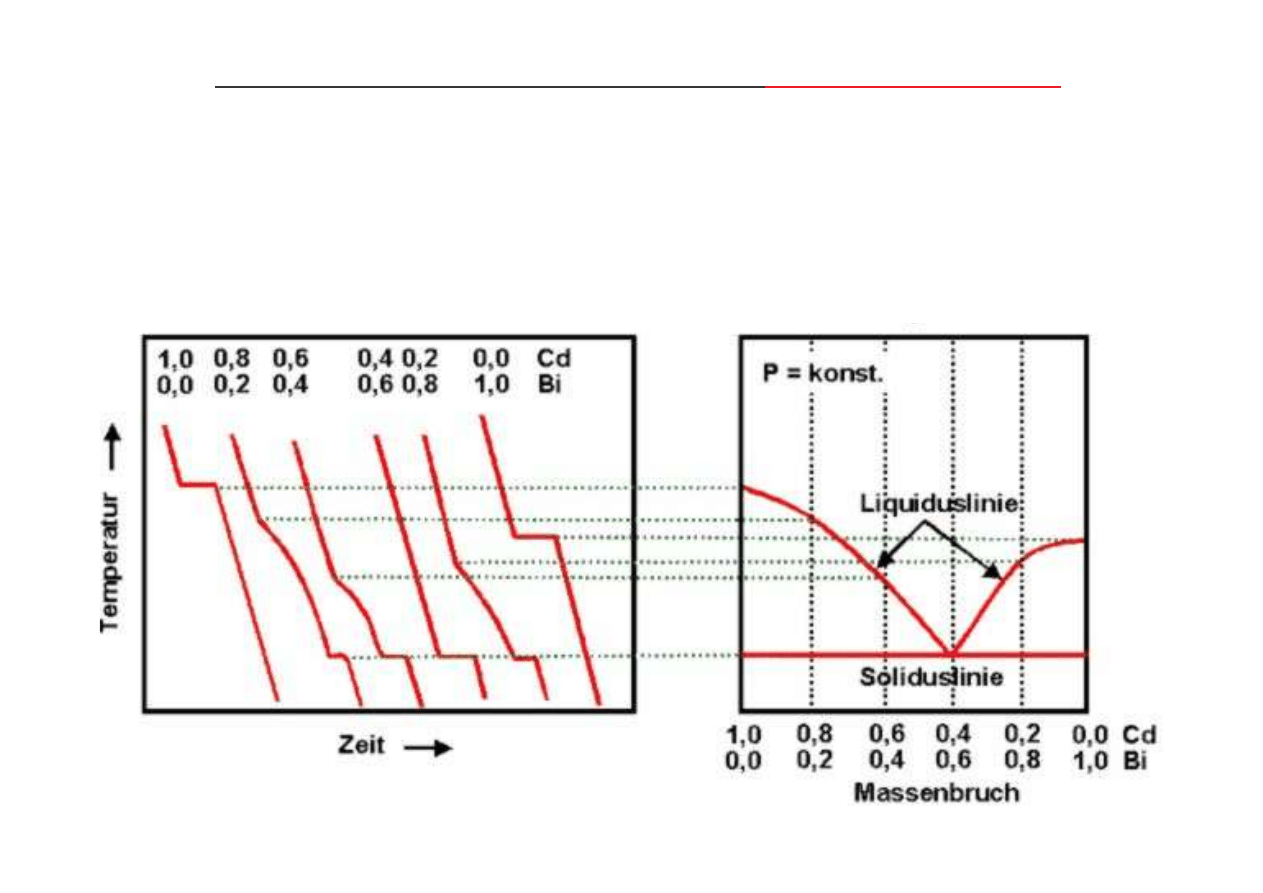
otrzymywanie wykresu fazowego układu Bi-Cd na podstawie krzywych chłodzenia stopów:

Wykres równowagi fazowej z izotermiczn

przemian eutektyczn

składniki układu:

- nie rozpuszczaj si w stanie stałym,

- nie tworz faz po rednich,

- nie s polimorficzne.

(http://ac16.uni-paderborn.de/lehrveranstaltungen/)

krzywe chłodzenia:

wykres fazowy:

(+-)

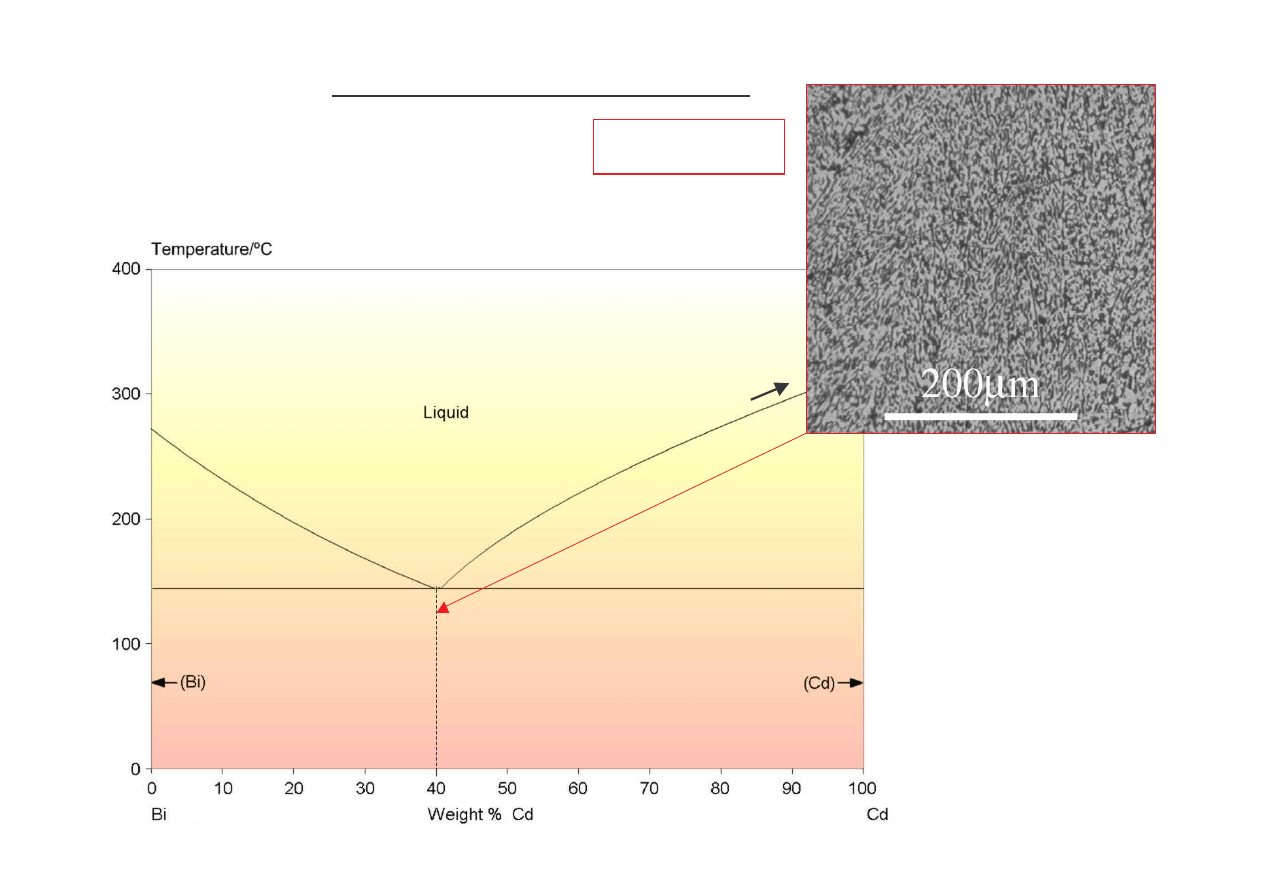
Bi + (Bi + Cd)

(B

i +

C

d)

Cd + (Bi + Cd)

L + Bi

L + Cd

L

Wykres równowagi układu Bi-Cd

271

321

144

Równanie izotermicznej przemiany eutektycznej:

L

E

↔

↔

↔

↔

(Bi + Cd)

E

mikrostruktura eutektyczna

(ciemny Cd, jasny Bi)

(prof. T.W. Clyne)

(www.doitpoms.ac.uk)

(+-)

BiCd40

(eutektyczny)

BiCd20

(przedeutektyczny)

(prof. T.W. Clyne)

(Bi + Cd)

Bi

Cd

Cd

Bi

(+-)

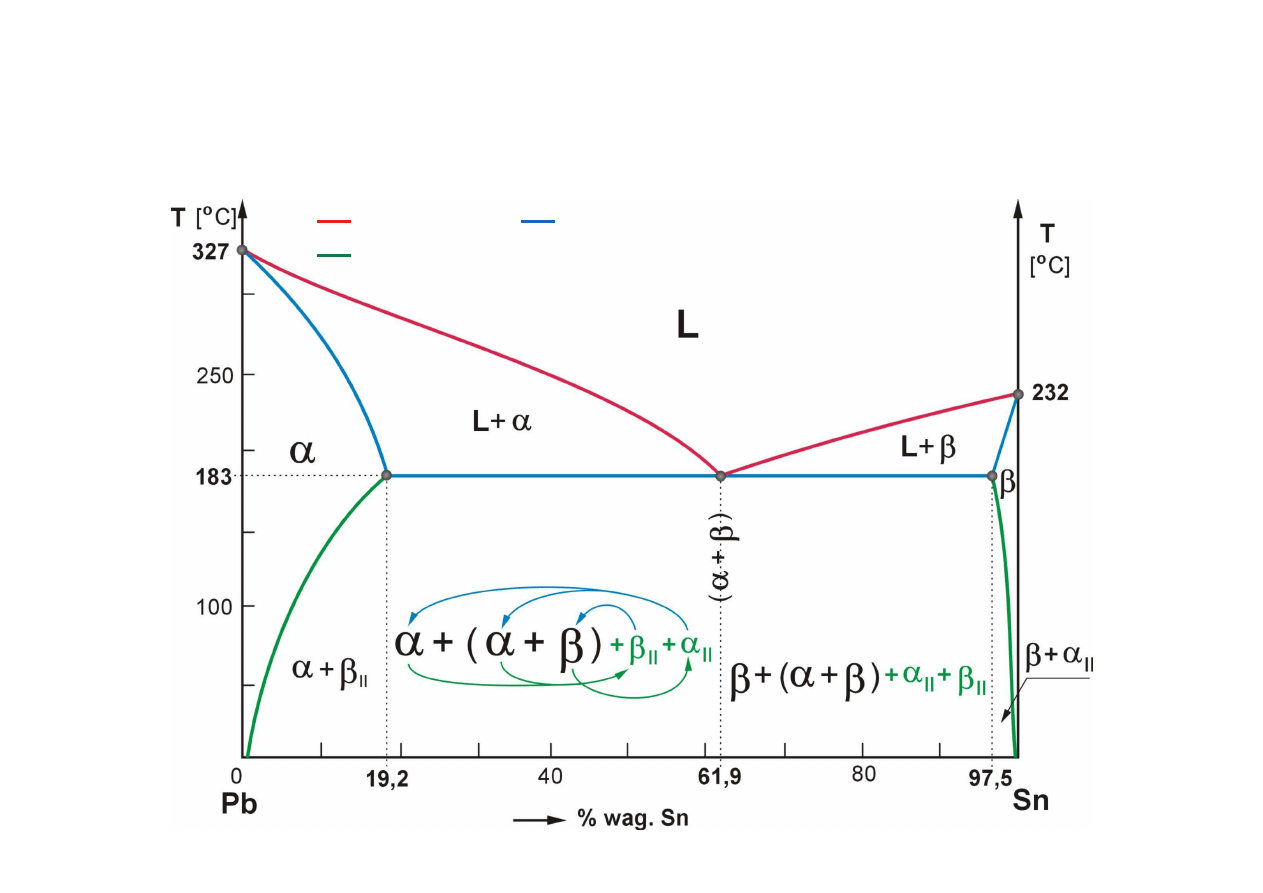
Przykład strukturalnego opisu wykresu równowagi (układ Pb-Sn)

fazy stałe:

αααα

- roztwór stały podstawowy, ró now złowy, graniczny Pb(Sn),

ββββ

- roztwór stały podstawowy, ró now złowy, graniczny Sn(Pb),

linie likwidus,

linie solidus,

linie solwus (linie granicznej rozpuszczalno ci),

C

D

E

F

G

A

B

(+!)

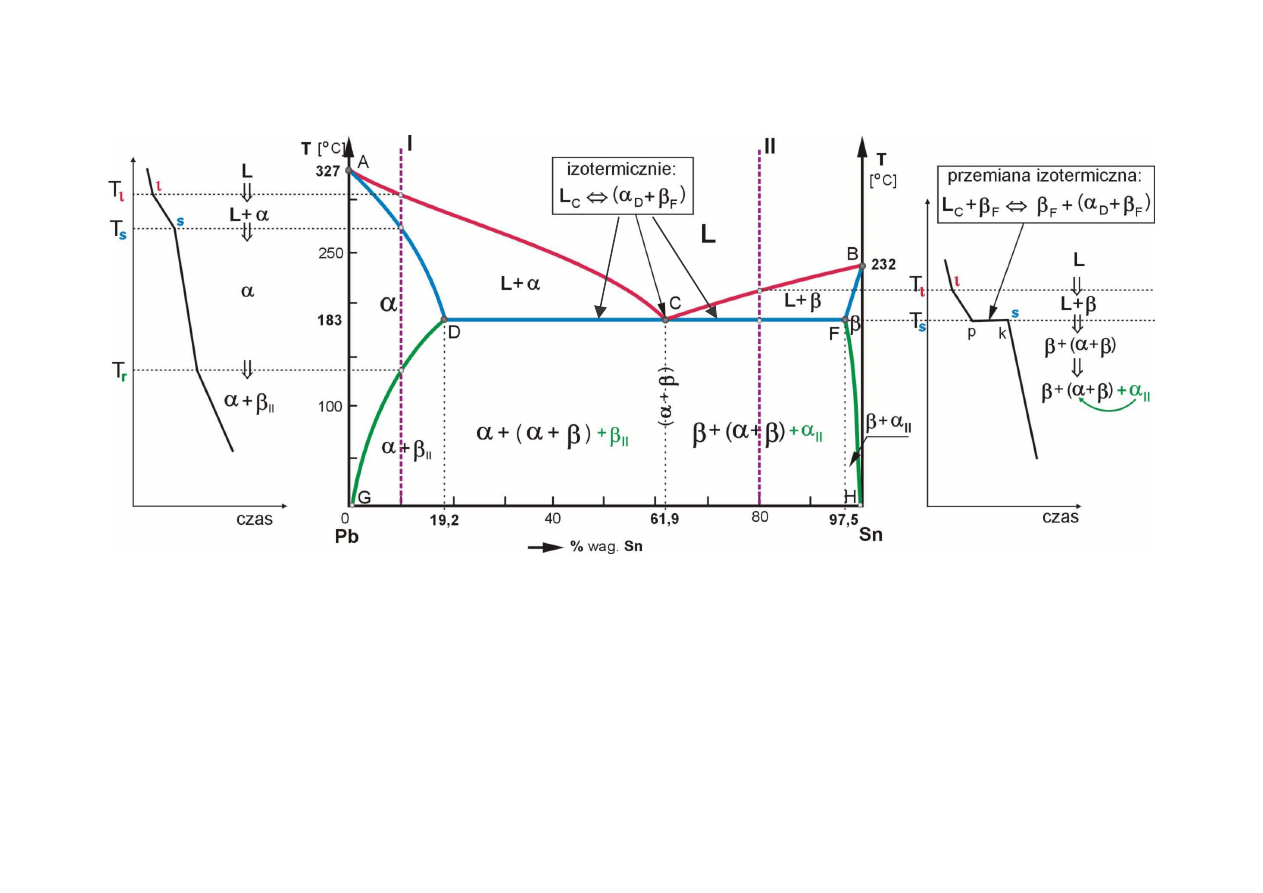
Przykład analizy stopów wykresu równowagi (układ Pb-Sn)

(

αααα

+

ββββ

) – eutektyczna mieszanina faz, krystalizuj ca w stałej temperaturze (s=0) –

składnik struktury

,

αααα

II

,

ββββ

II

-

fazy drugorz dowe

, krystalizuj ce po przekroczeniu linii granicznej rozpuszczalno ci,

- w stopach bez eutektyki jako

faza strukturalnie wolna

(zwykle na granicach ziaren),

- w stopach z eutektyk zwykle nie tworzy nowych osobnych wydziele lecz tylko pogrubia

wydzielenia wcze niej istniej ce,

- wszystkie stopy od D do F ko cz krzepni cie izotermiczn przemian eutektyczn , w której ciecz

(po osi gni ciu st enia punktu C) krzepnie w postaci eutektycznej mieszaniny faz,

(+!)

stop eutektyczny (ok. 38% Sn)

- eutektyka płytkowa (faza

β

ciemniejsza)

stop nadeutektyczny (ok. 60% Sn)

ββββ

(

strukturalnie wolna)

(

αααα

+

ββββ

)

(

αααα

+

ββββ

)

stop ok. 97% Sn; na granicach ziaren fazy

ββββ

(ciemna)

wydzielona faza

αααα

II

(jasna)

αααα

II

ββββ

Struktury wybranych stopów układu Pb-Sn:

(www.scielo.br) – C. S. Kiminamib

(www.sv.vt.edu/classes/MSE2094)

(+-)

stop przedeutektyczny (ok. 25% Sn)

(

αααα

+

ββββ

)

αααα

(

faza strukturalnie wolna)

stop eutektyczny (ok. 38% Sn)

Struktury po bardzo wolnym chłodzeniu

(inna budowa mieszaniny eutektycznej)

(www.scielo.br) – C. S. Kiminamib

(

składnik struktury)

(-+)

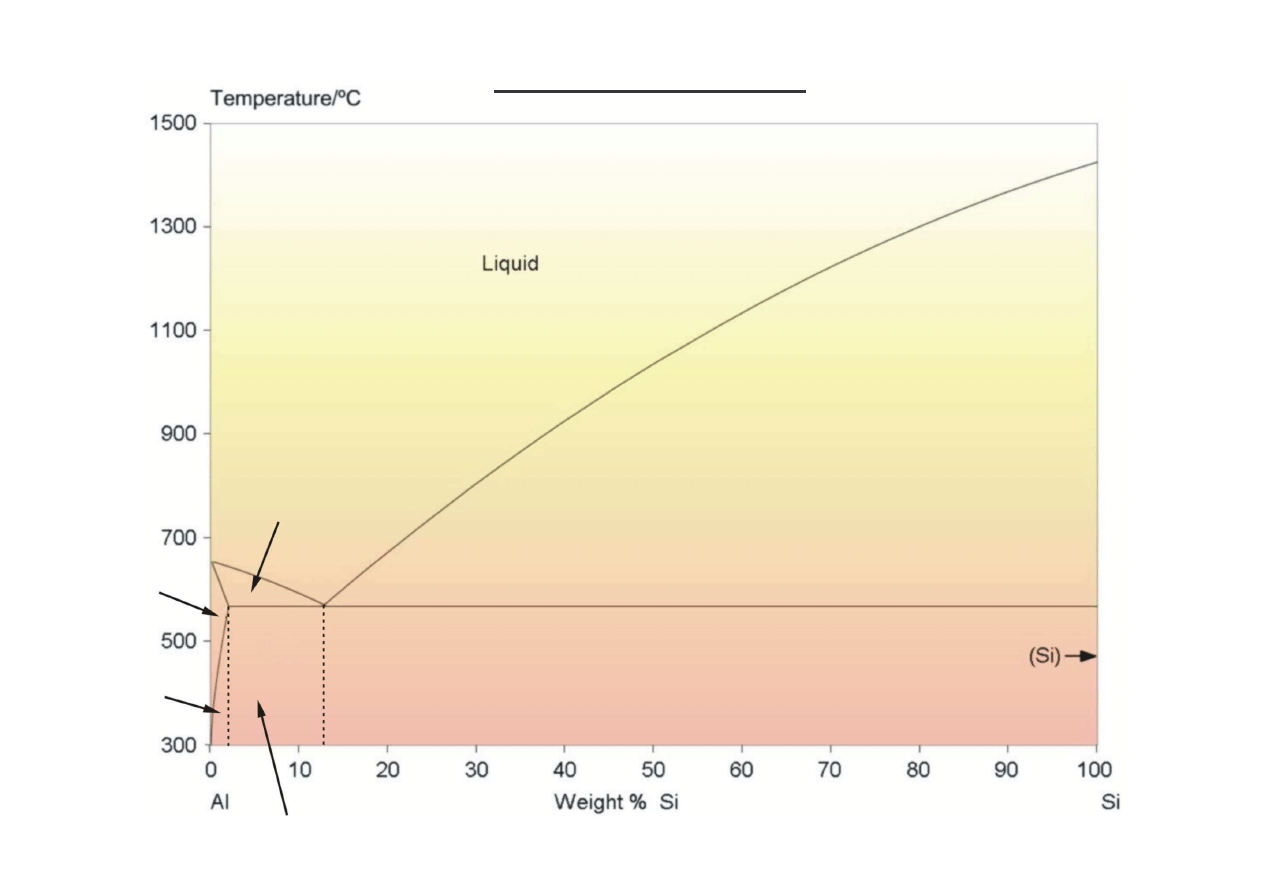
αααα

Si + (

αααα

+ Si)

(

αααα

+

S

i)

αααα

+ (

αααα

+ Si) +

Si

II

αααα

+ L

L

L + Si

αααα

+ Si

II

Wykres równowagi Al-Si

1414

660

577

12,6

1,65

(www.doitpoms.ac.uk)

A

B

C

D

E

(+)

stop eutektyczny niemodyfikowany, (

αααα

+ Si)

stop eutektyczny, nieprawidłowo modyfikowany

stop przedeutektyczny modyfikowany,

αααα

+ (

αααα

+ Si)

stop zaeutektyczny niemodyfikowany, Si + (

αααα

+ Si)

(-+)

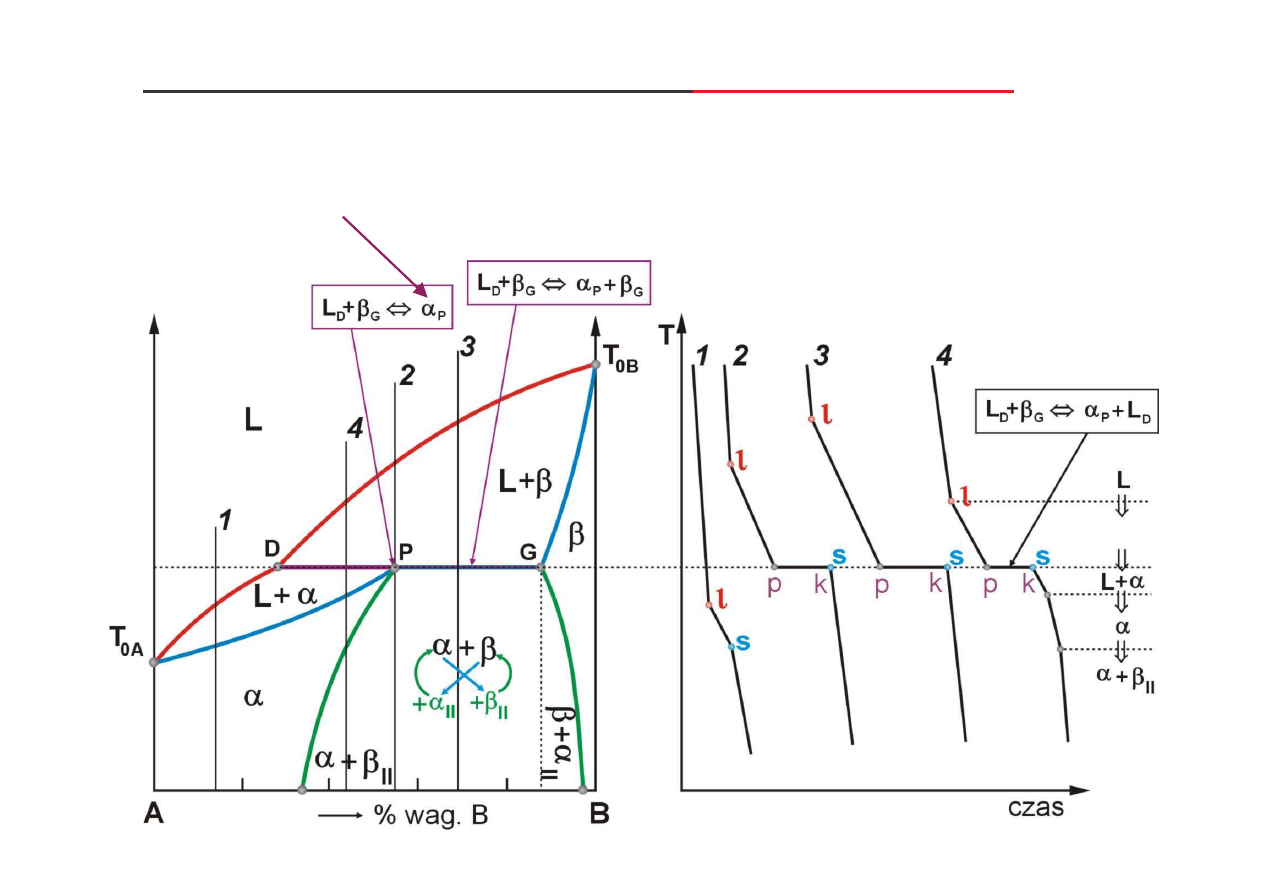
Wykres równowagi fazowej z izotermiczn

przemian perytektyczn

składniki układu:

- rozpuszczaj si w stanie stałym, tworz c roztwory stałe podstawowe graniczne,

- nie tworz faz po rednich,

- nie s polimorficzne.

perytektyka

jest faz (tutaj roztwór

αααα

) powstaj c w wyniku swoistej reakcji dwóch faz (tutaj L oraz

ββββ

),

(wi cej, patrz: R. Haimann, cz. 1)

(+)

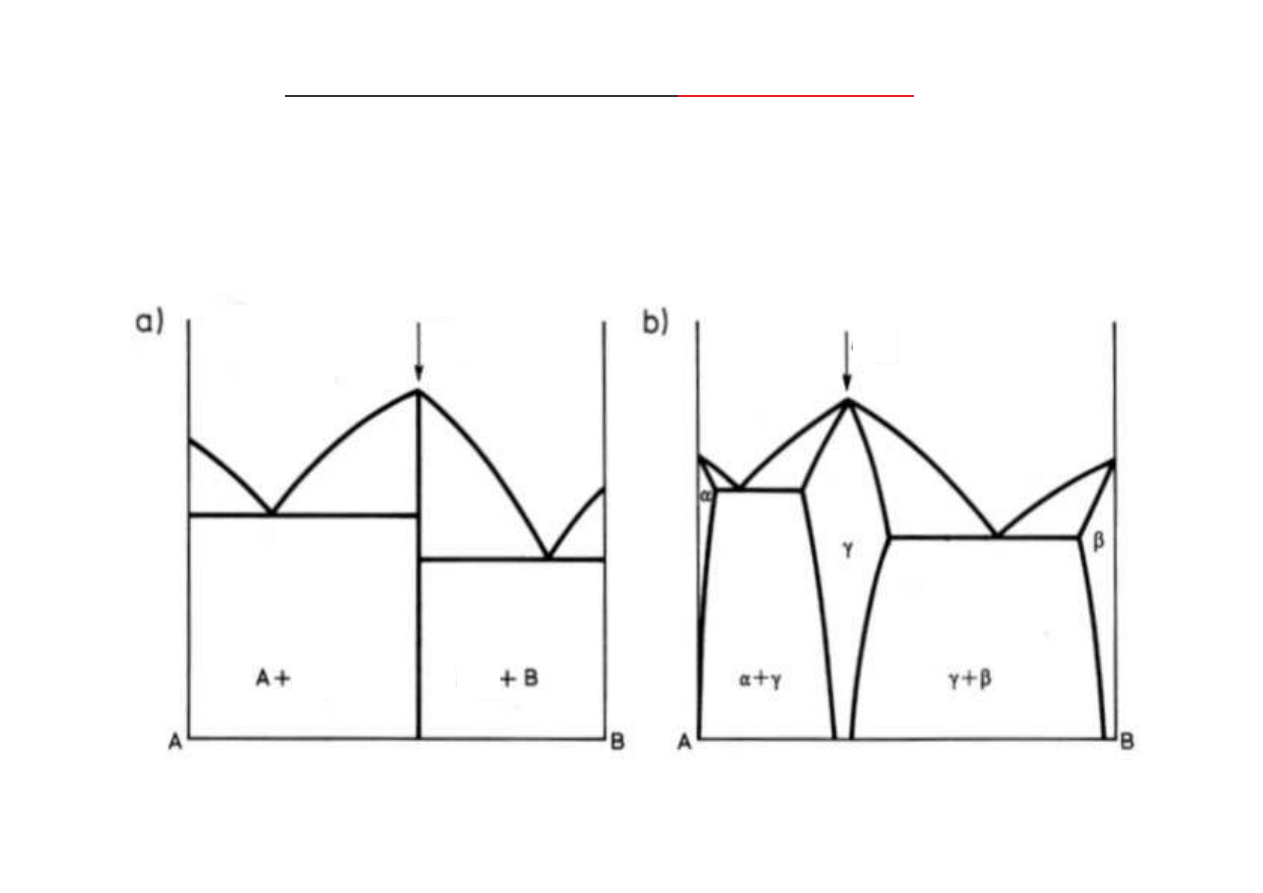
Zło one wykresy równowagi z

fazami po rednimi

wykresy z faz po redni trwał

(krystalizuj c bezpo rednio z cieczy)

a) faza wyst puje przy ci le okre lonym stosunku stechiometrycznym (A

n

B

m

),

b) faza wyst puje w pewnym zakresie st e jako

roztwór stały wtórny

– A

n

B

m

(A,B),

fazy po rednie dziel wykres zło ony na wykresy proste, które rozpatrujemy niezale nie,

A

n

B

m

A

n

B

m

A

n

B

m

A

n

B

m

(+)

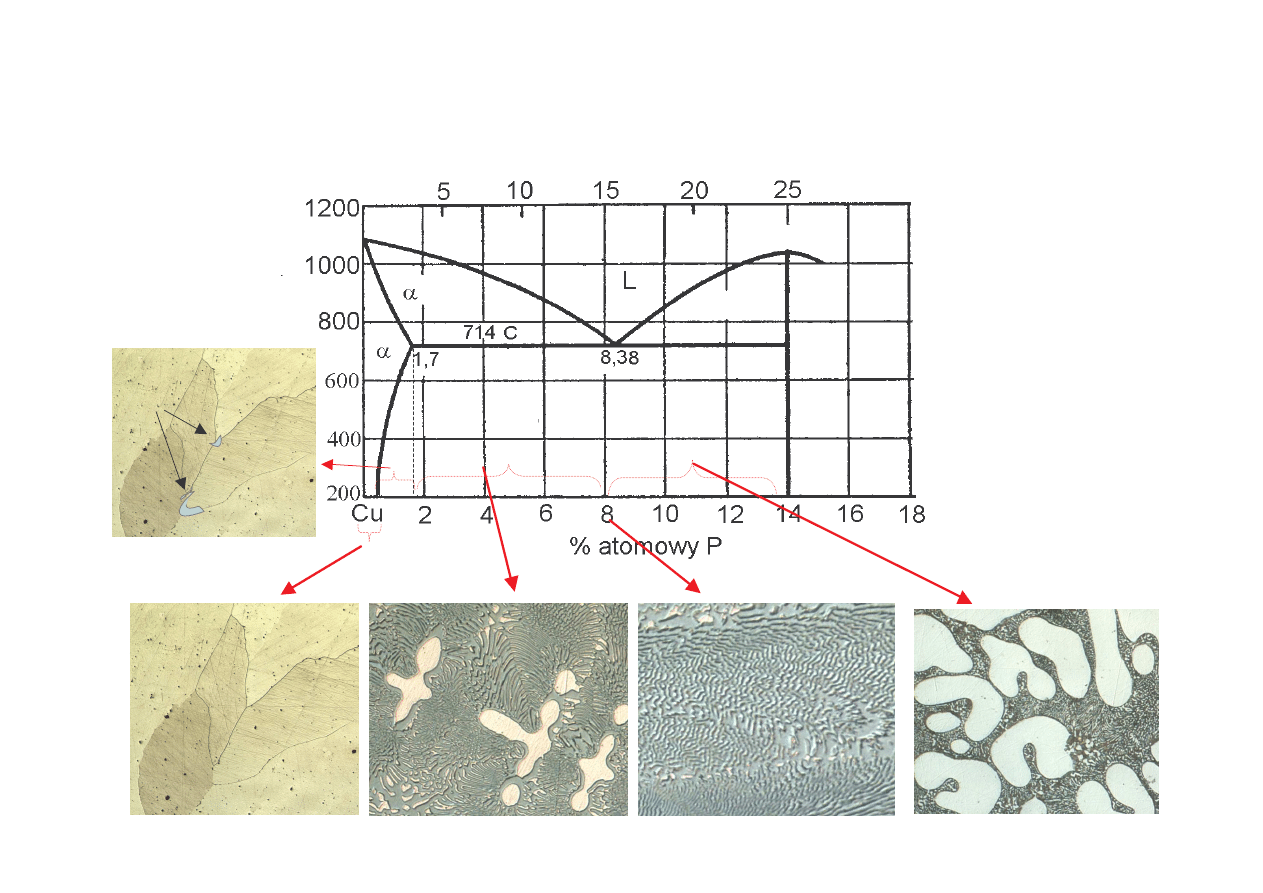
Cu

3

P

L + Cu

3

P

°

% masowy P

°C

+ L

+ Cu

3

P

αααα

(

αααα

+ Cu

3

P)

(

αααα

+ Cu

3

P)

(

αααα

+ Cu

3

P)

αααα

Cu

3

P

αααα

Cu

3

P

II

(za B. Ku nick )

przykład wykresu z trwał faz po redni (mi dzymetaliczn )

układ Cu-P:

(+-)

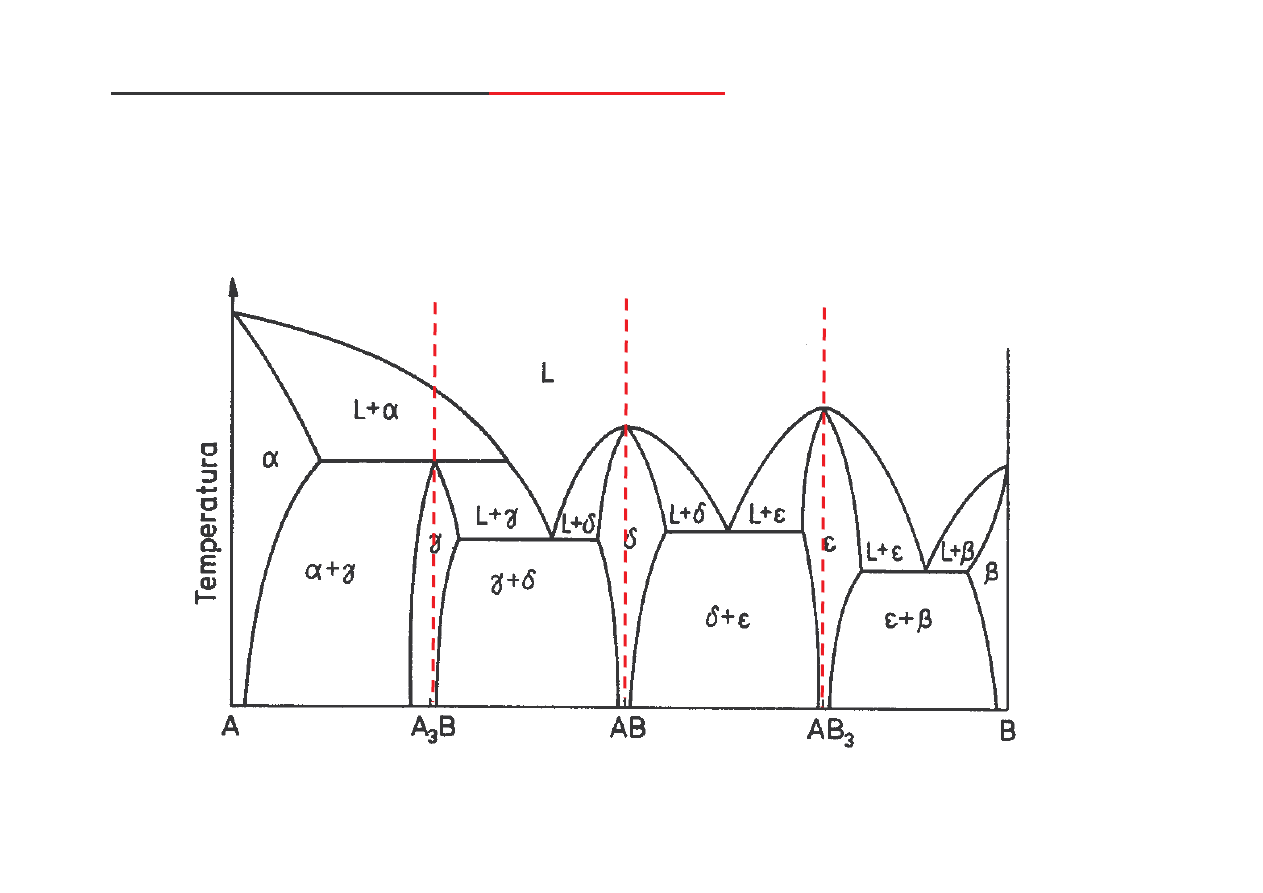
Zło ony wykres równowagi z

fazami po rednimi

składniki układu:

• rozpuszczaj si w stanie stałym, tworz c roztwory stałe podstawowe graniczne,
• tworz fazy po rednie: AB, AB

3

(trwałe) oraz A

3

B (nietrwała) - wyst puj jako roztwory stałe wtórne,

• nie s polimorficzne.

(za B. Ku nick )

(+-)

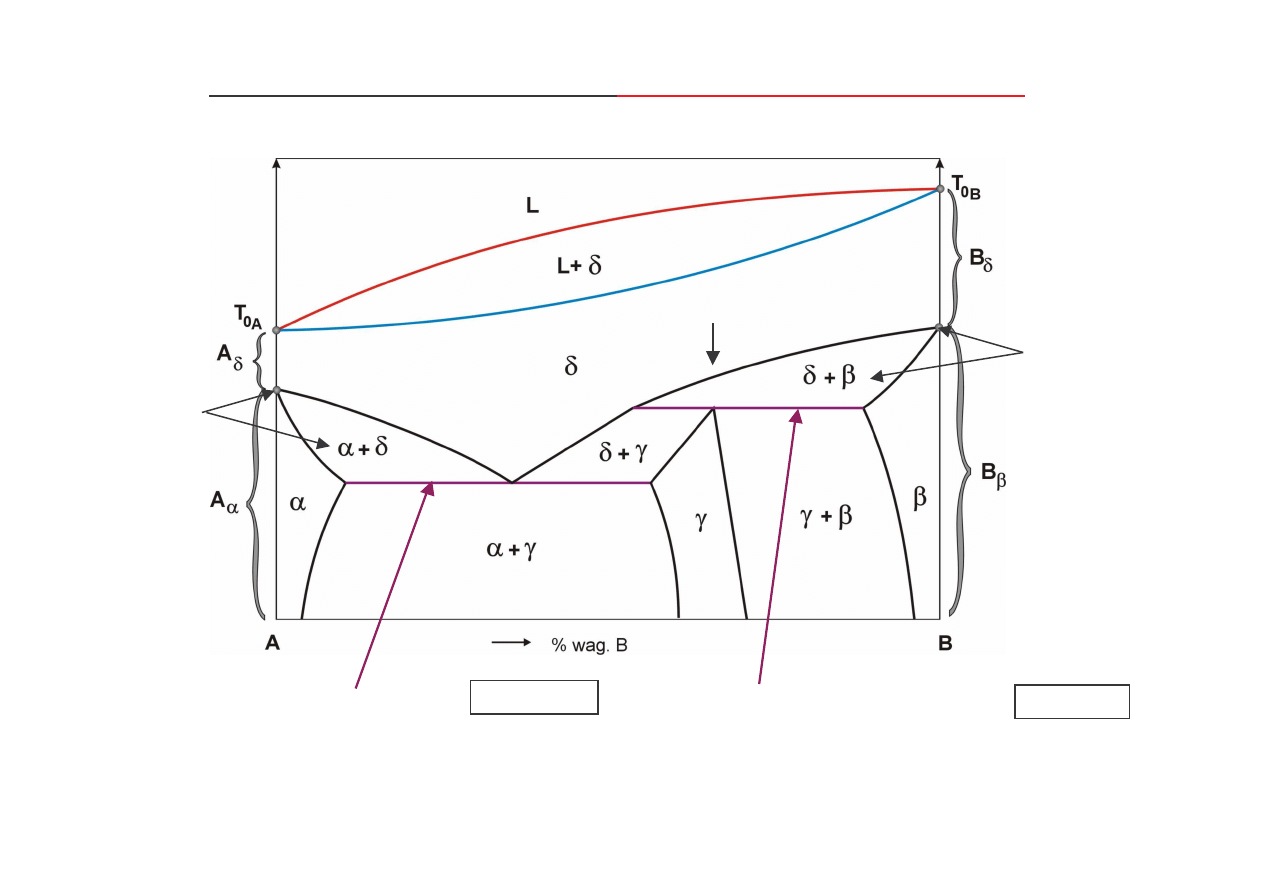
Zło one wykresy równowagi ze

składnikami wielopostaciowymi

wykresy składaj si z wykresów prostych poło onych jeden nad drugim,

izotermiczna przemiana

eutektoidalna

:

δδδδ ↔

↔

↔

↔

(

αααα

+

γγγγ

)

izotermiczna przemiana

perytektoidalna

:

δδδδ

+

ββββ ↔

↔

↔

↔ γγγγ

przemiana

alotropowa

przemiana

alotropowa

δδδδ

-

roztwór stały podstawowy ci gły od

A

δδδδ

(B)

do

B

δδδδ

(A)

,

αααα

oraz

ββββ

-

roztwory stałe podstawowe graniczne

A

αααα

(B)

oraz

B

ββββ

(A),

γγγγ

-

roztwór stały wtórny

A

n

B

m

(A,B)

A

n

B

m

{

fazy stałe:

C

D

E

F

G

H

K

P

M

N

(+)

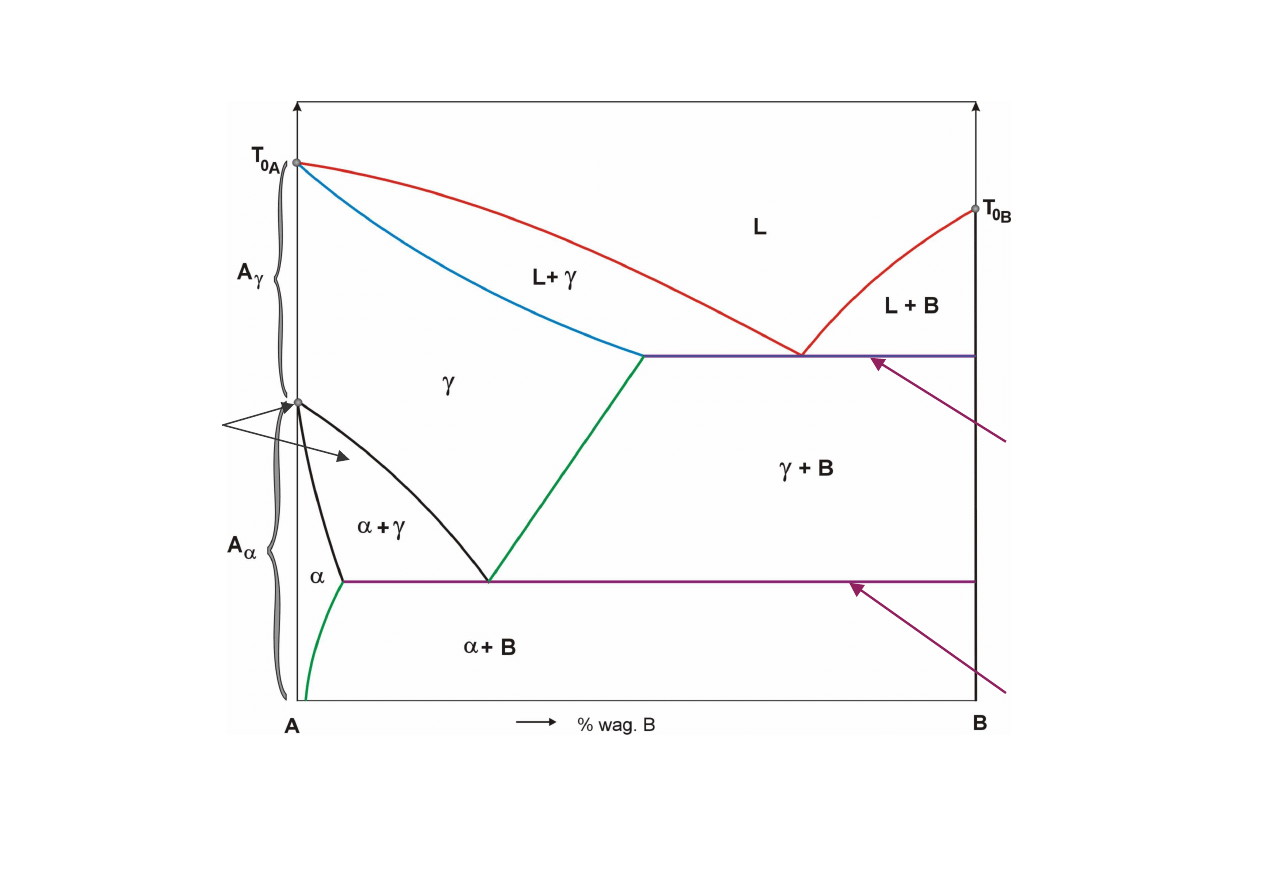
γγγγ

-

roztwór stały podstawowy graniczny

A

γγγγ

(B)

,

αααα

-

roztwór stały podstawowy graniczny

A

αααα

(B),

B -

czysty składnik

{

fazy stałe:

przemiana

eutektyczna

przemiana

eutektoidalna

przemiana

alotropowa

C

D

E

F

G

H

K

(+)