Instrukcja nr 4. Azymut, czwartak, rachunek współrzędnych

Kierunek Architektura Krajobrazu sem. II – studia stacjonarne PS

7-8

Opracował:

dr inż. Piotr Krzysztof Tuz Katedra Systemów Inżynierii Środowiska Politechnika Białostocka

wersja z dnia 2011-11-14

Strona 1

1.1

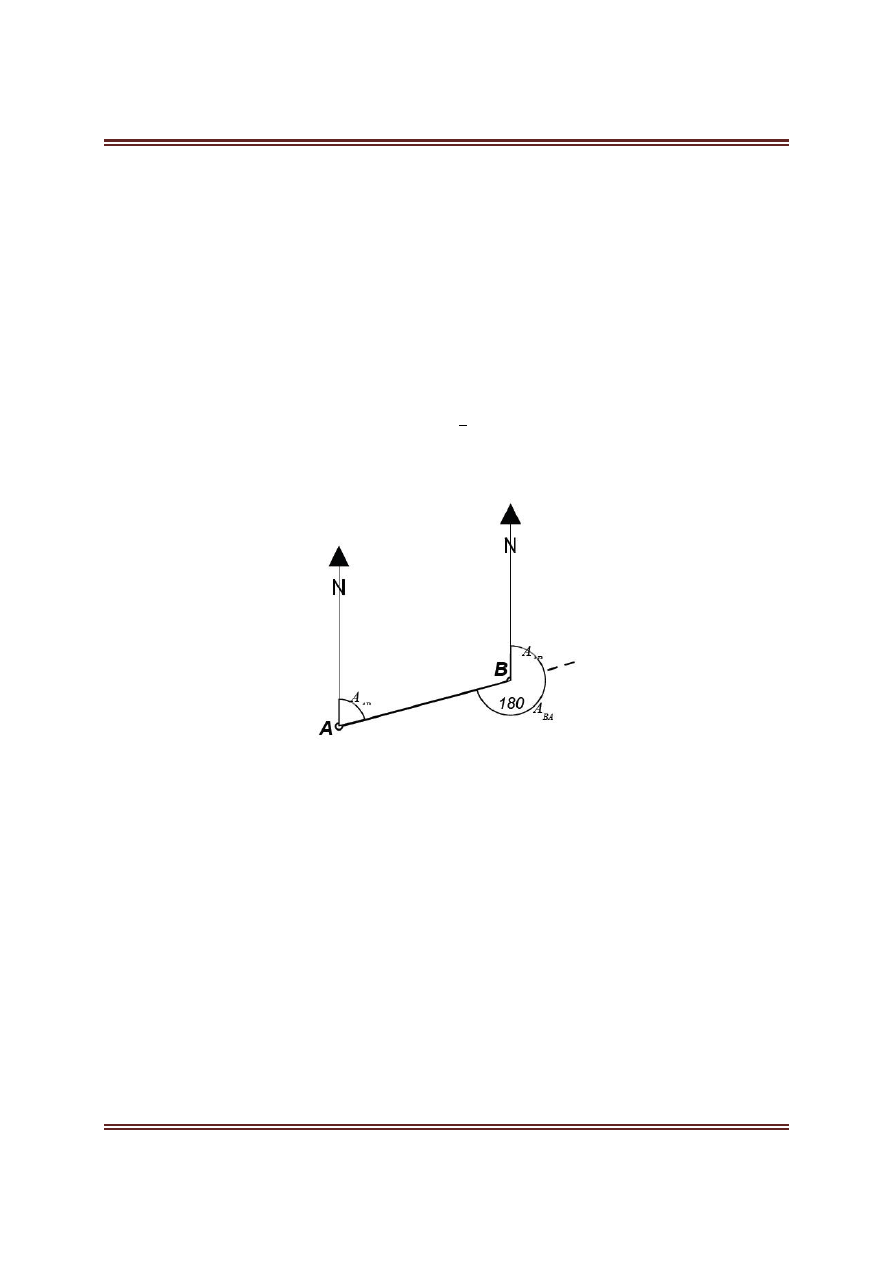
Azymutem A

AB

boku AB nazywamy kąt poziomy, zawarty w przedziale od 0 do 400

g

, pomiędzy kierun-

kiem północy wychodzącym z punktu A, a danym bokiem AB, liczony od kierunku północy w prawo,

czyli zgodnie z ruchem wskazówek zegara (1). Jeśli punktem początkowym boku, dla którego okre-

ślamy azymut jest punkt B, wtedy po wyprowadzeniu z niego kierunku północy i zakreśleniu kąta w

prawo pomiędzy północą a bokiem BA otrzymamy azymut boku odwrotnego, oznaczony symbolem:

A

BA

. Zgodnie z rys. 1 azymut ten różni się od azymutu boku AB o wartość kąta półpełnego:

A

BA

= A

AB

+200

g

W powyższym wzorze znak plus odnosi się do azymutów wyjściowych mniejszych od 200

g

, zaś znak

minus dotyczy azymutów wyjściowych przekraczających 200

g

.

Rys.1. Azymut linii głównej i odwrotnej (7).

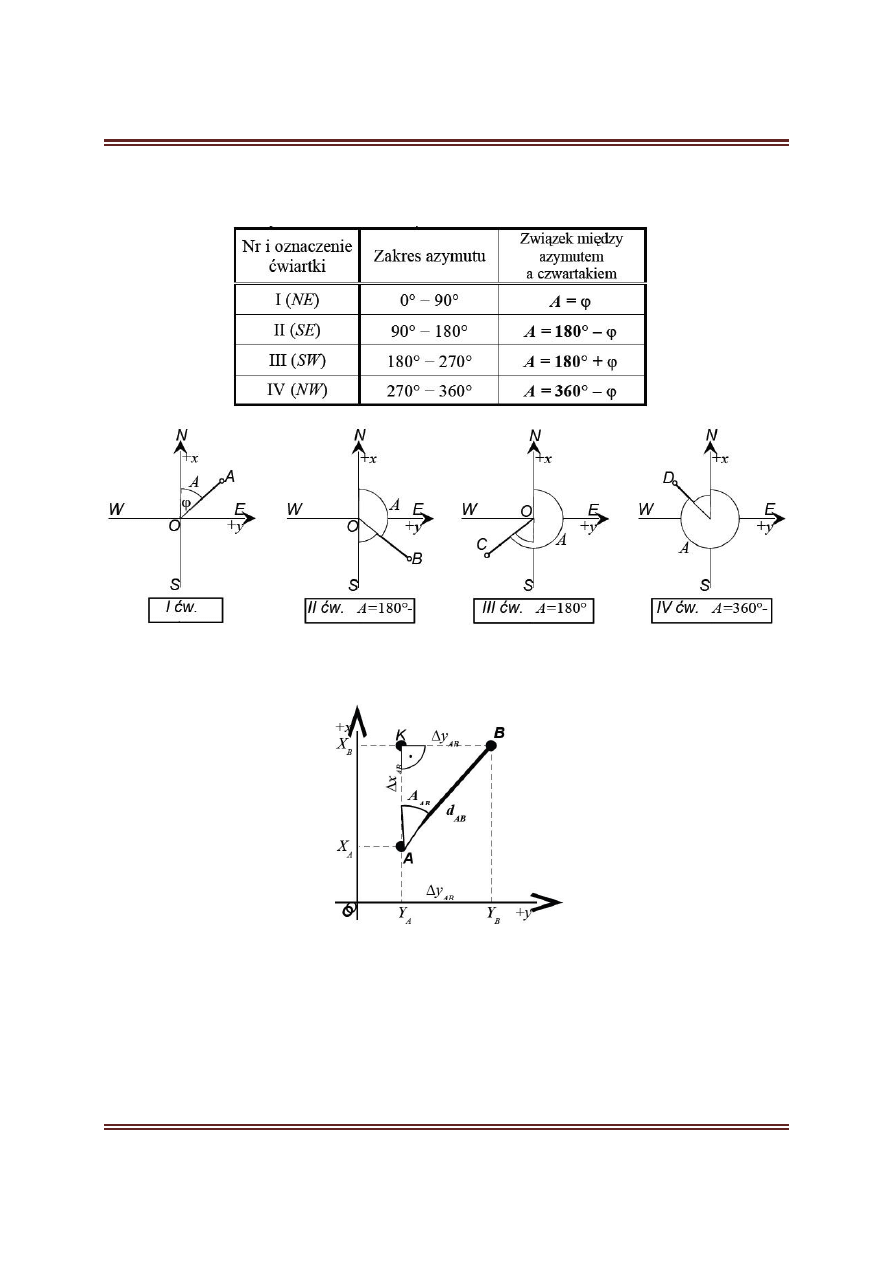
Czwartak linii AB jest definiowany jako kąt ostry zawarty pomiędzy linią osi x, czyli jej dodatnim lub

ujemnym kierunkiem, a danym bokiem AB. W ćwiartkach: I i IV ramieniem wyjściowym czwartaków

jest prosta skierowana na północ, natomiast w ćwiartkach: II i III ramię to stanowi prosta skierowana

na południe.

Na podstawie rysunku 2 można określić zestawione w tabeli 1 zależności pomiędzy azymutem a

czwartakiem w poszczególnych ćwiartkach układu współrzędnych prostokątnych. Zależności te po-

zwalają na ustalenie orientacji dowolnego kierunku, czyli obliczenie jego azymutu na podstawie war-

tości czwartaka φ.

Instrukcja nr 4. Azymut, czwartak, rachunek współrzędnych

Kierunek Architektura Krajobrazu sem. II – studia stacjonarne PS

7-8

Opracował:

dr inż. Piotr Krzysztof Tuz Katedra Systemów Inżynierii Środowiska Politechnika Białostocka

wersja z dnia 2011-11-14

Strona 2

Tabela 1. Związek pomiędzy azymutem i czwartakiem w poszczególnych ćwiartkach geodezyjnego

układu współrzędnych (7)

Rys. 2. Azymuty w poszczególnych ćwiartkach (7).

Związek pomiędzy przyrostami współrzędnych a azymutem i długością boku tłumaczy rysunek 3.

Rys. 3. Związek pomiędzy przyrostami współrzędnych a azymutem i długością boku (7).

Na podstawie zależności dla trójkąta ABK możemy określić:

ΔX

AB

=X

B

-X

A

ΔY

AB

=Y

B

-Y

A

Instrukcja nr 4. Azymut, czwartak, rachunek współrzędnych

Kierunek Architektura Krajobrazu sem. II – studia stacjonarne PS

7-8

Opracował:

dr inż. Piotr Krzysztof Tuz Katedra Systemów Inżynierii Środowiska Politechnika Białostocka

wersja z dnia 2011-11-14

Strona 3

Jednocześnie możemy określić znaki przyrostów współrzędnych w różnych ćwiartkach i zależność

azymutu i czwartaka.

Tabela 2. Zależność pomiędzy azymutem i czwartakiem oraz przyrostami współrzędnych w różnych

ćwiartkach.

1.2. Obliczenie współrzędnych punktu leżącego na prostej.

Funkcje trygonometryczne azymutu boku AB: sin A, cos A obliczone wg wzorów noszą nazwę współ-

czynników kierunkowych boku AB.

Ostateczne wzory na obliczenie współrzędnych punktu posiłkowego P na prostej AB przyjmą postać:

X

P

= X

A

+ L

AP

* cos A

AB

Y

P

= Y

A

+ L

AP

* sin A

AB

Odległość L

AP

, stanowi tzw. miarę bieżącą punktu P. Po jej zmierzeniu należy kontynuować wyzna-

czanie innych miar bieżących do dalszych punktów posiłkowych i zakończyć pomiar odległości na

Instrukcja nr 4. Azymut, czwartak, rachunek współrzędnych

Kierunek Architektura Krajobrazu sem. II – studia stacjonarne PS

7-8

Opracował:

dr inż. Piotr Krzysztof Tuz Katedra Systemów Inżynierii Środowiska Politechnika Białostocka

wersja z dnia 2011-11-14

Strona 4

punkcie B, w wyniku czego otrzymujemy miarę końcową, czyli długość boku AB - d

AB

„pomierzoną”.

Miara ta powinna być zgodna z długością d

AB

„obliczoną”, uzyskaną ze współrzędnych.

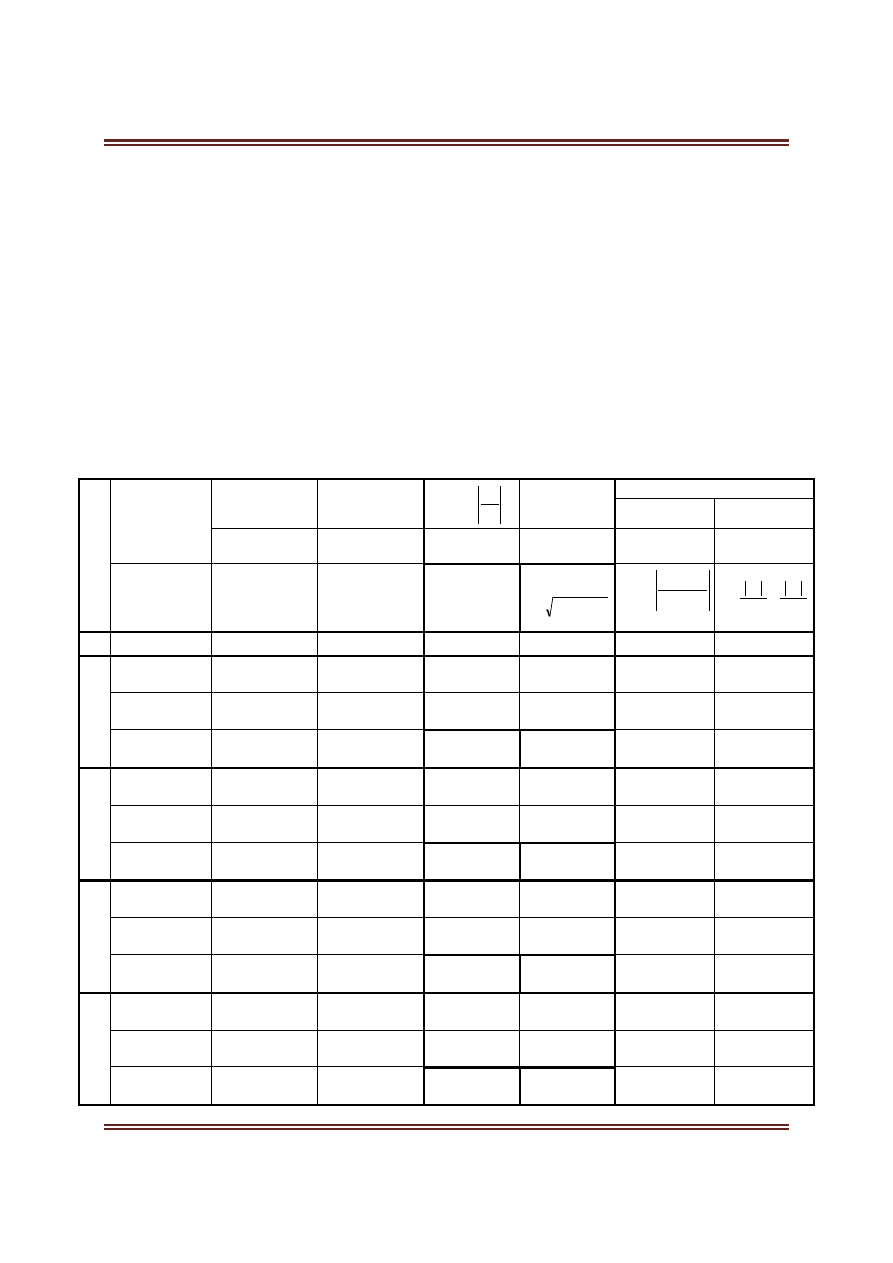
Tabela 3.

Obliczenie azymutu i długości ze współrzędnych – przykłady obliczeniowe ze sprawdzeniem

L.p.

Oznaczenia
punktów: B

A

X

B

Y

B

tg



=




y
x

cos



Kontrola



x+



y



X

A

Y

A

Czwartak



sin





x–



y

A+(50

g

)

Oznaczenie

zwrotu

boku: A



B



x

AB

= X

B

– X

A



y

AB

= Y

B

– Y

A

Azymut A

AB

Odległość

d

x

y









2

2

tg

 












x

y

x

y

d

x

y









cos

sin





1

2

3

4

5

6

7

8

1

101

1000,00

1100,00

0,5

0,8944

150,00m

79,5167

g

100

900,00

1050,00

29,5167

g

0,4472

50,00m

79,5167

g

A

100-101

+100,00

+50,00

29,5167

g

111,80 m

3

111,80=111,80

2

100

900,00

1050,00

0,5

-0,8944

-150m

79,5167

g

+200

g

101

1000,00

1100,00

29,5167

-0,4472

-50m

279,5167

g

A

101-100

-100,00

-50,00

229,5167

111,80

3

111,80=111,80

3

100

900,00

1050,00

0,5

-0,8944

-50m

20,4832

g

+200

g

102

1000,00

1000,00

29,5167

0,4472

-150m

220,4833

g

A

101-100

-100,00

+50,00

170,4833

111,80

1/3

111,80=111,80

4

102

1000,00

1000,00

0,5

0,8944

50m

20,4832

g

100

900,00

1050,00

29,5167

-0,4472

150m

(4)20,4833

g

A

101-100

100,00

-50,00

370,4833

111,80

1/3

111,80=111,80

Instrukcja nr 4. Azymut, czwartak, rachunek współrzędnych

Kierunek Architektura Krajobrazu sem. II – studia stacjonarne PS

7-8

Opracował:

dr inż. Piotr Krzysztof Tuz Katedra Systemów Inżynierii Środowiska Politechnika Białostocka

wersja z dnia 2011-11-14

Strona 5

A

B

Zadanie do samodzielnego obliczenia:

Oblicz kąty trójkąta OAB ze współrzędnych wykorzystując poznane formuły

Nr punktu

X

Y

A

100,10

- 20,10

O

- 200,11

80,42

B

84,62

284,57

Literatura:

1.Tatarczyk J.; Wybrane zagadnienia z instrumentoznawstwa geodezyjnego. Skrypt uczelniany AGH,

nr 982, Kraków, 1985.

2. Jerzy Szymoński – Instrumentoznawstwo geodezyjne.

3. Robert Krzyżek – materiały dydaktyczne do zajęć z geodezji I

4. Ćwiczenia z geodezji I. Praca zbiorowa pod redakcją J. Belucha. Wydawnictwa Naukowo –
Dydaktyczne AGH, Kraków, 2007.

5. Elementy geodezji w pomiarach inżynierskich / pod red. Ryszarda Józefa Grabowskiego ; [aut.
Eugenia Bajkowska i in.]. Białystok, 1991.

6. Osada E.: Wykłady z geodezji i geoinformatyki. Niwelacja. Wydawnictwo Naukowe Dolnośląskiej
Szkoły Wyższej, 2009.

7. Jagielski A. Geodezja I.

Wydawnictwo GEODPIS / ISBN: 83-922884-0-8 / Wydanie 2 - zmodyfikowane

(2005)

O