
Zadanie 6.
1. Analiza modelu wyboczeniowego:
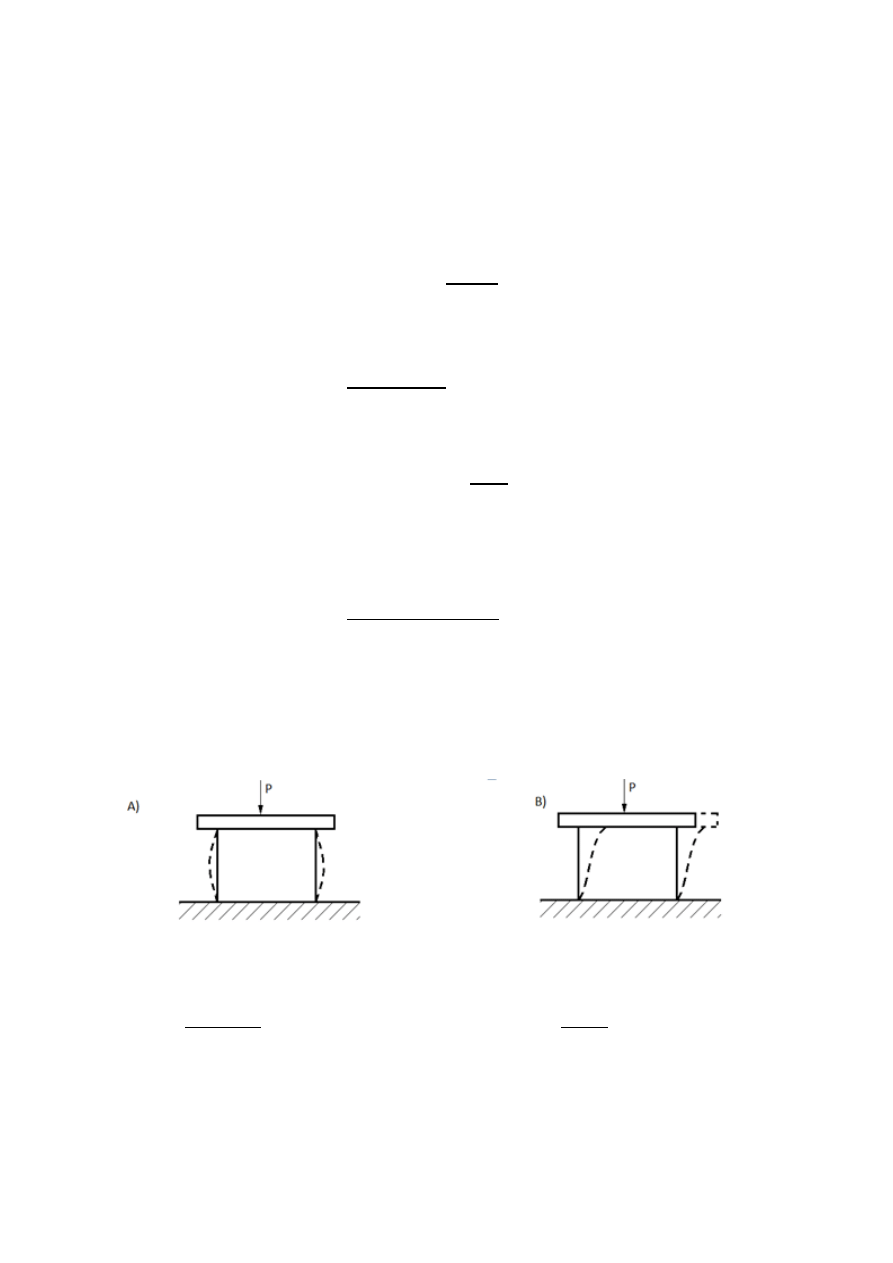
Najmniej korzystnym przypadkiem wyboczenia w przedstawionym układzie jest
wyboczenie jednego z prętów w sposób przedstawiony na rysunku obok. W związku z
tym w poniższych obliczeniach zostaną wykorzystane poniższe dane:
µ = 2, l
w
= 2*h
2. Momenty bezwładności przekrojów prętów:
2.1 pręt o przekroju kwadratowym:
2.2 pręt o przekroju trójkątnym:
3. Pola przekroju prętów:
3.1 pole przekroju pręta kwadratowego:
3.2 pole przekroju pręta trójkątnego:

4. Smukłość graniczna:
√
√
5. Smukłości prętów:
,
gdzie:
s – smukłość,
i
min
– minimalny promień bezwładności,
l
w
– długość wyboczeniowa.
√
,
gdzie:
I
min
– minimalny moment bezwładności,
A - pole przekroju pręta.
5.1 minimalne promienie bezwładności:
5.1.1 pręta o przekroju kwadratowym:
√
5.1.2 pręta o przekroju trójkątnym:
√
5.2 smukłości prętów:
5.2.1 pręt o przekroju kwadratowym:
5.2.2 pręt o przekroju trójkątnym:
Pręt o większej smukłości ulegnie wyboczeniu przy mniejszej sile oddziaływującej na niego, więc jest
to bardziej niekorzystny przypadek:
138,564 > S
gr
6. Zastosowanie wzoru Eulera:
7. Dopuszczalna siła:
,
gdzie:
n – współczynnik bezpieczeństwa.
8. Pozostałe przypadki
Poddajmy analizie również pozostałe możliwości wyboczenia prętów układu, z racji, że pręt o
przekroju kwadratowym ma mniejszą wytrzymałość, wykorzystamy jego dane do poniższych
obliczeń, jako najsłabsze ogniwo układu :
µ=0,7, l
w
=0,7*h
µ=1, l
w
=h
s<s
gr
s<s
gr
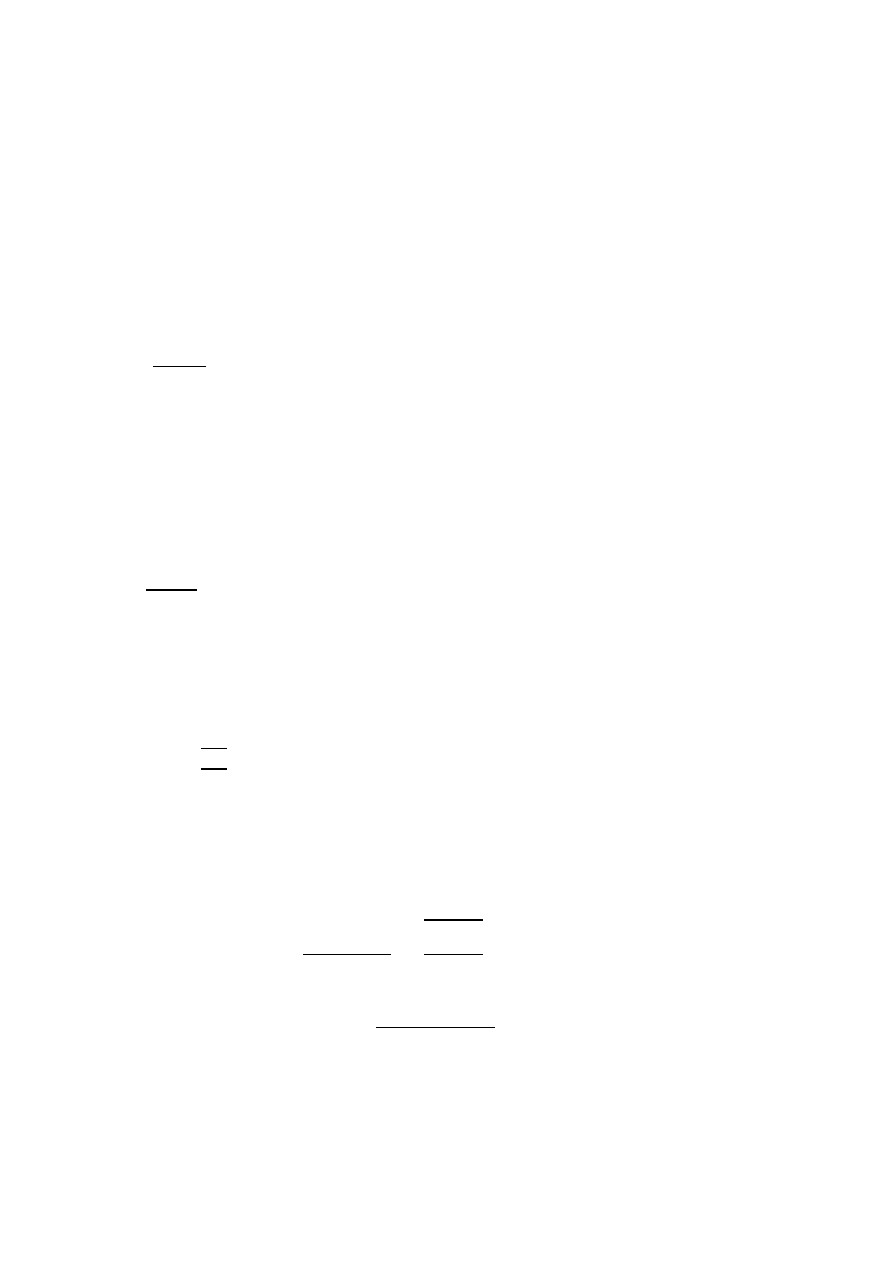
Ponieważ s<s
gr
w przypadkach tych zachodzi odkształcenie sprężysto-plastyczne, zastosujemy więc
wzory Johnssona-Ostenfelda i Tetmajera otrzymane wartości.
Wzór Tetmajera:
,
gdzie:
,
.
Wzór Johnssona-Ostenfelda:
,
gdzie:
,
.
Powyższy wzór można stosować, jeśli spełniony jest warunek:
gdzie:
√
.
8.1) Przypadek A:
Zastosowanie wzoru Tetmajera:
√
Zastosowanie wzoru Johnssona-Ostenfelda:
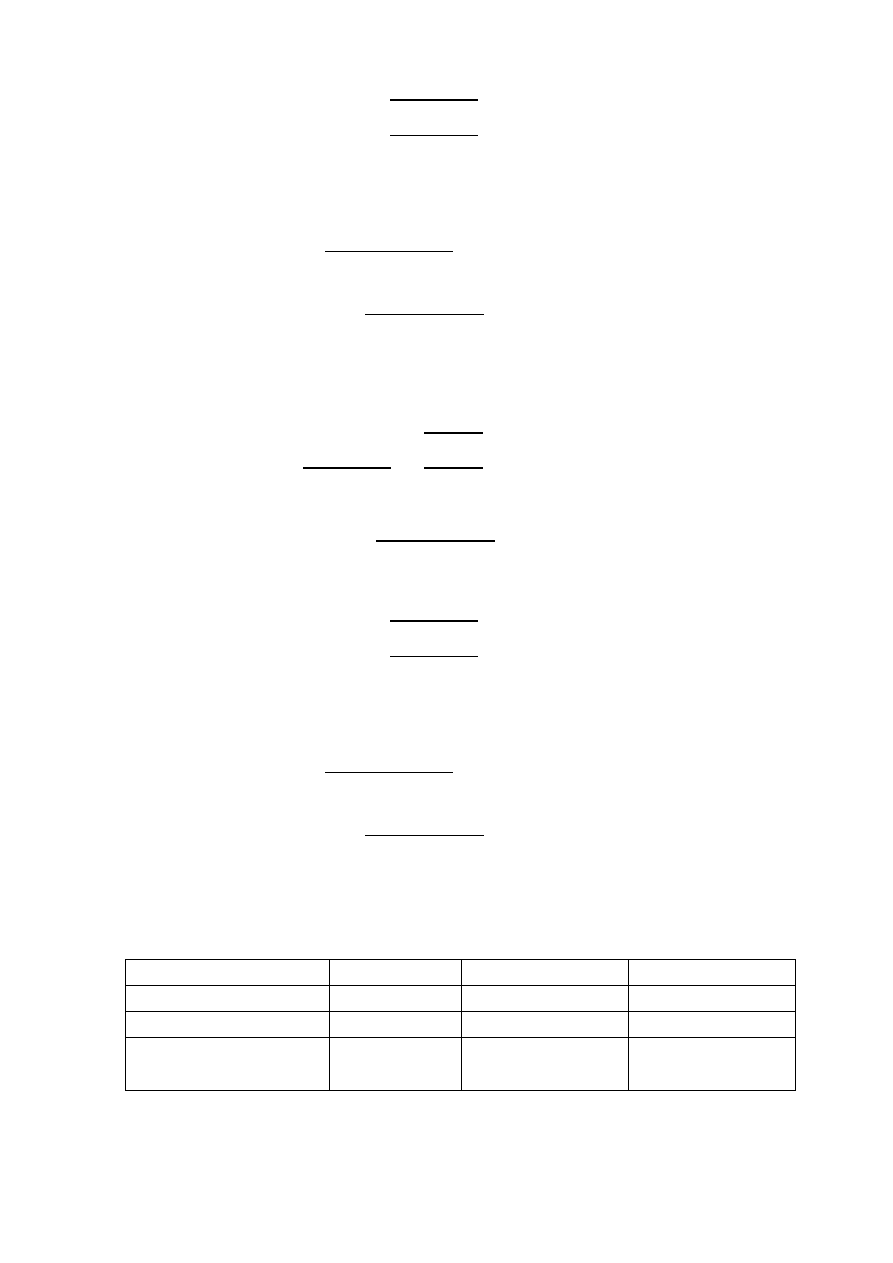
√
8.2) Przypadek B:
Zastosowanie wzoru Tetmajera:
√
Zastosowanie wzoru Johnssona-Ostenfelda:
√
9. Porównanie wyników
µ=2
µ=1
µ=0,7
Wzór Eulera
27,417 kN
-
-
Wzór Tetmajera
-
56,565 kN
58,795 kN
Wzór Johnssona-
Ostenfelda
-
54,67 kN
58,429 kN
Wyszukiwarka
Podobne podstrony:
6 M3 MichalskiJ PazderskiJ ZAD6
M3 6 4
10 M3 JankowskiM MuszyńskiA ZAD10
M3 2 2
michalpasterski pl 10 sposobw na nieograniczon motywacj
M3, WSFiZ Warszawa, Semestr II, Technologie informacyjne - ćwiczenia (e-learning) (Grzegorz Stanio)
zad6, Informatyka i Ekonometria 3 rok, Ekonometria, sliwka
Medytacja Przesłanie Archanioła Michała
fiz m3 teoria
1 3 m3 wstep
M3 2 1
ECCC Sylabus IT M3 A
M3 1 7
pielegn srod rodz m3
M3, weterynaria uwm III rok, patofizjo
prob tabela5, od michała, od micha, TPL
BIBL-TAL, Poradowski Michał ks
MICHALKIEWICZ - LOGIKA WYSTARCZY, chomikowane nowe
więcej podobnych podstron