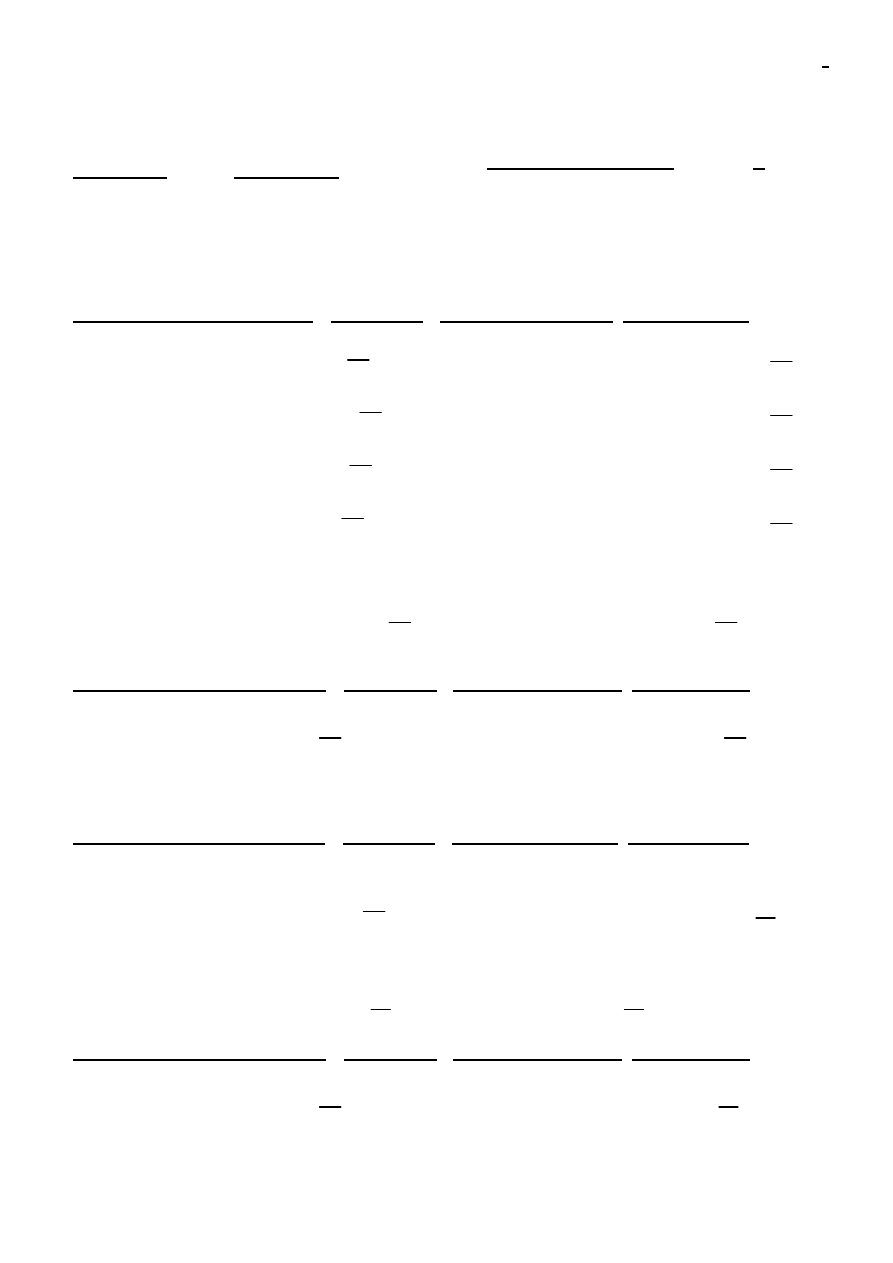
1

gsp g1 g2

+

g3

+

g4

+

:=

gksp 4.29

kN

m

2

=

gsp 5.00

kN

m

2

=

Obciążenia zmienne gk γk g

q gk1 6

kN

m

2

:=

γk 1.2

:=

gzp gk1 γk

⋅

:=

gzp 7.2

kN

m

2

=

Zestawienie obciążeń: ŻEBRO

Obciążenia stałe gk γk g

Płyta gk1 gksp Lp

⋅

:=

Ciężar żebra gk2 bz hz hf

−

(

)

⋅

25

⋅

kN

m

3

⋅

:=

γk2 1.1

:=

g1 gsp Lp

⋅

:=

g2 gk2 γk2

⋅

:=

g2 1.65

kN

m

=

Razem obciążenia stałe:

gksz

gk1 gk2

+

:=

gsz g1 g2

+

:=

gksz 13.51

kN

m

=

gsz 15.66

kN

m

=

Obciążenia zmienne gk γk g

q gk1 6

kN

m

2

Lp

:=

γk 1.2

:=

gzz gk1 γk

⋅

:=

gzz 20.16

kN

m

=

Projekt z konstrukcji żelbetowych.

Rozplanowanie:

Wymiary elwmentów:

Element Rozpiętość
Żebro Lz 5.50m

:=

Podciąg Lp 2.80m

:=

Podciąg/Żebro główne Lpz 8.40m

:=

Element h b
Strop hf 0.1m

:=

Żebro hz 0.4m

:=

bz 0.2m

:=

Podciąg hp 0.55m

:=

bp 0.3m

:=

Zestawienie obciążeń: PŁYTA

Obciążenia stałe gk γk g

Płyty gk1 0.72

kN

m

2

:=

γk1 1.2

:=

Wylewka cementowa 5 cm gk2 1.05

kN

m

2

:=

γk2 1.3

:=

Styropian gk3 0.02

kN

m

2

:=

γk3 1.2

:=

Płyta żelbetowa gk4 2.5

kN

m

2

:=

γk4 1.1

:=

g1 gk1 γk1

⋅

:=

g1 0.86

kN

m

2

=

g2 gk2 γk2

⋅

:=

g2 1.37

kN

m

2

=

g3 gk3 γk3

⋅

:=

g3 0.02

kN

m

2

=

g4 gk4 γk4

⋅

:=

g4 2.75

kN

m

2

=

Razem obciążenia stałe:

gksp gk1 gk2

+

gk3

+

gk4

+

:=

2

gzz 20.16

kN

m

=

Gzp 110.88 kN

=

Rozpiętoć

Lp 2.9m

:=

Lz 5.5m

=

Lpz 8.4m

=

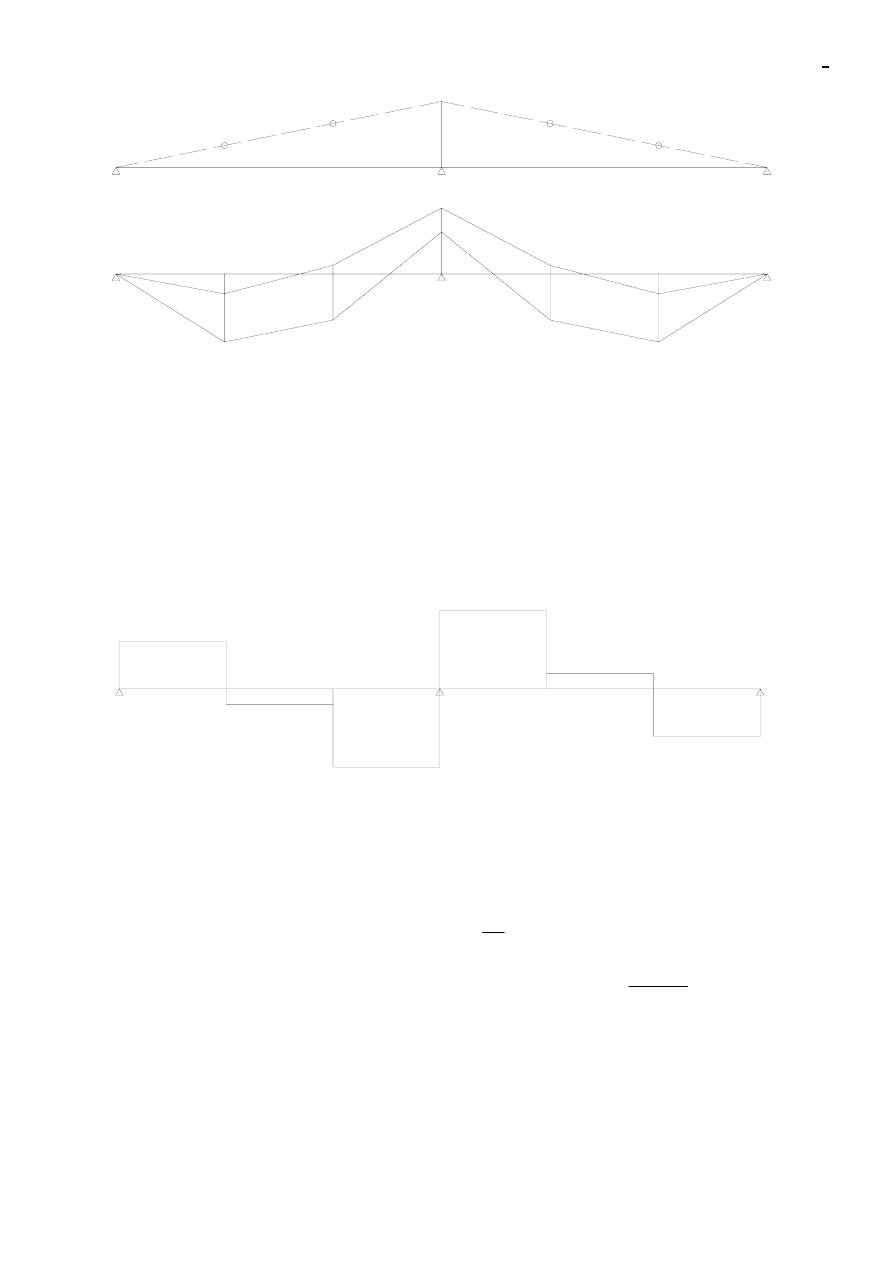
Obwiednia momentów dla płyty

M1max

0.0781 gsp

⋅

0.1 gzp

⋅

+

(

)

Lp

2

⋅

:=

M1max 9.34kN

=

M1

0.0781 gsp

⋅

0.0263 gzp

⋅

−

(

)

Lp

2

⋅

:=

M2max

0.0331 gsp

⋅

0.0787 gzp

⋅

+

(

)

Lp

2

⋅

:=

M2max 6.16kN

=

M2

0.0331 gsp

⋅

0.0461 gzp

⋅

−

(

)

Lp

2

⋅

:=

M3max

0.0462 gsp

⋅

0.0855 gzp

⋅

+

(

)

Lp

2

⋅

:=

M3max 7.12kN

=

M1 1.69kN

=

M2

1.40

−

kN

=

MBmax

0.105

−

gsp

⋅

0.119 gzp

⋅

−

(

)

Lp

2

⋅

:=

MBmax

11.62

−

kN

=

MCmax

0.079

−

gsp

⋅

0.111 gzp

⋅

−

(

)

Lp

2

⋅

:=

MCmax

10.05

−

kN

=

MDmax

0.079

−

gsp

⋅

0.044 gzp

⋅

−

(

)

Lp

2

⋅

:=

MDmax

5.99

−

kN

=

9.34

11.62

6.16

10.05

7.12

Obwiednie momentów dla PŁYTY

1.69

1.40

1.40

Zestawienie obciążeń: PODCIĄG

Obciążenia stałe Gk γk G

Obciążenia z żeber Gk1 gksz Lz

⋅

:=

Ciężar podciągu Gk2 bp hp hf

−

(

)

⋅

25

⋅

kN

m

3

Lp

⋅

:=

γk 1.1

:=

G1 gsz Lz

⋅

:=

G1 86.12 kN

=

G2 Gk2 γk

⋅

:=

G2 10.39 kN

=

Razem obciążenia stałe:

Gksp Gk1 Gk2

+

:=

Gsp G1 G2

+

:=

Gksp 83.77 kN

=

Gsp 96.52 kN

=

Obciążenia zmienne Gk γk G

q Gk1 g

k1

Lz

⋅

:=

γk 1.2

:=

Gzp Gk1 γk

⋅

:=

Gzp 110.88kN

=

Wyniki z tablic Winklera

PŁYTA

ŻEBRO

PODCIĄG

gsp 5.00

kN

m

2

=

gsz 15.66

kN

m

=

Gsp 96.52 kN

=

Obciążenia stałe

Obciążenia zmienne

gzp 7.2

kN

m

2

=

3

207.40

207.40

96.52

96.52

580.72

270.26

MBmax

425.52

−

kNm

=

MBmax

0.333

−

Gsp

⋅

0.167 Gzp

⋅

−

(

)

Lpz

⋅

:=

M1max 438.91 kNm

=

M1max

0.222 Gsp

⋅

0.278 Gzp

⋅

+

(

)

Lpz

⋅

:=

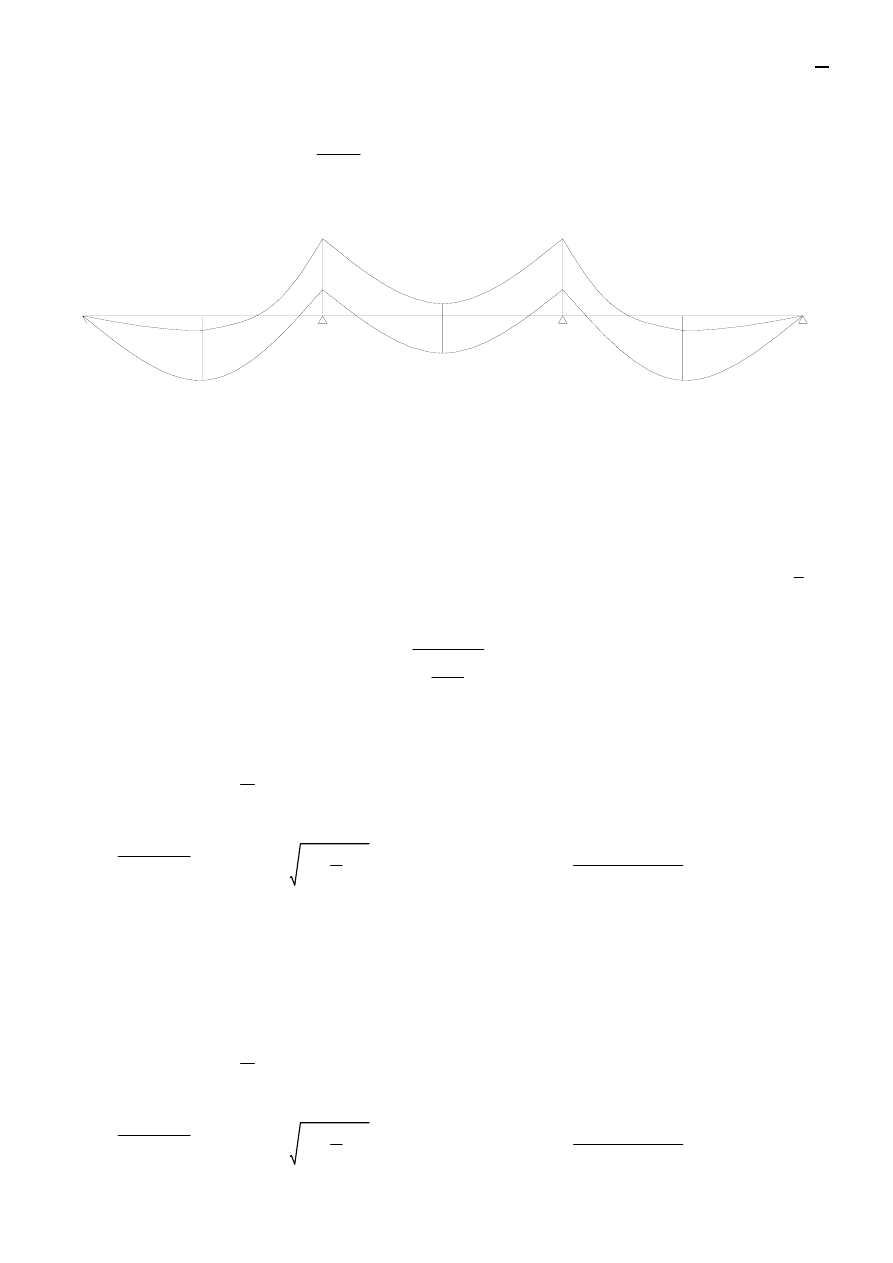
Obwiednia momentów dla podciągu

84.34

120.09

107.70

120.09

107.70

84.34

Obwiednia sił poprzecznych ŻEBRA

QBPmax 107.70 kN

=

QBPmax

0.5 gsz

⋅

0.583 gzz

⋅

+

(

)

Lz

⋅

:=

QBLmax

120.09

−

kN

=

QBLmax

0.6

−

gsz

⋅

0.617 gzz

⋅

−

(

)

Lz

⋅

:=

QAmax 84.34 kN

=

QAmax

0.4 gsz

⋅

0.45 gzz

⋅

+

(

)

Lz

⋅

:=

Obwiednie sił poprzecznych dla żebra

99.49

118.72

57.58

118.72

99.49

Obwiednia momentów dla ŻEBRA

22.65

18.65

22.65

M2

18.65

−

kNm

=

M1 22.647 kNm

=

MBmax

118.72

−

kNm

=

MBmax

0.1

−

gsz

⋅

0.117 gzz

⋅

−

(

)

Lz

2

⋅

:=

M2

0.025 gsz

⋅

0.05 gzz

⋅

−

(

)

Lz

2

⋅

:=

M2max 57.58 kNm

=

M2max

0.025 gsz

⋅

0.075 gzz

⋅

+

(

)

Lz

2

⋅

:=

M1

0.08 gsz

⋅

0.025 gzz

⋅

−

(

)

Lz

2

⋅

:=

M1max 99.49 kNm

=

M1max

0.08 gsz

⋅

0.101 gzz

⋅

+

(

)

Lz

2

⋅

:=

Obwiednia momentów dla żebra

4

a1 3cm

:=

Otulina dla środowiska wilgotnego z mrozem:

hf 0.1m

:=

Grubość płyty:

ξeff.lim 0.63

=

ξeff.lim 0.8

εcu

εcu εs

+









⋅

:=

Graniczna wartość względem wysokości strefy ściskania przekroju:

εs 9.5 10

4

−

×

=

εs

fyd

Es

:=

Es

200 10

3

MPa

⋅

:=

Moduł sprężystości stali zwykłej

fcd 10.6MPa

:=

α

0.85

:=

εcu 0.0035

:=

fyk 220MPa

:=

fyd 190MPa

:=

Leff Lp

:=

Dane do projektowania:

•

Płyta: Beton B20, Stal A0

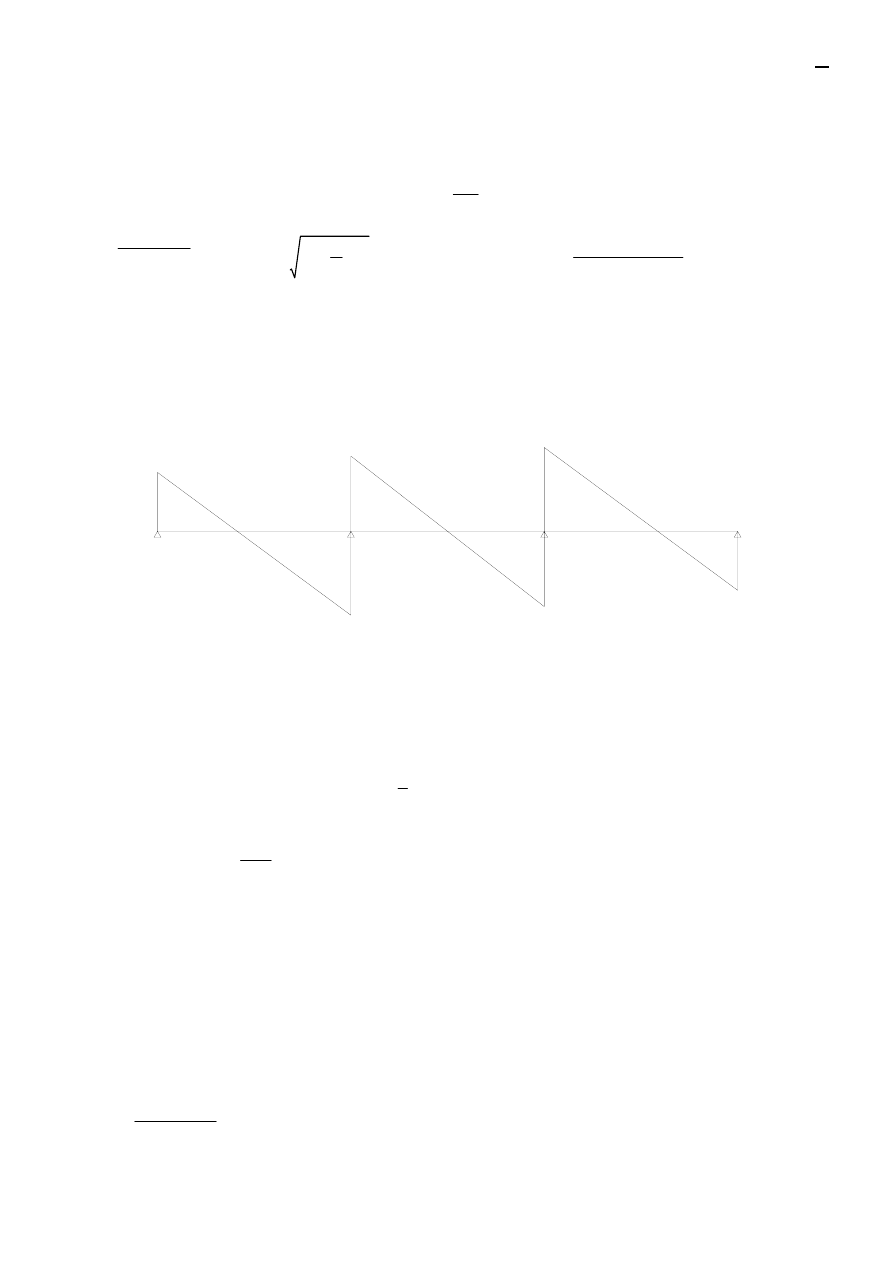
156.74

50.66

258.06

258.06

50.66

156.75

Obwiednia sił poprzecznych PODCIĄG

QCmax 45.86 kN

=

QCmax

0.667 Gsp

⋅

0.167 Gzp

⋅

−

(

)

:=

QBmax 406.29 kN

=

QBmax

2.677 Gsp

⋅

1.334 Gzp

⋅

+

(

)

:=

QBPmax 147.27 kN

=

QBPmax

1.334 Gsp

⋅

0.167 Gzp

⋅

+

(

)

:=

QBLmax

258.15

−

kN

=

QBLmax

1.334

−

Gsp

⋅

1.167 Gzp

⋅

−

(

)

:=

QAmax 156.74 kN

=

QAmax

0.667 Gsp

⋅

0.833 Gzp

⋅

+

(

)

:=

Obwiednia sił poprzecznych dla podciągu

425.52

141.84

283.68

141.84

283.68

297.04

270.26

297.04

438.88

425.52

13.42

128.42

128.42

13.42

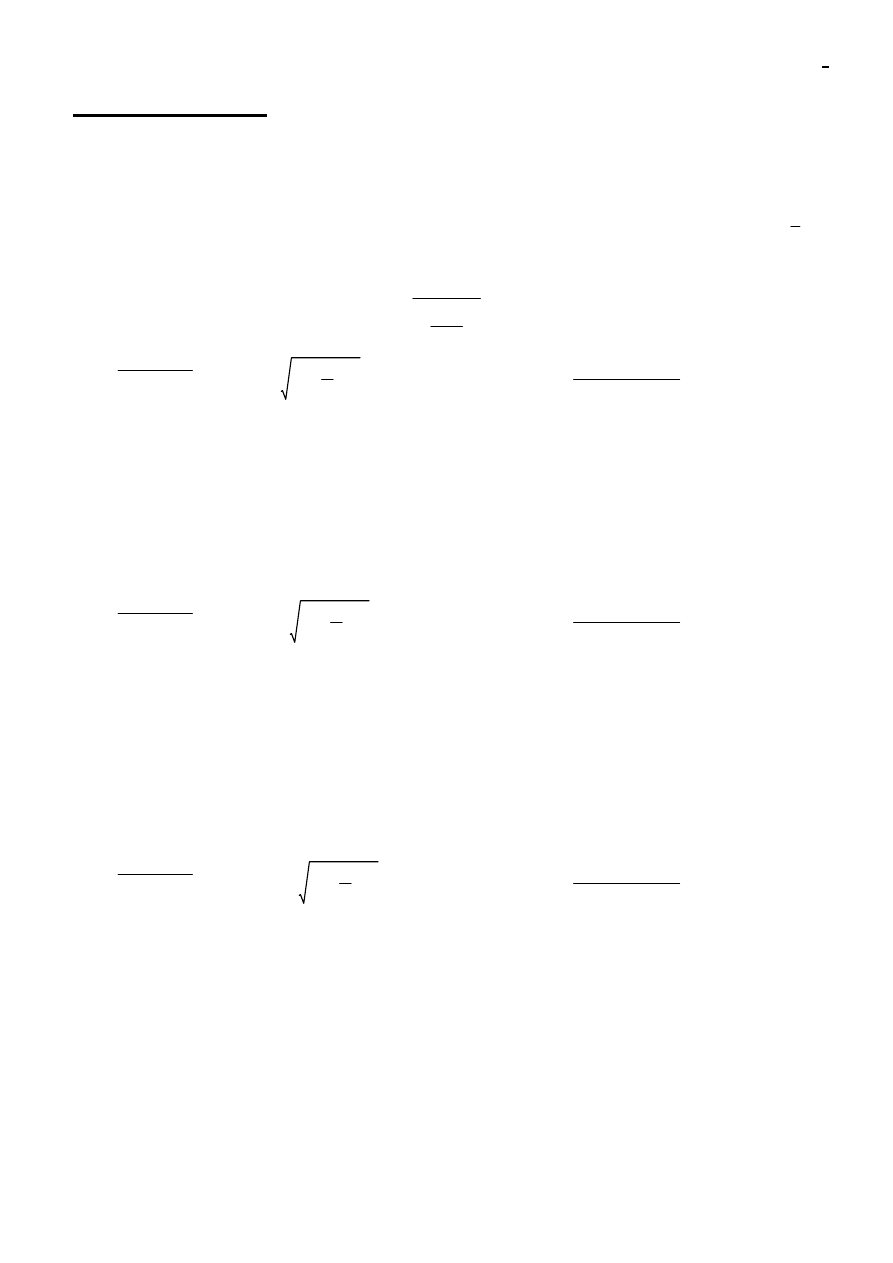
5

Przyjęta średnica prętów:

φ

10mm

:=

ms

M

fcd 1

⋅ m

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

1

⋅ m d

⋅ ξeff

⋅

fyd

:=

As1 5.474 cm

2

=

Przyjmuję

φ10 co 14 cm co odpowiada 5.61cm

2

Przęsło CD

•

M

7.12kNm

:=

Przyjęta średnica prętów:

φ

10mm

:=

ms

M

fcd 1

⋅ m

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

1

⋅ m d

⋅ ξeff

⋅

fyd

:=

As1 6.437 cm

2

=

Przyjmuję

φ10 co 11 cm co odpowiada 7.14cm

2

Wymiarowanie plyty

Wymiarowanie dołem

Przęsło AB

•

M

9.34kNm

:=

Przyjęta średnica prętów:

φ

10mm

:=

Wysokość użyteczna przekroju

d

hf a1

−

φ
2

−

:=

Minimalna powierzchnia zbrojenia dla szerokości 1 metra:

As.min max 0.0015 1

⋅ m d

⋅

0.6 1

⋅ m d

⋅

fyk

MPa













:=

As.min 1.773 cm

2

=

ms

M

fcd 1

⋅ m

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

1

⋅ m d

⋅ ξeff

⋅

fyd

:=

As1 8.827 cm

2

=

Przyjmuję

φ10 co 8 cm co odpowiada 9.817cm

2

Przęsło BC

•

M

6.16kNm

:=

6

Obciazenia stale:

p

gzp

:=

Obciazenia zmienne:

Podpora B

•

M

11.62kNm

:=

Przyjęta średnica prętów:

φ

10mm

:=

Wysokość użyteczna przekroju

d

hf a1

−

φ
2

−

:=

Minimalna powierzchnia zbrojenia dla szerokości 1 metra:

As.min max 0.0015 1

⋅ m d

⋅

0.6 1

⋅ m d

⋅

fyk

MPa













:=

As.min 1.773 cm

2

=

Przypadek a)

M'

M

q

p

+

(

) Lp

⋅

2

bz m

⋅

2

⋅

−

:=

M'

9.851 kNm

=

ms

M'

fcd 1

⋅ m

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

1

⋅ m d

⋅ ξeff

⋅

fyd

:=

As1 9.414 cm

2

=

Wymiarowanie górą:

M1 11.62kNm

:=

M2 1.40kNm

:=

M'

0.5 M1 M2

+

(

)

⋅

:=

M'

6.51 kNm

=

Przyjęta średnica prętów:

φ

12mm

:=

Wysokość użyteczna przekroju

d

hf a1

−

φ
2

−

:=

Minimalna powierzchnia zbrojenia dla szerokości 1 metra:

As.min max 0.0015 1

⋅ m d

⋅

0.6 1

⋅ m d

⋅

fyk

MPa













:=

As.min 1.745 cm

2

=

ms

M'

fcd 1

⋅ m

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

1

⋅ m d

⋅ ξeff

⋅

fyd

:=

As1 5.934 cm

2

=

Przyjmuję

φ12 co 16 cm co odpowiada 7.069 cm

2

Wymiarowanie na moment podporowy

q

gsp

:=

7

Przyjnuję

φ10 co 10 cm co odpowiada 7.854cm

2

Przyjmujemy wieksza powierzchnię zbrojenia

As1 5.731 cm

2

=

As1

α fcd

⋅

1

⋅ m d'

⋅ ξeff

⋅

fyd

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

ms

M

fcd 1

⋅ m

⋅

d'

2

⋅

:=

d'

d

bz

6

+

:=

Przypadek b)

As1 7.656 cm

2

=

As1

α fcd

⋅

1

⋅ m d

⋅ ξeff

⋅

fyd

:=

ξeff ξeff.lim

<

1

=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ms

M'

fcd 1

⋅ m

⋅

d

2

⋅

:=

M'

8.281 kNm

=

M'

M

q

p

+

(

) Lp

⋅

2

bz m

⋅

2

⋅

−

:=

Przypadek a)

φ

10mm

:=

Przyjęta średnica prętów:

M

10.05kNm

:=

Podpora C

•

Przyjmuję

φ10 co 8 cm co odpowiada 9.817cm

2

Przyjmujemy wiekszą powierzchnię zbrojenia

As1 6.701 cm

2

=

As1

α fcd

⋅

1

⋅ m d'

⋅ ξeff

⋅

fyd

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

ms

M

fcd 1

⋅ m

⋅

d'

2

⋅

:=

d'

d

bz

6

+

:=

Przypadek b)

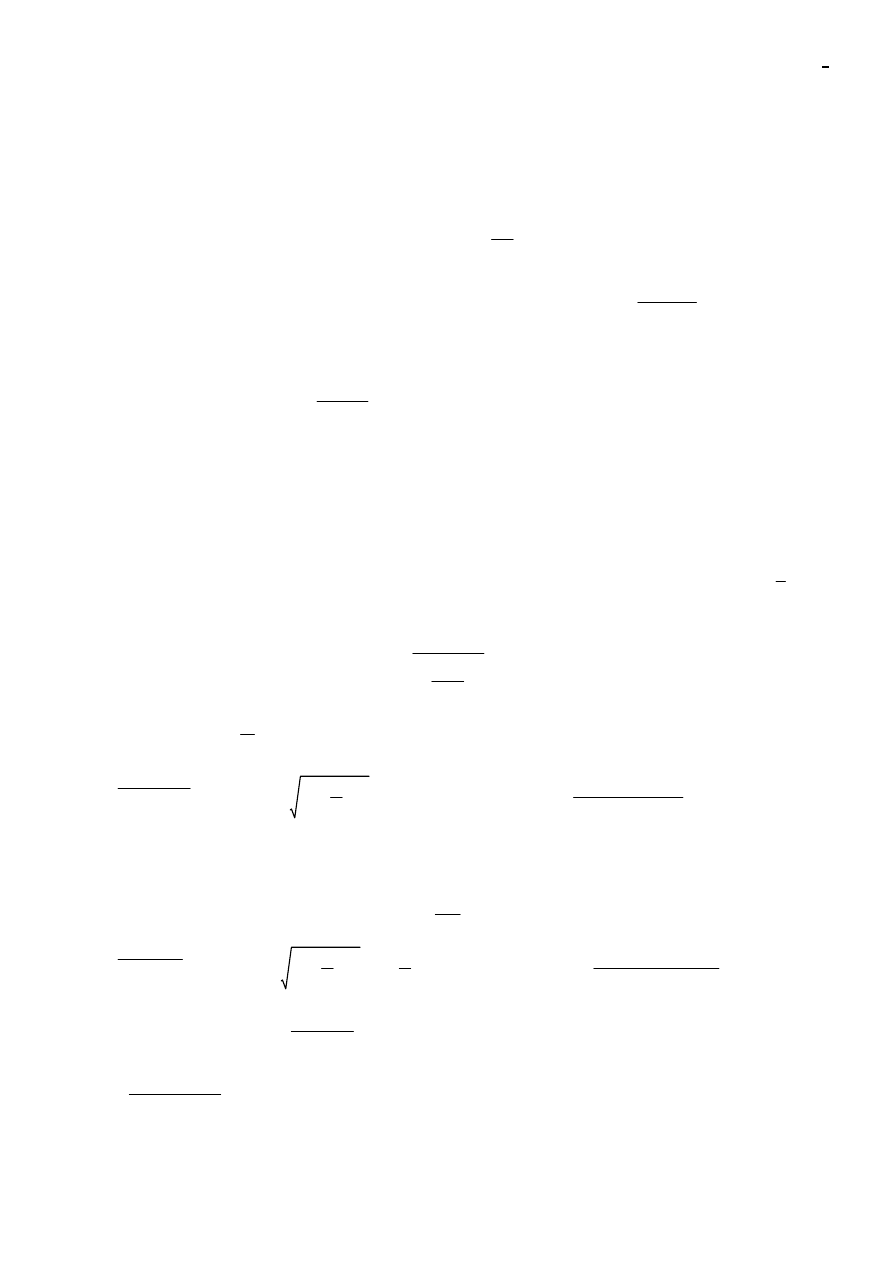
8

Mp M

>

1

=

Pozornie teowy

ms

M

fcd beff

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

beff

⋅

d

⋅ ξeff

⋅

fyd

:=

As1 18.576 cm

2

=

Przyjnuję 6 prętów

φ25 co odpowiada 29.45cm

2

Podpora B

•

M

425.52kNm

:=

q

Gsp Gzp

+

:=

M'

M

q

bp

2

Lpz

⋅

−

:=

ms

M'

fcd bp

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

1

2

α

ms

⋅

−

0.255

−

=

A's1

α fcd

⋅

bp

⋅

ξeff.lim

⋅

d

⋅

fyd

:=

M'sd α fcd

⋅

bp

⋅

ξeff.lim

⋅

d

⋅

d

ξeff.lim d

⋅

2

−










⋅

:=

M'sd 263.765 kNm

=

∆Msd M' M'sd

−

:=

∆Msd 159.533kNm

=

A''s1

∆Msd

fyd d 5cm

−

(

)

⋅

:=

As2 A''s1

:=

As1 A's1 A''s1

+

:=

As2 10.14 cm

2

=

As1 29.20 cm

2

=

Przyjmuje 6 prętów

φ25 (29.45 cm

2

)

Podciąg: Beton B20, Stal AIII

Zmiana danych dla stali:

Obliczeniowa granica plastyczności stali uzwojenia AIII

fyd 350MPa

:=

Odksztalcenie stali odpowiadajace naprężeniu fyd

εs

fyd

Es

:=

εs 1.75 10

3

−

×

=

Graniczna wartość względem wysokości strefy ściskania przekroju:

ξeff.lim 0.8

εcu

εcu εs

+









⋅

:=

ξeff.lim 0.53

=

Charakterystyczna granica plastyczności stali zbrojeniowej

fyk 355MPa

:=

Efektywna szerokość:

beff bp

Lpz 0.7

⋅

5

+

:=

beff 1.476 m

=

Przeslo AB

•

M

438.88kNm

:=

Przyjęta średnica prętów:

φ

25mm

:=

φs 8mm

:=

Wysokość użyteczna przekroju

d

hp a1

−

φ
2

−

φs

−

:=

As.min max 0.0015 1

⋅ m d

⋅

0.6 beff

⋅

d

⋅

fyk

MPa













:=

As.min 12.461 cm

2

=

Mp α fcd

⋅

beff

⋅

hf

⋅

d

hf

2

−










⋅

:=

Mp 597.779 kNm

=

9

d

49.95 cm

=

Wytrzymałoć charakterystyczna na ściskanie:

fck 16MPa

:=

Współczynnik doprowadzenia do podpory zbrojenia:

k

1

:=

Wytrzymałoć na ścinanie:

τRd 0.22MPa

:=

Powierzchnia głównego zbrojenia rozciąganego w przekroju:

AsL 29.45cm

2

:=

π φs

2

⋅

4

0.503 cm

2

=

Naprężenie:

σcp 0Pa

:=

Współczynnik:

ν

0.7

fck

MPa

200

−

:=

Współczynnik:

z

0.9 d

⋅

:=

z

44.96 cm

=

Przyjmujemy:

cot

θ

( )

1

=

Pole strzemion/a:

Asw1 4 0.503

⋅

cm

2

:=

Strzemiona dwucięte

Granica plastyczności strzemion:

fywd1 fyd

:=

Wymiarowanie podciągu na ścinanie.

VRd1 - graniczna siła poprzeczna ze względu na ukośne rozciąganie powstające przy ścinaniu w elemencie nie

mającym poprzecznego zbrojenia na ścinanie

VRd2 - graniczna siła poprzeczna ze względu na ukośne ściskanie, powstające przy ścinaniu w elementach

zginanych

VRd3 - graniczna siła poprzeczna ze względu na rozciąganie poprzecznego zbrojenia na rozciąganie

poprzecznego zbrojenia na ścinanie

Dane projektowe:

Strzemiona A0, Beton B20

Przepisanie danych dla stali A0:

Obliczeniowa granica plastyczności stali uzwojenia:

fyd 190MPa

:=

fctd 0.87MPa

:=

Charakterystyczna granica plastyczności stali zbrojeniowej

fyk 220MPa

:=

Moduł sprężystości stali zwykłej

Es

200 10

3

MPa

⋅

:=

Odkształcenie stali odpowiadajace naprezeniu fyd

εs

fyd

Es

:=

εs 9.5 10

4

−

×

=

Otulina dla środowiska wilgotnego z mrozem:

a1 3cm

:=

Średnica zbrojenia głównego: φ

25mm

:=

Średnica strzemion:

φs 8mm

:=

Wysokość użyteczna przekroju

d

hp a1

−

φ
2

−

φs

−

:=

10

Vsd VRd1

>

0

=

Odcinek I-go rodzaju

VRd2 ν fcd

⋅

bp

⋅

z

⋅ 0.5

⋅

:=

Vsd

1
5

VRd2

<

1

=

s2 0.6 d

⋅

:=

s2 0.30m

=

Vsd 258.06kN

:=

Stopień zbrojenia: ρL

AsL

bp d

⋅

:=

ρL 0.02

=

VRd1

0.35 k

⋅ fctd

⋅

1.2

40

ρL

⋅

+

(

)

⋅

0.15

σcp

⋅

+





bp

⋅

d

⋅

:=

Vsd VRd1

>

1

=

VRd2 ν fcd

⋅

bp

⋅

z

⋅ 0.5

⋅

:=

Vsd VRd2

<

1

=

Maksymalny rozstaw strzemion tak aby był spełniony warunek poniżej:

s1 0.06m

:=

VRd3

Asw1 fywd1

⋅

s1

z

⋅ 1

⋅

:=

Vsd VRd3

≤

1

=

Vsd 156.74kN

:=

Stopień zbrojenia: ρL

AsL

bp d

⋅

:=

ρL 0.02

=

VRd1

0.35 k

⋅ fctd

⋅

1.2

40

ρL

⋅

+

(

)

⋅

0.15

σcp

⋅

+





bp

⋅

d

⋅

:=

Vsd VRd1

>

1

=

VRd1 90.625 kN

=

VRd2 ν fcd

⋅

bp

⋅

z

⋅ 0.5

⋅

:=

Vsd VRd2

<

1

=

Maksymalny rozstaw strzemion tak aby był spełniony warunek poniżej:

s1 0.10m

:=

VRd3

Asw1 fywd1

⋅

s1

z

⋅ 1

⋅

:=

Vsd VRd3

≤

1

=

Vsd 50.66kN

:=

Stopień zbrojenia: ρL

AsL

bp d

⋅

:=

ρL 0.02

=

VRd1

0.35 k

⋅ fctd

⋅

1.2

40

ρL

⋅

+

(

)

⋅

0.15

σcp

⋅

+





bp

⋅

d

⋅

:=

11

Mp 270.931 kNm

=

Mp M

>

1

=

Pozornie teowy

ms

M

fcd beff

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

beff

⋅

d

⋅ ξeff

⋅

fyd

:=

As1 8.277 cm

2

=

Przyjnuję 4 prętów

φ20 co odpowiada 12.57cm

2

Przeslo BC

•

M

57.58kNm

:=

Mp α fcd

⋅

beff

⋅

hf

⋅

d

hf

2

−










⋅

:=

Mp 270.931 kNm

=

Mp M

>

1

=

Pozornie teowy

ms

M

fcd beff

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

beff

⋅

d

⋅ ξeff

⋅

fyd

:=

As1 4.692 cm

2

=

Żebro: Beton B20, Stal AIII

fyd 350MPa

:=

Efektywna szerokość:

beff bz

Lz 0.7

⋅

5

+

:=

beff 0.97m

=

99.49

118.72

57.58

118.72

99.49

Obwiednia momentów dla ŻEBRA

22.65

18.65

22.65

A

B

C

D

Przeslo AB

•

φ

20mm

:=

M

99.49kNm

:=

Przyjęta średnica prętów:

φ

20mm

:=

Wysokość użyteczna przekroju

d

hz a1

−

φ
2

−

:=

As.min max 0.0015 1

⋅ m d

⋅

0.6 beff

⋅

d

⋅

fyk

MPa













:=

As.min 9.524 cm

2

=

Współczynnik:

z

0.9 d

⋅

:=

Mp α fcd

⋅

beff

⋅

hf

⋅

d

hf

2

−










⋅

:=

12

Średnica zbrojenia głównego: φ

20mm

:=

Otulina dla środowiska wilgotnego z mrozem:

a1 3cm

:=

AsL 15.70cm

2

:=

Wysokość użyteczna przekroju

d

hz a1

−

φ
2

−

φs

−

:=

d

35.2 cm

=

Stopień zbrojenia: ρL

AsL

bp d

⋅

:=

ρL 0.015

=

Vsd 120.09kN

:=

VRd1

0.35 k

⋅ fctd

⋅

1.2

40

ρL

⋅

+

(

)

⋅

0.15

σcp

⋅

+





bz

⋅

d

⋅

:=

Vsd VRd1

>

1

=

VRd2 ν fcd

⋅

bp

⋅

z

⋅ 0.5

⋅

:=

Vsd VRd2

<

1

=

Maksymalny rozstaw strzemion tak aby był spełniony warunek poniżej:

s1 0.10m

:=

VRd3

Asw1 fywd1

⋅

s1

z

⋅ 1

⋅

:=

Vsd VRd3

≤

1

=

Przyjmuje 4 pręty

φ20 (12.57 cm

2

)

As1 As.min

<

1

=

Podpora B

•

M

118.72kNm

:=

q

gsz gzz

+

:=

M'

M

q m

⋅

bz

2

Lz

⋅

−

:=

ms

M'

fcd beff

⋅

d

2

⋅

:=

ξeff 1

1

2

α

ms

⋅

−

−

:=

ξeff ξeff.lim

<

1

=

As1

α fcd

⋅

beff

⋅

d

⋅ ξeff

⋅

fyd

:=

As1 9.952 cm

2

=

Przyjmuje 4 pręty

φ20 (12.57 cm

2

)

Wymiarowanie przypodporowe odcinka żebra na ścinanie.

Strzemiona A0, Beton B20

84.34

120.09

107.70

120.09

107.70

84.34

Obwiednia sił poprzecznych ŻEBRA

Średnica strzemion:

φs 8mm

:=

Pole strzemion/a:

Asw1 4 0.503

⋅

cm

2

:=

Strzemiona dwucięte

13

φ

25mm

:=

Wymagana długość zakotwienia dla podciągu

Przyczepnoć obliczeniowa:

fbd

2MPa

:=

Podstawowa długość zakotwienia:

Lb

φ
4

fyd
fbd

⋅

:=

Lb 109.375 cm

=

As.req 29.957cm

2

:=

As.prov

34.36cm

2

:=

Współczynnik efektywności zakotwienia:

αa 1

:=

Wymagana długość zakotwienia:

Lb.net αa Lb

⋅

As.req

As.prov

⋅

:=

Lb.net 95.36 cm

=