
PROJEKT MONOLITYCZNEJ
RAMY ŻELBETOWEJ

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
1
Zawartość projektu:
str.
1. Skrócony opis techniczny obiektu
2
2. Rozplanowanie rozmieszczenia dylatacji
3. Dobór konstrukcji stropu, stropodachu oraz ścian osłonowych
4. Zebranie obciążeń
5. Wstępne zaprojektowanie przekrojów
6. Dobór elementów stężających
7. Schematy obciążeń
8. Obliczenia statyczno – wytrzymałościowe układu ramowego
a) Wymiarowanie przekrojów na zginanie
b) Wymiarowanie przekrojów na ścinanie
c) Stan graniczny użytkowalności
d) Wymiarowanie przekrojów na ściskanie
e) Warunki konstrukcyjne kotwienia i łączenia prętów
f) Wymiarowanie stóp fundamentowych
9. Zestawienie stali zbrojeniowej
10. Literatura i normy

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
2
1. Skrócony opis techniczny obiektu
Obiekt stanowi rama żelbetowa o długości L=78,0[m], szerokości B=18,6[m] i całkowitej
wysokości H=10,35[m]. Pochylenie rygla dachowego wynosi α=13º. Obiekt posadowiony jest
na terenie typu B w miejscowości Kielce, zatem leży w II strefie obciążenia śniegiem i I
strefie obciążenia wiatrem. Obciążenia są przekazywane poprzez stopy żelbetowe na grunt,
którym jest mało wilgotny piasek drobnoziarnisty o stopniu zagęszczenia I
D
=0,7. Słupy
rozstawione są w odległości 6,0[m].
2. Rozplanowanie rozmieszczenia dylatacji
Dylatacje o szerokości osiowej między słupami 0,6[m] planuje się wykonać w odległości, co
30,0[m] od czoła obiektu wg poniższego rysunku:
3. Dobór konstrukcji stropu, stropodachu oraz ścian osłonowych.
Konstrukcję stropu stanowi układ warstw, których przekrój przedstawiony jest na poniższym
rysunku, których elementem nośnym jest płyta żelbetowa o grubości 0,24[m].
Konstrukcję stropodachu stanowi układ warstw, z których zasadniczym elementem są płyty
panwiowe, natomiast zewnetrzną pokrywę tworzy blacha stalowa.
Konstrukcja ścian osłonowych została wykonana z lekkich ognioodpornych płyt
warstwowych o grubości 0,24[m]. Okładziny zewnętrzne wykonane są z blachy stalowej
cynkowanej na gorąco, natomiast rdzeń stanowi wełna mineralna. Płyty spełniają wymagania
normy ISO 9001.

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
3
4. Zebranie obciążeń
a) Obciążenie śniegiem wg PN-80/B-02010
Obciążenie charakterystyczne:
C
Q
S
k
k
⋅
=
Dla zadanego obiektu wartości obciążenia charakterystycznego śniegiem gruntu i
współczynnika kształtu dachu wynoszą:
[
]
[
]
2
2
/
72
,
0
8
,
0
9
,
0
8
,
0
/
9
,
0
m
kN
C
Q
S
C
m
kN
Q
k
k
k
=
⋅
=
⋅
=
=
=
Obciążenie obliczeniowe wynosi:
[
]
2
/
008
,
1
4
,
1
72
,
0
m
kN
S
S
f
k
=
⋅
=
⋅
=
γ
b) Obciążenie wiatrem wg PN-77/B-02011
Obciążenie charakterystyczne:
β
⋅
⋅
⋅
=
C
C
q
p
e
k
k
Dla zadanego obiektu wartości charakterystycznego ciśnienia prędkości wiatru i
współczynnika ekspozycji wynoszą:
[ ]
[
]
8
,
0
/
25
,
0
250
2
=
=
=
e
k
C
m
kN
Pa
q
Dla budynku o szkielecie żelbetowym i wysokości
[ ]
m
H
50
<
okres drgań własnych wynosi:
216
,
0
6
,
18
35
,
10
09
,
0
09
,
0
=
⋅
=
⋅
=
B
H
T
natomiast logarytmiczny dekrement tłumienia drgań wynosi:
15
,
0
=
∆
Z powyższych wartości wynika (punkt ich przecięcia na wykresie znajduje się w polu B), iż
budynek jest niepodatny na dynamiczne działanie porywów wiatru, zatem wartość
współczynnika działania porywów wiatru wynosi:
8
,
1
=
β
Ponieważ obiekt zakwalifikowany jest do budowli zamkniętych wartość współczynnika
aerodynamicznego zależy jedynie od wartości współczynnika ciśnienia zewnętrznego C
z
.
z
w
z
p
w
C
C
C
C
C
=
−
=
=
0
Wartości współczynnika C
z
dla połaci dachu dwuspadowego określone zostały na podstawie
stosunku
2
11
,
0
0
,
78
2
,
8
≤
=
=
L
h
oraz kąta nachylenia połaci dachowej i zostały przedstawione na
poniższym schemacie:
Wartości współczynnika C
z
dla ścian osłonowych określone zostały na podstawie stosunków:
2
13
,
0
0
,
78
35
,
10
≤
=
=
L
H
oraz
1
24
,
0
0
,
78
6
,
18
≤
=
=
L
B
i przedstawione są na poniższym schemacie:
Obciążenie charakterystyczne dla ściany nawietrznej:
(
)
[
]
2
/
252
,
0
8
,
1
7
,
0
8
,
0
25
,
0
m
kN
p
k
=
⋅
+
⋅
⋅
=
Obciążenie charakterystyczne dla ściany zawietrznej:
(
)
[
]
2
/
144
,
0
8
,
1
4
,
0
8
,
0
25
,
0
m
kN
p
k
−
=
⋅
−
⋅
⋅
=
Obciążenie charakterystyczne dla ścian równoległych do kierunku działania wiatru:
(
)
[
]
2
/
252
,
0
8
,
1
7
,
0
8
,
0
25
,
0
m
kN
p
k
−
=
⋅
−
⋅
⋅
=
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
4
Obciążenie charakterystyczne dla połaci nawietrznej:
(
)
[
]
2
/
324
,
0
8
,
1
9
,
0
8
,
0
25
,
0
m
kN
p
kp
−
=
⋅
−
⋅
⋅
=
Obciążenie charakterystyczne dla połaci zawietrznej:
(
)
[
]
2
/
144
,
0
8
,
1
4
,
0
8
,
0
25
,
0
m
kN
p
ks
−
=
⋅
−
⋅
⋅
=
Obciążenie obliczeniowe:
f
k
p
p
γ
⋅
=
Obciążenie obliczeniowe dla ściany nawietrznej:
[
]
2
/
3276
,
0
3
,
1
252
,
0
m
kN
p
p
f
k
=
⋅
=
⋅
=
γ
Obciążenie obliczeniowe dla ściany zawietrznej:
[
]
2
/
1872
,
0
3
,
1
144
,
0
m
kN
p
p
f
k
−
=
⋅
−
=
⋅
=
γ
Obciążenie obliczeniowe dla ścian równoległych do kierunku działania wiatru:
[
]
2
/
3276
,
0
3
,
1
252
,
0
m
kN
p
p
f
k
−
=
⋅
−
=
⋅
=
γ
Obciążenie obliczeniowe dla połaci nawietrznej (parcie wiatru):
[
]
2
/
4212
,
0
3
,
1
324
,
0
m
kN
p
p
f
kp
−
=
⋅
−
=
⋅
=
γ
Obciążenie obliczeniowe dla połaci zawietrznej (ssanie wiatru):
[
]
2
/
1872
,
0
3
,
1
144
,
0
m
kN
p
p
f
ks
−
=
⋅
−
=
⋅
=
γ
c) Zebranie obciążeń dla poszczególnych konstrukcji ramy
Dla stropu:
Lp. Rodzaj
obciążenia
Obc. charakterystyczne
[kN/m
2
]
f
γ
Obc. obliczeniowe
[kN/m
2
]
1. Obciążenia stałe wg PN-82/B-02001:
-posadzka (lastriko)
22,0 kN/m
3
x 0,02 m
0,44 1,3
0,572
-gładź cementowa
21,0 kN/m
3
x 0,03 m
0,63 1,3
0,819
-styropian
0,45 kN/m
3
x 0,04 m
0,018 1,2
0,022
-papa
11,0 kN/m
3
x 0,005 m
0,055 1,2
0,066
-płyta żelbetowa
25,0 kN/m
3
x 0,24 m
6,0 1,1
6,6
-tynk cem.-wap.
19,0 kN/m
3
x 0,015 m
0,285 1,3
0,371
suma g
k
=7,428 g=8,45
2.
Obciążenie zmienne
(charakterystyczne użytkowe)
q
k
=15,0 1,2
q=18,0
Obciążenie całkowite g
k
+q
k
=22,428 g+q=26,45
Obciążenie całkowite na 6mb
158,7 [kN/m]
Dla stropodachu:
Lp. Rodzaj
obciążenia
Obc. charakterystyczne
[kN/m
2
]
f
γ
Obc. obliczeniowe
[kN/m
2
]
1. Obciążenia stałe wg PN-82/B-02001:
-blacha stalowa
0,35
1,2
0,42
-gładź cementowa
21,0 kN/m
3
x 0,03 m
0,63 1,3
0,819
-styropian
0,45 kN/m
3
x 010 m
0,045 1,2
0,054
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
5
-papa
11,0 kN/m
3
x 0,005 m
0,055 1,2
0,066
-płyty panwiowe
25,0 kN/m
3
x 0,15 m
3,75 1,2
4,5
-tynk cem.-wap.
19,0 kN/m
3
x 0,015 m
0,285 1,3
0,371
suma g
k
=5,115 g=6,23
2.
Obciążenie zmienne
(śniegiem)
q
k
=0,72 1,4
q=1,008
Obciążenie całkowite g
k
+q
k
=5,835
g+q=7,238
Obciążenie całkowite na 6mb
43,428 [kN/m]
Dla ścian osłonowych dobrano lekkie ognioodporne płyty warstwowe PAROC grubości
24[cm] o obciążeniu charakterystycznym 1,389 [kN/m
2
]i obliczeniowym 1,667 [kN/m
2
].
5. Wstępne zaprojektowanie przekrojów
Do celów projektowych zakładam:
- klasę betonu B-30: f
cd
=16,7[MPa] f
ctm
=2,6[MPa]
- zbrojenie A-III: f
yd
=350[MPa] E
S
=200[GPa]
- klasę środowiska XC3
- początkową średnica zbrojenia Φ=20[mm]
- stopień zbrojenia na poziomie ρ=1%=0,01
Określenie grubości otulenia prętów zbrojenia (Φ
s
-pomijamy):
[ ]
[ ]
[ ]
[ ]
[ ]
mm
c
a
mm
c
c
c
mm
mm
d
mm
c
s
nom
nom
g
36
2
20
0
26
2
26
5
21
20
21
5
16
5
20
max
1
min
min
=
+
+
=
+
+
=
=
+
=
∆
+
=
=
+
=
+
≥
=
≥
=
φ
φ
φ
Przyjmuję grubość otulenia a
1
=4,0[cm].
a) Obliczenie wymiarów geometrycznych przekroju rygla stropu (b
w
=0,35[m]):
Obliczenie momentu przęsłowego:
[ ]
[ ]
(
)
( )
[
]
kNm
l
p
M
m
kN
c
l
q
g
p
m
kN
m
m
m
kN
c
eff
wl
wl
095
,
1025
8
0
,
7
363
,
167
8
363
,
167
663
,
8
0
,
6
45
,
26
663
,
8
1
,
1
9
,
0
35
,
0
25
2
2
3
=
⋅
=
⋅
=
=
+
⋅
=
+
⋅
+
=
=
⋅
⋅
⋅
=
[
]
kNm
M
M
sd
822
,
768
095
,
1025
75
,
0
75
,
0
=
⋅
=
⋅
=
Obliczenie użytecznej wysokości przekroju:
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
6
[ ]
m
A
b
f
M
d
A
f
f
w
cd
sd
eff
eff
eff
eff
cd
yd
eff
837
,
0
1876
,
0
35
,
0
16700
822
,
768
1876
,
0
8952
,
0
2096
,
0
8952
,
0
2096
,
0
5
,
0
1
5
,
0
1
2096
,
0
01
,
0
7
,
16
350
0
0
=
⋅
⋅
=
⋅
⋅
=
=
⋅
=
⋅
=
=
⋅
−
=
⋅
−
=
=
⋅
=
⋅
=
ζ
ξ
ξ
ζ
ρ
ξ
Obliczenie wysokości przekroju:
[ ]
[ ]
m
m
a
d
h
9
,
0
877
,
0
04
,
0
837
,
0
1
≈
=
+
=
+
=
Sprawdzenie stanu granicznego ugięcia:
[ ]
[ ]
[
]
[
]
283
,
16
857
,
0
19
19
133
,
6
773
,
331
250
86
,
0
0
,
7
250
250
773
,
331
00301
,
0
86
,
0
8952
,
0
822
,
768
00301
,
0
86
,
0
35
,
0
01
,
0
857
,
0
0
,
7
03
,
0
200
200
86
,
0
04
,
0
9
,
0
1
2
lim
1
1
=
⋅
=
⋅
≤
=
⋅
=
⋅
≠
=
⋅
⋅
=
⋅
⋅
=
=
⋅
⋅
=
⋅
⋅
=
=
⋅
=
⋅
=
=
−
=
−
=
n
d
l
MPa
MPa
A
d
M
m
d
b
A
l
a
n
m
a
h
d
s
eff
s
eff
sd
s
s
eff
σ
ζ
σ
ρ
b) Obliczenie wymiarów geometrycznych przekroju rygla stropodachu (b
w
=0,35[m]) dla
rozpiętości maksymalnej 7,0[m] (dla rozpiętości 5,8[m] przyjmuję wartość taką samą
jak dla 7,0[m]):
Obliczenie momentu przęsłowego:
[ ]
[ ]
(
)
( )
[
]
kNm
l
p
M
m
kN
c
l
q
g
p
m
kN
m
m
m
kN
c
eff
wl
wl
473
,
295
8
0
,
7
241
,
48
8
241
,
48
813
,
4
0
,
6
238
,
7
813
,
4
1
,
1
5
,
0
35
,
0
25
2
2
3
=
⋅
=
⋅
=
=
+
⋅
=
+
⋅
+
=
=
⋅
⋅
⋅
=
[
]
kNm
M
M
sd
605
,
221
473
,
295
75
,
0
75
,
0
=
⋅
=
⋅
=
Obliczenie użytecznej wysokości przekroju:
[ ]
m
A
b
f
M
d
A
f
f
w
cd
sd
eff
eff
eff
eff
cd
yd
eff
45
,
0
1876
,
0
35
,
0
16700
605
,
221
1876
,
0
8952
,
0
2096
,
0
8952
,
0
2096
,
0
5
,
0
1
5
,
0
1
2096
,
0
01
,
0
7
,
16
350
0
0
=
⋅
⋅
=
⋅
⋅
=
=
⋅
=
⋅
=
=
⋅
−
=
⋅
−
=
=
⋅
=
⋅
=
ζ
ξ
ξ
ζ
ρ
ξ
Obliczenie wysokości przekroju:
[ ]
[ ]
m
m
a
d
h
5
,
0
49
,
0
04
,
0
45
,
0
1
≈
=
+
=
+
=
Sprawdzenie stanu granicznego ugięcia:

Katedra Konstrukcji Betonowych Projekt ramj
7
[ ]
[ ]
[
]
[
]
283
,
16
857
,
0
19
19
382
,
11
253
,
334
250
46
,
0
0
,
7
250
250
253
,
334
00161
,
0
46
,
0
8952
,
0
605
,
221
00161
,
0
46
,
0
35
,
0
01
,
0
857
,
0
0
,
7
03
,
0
200
200
46
,
0
04
,
0
5
,
0
1
2
lim
1
1
=
⋅
=
⋅
≤
=
⋅
=
⋅
≠
=
⋅
⋅
=
⋅
⋅
=
=
⋅
⋅
=
⋅
⋅
=
=
⋅
=
⋅
=
=
−
=
−
=
n
d
l
MPa
MPa
A
d
M
m
d
b
A
l
a
n
m
a
h
d
s
eff
s
eff
sd
s
s
eff
σ
ζ
σ
ρ
Sprawdzenie stanu granicznego ugięcia rygla stropodachu (b
w
=0,35[m]) dla rozpiętości
5,8[m]:
( )
[
]
[
]
kNm
M
M
kNm
l
p
M
sd
eff
139
,
152
851
,
202
75
,
0
75
,
0
851
,
202
8
8
,
5
241
,
48
8
2
2
=
⋅
=
⋅
=
=
⋅
=
⋅
=
[ ]
[ ]
[
]
[
]
19
736
,
13
476
,
229
250
46
,
0
8
,
5
250
250
476
,
229
00161
,
0
46
,
0
8952
,
0
139
,
152
00161
,
0
46
,
0
35
,
0
01
,
0
029
,
0
200
8
,
5
200
2
lim
≤
=
⋅
=
⋅
≠
=
⋅
⋅
=
⋅
⋅
=
=
⋅
⋅
=
⋅
⋅
=
=
=
=
s
eff
s
eff
sd
s
s
eff
d
l
MPa
MPa
A
d
M
m
d
b
A
m
l
a
σ
ζ
σ
ρ
c) Określenie wymiarów geometrycznych przekroju słupa:
[ ]
[ ]
m
b
h
m
b
b
sl
sl
w
sl
6
,
0
525
,
0
35
,
0
5
,
1
5
,
1
35
,
0
≈
=
⋅
=
⋅
≥
=
=
6. Dobór elementów stężających
Dobrano elementy stężające znajdujące się w węzłach ramy o wymiarach przekroju
poprzecznego:
- górne elementy stężające: szerokość 0,25[m], wysokość 0,4[m]
- dolne elementy stężające: szerokość 0,25[m], wysokość 0,5[m]
7. Schematy obciążeń
a) Ciężar własny
Ciężar ściany:
[ ]
kN
008
,
40
0
,
6
0
,
4
667
,
1
=
⋅
⋅
Ciężar górnego elementu stężającego:
[ ]
kN
P
5
,
16
0
,
6
1
,
1
0
,
25
4
,
0
25
,
0
1
=
⋅
⋅
⋅
⋅
=
Ciężar dolnego elementu stężającego wraz z ciężarem ściany osłonowej znajdującej się
bezpośrednio nad nim:
[ ]
kN
P
633
,
60
008
,
40
625
,
20
008
,
40
0
,
6
1
,
1
0
,
25
5
,
0
25
,
0
2
=
+
=
+
⋅
⋅
⋅
⋅
=
Ciężar stropu:
[
]
m
kN
q
7
,
50
1
=
Ciężar stropodachu:
[
]
m
kN
q
38
,
37
2
=
Ciężar słupa:
[
]
m
kN
q
s
775
,
5
1
,
1
0
,
25
6
,
0
35
,
0
=
⋅
⋅
⋅
=

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
8
Moment występujący przy górnym stężeniu:
[
]
kNm
e
P
M
888
,
2
175
,
0
5
,
16
1
1
1
=
⋅
=
⋅
=
Moment występujący przy dolnym stężeniu:
[
]
kNm
e
P
M
611
,
10
175
,
0
633
,
60
2
2
2
=
⋅
=
⋅
=
b) Obciążenie użytkowe
c) Obciążenie śniegiem
d) Obciążenie wiatrem z lewej strony
e) Obciążenie wiatrem z prawej strony
8. Obliczenia statyczno-wytrzymałościowe układu ramowego
a) Wymiarowanie przekrojów na zginanie
Rygiel stropu nr 7
Dane geometryczne rygla i wytrzymałościowe betonu B-30 i stali A-III:
[ ]
[ ]
[ ]
[ ]
m
a
m
d
m
h
m
b
04
,
0
86
,
0
90
,
0
35
,
0
=
=
=
=
[
]
[
]
[
]
[
]
MPa
f
MPa
f
MPa
f
MPa
f
yk
yd
ctm
cd
410
350
6
,
2
7
,
16
=
=
=
=
Wyznaczenie minimalnego zbrojenia:
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
913
,
3
10
913
,
3
86
,
0
35
,
0
0013
,
0
0013
,
0
963
,
4
10
963
,
4
86
,
0
35
,
0
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
b
cm
m
d
b
f
f
A
yk
ctm
S
•
węzeł 5 i 6
[
]
kNm
M
M
Sd
133
,
440
max
7
=
=
[ ]
[ ]
2
2
3
1
lim
,
0
2
2
0
454
,
15
10
5454
,
1
9462
,
0
86
,
0
350000
133
,
440
9462
,
0
1076
,
0
5
,
0
1
5
,
0
1
53
,
0
1076
,
0
1018
,
0
2
1
1
2
1
1
1018
,
0
)
86
,
0
(
35
,
0
16700
133
,
440
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie górą 6Φ20 o A
S1
=18,85[cm
2
] i montażowe dołem 4Φ12 o A
S1
=4,52[cm
2
].
Stopień zbrojenia w węźle:
%
626
,
0
%
100
86
35
85
,
18
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
•
przęsło
[
]
kNm
M
M
Sd
660
,
592
max
7
=
=

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
9
[ ]
[ ]
2
2
3
1
lim
,
0
2
2
0
263
,
21
10
1263
,
2
926
,
0
86
,
0
350000
660
,
592
926
,
0
1481
,
0
5
,
0
1
5
,
0
1
53
,
0
1481
,
0
1371
,
0
2
1
1
2
1
1
1371
,
0
)
86
,
0
(
35
,
0
16700
660
,
592
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie dołem na moment przęsłowy 7Φ20 o A
S1
=21,99[cm
2
] i montażowe górą
4Φ12 o A
S1
=4,52[cm
2
]
Stopień zbrojenia w przęśle:
%
731
,
0
%
100
86
35
99
,
21
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
Rygiel stropodachu nr 8 = nr 11
Dane geometryczne rygla i wytrzymałościowe betonu B-30 i stali A-III:
[ ]
[ ]
[ ]
[ ]
m
a
m
d
m
h
m
b
04
,
0
46
,
0
50
,
0
35
,
0
=
=
=
=
[
]
[
]
[
]
[
]
MPa
f
MPa
f
MPa
f
MPa
f
yk
yd
ctm
cd
410
350
6
,
2
7
,
16
=
=
=
=
Wyznaczenie minimalnego zbrojenia:
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
093
,
2
10
093
,
2
46
,
0
35
,
0
0013
,
0
0013
,
0
,655
2
10
655
,
2
46
,
0
35
,
0
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
b
cm
m
d
b
f
f
A
yk
ctm
S
•
węzeł 8 = 10
[
]
kNm
M
M
Sd
746
,
151
max
11
,
8
=
=
[ ]
[ ]
2
2
3
1
lim
,
0
2
2
0
09
,
10
10
009
,
1
9343
,
0
46
,
0
350000
746
,
151
9343
,
0
1313
,
0
5
,
0
1
5
,
0
1
53
,
0
1313
,
0
1227
,
0
2
1
1
2
1
1
1227
,
0
)
46
,
0
(
35
,
0
16700
746
,
151
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie górą 4Φ20 o A
S1
=12,57[cm
2
] i montażowe dołem 2Φ12 o A
S1
=2,26[cm
2
]
Stopień zbrojenia w węźle:
%
781
,
0
%
100
46
35
57
,
12
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
•
węzeł 7 = 11
[
]
kNm
M
M
Sd
923
,
94
max
11
,
8
=
=

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
10
[ ]
[ ]
2
2
4
1
lim
,
0
2
2
0
14
,
6
10
141
,
6
96
,
0
46
,
0
350000
923
,
94
96
,
0
0799
,
0
5
,
0
1
5
,
0
1
53
,
0
0799
,
0
0767
,
0
2
1
1
2
1
1
0767
,
0
)
46
,
0
(
35
,
0
16700
923
,
94
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie górą 3Φ20 o A
S1
=9,42[cm
2
] i montażowe dołem 2Φ12 o A
S1
=2,26[cm
2
]
Stopień zbrojenia w węźle:
%
585
,
0
%
100
46
35
42
,
9
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
•
przęsło:
[
]
kNm
M
M
Sd
949
,
92
max
11
,
8
=
=
[ ]
[ ]
2
2
4
1
lim
,
0
2
2
0
01
,
6
10
008
,
6
9609
,
0
46
,
0
350000
949
,
92
9609
,
0
0782
,
0
5
,
0
1
5
,
0
1
53
,
0
0782
,
0
0752
,
0
2
1
1
2
1
1
0752
,
0
)
46
,
0
(
35
,
0
16700
949
,
92
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie dołem na moment przęsłowy 3Φ20 o A
S1
=9,42[cm
2
] i montażowe górą
2Φ12 o A
S1
=2,26[cm
2
]
Stopień zbrojenia w przęśle:
%
585
,
0
%
100
46
35
42
,
9
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
Rygiel stropodachu nr 9 = nr 10 (zakrzywiony)
Dane geometryczne rygla i wytrzymałościowe betonu B-30 i stali A-III:
[ ]
[ ]
[ ]
[ ]
m
a
m
d
m
h
m
b
04
,
0
46
,
0
50
,
0
35
,
0
=
=
=
=
[
]
[
]
[
]
[
]
MPa
f
MPa
f
MPa
f
MPa
f
yk
yd
ctm
cd
410
350
6
,
2
7
,
16
=
=
=
=
Wyznaczenie minimalnego zbrojenia:
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
093
,
2
10
093
,
2
46
,
0
35
,
0
0013
,
0
0013
,
0
,655
2
10
655
,
2
46
,
0
35
,
0
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
b
cm
m
d
b
f
f
A
yk
ctm
S
•
węzeł 8 = 10:
[
]
kNm
M
M
Sd
568
,
188
max
10
,
9
=
=

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
11
[ ]
[ ]
2
2
3
1
lim
,
0
2
2
0
77
,
12
10
277
,
1
9169
,
0
46
,
0
350000
586
,
188
9169
,
0
1663
,
0
5
,
0
1
5
,
0
1
53
,
0
1663
,
0
1525
,
0
2
1
1
2
1
1
1525
,
0
)
46
,
0
(
35
,
0
16700
568
,
188
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie górą 5Φ20 o A
S1
=15,71[cm
2
] i montażowe dołem 3Φ12 o A
S1
=3,39[cm
2
]
Stopień zbrojenia w węźle:
%
976
,
0
%
100
46
35
71
,
15
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
•
węzeł 9 - załamanie (M
max
przy węźle):
[
]
kNm
M
M
Sd
617
,
82
max
10
,
9
=
=
[ ]
[ ]
2
2
4
1
lim
,
0
2
2
0
32
,
5
10
315
,
5
9654
,
0
46
,
0
350000
617
,
82
9654
,
0
0692
,
0
5
,
0
1
5
,
0
1
53
,
0
0692
,
0
0668
,
0
2
1
1
2
1
1
0668
,
0
)
46
,
0
(
35
,
0
16700
617
,
82
cm
m
d
f
M
A
A
d
b
f
M
A
eff
yd
sd
S
eff
eff
eff
eff
cd
sd
=
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
−
=
−
=
=
≤
=
⋅
−
−
=
−
−
=
=
⋅
⋅
=
⋅
⋅
=
−
ζ
ξ
ζ
ξ
ξ
Przyjęto zbrojenie dołem przy wężle 2Φ20 o A
S1
=6,28[cm
2
] i montażowe górą 2Φ12 o
A
S1
=2,26[cm
2
]
Stopień zbrojenia:
%
39
,
0
%
100
46
35
28
,
6
%
100
1
=
⋅
⋅
=
⋅
⋅
=
d
b
A
S
L
ρ
b) Wymiarowanie przekrojów na ścinanie
Nie zastosowano prętów odgiętych, gdyż założono, iż całkowitą siłę poprzeczną przenoszą
strzemiona prostopadłe do osi belki.
Określenie minimalnej średnicy strzemion z warunków normowych:
[ ]
[ ]
[ ]
mm
mm
mm
s
s
8
4
20
2
,
0
2
,
0
5
,
4
=
⇒
=
⋅
=
⋅
≥
φ
φ
φ
Rygiel stropu nr 7 (węzeł 5 i 6)
Przyjmuję strzemiona czterocięte Φ8 ze stali A-I.
[ ]
kN
V
V
Sd
245
,
586
max
7
7
=
=
Obliczenie siły tnącej w odległości a
1
i d od lica podpory:
(
)
[ ]
(
)
[ ]
kN
q
g
d
V
V
kN
q
g
a
V
V
k
Sd
d
Sd
Sd
k
Sd
018
,
393
575
,
166
86
,
0
273
,
536
273
,
536
575
,
166
3
,
0
245
,
586
7
,
7
,
1
7
7
,
=
⋅
−
=
+
⋅
−
=
=
⋅
−
=
+
⋅
−
=
Obliczenie nośności odcinków pierwszego rodzaju:

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
12
(
)
=
⋅
=
⋅
≤
=
⋅
=
=
≥
=
−
=
−
=
≤
=
⋅
=
⋅
=
2
2
1
3340
16700
2
,
0
2
,
0
879
,
142
9
,
0
35
,
0
007
,
45
0
,
1
74
,
0
86
,
0
6
,
1
6
,
1
01
,
0
00626
,
0
86
35
85
,
18
m
kN
f
m
kN
A
N
k
d
k
d
b
A
cd
c
Sd
cp
S
L
σ
ρ
(
)
[
]
(
)
[
]
[ ]
kN
f
k
d
b
V
cp
L
ctd
Rd
811
,
189
879
,
142
15
,
0
00626
,
0
40
2
,
1
1200
0
,
1
35
,
0
86
,
0
35
,
0
15
,
0
40
2
,
1
35
,
0
1
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
σ
ρ
1
,
Rd
d
Sd
V
V
≥
Ponieważ warunek nie jest spełniony, należy policzyć nośność odcinków drugiego rodzaju
(dozbrajanie na ścinanie jest potrzebne), ponadto przekrój obciążony jest dodatkowo siłami
ściskającymi, więc nośność odcinków drugiego należy zredukować.
[ ]
[ ]
kN
z
b
f
V
f
m
d
z
cd
Rd
ck
488
,
1221
774
,
0
35
,
0
16700
54
,
0
5
,
0
5
,
0
54
,
0
250
25
1
6
,
0
250
1
6
,
0
774
,
0
86
,
0
9
,
0
9
,
0
2
=
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
=
−
⋅
=
−
⋅
=
=
⋅
=
⋅
=
ν
ν
[ ]
kN
V
V
f
m
kN
f
m
kN
Rd
c
red
Rd
cd
cp
c
cd
cp
939
,
1231
488
,
1221
009
,
1
009
,
1
16700
879
,
142
1
1
4175
16700
25
,
0
25
,
0
879
,
142
0
2
,
2
2
2
=
⋅
=
⋅
=
=
+
=
+
=
=
⋅
=
⋅
<
=
<
α
σ
α
σ
red
Rd
d
Sd
Rd
V
V
V
,
2
,
1
≤
≤
Obliczenie długości odcinka ścinania drugiego rodzaju:
[ ]
m
q
g
V
V
l
Rd
k
Sd
t
12
,
2
575
,
166
36
,
183
273
,
536
1
,
=
−
=
+
−
=
Określenie maksymalnego rozstawu ramion strzemion:
[ ]
[ ]
=
⋅
=
⋅
≤
cm
d
cm
s
645
,
0
86
,
0
75
,
0
75
,
0
40
max
1
Obliczenie odległości między
strzemionami:
[ ]
m
z
V
f
A
s
d
Sd
ywd
sw
125
,
0
5
,
1
774
,
0
018
,
393
210000
000201
,
0
cot
5
,
1
cot
,
1
1
1
=
⋅
⋅
⋅
=
⋅
⋅
⋅
≤
=
θ
θ
Przyjęto na odcinku l
t
=2,12[m] strzemiona w rozstawie 0,12[m] i w rozstawie 0,20[m] na
pozostałym.
Obliczenie nośności odcinków drugiego rodzaju, gdy zbrojenie na ścinanie składa się tylko ze
strzemion prostopadłych do osi belki:
[ ]
kN
z
b
f
V
cd
Rd
527
,
1127
5
,
1
1
5
,
1
774
,
0
35
,
0
16700
54
,
0
cot
1
cot
2
2
2
=
+
⋅
⋅
⋅
⋅
=
+
⋅
⋅
⋅
⋅
=
θ
θ
ν
[ ]
kN
z
s
f
A
V
ywd
sw
Rd
508
,
408
5
,
1
774
,
0
12
,
0
210000
000201
,
0
cot
1
1
1
3
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
θ
3
2
,
,
Rd
Rd
d
Sd
V
V
V
≤
Stopień zbrojenia strzemionami na ścinanie:

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
13
0017
,
0
240
25
08
,
0
08
,
0
00479
,
0
12
35
0106
,
2
min
1
1
1
1
=
⋅
=
⋅
=
≥
=
⋅
=
⋅
=
yk
ck
w
w
sw
w
f
f
s
b
A
ρ
ρ
ρ
Obliczenie nośności zbrojenia rozciąganego (głównego) na odcinkach drugiego rodzaju w
odległości l
t
od podpory 5 i 6:
[ ]
[ ]
[ ]
[ ]
kN
f
A
F
kN
F
z
M
F
kN
V
F
m
l
yd
S
td
td
Sd
td
l
Sd
td
t
t
65
,
769
350000
002199
,
0
69
,
738
83
,
174
774
,
0
428
,
436
83
,
174
5
,
1
106
,
233
5
,
0
cot
5
,
0
12
,
2
1
,
=
⋅
=
⋅
≤
=
+
=
∆
+
=
=
⋅
⋅
=
⋅
⋅
=
∆
=
θ
Obliczenie nośności zbrojenia rozciąganego (głównego) na odcinkach drugiego rodzaju w
odległości a
L
od podpory 5 i 6:
[ ]
[ ]
[ ]
[ ]
kN
f
A
F
kN
F
z
M
F
kN
V
F
m
z
a
yd
S
td
td
Sd
td
a
Sd
td
L
L
65
,
769
350000
002199
,
0
301
,
474
358
,
297
774
,
0
954
,
136
358
,
297
5
,
1
477
,
396
5
,
0
cot
5
,
0
581
,
0
5
,
1
774
,
0
5
,
0
cot
5
,
0
1
,
=
⋅
=
⋅
≤
=
+
=
∆
+
=
=
⋅
⋅
=
⋅
⋅
=
∆
=
⋅
⋅
=
⋅
⋅
=
θ
θ
Nie ma potrzeby dokonywania dodatkowego dozbrajania na ścinanie, gdyż warunki nośności
zbrojenia zostały spełnione.
Rygiel stropodachu nr 8 i 11 (węzeł 7 i 11)
[ ]
kN
V
V
Sd
213
,
132
max
11
,
8
11
,
8
=
=
Siła tnąca w odległości a
1
i d od lica podpory:
[ ]
[ ]
kN
V
kN
V
d
Sd
k
Sd
007
,
98
830
,
116
11
,
8
,
11
,
8
,
=
=
Obliczenie nośności odcinków pierwszego rodzaju:
(
)
=
⋅
=
⋅
≤
=
⋅
=
=
≥
=
−
=
−
=
≤
=
⋅
=
⋅
=
2
2
1
3340
16700
2
,
0
2
,
0
811
,
285
5
,
0
35
,
0
017
,
50
0
,
1
14
,
1
46
,
0
6
,
1
6
,
1
01
,
0
00585
,
0
46
35
42
,
9
m
kN
f
m
kN
A
N
k
d
k
d
b
A
cd
c
Sd
cp
S
L
σ
ρ
(
)
[
]
(
)
[
]
[ ]
kN
f
k
d
b
V
cp
L
ctd
Rd
445
,
117
811
,
285
15
,
0
00585
,
0
40
2
,
1
1200
14
,
1
35
,
0
46
,
0
35
,
0
15
,
0
40
2
,
1
35
,
0
1
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
σ
ρ
1
,
Rd
d
Sd
V
V
≤
Ponieważ warunek jest spełniony, dozbrajanie na ścinanie nie jest potrzebne, występują zatem
tylko odcinki pierwszego rodzaju. Przekrój obciążony jest dodatkowo siłami ściskającymi,
więc nośność odcinków pierwszego rodzaju należy zredukować.

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
14
[ ]
[ ]
kN
z
b
f
V
f
m
d
z
cd
Rd
ck
354
,
653
414
,
0
35
,
0
16700
54
,
0
5
,
0
5
,
0
54
,
0
250
25
1
6
,
0
250
1
6
,
0
414
,
0
46
,
0
9
,
0
9
,
0
2
=
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
=
−
⋅
=
−
⋅
=
=
⋅
=
⋅
=
ν
ν
[ ]
kN
V
V
f
m
kN
f
m
kN
Rd
c
red
Rd
cd
cp
c
cd
cp
536
,
664
354
,
653
017
,
1
017
,
1
16700
811
,
285
1
1
4175
16700
25
,
0
25
,
0
811
,
285
0
2
,
2
2
2
=
⋅
=
⋅
=
=
+
=
+
=
=
⋅
=
⋅
<
=
<
α
σ
α
σ
red
Rd
Rd
d
Sd
V
V
V
,
2
1
,
≤
≤
Określenie maksymalnego rozstawu ramion strzemion posrednich:
[ ]
[ ]
=
⋅
=
⋅
≤
cm
d
cm
s
345
,
0
46
,
0
75
,
0
75
,
0
40
max
1
Przyjęto strzemiona montażowe w rozstawie 0,20[m].
Rygiel stropodachu nr 8 i 11 (węzeł 8 i 10)
[ ]
kN
V
V
Sd
954
,
148
max
11
,
8
11
,
8
=
=
Siła tnąca w odległości a
1
i d od lica podpory:
[ ]
[ ]
kN
V
kN
V
d
Sd
k
Sd
690
,
113
046
,
135
11
,
8
,
11
,
8
,
=
=
Obliczenie nośności odcinków pierwszego rodzaju:
(
)
=
⋅
=
⋅
≤
=
⋅
=
=
≥
=
−
=
−
=
≤
=
⋅
=
⋅
=
2
2
1
3340
16700
2
,
0
2
,
0
811
,
285
5
,
0
35
,
0
017
,
50
0
,
1
14
,
1
46
,
0
6
,
1
6
,
1
01
,
0
00781
,
0
46
35
57
,
12
m
kN
f
m
kN
A
N
k
d
k
d
b
A
cd
c
Sd
cp
S
L
σ
ρ
(
)
[
]
(
)
[
]
[ ]
kN
f
k
d
b
V
cp
L
ctd
Rd
488
,
123
811
,
285
15
,
0
00781
,
0
40
2
,
1
1200
14
,
1
35
,
0
46
,
0
35
,
0
15
,
0
40
2
,
1
35
,
0
1
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
σ
ρ
1
,
Rd
d
Sd
V
V
≤
Ponieważ warunek jest spełniony, dozbrajanie na ścinanie nie jest potrzebne, występują zatem
tylko odcinki pierwszego rodzaju. Przekrój obciążony jest dodatkowo siłami ściskającymi,
więc nośność odcinków pierwszego rodzaju należy zredukować.
[ ]
[ ]
kN
z
b
f
V
f
m
d
z
cd
Rd
ck
354
,
653
414
,
0
35
,
0
16700
54
,
0
5
,
0
5
,
0
54
,
0
250
25
1
6
,
0
250
1
6
,
0
414
,
0
46
,
0
9
,
0
9
,
0
2
=
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
=
−
⋅
=
−
⋅
=
=
⋅
=
⋅
=
ν
ν

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
15
[ ]
kN
V
V
f
m
kN
f
m
kN
Rd
c
red
Rd
cd
cp
c
cd
cp
536
,
664
354
,
653
017
,
1
017
,
1
16700
811
,
285
1
1
4175
16700
25
,
0
25
,
0
811
,
285
0
2
,
2
2
2
=
⋅
=
⋅
=
=
+
=
+
=
=
⋅
=
⋅
<
=
<
α
σ
α
σ
red
Rd
Rd
d
Sd
V
V
V
,
2
1
,
≤
≤
Określenie maksymalnego rozstawu ramion strzemion pośrednich:
[ ]
[ ]
=
⋅
=
⋅
≤
cm
d
cm
s
345
,
0
46
,
0
75
,
0
75
,
0
40
max
1
Przyjęto strzemiona montażowe w rozstawie 0,20[m].
Rygiel stropodachu nr 9 i 10 (węzeł 8 i 10)
[ ]
kN
V
V
Sd
701
,
158
max
10
,
9
10
,
9
=
=
Siła tnąca w odległości a
1
i d od lica podpory:
[ ]
[ ]
kN
V
kN
V
d
Sd
k
Sd
924
,
125
773
,
144
10
,
9
,
10
,
9
,
=
=
Obliczenie nośności odcinków pierwszego rodzaju:
(
)
=
⋅
=
⋅
≤
=
⋅
=
=
≥
=
−
=
−
=
≤
=
⋅
=
⋅
=
2
2
1
3340
16700
2
,
0
2
,
0
029
,
557
5
,
0
35
,
0
48
,
97
0
,
1
14
,
1
46
,
0
6
,
1
6
,
1
01
,
0
00976
,
0
46
35
71
,
15
m
kN
f
m
kN
A
N
k
d
k
d
b
A
cd
c
Sd
cp
S
L
σ
ρ
(
)
[
]
(
)
[
]
[ ]
kN
f
k
d
b
V
cp
L
ctd
Rd
051
,
136
029
,
557
15
,
0
00976
,
0
40
2
,
1
1200
14
,
1
35
,
0
46
,
0
35
,
0
15
,
0
40
2
,
1
35
,
0
1
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
σ
ρ
1
,
Rd
d
Sd
V
V
≤
Ponieważ warunek jest spełniony, dozbrajanie na ścinanie nie jest potrzebne, występują zatem
tylko odcinki pierwszego rodzaju. Przekrój obciążony jest dodatkowo siłami ściskającymi,
więc nośność odcinków pierwszego rodzaju należy zredukować.
[ ]
[ ]
kN
z
b
f
V
f
m
d
z
cd
Rd
ck
354
,
653
414
,
0
35
,
0
16700
54
,
0
5
,
0
5
,
0
54
,
0
250
25
1
6
,
0
250
1
6
,
0
414
,
0
46
,
0
9
,
0
9
,
0
2
=
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
=
−
⋅
=
−
⋅
=
=
⋅
=
⋅
=
ν
ν
[ ]
kN
V
V
f
m
kN
f
m
kN
Rd
c
red
Rd
cd
cp
c
cd
cp
147
,
675
354
,
653
033
,
1
033
,
1
16700
029
,
557
1
1
4175
16700
25
,
0
25
,
0
029
,
557
0
2
,
2
2
2
=
⋅
=
⋅
=
=
+
=
+
=
=
⋅
=
⋅
<
=
<
α
σ
α
σ
red
Rd
Rd
d
Sd
V
V
V
,
2
1
,
≤
≤
Określenie maksymalnego rozstawu ramion strzemion pośrednich:
[ ]
[ ]
=
⋅
=
⋅
≤
cm
d
cm
s
345
,
0
46
,
0
75
,
0
75
,
0
40
max
1

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
16
Przyjęto strzemiona montażowe w rozstawie 0,20[m].
Rygiel stropodachu nr 9 i 10 (węzeł 9 - zakrzywiony)
[ ]
kN
V
V
Sd
616
,
13
max
10
,
9
10
,
9
=
=
Obliczenie minimalnego sumarycznego pola przekroju powierzchni strzemion:
[ ]
[
]
[
]
[ ]
2
2
37
,
2
2
13
sin
210
350
28
,
6
2
2
sin
2
13
210
350
28
,
6
cm
f
f
A
A
MPa
f
MPa
f
cm
A
ywd
yd
S
sw
ywd
yd
S
=
⋅
⋅
⋅
=
⋅
⋅
⋅
≥
°
=
=
=
=
∑
α
α
Określenie maksymalnej długości rozstawienia strzemion:
[ ] [ ]
[ ]
cm
cm
mm
16
2
8
8
2
20
=
⋅
=
⋅
=
=
φ
φ
Przyjęto strzemiona dwucięte Φ8 ze stali A-I w rozstawie 8 cm na długości 16 cm z każdej
strony załamania:
[ ]
[ ]
[ ]
[ ]
2
2
2
2
37
,
2
03
,
5
4
8
,
0
2
5
4
2
5
8
,
0
8
cm
cm
A
cm
mm
s
sw
s
≥
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
=
=
∑
π
φ
π
φ
c) Stan graniczny użytkowalności
Rygiel stropu nr 7
Moment zginający od kombinacji obciążeń długotrwałych (charakterystycznych: obciążenia
stałe+60%zmiennych):
(
)
[
]
kNm
q
g
q
g
M
M
q
g
q
g
M
M
k
k
d
Sd
d
k
Sd
k
k
d
k
Sd
d
Sd
337
,
370
45
,
26
428
,
22
749
,
436
)
(
)
(
=
⋅
=
+
+
⋅
=
⇒
+
+
=
Moment zginający od obciążeń całkowitych (charakterystycznych):
(
)
[
]
kNm
q
g
q
g
M
M
q
g
q
g
M
M
k
k
Sd
k
Sd
k
k
k
Sd
Sd
54
,
502
45
,
26
428
,
22
66
,
592
)
(
)
(
=
⋅
=
+
+
⋅
=
⇒
+
+
=
Wymiary geometryczne rygla:
[ ]
[ ]
[ ]
[ ]
m
a
m
d
m
h
m
b
04
,
0
86
,
0
90
,
0
35
,
0
=
=
=
=
[ ]
m
l
eff
0
,
7
=
Zbrojenie ze stali A-III:
[
]
[
]
[
]
[
]
MPa
GPa
E
MPa
f
MPa
f
s
yk
yd
200000
200
410
350
=
=
=
=
Beton B-30:
[
]
[
]
MPa
f
MPa
f
ctm
cd
6
,
2
7
,
16
=
=
[
]
[
]
MPa
f
MPa
f
ctk
ck
8
,
1
25
=
=
[
]
[
]
MPa
GPa
E
cm
31000
31
=
==
Ugięcie
Obliczenie wskaźnika wytrzymałości przekroju betonu oraz momentu rysującego:
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
17
[ ]
[
]
[
]
[
]
kNm
M
kNm
MNm
W
f
M
m
h
b
W
Sd
C
ctm
Cr
C
54
,
502
85
,
122
12285
,
0
04725
,
0
6
,
2
04725
,
0
6
9
,
0
35
,
0
6
3
2
2
=
<
=
=
⋅
=
⋅
=
=
⋅
=
⋅
=
Przekrój pracuje jako zarysowany (faza II).
0
,
1
1
=
β
- dla prętów żebrowanych:
5
,
0
2
=
β
- przy obciążeniu długotrwałym
Obliczenie stosunku naprężeń w zbrojeniu rozciąganym z warunku:
332
,
0
337
,
370
85
,
122
=
=
=
d
Sd
Cr
s
sr
M
M
σ
σ
Obliczenie współczynnika zależny od schematu statycznego i typu obciążenia:
0887
,
0
660
,
592
10
133
,
440
133
,
440
1
48
5
10
1
48
5
=
⋅
+
−
⋅
=
⋅
+
−
⋅
=
prz
B
A
k
M
M
M
α
Założona wilgotność względna powietrza wynosi RH=50%.
Określenie współczynnika pełzania na podstawie miarodajnego przekroju elementu:
(
)
[ ]
( )
69
,
2
,
252
900
350
2
900
350
2
2
0
0
=
⇒
=
+
⋅
⋅
⋅
=
⋅
=
t
t
mm
u
A
h
c
φ
( )
[
]
81
,
23
08
,
8401
200000
08
,
8401
69
,
2
1
31000
,
1
,
,
0
,
=
=
=
=
+
=
+
=
eff
c
s
t
e
cm
eff
c
E
E
MPa
t
t
E
E
α
φ
J
I
– moment bezwładności przekroju sprowadzonego przekroju w fazie niezarysowanej.
[ ]
m
A
h
b
d
A
h
b
x
S
t
e
S
t
e
I
51
,
0
002199
,
0
81
,
23
9
,
0
35
,
0
86
,
0
002199
,
0
81
,
23
9
,
0
35
,
0
5
,
0
5
,
0
2
1
,
1
,
2
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
α
α
(
)
(
)
(
)
(
)
[ ]
4
2
3
3
2
1
,
3
3
0288
,
0
51
,
0
86
,
0
002199
,
0
81
,
23
3
51
,
0
9
,
0
35
,
0
3
51
,
0
35
,
0
3
3
m
x
d
A
x
h
b
x
b
J
I
S
t
e
I
I
I
=
−
⋅
⋅
+
−
⋅
+
⋅
=
=
−
⋅
⋅
+
−
⋅
+
⋅
=
α
J
II
– moment bezwładności przekroju sprowadzonego przekroju w fazie zarysowanej.
[ ]
m
A
d
b
b
A
x
S
t
e
S
t
e
II
38
,
0
002199
,
0
81
,
23
86
,
0
35
,
0
2
1
1
35
,
0
002199
,
0
81
,
23
2
1
1
1
,
1
,
=
⋅
⋅
⋅
+
+
−
⋅
⋅
=
⋅
⋅
⋅
+
+
−
⋅
⋅
=
α
α
(
)
(
)
[ ]
4
2
3
2
1
,
3
0185
,
0
38
,
0
86
,
0
002199
,
0
81
,
23
3
38
,
0
35
,
0
3
m
x
d
A
x
b
J
II
S
t
e
II
II
=
−
⋅
⋅
+
⋅
=
−
⋅
⋅
+
⋅
=
α
642
,
0
0288
,
0
0185
,
0
=
=
I
II
J
J
Sztywność przekroju zarysowanego przy obciążeniu długotrwałym:
(
) (
)
[
]
[
]
2
2
2
2
2
1
,
158548
548
,
158
642
,
0
1
332
,
0
5
,
0
0
,
1
1
0185
,
0
08
,
8401
1
1
kNm
MNm
J
J
J
E
B
I
II
s
sr
II
eff
c
=
=
=
−
⋅
⋅
⋅
−
⋅
=
−
⋅
⋅
⋅
−
⋅
=
∞
σ
σ
β
β
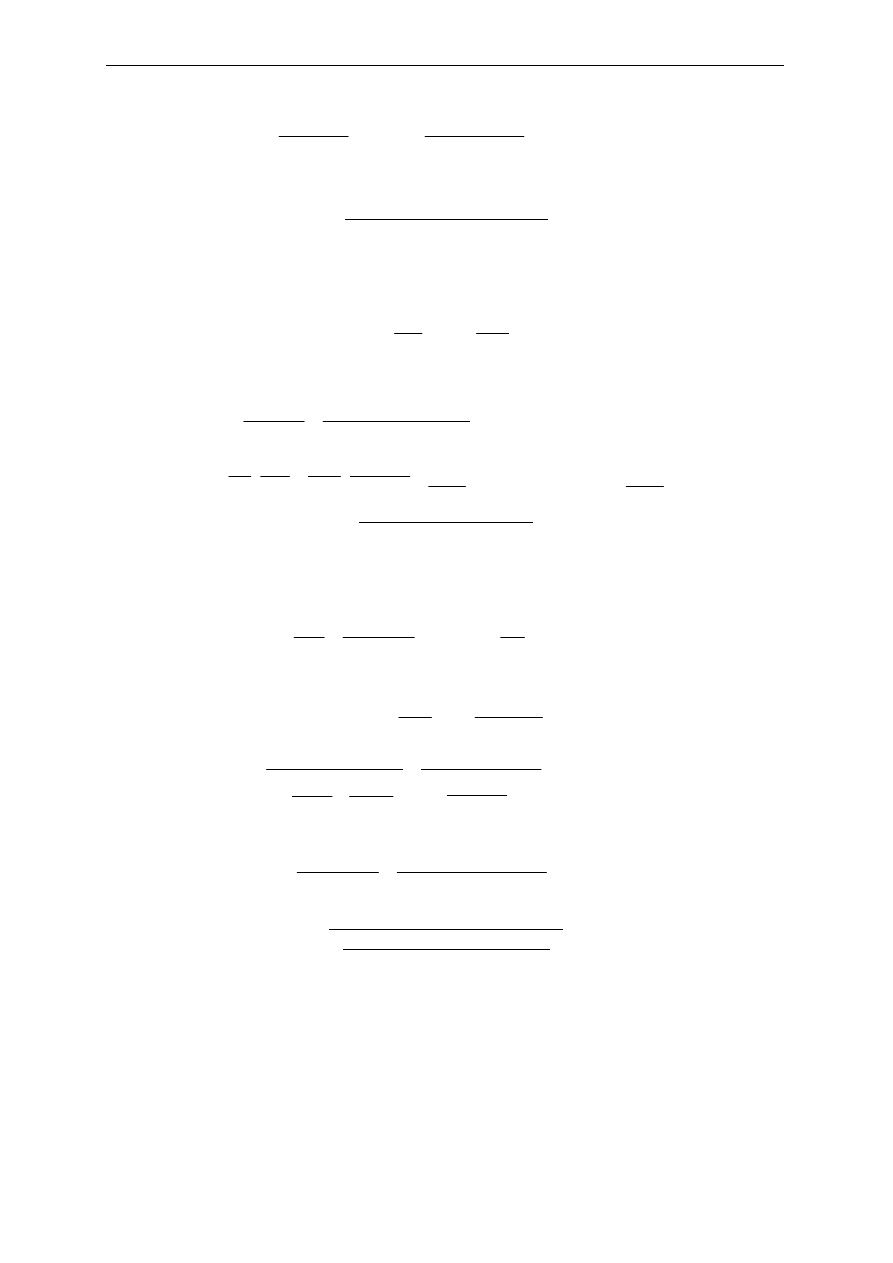
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
18
[ ]
[ ]
mm
m
B
l
M
a
eff
d
Sd
k
10
01
,
0
158548
0
,
7
337
,
370
0887
,
0
2
2
=
=
⋅
⋅
=
⋅
⋅
=
∞
α
[ ]
[ ]
[ ]
[ ]
mm
a
m
m
l
m
eff
30
5
,
7
0
,
7
0
,
6
lim
=
⇒
<
=
<
[ ]
[ ]
mm
a
mm
a
30
10
lim
=
<
=
Powyższe obliczenie ugięcia można byłoby pominąć, ograniczając ugięcie do wartości
[ ]
mm
a
3
,
0
lim
=
gdyż stosunek rozpiętości l
eff
do wysokości użytecznej d elementów o
określonym stopniu ρ
L
zbrojenia podłużnego jest mniejszy od wartości normowej
zamieszczonej w tablicy 13 (PN-B-03264:2002):
[ ]
[
]
[
]
71
,
25
857
,
0
30
30
833
,
8
385
,
230
250
86
,
0
0
,
7
250
250
385
,
230
002199
,
0
86
,
0
85
,
0
337
,
370
85
,
0
731
,
0
002199
,
0
857
,
0
0
,
7
03
,
0
200
200
1
2
lim
1
=
⋅
=
⋅
≤
=
⋅
=
⋅
≠
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
=
=
⋅
=
⋅
=
n
d
l
MPa
MPa
A
d
M
m
A
l
a
n
s
eff
s
d
Sd
s
L
s
eff
σ
ζ
σ
ζ
ρ
Szerokość rys ukośnych
Ze względu na możliwość przekroczenia szerokości rys ukośnych zmniejszono rozstaw
strzemion do wartości
[ ]
[ ]
m
cm
s
1
,
0
10
1
=
=
, wynikiem takiego zabiegu będą mniejsze rysy
oraz większa nośność na ścinanie odcinków drugiego rodzaju
Obliczenie naprężeń ścinających:
[
]
[ ]
mm
b
s
A
MPa
m
kN
d
b
V
w
w
sw
w
w
w
w
Sd
345
,
464
0
8
0
,
1
00574
,
0
3
1
3
1
00574
,
0
35
,
0
1
,
0
000201
,
0
0
0
95
,
1
66
,
1947
86
,
0
35
,
0
245
,
586
2
2
2
1
1
1
1
1
2
1
2
2
=
+
⋅
⋅
=
⋅
+
⋅
⋅
=
=
⋅
=
+
⋅
=
+
=
=
=
=
⋅
=
⋅
=
φ
η
ρ
φ
η
ρ
λ
ρ
ρ
ρ
ρ
τ
Obliczenie szerokości rys ukośnych:
[ ]
mm
f
E
w
ck
s
w
k
25
,
0
25
200000
00574
,
0
345
,
464
95
,
1
4
4
2
2
=
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
ρ
λ
τ
[ ]
[ ]
mm
w
mm
w
k
3
,
0
25
,
0
lim
=
<
=
Szerokość rys prostopadłych
[
]
[
]
kNm
M
kNm
M
d
Sd
Cr
337
,
370
85
,
122
=
<
=
Przekrój pracuje jako zarysowany (faza II).
7
,
1
=
β
- przy obciążeniu bezpośrednim
Obliczenie średniego, końcowego rozstawu rys:
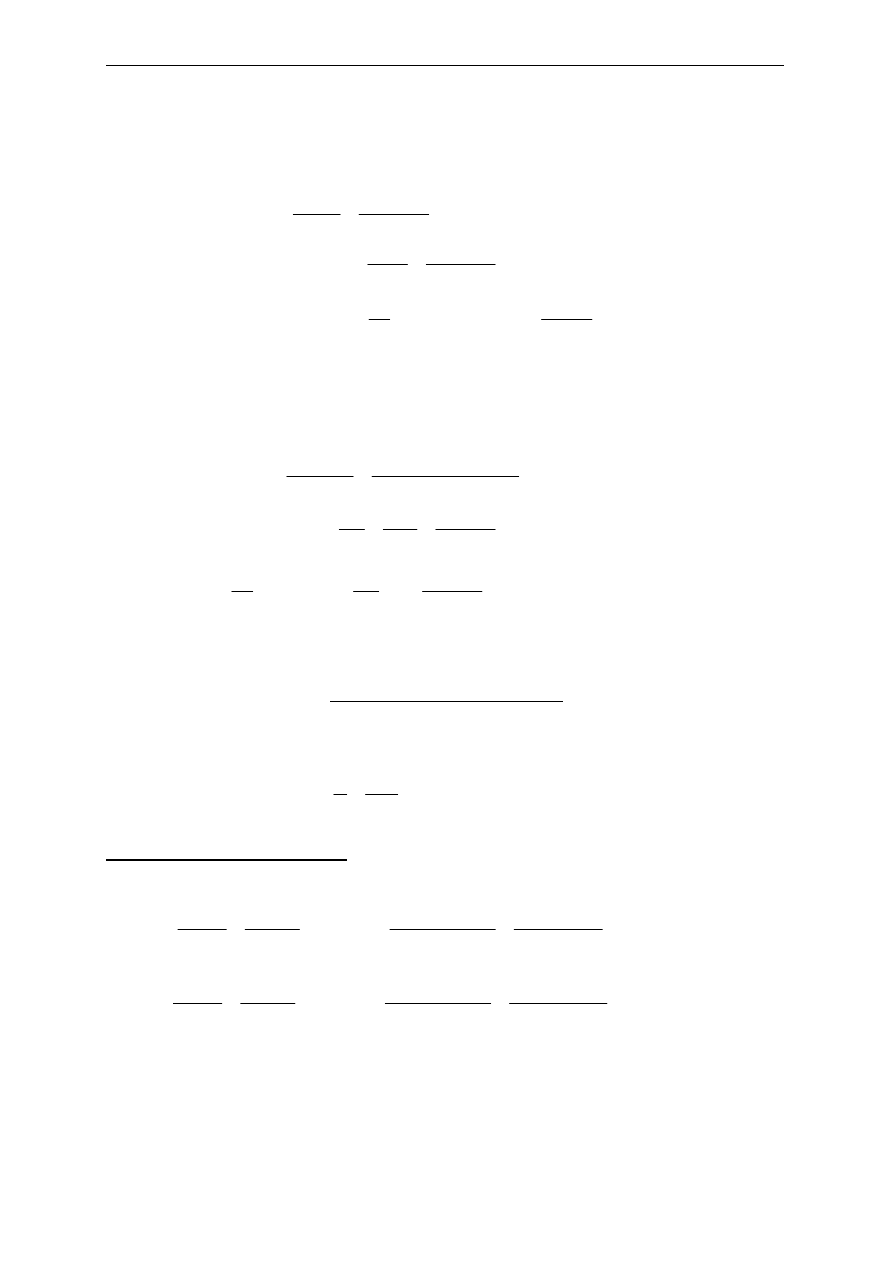
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
19
[ ]
[ ]
[ ]
[ ]
mm
k
k
s
A
A
m
b
m
x
h
m
a
A
k
k
r
rm
eff
ct
s
r
II
eff
ct
85
,
81
0628
,
0
20
5
,
0
8
,
0
25
,
0
50
25
,
0
50
0628
,
0
035
,
0
002199
,
0
035
,
0
35
,
0
1
,
0
17
,
0
3
38
,
0
9
,
0
3
1
,
0
04
,
0
5
,
2
5
,
2
min
5
,
0
8
,
0
2
1
,
2
1
,
2
1
=
⋅
⋅
⋅
+
=
⋅
⋅
⋅
+
=
=
=
=
=
⋅
=
⋅
=
−
=
−
=
⋅
=
⋅
=
=
=
ρ
φ
ρ
Obliczenie średniego odkształcenia zbrojenia rozciąganego:
[
]
[
]
00109
,
0
332
,
0
5
,
0
0
,
1
1
200000
385
,
230
1
332
,
0
337
,
370
85
,
122
385
,
230
002199
,
0
86
,
0
85
,
0
337
,
370
85
,
0
%
731
,
0
5
,
0
0
,
1
2
2
2
1
1
2
1
=
⋅
⋅
−
⋅
=
⋅
⋅
−
⋅
=
=
=
=
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
=
=
s
sr
s
s
sm
d
Sd
Cr
s
sr
S
d
Sd
s
L
E
M
M
MPa
A
d
M
σ
σ
β
β
σ
ε
σ
σ
ζ
σ
ζ
ρ
β
β
Obliczenie szerokości rys prostopadłych:
[ ]
mm
s
w
sm
rm
k
15
,
0
00109
,
0
85
,
81
7
,
1
=
⋅
⋅
=
⋅
⋅
=
ε
β
[ ]
[ ]
mm
w
mm
w
k
3
,
0
15
,
0
lim
=
<
=
Powyższego obliczenia szerokości rys prostopadłych nie można byłoby pominąć,
ograniczając szerokość rys do wartości
[ ]
mm
w
3
,
0
lim
=
, gdyż nie jest spełniony podstawowy
warunek na wartość stosunku (Załącznik D - PN-B-03264:2002):
(
)
95
,
0
85
,
0
956
,
0
9
,
0
86
,
0
÷
∉
=
=
h
d
Rygiel stropodachu nr 8 = nr11
Moment zginający od kombinacji obciążeń długotrwałych (charakterystycznych: obciążenia
stałe+60%zmiennych):
(
)
[
]
kNm
q
g
q
g
M
M
q
g
q
g
M
M
k
k
d
Sd
d
k
Sd
k
k
d
k
Sd
d
Sd
394
,
69
238
,
7
835
,
5
08
,
86
)
(
)
(
=
⋅
=
+
+
⋅
=
⇒
+
+
=
Moment zginający od obciążeń całkowitych (charakterystycznych):
(
)
[
]
kNm
q
g
q
g
M
M
q
g
q
g
M
M
k
k
Sd
k
Sd
k
k
k
Sd
Sd
932
,
74
238
,
7
835
,
5
949
,
92
)
(
)
(
=
⋅
=
+
+
⋅
=
⇒
+
+
=
Wymiary geometryczne rygla:

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
20
[ ]
[ ]
[ ]
[ ]
m
a
m
d
m
h
m
b
04
,
0
46
,
0
50
,
0
35
,
0
=
=
=
=
[ ]
m
l
eff
8
,
5
=
Zbrojenie ze stali A-III:
[
]
[
]
[
]
[
]
MPa
GPa
E
MPa
f
MPa
f
s
yk
yd
200000
200
410
350
=
=
=
=
Beton B-30:
[
]
[
]
MPa
f
MPa
f
ctm
cd
6
,
2
7
,
16
=
=
[
]
[
]
MPa
f
MPa
f
ctk
ck
8
,
1
25
=
=
[
]
[
]
MPa
GPa
E
cm
31000
31
=
==
Ugięcie
Obliczenie wskaźnika wytrzymałości przekroju betonu oraz momentu rysującego:
[ ]
[
]
[
]
[
]
kNm
M
kNm
MNm
W
f
M
m
h
b
W
Sd
C
ctm
Cr
C
932
,
74
92
,
37
03792
,
0
01458
,
0
6
,
2
01458
,
0
6
5
,
0
35
,
0
6
3
2
2
=
<
=
=
⋅
=
⋅
=
=
⋅
=
⋅
=
Przekrój pracuje jako zarysowany (faza II).
0
,
1
1
=
β
- dla prętów żebrowanych:
5
,
0
2
=
β
- przy obciążeniu długotrwałym
Obliczenie stosunku naprężeń w zbrojeniu rozciąganym z warunku:
546
,
0
394
,
69
92
,
37
=
=
=
d
Sd
Cr
s
sr
M
M
σ
σ
Obliczenie współczynnika zależny od schematu statycznego i typu obciążenia:
0765
,
0
949
,
92
10
746
,
151
923
,
94
1
48
5
10
1
48
5
=
⋅
+
−
⋅
=
⋅
+
−
⋅
=
prz
B
A
k
M
M
M
α
Założona wilgotność względna powietrza wynosi RH=50%.
Określenie współczynnika pełzania na podstawie miarodajnego przekroju elementu:
(
)
[ ]
( )
74
,
2
,
206
500
350
2
500
350
2
2
0
0
=
⇒
=
+
⋅
⋅
⋅
=
⋅
=
t
t
mm
u
A
h
c
φ
( )
[
]
13
,
24
77
,
8288
200000
77
,
8288
74
,
2
1
31000
,
1
,
,
0
,
=
=
=
=
+
=
+
=
eff
c
s
t
e
cm
eff
c
E
E
MPa
t
t
E
E
α
φ
J
I
– moment bezwładności przekroju sprowadzonego przekroju w fazie niezarysowanej.
[ ]
m
A
h
b
d
A
h
b
x
S
t
e
S
t
e
I
27
,
0
000942
,
0
13
,
24
5
,
0
35
,
0
46
,
0
000942
,
0
13
,
24
5
,
0
35
,
0
5
,
0
5
,
0
2
1
,
1
,
2
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
α
α
(
)
(
)
(
)
(
)
[ ]
4
2
3
3
2
1
,
3
3
00454
,
0
27
,
0
46
,
0
000942
,
0
13
,
24
3
27
,
0
5
,
0
35
,
0
3
27
,
0
35
,
0
3
3
m
x
d
A
x
h
b
x
b
J
I
S
t
e
I
I
I
=
−
⋅
⋅
+
−
⋅
+
⋅
=
=
−
⋅
⋅
+
−
⋅
+
⋅
=
α
J
II
– moment bezwładności przekroju sprowadzonego przekroju w fazie zarysowanej.
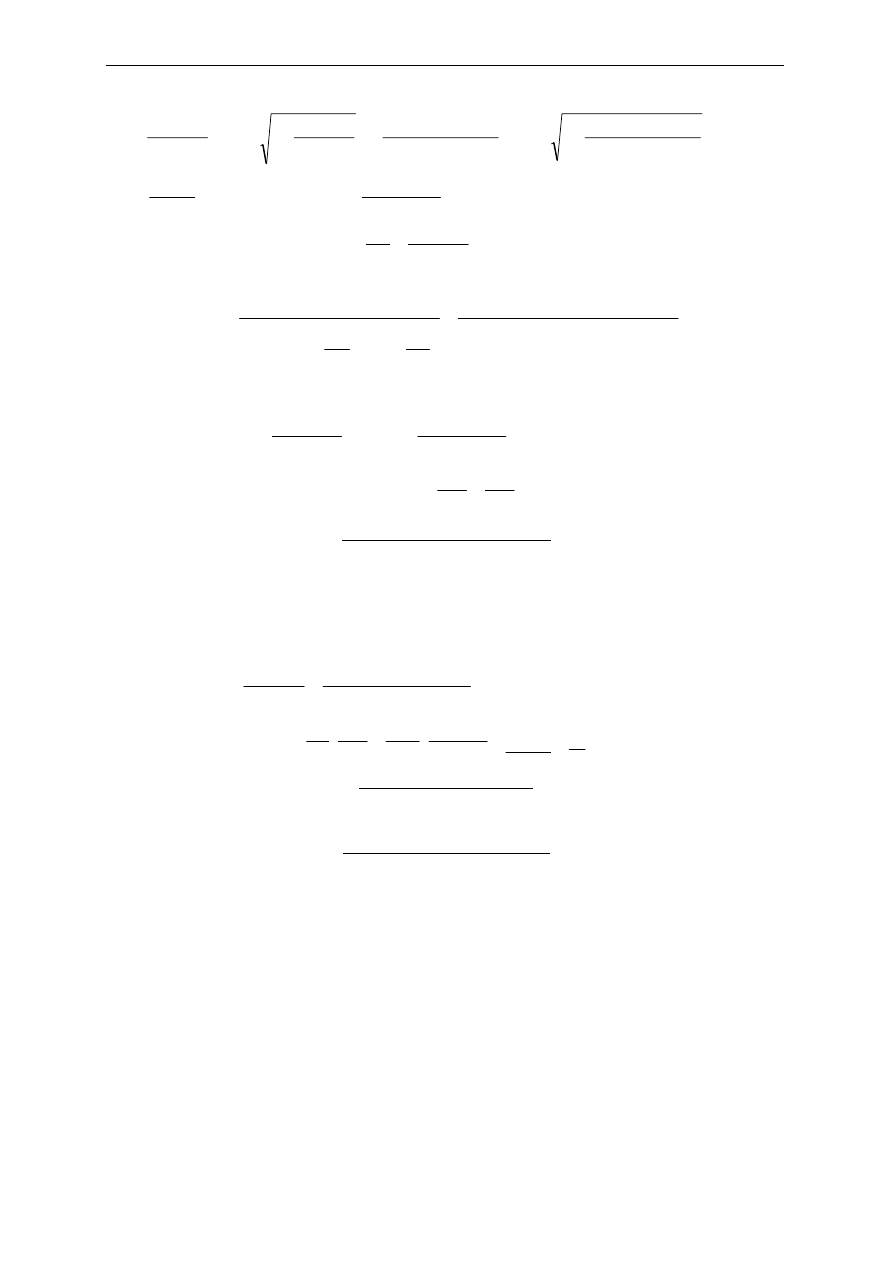
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
21
[ ]
m
A
d
b
b
A
x
S
t
e
S
t
e
II
19
,
0
000942
,
0
13
,
24
46
,
0
35
,
0
2
1
1
35
,
0
000942
,
0
13
,
24
2
1
1
1
,
1
,
=
⋅
⋅
⋅
+
+
−
⋅
⋅
=
⋅
⋅
⋅
+
+
−
⋅
⋅
=
α
α
(
)
(
)
[ ]
4
2
3
2
1
,
3
00246
,
0
19
,
0
46
,
0
000942
,
0
13
,
24
3
19
,
0
35
,
0
3
m
x
d
A
x
b
J
II
S
t
e
II
II
=
−
⋅
⋅
+
⋅
=
−
⋅
⋅
+
⋅
=
α
542
,
0
00454
,
0
00246
,
0
=
=
I
II
J
J
Sztywność przekroju zarysowanego przy obciążeniu długotrwałym:
(
) (
)
[
]
[
]
2
2
2
2
2
1
,
21884
884
,
21
542
,
0
1
546
,
0
5
,
0
0
,
1
1
00246
,
0
77
,
8288
1
1
kNm
MNm
J
J
J
E
B
I
II
s
sr
II
eff
c
=
=
=
−
⋅
⋅
⋅
−
⋅
=
−
⋅
⋅
⋅
−
⋅
=
∞
σ
σ
β
β
[ ]
[ ]
mm
m
B
l
M
a
eff
d
Sd
k
2
,
8
0082
,
0
21884
8
,
5
394
,
69
0765
,
0
2
2
=
=
⋅
⋅
=
⋅
⋅
=
∞
α
[ ]
[ ]
[ ]
[ ]
mm
m
l
a
m
m
l
eff
eff
29
029
,
0
200
8
,
5
200
0
,
6
8
,
5
lim
=
=
=
=
⇒
<
=
[ ]
[ ]
mm
a
mm
a
29
2
,
8
lim
=
<
=
Powyższe obliczenie ugięcia można byłoby pominąć, ograniczając ugięcie do wartości
[ ]
mm
a
29
,
0
lim
=
gdyż stosunek rozpiętości l
eff
do wysokości użytecznej d elementów o
określonym stopniu ρ
L
zbrojenia podłużnego jest mniejszy od wartości normowej
zamieszczonej w tablicy 13 (PN-B-03264:2002):
[ ]
[
]
[
]
35
731
,
16
406
,
188
250
46
,
0
8
,
5
250
250
406
,
188
000942
,
0
46
,
0
85
,
0
394
,
69
85
,
0
585
,
0
000942
,
0
2
≤
=
⋅
=
⋅
≠
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
=
s
eff
s
d
Sd
s
L
s
d
l
MPa
MPa
A
d
M
m
A
σ
ζ
σ
ζ
ρ
Szerokość rys ukośnych
Sprawdzenie szerokości rys ukośnych przy w
lim
=0,3 mm nie jest potrzebne, gdyż zastosowane
strzemiona prostopadłe zapewniają przy
75
,
1
5
,
1
cot
≤
=
θ
wystarczającą nośność na ścinanie.
Szerokość rys prostopadłych
[
]
[
]
kNm
M
kNm
M
d
Sd
Cr
394
,
69
92
,
37
=
<
=
Przekrój pracuje jako zarysowany (faza II).
7
,
1
=
β
- przy obciążeniu bezpośrednim
Obliczenie średniego, końcowego rozstawu rys:
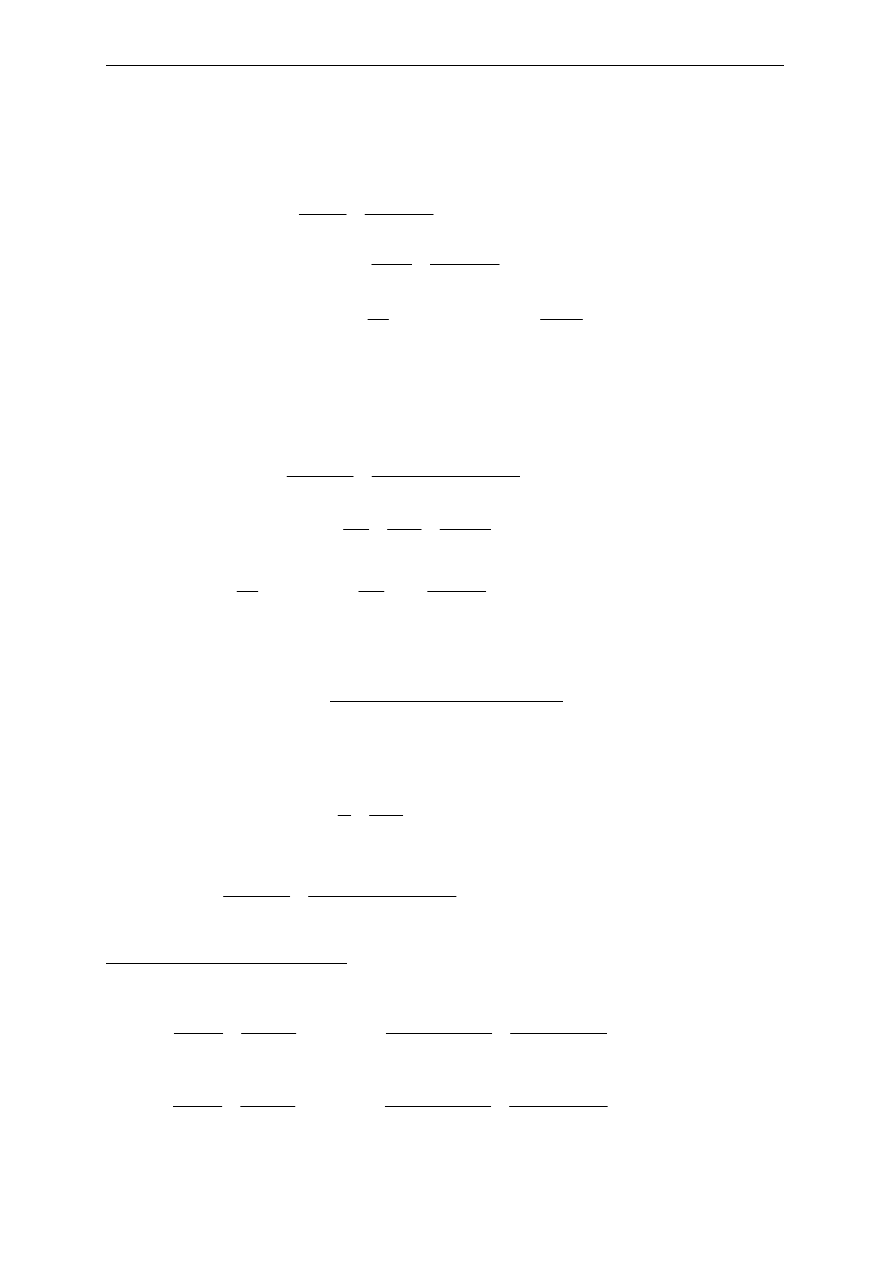
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
22
[ ]
[ ]
[ ]
[ ]
mm
k
k
s
A
A
m
b
m
x
h
m
a
A
k
k
r
rm
eff
ct
s
r
II
eff
ct
07
,
124
027
,
0
20
5
,
0
8
,
0
25
,
0
50
25
,
0
50
027
,
0
035
,
0
000942
,
0
035
,
0
35
,
0
1
,
0
1
,
0
3
19
,
0
5
,
0
3
1
,
0
04
,
0
5
,
2
5
,
2
min
5
,
0
8
,
0
2
1
,
2
1
,
2
1
=
⋅
⋅
⋅
+
=
⋅
⋅
⋅
+
=
=
=
=
=
⋅
=
⋅
=
−
=
−
=
⋅
=
⋅
=
=
=
ρ
φ
ρ
Obliczenie średniego odkształcenia zbrojenia rozciąganego:
[
]
[
]
0008
,
0
546
,
0
5
,
0
0
,
1
1
200000
406
,
188
1
546
,
0
394
,
69
92
,
37
406
,
188
000942
,
0
46
,
0
85
,
0
394
,
69
85
,
0
%
585
,
0
5
,
0
0
,
1
2
2
2
1
1
2
1
=
⋅
⋅
−
⋅
=
⋅
⋅
−
⋅
=
=
=
=
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
=
=
s
sr
s
s
sm
d
Sd
Cr
s
sr
S
d
Sd
s
L
E
M
M
MPa
A
d
M
σ
σ
β
β
σ
ε
σ
σ
ζ
σ
ζ
ρ
β
β
Obliczenie szerokości rys prostopadłych:
[ ]
mm
s
w
sm
rm
k
17
,
0
0008
,
0
07
,
124
7
,
1
=
⋅
⋅
=
⋅
⋅
=
ε
β
[ ]
[ ]
mm
w
mm
w
k
3
,
0
17
,
0
lim
=
<
=
Powyższe obliczenie szerokości rys prostopadłych można byłoby pominąć, ograniczając
szerokość rys do wartości
[ ]
mm
w
3
,
0
lim
=
gdyż zastosowana średnica prętów zbrojenia nie
przekroczyła wartości maksymalnej wynikającej z tablicy D.1 (Załącznik D – PN-B-
03264:2002) i poniższych warunków:
(
)
[
]
[ ]
mm
MPa
A
d
M
h
d
S
d
Sd
s
L
25
406
,
188
000942
,
0
46
,
0
85
,
0
394
,
69
85
,
0
%
585
,
0
95
,
0
85
,
0
92
,
0
5
,
0
46
,
0
max
1
=
⇒
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
÷
∈
=
=
φ
ζ
σ
ζ
ρ
Rygiel stropodachu nr 9 + nr10
Moment zginający od kombinacji obciążeń długotrwałych (charakterystycznych: obciążenia
stałe+60%zmiennych):
(
)
[
]
kNm
q
g
q
g
M
M
q
g
q
g
M
M
k
k
d
Sd
d
k
Sd
k
k
d
k
Sd
d
Sd
963
,
62
238
,
7
835
,
5
102
,
78
)
(
)
(
=
⋅
=
+
+
⋅
=
⇒
+
+
=
Moment zginający od obciążeń całkowitych (charakterystycznych):
(
)
[
]
kNm
q
g
q
g
M
M
q
g
q
g
M
M
k
k
Sd
k
Sd
k
k
k
Sd
Sd
603
,
66
238
,
7
835
,
5
617
,
82
)
(
)
(
=
⋅
=
+
+
⋅
=
⇒
+
+
=
Wymiary geometryczne rygla:
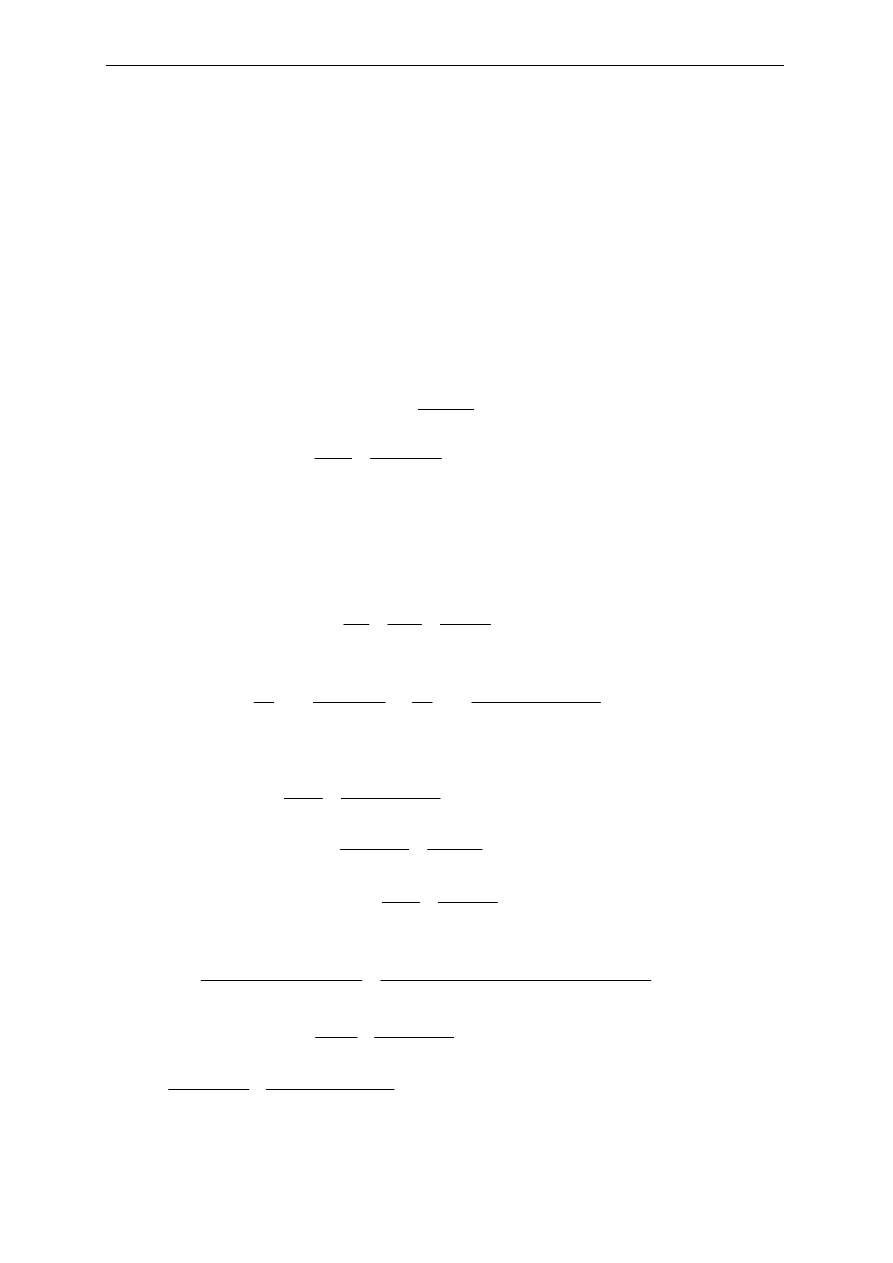
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
23
[ ]
[ ]
[ ]
[ ]
m
a
m
d
m
h
m
b
04
,
0
46
,
0
50
,
0
35
,
0
=
=
=
=
[ ]
m
l
eff
0
,
7
=
Zbrojenie ze stali A-III:
[
]
[
]
[
]
[
]
MPa
GPa
E
MPa
f
MPa
f
s
yk
yd
200000
200
410
350
=
=
=
=
Beton B-30:
[
]
[
]
MPa
f
MPa
f
ctm
cd
6
,
2
7
,
16
=
=
[
]
[
]
MPa
f
MPa
f
ctk
ck
8
,
1
25
=
=
[
]
[
]
MPa
GPa
E
cm
31000
31
=
==
Ugięcie
Obliczenie wskaźnika wytrzymałości przekroju betonu oraz momentu rysującego:
[ ]
[
]
[
]
[
]
kNm
M
kNm
MNm
W
f
M
m
h
b
W
Sd
C
ctm
Cr
C
603
,
66
92
,
37
03792
,
0
01458
,
0
6
,
2
01458
,
0
6
5
,
0
35
,
0
6
3
2
2
=
<
=
=
⋅
=
⋅
=
=
⋅
=
⋅
=
Przekrój pracuje jako zarysowany (faza II).
0
,
1
1
=
β
- dla prętów żebrowanych:
5
,
0
2
=
β
- przy obciążeniu długotrwałym
Obliczenie stosunku naprężeń w zbrojeniu rozciąganym z warunku:
569
,
0
603
,
66
92
,
37
=
=
=
d
Sd
Cr
s
sr
M
M
σ
σ
Obliczenie współczynnika zależny od schematu statycznego i typu obciążenia:
0566
,
0
617
,
82
10
568
,
188
568
,
188
1
48
5
10
1
48
5
=
⋅
+
−
⋅
=
⋅
+
−
⋅
=
prz
B
A
k
M
M
M
α
Założona wilgotność względna powietrza wynosi RH=50%.
Określenie współczynnika pełzania na podstawie miarodajnego przekroju elementu:
(
)
[ ]
( )
74
,
2
,
206
500
350
2
500
350
2
2
0
0
=
⇒
=
+
⋅
⋅
⋅
=
⋅
=
t
t
mm
u
A
h
c
φ
( )
[
]
13
,
24
77
,
8288
200000
77
,
8288
74
,
2
1
31000
,
1
,
,
0
,
=
=
=
=
+
=
+
=
eff
c
s
t
e
cm
eff
c
E
E
MPa
t
t
E
E
α
φ
J
I
– moment bezwładności przekroju sprowadzonego przekroju w fazie niezarysowanej.
[ ]
m
A
h
b
d
A
h
b
x
S
t
e
S
t
e
I
27
,
0
000628
,
0
13
,
24
5
,
0
35
,
0
46
,
0
000628
,
0
13
,
24
5
,
0
35
,
0
5
,
0
5
,
0
2
1
,
1
,
2
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
α
α
(
)
(
)
(
)
(
)
[ ]
4
2
3
3
2
1
,
3
3
00426
,
0
27
,
0
46
,
0
000628
,
0
13
,
24
3
27
,
0
5
,
0
35
,
0
3
27
,
0
35
,
0
3
3
m
x
d
A
x
h
b
x
b
J
I
S
t
e
I
I
I
=
−
⋅
⋅
+
−
⋅
+
⋅
=
=
−
⋅
⋅
+
−
⋅
+
⋅
=
α
J
II
– moment bezwładności przekroju sprowadzonego przekroju w fazie zarysowanej.
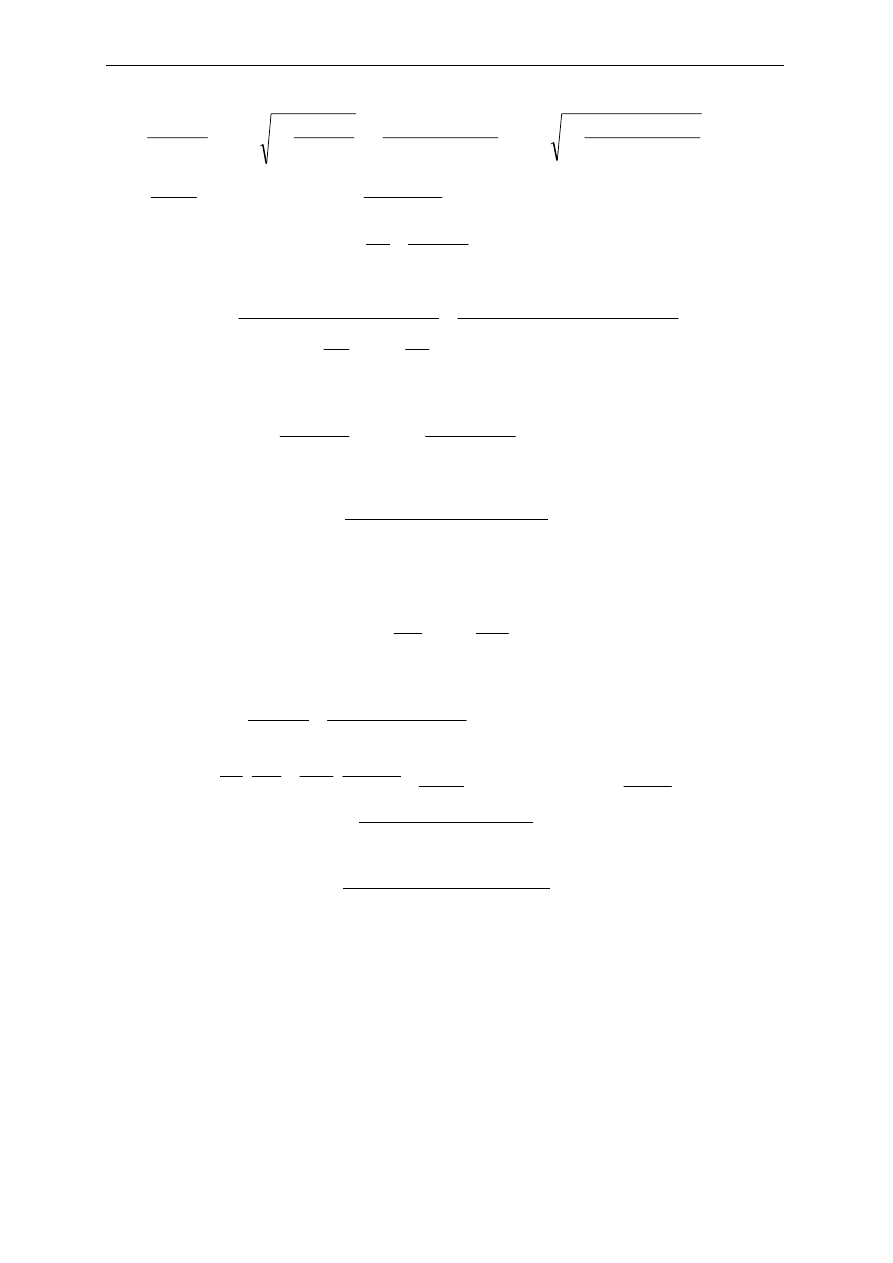
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
24
[ ]
m
A
d
b
b
A
x
S
t
e
S
t
e
II
16
,
0
000628
,
0
13
,
24
46
,
0
35
,
0
2
1
1
35
,
0
000628
,
0
13
,
24
2
1
1
1
,
1
,
=
⋅
⋅
⋅
+
+
−
⋅
⋅
=
⋅
⋅
⋅
+
+
−
⋅
⋅
=
α
α
(
)
(
)
[ ]
4
2
3
2
1
,
3
00184
,
0
16
,
0
46
,
0
000628
,
0
13
,
24
3
16
,
0
35
,
0
3
m
x
d
A
x
b
J
II
S
t
e
II
II
=
−
⋅
⋅
+
⋅
=
−
⋅
⋅
+
⋅
=
α
432
,
0
00426
,
0
00184
,
0
=
=
I
II
J
J
Sztywność przekroju zarysowanego przy obciążeniu długotrwałym:
(
) (
)
[
]
[
]
2
2
2
2
2
1
,
16796
796
,
16
432
,
0
1
569
,
0
5
,
0
0
,
1
1
00184
,
0
77
,
8288
1
1
kNm
MNm
J
J
J
E
B
I
II
s
sr
II
eff
c
=
=
=
−
⋅
⋅
⋅
−
⋅
=
−
⋅
⋅
⋅
−
⋅
=
∞
σ
σ
β
β
[ ]
[ ]
mm
m
B
l
M
a
eff
d
Sd
k
11
011
,
0
16796
0
,
7
603
,
66
0566
,
0
2
2
=
=
⋅
⋅
=
⋅
⋅
=
∞
α
[ ]
[ ]
[ ]
[ ]
mm
a
m
m
l
m
eff
30
5
,
7
0
,
7
0
,
6
lim
=
⇒
<
=
<
[ ]
[ ]
mm
a
mm
a
30
11
lim
=
<
=
Powyższe obliczenie ugięcia można byłoby pominąć, ograniczając ugięcie do wartości
[ ]
mm
a
3
,
0
lim
=
gdyż stosunek rozpiętości l
eff
do wysokości użytecznej d elementów o
określonym stopniu ρ
L
zbrojenia podłużnego jest mniejszy od wartości normowej
zamieszczonej w tablicy 13 (PN-B-03264:2002):
[ ]
[
]
[
]
995
,
29
857
,
0
35
30
851
,
14
173
,
256
250
46
,
0
0
,
7
250
250
173
,
256
000628
,
0
46
,
0
9
,
0
603
,
66
9
,
0
39
,
0
000628
,
0
857
,
0
0
,
7
03
,
0
200
200
1
2
lim
1
=
⋅
=
⋅
≤
=
⋅
=
⋅
≠
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
=
=
⋅
=
⋅
=
n
d
l
MPa
MPa
A
d
M
m
A
l
a
n
s
eff
s
d
Sd
s
L
s
eff
σ
ζ
σ
ζ
ρ
Szerokość rys ukośnych
Sprawdzenie szerokości rys ukośnych przy w
lim
=0,3 mm nie jest potrzebne, gdyż zastosowane
strzemiona prostopadłe zapewniają przy
75
,
1
5
,
1
cot
≤
=
θ
wystarczającą nośność na ścinanie.
Szerokość rys prostopadłych
[
]
[
]
kNm
M
kNm
M
d
Sd
Cr
603
,
66
92
,
37
=
<
=
Przekrój pracuje jako zarysowany (faza II).
7
,
1
=
β
- przy obciążeniu bezpośrednim
Obliczenie średniego, końcowego rozstawu rys:
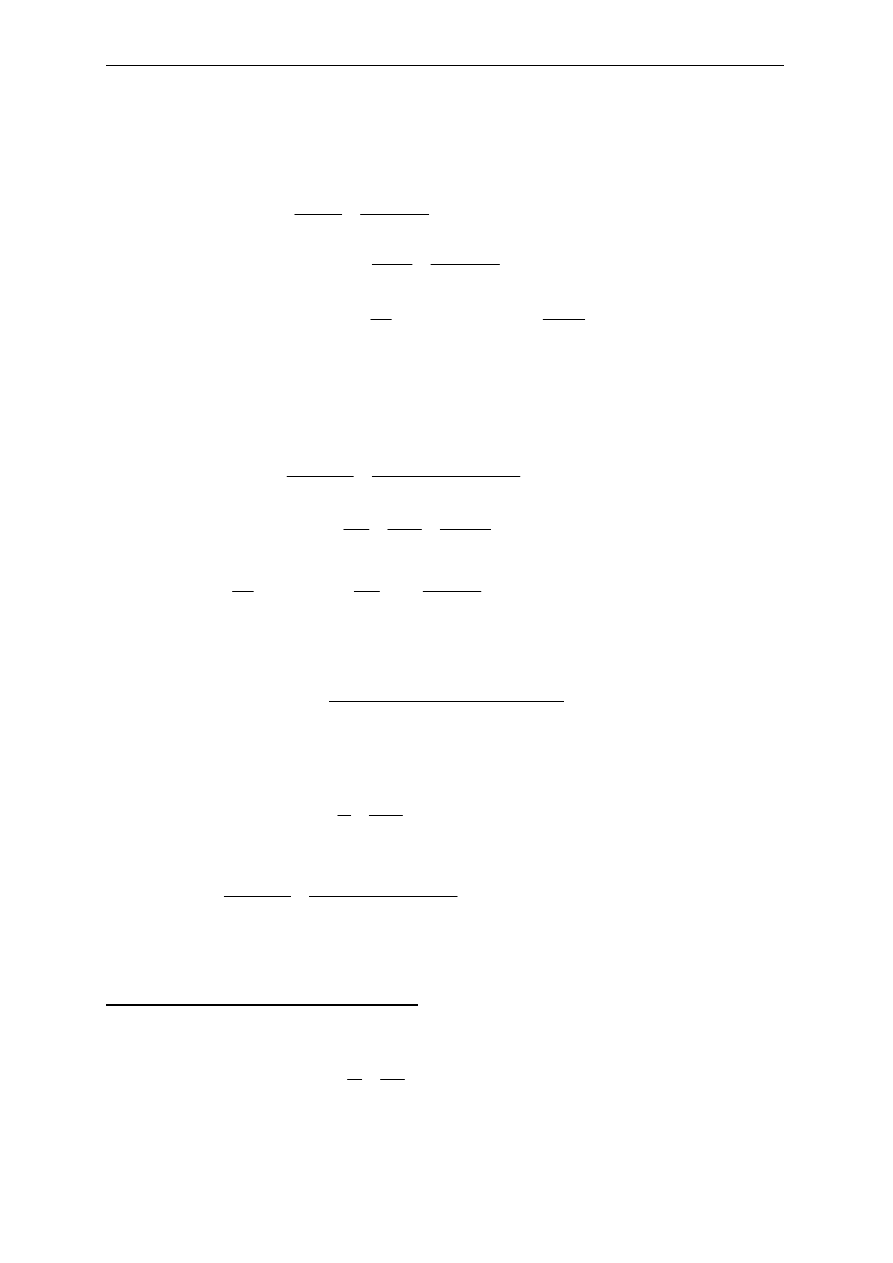
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
25
[ ]
[ ]
[ ]
[ ]
mm
k
k
s
A
A
m
b
m
x
h
m
a
A
k
k
r
rm
eff
ct
s
r
II
eff
ct
11
,
161
018
,
0
20
5
,
0
8
,
0
25
,
0
50
25
,
0
50
018
,
0
035
,
0
000628
,
0
035
,
0
35
,
0
1
,
0
11
,
0
3
16
,
0
5
,
0
3
1
,
0
04
,
0
5
,
2
5
,
2
min
5
,
0
8
,
0
2
1
,
2
1
,
2
1
=
⋅
⋅
⋅
+
=
⋅
⋅
⋅
+
=
=
=
=
=
⋅
=
⋅
=
−
=
−
=
⋅
=
⋅
=
=
=
ρ
φ
ρ
Obliczenie średniego odkształcenia zbrojenia rozciąganego:
[
]
[
]
00107
,
0
569
,
0
5
,
0
0
,
1
1
200000
173
,
256
1
569
,
0
603
,
66
92
,
37
173
,
256
000628
,
0
46
,
0
90
,
0
603
,
66
90
,
0
%
39
,
0
5
,
0
0
,
1
2
2
2
1
1
2
1
=
⋅
⋅
−
⋅
=
⋅
⋅
−
⋅
=
=
=
=
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
=
=
s
sr
s
s
sm
d
Sd
Cr
s
sr
S
d
Sd
s
L
E
M
M
MPa
A
d
M
σ
σ
β
β
σ
ε
σ
σ
ζ
σ
ζ
ρ
β
β
Obliczenie szerokości rys prostopadłych:
[ ]
mm
s
w
sm
rm
k
29
,
0
00107
,
0
11
,
161
7
,
1
=
⋅
⋅
=
⋅
⋅
=
ε
β
[ ]
[ ]
mm
w
mm
w
k
3
,
0
29
,
0
lim
=
<
=
W powyższym przypadku obliczenia szerokości rys prostopadłych nie można byłoby
pominąć, ograniczając szerokość rys do wartości
[ ]
mm
w
3
,
0
lim
=
, gdyż zastosowana średnica
prętów zbrojenia przekroczyła wartość maksymalną wynikającą z tablicy D.1 (Załącznik D
PN-B-03264:2002) i poniższych warunków:
(
)
[
]
[ ]
mm
MPa
A
d
M
h
d
S
d
Sd
s
L
18
173
,
256
000628
,
0
46
,
0
90
,
0
603
,
66
90
,
0
%
39
,
0
95
,
0
85
,
0
92
,
0
5
,
0
46
,
0
max
1
=
⇒
=
⋅
⋅
=
⋅
⋅
=
=
⇒
=
÷
∈
=
=
φ
ζ
σ
ζ
ρ
d) Wymiarowanie przekrojów na ściskanie
Słup nr 1 = nr 4 – zbrojenie symetryczne
Określenie długości obliczeniowej i smukłości słupa:
[ ]
(
)
30
7
667
,
13
6
,
0
2
,
8
2
,
8
2
,
8
0
,
1
0
0
≤
>
=
=
=
=
⋅
=
⋅
=
lecz
h
l
m
l
l
col
λ
β
Nośność należy sprawdzić z uwzględnieniem smukłości elementów i wpływu obciążeń
długotrwałych.
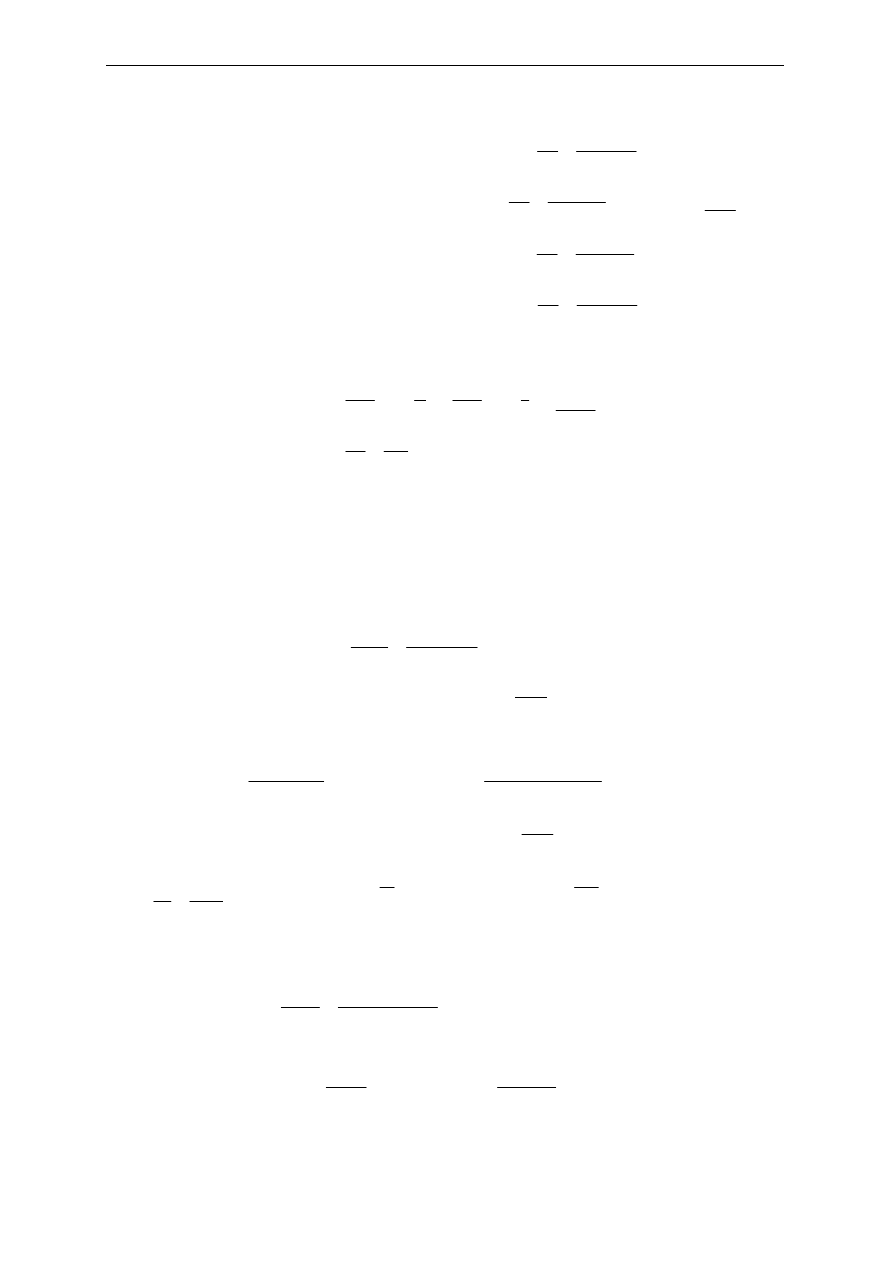
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
26
Wyznaczenie maksymalnego mimośrodu konstrukcyjnego:
[
]
[ ]
[ ]
[
]
[ ]
[ ]
[ ]
[
]
[ ]
[ ]
[
]
[ ]
m
N
M
e
kNm
M
kN
N
m
N
M
e
kNm
M
kN
N
m
N
M
e
kN
N
kNm
M
m
N
M
e
kN
N
kNm
M
e
e
e
e
19
,
0
532
,
259
538
,
48
538
,
48
532
,
259
55
,
0
039
,
128
151
,
70
151
,
70
039
,
128
max
59
,
0
849
,
155
035
,
92
849
,
155
035
,
92
24
,
0
546
,
256
620
,
61
546
,
256
620
,
61
min
max
min
max
=
=
=
⇒
=
→
=
=
=
=
⇒
=
→
=
⇐
=
=
=
⇒
=
→
=
=
=
=
⇒
=
→
=
Wyznaczenie maksymalnego mimośrodu niezamierzonego (n - pierwsza kondygnacja licząc
od góry):
[ ]
[ ]
[ ]
=
=
=
+
⋅
=
+
⋅
=
m
m
h
m
n
l
e
col
a
01
,
0
02
,
0
30
6
,
0
30
027
,
0
1
1
1
600
2
,
8
1
1
600
max
Obliczenie mimośrodu początkowego siły ściskającej względem środka ciężkości przekroju
betonu:
[ ]
[ ]
m
m
e
e
e
e
a
62
,
0
617
,
0
59
,
0
027
,
0
0
≈
=
+
=
+
=
Obliczenie zwiększonego mimośrodu początkowego:
[ ]
[
]
[ ]
[
]
=
=
=
−
−
⋅
⋅
⋅
=
−
−
⋅
⋅
⋅
=
=
=
=
=
=
⋅
=
⋅
=
2
4
2
2
2
1
2
4
3
3
200000
200
0001325
,
0
2
04
,
0
04
,
0
6
,
0
56
,
0
35
,
0
01
,
0
2
01
,
0
%
1
31000
31
0063
,
0
12
6
,
0
35
,
0
12
m
MN
GPa
E
m
a
a
h
d
b
J
m
MN
GPa
E
m
h
b
J
s
s
cm
c
ρ
ρ
=
⋅
−
⋅
−
=
⋅
−
⋅
−
>
=
=
05
,
0
196
,
0
7
,
16
01
,
0
6
,
0
2
,
8
01
,
0
50
,
0
01
,
0
01
,
0
50
,
0
03
,
1
6
,
0
62
,
0
0
0
cd
f
h
l
h
e
Wilgotność względna powietrza wynosi RH=50%.
Miarodajny przekrój elementu wynosi:
(
)
[ ]
(
)
72
,
2
,
221
600
350
2
600
350
2
2
0
0
=
∞
⇒
=
+
⋅
⋅
⋅
=
⋅
=
t
mm
u
A
h
c
φ
[ ]
(
)
088
,
2
72
,
2
849
,
155
679
,
124
5
,
0
1
,
5
,
0
1
679
,
124
849
,
155
8
,
0
8
,
0
0
,
,
=
⋅
⋅
+
=
∞
⋅
⋅
+
=
=
⋅
=
⋅
=
t
N
N
k
kN
N
N
Sd
lt
Sd
lt
Sd
lt
Sd
φ
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
27
[ ]
[ ]
[ ]
[ ]
018
,
1
8925
849
,
155
1
1
1
1
8032
8925
9
,
0
9
,
0
849
,
155
8925
925
,
8
0001325
,
0
200000
1
,
0
6
,
0
62
,
0
1
,
0
11
,
0
088
,
2
2
0063
,
0
31000
2
,
8
9
1
,
0
1
,
0
11
,
0
2
9
2
0
2
0
=
−
=
−
=
=
⋅
=
⋅
≤
=
=
=
⋅
+
+
+
⋅
⋅
⋅
⋅
=
=
⋅
+
+
+
⋅
⋅
⋅
⋅
=
crit
Sd
crit
Sd
s
s
lt
c
cm
crit
N
N
kN
N
kN
N
kN
MN
J
E
h
e
k
J
E
l
N
η
[ ]
m
e
e
tot
63
,
0
62
,
0
018
,
1
0
=
⋅
=
⋅
=
η
Obliczenie mimośrodu względem środka ciężkości zbrojenia rozciąganego
[ ]
m
a
h
e
e
tot
s
89
,
0
04
,
0
6
,
0
5
,
0
63
,
0
5
,
0
1
1
=
−
⋅
+
=
−
⋅
+
=
Obliczenie powierzchni zbrojenia ściskanego przy założeniu ściskania z dużym mimośrodem:
[ ]
m
d
x
eff
eff
297
,
0
56
,
0
53
,
0
lim
,
lim
,
=
⋅
=
⋅
=
ξ
[ ]
[ ]
[ ]
m
a
m
x
x
m
b
f
N
x
eff
eff
cd
Sd
eff
08
,
0
04
,
0
2
2
027
,
0
027
,
0
35
,
0
16700
0
,
1
849
,
155
2
lim
,
=
⋅
=
⋅
<
=
≤
=
⋅
⋅
=
⋅
⋅
=
α
[ ]
[ ]
2
2
4
2
1
2
1
168
,
3
10
168
,
3
1
04
,
0
56
,
0
89
,
0
350000
849
,
155
1
cm
m
a
d
e
f
N
A
A
s
yd
Sd
S
S
=
⋅
=
=
−
−
⋅
=
−
−
⋅
=
=
−
Wyznaczenie zbrojenia minimalnego:
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
=
⋅
=
−
−
2
2
4
2
2
4
min
88
,
5
10
88
,
5
56
,
0
35
,
0
003
,
0
003
,
0
668
,
0
10
668
,
0
350000
849
,
155
15
,
0
15
,
0
max
cm
m
d
b
cm
m
f
N
A
yd
Sd
S
[ ]
2
2
1
88
,
5
cm
A
A
S
S
=
=
Przyjąłem zbrojenie symetryczne 3Φ20 o A
S1
= A
S2
=9,425[cm
2
], o większym przekroju aby
osiągnąć założony stopień zbrojenia.
Obliczenie stopnia zbrojenia obliczonego:
[ ]
%
898
,
0
%
100
60
35
85
,
18
85
,
18
425
,
9
425
,
9
2
1
2
2
1
=
⋅
⋅
=
⋅
+
=
=
+
=
+
h
b
A
A
cm
A
A
S
S
S
S
ρ
Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a
stopniem zbrojenia założonym:
%
20
%
2
,
10
%
100
0
,
1
0
,
1
898
,
0
=
∆
<
=
⋅
−
=
−
=
∆
dop
zal
zal
ρ
ρ
ρ
Sprawdzenie nośności przekroju słupa prostokątnego, mimośrodowo ściskanego:
[ ]
m
d
x
eff
eff
297
,
0
56
,
0
53
,
0
lim
,
lim
,
=
⋅
=
⋅
=
ξ

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
28
[ ]
[ ]
m
a
e
d
e
m
a
h
e
e
s
s
tot
s
37
,
0
04
,
0
89
,
0
56
,
0
89
,
0
04
,
0
6
,
0
5
,
0
63
,
0
5
,
0
2
1
2
1
1
−
=
−
−
=
−
−
=
=
−
⋅
+
=
−
⋅
+
=
(
) (
)
(
)
(
) (
)
(
)
[ ]
lim
,
4
4
2
2
2
1
1
2
2
2
2
2
97
,
0
35
,
0
7
,
16
0
,
1
)
37
,
0
(
10
425
,
9
89
,
0
10
425
,
9
350
2
04
,
0
37
,
0
04
,
0
37
,
0
2
eff
eff
cd
s
S
s
S
yd
s
s
eff
x
x
m
b
f
e
A
e
A
f
a
e
a
e
x
>
=
⋅
⋅
−
⋅
⋅
−
⋅
⋅
⋅
⋅
+
−
−
+
−
−
−
=
=
⋅
⋅
⋅
−
⋅
⋅
⋅
+
−
+
−
−
=
−
−
α
(
)
(
)
37
,
0
)
37
,
0
(
10
425
,
9
350
89
,
0
10
425
,
9
350
1
47
,
0
2
35
,
0
7
,
16
0
,
1
2
1
2
2
03
,
0
35
,
0
7
,
16
0
,
1
47
,
0
56
,
0
89
,
0
10
425
,
9
350
2
04
,
0
37
,
0
2
47
,
0
53
,
0
1
1
4
4
2
2
1
1
4
1
1
2
2
lim
,
=
−
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
⋅
−
⋅
⋅
⋅
=
−
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
−
−
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
−
=
=
−
=
−
=
−
−
−
s
S
yd
s
S
yd
cd
cd
s
S
yd
s
eff
e
A
f
e
A
f
p
b
f
B
b
f
p
d
e
A
f
a
e
A
p
α
α
ξ
(
)
64
,
0
37
,
0
03
,
0
03
,
0
2
2
=
+
−
+
=
+
+
−
=
B
A
A
x
eff
0
,
1
0
,
1
14
,
1
56
,
0
64
,
0
−
=
⇒
>
=
=
=
s
eff
eff
d
x
κ
ξ
(
)
[ ]
[ ]
kN
kN
A
f
A
f
x
b
f
N
s
S
yd
S
yd
eff
cd
Sd
55
,
4400
55,849
1
0
,
1
10
425
,
9
350000
10
425
,
9
350000
64
,
0
35
,
0
16700
0
,
1
849
,
155
4
4
1
2
≤
−
⋅
⋅
⋅
−
⋅
⋅
+
⋅
⋅
⋅
≤
⋅
⋅
−
⋅
+
⋅
⋅
⋅
≤
−
−
κ
α
(
)
(
)
(
)
(
)
[
]
[
]
kNm
kNm
a
d
A
f
x
d
x
b
f
e
N
S
yd
eff
eff
cd
s
Sd
327
,
1069
38,706
1
04
,
0
56
,
0
10
425
,
9
350000
64
,
0
5
,
0
56
,
0
64
,
0
35
,
0
16700
0
,
1
89
,
0
849
,
155
5
,
0
4
2
2
1
≤
−
⋅
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
≤
⋅
−
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
≤
⋅
−
α
Przyjęcie średnicy strzemion:
[ ]
[ ]
[ ]
mm
mm
mm
s
zal
s
8
5
,
4
4
20
2
,
0
2
,
0
=
=
⋅
=
⋅
≥
φ
φ
φ
Wyznaczenie rozstawu strzemion:
[ ]
[ ]
(
)
[ ]
[ ]
[ ]
=
=
≤
=
=
⋅
=
⋅
≤
mm
cm
mm
cm
mm
s
L
400
35
350
b
%
3
30
300
20
15
15
min
sl
ρ
φ
Przyjęto strzemiona dwucięte Φ8 w rozstawie 20[cm] i w rozstawie 10[cm] na długości
zakładu.
Słup nr 2 = nr 3 – zbrojenie symetryczne
Określenie długości obliczeniowej i smukłości słupa:
[ ]
7
7
6
,
0
2
,
4
2
,
4
2
,
4
0
,
1
0
0
≤
=
=
=
=
⋅
=
⋅
=
h
l
m
l
l
col
λ
β

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
29
Nośność sprawdzamy bez uwzględnienia smukłości elementu i wpływu obciążeń
długotrwałych.
Wyznaczenie maksymalnego mimośrodu konstrukcyjnego:
[
]
[ ]
[ ]
[
]
[ ]
[ ]
[ ]
[
]
[ ]
[ ]
[
]
[ ]
m
N
M
e
kNm
M
kN
N
m
N
M
e
kNm
M
kN
N
m
N
M
e
kN
N
kNm
M
m
N
M
e
kN
N
kNm
M
e
e
e
e
13
,
0
025
,
965
022
,
123
022
,
123
025
,
965
15
,
0
640
,
509
998
,
77
998
,
77
640
,
509
14
,
0
022
,
921
706
,
129
022
,
921
706
,
129
max
28
,
0
972
,
898
427
,
252
972
,
898
427
,
252
min
max
min
max
=
=
=
⇒
=
→
=
=
=
=
⇒
=
→
=
=
=
=
⇒
=
→
=
⇐
=
=
=
⇒
=
→
=
Wyznaczenie maksymalnego mimośrodu niezamierzonego (n – druga kondygnacja licząc od
góry):
[ ]
[ ]
[ ]
=
=
=
+
⋅
=
+
⋅
=
m
m
h
m
n
l
e
col
a
01
,
0
02
,
0
30
6
,
0
30
0105
,
0
2
1
1
600
2
,
4
1
1
600
max
Obliczenie mimośrodu początkowego siły ściskającej względem środka ciężkości przekroju
betonu:
[ ]
m
e
e
e
e
a
3
,
0
28
,
0
02
,
0
0
=
+
=
+
=
Obliczenie zwiększonego mimośrodu początkowego:
[ ]
m
e
e
tot
3
,
0
3
,
0
0
,
1
0
,
1
0
=
⋅
=
⋅
=
=
η
η
Obliczenie mimośrodu względem środka ciężkości zbrojenia rozciąganego:
[ ]
m
a
h
e
e
tot
s
56
,
0
04
,
0
6
,
0
5
,
0
3
,
0
5
,
0
1
1
=
−
⋅
+
=
−
⋅
+
=
Obliczenie powierzchni zbrojenia ściskanego przy założeniu ściskania z dużym mimośrodem:
[ ]
m
d
x
eff
eff
297
,
0
56
,
0
53
,
0
lim
,
lim
,
=
⋅
=
⋅
=
ξ
[ ]
[ ]
[ ]
m
a
m
x
x
m
b
f
N
x
eff
eff
cd
Sd
eff
08
,
0
04
,
0
2
2
154
,
0
154
,
0
35
,
0
16700
0
,
1
972
,
898
2
lim
,
=
⋅
=
⋅
>
=
≤
=
⋅
⋅
=
⋅
⋅
=
α
(
)
(
)
[ ]
[ ]
2
2
4
2
1
2
1
803
,
3
10
803
,
3
04
,
0
56
,
0
350000
35
,
0
16700
0
,
1
2
972
,
898
56
,
0
56
,
0
972
,
898
2
cm
m
a
d
f
b
f
N
d
e
N
A
A
yd
cd
Sd
s
Sd
S
S
=
⋅
=
−
⋅
⋅
⋅
⋅
+
−
⋅
=
=
−
⋅
⋅
⋅
⋅
+
−
⋅
=
=
−
α
Wyznaczenie zbrojenia minimalnego:
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
30
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
=
⋅
=
−
−
2
2
4
2
2
4
min
88
,
5
10
88
,
5
56
,
0
35
,
0
003
,
0
003
,
0
853
,
3
10
853
,
3
350000
972
,
898
15
,
0
15
,
0
max
cm
m
d
b
cm
m
f
N
A
yd
Sd
S
[ ]
2
2
1
88
,
5
cm
A
A
S
S
=
=
Przyjąłem zbrojenie symetryczne 3Φ20 o A
S1
= A
S2
=9,425[cm
2
] , o większym przekroju aby
osiągnąć założony stopień zbrojenia.
Obliczenie stopnia zbrojenia obliczonego:
[ ]
%
898
,
0
%
100
60
35
85
,
18
85
,
18
425
,
9
425
,
9
2
1
2
2
1
=
⋅
⋅
=
⋅
+
=
=
+
=
+
h
b
A
A
cm
A
A
S
S
S
S
ρ
Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a
stopniem zbrojenia założonym:
%
20
%
2
,
10
%
100
0
,
1
0
,
1
898
,
0
=
∆
<
=
⋅
−
=
−
=
∆
dop
zal
zal
ρ
ρ
ρ
Sprawdzenie nośności przekroju słupa prostokątnego, mimośrodowo ściskanego:
[ ]
m
d
x
eff
eff
297
,
0
56
,
0
53
,
0
lim
,
lim
,
=
⋅
=
⋅
=
ξ
[ ]
[ ]
m
a
e
d
e
m
a
h
e
e
s
s
tot
s
04
,
0
04
,
0
56
,
0
56
,
0
56
,
0
04
,
0
6
,
0
5
,
0
3
,
0
5
,
0
2
1
2
1
1
−
=
−
−
=
−
−
=
=
−
⋅
+
=
−
⋅
+
=
(
) (
)
(
)
(
) (
)
(
)
[ ]
lim
,
4
4
2
2
2
1
1
2
2
2
2
2
35
,
0
35
,
0
7
,
16
0
,
1
)
04
,
0
(
10
425
,
9
56
,
0
10
425
,
9
350
2
04
,
0
04
,
0
04
,
0
04
,
0
2
eff
eff
cd
s
S
s
S
yd
s
s
eff
x
x
m
b
f
e
A
e
A
f
a
e
a
e
x
>
=
⋅
⋅
−
⋅
⋅
−
⋅
⋅
⋅
⋅
+
−
−
+
−
−
−
=
=
⋅
⋅
⋅
−
⋅
⋅
⋅
+
−
+
−
−
=
−
−
α
(
)
(
)
19
,
0
)
04
,
0
(
10
425
,
9
350
56
,
0
10
425
,
9
350
1
47
,
0
2
35
,
0
7
,
16
0
,
1
2
1
2
2
16
,
0
35
,
0
7
,
16
0
,
1
47
,
0
56
,
0
56
,
0
10
425
,
9
350
2
04
,
0
04
,
0
2
47
,
0
53
,
0
1
1
4
4
2
2
1
1
4
1
1
2
2
lim
,
=
−
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
⋅
−
⋅
⋅
⋅
=
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
−
−
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
−
=
=
−
=
−
=
−
−
−
s
S
yd
s
S
yd
cd
cd
s
S
yd
s
eff
e
A
f
e
A
f
p
b
f
B
b
f
p
d
e
A
f
a
e
A
p
α
α
ξ
3
,
0
19
,
0
16
,
0
16
,
0
2
2
=
+
+
−
=
+
+
−
=
B
A
A
x
eff
(
)
(
)
957
,
0
1
53
,
0
1
54
,
0
1
2
1
1
1
2
54
,
0
56
,
0
3
,
0
lim
,
=
−
−
−
⋅
=
−
−
−
⋅
=
=
=
=
eff
eff
s
eff
eff
d
x
ξ
ξ
κ
ξ
[ ]
[ ]
kN
kN
A
f
A
f
x
b
f
N
s
S
yd
S
yd
eff
cd
Sd
685
,
1767
972
,
898
957
,
0
10
425
,
9
350000
10
425
,
9
350000
3
,
0
35
,
0
16700
0
,
1
972
,
898
4
4
1
2
≤
⋅
⋅
⋅
−
⋅
⋅
+
⋅
⋅
⋅
≤
⋅
⋅
−
⋅
+
⋅
⋅
⋅
≤
−
−
κ
α
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
31
(
)
(
)
(
)
(
)
[
]
[
]
kNm
kNm
a
d
A
f
x
d
x
b
f
e
N
S
yd
eff
eff
cd
s
Sd
47
,
890
03,424
5
04
,
0
56
,
0
10
425
,
9
350000
3
,
0
5
,
0
56
,
0
3
,
0
35
,
0
16700
0
,
1
56
,
0
972
,
898
5
,
0
4
2
2
1
≤
−
⋅
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
≤
⋅
−
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
≤
⋅
−
α
Przyjęcie średnicy strzemion:
[ ]
[ ]
[ ]
mm
mm
mm
s
zal
s
8
5
,
4
4
20
2
,
0
2
,
0
=
=
⋅
=
⋅
≥
φ
φ
φ
Wyznaczenie rozstawu strzemion:
[ ]
[ ]
(
)
[ ]
[ ]
[ ]
=
=
≤
=
=
⋅
=
⋅
≤
mm
cm
mm
cm
mm
s
L
400
35
350
b
%
3
30
300
20
15
15
min
sl
ρ
φ
Przyjęto strzemiona dwucięte Φ8 w rozstawie 20[cm] i w rozstawie 10[cm] na długości
zakładu.
Słup nr 5 = nr 6 – zbrojenie symetryczne
Określenie długości obliczeniowej i smukłości słupa:
[ ]
(
)
30
7
898
,
8
6
,
0
339
,
5
339
,
5
339
,
5
0
,
1
0
0
≤
>
=
=
=
=
⋅
=
⋅
=
lecz
h
l
m
l
l
col
λ
β
Nośność należy sprawdzić z uwzględnieniem smukłości elementów i wpływu obciążeń
długotrwałych.
Wyznaczenie maksymalnego mimośrodu konstrukcyjnego:
[
]
[ ]
[ ]
[
]
[ ]
[ ]
[ ]
[
]
[ ]
[ ]
[
]
[ ]
m
N
M
e
kNm
M
kN
N
m
N
M
e
kNm
M
kN
N
m
N
M
e
kN
N
kNm
M
m
N
M
e
kN
N
kNm
M
e
e
e
e
17
,
0
617
,
274
831
,
47
831
,
47
617
,
274
21
,
0
177
,
365
503
,
76
503
,
76
177
,
365
19
,
0
636
,
324
151
,
62
636
,
324
151
,
62
max
53
,
0
665
,
352
864
,
188
665
,
352
864
,
188
min
max
min
max
=
=
=
⇒
=
→
=
=
=
=
⇒
=
→
=
=
=
=
⇒
=
→
=
⇐
=
=
=
⇒
=
→
=
Wyznaczenie maksymalnego mimośrodu niezamierzonego (n – pierwsza kondygnacja licząc
od góry):
[ ]
[ ]
[ ]
=
=
=
+
⋅
=
+
⋅
=
m
m
h
m
n
l
e
col
a
01
,
0
02
,
0
30
6
,
0
30
018
,
0
1
1
1
600
339
,
5
1
1
600
max
Obliczenie mimośrodu początkowego siły ściskającej względem środka ciężkości przekroju
betonu:
[ ]
m
e
e
e
e
a
55
,
0
53
,
0
02
,
0
0
=
+
=
+
=
Obliczenie zwiększonego mimośrodu początkowego:
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
32
[ ]
[
]
[ ]
[
]
=
=
=
−
−
⋅
⋅
⋅
=
−
−
⋅
⋅
⋅
=
=
=
=
=
=
⋅
=
⋅
=
2
4
2
2
2
1
2
4
3
3
200000
200
0001325
,
0
2
04
,
0
04
,
0
6
,
0
56
,
0
35
,
0
01
,
0
2
01
,
0
%
1
31000
31
0063
,
0
12
6
,
0
35
,
0
12
m
MN
GPa
E
m
a
a
h
d
b
J
m
MN
GPa
E
m
h
b
J
s
s
cm
c
ρ
ρ
=
⋅
−
⋅
−
=
⋅
−
⋅
−
>
=
=
05
,
0
244
,
0
7
,
16
01
,
0
6
,
0
339
,
5
01
,
0
50
,
0
01
,
0
01
,
0
50
,
0
92
,
0
6
,
0
55
,
0
0
0
cd
f
h
l
h
e
Wilgotność względna powietrza wynosi RH=50%.
Miarodajny przekrój elementu wynosi:
(
)
[ ]
(
)
72
,
2
,
221
600
350
2
600
350
2
2
0
0
=
∞
⇒
=
+
⋅
⋅
⋅
=
⋅
=
t
mm
u
A
h
c
φ
[ ]
(
)
088
,
2
72
,
2
665
,
352
132
,
282
5
,
0
1
,
5
,
0
1
132
,
282
665
,
352
8
,
0
8
,
0
0
,
,
=
⋅
⋅
+
=
∞
⋅
⋅
+
=
=
⋅
=
⋅
=
t
N
N
k
kN
N
N
Sd
lt
Sd
lt
Sd
lt
Sd
φ
[ ]
[ ]
[ ]
[ ]
032
,
1
11441
665
,
352
1
1
1
1
10297
11441
9
,
0
9
,
0
665
,
352
11441
441
,
11
0001325
,
0
200000
1
,
0
6
,
0
55
,
0
1
,
0
11
,
0
088
,
2
2
0063
,
0
31000
339
,
5
9
1
,
0
1
,
0
11
,
0
2
9
2
0
2
0
=
−
=
−
=
=
⋅
=
⋅
≤
=
=
=
⋅
+
+
+
⋅
⋅
⋅
⋅
=
=
⋅
+
+
+
⋅
⋅
⋅
⋅
=
crit
Sd
crit
Sd
s
s
lt
c
cm
crit
N
N
kN
N
kN
N
kN
MN
J
E
h
e
k
J
E
l
N
η
[ ]
m
e
e
tot
57
,
0
62
,
0
032
,
1
0
=
⋅
=
⋅
=
η
Obliczenie mimośrodu względem środka ciężkości zbrojenia rozciąganego
[ ]
m
a
h
e
e
tot
s
83
,
0
04
,
0
6
,
0
5
,
0
57
,
0
5
,
0
1
1
=
−
⋅
+
=
−
⋅
+
=
Obliczenie powierzchni zbrojenia ściskanego przy założeniu ściskania z dużym mimośrodem:
[ ]
m
d
x
eff
eff
297
,
0
56
,
0
53
,
0
lim
,
lim
,
=
⋅
=
⋅
=
ξ
[ ]
[ ]
[ ]
m
a
m
x
x
m
b
f
N
x
eff
eff
cd
Sd
eff
08
,
0
04
,
0
2
2
06
,
0
06
,
0
35
,
0
16700
0
,
1
665
,
352
2
lim
,
=
⋅
=
⋅
<
=
≤
=
⋅
⋅
=
⋅
⋅
=
α
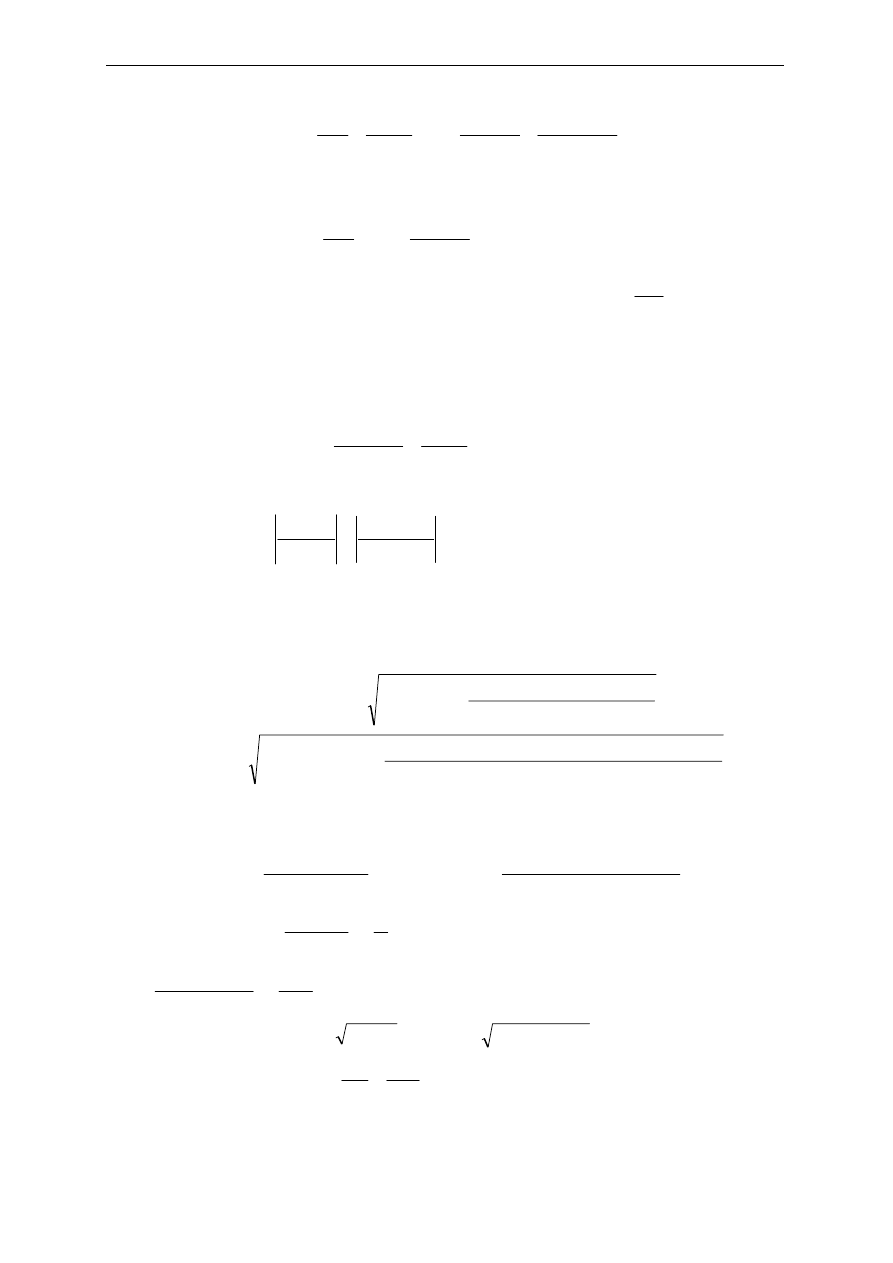
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
33
[ ]
[ ]
2
2
4
2
1
2
1
007
,
6
10
007
,
6
1
04
,
0
56
,
0
83
,
0
350000
665
,
352
1
cm
m
a
d
e
f
N
A
A
s
yd
Sd
S
S
=
⋅
=
=
−
−
⋅
=
−
−
⋅
=
=
−
Wyznaczenie zbrojenia minimalnego:
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
=
⋅
=
−
−
2
2
4
2
2
4
min
88
,
5
10
88
,
5
56
,
0
35
,
0
003
,
0
003
,
0
511
,
1
10
511
,
1
350000
665
,
352
15
,
0
15
,
0
max
cm
m
d
b
cm
m
f
N
A
yd
Sd
S
[ ]
2
2
1
007
,
6
cm
A
A
S
S
=
=
Przyjąłem zbrojenie symetryczne 3Φ20 o A
S1
= A
S2
=9,425[cm
2
], o większym przekroju aby
osiągnąć założony stopień zbrojenia.
Obliczenie stopnia zbrojenia obliczonego:
[ ]
%
898
,
0
%
100
60
35
85
,
18
85
,
18
425
,
9
425
,
9
2
1
2
2
1
=
⋅
⋅
=
⋅
+
=
=
+
=
+
h
b
A
A
cm
A
A
S
S
S
S
ρ
Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a
stopniem zbrojenia założonym:
%
20
%
2
,
10
%
100
0
,
1
0
,
1
898
,
0
=
∆
<
=
⋅
−
=
−
=
∆
dop
zal
zal
ρ
ρ
ρ
Sprawdzenie nośności przekroju słupa prostokątnego, mimośrodowo ściskanego:
[ ]
m
d
x
eff
eff
297
,
0
56
,
0
53
,
0
lim
,
lim
,
=
⋅
=
⋅
=
ξ
[ ]
[ ]
m
a
e
d
e
m
a
h
e
e
s
s
tot
s
31
,
0
04
,
0
83
,
0
56
,
0
83
,
0
04
,
0
6
,
0
5
,
0
57
,
0
5
,
0
2
1
2
1
1
−
=
−
−
=
−
−
=
=
−
⋅
+
=
−
⋅
+
=
(
) (
)
(
)
(
) (
)
(
)
[ ]
lim
,
4
4
2
2
2
1
1
2
2
2
2
2
85
,
0
35
,
0
7
,
16
0
,
1
)
31
,
0
(
10
425
,
9
83
,
0
10
425
,
9
350
2
04
,
0
31
,
0
04
,
0
31
,
0
2
eff
eff
cd
s
S
s
S
yd
s
s
eff
x
x
m
b
f
e
A
e
A
f
a
e
a
e
x
>
=
⋅
⋅
−
⋅
⋅
−
⋅
⋅
⋅
⋅
+
−
−
+
−
−
−
=
=
⋅
⋅
⋅
−
⋅
⋅
⋅
+
−
+
−
−
=
−
−
α
(
)
(
)
34
,
0
)
31
,
0
(
10
425
,
9
350
83
,
0
10
425
,
9
350
1
47
,
0
2
35
,
0
7
,
16
0
,
1
2
1
2
2
006
,
0
35
,
0
7
,
16
0
,
1
47
,
0
56
,
0
83
,
0
10
425
,
9
350
2
04
,
0
31
,
0
2
47
,
0
53
,
0
1
1
4
4
2
2
1
1
4
1
1
2
2
lim
,
=
−
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
⋅
−
⋅
⋅
⋅
=
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
−
−
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
−
=
=
−
=
−
=
−
−
−
s
S
yd
s
S
yd
cd
cd
s
S
yd
s
eff
e
A
f
e
A
f
p
b
f
B
b
f
p
d
e
A
f
a
e
A
p
α
α
ξ
58
,
0
34
,
0
006
,
0
006
,
0
2
2
=
+
+
−
=
+
+
−
=
B
A
A
x
eff
0
,
1
0
,
1
03
,
1
56
,
0
58
,
0
−
=
⇒
>
=
=
=
s
eff
eff
d
x
κ
ξ

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
34
(
)
[ ]
[ ]
kN
kN
A
f
A
f
x
b
f
N
s
S
yd
S
yd
eff
cd
Sd
85
,
4049
665
,
352
0
,
1
10
425
,
9
350000
10
425
,
9
350000
58
,
0
35
,
0
16700
0
,
1
665
,
352
4
4
1
2
≤
−
⋅
⋅
⋅
−
⋅
⋅
+
⋅
⋅
⋅
≤
⋅
⋅
−
⋅
+
⋅
⋅
⋅
≤
−
−
κ
α
(
)
(
)
(
)
(
)
[
]
[
]
kNm
kNm
a
d
A
f
x
d
x
b
f
e
N
S
yd
eff
eff
cd
s
Sd
862
,
1086
92,712
2
04
,
0
56
,
0
10
425
,
9
350000
58
,
0
5
,
0
56
,
0
58
,
0
35
,
0
16700
0
,
1
83
,
0
665
,
352
5
,
0
4
2
2
1
≤
−
⋅
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
≤
⋅
−
⋅
⋅
+
⋅
−
⋅
⋅
⋅
⋅
≤
⋅
−
α
Przyjęcie średnicy strzemion:
[ ]
[ ]
[ ]
mm
mm
mm
s
zal
s
8
5
,
4
4
20
2
,
0
2
,
0
=
=
⋅
=
⋅
≥
φ
φ
φ
Wyznaczenie rozstawu strzemion:
[ ]
[ ]
(
)
[ ]
[ ]
[ ]
=
=
≤
=
=
⋅
=
⋅
≤
mm
cm
mm
cm
mm
s
L
400
35
350
b
%
3
30
300
20
15
15
min
sl
ρ
φ
Przyjęto strzemiona dwucięte Φ8 w rozstawie 20[cm] i w rozstawie 10[cm] na długości
zakładu.
e) Warunki konstrukcyjne kotwienia i łączenia prętów
Obliczenie podstawowej długości zakotwienia prętów (dla dobrych warunków przyczepności
pretów zbrojenia do betonu):
[ ]
m
f
f
l
bd
yd
b
a
65
,
0
7
,
2
350
4
02
,
0
4
0
,
1
=
⋅
=
⋅
=
=
φ
α
Obliczenie minimalnej długości zakotwienia prętów rozciąganych:
[ ]
[ ]
[ ]
[ ]
=
=
⋅
=
⋅
≥
=
⋅
=
⋅
=
m
mm
m
m
l
l
b
b
1
,
0
100
2
,
0
02
,
0
10
10
195
,
0
65
,
0
3
,
0
3
,
0
min
,
φ
Obliczenie minimalnej długości zakotwienia prętów ściskanych:
[ ]
[ ]
[ ]
[ ]
=
=
⋅
=
⋅
≥
=
⋅
=
⋅
=
m
mm
m
m
l
l
b
b
1
,
0
100
2
,
0
02
,
0
10
10
39
,
0
65
,
0
6
,
0
6
,
0
min
,
φ
Rygiel stropu nr 7
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przywęzłowego dla węzła nr 5 = 6:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
53
,
0
85
,
18
454
,
15
65
,
0
0
,
1
85
,
18
454
,
15
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przęsłowego:
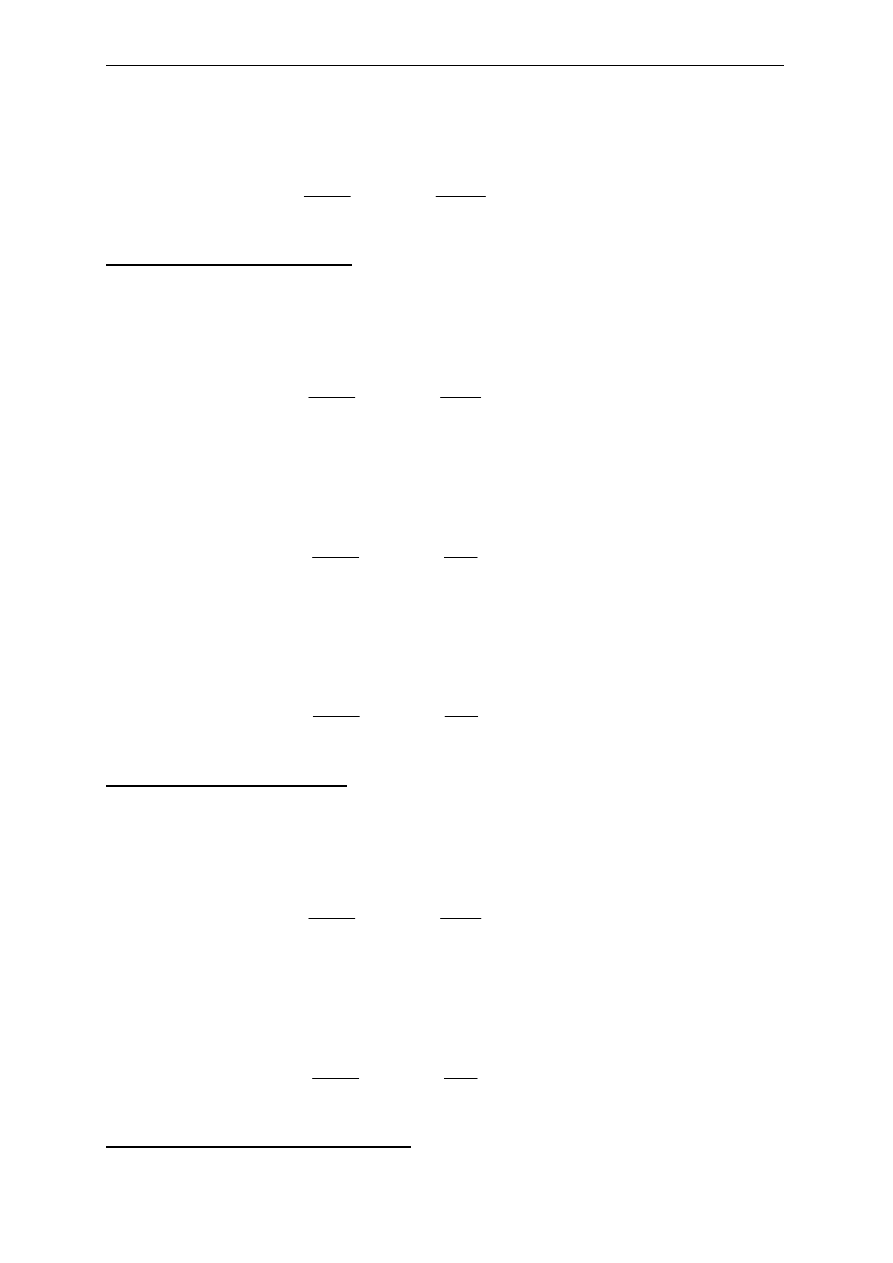
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
35
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
63
,
0
99
,
21
263
,
21
65
,
0
0
,
1
99
,
21
263
,
21
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Rygiel stropodachu nr 8 = nr 11
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przywęzłowego dla węzła nr 8 = 10:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
52
,
0
57
,
12
09
,
10
65
,
0
0
,
1
57
,
12
09
,
10
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przywęzłowego dla węzła nr 7 = 11:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
42
,
0
42
,
9
14
,
6
65
,
0
0
,
1
42
,
9
14
,
6
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przęsłowego:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
41
,
0
42
,
9
01
,
6
65
,
0
0
,
1
42
,
9
01
,
6
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Rygiel stropodachu nr9 = nr 10
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przywęzłowego dla węzła nr 8 = 10:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
53
,
0
71
,
15
77
,
12
65
,
0
0
,
1
71
,
15
77
,
12
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego
przęsłowego:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
2
,
0
55
,
0
28
,
6
32
,
5
65
,
0
0
,
1
28
,
6
32
,
5
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
=
α
Słup nr 1 = nr 4, nr 2 = nr 3, nr 5 = nr 6
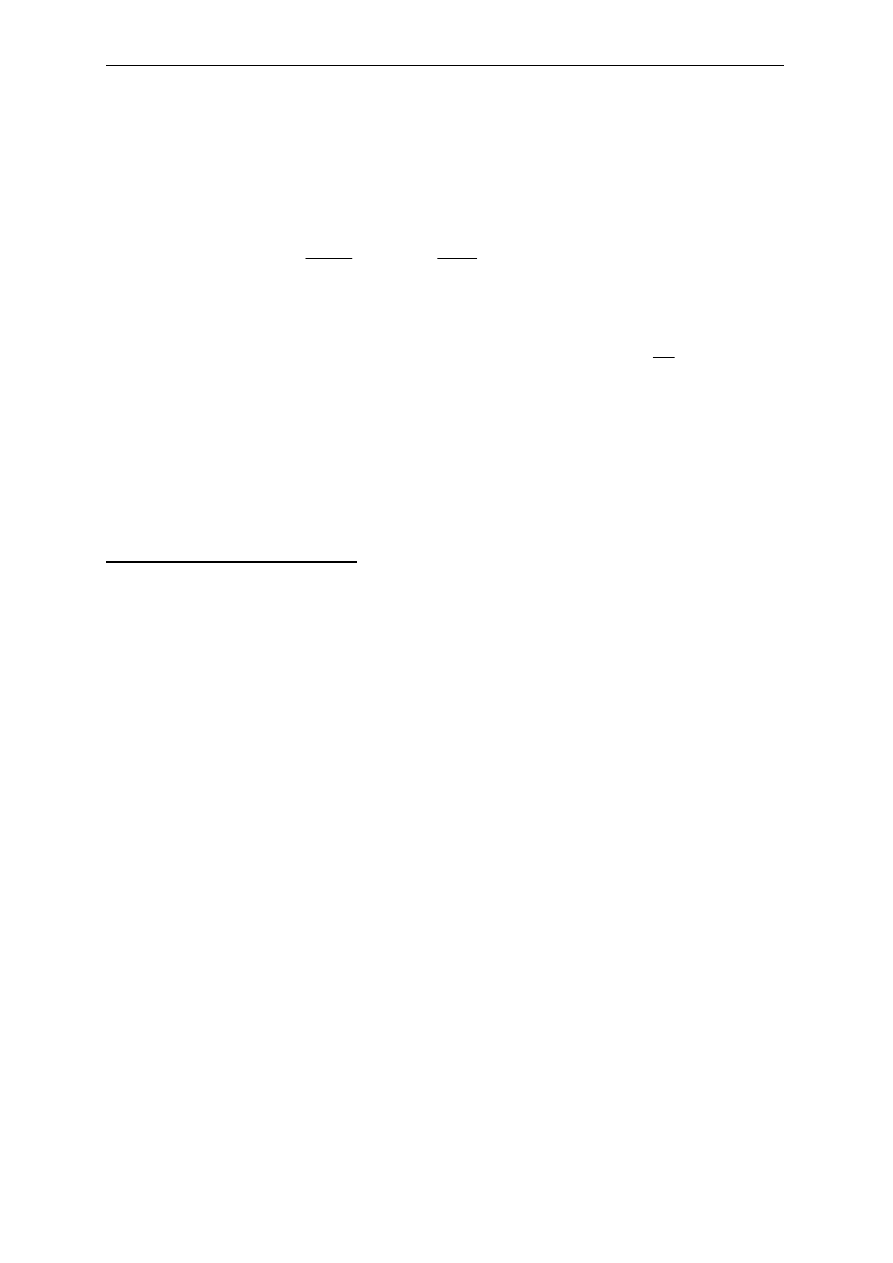
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
36
Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego:
[ ]
[ ]
[ ]
[ ]
m
l
m
A
A
l
l
cm
A
cm
A
b
prov
S
reg
S
b
a
bd
prov
S
reg
S
39
,
0
41
,
0
85
,
18
76
,
11
65
,
0
0
,
1
85
,
18
425
,
9
425
,
9
76
,
11
88
,
5
88
,
5
min
,
,
,
2
,
2
,
=
≥
=
⋅
⋅
=
⋅
⋅
=
=
+
=
=
+
=
α
Obliczenie obliczeniowej wymaganej długości zakładu:
[ ]
[ ]
[ ]
m
mm
m
l
l
b
a
s
2
,
0
200
195
,
0
65
,
0
0
,
1
0
,
1
3
,
0
3
,
0
0
,
1
1
min
,
1
=
≥
=
⋅
⋅
⋅
=
⋅
⋅
⋅
≥
=
α
α
α
[ ]
[ ]
m
l
m
l
l
s
bd
s
2
,
0
41
,
0
0
,
1
41
,
0
min
,
1
=
≥
=
⋅
=
⋅
=
α
f) Wymiarowanie stóp fundamentowych
Przy obliczeniach wg I stanu granicznego wartość obliczeniowa działającego obciążenia N
r
powinna spełniać warunek:
fNL
r
Q
m
N
⋅
≤
Stopa fundamentowa nr 2 = nr 3
Wielkości obciążenia działającego na stopę (obliczeniowe):
[ ]
[ ]
[
]
kNm
M
kN
T
kN
N
022
,
123
119
,
88
025
,
965
=
−
=
=
Przyjmuję posadowienie fundamentu na głębokości 1,0[m] (równej głębokości przemarzania
gruntów w miejscowości Kielce h
z
=1,0[m]) na chudym betonie grubości minimum 10[cm]
wykonanym z betonu B-10.
Przyjęcie wstępnych wymiarów stopy fundamentowej, przy założeniu, że minimalna
wysokość stopy ze względu na długość zakotwienia prętów głównych słupa wynosi h= m:
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
m
h
m
b
m
H
D
h
m
D
m
H
m
B
m
L
f
f
f
6
,
0
35
,
0
4
,
0
,6
0
-
,0
1
-
0
,
1
6
,
0
5
,
1
0
,
2
min
min
=
=
=
=
=
=
=
=
=
Obliczenie objętości stopy fundamentowej i gruntu nad odsadzkami fundamentu:
[ ]
3
88
,
1
4
,
0
6
,
0
35
,
0
6
,
0
5
,
1
0
,
2
m
h
h
b
H
B
L
V
f
f
f
=
⋅
⋅
+
⋅
⋅
=
⋅
⋅
+
⋅
⋅
=
[ ]
3
min
12
,
1
88
,
1
0
,
1
5
,
1
0
,
2
m
V
D
B
L
V
f
g
=
−
⋅
⋅
=
−
⋅
⋅
=
Obliczenie ciężarów stopy i gruntu nad odsadzkami fundamentu:
[ ]
kN
V
G
f
r
f
81
,
51
88
,
1
25
1
,
1
25
2
,
1
=
⋅
⋅
=
⋅
⋅
=
[ ]
kN
V
G
g
r
g
50
,
22
12
,
1
8
,
16
2
,
1
7
,
16
2
,
1
=
⋅
⋅
=
⋅
⋅
=
Obliczenie całkowitego obciążenia działającego na grunt w poziomie posadowienia:
[ ]
kN
G
G
N
N
r
g
r
f
r
33
,
1039
50
,
22
81
,
51
025
,
965
=
+
+
=
+
+
=

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
37
Sprawdzenie czy wypadkowa obciążeń znajduje się w rdzeniu przekroju podstawy:
[
]
kNm
D
T
M
M
r
903
,
34
0
,
1
119
,
88
022
,
123
min
=
⋅
−
=
⋅
+
=
[ ]
[ ]
m
L
m
N
M
e
r
r
L
33
,
0
6
0
,
2
6
03
,
0
33
,
1039
903
,
34
=
=
<
=
=
=
Ponieważ wypadkowa znajduje się w rdzeniu podstawy fundamentu, to pod fundamentem
wystąpią naprężenia tylko jednego znaku (ściskające). Naprężenia te wynoszą:
[ ]
kPa
L
e
B
L
N
q
L
r
r
348
,
381
0
,
2
03
,
0
6
1
5
,
1
0
,
2
33
,
1039
6
1
max
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
=
[ ]
kPa
L
e
B
L
N
q
L
r
r
542
,
311
0
,
2
03
,
0
6
1
5
,
1
0
,
2
33
,
1039
6
1
min
=
⋅
−
⋅
⋅
=
⋅
−
⋅
⋅
=
0
,
2
22
,
1
542
,
311
348
,
381
min
max
<
=
=
r
r
q
q
Parametry geotechniczne gruntu (piasek drobny) na którym ma być posadowiona stopa
fundamentowa:
7
,
0
=
D
I
'
21
28
°
=
Φ
r
u
=
⋅
3
)
(
8
,
16
m
kN
g
n
ς
=
⋅
=
⋅
=
⋅
3
)
(
)
(
)
(
1
,
15
m
kN
g
g
g
r
B
r
D
r
ς
ς
ς
50
,
26
=
C
N
30
,
15
=
D
N
79
,
5
=
B
N
Zredukowane wymiary stopy fundamentowej wynoszą:
[ ]
m
e
L
L
L
94
,
1
03
,
0
2
0
,
2
2
=
⋅
−
=
⋅
−
=
[ ]
m
B
B
5
,
1
=
=
Współczynnik uwzględniający wpływ nachylenia wypadkowej:
085
,
0
33
,
1039
119
,
88
=
=
=
r
r
L
N
T
tg
δ
54
,
0
35
,
28
=
=
Φ
tg
tg
r
157
,
0
54
,
0
085
,
0
=
=
Φ
r
r
L
tg
tg
δ
85
,
0
=
C
i
86
,
0
=
D
i
76
,
0
=
B
i
Obliczenie waruneku I stanu granicznego nośności:
[ ]
kN
i
L
g
N
L
B
i
D
g
N
L
B
L
B
Q
B
r
B
B
D
r
D
D
fNL
237
,
1479
76
,
0
94
,
1
1
,
15
79
,
5
94
,
1
5
,
1
25
,
0
1
86
,
0
0
,
1
1
,
15
30
,
15
94
,
1
5
,
1
5
,
1
1
94
,
1
5
,
1
25
,
0
1
5
,
1
1
min
=
=
⋅
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
=
=
⋅
⋅
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
=
ς
ς
Ponieważ parametry geotechniczne zostały wyznaczone metodą B, należy zmniejszyć
współczynnik korekcyjny m=0,9 o 10%.
[ ]
[ ]
kN
kN
Q
N
fNL
r
182
,
1198
237
,
1479
81
,
0
33
,
1039
9
,
0
9
,
0
=
⋅
≤
⋅
⋅
≤
Obliczenie zbrojenia stopy fundamentowej metodą wydzielonych wsporników:
Stopa fundamentowa zaprojektowana będzie na parametry wytrzymałościowe betonu B-30 i
stali A-III.
Graniczny opór gruntu pod stopą wynosi:

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
38
=
⋅
=
=
2
443
,
346
5
,
1
0
,
2
33
,
1039
m
kN
A
N
f
r
gr
σ
Przyjmuję w stopie żelbetowej kąt rozchodzenia się naprężeń
0
,
1
45
=
⇒
°
=
α
α
tg
Obliczenie momentów zginających wsporniki:
(
) (
)
(
) (
)
[
]
(
) (
)
(
) (
)
[
]
kNm
h
L
b
B
M
kNm
b
B
h
L
M
gr
gr
816
,
87
24
6
,
0
0
,
2
2
35
,
0
5
,
1
443
,
346
24
2
781
,
94
24
35
,
0
5
,
1
2
6
,
0
0
,
2
443
,
346
24
2
2
2
2
2
2
1
=
+
⋅
⋅
−
⋅
=
+
⋅
⋅
−
⋅
=
=
+
⋅
⋅
−
⋅
=
+
⋅
⋅
−
⋅
=
σ
σ
Przyjęto grubość otulenia prętów zbrojenia
[ ]
m
a
08
,
0
=
[ ]
[ ]
m
d
z
m
a
h
d
468
,
0
52
,
0
9
,
0
9
,
0
52
,
0
08
,
0
6
,
0
=
⋅
=
⋅
=
=
−
=
−
=
Obliczenie zbrojenia stopy:
[ ]
[ ]
[ ]
[ ]
2
2
4
2
2
2
2
4
1
1
361
,
5
10
361
,
5
468
,
0
350000
816
,
87
786
,
5
10
786
,
5
468
,
0
350000
781
,
94
cm
m
z
f
M
A
cm
m
z
f
M
A
yd
S
yd
S
=
⋅
=
⋅
=
⋅
=
=
⋅
=
⋅
=
⋅
=
−
−
Wyznaczenie minimalnej powierzchni zbrojenia:
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
,
52
,
13
10
52
,
13
52
,
0
0
,
2
0013
,
0
0013
,
0
147
,
17
10
147
,
17
52
,
0
0
,
2
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
L
cm
m
d
L
f
f
A
yk
ctm
SL
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
,
14
,
10
10
14
,
10
52
,
0
5
,
1
0013
,
0
0013
,
0
86
,
12
10
86
,
12
52
,
0
5
,
1
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
B
cm
m
d
B
f
f
A
yk
ctm
SB
Ostatecznie przyjęto zbrojenie większe od minimalnego złożone z 16Φ12 o A
S
=18,096[cm
2
]
prostopadle do dłuższego boku i 12
Φ12 o A
S
=13,572[cm
2
] równoległe do niego.
Z rozkładu naprężeń w stopie wynika, że istnieje konieczność sprawdzenia warunku na
przebicie:
[ ]
[
]
[ ]
[ ]
m
d
m
b
b
b
m
kN
MPa
f
m
A
m
kN
m
ctd
gr
52
,
0
83
,
0
2
31
,
1
35
,
0
2
1200
2
,
1
32
,
0
31
,
1
08
,
0
2
08
,
0
08
,
0
2
5
,
1
14
,
0
443
,
346
2
1
2
2
2
=
=
+
=
+
=
=
=
=
⋅
+
⋅
⋅
+
⋅
=
=
σ
[ ]
[ ]
kN
d
b
f
N
kN
A
m
ctd
Rd
gr
92
,
517
52
,
0
83
,
0
1200
862
,
110
32
,
0
443
,
346
=
⋅
⋅
=
⋅
⋅
=
≤
=
⋅
=
⋅
σ
Stopa fundamentowa nr 1 = nr 4
Wielkości obciążenia działającego na stopę (obliczeniowe):

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
39
[ ]
[ ]
[
]
kNm
M
kN
T
kN
N
538
,
48
849
,
15
532
,
259
=
−
=
=
Przyjmuję posadowienie fundamentu na głębokości 1,0[m] (równej głębokości przemarzania
gruntów w miejscowości Kielce h
z
=1,0[m]) na chudym betonie grubości minimum 10[cm]
wykonanym z betonu B-10.
Przyjęcie wstępnych wymiarów stopy fundamentowej, przy założeniu, że minimalna
wysokość stopy ze względu na długość zakotwienia prętów głównych słupa wynosi h= m:
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
m
h
m
b
m
H
D
h
m
D
m
H
m
B
m
L
f
f
f
6
,
0
35
,
0
4
,
0
,6
0
-
,0
1
-
0
,
1
6
,
0
5
,
1
0
,
2
min
min
=
=
=
=
=
=
=
=
=
Obliczenie objętości stopy fundamentowej i gruntu nad odsadzkami fundamentu:
[ ]
3
88
,
1
4
,
0
6
,
0
35
,
0
6
,
0
5
,
1
0
,
2
m
h
h
b
H
B
L
V
f
f
f
=
⋅
⋅
+
⋅
⋅
=
⋅
⋅
+
⋅
⋅
=
[ ]
3
min
12
,
1
88
,
1
0
,
1
5
,
1
0
,
2
m
V
D
B
L
V
f
g
=
−
⋅
⋅
=
−
⋅
⋅
=
Obliczenie ciężarów stopy i gruntu nad odsadzkami fundamentu:
[ ]
kN
V
G
f
r
f
81
,
51
88
,
1
25
1
,
1
25
2
,
1
=
⋅
⋅
=
⋅
⋅
=
[ ]
kN
V
G
g
r
g
50
,
22
12
,
1
8
,
16
2
,
1
7
,
16
2
,
1
=
⋅
⋅
=
⋅
⋅
=
Obliczenie całkowitego obciążenia działającego na grunt w poziomie posadowienia:
[ ]
kN
G
G
N
N
r
g
r
f
r
84
,
333
50
,
22
81
,
51
532
,
259
=
+
+
=
+
+
=
Sprawdzenie czy wypadkowa obciążeń znajduje się w rdzeniu przekroju podstawy:
[
]
kNm
D
T
M
M
r
689
,
32
0
,
1
849
,
15
538
,
48
min
=
⋅
−
=
⋅
+
=
[ ]
[ ]
m
L
m
N
M
e
r
r
L
33
,
0
6
0
,
2
6
1
,
0
84
,
333
689
,
32
=
=
<
=
=
=
Ponieważ wypadkowa znajduje się w rdzeniu podstawy fundamentu, to pod fundamentem
wystąpią naprężenia tylko jednego znaku (ściskające). Naprężenia te wynoszą:
[ ]
kPa
L
e
B
L
N
q
L
r
r
969
,
143
0
,
2
1
,
0
6
1
5
,
1
0
,
2
84
,
333
6
1
max
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
=
[ ]
kPa
L
e
B
L
N
q
L
r
r
591
,
78
0
,
2
1
,
0
6
1
5
,
1
0
,
2
84
,
333
6
1
min
=
⋅
−
⋅
⋅
=
⋅
−
⋅
⋅
=
0
,
2
83
,
1
591
,
78
969
,
143
min
max
<
=
=
r
r
q
q
Parametry geotechniczne gruntu (piasek drobny) na którym ma być posadowiona stopa
fundamentowa:
7
,
0
=
D
I
'
21
28
°
=
Φ
r
u
=
⋅
3
)
(
8
,
16
m
kN
g
n
ς
=
⋅
=
⋅
=
⋅
3
)
(
)
(
)
(
1
,
15
m
kN
g
g
g
r
B
r
D
r
ς
ς
ς
50
,
26
=
C
N
30
,
15
=
D
N
79
,
5
=
B
N
Zredukowane wymiary stopy fundamentowej wynoszą:

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
40
[ ]
m
e
L
L
L
8
,
1
1
,
0
2
0
,
2
2
=
⋅
−
=
⋅
−
=
[ ]
m
B
B
5
,
1
=
=
Współczynnik uwzględniający wpływ nachylenia wypadkowej:
048
,
0
84
,
333
849
,
15
=
=
=
r
r
L
N
T
tg
δ
54
,
0
35
,
28
=
=
Φ
tg
tg
r
088
,
0
54
,
0
048
,
0
=
=
Φ
r
r
L
tg
tg
δ
89
,
0
=
C
i
9
,
0
=
D
i
83
,
0
=
B
i
Obliczenie waruneku I stanu granicznego nośności:
[ ]
kN
i
L
g
N
L
B
i
D
g
N
L
B
L
B
Q
B
r
B
B
D
r
D
D
fNL
528
,
1497
83
,
0
8
,
1
1
,
15
79
,
5
8
,
1
5
,
1
25
,
0
1
9
,
0
0
,
1
1
,
15
30
,
15
8
,
1
5
,
1
5
,
1
1
8
,
1
5
,
1
25
,
0
1
5
,
1
1
min
=
=
⋅
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
=
=
⋅
⋅
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
=
ς
ς
Ponieważ parametry geotechniczne zostały wyznaczone metodą B, należy zmniejszyć
współczynnik korekcyjny m=0,9 o 10%.
[ ]
[ ]
kN
kN
Q
N
fNL
r
997
,
1212
528
,
1497
81
,
0
33,84
3
9
,
0
9
,
0
=
⋅
≤
⋅
⋅
≤
Obliczenie zbrojenia stopy fundamentowej metodą wydzielonych wsporników:
Stopa fundamentowa zaprojektowana będzie na parametry wytrzymałościowe betonu B-30 i
stali A-III.
Graniczny opór gruntu pod stopą wynosi:
=
⋅
=
=
2
28
,
111
5
,
1
0
,
2
84
,
333
m
kN
A
N
f
r
gr
σ
Przyjmuję w stopie żelbetowej kąt rozchodzenia się naprężeń
0
,
1
45
=
⇒
°
=
α
α
tg
Obliczenie momentów zginających wsporniki:
(
) (
)
(
) (
)
[
]
(
) (
)
(
) (
)
[
]
kNm
h
L
b
B
M
kNm
b
B
h
L
M
gr
gr
207
,
28
24
6
,
0
0
,
2
2
35
,
0
5
,
1
28
,
111
24
2
444
,
30
24
35
,
0
5
,
1
2
6
,
0
0
,
2
28
,
111
24
2
2
2
2
2
2
1
=
+
⋅
⋅
−
⋅
=
+
⋅
⋅
−
⋅
=
=
+
⋅
⋅
−
⋅
=
+
⋅
⋅
−
⋅
=
σ
σ
Przyjęto grubość otulenia prętów zbrojenia
[ ]
m
a
08
,
0
=
[ ]
[ ]
m
d
z
m
a
h
d
468
,
0
52
,
0
9
,
0
9
,
0
52
,
0
08
,
0
6
,
0
=
⋅
=
⋅
=
=
−
=
−
=
Obliczenie zbrojenia stopy:
[ ]
[ ]
[ ]
[ ]
2
2
4
2
2
2
2
4
1
1
722
,
1
10
722
,
1
468
,
0
350000
207
,
28
859
,
1
10
859
,
1
468
,
0
350000
444
,
30
cm
m
z
f
M
A
cm
m
z
f
M
A
yd
S
yd
S
=
⋅
=
⋅
=
⋅
=
=
⋅
=
⋅
=
⋅
=
−
−
Wyznaczenie minimalnej powierzchni zbrojenia:
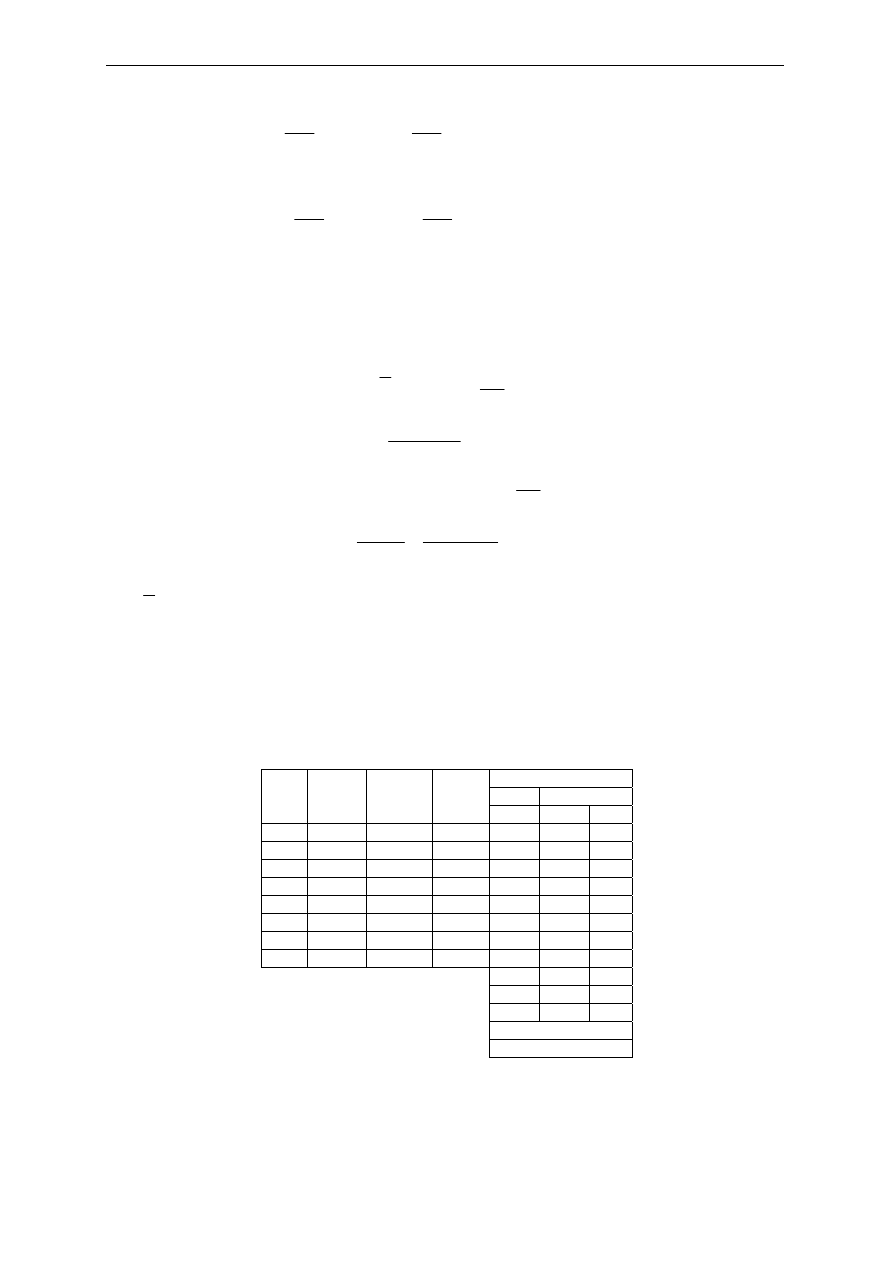
Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
41
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
,
52
,
13
10
52
,
13
52
,
0
0
,
2
0013
,
0
0013
,
0
147
,
17
10
147
,
17
52
,
0
0
,
2
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
L
cm
m
d
L
f
f
A
yk
ctm
SL
[ ]
[ ]
[ ]
[ ]
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
−
−
2
2
4
2
2
4
min
,
14
,
10
10
14
,
10
52
,
0
5
,
1
0013
,
0
0013
,
0
86
,
12
10
86
,
12
52
,
0
5
,
1
410
6
,
2
26
,
0
26
,
0
max
cm
m
d
B
cm
m
d
B
f
f
A
yk
ctm
SB
Ostatecznie przyjęto zbrojenie większe od minimalnego złożone z 16Φ12 o A
S
=18,096[cm
2
]
prostopadle do dłuższego boku i 12
Φ12 o A
S
=13,572[cm
2
] równoległe do niego.
Z rozkładu naprężeń w stopie wynika, że istnieje konieczność sprawdzenia warunku na
przebicie:
[ ]
[
]
[ ]
[ ]
m
d
m
b
b
b
m
kN
MPa
f
m
A
m
kN
m
ctd
gr
52
,
0
83
,
0
2
31
,
1
35
,
0
2
1200
2
,
1
32
,
0
31
,
1
08
,
0
2
08
,
0
08
,
0
2
5
,
1
14
,
0
28
,
111
2
1
2
2
2
=
=
+
=
+
=
=
=
=
⋅
+
⋅
⋅
+
⋅
=
=
σ
[ ]
[ ]
kN
d
b
f
N
kN
A
m
ctd
Rd
gr
92
,
517
52
,
0
83
,
0
1200
61
,
35
32
,
0
28
,
111
=
⋅
⋅
=
⋅
⋅
=
≤
=
⋅
=
⋅
σ
9. Zestawienie stali zbrojeniowej
Poniższa tabela przedstawia zestawienie stali zbrojeniowej użytej do wykonania
monolitycznej ramy żelbetowej, ponieważ jest ona symetryczna dane dotyczą połowy ramy i
tylko ostatnia wartość odnosi się do całości.
Długość łączna [m]
A-I A-III
Nr
pręta
Rodzaj
stali
Długość
[cm]
Liczba
sztuk
Φ8
Φ12 Φ20
1
2
3
4
5
6
7
8
Długość razem [m]
Masa
jednostkowa
[kg/m] 0,395 0,888 2,47
Masa [kg]
Masa ogółem [kg]
Wykonać x 2
10. Literatura i normy:

Katedra Konstrukcji Betonowych Projekt ramy zelbetowej
42
• PN-B-03264:2002 - Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i
projektowanie.
• PN-82/B-02001 - Obciążenia budowli. Obciążenia stałe.
• PN-82/B-02003 - Obciążenia budowli. Obciążenia zmienne technologiczne.
• PN-80/B-02010 - Obciążenia w obliczeniach statycznych. Obciążenie śniegiem.
• PN-77/B-02011 - Obciążenia w obliczeniach statycznych. Obciążenie wiatrem.
• PN-81/B-03020 - Grunty budowlane. Posadowienie bezpośrednie budowli. Obliczenia
statyczne i projektowanie.
• Grabiec K., Bogucka J., Grabiec-Mizera T. „Obliczanie przekrojów w elementach
żelbetowych i betonowych”
Wyszukiwarka
Podobne podstrony:
beton rama2 proj
beton strop proj
BETON PROJ 1 A4
BETON PROJ 1 A4
proj beton
mapy do celow proj
9 Zginanie uko Ťne zbrojenie min beton skr¦Öpowany
Proj syst log wykl 6
Bud II ćw proj 4
Instrukcja do zad proj 13 Uklad sterowania schodow ruchom
beton towarowy
beton projekt
beton ustroju nosnego
Cz Mesjasz Kierowanie Ludzmi w Zarz Proj 1
proj 7
Beton CALY id 82986 Nieznany (2)
15 Slowek G i inni Beton natrys Nieznany
więcej podobnych podstron