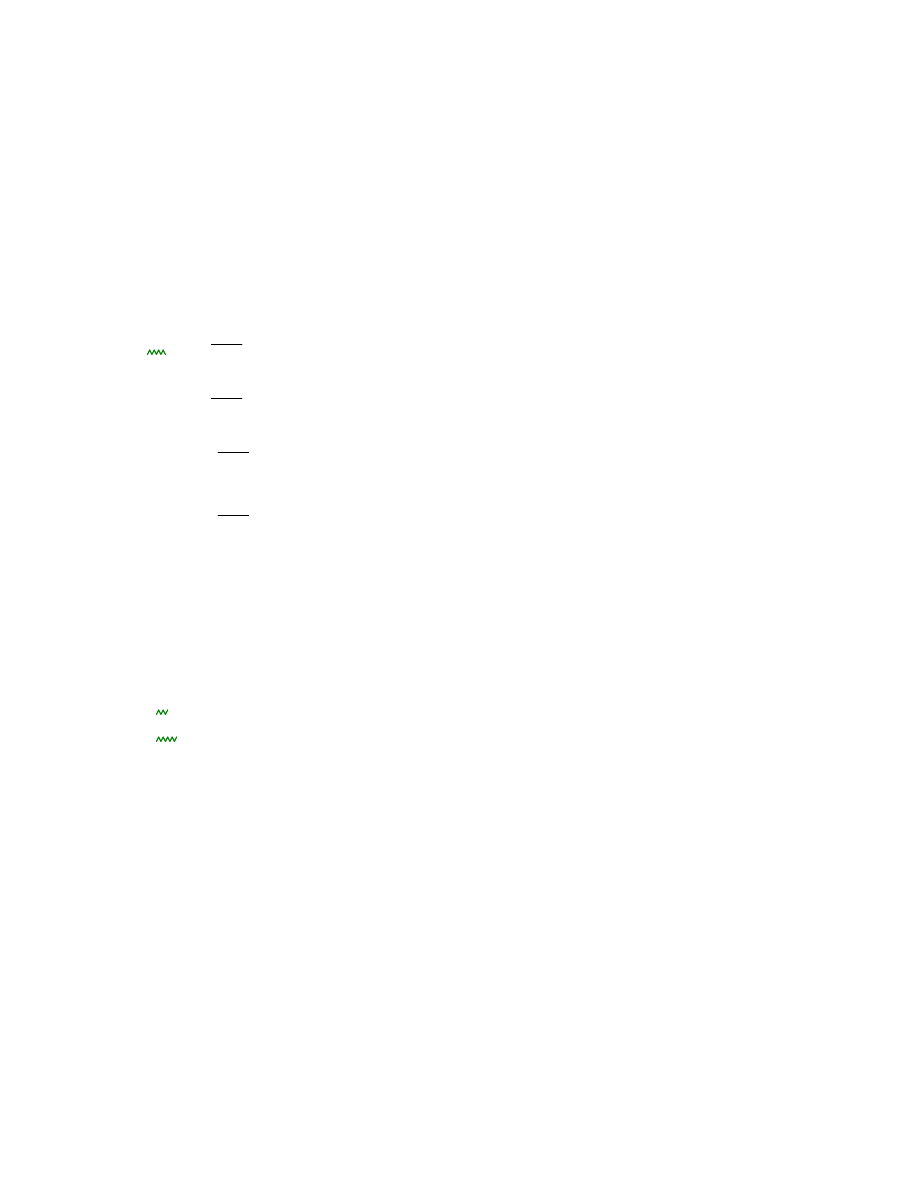
3. Projektowanie połączenia belki drugorzędnej do
żebra podciągu, przenoszącego siłę reakcji o wartości
25kN.
3.1 Dane:
Stal gatunku: S355
Śruby: M16 klasy 5.8
fy
355
N
mm
2
fu
360
N
mm
2
fyb
400
N
mm
2
fub
500
N
mm
2
A
As
157 mm
2
d
16 mm
γM2
1.25
γM0 1
t
8 mm
tw
6.6 mm
d0
18 mm
Sprawdzenie poprawności rozmieszczenia łączenia
e1
50 mm
> 1.2 d
0
0.022 m
e2
50 mm
> 1.2 d
0
0.022 m
p1
80 mm
> 2.2 d
0
0.04 m
Płaszczyzna ścinanie nie przechodzi przez gwitowną część śruby więc α
ν
0.5
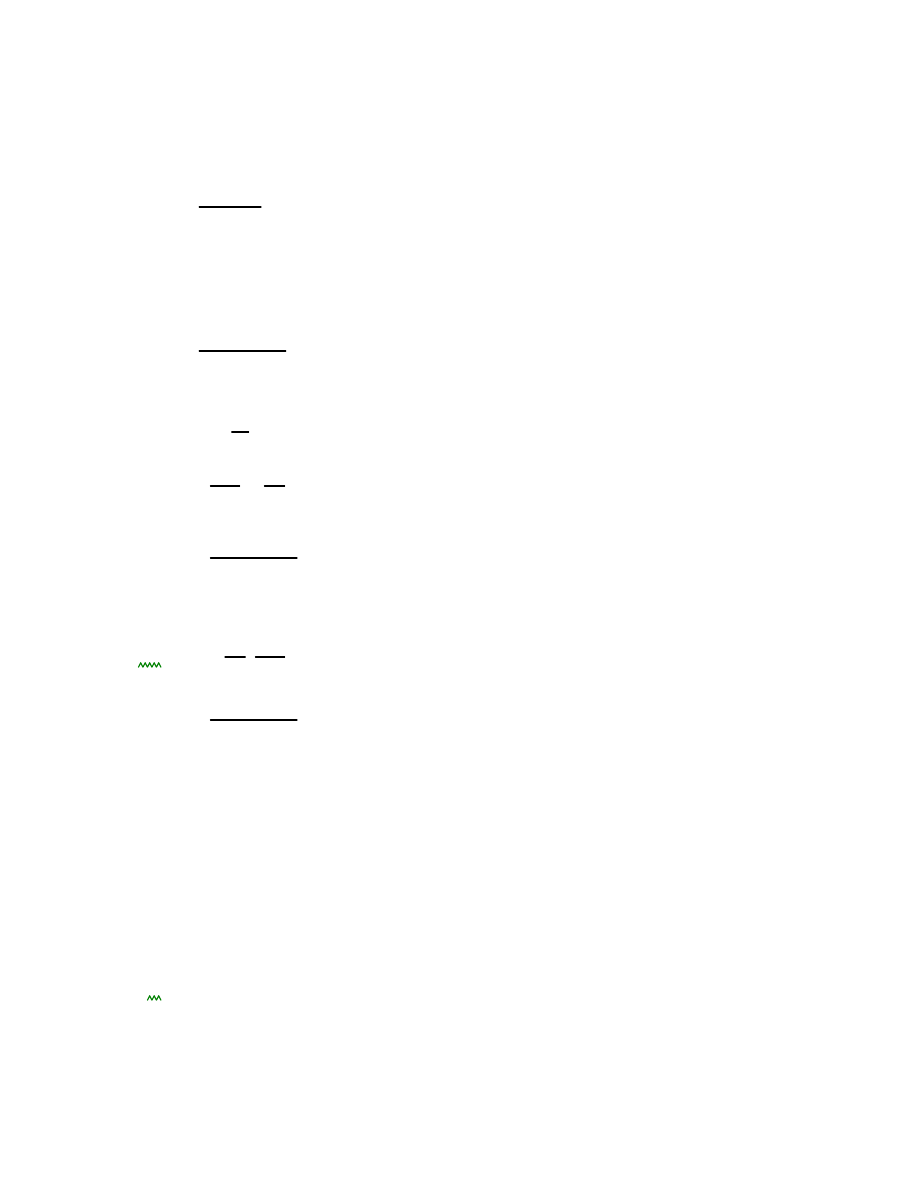
3.2 Nośność śruby na ścinaine wynosi:
Fv.Rd
αν fub
As
γM2
3.14
10
4
N
3.3 Nośność śruby na docisk do środnika belki:
Śruba skrajna
Fb.Rd
k1 αb
fu
d
t
w
γM2
k1
k1
min 2.8
e2
d0
1.7
2.5
2.5
αb
min
e1
3 d0
1
fub
fu
0.926
Fb.Rd.1
k1 αb
fu
d
t
w
γM2
7.04
10
4
N
Śruba pośrednia
αb
min 1
fub
fu
p1
3 d0
1
Fb.Rd.2
k1 αb
fu
d
t
w
γM2
7.603
10
4
N
Grubośc żebra t= 8 mm jest większa od grubości środnika belki t
w
= 6 mm, a więc nośność na
docisk do ścianki jego otworów nie jest miarodajna.
3.4 Nośność grupy łączników.
Ze wzglęgu na to, że nośność na scinanie łącznika F
ν,Rd
jest większa od nośności na docisk
F
b,Rd
obliczeniowa nośność grupy łączników jest równa sumie nośności pojedynczych łączników
na docisk:
F
Fb.Rd.1 Fb.Rd.2
1.464
10
5
N
> F
Ed
2.5
10
4
N
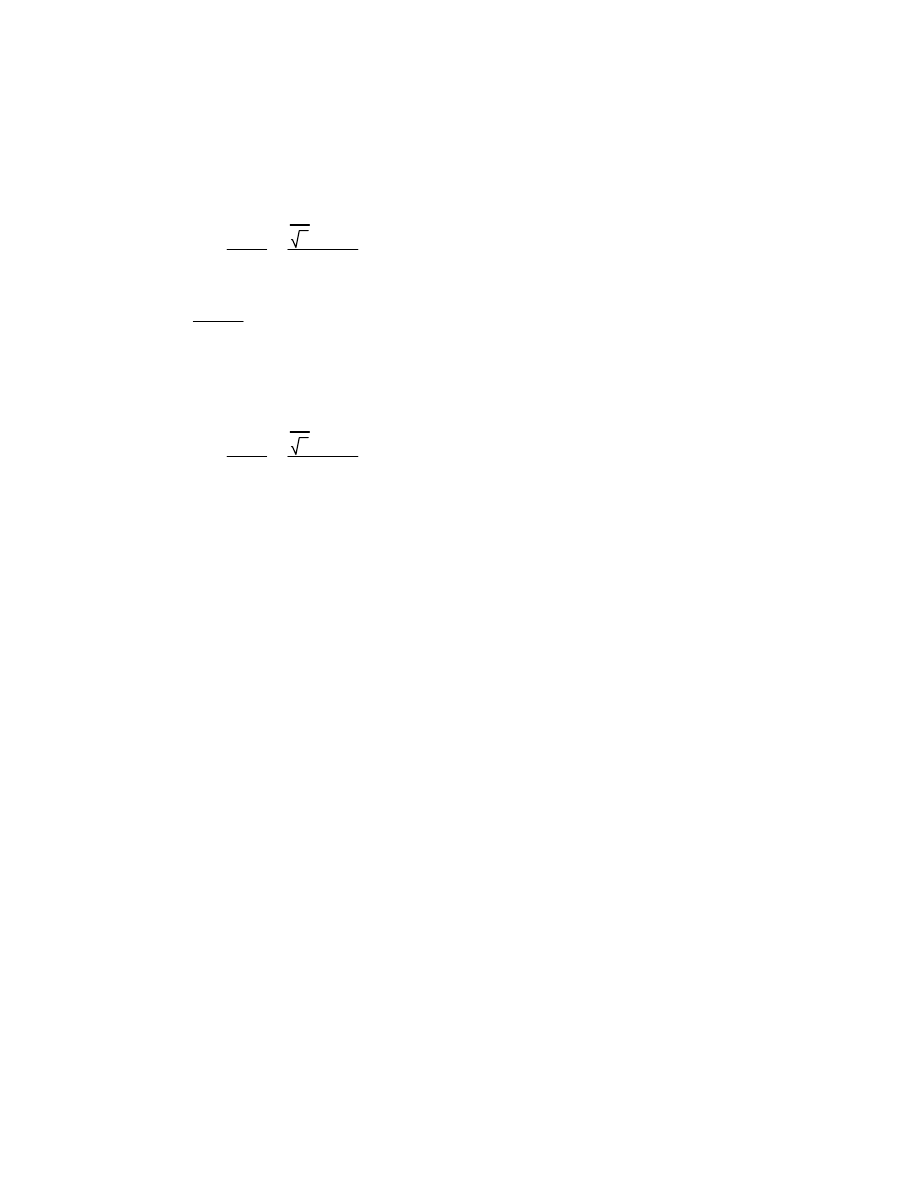
3.5 Nośność na rozerwanie blokowe panelu środnika belki
oblicza się ze wzoru:
Veff.l.Rd
fu Ant
γM2
1
3
fy
A
nv
γM0
Ant
Ant
e2 d0
2
tw
1.056
10
4
m
2
Anv
p1 e1
1.5 d0
tw
6.798
10
4
m
2
Veff.l.Rd
fu Ant
γM2
1
3
fy
A
nv
γM0
1.697
10
5
N
>
FEd 2.5 10
4
N