wer. 2014 MT

1

LABORATORIUM MECHANIKI EKSPERYMENTALNEJ

Instrukcja do ćwiczenia

4

Wyznaczanie współczynnika restytucji

Cel

ć

wiczenia

Celem

ć

wiczenia jest zapoznanie z podstawami modelowego opisu zderze

ń

oraz

sposobem do

ś

wiadczalnego wyznaczania współczynnika restytucji.

Literatura

1.

J.Leyko, Mechanika Ogólna, tom II.

2.

R. Grybo

ś

, Teoria uderzenia w dyskretnych układach mechanicznych

Zagadnienia kontrolne

1. Pop

ę

d siły

2. Zale

ż

no

ść

mi

ę

dzy p

ę

dem i pop

ę

dem

3. Zasada zachowania p

ę

du

4. Iloczyn skalarny i wektorowy
5. Definicja kr

ę

tu

6. Zasada kr

ę

tu

7. Zasada zachowania kr

ę

tu

8. Moment bezwładno

ś

ci ciała wzgl

ę

dem osi

9. Współczynnik restytucji
10. Definicja zderzenia
11. Zderzenia niespr

ęż

yste i spr

ęż

yste

12. Zderzenie proste i

ś

rodkowe

13. Energia kinetyczna w ruchu obrotowym
14. Wyznaczanie

ś

rodka ci

ęż

ko

ś

ci ciała zło

ż

onego z układu kilku podstawowych brył

15. Wahadło fizyczne – opis matematyczny ruchu i wnioski z niego wynikaj

ą

ce

16. Okres i cz

ę

sto

ść

kołowa waha

ń

wahadła fizycznego, zale

ż

no

ść

pomi

ę

dzy okresem

a cz

ę

sto

ś

ci

ą

17. Wyznaczanie momentu bezwładno

ś

ci wahadła na podstawie pomiaru okresu

ruchu
18. Przebieg

ć

wiczenia

1. Podstawy teoretyczne zwi

ą

zane z realizacj

ą

ć

wiczenia

Uwaga!

Poni

ż

sze wprowadzenie nie wyczerpuje tematu i jest jedynie, krótkim opisem

zagadnie

ń

pozwalaj

ą

cym zrozumie

ć

ogólnie przebieg

ć

wiczenia i metod

ę

pomiarow

ą

.

Aby móc odpowiedzie

ć

na wy

ż

ej przedstawione zagadnienia kontrolne nale

ż

y oprócz

instrukcji si

ę

gn

ąć

do

ź

ródeł literaturowych.

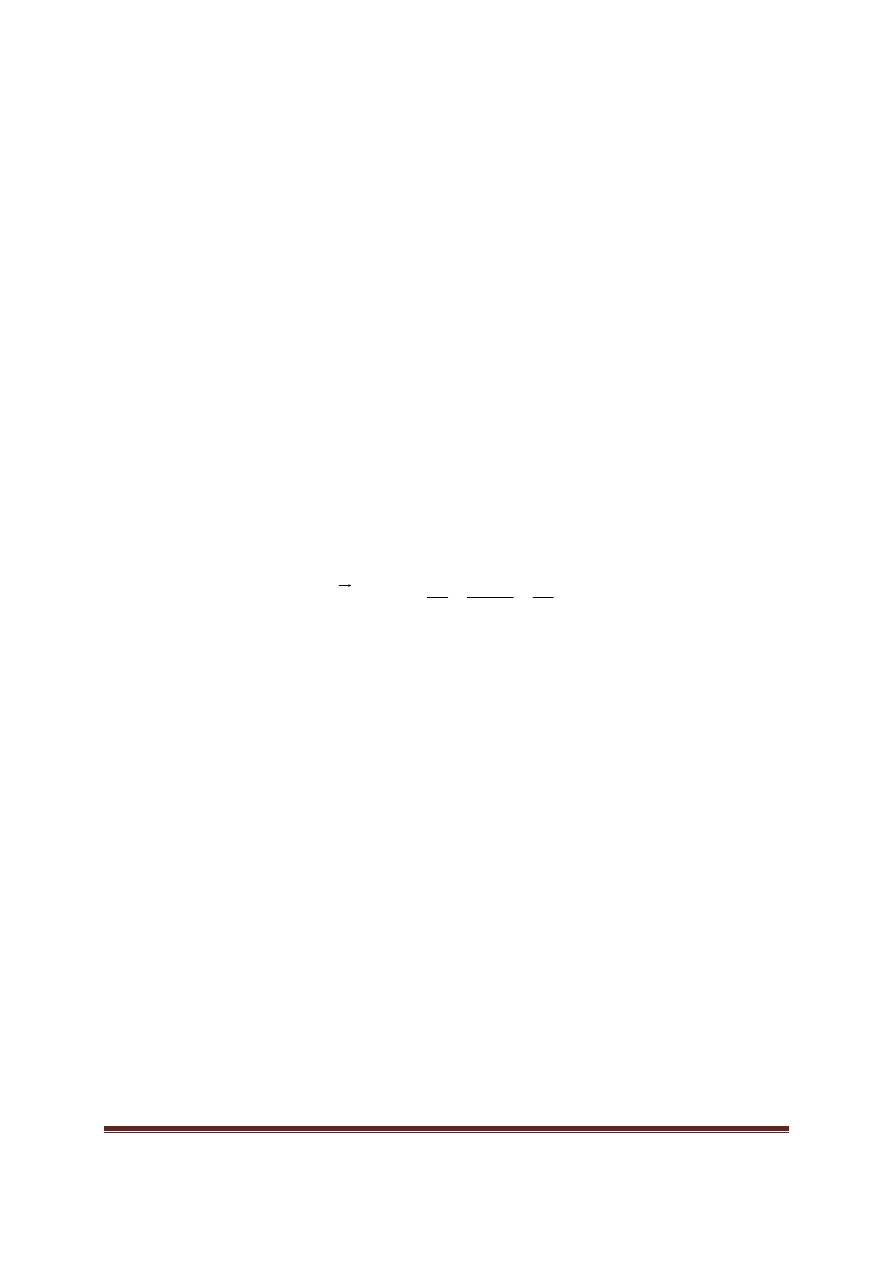
wer. 2014 MT

2

1.1. Wprowadzenie

W niektórych sytuacjach mamy do czynienia z siłami, które działaj

ą

na ciało w

okresie bardzo krótkiego przedziału czasu, osi

ą

gaj

ą

c bardzo du

ż

e warto

ś

ci chwilowe.

Tego rodzaju siły pojawiaj

ą

si

ę

przy zderzeniach ciał materialnych.

Analiza teoretyczna dotyczy najcz

ęś

ciej zderzenia doskonale spr

ęż

ystego lub

doskonale niespr

ęż

ystego (plastycznego). W praktyce mamy do czynienia ze

zderzeniami spr

ęż

ysto-plastycznymi i wówczas nale

ż

y uwzgl

ę

dni

ć

własno

ś

ci fizyczne

zderzaj

ą

cych si

ę

ciał. Własno

ś

ci te charakteryzuje współczynnik uderzenia, tzw.

współczynnik restytucji, który okre

ś

la jaka cz

ęść

p

ę

du ciała zostaje odzyskana po

zderzeniu.

W analizie zderze

ń

wprowadza si

ę

poj

ę

cia uderzenia prostego i

ś

rodkowego.

Zderzenie dwóch ciał nazywamy prostym, je

ś

li pr

ę

dko

ś

ci punktów, w których stykaj

ą

si

ę

ciała, s

ą

skierowane wzdłu

ż

wspólnej normalnej do powierzchni obu ciał.

Zderzenie nazywamy

ś

rodkowym je

ś

li wspomniana normalna przechodzi przez

ś

rodki mas uderzaj

ą

cych ciał. Dalej zakłada

ć

b

ę

dziemy,

ż

e podczas realizacji

ć

wiczenia dochodzi do zderzenia prostego (obrót ciała powodowany zderzeniem jest

pomijany). Dodatkowo przy wyznaczaniu współczynnika restytucji pomija si

ę

tarcie.

Rozpatrzmy jedno z ciał bior

ą

cych udział w zderzeniu i zapiszmy drug

ą

zasad

ę

dynamiki Newtona:

( )

dt

p

d

dt

v

m

d

dt

v

d

m

a

m

F

r

r

r

r

=

=

=

=

gdzie

p

r

jest p

ę

dem.

Bior

ą

c pod uwag

ę

,

ż

e siła zale

ż

y od czasu mo

ż

emy napisa

ć

:

dt

t

F

p

d

)

(

r

r

=

Dla całego procesu zderzenia:

∫

∫

=

konc

pocz

konc

pocz

t

t

p

p

dt

t

F

p

d

)

(

r

r

r

r

gdzie indeksy pocz i konc odnosz

ą

si

ę

do wielko

ś

ci przed i po zderzeniu.

Lewa strona równania stanowi zmian

ę

p

ę

du ciała. Prawa strona zale

ż

na od czasu

działania i wielko

ś

ci siły, stanowi pop

ę

d siły.

W wyniku zderzenia dwóch ciał i braku oddziaływa

ń

zewn

ę

trznych ulega zmianie p

ę

d

poszczególnych ciał bior

ą

cych udział w zderzeniu (nie zmienia si

ę

natomiast

całkowity p

ę

d układu tzn. p

ę

du kładu przed i po zderzeniu s

ą

sobie równe – zasada

zachowania p

ę

du).

Oznaczaj

ą

c chwil

ę

pojawienia si

ę

siły jako t

0

i czas jej trwania jako

τ

mamy:

τ

+

=

0

t

t

konc

i ostatecznie pop

ę

d (impuls) siły mo

ż

emy wyrazi

ć

jako:

∫

+

=

τ

0

0

)

(

t

t

dt

t

F

S

r

r

wer. 2014 MT

3

Na rysunku 1 znajduje si

ę

przykładowy przebieg czasowy warto

ś

ci siły. Zgodnie z

powy

ż

szym moduł pop

ę

du siły stanowi pole powierzchni pod krzyw

ą

F(t).

Rys.1. Warto

ść

chwilowa siły w funkcji czasu

Proces zderzenia mo

ż

na podzieli

ć

na dwie fazy. Pierwsza z nich charakteryzuje si

ę

wzrostem siły chwilowej i narastaniem odkształce

ń

. Odkształcenia maj

ą

charakter

zarówno lokalny (w miejscu zetkni

ę

cia si

ę

ciał), jak i ogólny (obejmuj

ą

cy zasi

ę

giem

cał

ą

obj

ę

to

ść

zderzaj

ą

cych si

ę

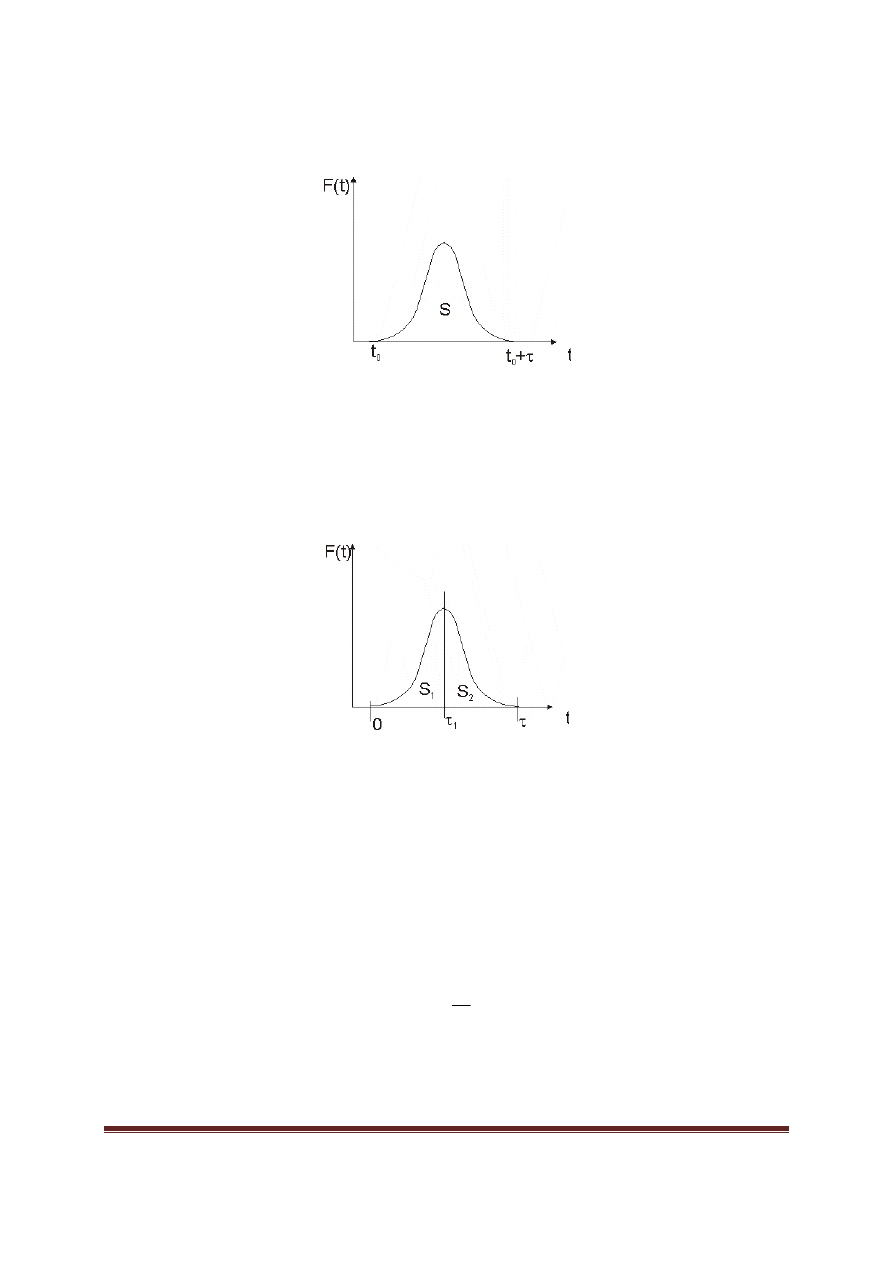
ciał). Stan ten trwa do chwili

1

τ

=

t

(patrz rysunek 2).

Rys.2. Dwie fazy zderzenia. Dla uproszczenia przyj

ę

to,

pocz

ą

tek zderzenia w chwili t=0

W chwili tej siła i lokalne odkształcenia osi

ą

gaj

ą

warto

ść

maksymaln

ą

. W kolejnej

fazie trwaj

ą

cej do chwili

τ

nast

ę

puje spadek siły do zera i zanikanie odkształce

ń

lokalnych. Oznaczaj

ą

c odpowiednie impulsy siły jak na rysunku 2 mo

ż

emy napisa

ć

,

ż

e całkowity pop

ę

d siły wynosi:

2

1

S

S

S

r

r

r

+

=

W celu scharakteryzowania stopnia spr

ęż

ysto

ś

ci zderzenia wprowadza si

ę

współczynnik restytucji R, wyra

ż

aj

ą

cy jaka cz

ęść

impulsu pierwszej fazy zderzenia

zostaje odzyskana w drugiej fazie.

1

2

S

S

R

=

Je

ż

eli przebieg czasowy siły chwilowej w drugiej fazie, jest zwierciadlanym odbiciem

przebiegu w pierwszej fazie, to S

2

= S

1

, a R=1. Ma to miejsce wówczas gdy

odkształcenia lokalne i ogólne s

ą

wył

ą

cznie spr

ęż

yste i zderzeniu nie towarzysz

ą

ż

adne straty energii kinetycznej (zderzenie idealnie spr

ęż

yste). Drugi skrajny

wer. 2014 MT

4

przypadek stanowi zderzenie plastyczne (całkowicie niespr

ęż

yste), w którym ciała

doznaj

ą

odkształce

ń

trwałych, a wi

ę

c nie zanikaj

ą

cych mimo tego,

ż

e siła chwilowa

maleje do zera. Przy zderzeniu plastycznym istnieje tylko pierwsza faza, czyli S

2

=0,

S

1

=S, oraz R=0.

W warunkach rzeczywistych mamy do czynienia z przypadkami po

ś

rednimi

czyli zderzeniami elasto-plastycznymi (niespr

ęż

ystymi) dla których 0< R <1.

1.2. Zasada zmienno

ś

ci kr

ę

tu dla sił chwilowych

Rozpatrzmy ciało poddane działaniu siły chwilowej

F

r

w punkcie A.

Rys.3. Impuls sił chwilowych działaj

ą

cych na ciało sztywne.

Pocz

ą

tek układu współrz

ę

dnych le

ż

y w

ś

rodku masy.

Niech

K

r

oznacza wektor kr

ę

tu ciała wzgl

ę

dem

ś

rodka masy. Siła chwilowa

F

r

, której

impuls wynosi

S

r

, działa na promieniu – wektorze

r

r

.

Na podstawie zasady kr

ę

tu:

F

r

dt

K

d

r

r

r

×

=

Po scałkowaniu otrzymamy:

(

)

∫

×

=

−

τ

τ

0

)

(

dt

t

F

r

K

K

r

r

r

r

gdzie:

τ

K

r

oznacza kr

ę

t po zderzeniu

,

natomiast

K

r

- tu

ż

przed zderzeniem

Załó

ż

my,

ż

e

r

r

nie ulega zmianie w czasie działania siły chwilowej. Wówczas:

(

)

( )

S

r

dt

t

F

r

dt

t

F

r

r

r

r

r

r

×

=

×

=

×

∫

∫

τ

τ

0

0

)

(

Zatem równanie zasady zmienno

ś

ci kr

ę

tu dla sił chwilowych przyjmuje posta

ć

:

S

r

K

r

r

r

×

=

∆

(1)

1.3. Układ rzeczywisty

Rozpatrzmy zderzenie wahadła fizycznego 1 (bijaka) z nieruchomym

wahadłem fizycznym 2. Układ zaprezentowano na rysunku 4.

wer. 2014 MT

5

wahadło 2

h

1

wahadło 1
(bijak)

h

2

I

2

ω

2

=0

ω

1

=0

l

I

1

Rys.4. Wahadła w spoczynku (stykaj

ą

si

ę

swobodnie)

Przez I oznaczono odpowiednie momenty bezwładno

ś

ci wahadeł wzgl

ę

dem osi

obrotu, h poło

ż

enie

ś

rodków mas,

ω

pr

ę

dko

ś

ci k

ą

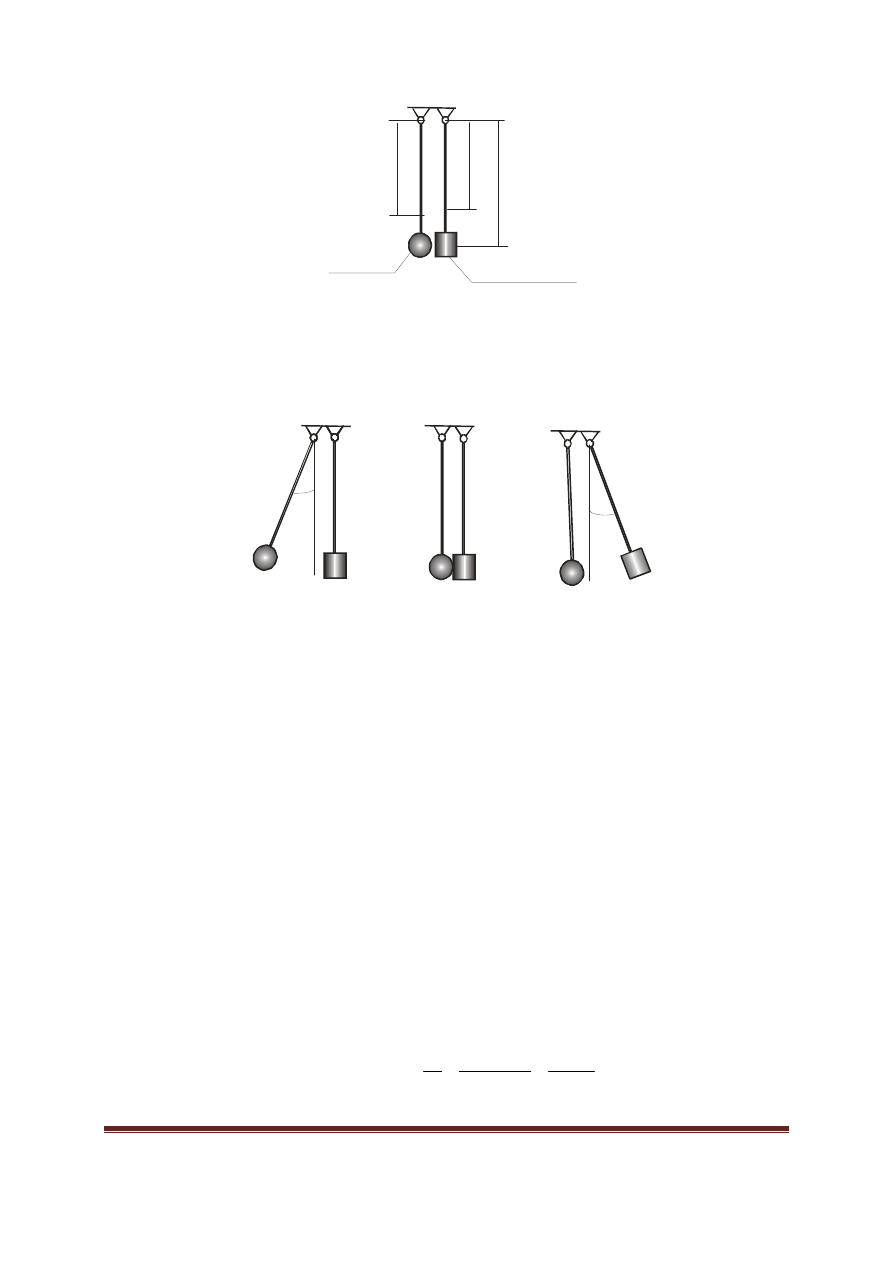
towe. Na rysunku 5 przedstawiono

poszczególne fazy ruchu zwi

ą

zane z prowadzonym podczas

ć

wiczenia

eksperymentem.

ω

1

=0

ω

2

=0

α

0

α

max

ω

*

1

a)

b)

c)

ω

1

ω

2

=0

ω

2

Rys.5. Kolejne fazy ruchu układu, a) wahadło 1 wychylone o k

ą

t

α

0

, b) wahadło 1 uderza w drugie z

pr

ę

dko

ś

ci

ą

k

ą

tow

ą

ω

1

, c) wahadło 2 wychyla si

ę

o k

ą

t

α

max

Skorzystamy z zasady zachowania kr

ę

tu, która mówi

,

ż

e przyrost kr

ę

tu ciała

materialnego wzgl

ę

dem bieguna wywołany działaniem siły chwilowej równy jest

momentowi jej impulsu wzgl

ę

dem tego

ż

bieguna (wzór 1). Poniewa

ż

ruch odbywa si

ę

w jednej płaszczy

ź

nie wi

ę

c kierunki wektorów kr

ę

tu obu wahadeł s

ą

równoległe.

Mo

ż

emy wi

ę

c zrezygnowa

ć

z opisu wektorowego.

Dla pierwszego okresu zderzenia mamy:







=

−

=

−

1

2

1

1

1

1

lS

I

lS

I

I

ω

ω

ω

(2)

gdzie:

ω

1

– pr

ę

dko

ść

k

ą

towa wahadła 1 przed zderzeniem,

ω

pr

ę

dko

ść

k

ą

towa w

ś

rodkowej fazie zderzenia (pr

ę

dko

ść

k

ą

towa zderzenia wahadeł).

Dla drugiej fazy zderzenia mamy:







=

−

−

=

−

2

2

2

2

2

1

*

1

1

lS

I

I

lS

I

I

ω

ω

ω

ω

(3)

gdzie:

ω

*

1

jest pr

ę

dko

ś

ci

ą

wahadła 1 po zderzeniu,

ω

2

jest pr

ę

dko

ś

ci

ą

wahadła 2.

Wykorzystuj

ą

c definicj

ę

współczynnika restytucji oraz powy

ż

sze układy

równa

ń

otrzymamy:

ω

ω

ω

ω

ω

ω

−

=

−

=

=

2

2

2

2

2

1

2

I

I

I

S

S

R

(4)

Z układu równa

ń

(2) mo

ż

emy wyznaczy

ć

nieznane

ω

:

wer. 2014 MT

6

2

1

1

1

I

I

I

+

=

ω

ω

(5)

Aby wyznaczy

ć

pr

ę

dko

ś

ci k

ą

towe nale

ż

y przyrówna

ć

energi

ę

kinetyczn

ą

T do

pracy L sił ci

ęż

ko

ś

ci.

)

cos

1

(

2

1

0

1

1

2

1

1

α

ω

−

=

gh

m

I

(6)

gdzie: m

1

masa pierwszego wahadła.

Powy

ż

sze równanie prowadzi do:

1

0

1

1

1

)

cos

1

(

2

I

gh

m

α

ω

−

=

(7a)

Analogicznie mo

ż

na wyznaczy

ć

ω

2

co daje:

2

max

2

2

2

)

cos

1

(

2

I

gh

m

α

ω

−

=

(7b)

Momenty bezwładno

ś

ci wahadeł mo

ż

na wyznaczy

ć

do

ś

wiadczalnie za

pomoc

ą

wzoru:

2

2

4

π

i

i

i

i

T

gh

m

I

=

(8)

gdzie: T

i

–

ś

redni okres waha

ń

i – tego wahadła fizycznego, h

i

– odległo

ść

ś

rodka

masy od osi obrotu wahadła (wyznaczona na podstawie oblicze

ń

).

2. Realizacja

ć

wiczenia

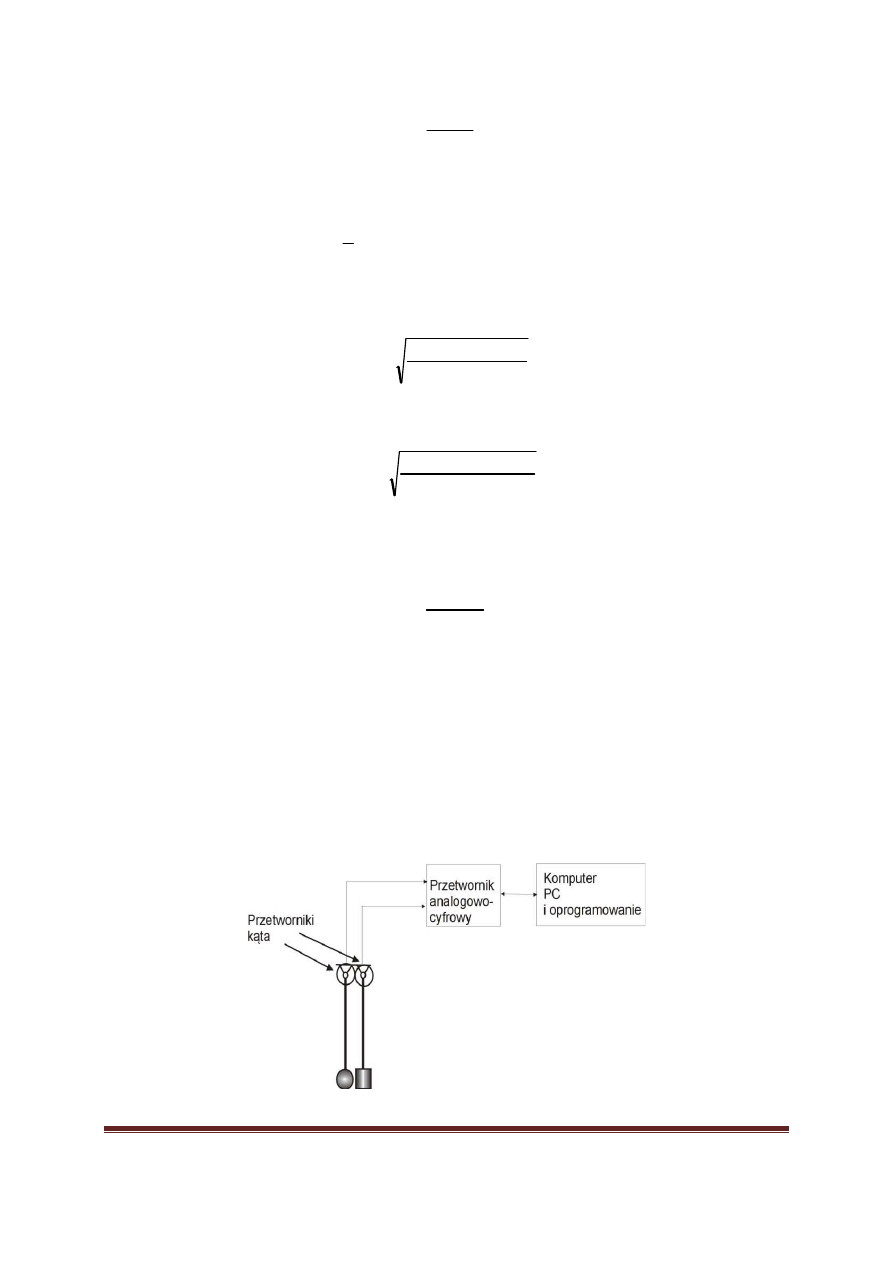
2.1. Stanowisko do realizacji pomiaru

Stanowisko do realizacji pomiaru składa si

ę

z dwóch wahadeł osadzonych na

osiach przetworników k

ą

ta, przetwornika analogowo cyfrowego i komputera wraz z

dedykowanym oprogramowaniem (rys. 6).

Rys.6. Schemat stanowiska i toru pomiarowego

wer. 2014 MT

7

Oprogramowanie pozwala na pomiar okresu waha

ń

wahadeł oraz rejestracj

ę

zmian k

ą

tów podczas zderzenia.

2.2. Przebieg

ć

wiczenia

Ogólny schemat procedury pomiarowej jest nast

ę

puj

ą

cy.

1) Zidentyfikuj par

ę

bijak i wahadło uderzane dla zadanego przez

prowadz

ą

cego wariantu

ć

wiczenia (patrz tabela 1). Na fotografii 1 przedstawiono

dost

ę

pne wahadła bijaków i wahadła uderzane wraz z przyj

ę

tymi oznaczeniami.

Fot.1. Zestaw wahadeł bijaków i wahadeł uderzanych dost

ę

pnych w

ć

wiczeniu

Tabela 1. Warianty

ć

wiczenia

Nr
wariantu

Wahadło bijaka

Wahadło uderzane

Oznaczenie

Materiał

Oznaczenie

Materiał

1

BMO

Mosi

ą

dz

WST

Stal

2

BMO

Mosi

ą

dz

WMO

Mosi

ą

dz

3

BMO

Mosi

ą

dz

WAL1

Aluminium

4

BMO

Mosi

ą

dz

WAL2

Aluminium

5

BST

Stal

WST

Stal

6

BST

Stal

WMO

Mosi

ą

dz

7

BST

Stal

WAL1

Aluminium

8

BST

Stal

WAL2

Aluminium

9

BMO1

Mosi

ą

dz

WST

Stal

10

BMO1

Mosi

ą

dz

WMO

Mosi

ą

dz

11

BMO1

Mosi

ą

dz

WAL1

Aluminium

12

BMO1

Mosi

ą

dz

WAL2

Aluminium

wer. 2014 MT

8

2) Wyznacz masy wahadeł, długo

ść

l

(patrz rys. 4) od punktu zawieszenia do punktu

zderzenia. W przypadku bijaka BMO1 przyjmij,

ż

e zderzenie zachodzi na połowie

wysoko

ś

ci walca bijaka.

3) Zmierz wahadła, narysuj je i zwymiaruj. Zaznacz tak

ż

e na rysunku długo

ść

l .

4)

Wyznacz teoretyczne poło

ż

enie

ś

rodka masy obu wahadeł w odniesieniu do

punktu zawieszenia. W tym celu przyjmij,

ż

e wszystkie elementy wahadła wykonane

s

ą

z tego samego materiału i tworz

ą

brył

ę

jednorodn

ą

. Licz

ą

c wi

ę

c obj

ę

to

ś

ci

podstawowych brył, z których składa si

ę

wahadło, mo

ż

na przyj

ąć

,

ż

e

ś

rodek masy

cało

ś

ci (wahadła) b

ę

dzie miał współrz

ę

dn

ą

:

∑

∑

∑

∑

=

=

=

=

=

=

N

i

i

N

i

i

i

N

i

i

N

i

i

i

c

V

V

h

m

m

h

h

1

1

1

1

gdzie: V

i

i m

i

s

ą

odpowiednio obj

ę

to

ś

ci

ą

i mas

ą

elementarnej bryły, N – liczb

ą

elementarnych brył, natomiast h

i

poło

ż

eniem

ś

rodka masy elementarnej bryły i.

5) Reguluj

ą

c wysoko

ść

nó

ż

ek podstawy stanowiska wypoziomuj podstaw

ę

.

6) Zawie

ś

wahadło bijaka w uchwycie przetwornika 1 i zmierz za pomoc

ą

programu

okres waha

ń

tego wahadła (parametry akwizycji - patrz instrukcja obsługi programu

w zał

ą

czniku Z1).

7) Zawie

ś

wahadło uderzane w uchwycie przetwornika 2 i dokonaj pomiaru jak wy

ż

ej.

8) Na podstawie wzoru 8 oblicz momenty bezwładno

ś

ci wahadeł.

9) Dla zadanego wariantu

ć

wiczenia dokonaj za pomoc

ą

programu rejestracji

przebiegu zderzenia (patrz instrukcja obsługi programu w zał

ą

czniku Z1).

Uwaga!

W przypadku gdy spoczywaj

ą

ce swobodnie wahadła nie b

ę

d

ą

w pobli

ż

u

pozycji zerowej (odczyty warto

ś

ci k

ą

ta b

ę

d

ą

ró

ż

ne od zera o wi

ę

cej ni

ż

1

o

) przerwij

pomiar i dokonaj kalibracji toru (patrz zał

ą

cznik Z1).

10) Uzyskane rejestracje zapisuj na dysku. B

ę

d

ą

one potrzebne do dalszego

opracowania wyników

ć

wiczenia (w celu skopiowania danych konieczne jest

posiadanie pami

ę

ci zewn

ę

trznej typu flash). W celu umo

ż

liwienia weryfikacji

wyników zapisuj je zgodnie z opisem, który znajdziesz na stanowisku.
Rejestracje wykonaj dla podanych w arkuszu sprawozdania k

ą

tów pocz

ą

tkowych

α

o

.

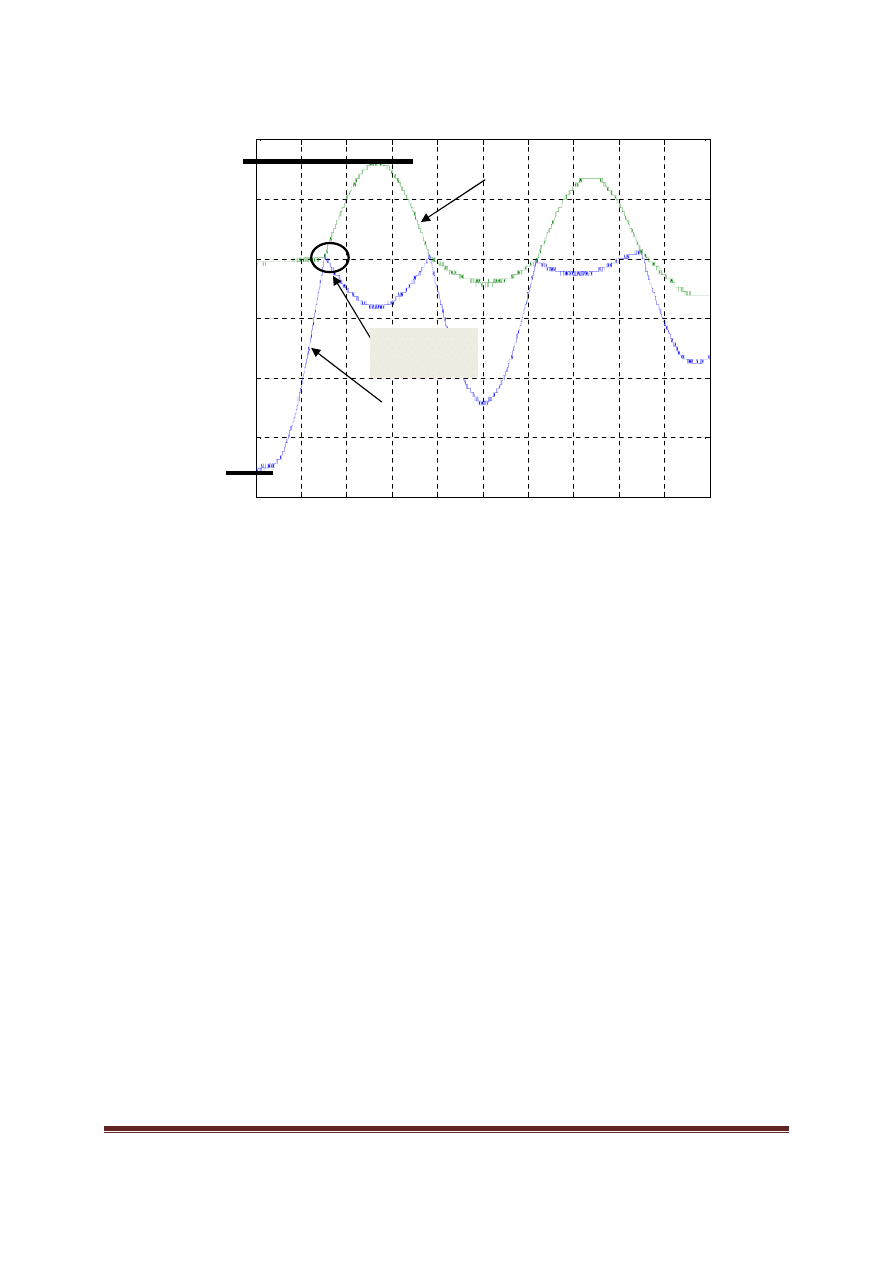
11) Z uzyskanych rejestracji odczytaj

α

o

i

α

max

czyli odpowiednio k

ą

t pocz

ą

tkowy

wychylenia bijaka (wahadła 1) i maksymalny k

ą

t jaki osi

ą

gnie wahadło uderzane

(wahadło 2) po pierwszym zderzeniu (patrz rysunek 7). Praktycznie b

ę

d

ą

to

odpowiednio minimalny (bior

ą

c pod uwag

ę

ujemny znak) k

ą

t wychylenia wahadła 1 i

maksymalny k

ą

t wychylenia wahadła 2 jakie zostały zarejestrowane w pliku.

wer. 2014 MT

9

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

-20

-15

-10

-5

0

5

10

Czas [s]

K

a

t

w

y

c

h

y

le

n

ia

z

p

o

lo

z

e

n

ia

r

o

w

n

o

w

a

g

i

Rys.7. Przykładowy wynik rejestracji ruchu obu wahadeł

Nale

ż

y pami

ę

ta

ć

,

ż

e do oblicze

ń

odpowiednie k

ą

ty nale

ż

y przyjmowa

ć

jako

dodatnie, pomijaj

ą

c informacj

ę

o kierunku ich odmierzania.

12) Wyznacz pr

ę

dko

ś

ci k

ą

towe

ω

1

i

ω

2

ze wzorów (7a) i (7b) oraz

ω

ze wzoru (5).

13) Wyznacz współczynnik restytucji ze wzoru (4) dla ka

ż

dego zarejestrowanego

przypadku i oszacuj jego niepewno

ść

pomiarow

ą

(patrz zał

ą

cznik Z2). Załó

ż

,

ż

e R

nie zale

ż

y istotnie od

ω

1

i wyznacz

ś

redni

ą

wa

ż

on

ą

R z uwzgl

ę

dnieniem niepewno

ś

ci

pomiarowych. Sprawd

ź

to zało

ż

enie rysuj

ą

c wykres R(

ω

1

) wraz z niepewno

ś

ciami

pomiarowymi.
Uwaga!
Odrzu

ć

wyniki bł

ę

dne – sprzeczne z rzeczywisto

ś

ci

ą

, je

ś

li takie wyst

ę

puj

ą

(nie

uwzgl

ę

dniaj ich w

ś

redniej ani na wykresie R(

ω

1

)).

14) Przekształcaj

ą

c drugie równanie w układzie równa

ń

(2) wyznacz impuls siły S

1

a

nast

ę

pnie znaj

ą

c współczynnik restytucji wyznacz impuls siły S

2

.

15) Sporz

ą

d

ź

wykres oszacowania

ś

redniej siły podczas zderzenia w pierwszej

i drugiej jego fazie w zale

ż

no

ś

ci od pr

ę

dko

ś

ci k

ą

towej bijaka podczas zderzenia

zakładaj

ą

c,

ż

e czasy pierwszej i drugiej fazy zderzenia wynosz

ą

T=0,005 ±0,001s.

Na wykresie uwzgl

ę

dnij niepewno

ś

ci pomiarowe.

Bior

ą

c pod uwag

ę

definicj

ę

pop

ę

du siły dla okre

ś

lonego jej kierunku:

∫

=

T

dt

t

F

S

0

)

(

oraz definicj

ę

warto

ś

ci

ś

redniej:

Bijak

(wahadło 1)

Wahadło uderzane

(wahadło 2)

Kąt wychylenia początkowego

wahadła 1 ( α

o

)

Pierwsze

zderzenie

Kąt wychylenia końcowego wahadła 2

( α

max

)

wer. 2014 MT

10

∫

=

T

sr

dt

t

F

T

F

0

)

(

1

mo

ż

emy zapisa

ć

:

S

dt

t

F

T

F

T

sr

=

=

∫

0

)

(

Tak wi

ę

c mo

ż

emy oszacowa

ć

ś

redni

ą

warto

ść

siły jako:

T

S

F

sr

=

Wszystkie wyniki wpisz do odpowiednich tabel zgodnie z poleceniami

zawartymi w arkuszu sprawozdania. Sporz

ą

d

ź

wymagane wykresy. Opracuj wnioski

dotycz

ą

ce warto

ś

ci wyznaczonego współczynnika restytucji, jego tendencji zmian w

funkcji pr

ę

dko

ś

ci k

ą

towej bijaka podczas zderzenia, warto

ś

ci niepewno

ś

ci

pomiarowej i dokładno

ś

ci metody itp. Spróbuj tak

ż

e porówna

ć

otrzymane wyniki R z

danymi literaturowymi. Zastanów si

ę

nad przyczynami wyst

ą

pienia bł

ę

dów grubych

prowadz

ą

cych do wyników sprzecznych z rzeczywisto

ś

ci

ą

(je

ś

li takie wyst

ą

pi

ą

).

Skomentuj uzyskane warto

ś

ci

ś

rednie sił wyst

ę

puj

ą

ce podczas zderzenia.

UWAGA !!!

Wahadła nale

ż

y montowa

ć

i demontowa

ć

bardzo ostro

ż

nie, by nie uszkodzi

ć

przetworników k

ą

ta obrotu. Na osiach przetworników k

ą

ta s

ą

zamontowane

aluminiowe pier

ś

cienie – uchwyty słu

żą

ce do zawieszenia wahadeł. NIE

DEMONTOWA

Ć

TYCH UCHWYTÓW. Na płaszczy

ź

nie czołowej ka

ż

dego z

uchwytów znajduje si

ę

ś

ruba zaciskowa do mocowania wahadła.

Ś

RUB

Ę

NALE

Ż

Y

DOKR

Ę

CA

Ć

PALCAMI, NIE STOSOWA

Ć

NARZ

Ę

DZI (KOMBINEREK, KLUCZY

ITP.) Mas

ę

uchwytu i

ś

ruby zaciskowej pomin

ąć

przy obliczeniach.

Wahadła nale

ż

y wkłada

ć

do otworów w uchwycie bez stosowania nadmiernej

siły.

Ś

ruba zaciskowa powinna by

ć

odpowiednio wykr

ę

cona, by pr

ę

t wahadła wsun

ą

ł

si

ę

do ko

ń

ca otworu mocuj

ą

cego. Nie wkłada

ć

i nie zdejmowa

ć

wahadeł „na sił

ę

”, nie

nagina

ć

pr

ę

tów wahadeł. Ewentualne problemy z monta

ż

em wahadeł zgłosi

ć

prowadz

ą

cemu zaj

ę

cia.

Wahadło nale

ż

y zwa

ż

y

ć

i zwymiarowa

ć

jako cało

ść

. NIE WYKR

Ę

CA

Ć

PR

Ę

TA

WAHADŁA. Poło

ż

enie

ś

rodka masy wahadła obliczy

ć

na podstawie wymiarów

przyjmuj

ą

c,

ż

e wahadło wykonane jest w cało

ś

ci z jednego materiału. Przy

obliczeniach pomin

ąć

niewielkie otwory technologiczne, podtoczenia itp.

WAHADŁA SŁU

ŻĄ

WYŁ

Ą

CZNIE DO REALIZACJI

Ć

WICZENIA.

S

Ą

PODATNE NA USZKODZENIE, NP. ZGI

Ę

CIE PR

Ę

TA.

WYKORZYSTYWANIE ICH W SPOSÓB NIEZGODNY Z NINIEJSZ

Ą

INSTRUKCJ

Ą

UZNANE B

Ę

DZIE ZA NIEPRZYGOTOWANIE DO

Ć

WICZENIA Z WSZYSTKIMI

TEGO KONSEKWENCJAMI.

wer. 2014 MT

11

ZAŁ

Ą

CZNIKI

Z1. Opis programu komputerowego

Poni

ż

ej podano informacje uzupełniaj

ą

ce dotycz

ą

ce obsługi stosowanego

oprogramowania komputerowego „WspRestytucji”.

Przed przyst

ą

pieniem do bada

ń

nale

ż

y sprawdzi

ć

czy stanowisko jest

wypoziomowane. W razie potrzeby nale

ż

y je wypoziomowa

ć

i ustali

ć

nowe warto

ś

ci

napi

ę

cia z przetworników k

ą

ta, odpowiadaj

ą

ce poło

ż

eniu zerowemu wahadeł. W tym

celu nale

ż

y nacisn

ąć

Ctrl+K i stosowa

ć

si

ę

do polecania wy

ś

wietlonego przez

program. Pocz

ą

tkowe warto

ś

ci k

ą

ta dla swobodnie spoczywaj

ą

cych wahadeł nie

powinny ró

ż

ni

ć

si

ę

od zera wi

ę

cej ni

ż

1 stopie

ń

.

Ć

wiczenie wykonywane jest w dwóch etapach. W pierwszym etapie nale

ż

y

wykona

ć

wszystkie pomiary wst

ę

pne słu

żą

ce okre

ś

leniu momentów bezwładno

ś

ci

poszczególnych wahadeł (patrz wzór 8).

W celu okre

ś

lenia okresu waha

ń

wahadeł nale

ż

y montowa

ć

je w stanowisku

pojedynczo. Aby unikn

ąć

pomyłki nale

ż

y montowa

ć

wahadło bijaka (nr 1) na osi z

lewej strony stanowiska, a wahadło uderzane (nr 2) na osi z prawej strony
stanowiska (zgodnie z rysunkiem 6).

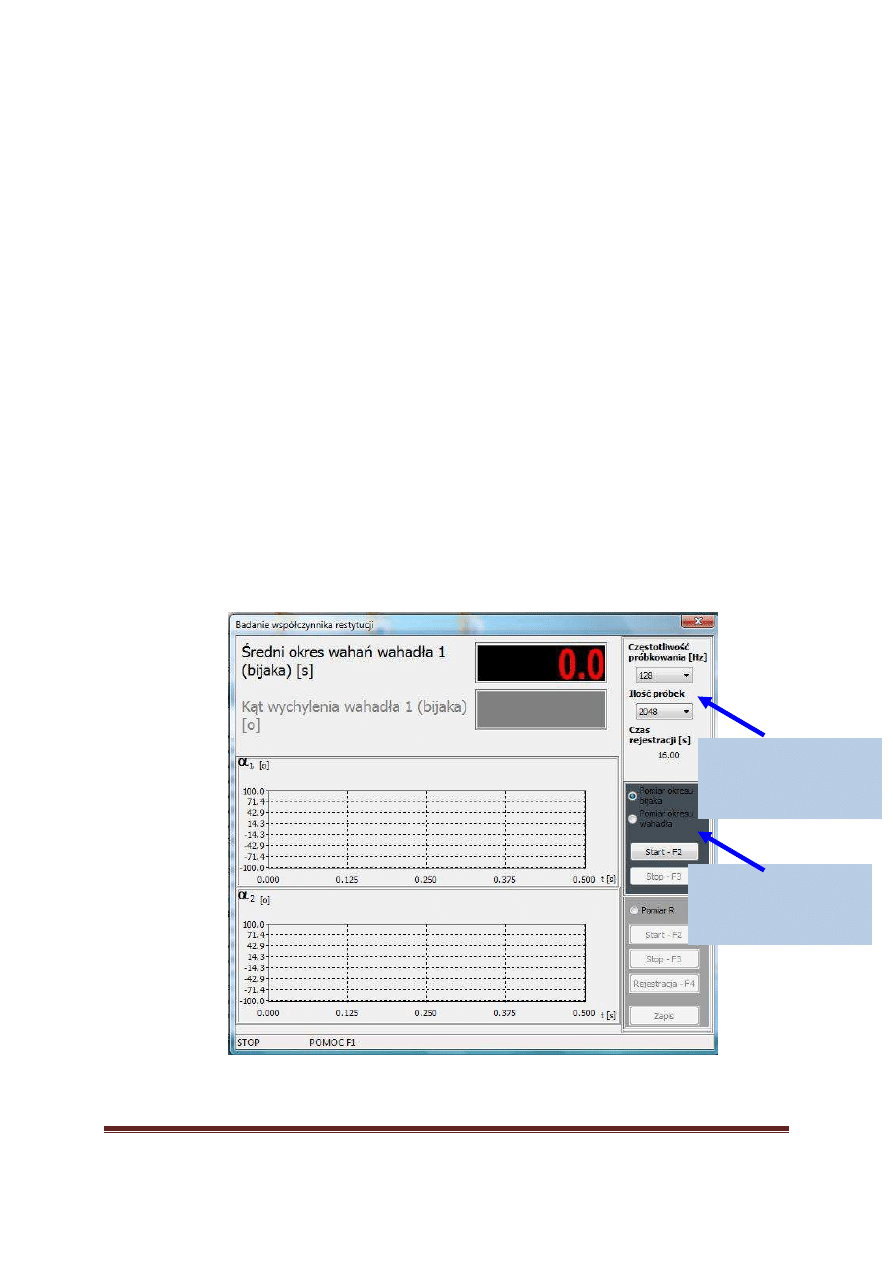
W oknie głównym programu wybra

ć

, którego wahadła w danym momencie ma

dotyczy

ć

pomiar (patrz rysunek 8).

Rys.8. Okno główne programu – etap przygotowania do pomiaru okresów waha

ń

wahadeł

Wybór trybu pomiaru

okresu poszczególnych

wahadeł

Wybór parametrów

próbkowania

wer. 2014 MT

12

Nale

ż

y tak

ż

e dobra

ć

parametry akwizycji sygnału, tak aby czas rejestracji

wynosił co najmniej 64 sek (liczba próbek 8192, cz

ę

stotliwo

ść

próbkowania 128Hz).

Pami

ę

taj aby k

ą

t pocz

ą

tkowy wychylenia danego wahadła podczas pomiaru okresu

waha

ń

nie przekraczał 10

o

.

Czas rejestracji T

r

wynika z ustawionych parametrów: cz

ę

stotliwo

ś

ci

próbkowania (fp [Hz]) i ilo

ś

ci próbek (N) wg wzoru:

fp

N

T

r

=

[s]

(Z1)

Dłu

ż

szy czas rejestracji pozwoli na uzyskanie wi

ę

kszej liczby u

ś

rednie

ń

okresu.

Pami

ę

taj aby zapisa

ć

w arkuszu pomiarowym parametry rejestracji sygnału.

Nast

ę

pnie nale

ż

y wychyli

ć

badane wahadło z poło

ż

enia równowagi i klikn

ąć

"Start-F2" (lub nacisn

ąć

klawisz F2). Program rozpocznie pomiar warto

ś

ci chwilowej

wychylenia wahadła wzgl

ę

dem poło

ż

enia równowagi. K

ą

t ujemny b

ę

dzie

wskazywany dla wychylenia w kierunku zgodnym z ruchem wskazówek zegara. Aby
dokona

ć

poprawnego pomiaru okresu nale

ż

y zada

ć

wychylenie pocz

ą

tkowe poni

ż

ej

10

o

i pu

ś

ci

ć

swobodnie wahadło. Program automatycznie rozpocznie rejestracj

ę

po

przej

ś

ciu wahadła przez poło

ż

enie równowagi a nast

ę

pnie sam zatrzyma rejestracj

ę

po odczytaniu zadanej liczby próbek. Oczekiwanie na ruch wahadła mo

ż

na przerwa

ć

poprzez „Stop” (F3).

Ś

redni okres waha

ń

mo

ż

na odczyta

ć

w odpowiednim polu okna głównego.

Wyniki pomiaru jak i parametry akwizycji sygnału nale

ż

y wpisa

ć

w arkusz

sprawozdania. Powy

ż

sza procedura musi by

ć

przeprowadzona dla obu wahadeł.

W drugim etapie

ć

wiczenia nale

ż

y dokona

ć

pomiarów odpowiednich k

ą

tów

wychyle

ń

wahadeł. W tym celu nale

ż

y zamontowa

ć

oba wahadła i zarejestrowa

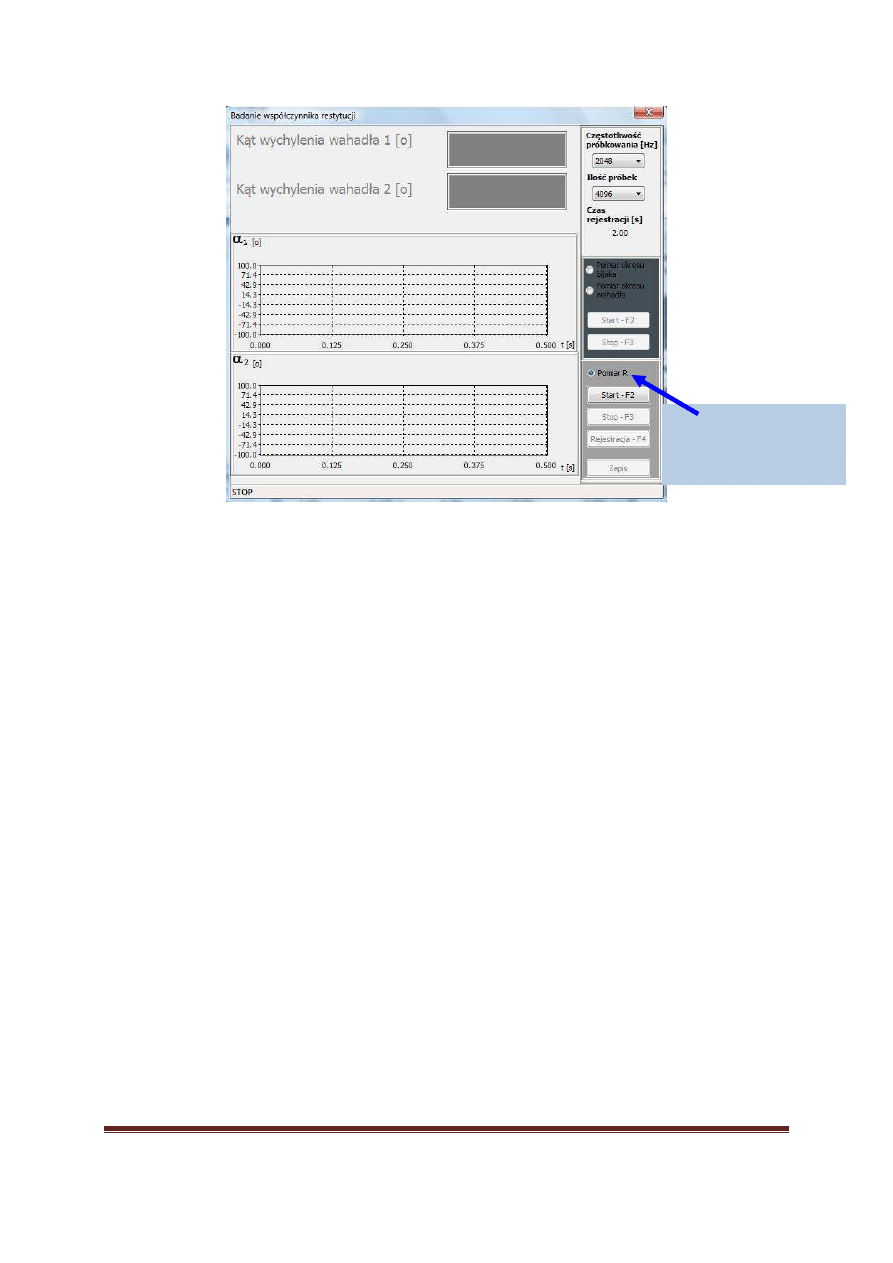
ć

sygnał podczas ich zderzenia. W oknie głównym programu (rys. 9) nale

ż

y zaznaczy

ć

opcj

ę

pomiaru R i ustawi

ć

odpowiednie parametry akwizycji. Zalecane jest ustawienie

du

ż

ej cz

ę

stotliwo

ś

ci próbkowania tak

,

aby odwzorowanie przebiegu czasowego było

jak najdokładniejsze. Wynikowy czas rejestracji powinien pozwoli

ć

na uchwycenie

momentu zderzenia i zatrzymania ruchu wahadła 2 w maksymalnym wychyleniu po
zderzeniu. Zaleca si

ę

aby wynikowy czas rejestracji wynosił 1s (cz

ę

stotliwo

ść

próbkowania 8192 Hz, liczba próbek 8192).

wer. 2014 MT

13

Rys.9. główne programu – etap przygotowania do rejestracji zderzenia

Nast

ę

pnie nale

ż

y wybra

ć

polecenie „Start – F2” (lub nacisn

ąć

klawisz F2). W

polach rozmieszczonych u góry okna głównego mo

ż

na obserwowa

ć

aktualne

warto

ś

ci k

ą

ta wychyle

ń

ka

ż

dego z wahadeł. Wahadło bijaka nale

ż

y wychyli

ć

o

wybrany k

ą

t z pozycji równowagi

,

a wahadło 2 powinno pozostawa

ć

w pozycji

równowagi. Dla wahadła 2 wy

ś

wietlana warto

ść

k

ą

ta powinna by

ć

bliska zeru (mo

ż

e

ona nieco oscylowa

ć

wokół zera, ze wzgl

ę

du na wyst

ę

puj

ą

cy szum). Maksymalny k

ą

t

wychylenia wahadła bijaka to 60

o

. W kolejnym kroku nale

ż

y nacisn

ąć

klawisz F4 lub

wybra

ć

polecenie „Rejestracja” a nast

ę

pnie pu

ś

ci

ć

bijak tak

,

aby rozpocz

ą

ł si

ę

jego

swobodny ruch (nie nale

ż

y nadawa

ć

pr

ę

dko

ś

ci pocz

ą

tkowej bijakowi).

Uwaga !
Nale

ż

y pami

ę

ta

ć

aby wahadło bijaka uwolni

ć

dopiero po rozpocz

ę

ciu

rejestracji tak aby k

ą

t pocz

ą

tkowy mógł zosta

ć

jednoznacznie odczytany z

otrzymanej rejestracji. Zwłoka ta nie mo

ż

e by

ć

zbyt długa gdy

ż

rejestracja musi obj

ąć

tak

ż

e moment gdy wahadło 2 po zderzeniu osi

ą

gnie warto

ść

maksymaln

ą

.

Poprawno

ść

rejestracji nale

ż

y sprawdzi

ć

obserwuj

ą

c wykresy przebiegów czasowych

wy

ś

wietlanych przez program.

Po upływie zadanego czasu rejestracji program automatycznie zatrzyma

akwizycj

ę

sygnału i wy

ś

wietli przebieg czasowy zmian k

ą

tów ka

ż

dego z wahadeł.

Wynik rejestracji nale

ż

y zapisa

ć

nadaj

ą

c nazw

ę

folderów i plików wg schematu

wyja

ś

nionego wy

ż

ej. Zapisany plik b

ę

dzie podstaw

ą

do dalszych oblicze

ń

. Zapisany

plik z wynikami w postaci tekstowej mo

ż

e zosta

ć

łatwo otwarty za pomoc

ą

takich

programów jak: Notatnik, Excel, Word, Matlab, Statistica itp. Pami

ę

taj aby

niezale

ż

nie zanotowa

ć

w arkuszu pomiarowym parametry rejestracji sygnału

(cz

ę

stotliwo

ść

próbkowania i liczb

ę

próbek).

Rejestracje nale

ż

y powtórzy

ć

dla zadanych (patrz arkusz sprawozdania)

warto

ś

ci k

ą

tów wychyle

ń

pocz

ą

tkowych bijaka.

Wybór trybu rejestracji

zderzenia w celu

wyznaczenia wsp. R

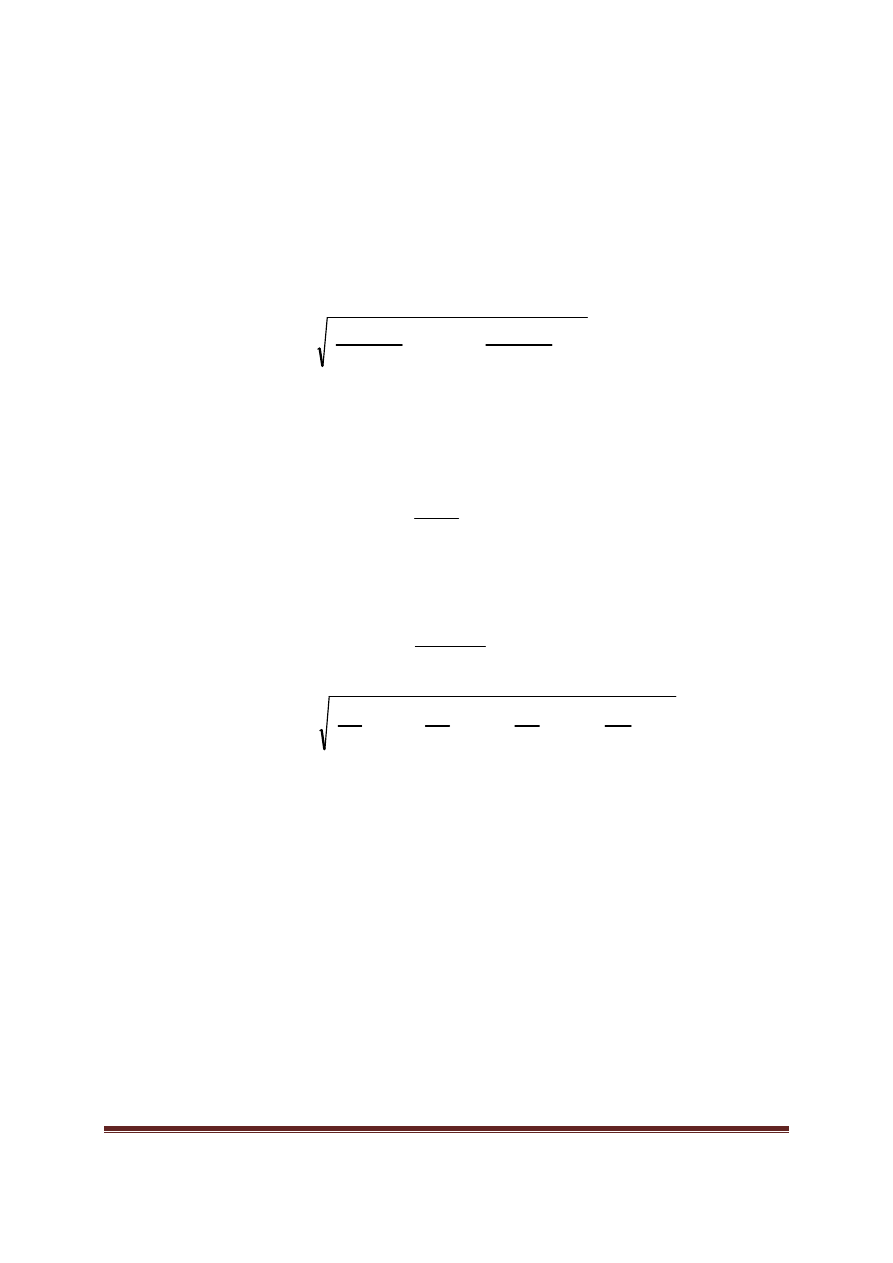
wer. 2014 MT

14

Z2. Oszacowanie niepewno

ś

ci pomiarowej

Pomiary wst

ę

pne

Mierz

ą

c wielko

ś

ci geometryczne i okre

ś

laj

ą

mas

ę

notuj w arkuszu

sprawozdania niepewno

ść

pomiaru. Przyjmij,

ż

e w przypadku pomiaru suwmiark

ą

,

ż

e

wynosi ona ±0,1 mm. W przypadku pomiary masy przyjmij niepewno

ść

±1 g.

Warto

ść

niepewno

ś

ci pomiaru Q(x,... z) otrzymanego metod

ą

po

ś

redni

ą

, przy

zało

ż

eniu,

ż

e niepewno

ś

ci poszczególnych pomiarów s

ą

niezale

ż

ne i losowe, mo

ż

e

zosta

ć

obliczona ze wzoru:

2

2

)

,...

(

...

)

,...

(













∆

∂

∂

+

+













∆

∂

∂

=

∆

z

z

z

x

Q

x

x

z

x

Q

Q

(Z2)

gdzie:

∆

Q jest szacowan

ą

niepewno

ś

ci

ą

wielko

ś

ci mierzonej metod

ą

po

ś

redni

ą

,

∆

x ...

∆

z niepewno

ś

ciami wielo

ś

ci mierzonych bezpo

ś

rednio/po

ś

rednio, od których zale

ż

y

wielko

ść

Q.

Oszacowanie poło

ż

enia

ś

rodka masy wyznaczamy ze wzoru:

∑

∑

=

=

=

N

i

i

N

i

i

i

c

V

V

h

h

1

1

(Z3)

Bior

ą

c pod uwag

ę

,

ż

e wahadła mo

ż

na zamodelowa

ć

jako zło

ż

enie dwóch brył

(pr

ę

ta i walca lub kuli) mo

ż

emy zapisa

ć

:

2

1

2

2

1

1

V

V

V

h

V

h

h

c

+

+

=

.

(Z4)

St

ą

d:

2

2

2

2

1

1

2

2

2

2

1

1













∆

∂

∂

+













∆

∂

∂

+













∆

∂

∂

+













∆

∂

∂

=

∆

V

V

h

V

V

h

h

h

h

h

h

h

h

c

c

c

c

c

(Z5)

Bior

ą

c pod uwag

ę

,

ż

e mamy tutaj do czynienia z oszacowaniem niepewno

ś

ci, nie

jest wymagane bardzo dokładne jej obliczenie. Okazuje si

ę

(co łatwo sprawdzi

ć

),

ż

e

dla rozpatrywanego zestawu wahadeł istotny jest w zasadzie tylko jeden składnik
powy

ż

szej sumy zwi

ą

zany z niepewno

ś

ci

ą

wyznaczenia obj

ę

to

ś

ci kuli lub walca

bijaka lub wahadła uderzanego (reszta jest innego rz

ę

du wielko

ś

ci). Po podstawieniu

warto

ś

ci niepewno

ś

ci oszacowania

ś

rodka masy dla wszystkich wahadeł s

ą

rz

ę

du (w

przybli

ż

eniu) ±1 mm i tak

ą

warto

ść

nale

ż

y przyj

ąć

w dalszych analizach. Z tak

ą

niepewno

ś

ci

ą

nale

ż

y te

ż

wyrazi

ć

ostateczne poło

ż

enie

ś

rodków masy.

Pomiary okresu waha

ń

Od wyboru parametrów akwizycji zale

ż

y niepewno

ść

pomiarowa uzyskanego

okresu. Pomiar okresu waha

ń

odbywa si

ę

za pomoc

ą

transformaty Fouriera z

dziedziny czasu w dziedzin

ę

cz

ę

stotliwo

ś

ci. Rzutuje to na sposób wyznaczania

niepewno

ś

ci

pomiarowej

uzyskanego

okresu.

Rozdzielczo

ść

df

pomiaru

cz

ę

stotliwo

ś

ci waha

ń

wahadła mo

ż

e by

ć

przedstawiona jako:

wer. 2014 MT

15

]

[

1

Hz

T

df

r

=

.

(Z6)

gdzie T

r

czas rejestracji.

Je

ś

li oznaczymy cz

ę

stotliwo

ść

ruchu wahadła przez f

o

[Hz] a odpowiadaj

ą

cy mu

okres jego waha

ń

jako T

o

mo

ż

emy zapisa

ć

:

]

[

1

s

f

T

o

o

=

.

(Z7)

Wobec powy

ż

szego niepewno

ść

pomiaru okresu mo

ż

e by

ć

wyznaczona jako (patrz

wzór Z2):

N

fpT

Nf

fp

df

f

f

f

T

T

o

o

o

o

o

o

2

2

0

2

1

=

=

=

∆

∂

∂

=

∆

[s].

(Z8)

Podstawiaj

ą

c odpowiednie warto

ś

ci (okresy wahadeł s

ą

zbli

ż

one) mo

ż

na oszacowa

ć

powy

ż

sz

ą

niepewno

ść

jako ± 0,01s. Tak

ą

warto

ść

nale

ż

y przyj

ąć

dla ka

ż

dego z

rozpatrywanych wahadeł.

Okre

ś

lenie momentu bezwładno

ś

ci

Aby wyznaczy

ć

niepewno

ść

pomiaru momentów bezwładno

ś

ci nale

ż

y skorzysta

ć

ze

wzoru ogólnego (Z2) z zał

ą

cznika i niepewno

ś

ci obliczonych/przyj

ę

tych wcze

ś

niej.

Przyspieszenie ziemskie przyjmij jako 9,807 ± 0,001 m/s

2

. Do dalszych działa

ń

przyjmij warto

ś

ci momentu bezwładno

ś

ci wyra

ż

one za pomoc

ą

trzech cyfr

znacz

ą

cych.

Pomiary k

ą

tów wychyle

ń

Przyjmij niepewno

ś

ci pomiaru k

ą

tów

α

o

i

α

max

wynosz

ą

c

ą

±0,1

o

.

Okre

ś

lenie niepewno

ś

ci pr

ę

dko

ś

ci k

ą

towych

Skorzystaj ze wzoru Z2 i niepewno

ś

ci obliczonych wcze

ś

niej. Przy uwzgl

ę

dnianiu

niepewno

ś

ci pomiaru k

ą

ta pami

ę

taj o zamianie stopni na radiany.

Okre

ś

lenie współczynnika restytucji

Dla ka

ż

dego k

ą

ta pocz

ą

tkowego okre

ś

l współczynnik restytucji oraz

niepewno

ść

jego pomiaru (korzystaj

ą

c z wzoru Z2). Nast

ę

pne okre

ś

l

ś

redni

ą

warto

ść

współczynnika restytucji uwzgl

ę

dniaj

ą

c ró

ż

ne niepewno

ś

ci jego pomiaru.

Pomiary obarczone wi

ę

ksza niepewno

ś

ci

ą

powinny mie

ć

mniejszy wpływ na

ostateczny wynik ni

ż

pomiary okre

ś

lone z mniejsza niepewno

ś

ci

ą

. W tym celu

zastosuj oszacowanie R za pomoc

ą

ś

redniej wa

ż

onej:

∑

∑

=

i

i

i

sr

w

R

w

R

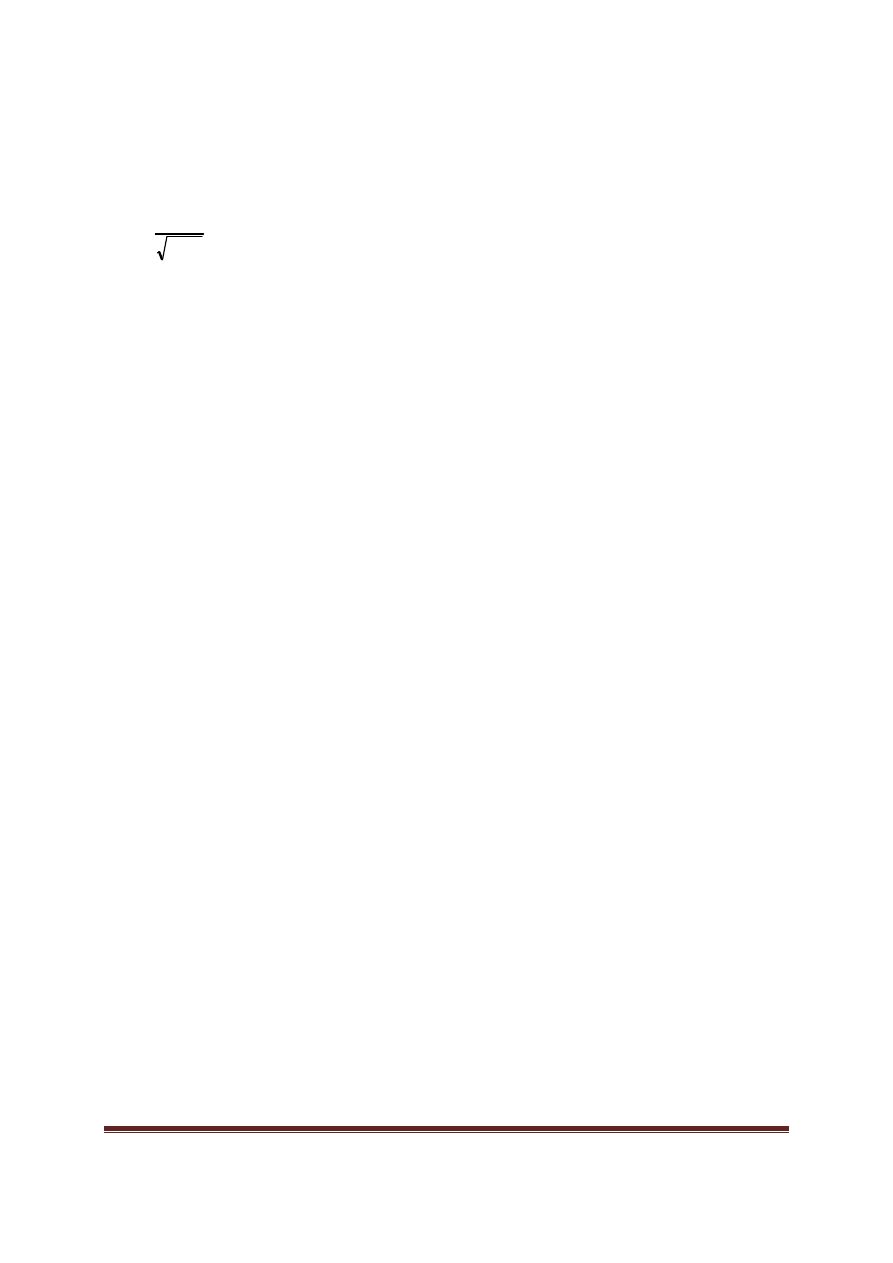
wer. 2014 MT

16

gdzie waga pomiaru i jest równa: 1/

∆

R

2

i

,

∆

R

i

niepewno

ś

ci

ą

oszacowania

współczynnika restytucji o indeksie i oraz R

i

jego warto

ś

ci

ą

.

Ostateczn

ą

niepewno

ść

pomiaru

ś

redniego współczynnika restytucji oszacuj za

pomoc

ą

wzoru:

∑

=

∆

i

sr

w

R

1

Uwaga!
Rysunek R(

ω

1

) powinien uwzgl

ę

dnia

ć

słupki bł

ę

du.

Okre

ś

lenie impulsu siły i

ś

redniej warto

ś

ci siły

Niepewno

ść

impulsu siły S

1

i S

2

okre

ś

l za pomoc

ą

wzoru Z2. Podobnie

wykonaj obliczenia dla

ś

rednich warto

ś

ci sił.

Uwaga!
Rysunek F

1

(

ω

1

) i F

2

(

ω

1

) powinien uwzgl

ę

dnia

ć

słupki bł

ę

du.