WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
1
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODTSAWY TEORII – CZĘŚC 3
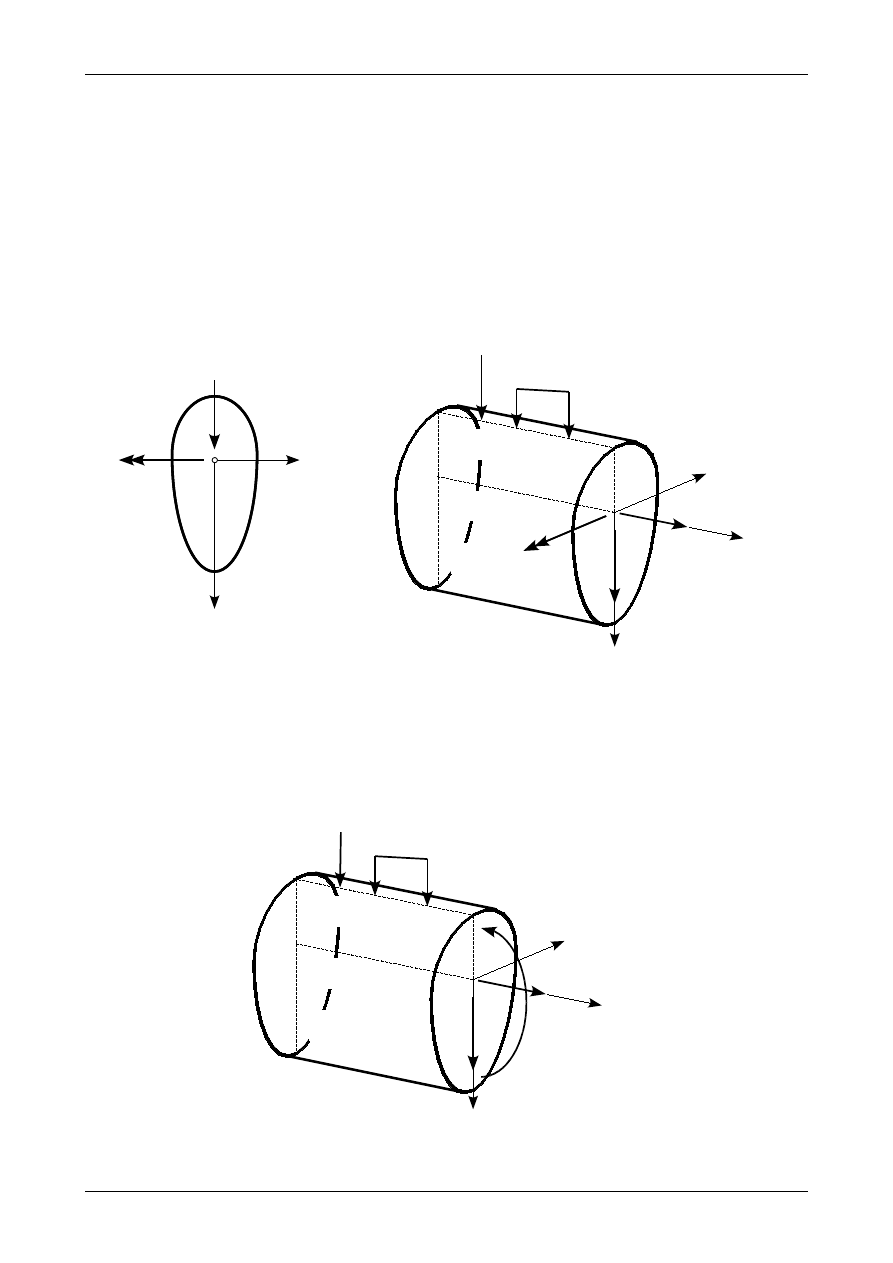
21 Pręty zginane i ścinane
W niniejszym rozdziale będziemy rozpatrywać naprężenia normalne i styczne, które powstają w
przekroju pręta od działania siły normalnej, siły poprzecznej i momentu zginającego. Obciążenie taki
występuje w belkach oraz ramach płaskich.
Wszystkie siły przekrojowe będziemy rozpatrywać w układzie osi głównych bezwładności. Wszystkie siły
czynne i bierne (reakcje) działające na układ prętowy będą działały w płaszczyźnie XY. Przykładowy przekrój
pręta oraz część pręta z działającymi siłami czynnymi i reakcjami oraz siłami przekrojowymi przedstawia
rysunek 62.
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
T=T
Y
M=M
Z
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
X
P
q(x)
N
M=M
Z
T
=
T
Y
sc
Rys. 62. Siły przekrojowe w belce lub ramie płaskiej.
Rysunek 63 przedstawia wektor dodatniego momentu zginającego, który jak wiadomo rozciąga dolną część
przekroju pręta. Zwrot wektora momentu zginającego ma ten sam kierunek co wkręcająca się śruba
prawoskrętna, która kręci się od dolnej do górnej części przekroju pręta.
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
X
P
q(x)
N
M
=M
Z
T
=
T
Y
Rys. 63. Dodatni moment zginający.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
2
Pomiędzy siłami przekrojowymi a obciążeniem q(x) istnieją zależności nazywane równaniami
różniczkowymi równowagi. Dla osi X skierowanej w prawo tak jak na rysunku 64 mają one postać
dT
x
dx
=−q
x
,
(288)
dM
x
dx
=T
x
.
(289)
Natomiast dla osi X skierowanej w lewo równania różniczkowe równowagi mają postać
dT
x
dx
=q
x
,
(290)
dM
x
dx
=−T
x
.
(291)
Y=Y
0
=Y
gl
X
N
T
=
T
Y
M=M
Z
Rys. 64. Widok sił przekrojowych z boku pręta.
Rysunek 64 przedstawia widok sił przekrojowych z boku pręta. Naprężenia normalne
σ
X
jakie powstają w
przekroju pręta są spowodowane działaniem siły normalnej i momentu zginającego. Oblicza się je ze wzoru
X
=
N
A
M
Z
I
Z
⋅y
,
(292)
w którym A oznacza pole powierzchni przekroju pręta, I
Z
oznacza główny moment bezwładności względem osi
Z=Z
gl
. Jak widać wartość naprężeń normalnych
σ
X
zależy tylko od zmiennej y. Oś, na której naprężenie
normalne
σ
X
osiąga wartość zero czyli oś obojętna w przypadku przekroju pręta będzie miała postać
N
A
M
Z
I
Z
⋅y
0
=0
,
(293)
czyli
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
3
y
0
=−
N
A
⋅
I
Z
M
Z
.
(294)
Wartość bezwzględną naprężenia stycznego
τ
XY
w punktach o jednakowej współrzędnej y wyznacza się ze
wzoru
∣
XY
∣
=
∣
T
Y
∣
⋅
∣
S
Z
y
∣
b
y⋅I
Z
,
(295)
w którym
S
Z
y
jest momentem statycznym względem głównej osi bezwładności Z=Z
gl
części przekroju
pręta leżącej poniżej lub powyżej punktu, w którym wyznaczamy naprężenia styczne
τ
XY
natomiast
b
y
jest szerokością przekroju w miejscu, w którym wyznaczmy naprężenia styczne
τ
XY
.
W przekrojach cienkościennych czyli składających się z figur, których jeden wymiar jest dużo większy niż
drugi pod wpływem siły poprzecznej T=T
Y
wystąpią także naprężenia styczne
τ
XZ.
. Naprężenia te wystąpią w
półkach przekroju dwuteowego lub teowego.
Wartość bezwzględną naprężenia stycznego
τ
XZ
wyznacza się ze wzoru
∣
XZ
∣
=
∣
T
Y
∣
⋅
∣
S
Z
z
∣
h
z⋅I
Z
,
(296)
w którym
S
Z
z
jest momentem stycznym względem głównej osi bezwładności Z=Z
gl
części przekroju półki
znajdującego po lewej lub prawej stronie punktu (w zależności od tego, w której z półek obliczamy naprężenie
styczne
τ
XZ
), w którym wyznaczamy naprężenia styczne
τ
XZ
. Natomiast
h
z
jest grubością półki w
miejscu, w którym wyznaczamy naprężenia styczne
τ
XZ
. Rysunki 65 i 66 przedstawiają część przekroju półki
oraz jej grubość wykorzystywaną we wzorze (296).
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
h
z
z
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
h
z
z
Rys. 65. Część przekroju półki oraz jej grubość wykorzystywana we wzorze (296).
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
4
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
h
z
z
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
h
z
z
Rys. 66. Część przekroju półki oraz jej grubość wykorzystywana we wzorze (296).
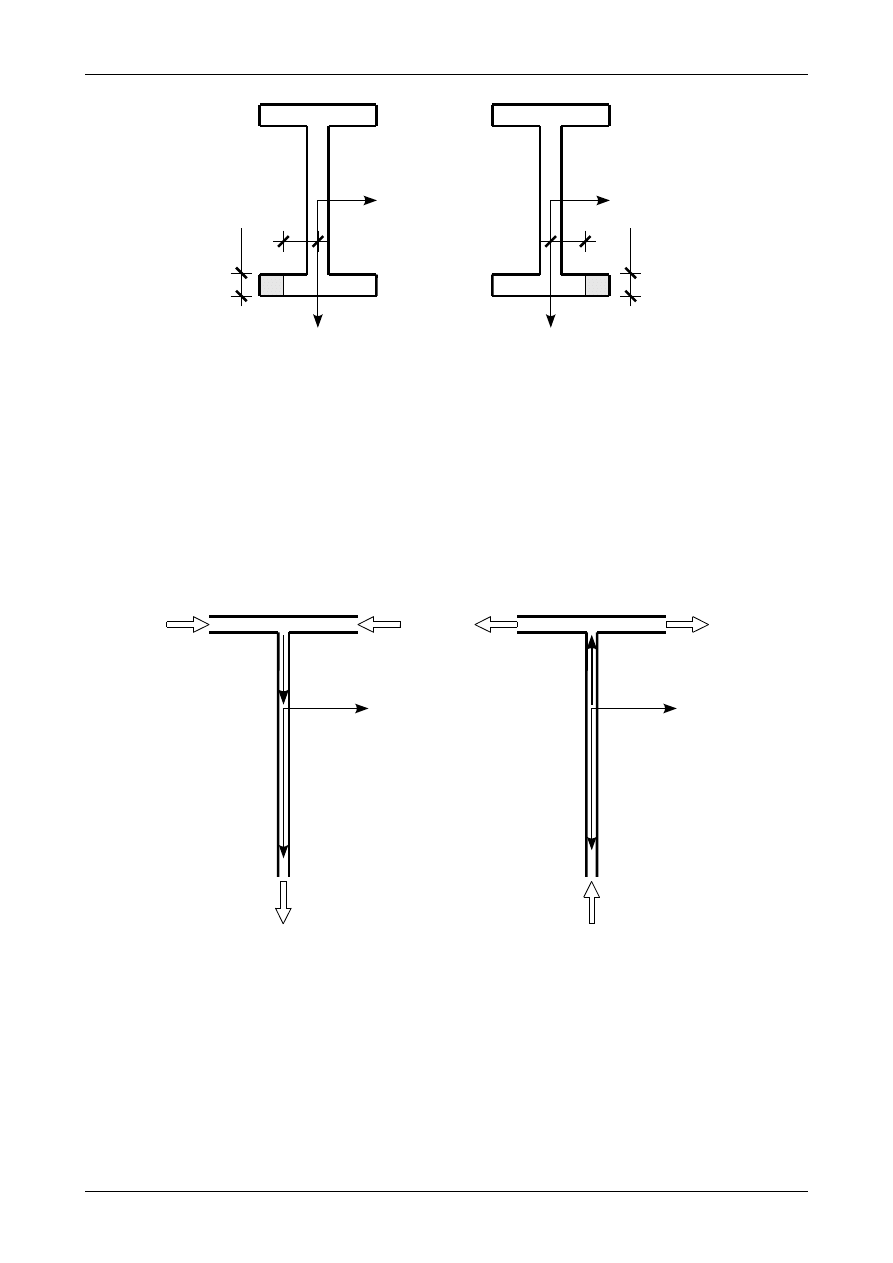
Ze wzoru (296) możemy wyznaczyć tylko wartość bezwzględną naprężenia stycznego
τ
XZ
. Chcąc wyznaczyć
znak tego naprężenia możemy się posłużyć modelem systemu rurek, w których płynie woda. Usuwamy
najkrótsze krawędzie, którymi woda będzie wpływać i wypływać. Jej wpływanie i wypływanie musi być takie,
żeby w środniku woda płynęła zgodnie ze zwrotem naprężeń stycznych
τ
XY
. Naprężenie styczne
τ
XZ
będzie
dodatnie, jeżeli będzie miało taki sam zwrot jak główna oś bezwładności Z=Z
gl
. Będzie natomiast ujemne,
jeżeli jego zwrot będzie przeciwny do zwrotu głównej osi bezwładności Z=Z
gl
. Rysunki 67 oraz 68
przedstawiają kierunki przepływu wody w systemie rurek w kształcie teownika i dwuteownika. Strzałki
pokazują kierunek przepływu wody. Na krawędziach półek naprężenia styczne
τ
XZ
wynoszą zero.
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
T=T
Y
T=T
Y
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
Rys. 67. Analogia wodna w przypadku teownika.
Rysunek 69 przedstawia przykładowe wykresy naprężeń w przekroju teowym natomiast rysunek 70
przedstawia wykresy naprężeń dla przekroju dwuteowego.
Jeżeli w przekroju siłą normalna wynosi zero to w środku ciężkości mamy tylko naprężenia styczne
τ
XY
. Stan
taki nazywa się czystym ścinaniem. Tensor naprężenia będzie miał postać
Dr inż. Janusz Dębiński
BZZ
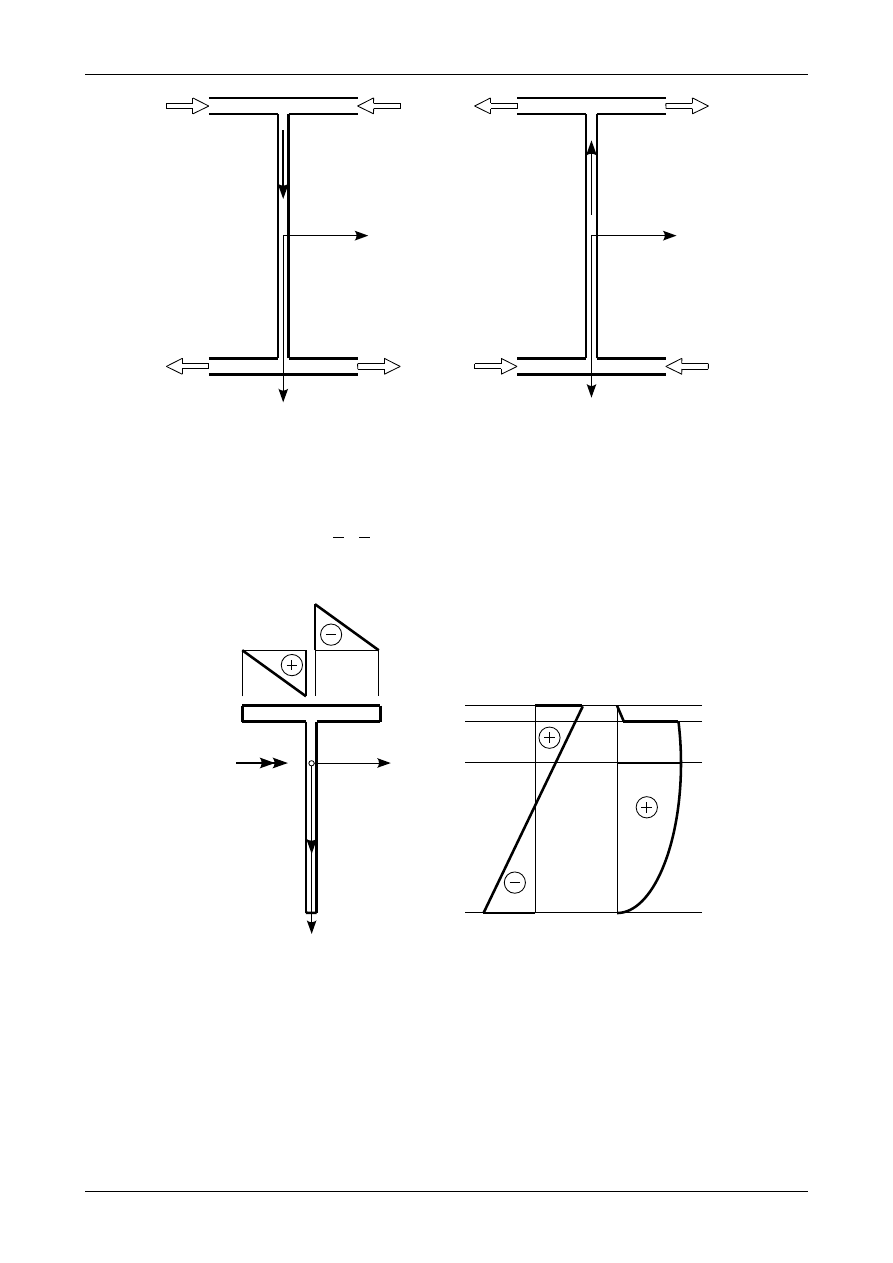
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
5
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
T=T
Y
T=T
Y
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
Rys. 68. Analogia wodna w przypadku dwuteownika.
=
=
[
0
0
0 0
0 0 0
]
.
(297)
Z=Z
0
=Z
gl
Y=Y
0
=Y
gl
X
XY
XZ
N>0
T=T
Y
M=M
Z
Rys. 69. Przykładowe wykresy naprężeń dla przekroju teowego.
Jak więc widać w przypadku czystego ścinania naprężenia główne nachylone są zawsze pod kątem plus
lub minus 45 stopni i mają wartość bezwzględną naprężenia stycznego. Aby łatwiej zapamiętać, które z
naprężeń głównych jest rozciągające a które ściskające posłużymy się pewną analogią. Wyobraźmy sobie, że
elementarny kwadrat zamieniamy w mechanizm wprowadzając w narożnikach przeguby. Układ ten
przedstawia rysunek 71 a). Układ ten może się poruszać, ponieważ posiada jeden stopnień swobody. Na
pionowy pręt układu działa siła o zwrocie naprężenia stycznego, która powoduje jego ruch. Jedna z
przekątnych układu zwiększa swoją długość (jest rozciągana) natomiast druga przekątna zmniejsza swoją
długość (jest ściskana). Położenie tych przekątnych pokazuje nam, który kierunek ma rozciągające naprężenie
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
6
główne a który kierunek ma ściskające naprężenie główne. Rysunek 72 przedstawia naprężenia główne dla
dodatnich naprężeń stycznych
τ
XY
natomiast rysunek 73 przedstawia naprężenia główne dla ujemnych
naprężeń stycznych
τ
XY
.
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
N>0
X
XY
XZ
XZ
T=T
Y
M=M
Z
Rys. 70. Przykładowe wykresy naprężeń dla przekroju dwuteowego.
a)
b)
c)
przekątna rozciągana
przekątna ściskana
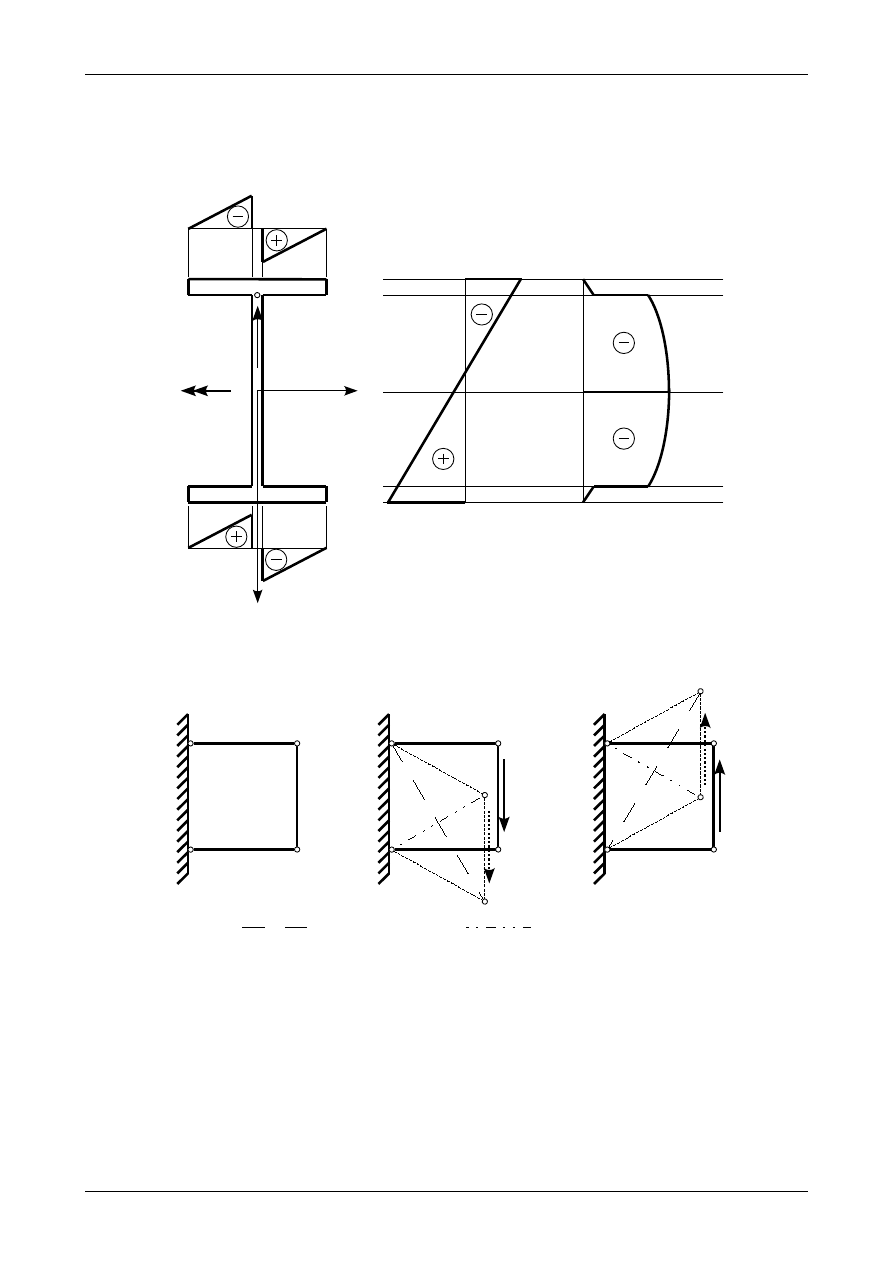
Rys. 71. Analogia mechaniczna do wyznaczenia kierunków głównych naprężeń rozciągających i ściskających.
W przypadku blachownic o przekroju dwuteowym lub teowym należy w jakiś sposób połączyć środnik i półki.
W przeciwnym wypadku każda blacha (środnik i półki) będzie pracowała osobno. Najczęściej stosowaną
metodą jest spawanie. W trakcie spawania poszczególne części łączy się za pomocą spoin. Przypadek taki
nazywa się często ścinaniem technicznym. Spoiną nazywamy tę część złącza, która składa się z metalu
stopionego podczas spawania. Może ona powstać wyłącznie z materiału rodzimego albo z udziałem materiału
doprowadzonego z zewnątrz, nazywanego spoiwem.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
7
X
Y
X
Y
X
gl
Y
gl
45
o
Rys. 72. Naprężenia główne dla dodatnich naprężeń stycznych
τ
XY
.
X
Y
X
Y
X
gl
Y
gl
45
o
Rys. 73. Naprężenia główne dla ujemnych naprężeń stycznych
τ
XY
.
Podstawowy podział spawania jest następujący:
•
spawanie łukiem elektrycznym z elektrodą topliwą lub nietopliwą,
•
spawanie gazowe.
Podstawowym i najbardziej rozpowszechnionym sposobem spawania elektrodą topliwą jest spawanie
elektrodą otuloną, potocznie nazywane ręcznym spawaniem łukowym. Źródłem ciepła jest łuk elektryczny
jarzący się między dwoma elektrodami. Jedną z elektrod może być spawany przedmiot natomiast druga
elektroda może służyć jako spoiwo (elektroda topliwa) lub może tylko służyć do utrzymania łuku (elektroda
nietopliwa), a spoina powstaje wyłącznie ze stopionego materiału rodzimego. Schemat technologii spawania tą
metodą pokazuje schematycznie rysunek 74.
Drugą metodą spawania elektrodą topliwą jest spawanie łukiem krytym. Schemat tej metody został pokazany
na rysunku 75.
Zamiast otuliny stosuje się topik w postaci proszku, pod którego warstwą jarzy się łuk między elektrodą
topliwą a przedmiotem spawania. Spawanie łukiem krytym odbywa się tylko automatycznie lub
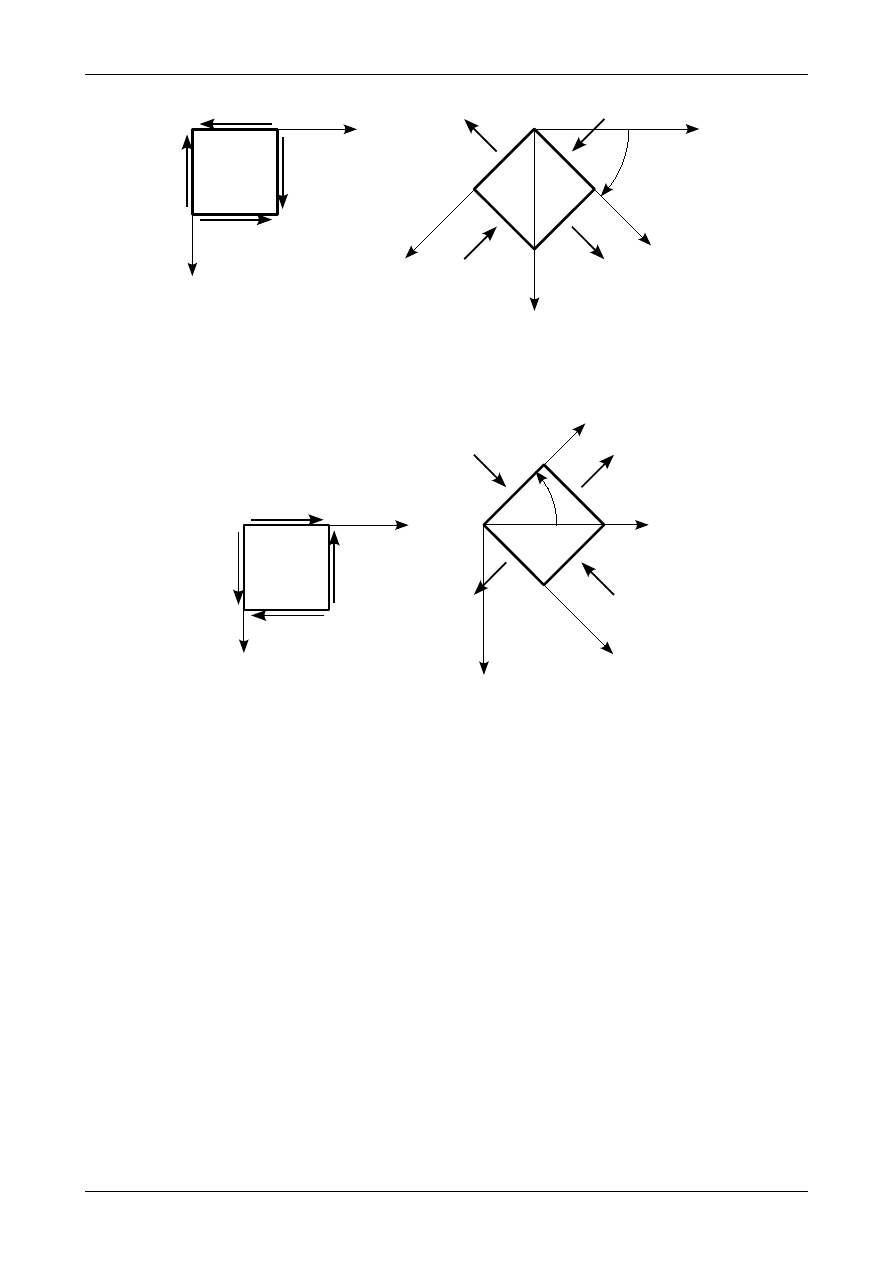
półautomatycznie. Łuk jarzy się niewidocznie pod warstwą topnika (D) zsypywanego z leja (A). Elektroda w
postaci drutu (B) jest podawana samoczynnie z bębna. Na spoinie (C) krzepnie żużel (F). Nadmiar topnika
(G) pozostały na spoinie jest zasysany z powrotem do leja zasypowego. Podkładka (E) jest stosowana w
pewnych przypadkach aby zapobiec wyciekaniu metalu. Proces ten charakteryzuje się bardzo wysoką
wydajnością (od 5 do 40 razy wydajniej niż przy spawaniu ręcznym).
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
8
Rys. 74. Schemat ręcznego spawania łukowego.
Rys. 75. Schemat spawania łukiem krytym.
Źródłem ciepła przy spawaniu gazowym jest płomień powstający ze spalania gazu palnego (najczęściej
acetylenu) zmieszanego z tlenem. Spawanie tą metodą nie jest stosowane do łączenia elementów
konstrukcyjnych, ponieważ procesowi temu towarzyszy o połowę niższa temperatura. W dodatku ciepło jest
rozprowadzane nierównomiernie, a także metal nie jest należycie zabezpieczony przed wpływem powietrza.
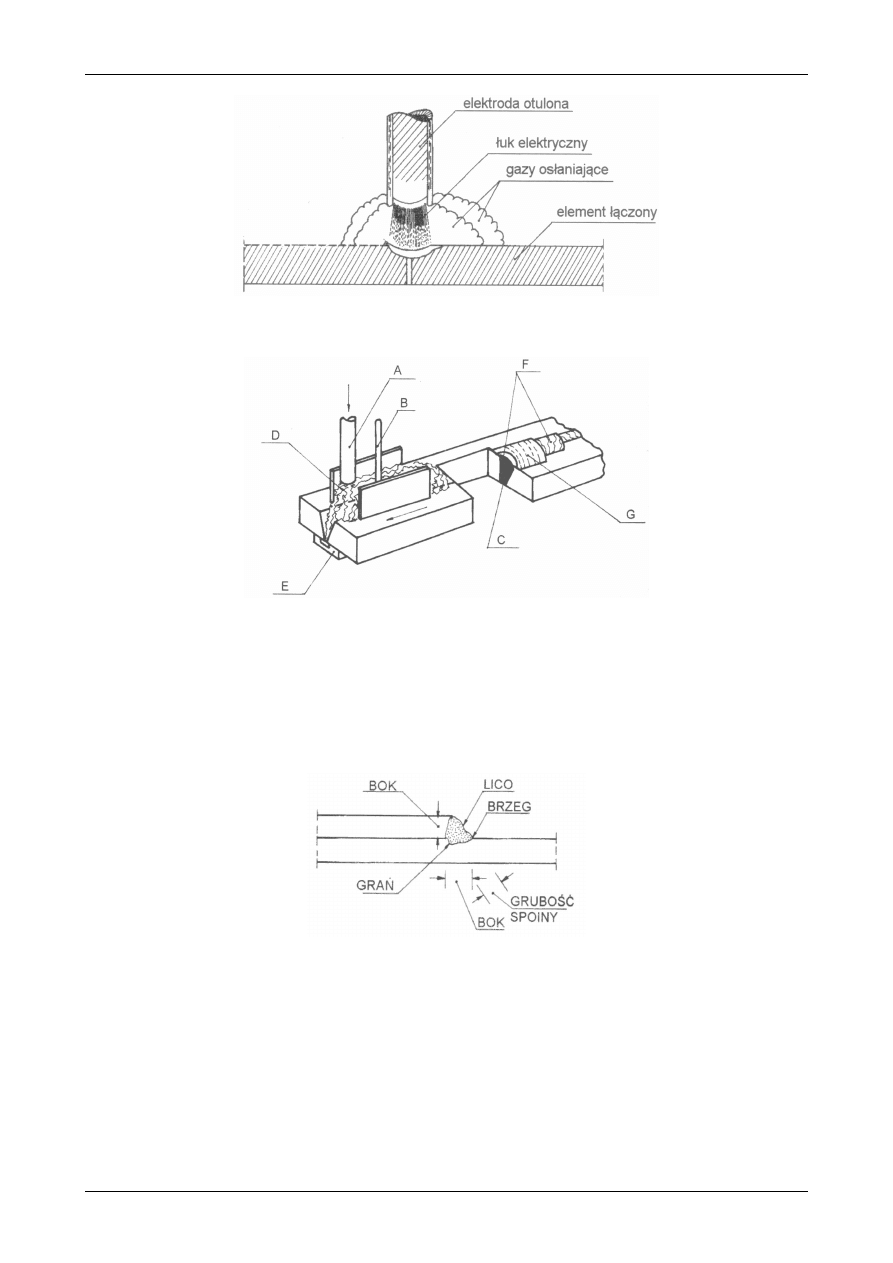
Rys. 76. Podstawowe elementy spoiny pachwinowej.
Do łączenia środnika z półką w przekroju dwuteowym i teowym stosuje się spoinę pachwinową. Nazwy
części spoiny pachwinowej pokazano na rysunku 76 natomiast na rysunku 77 pokazano widok takiej spoiny.
Na rysunku 78 pokazano przekrój przez spoinę pachwinową. Lico spoiny może być płaskie, wypukłe lub
wklęsłe. Grubością spoiny pachwinowej określa się wysokość trójkąta wpisanego w spoinę. Spoina
pachwinowa może być spoiną ciągłą lub przerywaną i wtedy nazywa się szwem spawanym. Jeżeli stosujemy
szew spawany to poszczególne spoiny szwu mogą leżeć po obu stronach naprzeciw siebie, albo przestawnie
wtedy, gdy poszczególne spoiny są układane po obu stronach na przemian.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
9
Rys. 77. Widok spoiny pachwinowej.
a)
a
a
a
b)
c)
Rys. 78. Przekrój przez spoinę pachwinową. Spoiny: a) płaska, b) wypukła, c) wklęsła. Grubość spoiny została
oznaczona jako a.
a
a
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
Rys. 79. Przekrój przez spoinę pachwinową łączącą środnik z półką.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
10
X
T
Y
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
h
S
s
g
T
Y
t
t
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
XY
XY
XY
XY
XY
XY
XY
XY
Rys. 80. Elementarne kostki naprężeń w środniku i półce dolnej.
Przekrój spoiny pachwinowej łączącej środnik z półką został pokazany na rysunku 79. Rysunek 80 pokazuje
elementarne kostki naprężeń z zaznaczonymi naprężeniami stycznymi
τ
XY
od siły poprzecznej T
Y
. Naprężenia
te zostały obliczone z wzoru (266) podstawiając do niego moment statyczny półki dolnej względem osi
Z=Z
0
=Z
gl
oraz dla górnej kostki jako b(y) grubość środnika g. Dla dolnej kostki należałoby do wzoru (266)
wstawić jako b(y) szerokość półki, jednak ze względów praktycznych przyjmuje się szerokość środnika czyli
tak samo jak dla kostki górnej. Sytuacja przedstawiona na rysunku 80 dotyczy przypadku, gdy pręt jest
wykonany z jednego kawałka metalu. Na styku środnik-półka powstanie siła, którą nazywamy siłą
rozwarstwiającą R. W przypadku blachownicy pręt jest wykonany z dwóch lub trzech blach, które są
połączone za pomocą spoin pachwinowych przedstawionych na rysunku 79. Naprężenia styczne na obu
kostkach występujące w pręcie wykonanym z jednego kawałka metalu zostaną przeniesione przez te spoiny.
Siła rozwarstwiająca próbuje przesunąć środnik względem półki. Jednak na przeszkodzie temu stoją spoiny
pachwinowe łączące środnik z półką.
X
R
R
Y=Y
0
=Y
gl
Z=Z
0
=Z
gl
T
Y
Rys. 81. Siły rozwarstwiające.
Ze względu na to, że siła poprzeczna T
Y
zmienia się na długości pręta siła rozwarstwiająca powinna także
zmieniać swoją wartość. Powodowałoby to, że spoiny pachwinowe łączące środnik z półką miałby na długości
pręta różną grubość. Ze względów technologicznych jest to nieopłacalne. W praktyce wystarczy znaleźć
ekstremalną siłę poprzeczną na długości pręta i dla tej siły zaprojektować spoiny pachwinowe o stałej
grubości na całej długości pręta.
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
11
Siła rozwarstwiająca jak istniałaby pomiędzy środnikiem i półką wynosi
R
=
XY
⋅g⋅L
,
(298)
w którym
τ
XY
oznacza naprężenie styczne na styku środnik-półka, g oznacza grubość środnika, L oznacza
długość pręta. Siła rozwarstwiająca przypadająca na parę spoin pachwinowych wynosi
R
=
sp
⋅2⋅a⋅L
.
(299)
We wzorze (299)
τ
sp
oznaczają naprężenia styczne w spoinie pachwinowej, natomiast a oznacza grubość
spoiny pachwinowej. Przyrównując do siebie siły rozwarstwiające (298) i (299) otrzymamy wzór na
obliczenie naprężeń stycznych w spoinie
τ
sp
.
sp
=
XY
⋅g
2
⋅a
(300)
Korzystając ze wzoru (266) naprężenia w punkcie leżącym na styku środnika i półki można wyliczyć ze wzoru
XY
=
∣T
Y
∣⋅∣S
Z
p
∣
g
⋅I
Z
,
(301)
w którym
S
Z
p
oznacza moment statyczny półki względem osi Z=Z
0
=Z
gl
. Podstawiając (301) do (300)
otrzymamy
sp
=
∣T
Y
∣⋅∣S
Z
p
∣
2
⋅a⋅I
Z
,
(302)
w którym T
Y
oznacza ekstremalną siłę poprzeczną na długości pręta.
Spoina pachwinowa może być także spoiną przerywaną. Spoinę taką razem z jej wymiarami przedstawia
rysunek 82. Zakłada się ponadto, że spoina pachwinowa jest symetryczna względem osi pręta. Siła
rozwarstwiająca przypadająca na jedną spoinę będzie wypadkową z naprężeń stycznych
τ
XY
z długości x
przedstawionej na rysunku 83. Długość x jest sumą długości spoiny l oraz odległości pomiędzy dwoma
spoinami przerywanymi e. Siła rozwarstwiająca R przypadająca na jedną parę spoin pachwinowych wynosi
R
=
XY
⋅g⋅x=
XY
⋅g⋅
l
e
.
(303)
We wzorze (303) g jest grubością środnika. Siła rozwarstwiająca przypadająca na parę spoin pachwinowych
przerywanych wynosi
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
12
R
=
sp
⋅2⋅a⋅l
.
(304)
l
e
l
e
l
Widok z boku
Widok z góry
Rys. 82. Widok z boku i z góry spoiny pachwinowej przerywanej.
l
e
l
e
l
l
R
R
e
2
e
2
x
Rys. 83. Siła rozwarstwiająca przypadająca na jedną parę spoin pachwinowych.
We wzorze (304) a oznacza grubość spoiny pachwinowej. Przyrównując do siebie wzory (303) oraz (304)
otrzymamy wzór na obliczenie naprężeń stycznych w pojedynczej spoinie pachwinowej w postaci
sp
=
XY
⋅g⋅
l
e
2
⋅a⋅l
.
(305)
Podstawiając wzór (301) na obliczenie naprężeń stycznych
τ
XY
otrzymamy ostatecznie
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
13
sp
=
∣T
Y
∣⋅∣S
Z
p
∣
2
⋅a⋅I
Z
⋅
l
e
l
,
(306)
w którym
S
Z
p
oznacza moment statyczny półki względem osi Z=Z
0
=Z
gl
.
22 Mimośrodowe działanie siły
W niniejszym rozdziale będziemy rozpatrywać działanie obciążenia, które działa w dowolnej
płaszczyźnie nie pokrywającej się z żadną osią główną przekroju pręta i przechodzącą przez środek ciężkości
przekroju pręta. Skupimy się tylko na działaniu momentu zginającego oraz siły normalnej. Pominiemy
natomiast działanie siły poprzecznej. Rysunek 84 przedstawia pręt, w którym płaszczyzna obciążenia czyli
płaszczyzna, na której działają wszystkie siły czynne i bierne (reakcje) nie pokrywa się z żadną z osi głównych
przekroju. Wektor momentu zginającego M jest zawsze prostopadły do płaszczyzny obciążenia.
Y
gl
Z
gl
M
X
P
q(x)
N
M
sc
Z
gl
Y
gl
Płaszczyzna
obciążenia
N>0
Rys. 84 Pręt obciążony w w płaszczyźnie nie pokrywającej się z żadną osią główną przekroju.
Y=Y
gl
Z=Z
gl
M
X
P
q(x)
N
M
sc
Z=Z
gl
Y=Y
gl
α
α
M
Z
M
Y
M
Z
M
Y
N>0
Rys. 85. Rozkład wektora momentu zginającego M na dwie składowe po kierunkach pokrywających się z osiami
głównymi.
Dr inż. Janusz Dębiński
BZZ
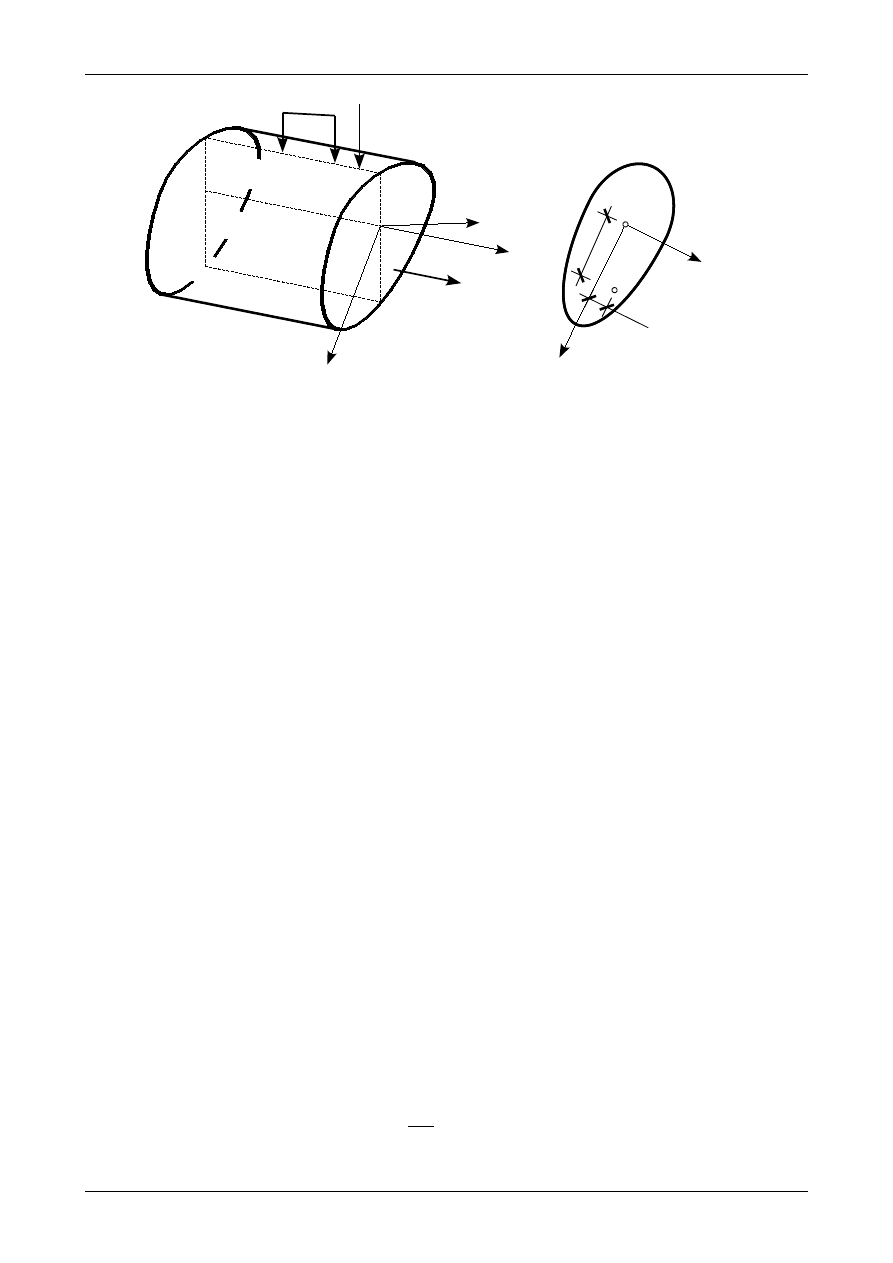
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
14
X
P
q(x)
N
Z=Z
gl
Y=Y
gl
Y=Y
gl
sc
N>0
Z=Z
gl
z
N
y
N
Rys. 86. Statycznie równoważne obciążenie przekroju pręta.
Wektor momentu zginającego M możemy rozłożyć na dwie składowe pokrywające się z osiami głównymi.
Przedstawia to rysunek 85. Wartość bezwzględna momentu zginającego po kierunku osi Y=Y
gl
wynosi
∣
M
Y
∣
=M⋅sin
.
(307)
Moment zginający po kierunku osi Z=Z
gl
wynosi
∣
M
Z
∣
=M⋅cos
.
(308)
Działanie sił przekrojowych przedstawionych na rysunku 85 możemy zastąpić statycznie równoważnym
obciążeniem przekroju pręta, w którym działanie składowych momentu zginającego zastąpimy przez
przeniesienie siły normalnej ze środka ciężkości do innego punktu o współrzędnych y
N
oraz z
N
. Rysunek 86
przedstawia taką sytuację.
Współrzędne y
N
i z
N
nie mogą być dowolne ale muszą spełniać następujące warunki
M
Y
=N⋅z
N
(309)
oraz
M
Z
=N⋅y
N
.
(310)
Współrzędne punktu przyłożenia siły normalnej wynoszą
z
N
=
M
Y
N
(311)
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
15
y
N
=
M
Z
N
.
(312)
Współrzędne y
N
oraz z
N
nazywają się mimośrodami a obciążenie pręta nazywa się obciążeniem
mimośrodowym.
Naprężenia normalne
σ
X
wyznacza się ze wzoru
X
=
N
A
M
Z
I
Z
⋅y
M
Y
I
Y
⋅z=A⋅yB⋅zC
.
(313)
W celu narysowania wykresu naprężeń normalnych należy w pierwszej kolejności wyznaczyć położenie osi
obojętnej. Jest to prosta, na której znajdują się punkty, w których naprężenie normalne
σ
X
równają się zero.
Oś obojętna ma postać
A
⋅yB⋅zC=0
.
(314)
Przenosząc wolny wyraz na drugą stronę otrzymamy
A
⋅yB⋅z=−C
.
(315)
Dzieląc obustronnie przez -C wzór (315) będzie miał postać
−
A
C
⋅y
−
B
C
⋅z=1
.
(316)
Wzór (316) możemy zapisać w postaci
y
−
C
A
z
−
C
B
=1
.
(317)
Równanie (317) opisuje postać odcinkową prostej. Prostą w postaci odcinkowej zapisujemy jako
y
y
0
z
Z
0
=1
.
(318)
W równaniu odcinkowym (318)
Dr inż. Janusz Dębiński
BZZ
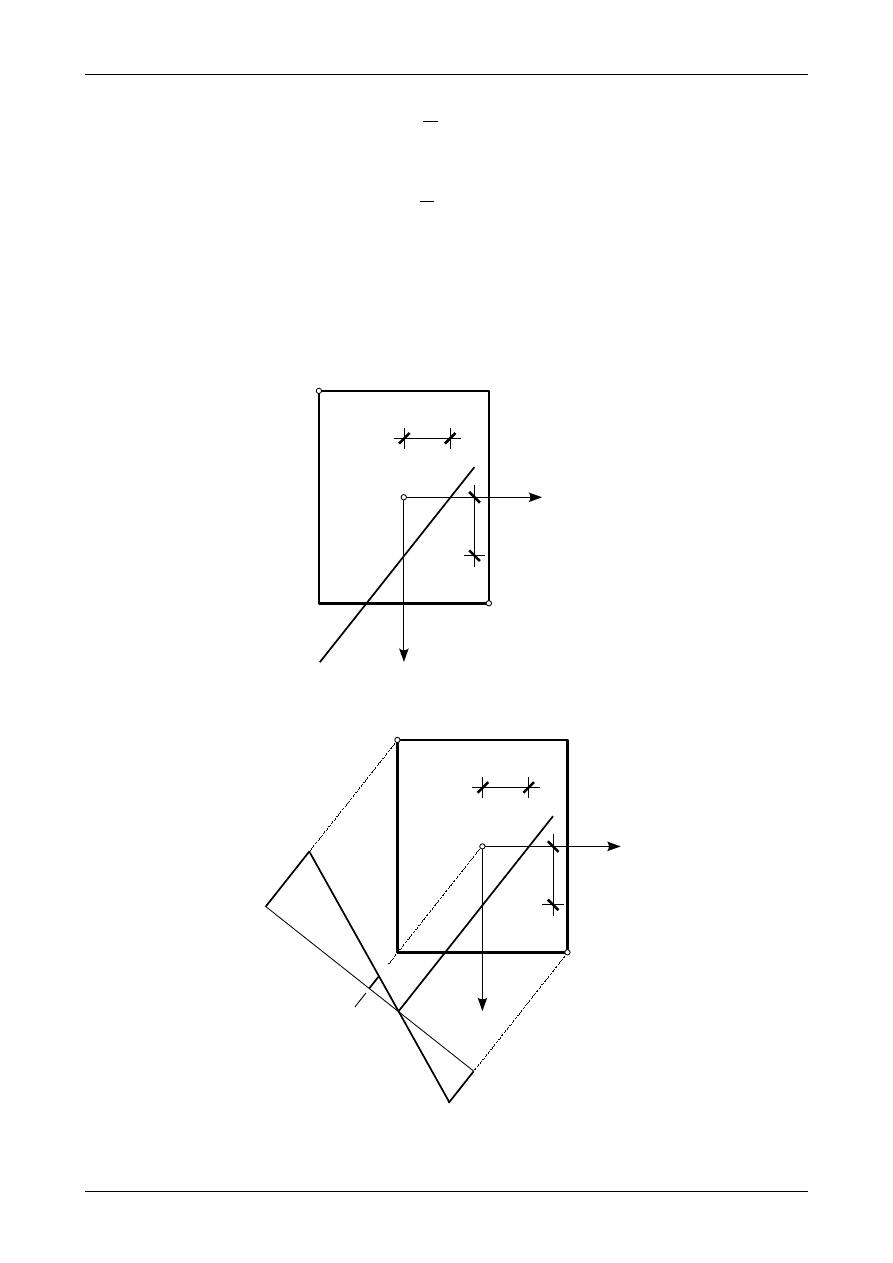
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
16
y
0
=−
C
A
(319)
z
0
=−
C
B
.
(320)
Położenie osi obojętnej w postaci odcinkowej w układzie osi środkowych przedstawia rysunek 87. Następnie
musimy znaleźć punkty przekroju, które są najbardziej oddalone od osi obojętnej (są to punkty 1 i 2). W
dalszej kolejności należy wyznaczyć naprężenie normalne w tych punktach podstawiając ich współrzędne do
wzoru (313). Naprężenia normalne będziemy odnosić na odcinku prostopadłym do osi obojętnej. Przykładowy
wykres naprężeń normalnych przedstawia rysunek 88.
sc
Z=Z
gl
Y=Y
gl
z
0
y
0
1
2
Rys. 87. Położenie osi obojętnej.
sc
Z=Z
gl
Y=Y
gl
z
0
y
0
1
2
X
X
1
X
2
N
A
Rys. 88. Przykładowy wykres naprężeń normalnych
σ
X
w przekroju.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
17
Jeżeli oś obojętna nie przecina przekroju pręt to w przekroju wystąpią naprężenia normalne
σ
X
jednakowego
znaku. W praktyce inżynierskiej bardzo często chcemy aby w przekroju działały tylko naprężenia jednego
znaku. Sytuacja taka zachodzi dla konstrukcji murowych, betonowych oraz przy projektowaniu fundamentów
i dotyczy naprężeń normalnych ściskających. Interesuje nas więc obszar przyłożenia siły normalnej by
naprężenia normalne
σ
X
były tego samego znaku. Obszar taki nazywa się rdzeniem przekroju.
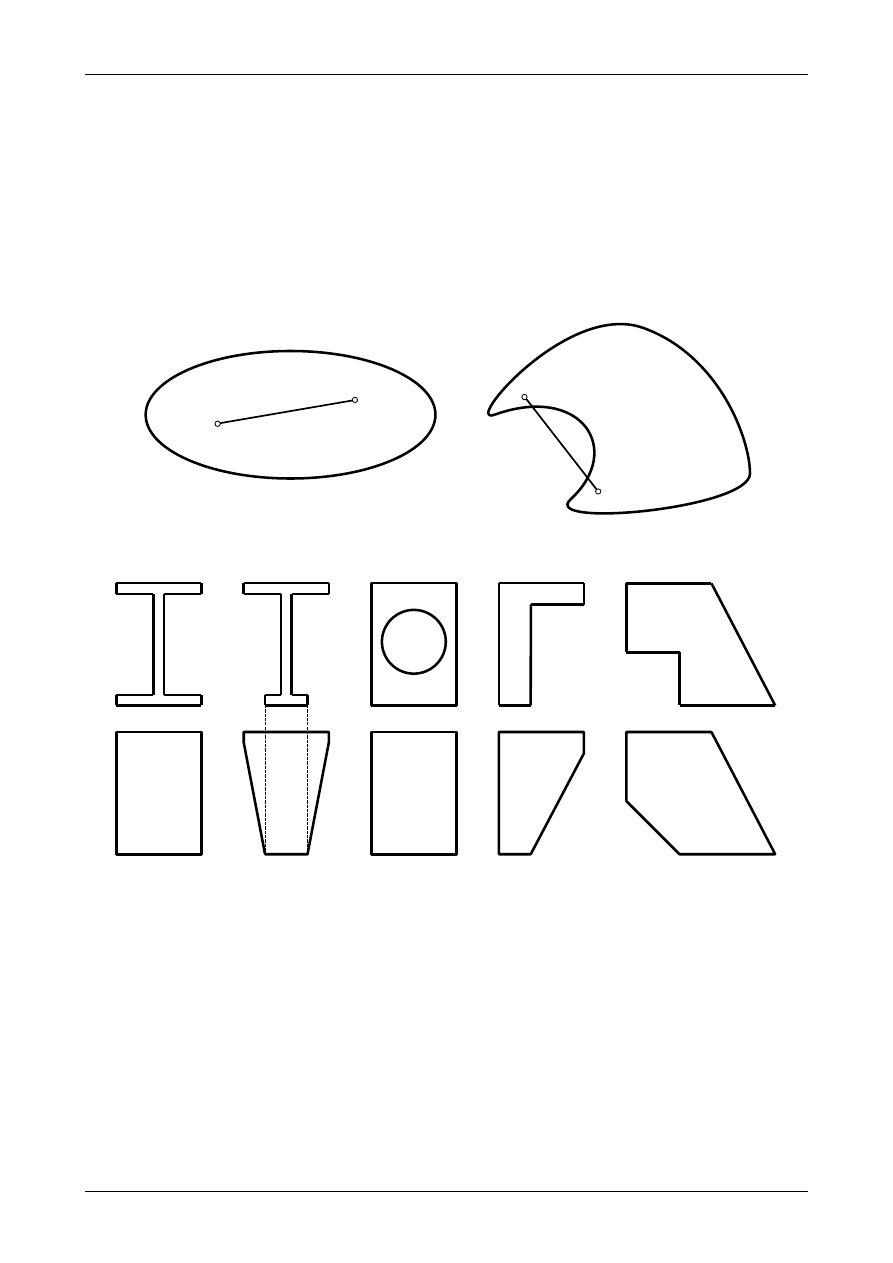
Z pojęciem rdzenia przekroju są związane pojęcia figury wklęsłej i wypukłej. Figurą wypukłą nazywamy taką
figurę, w której odcinek łączący dowolne dwa punkty tej figury cały znajduje się wewnątrz niej. Figurą
wklęsłą nazywamy taką figurę, w której odcinek łączący dowolne dwa punkty tej figury może częściowo
znajdować się poza nią. Rysunek 89 przedstawia figurę wklęsłą i wypukłą.
A
B
A
B
a)
b)
Rys. 89. Figury. a)wypukła, b)wklęsła.
1
2
3
4
1
2
3
4
5
6
1
2
3
4
1
2
3
4
5
1
2
3
4
5
Rys. 90. Figury wypukłe opisane na przekrojach wklęsłych.
Rdzeń przekroju posiada następujące właściwości:
1. jest figurą wypukłą,
2. zawiera środek ciężkości,
3. znajduje się wewnątrz konturu wypukłego,
4. jeżeli przekrój posiada jedną oś symetrii to i rdzeń przekroju jest względem tej samej osi symetryczny,
5. jeżeli przekrój posiada więcej niż jedną oś symetrii to i rdzeń przekroju jest względem tych samych osi
symetryczny,
Dr inż. Janusz Dębiński
BZZ
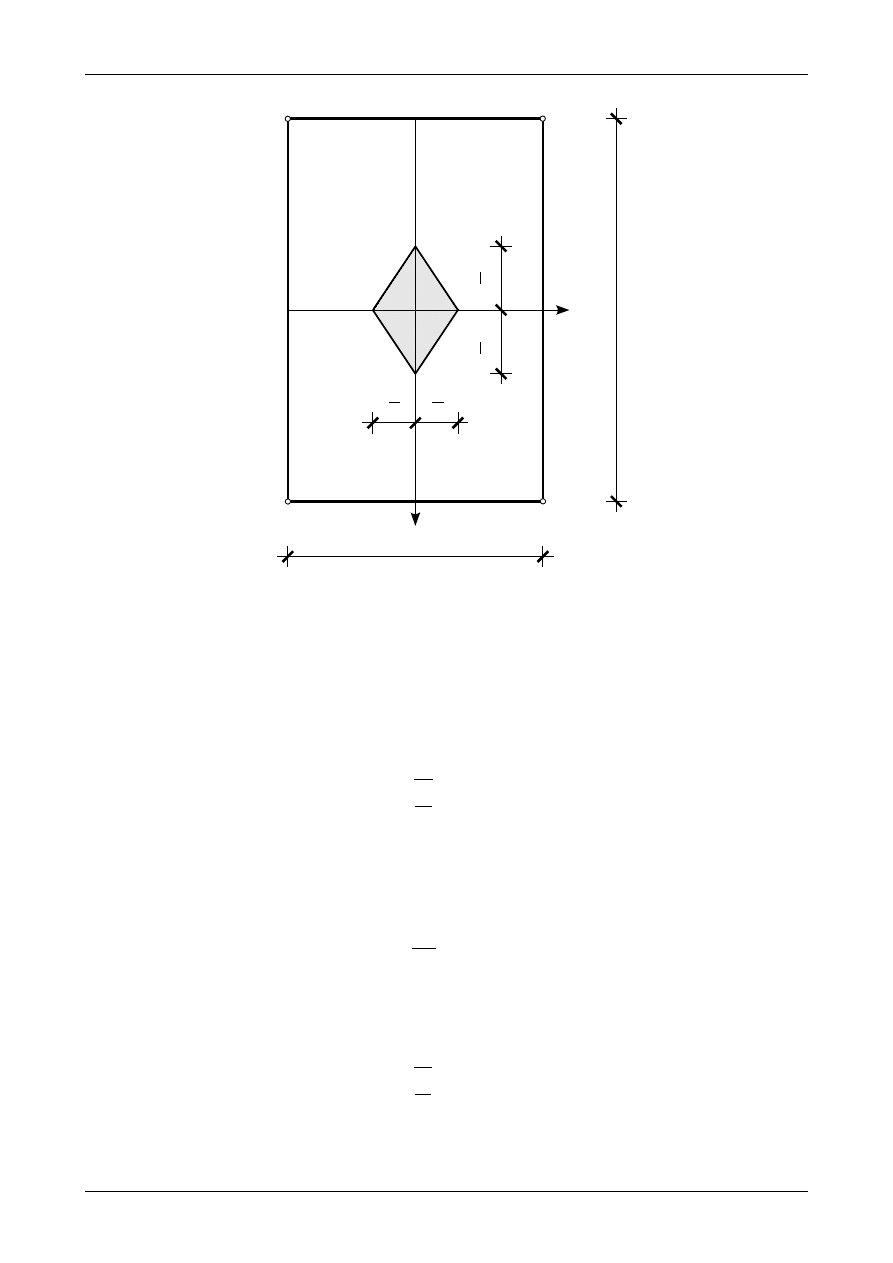
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
18
1
2
3
4
Z=Z
gl
Y=Y
gl
b
h
h
6
h
6
b
6
b
6
Rys. 91. Rdzeń przekroju dla prostokąta.
Rdzeń przekroju będziemy wyznaczać poprzez przykładanie siły normalnej w wierzchołkach konturu
zewnętrznego przekroju i obliczaniu odpowiadających im osi obojętnych. Jeżeli przekrój jest figurą wklęsłą to
zastępujemy go figurą wypukłą opisaną na nim. Rysunek 90 przedstawia kilka przykładów przekrojów
wklęsłych. Wierzchołki, w których należy przykładać siłę normalną zaznaczone są cyframi.
Wyrażenie
i
Z
=
I
Z
A
(321)
nazywamy promieniem bezwładności względem osi Z=Z
gl
. Współrzędna odcinkowa y
0
wynosi ostatecznie
y
0
=−
i
Z
2
y
N
.
(322)
Wyrażenie
i
Y
=
I
Y
A
(323)
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
19
nazywamy promieniem bezwładności względem osi Y=Y
gl
. Współrzędna odcinkowa z
0
wynosi ostatecznie
z
0
=−
i
Y
2
z
N
.
(324)
Wzory (322) i (324) dowodzą, że w układzie osi głównych współrzędne odcinkowe osi obojętnej znajdują się
po przeciwnej stronie niż współrzędne punktu przyłożenia siły normalnej. Dowodzi to, że oś obojętna w
układzie osi głównych przechodzi zawsze przez te ćwiartki układu współrzędnych, w których nie jest
przyłożona siła normalna.
Rysunek 91 przedstawia rdzeń przekroju dla prostokąta.
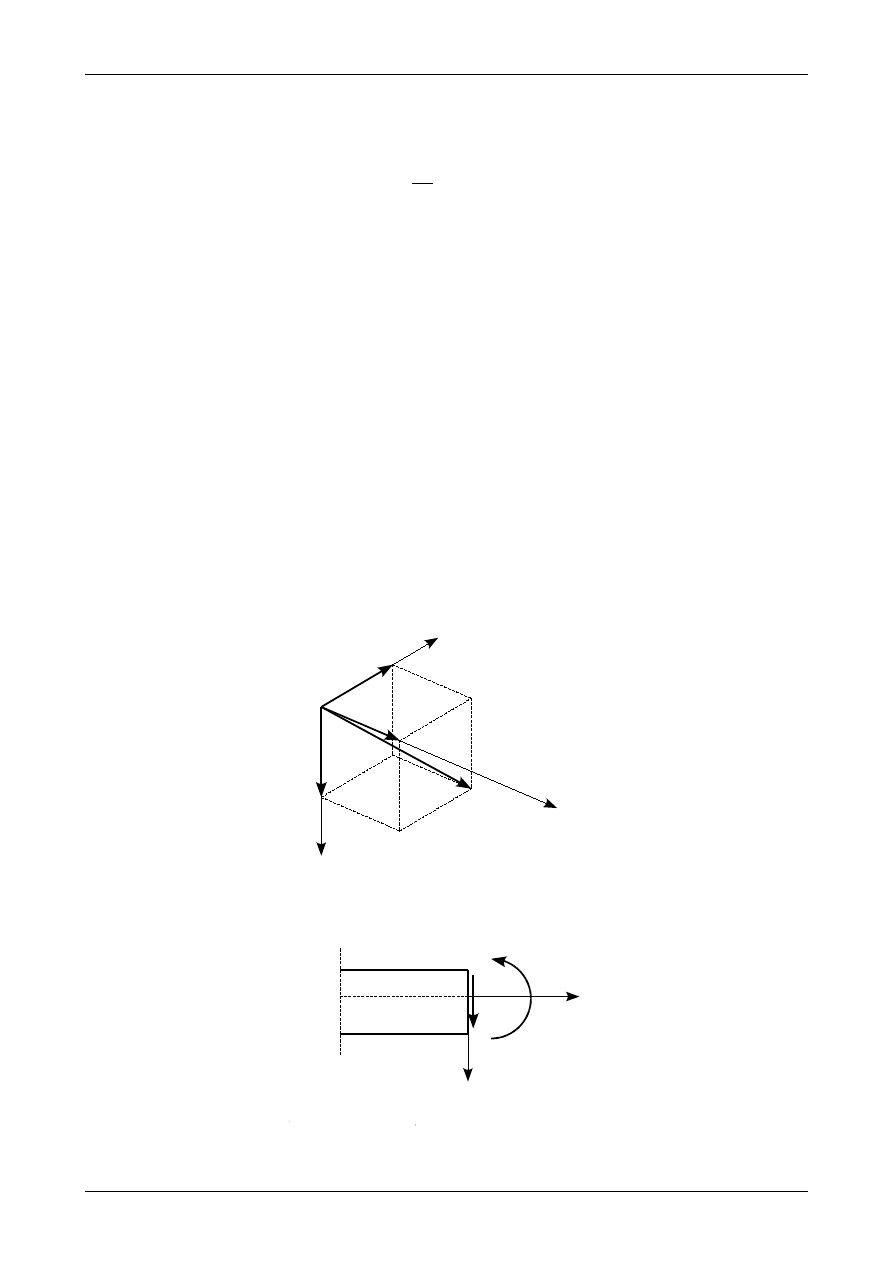
23 Ugięcia
Przemieszczenie belki będziemy opisywali za pomocą wektora przemieszczenia, który w układzie
współrzędnych XYZ będzie miał postać
f=u⋅iv⋅jw⋅k
.
(325)
Składowe wektora (325) w układzie XYZ przedstawia rysunek 92.
X
Y
Z
f
u
v
w
Rys. 92. Wektor przemieszczenia.
Y=Y
0
=Y
gl
X
T
=
T
Y
M=M
Z
Rys. 93. Obciążenie przekroju pręta.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
20
W niniejszym rozdziale ograniczymy się do przypadku, w którym płaszczyzna obciążenia pokrywa się z osią
główną bezwładności Y=Y
gl
. Obciążenie przekroju pręta przedstawia rysunek 93. Pominiemy wpływ siły
poprzecznej T=T
Z
na przemieszczenia belki. Przemieszczenia będą zależeć więc tylko od momentu
zginającego M=M
Z
.
Jeżeli obciążenie działa w płaszczyźnie XY to belka będzie doznawać tylko przemieszczeń po kierunku
głównej osi bezwładności Y=Y
gl
. Wektor przemieszczenia będzie miał tylko jedną składową czyli
f=v
.
(326)
Jeżeli przemieszczenie nastąpi w dół (zgodnie ze zwrotem osi Y) to będzie ono dodatnie, jeżeli do góry
(przeciwnie do zwrotu osi Y) to będzie ono ujemne. Przedstawia to rysunek 94.
v(x)
v>0
v<0
Rys. 94. Przykładowa linia ugięcia.
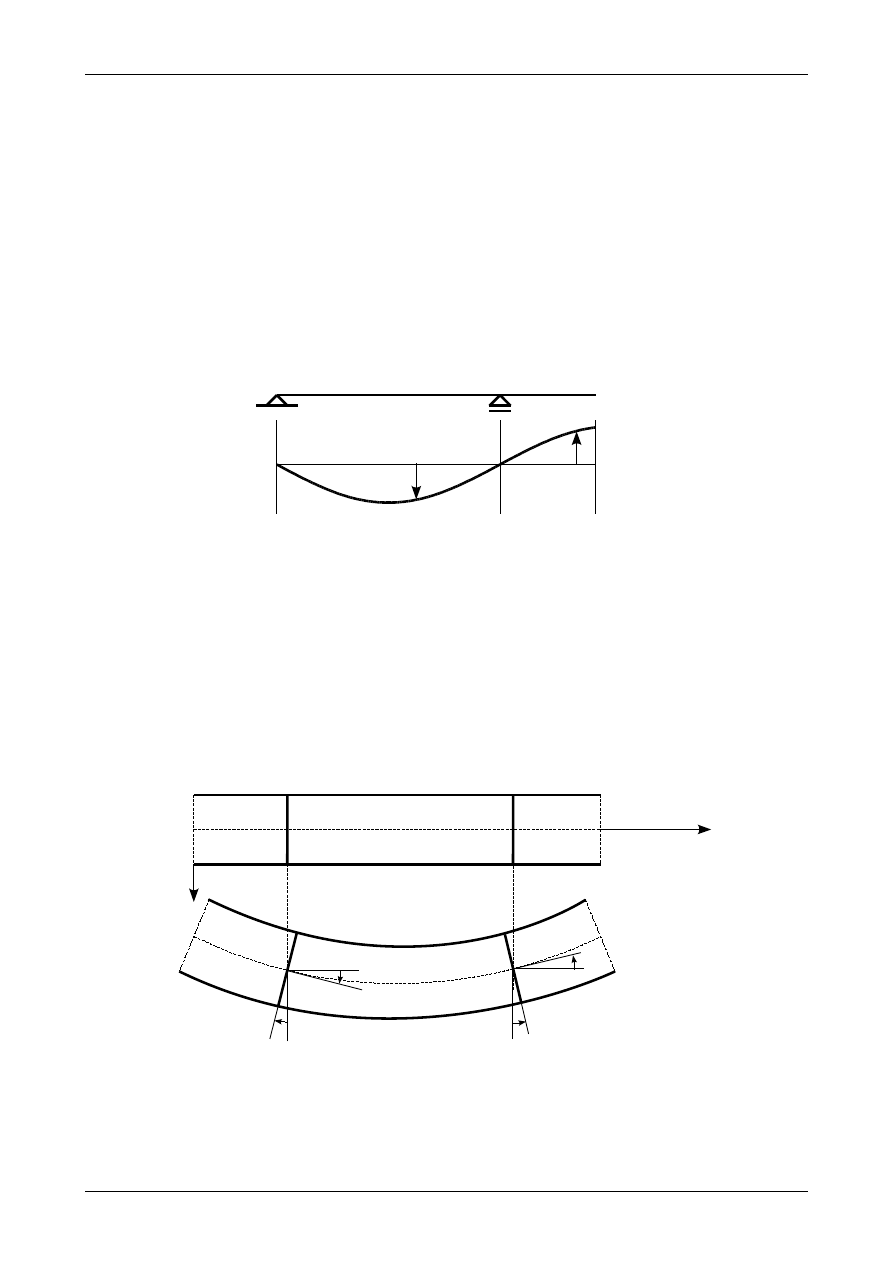
Oprócz linii ugięcia będzie ważny także wykres funkcji kąta obrotu przekroju pręta. Jak wiadomo przekrój
pręta jest zawsze prostopadły do osi pręta zarówno przed przyłożeniem obciążenia jak i po. Rysunek 95
przedstawia fragment pręta przed przyłożeniem i po przyłożeniu obciążenia. Oba przekroje, które przed
przyłożeniem obciążenia były pionowe obróciły się. Jeden z przekrojów obrócił się o kąt
φ
1
a drugi o kąt
φ
2
.
Na rysunku 95 zaznaczony jest schematycznie układ współrzędnych związany z przekrojem pręta. Jeżeli
obrót przekroju pręta nastąpi od osi X do osi Y to taki kąt obrotu jest dodatni natomiast jeżeli obrót
przekroju pręta nastąpi od osi Y do osi X to taki kąt obrotu jest kątem ujemnym. Jak widać na rysunku
95 kąt
φ
1
jest dodatni (obrót od osi X do osi Y) natomiast kąt
φ
2
jest ujemny (obrót od osi Y do osi X).
Jednostką kąta obrotu jest radian, który będziemy traktować jako jednostkę bezwymiarową.
1
2
1
0
2
0
X
Y
Rys. 95. Interpretacja kąta obrotu przekroju pręta.
Na rysunku 95 pokazane jest, że kąt obrotu przekroju jest także kątem nachylenia stycznej do linii ugięcia. Jak
wiadomo z rachunku różniczkowego tangens kąta nachylenia stycznej do wykresu funkcji w punkcie równa się
wartości pochodnej funkcji w tym punkcie. Ponieważ kąty obrotu przekroju pręta są wielkością bardzo małą
Dr inż. Janusz Dębiński
BZZ
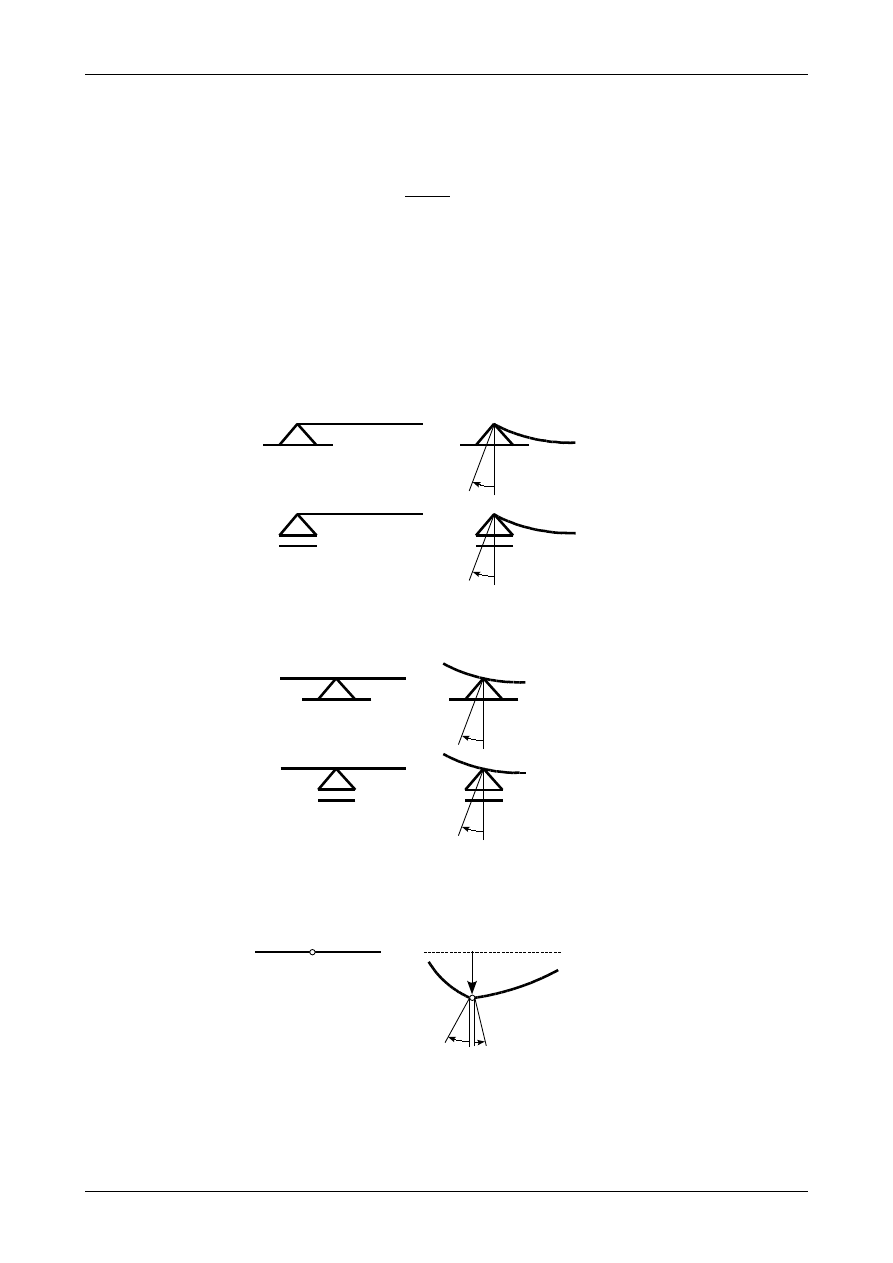
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
21
możemy przyjąć, że tangens kąta obrotu przekroju pręta równa się samemu kątowi obrotu wyrażonemu w
radianach. Możemy więc ogólnie zapisać, że
x =
d v
x
d x
.
(327)
Przy rozwiązywaniu zadań z wyznaczania ugięć bardzo potrzebne będą informacje o ugięciach i kątach
obrotów na różnego rodzaju więzach. Informacje te nazywają się warunkami brzegowymi. Na rysunku 96
przedstawione są warunki brzegowe dla podpór przegubowo-przesuwnej i przegubowo-nieprzesuwnej na
końcu belki. Jak widać dla tych podpór ugięcie v wynosi zawsze zero natomiast kąt obrotu jest różny od zera
(może istnieć przypadek szczególny kiedy kąt obrotu dla tych podpór będzie równy zero). Rysunek 97
przedstawia warunki brzegowe dla podpór przegubowo-przesuwnej i przegubowo-nieprzesuwnej na długości
belki. Warunki brzegowe są takie same jak opisane powyżej.
v
=0
≠0
v
=0
≠0
Rys. 96. Warunki brzegowe dla podpór przegubowo- przesuwnej i przegubowo-nieprzesuwnej na końcu belki.
v
=0
≠0
v
=0
≠0
Rys. 97. Warunki brzegowe dla podpór przegubowo- przesuwnej i przegubowo-nieprzesuwnej na długości belki.
v
≠0
L
≠0
P
≠0
L
≠
P
v
L
P
Rys. 98. Warunki brzegowe dla przegubu łączącego dwie belki proste.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
22
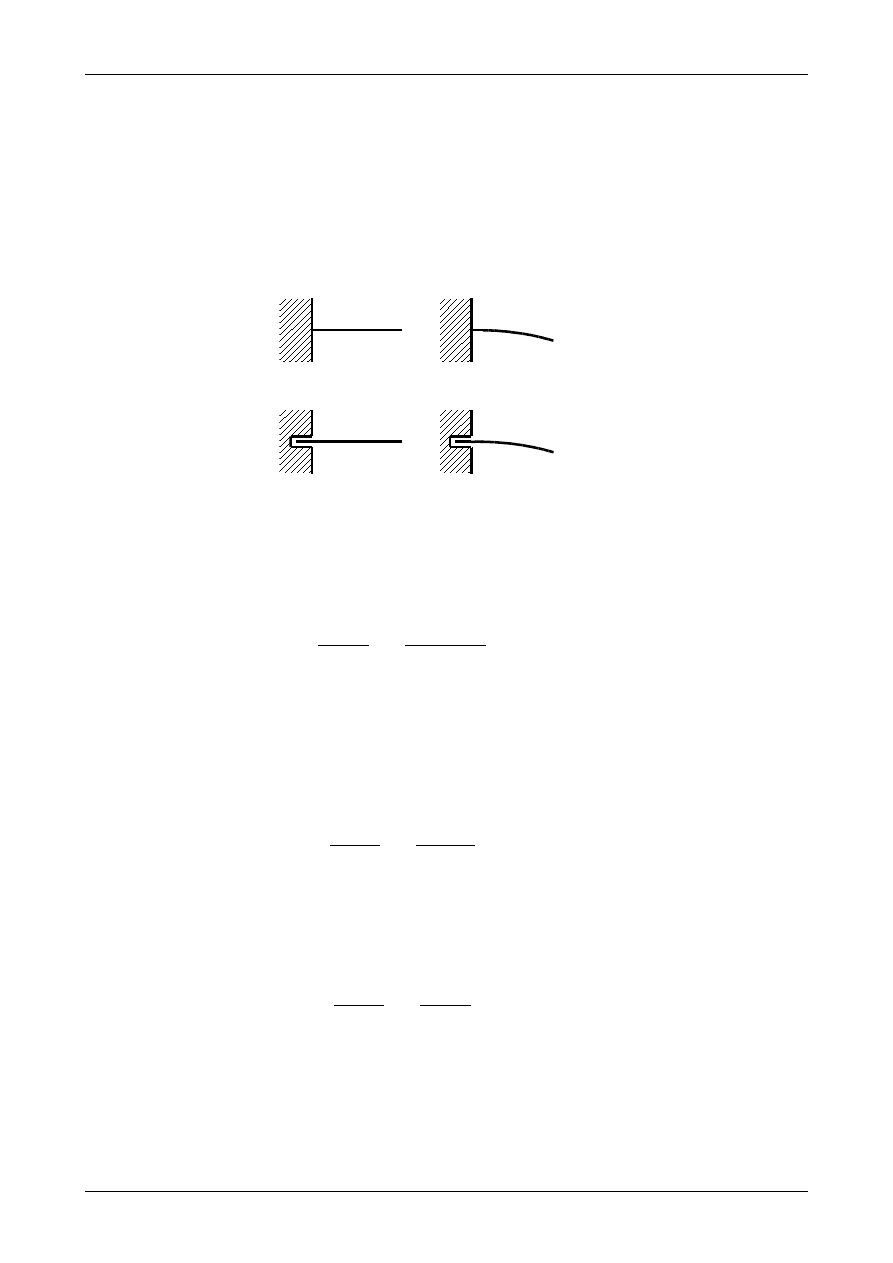
Rysunek 98 przedstawia warunki brzegowe dla przegubu łączącego dwie belki proste. Jak widać ugięcie w
przegubie jest różne od zera (może istnieć przypadek szczególny kiedy ugięcie w przegubie będzie równe
zero). W przegubie będziemy mieli dwa kąty obrotu: z lewej strony
φ
L
oraz z prawej strony
φ
P
.Jak widać oba
kąty są różne od zera oraz oba są od siebie różne (możliwy jest jednak szczególny przypadek, kiedy oba te
kąty będą sobie równe).
Ostatnimi podporami, dla których określimy warunki brzegowe są podpora ślizgowa oraz utwierdzenie. Dla
tych podpór nie ma żadnych przypadków szczególnych, ponieważ ugięcie oraz kąt obrotu są zawsze równe
zero. Podpory te oraz warunki brzegowe na nich przedstawia rysunek 99.
v
=0
=0
v
=0
=0
Rys. 99. Warunki brzegowe dla podpory ślizgowej i utwierdzenia.
Zależność pomiędzy funkcją ugięcia v(x) a funkcją momentu zginającego M(x)=M
Z
(x) nazywa się równaniem
różniczkowym linii ugięcia i ma postać
d
2
v
x
d x
2
=−
M
Z
x
E
x⋅I
Z
x
,
(328)
w którym E(x) jest funkcją wartości modułu Younga od położenia , I
Z
(x) jest funkcją momentu bezwładności
względem osi Z=Z
gl
od położenia. Ze względu na to, że będziemy rozpatrywać belki wykonane z materiału
izotropowego mającego w każdym punkcie te same właściwości więc moduł Younga będzie miał wartość stałą
a równanie różniczkowe równowagi będzie miało postać
d
2
v
x
d x
2
=−
M
Z
x
E
⋅I
Z
x
.
(329)
Jeżeli pewien odcinek belki będzie prętem pryzmatycznym czyli moment bezwładności będzie stały równanie
różniczkowe równowagi będzie miało postać
d
2
v
x
d x
2
=−
M
Z
x
E
⋅I
Z
.
(330)
Iloczyn modułu Younga oraz momentu bezwładności nazywamy sztywnością przekroju.
Jako przykład wyznaczenia ugięć obliczmy linię ugięcia i funkcję kąta obrotu dla belki swobodnie podpartej
obciążonej obciążeniem ciągłym równomiernie rozłożonym o wartości q. Belka ma długość L. Rysunek 100
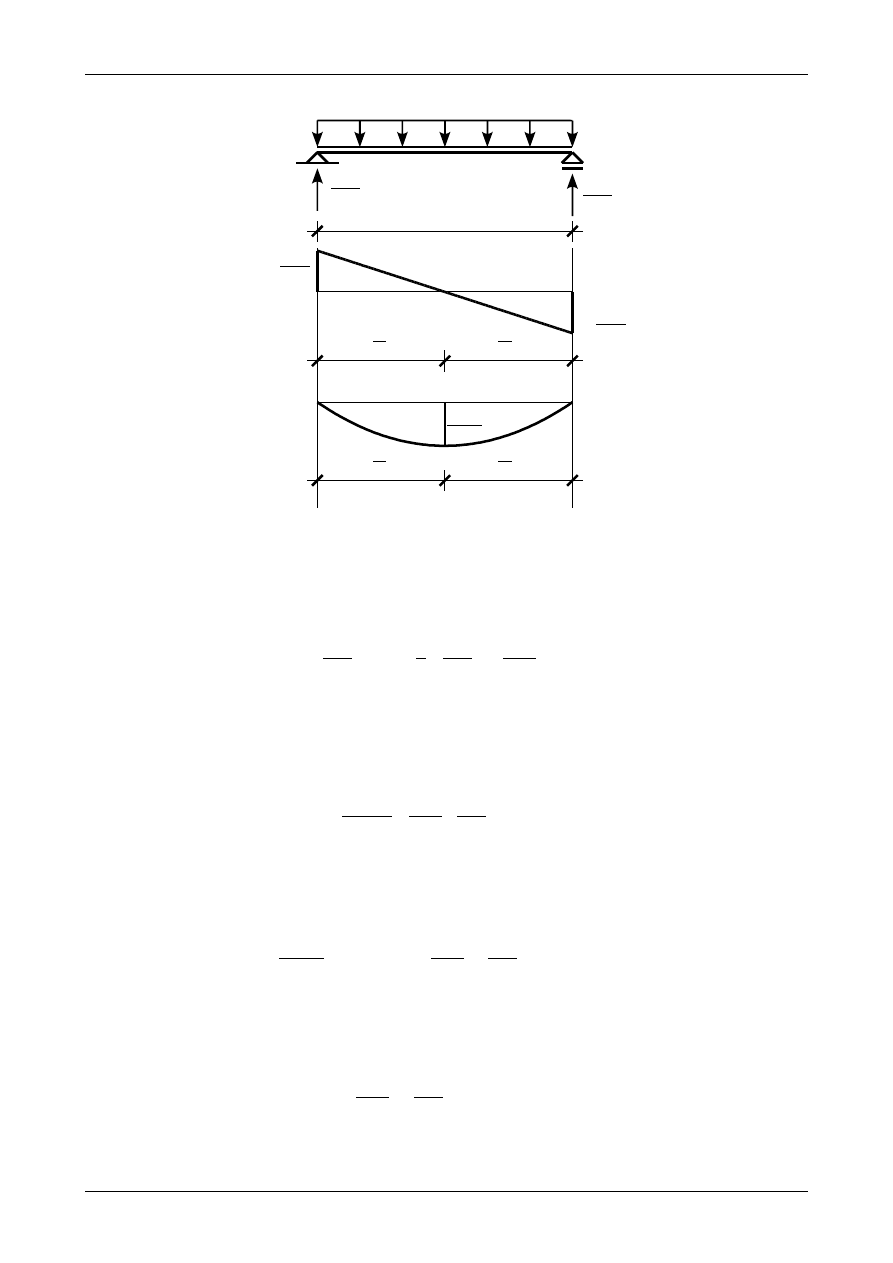
przedstawia belkę wraz z wykresami siły poprzecznej T(x) oraz momentu zginającego M(x).
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
23
q
L
T(x)
M(x)
q
⋅L
2
q
⋅L
2
q
⋅L
2
−
q
⋅L
2
0,0
0,0
L
2
L
2
L
2
L
2
q
⋅L
2
8
Rys. 100. Wykresy sił przekrojowych dla belki swobodnie podpartej z obciążeniem ciągłym równomiernie rozłożonym.
Moment zginający wynosi więc
M
x =
q
⋅L
2
⋅x−q⋅x⋅
x
2
=
q
⋅L
2
⋅x−
q
⋅x
2
2
.
(331)
Równanie różniczkowe równowagi będzie miało postać (zakładamy, że materiał jest jednorodny i pręt jest
pryzmatyczny)
E
⋅I
Z
⋅
d
2
v
x
d x
2
=
q
⋅x
2
2
−
q
⋅L
2
⋅x
.
(332)
Po pierwszym całkowaniu wzór (332) będzie miał postać
E
⋅I
Z
⋅
d v
x
d x
=E⋅I
Z
⋅ x=
q
⋅x
3
6
−
q
⋅L
4
⋅x
2
C
.
(333)
We wzorze (333) C oznacza pierwszą stałą całkowania. Po drugim całkowaniu otrzymamy wzór
E
⋅I
Z
⋅vx =
q
⋅x
4
24
−
q
⋅L
12
⋅x
3
C⋅xD
,
(334)
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
24
w którym D oznacza drugą stałą całkowania. Chcąc wyznaczyć wartości stałych całkowania należy wstawić
do równań (334) lub (333) dwa warunki brzegowe. Patrząc na rysunek 100 widać, że ugięcia nad podporami
wynoszą zero czyli otrzymamy
v
0=0
v
L =0
.
(335)
Podstawiając warunek pierwszy do równania (334) otrzymamy
q
⋅0
4
24
−
q
⋅L
12
⋅0
3
C⋅0D=0
,
(336)
czyli stała D wynosi jak widać zero. Zajmijmy się jeszcze jednostką tej stałej. Patrząc na równanie (334)
widać, że stała D musi mieć ten sam wymiar co iloczyn sztywności przekroju i ugięcia czyli
[
kN
⋅m
2
⋅m
]
=
[
kN
⋅m
3
]
.
(337)
Podstawiając warunek drugi do równania (334) otrzymamy
q
⋅L
4
24
−
q
⋅L
12
⋅L
3
C⋅L=0
.
(338)
W równaniu (338) zostało już uwzględnione, że stała D wynosi zero. Z równania (338) stała C wynosi
C
=
q
⋅L
3
24
.
(339)
Zajmijmy się jeszcze jednostką tej stałej. Patrząc na równanie (333) widać, że stała C musi mieć ten sam
wymiar co iloczyn sztywności przekroju i kąta obrotu przekroju. Kąt obrotu jak wiadomo jest bezwymiarowy
czyli stała C ma jednostkę
[
kN
⋅m
2
]
.
(340)
Ostatecznie funkcja kąta obrotu ma postać
x=
1
E
⋅I
Z
⋅
q
⋅x
3
6
−
q
⋅L
4
⋅x
2
q
⋅L
3
24
.
(341)
Ostatecznie linia ugięcia ma postać
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
25
v
x=
1
E
⋅I
Z
⋅
q
⋅x
4
24
−
q
⋅L
12
⋅x
3
q
⋅L
3
24
⋅x
.
(342)
Kąty obrotu przekrojów pręta na obu końcach belki wynoszą
0=
q
⋅L
3
24
⋅E⋅I
Z
.
(343)
oraz
L =−
q
⋅L
3
24
⋅E⋅I
Z
.
(344)
Miejsce zerowe wykresu kąta obrotu przekroju pręta znajduje się w miejscu
x
0
=
L
2
.
(345)
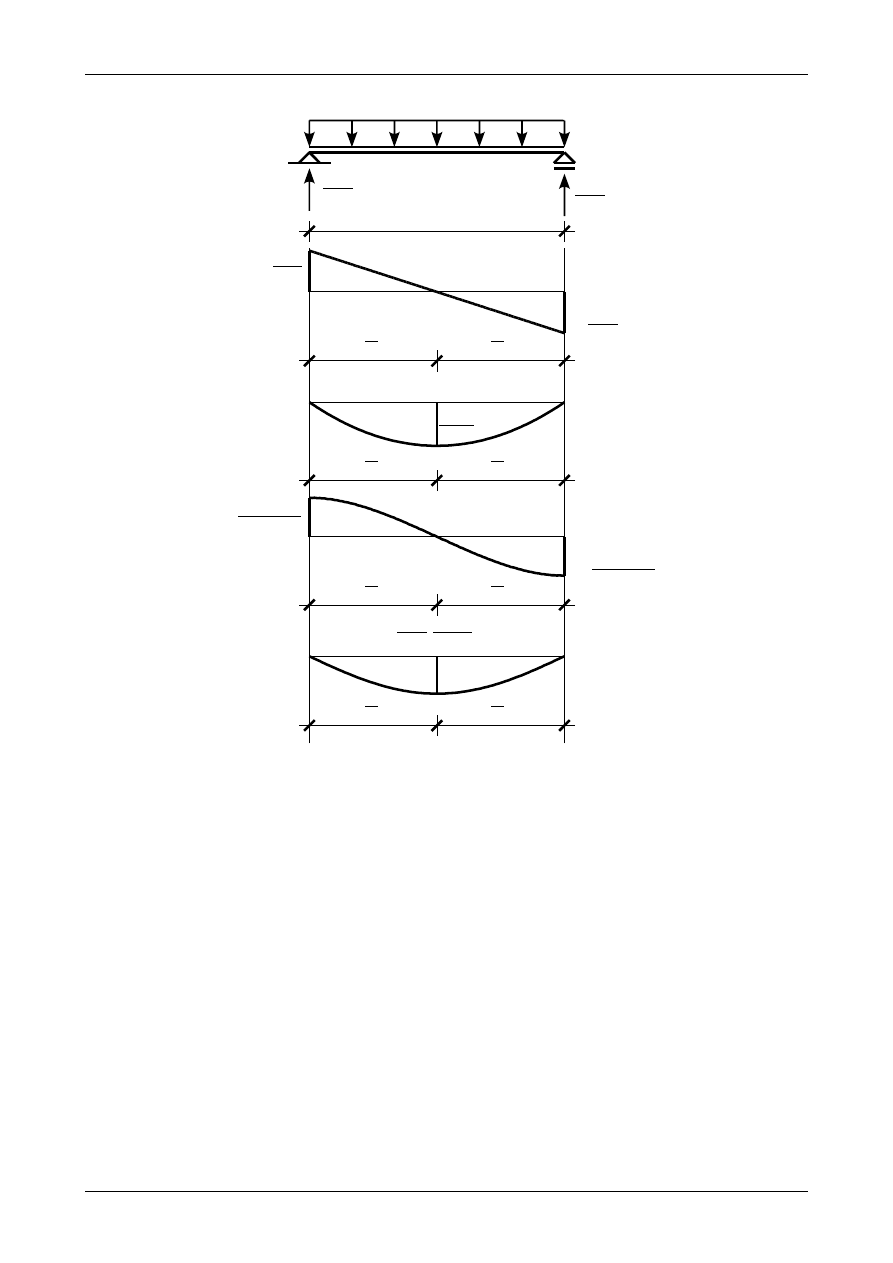
Rysunek 101 przedstawia wykres funkcji kąta obrotu przekroju. Ugięcia belki na obu końcach wynoszą
v
0=0
,
(346)
v
L=
1
E
⋅I
Z
⋅
q
⋅L
4
24
−
q
⋅L
12
⋅L
3
q
⋅L
3
24
⋅L
=0
.
(347)
Czyli jest to zgodne z warunkami brzegowymi (335). Ugięcie w środku belki czyli w miejscu zerowym funkcji
kąta obrotu przekroju wynosi
v
L
2
=
1
E
⋅I
Z
⋅
[
q
24
⋅
L
2
4
−
q
⋅L
12
⋅
L
2
3
q
⋅L
3
24
⋅
L
2
]
=
5
384
⋅
q
⋅L
4
E
⋅I
Z
.
(348)
Rysunek 101 przedstawia wykres linii ugięcia. Na wykresie tym widać, że funkcja kąta obrotu posiada
ekstremum w miejscu zerowym wykresu momentu zginającego M(x) natomiast linia ugięcia posiada
ekstremum w miejscu zerowym funkcji kąta obrotu przekroju pręta.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
26
q
L
T(x)
M(x)
q
⋅L
2
q
⋅L
2
q
⋅L
2
−
q
⋅L
2
0,0
0,0
L
2
L
2
L
2
L
2
q
⋅L
2
8
L
2
L
2
L
2
L
2
φ
(x)
v(x)
0,0
0,0
5
384
⋅
q
⋅L
4
E
⋅I
Z
q
⋅L
3
24
⋅E⋅I
Z
−
q
⋅L
3
24
⋅E⋅I
Z
Rys. 101. Wykresy funkcji kąta obroty przekroju pręta oraz linii ugięcia.
Belka przedstawiona powyżej składała się z jednego przedziału. W przypadku belek składających się z wielu
przedziałów należy obliczenia przeprowadzić we wszystkich przedziałach osobno zapisując odpowiednie
funkcje momentu zginającego M(x) i całkując każde z osobna otrzymać funkcję kąta obrotu przekroju pręta
oraz linię ugięcia. Liczba stałych i warunków brzegowych będzie się równała podwojonej liczbie przedziałów.
Liczbę stałych możemy zredukować do dwóch lecz musimy w specyficzny sposób zapisać wyrażenie na
moment zginający M(x). Sposób ten został zaproponowany przez Alfreda Clebscha.
Na początek przyjmiemy, że że belka jest wykonana z pręta pryzmatycznego czyli posiada stały moment
bezwładności I
Z
. Dodatkowo obciążenie ciągłe ograniczymy tylko do przypadku obciążenia ciągłego
równomiernie rozłożonego.
Metoda Clebscha pozwala na zredukowanie liczby stałych całkowania do dwóch bez względu na liczbę
przedziałów z obciążeniem na belce. Konieczne jest jednak przestrzeganie kilku zasad przy zapisie równania
momentu zginającego i jego całkowaniu.
Na początek należy przyjąć początek układu XY w lewym końcu belki. Wyrażenie na moment zginający w
dowolnym przedziale musi być wyrażone przez siły działające na lewą odciętą część belki.
Zapisując wyrażenie na moment zginający w dowolnym przedziale musimy uwzględnić w postaci
niezmienionej wszystkie człony wyrażenia na moment zginający w przedziałach poprzednich. Jeżeli obciążenie
ciągłe równomiernie rozłożone kończy się przed końcem belki to musimy je przedłużyć do samego końca belki
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
27
a w przedziałach, w których to obciążenie nie działa należy dodać obciążenie o tej samej wartości lecz
przeciwnie skierowane.
Wyrażenia na moment zginający, funkcję kąta obrotu przekroju oraz linię ugięcia będziemy zapisywali od razu
dla całej belki. Kreskami będziemy zaznaczać, gdzie kończy się odpowiednie wyrażenie. Jeżeli jakiś punkt
będzie się znajdował w odpowiednim przedziale to wyrażenie na moment zginający, funkcję kąta obrotu i linię
ugięcia będzie obowiązywało tylko do kreski kończącej dany przedział. Rysunek 102 przedstawia
przykładową belkę wraz ze wszystkimi siłami czynnymi i biernymi (reakcjami). Na belkę tą, w przedziale CD
działa obciążenie ciągłe równomierne rozłożone. Należy więc obciążenie to przeciągnąć do końca a w
przedziałach DE i EF dołożyć obciążenie o takiej samej wartości tylko skierowane do góry. Rysunek 103
przedstawia tak obciążoną belkę. Na rysunku tym zaznaczony jest także układ współrzędnych XY, którego
początek znajduje się w punkcie A. Belka jest prętem pryzmatycznym, czyli posiada stały moment
bezwładności I=I
Z
.
q
A
B
C
E
P
V
B
V
E
a
D
F
M
0
b
c
d
e
Rys. 102. Belka swobodnie podparta.
q
A
B
C
E
P
V
B
V
E
D
F
M
0
q
X
Y
a
b
c
d
e
Rys. 103. Statycznie równoważne obciążenie ciągłe równomiernie rozłożone.
Wyrażenie na moment zginający dla tej belki będzie miało postać
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
28
E
⋅I
Z
⋅v' ' =−
[
−P⋅
x
−0
1
∥
B
V
B
⋅
x
−a
1
∥
C
−
q
⋅
x
−b
2
2
M
0
⋅
x
−b
0
∥
D
q
⋅
x
−c
2
2
∥
E
V
E
⋅
x
−d
1
∥
F
]
.
(349)
Po uwzględnieniu minusa przed nawiasem wzór (349) będzie miało postać
E
⋅I
Z
⋅v' ' =P⋅
x
−0
1
∥
B
−V
B
⋅
x
−a
1
∥
C
q
⋅
x
−b
2
2
−M
0
⋅
x
−b
0
∥
D
−
q
⋅
x
−c
2
2
∥
E
−V
E
⋅
x
−d
1
∥
F
.
(350)
Po pierwszym całkowaniu otrzymamy równie funkcji kąta obrotu przekroju pręta w postaci
E
⋅I
Z
⋅v' =E⋅I
Z
⋅=C
P
⋅
x
−0
2
2
∥
B
−
V
B
⋅
x
−a
2
2
∥
C
q
⋅
x
−b
3
6
−
M
0
⋅
x
−b
1
1
∥
D
−
q
⋅
x
−c
3
6
∥
E
−
V
E
⋅
x
−d
2
2
∥
F
.
(351)
Całkując równanie (351) otrzymamy równanie linii ugięcia w postaci
E
⋅I
Z
⋅v=C⋅xD
P
⋅
x
−0
3
6
∥
B
−
V
B
⋅
x
−a
3
6
∥
C
q
⋅
x
−b
4
24
−
M
0
⋅
x
−b
2
2
∥
D
−
q
⋅
x
−c
4
24
∥
E
−
V
E
⋅
x
−d
3
6
∥
F
.
(352)
Chcąc wyznaczyć stałe C i D występujące w równaniach (351) i (352) należy podstawić warunki brzegowe.
Dla belki na rysunkach 102 i 103 będą to zerowe ugięcia na podporach B i E czyli
v
x=a=0
v
x=d=0
.
(353)
Podstawiając pierwszy warunek brzegowy do równania (352) i pamiętając, że punkt B znajduje się w
przedziale AB (czyli równanie (352) bierzemy tylko do punktu B) otrzymamy
C
⋅aD
P
⋅
a
−0
3
6
=C⋅aD
P
⋅a
3
6
=0
.
(354)
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
29
Podstawiając drugi warunek brzegowy do równania (352) i pamiętając, że punkt E należy do przedziału DE
(czyli równanie (352) bierzemy tylko do punktu E) otrzymamy
C
⋅
d
D
P
⋅
d
−0
3
6
−
V
B
⋅
d
−a
3
6
q
⋅
d
−b
4
24
−
M
0
⋅
d
−b
2
2
−
q
⋅
d
−c
4
24
=0
.
(355)
Równania (354) i (355) tworzą układ równań, w którym niewiadomymi są stałe C i D. Rozwiązując ten układ
otrzymamy wartości stałych całkowania. Podstawiając je do równań (351) i (352) wyznaczymy ostateczną
postać funkcji kąta obrotu przekroju pręta oraz linię ugięcia. Na koniec pozostaje nam narysowanie tych
funkcji. W tym celu użyteczne mogą być programy matematyczne lub arkusz kalkulacyjny.
Metoda obciążeń krzywiznami opiera się na podobieństwie różniczkowych równań równowagi oraz równania
różniczkowego linii ugięcia. Tabela 7.1 przedstawia powyższe wzory.
Tabela. 7.1. Różniczkowe równania równowagi i różniczkowe równanie linii ugięcia
Różniczkowe równania równowagi
Różniczkowe równanie linii ugięcia
M
x
v
x
d M
x
d x
=T x
d v
x
d dx
=x
dT
x
d x
=
d
2
M
x
d x
2
=−q x
d
2
v
x
d x
2
=−
M
x
E
⋅I
Z
x
=− x
Z porównania wzorów w czwartym wierszu Tabeli 7.1 wynika, że jeżeli jako obciążenie przyjmiemy moment
zginający podzielony przez sztywność przekroju (czyli krzywiznę
κ
(x)) czyli
q
*
x =
M
x
E
⋅I
Z
x
= x
(356)
to siła poprzeczna będzie równa kątowi obrotu przekroju pręta natomiast moment zginający będzie równy
ugięciu. Obciążenie q
*
(x) będziemy nazywali obciążeniem wtórnym. Siłę poprzeczną równą kątowi obrotu
przekroju pręta będziemy nazywali wtórną siłą poprzeczną. Moment zginający równy ugięciu będziemy
nazywali wtórnym momentem zginającym. Kąt obrotu będzie wynosił
x=T
*
x
.
(357)
We wzorze (357) T
*
oznacza właśnie wtórną siłę poprzeczną. Ugięcie będzie wynosiło
v
x=M
*
x
.
(358)
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
30
We wzorze (358) M
*
oznacza właśnie wtórny moment zginający. Pewnego wyjaśnienia wymaga sprawa
jednostek wielkości, które są wykorzystywane w tej metodzie wyznaczania ugięć. Moment zginający będziemy
wyrażali w
[kNm ]
.
(359)
Moduł Younga będziemy wyrażali w
[
kPa
]
=
[
kN
m
2
]
.
(360)
Moment bezwładności będziemy wyrażali w
[
m
4
]
.
(361)
Ostatecznie jednostką krzywizny
κ
(x) będzie
[
kNm
kN
m
2
⋅m
4
]
=
[
kNm
kNm
2
]
=
[
1
m
]
.
(362)
Analizując wzór (357) dochodzimy do wniosku, że jednostką wtórnej siły poprzecznej będzie wielkość
bezwymiarowa. Analizując wzór (358) dochodzimy do wniosku, że jednostką wtórnego momentu
zginającego jest metr.
Obciążeniem wtórnym q
*
(x) nie możemy obciążać belki rzeczywistej, ponieważ nie byłyby spełnione warunki
brzegowe. Musimy obciążać belkę nazywaną belką fikcyjną. Tabela 7.2 przedstawia podpory w belce
rzeczywistej i odpowiadające im podpory w belce fikcyjnej.
Tabela 7.2. Podpory w belce rzeczywistej i fikcyjnej.
Belka rzeczywista
Belka fikcyjna
A
A
A
A
A
A
A
A
v
A
=0
A
≠0
M
A
*
=0
T
A
*
≠0
B
B
B
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
31
Belka rzeczywista
Belka fikcyjna
v
B
=0
B
L
=
B
P
B
L
≠0
B
P
≠0
M
B
*
=0
T
B
*(L)
=T
B
*(P)
T
B
*(L)
≠0
T
B
*(P)
≠0
B
B
B
v
B
≠0
B
L
≠
B
P
B
L
≠0
B
P
≠0
M
B
*
≠0
T
B
*(L)
≠T
B
*(P)
T
B
*(L)
≠0
T
B
*(P)
≠0
A
B
A
B
A
B
A
B
v
A
=0
A
=0
v
B
≠0
B
≠0
M
A
*
=0
T
A
*
=0
M
B
*
≠0
T
B
*
≠0
Rysunek 104 przedstawia przykładową belkę wraz z obciążeniami czynnymi i biernymi. Jest to jak widać
belka o zmiennej sztywności. Rysunek 105 przedstawia wykresy momentu zginającego dla tej belki. Rysunek
106 przedstawia przerobiony wykres momentu zginającego w przedziale AB. Rysunek 107 przedstawia belkę
fikcyjną. Rysunek 108 przedstawia obciążenie fikcyjne dla belki wtórnej. Należy pamiętać, że jeżeli moment
zginający rozciąga dolną część przekroju pręta to obciążenie wtórne działa w dół a jeżeli moment zginający
rozciąga górną część przekroju pręta to obciążenie wtórne działa do góry. Mając już belkę fikcyjną oraz
obciążenie wtórne należy wyznaczyć wartości i zwroty reakcji wtórnych. W następnej kolejności możemy
wyznaczyć wartości wtórnej siły poprzecznej i wtórnego momentu zginającego w charakterystycznych
punktach. Wtórna siła poprzeczna będzie się równała kątowi obrotu a wtórny moment zginający ugięciu.
q
a
b
A
B
C
V
A
V
B
E
⋅I
Z
1
E
⋅I
Z
2
P
M
0
Rys. 104. Belka.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
32
q
a
b
A
B
C
V
A
V
B
E
⋅I
Z
1
E
⋅I
Z
2
P
M(x)
M
0
M
0
P⋅
b
Rys. 105. Wykresy sił przekrojowych dla belki.
q
a
b
A
B
C
V
A
V
B
E
⋅I
Z
1
E
⋅I
Z
2
P
M(x)
M
0
M
0
P⋅
b
M(x)
a
2
a
2
q
⋅a
2
8
M(x)
0,0
0,0
Rys. 106. Przerobiony wykres momentu zginającego w przedziale AB.
A
B
C
a
b
Rys. 107. Belka fikcyjna.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
33
a
2
a
2
A
B
C
a
b
P
⋅b
E
⋅I
Z
1
P
⋅b
E
⋅I
Z
2
M
0
E
⋅I
Z
1
q
⋅a
2
8
⋅E⋅I
Z
1
Rys. 108. Obciążenie wtórne belki fikcyjnej.
24 Stateczność
Wyboczenie pręta ściskanego osiowo jest jednym z przykładów utraty stateczności układu sprężystego.
W przypadku wyboczenia zniszczenie pręta następuje nie poprzez przekroczenie wytrzymałości na ściskanie
lecz poprzez zmianę jego kształtu i związanej z tym zmiany charakteru stanu naprężenia w pręcie. Siłę, przy
której będzie następowało zjawisko wyboczenia nazywamy siłą krytyczną. Siła krytyczna będzie funkcją
parametru, który nazywamy smukłością czyli
P
KR
= f
.
(363)
Zamiast siły krytycznej możemy także operować naprężeniem krytycznym, które wynosi
KR
=
P
KR
A
,
(364)
w którym A oznacza pole powierzchni przekroju pręta. Naprężenie krytyczne jest także funkcją smukłości
KR
=g
.
(365)
Smukłość wyznacza się ze wzoru
=
L
W
i
,
(366)
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
34
L
P
KR
L
P
KR
L
P
KR
L
P
KR
a)
b)
c)
d)
L
W
= L
L
W
=2⋅L
L
W
=0,7⋅L
L
W
=0,5⋅L
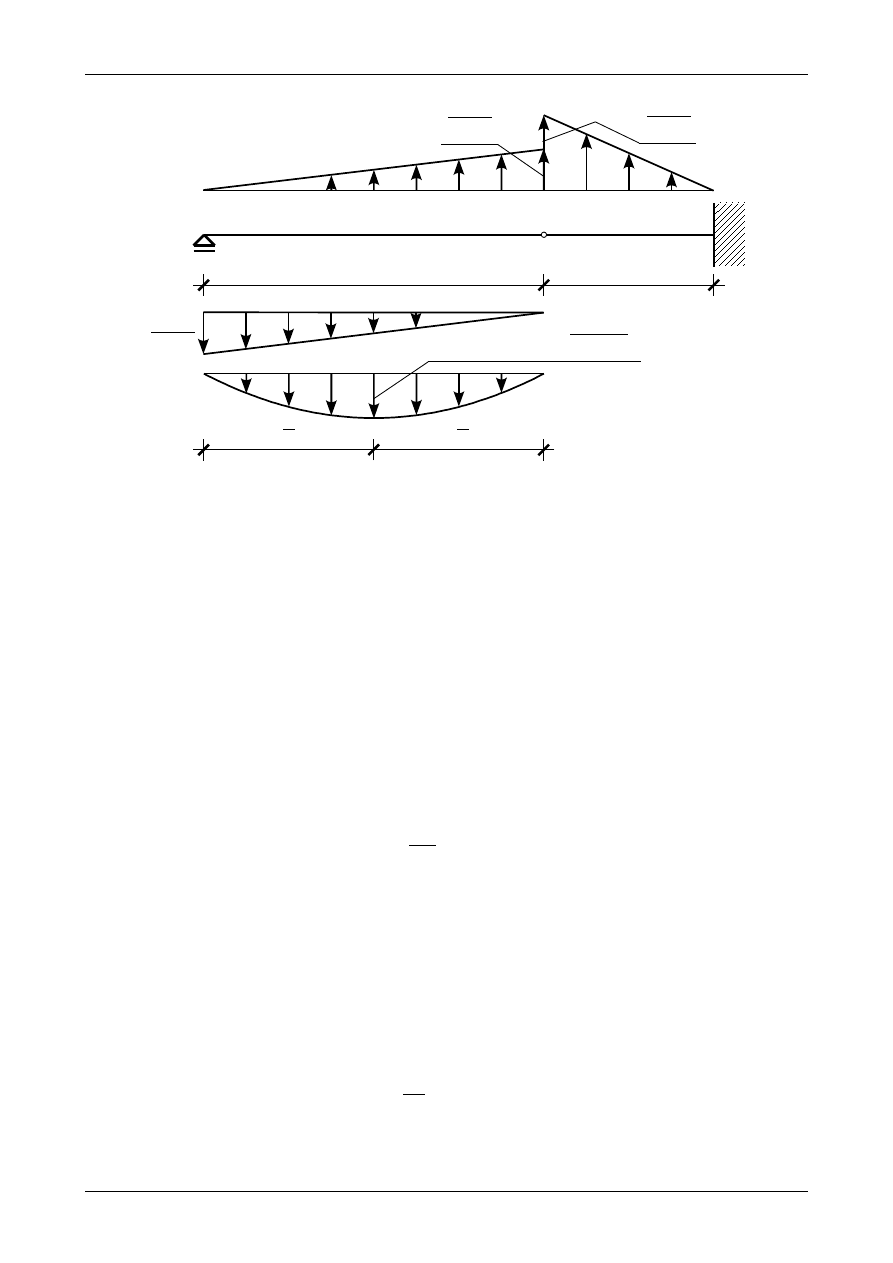
Rys. 109. Długości wyboczeniowe dla różnego rodzaju zamocowania pręta.
w którym L
W
jest tak zwaną długością wyboczeniową pręta. Rysunek 109 przedstawia cztery różne sposoby
zamocowania pręta i odpowiadające im długości wyboczeniowe. Natomiast
i
=
I
A
(367)
nazywa się promieniem bezwładności.
Smukłością graniczną nazywamy wyrażenie
GR
=⋅
E
SP
,
(368)
w którym E jest modułem Younga materiału, z którego wykonany jest pręt natomiast
σ
SP
oznacza granicę
sprężystości dla materiału, z którego wykonany jest pręt.
Jeżeli smukłość pręta jest mniejsza niż smukłość graniczna to mówimy, że pręt pracuje w zakresie
sprężysto-plastycznym. W zakresie tym największym naprężeniem normalnym jest granica plastyczności
σ
PL
, którą uznajemy jako naprężenie normalne, które powoduje zniszczenie pręta. W zakresie tym będziemy
przyjmować liniową zależność pomiędzy normalnym naprężeniem krytycznym a smukłością. Prostą tę nazywa
się prostą Tetmajera-Jasińskiego. Będzie ona miała równanie
KR
=
PL
−
PL
−
SP
GR
⋅
,
(369)
w którym
σ
PL
jest granicą plastyczności,
σ
SP
jest granicą sprężystości,
λ
GR
jest smukłością graniczną,
λ
jest
smukłością pręta.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
35
Jeżeli smukłość pręta jest większa niż smukłość graniczna to mówimy, że pręt pracuje w zakresie
sprężystym. Siłę krytyczną wyznacza się wtedy ze wzoru Eulera, który ma postać
P
KR
=
2
⋅E⋅I
L
W
2
,
(370)
w którym I oznacza mniejszy główny moment bezwładności.
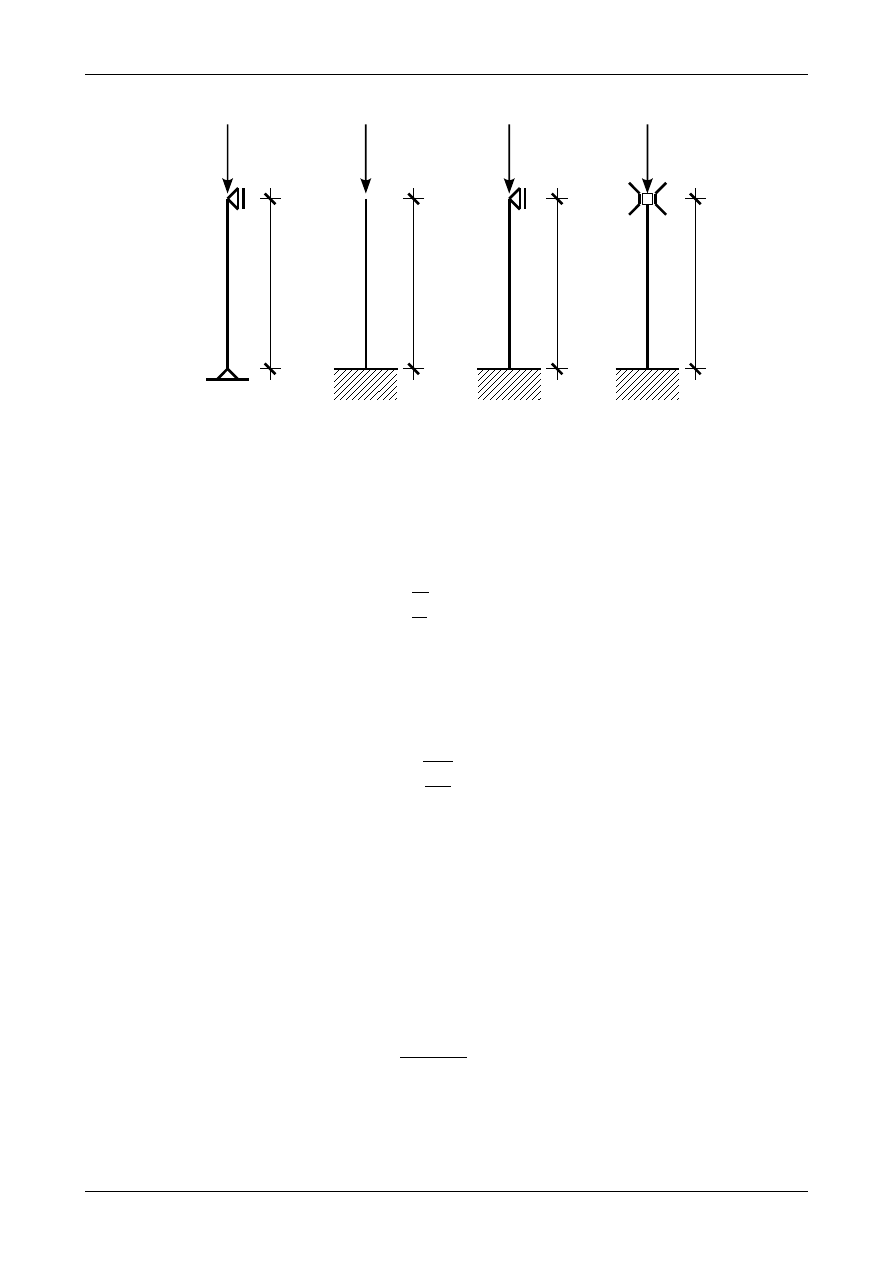
Wykres zależności pomiędzy naprężeniem krytycznym a smukłością przedstawia rysunek 110. Rysunek 111
przedstawia postacie wyboczeniowe kilku wybranych prętów. Postacie te są oczywiście zgodne z warunkami
brzegowymi występującymi na podporach.
KR
Zakres sprężysty
SP
GR
PL
KR
=
PL
−
PL
−
SP
GR
⋅
Zakres sprężysto-plastyczny
P
KR
=
2
⋅E⋅I
L
W
2
Rys. 110. Wykres zależności pomiędzy naprężeniem krytycznym i smukłością.
L
P
KR
L
P
KR
L
P
KR
L
P
KR
a)
b)
c)
d)
Rys. 111. Postacie wyboczeniowe.
Dr inż. Janusz Dębiński
BZZ
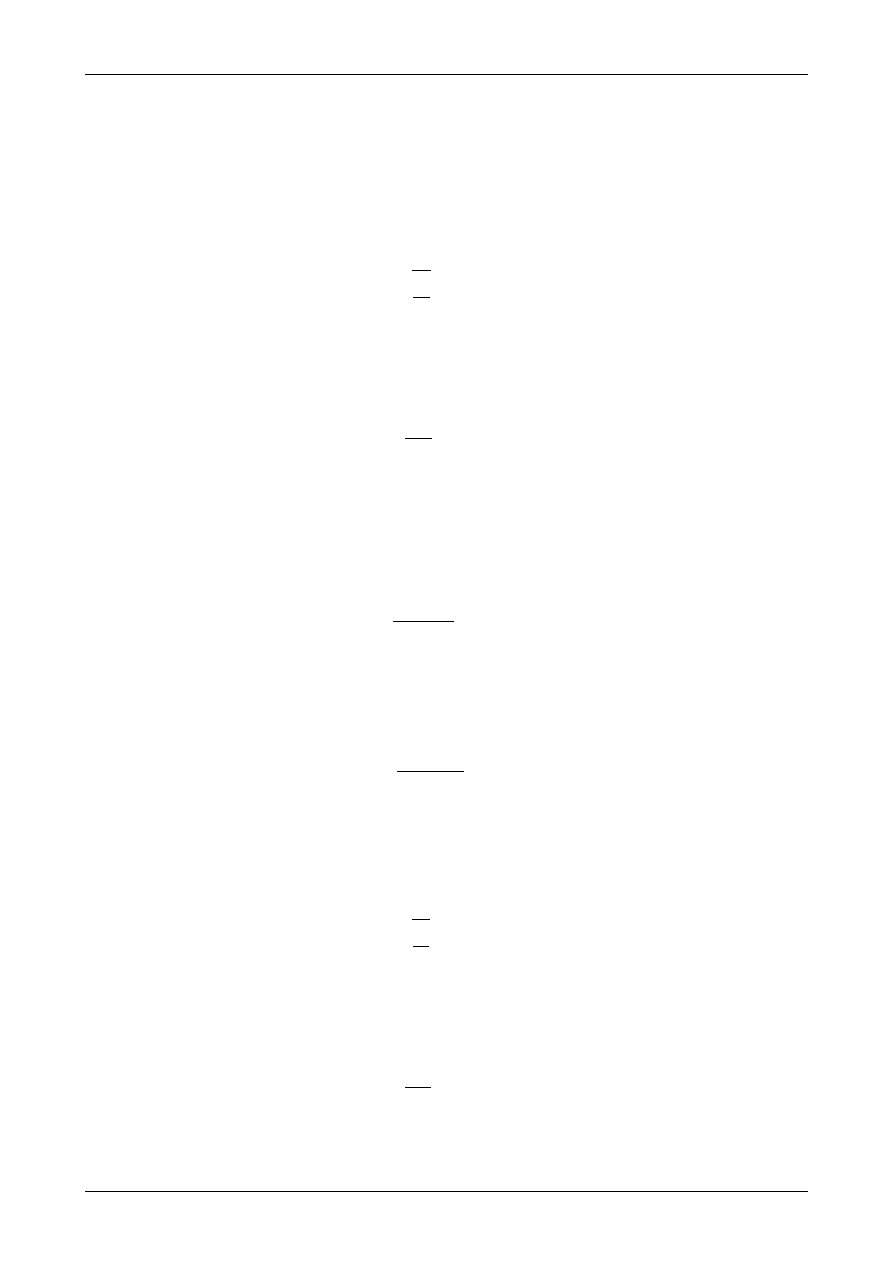
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
36
Wzory (366), (367), (369) i (370) obowiązują wtedy, gdy pręt jest podparty w ten sam sposób w obu
płaszczyznach pokrywających się z głównymi osiami bezwładności.
Jeżeli pręt jest podparty w różny sposób w płaszczyznach pokrywających się z głównymi osiami bezwładności
to nie da się od razu powiedzieć, w której płaszczyźnie nastąpi wyboczenie. Musimy więc sprawdzić
wyboczenie w obu płaszczyznach.
W płaszczyźnie XY (prostopadłej do osi Z=Z
gl
) musimy wyznaczyć promień bezwładności ze wzoru
i
Z
=
I
Z
A
.
(371)
następnie wyznaczamy smukłość pręta w tej płaszczyźnie ze wzoru
Z
=
L
W
Z
i
Z
,
(372)
w którym L
W
(Z)
jest długością wyboczeniową pręta w tej płaszczyźnie zależną od sposobu jego podparcia.
Smukłość pręta porównujemy ze smukłością graniczną i jeżeli pręt pracuje w zakresie sprężystym to siłę
krytyczną wyznaczamy ze wzoru
P
KR
=
2
⋅E⋅I
Z
L
W
Z
2
(373)
lub jeżeli pracuje w zakresie sprężysto-plastycznym to normalne naprężenie krytyczne wyznaczamy ze wzoru
KR
=
PL
−
PL
−
SP
GR
⋅
Z
.
(374)
Następnie wyznaczamy siłę krytyczną ze wzoru (364).
W płaszczyźnie XZ (prostopadłej do osi Y=Y
gl
) musimy wyznaczyć promień bezwładności ze wzoru
i
Y
=
I
Y
A
.
(375)
następnie wyznaczamy smukłość pręta w tej płaszczyźnie ze wzoru
Y
=
L
W
Y
i
Y
,
(376)
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
37
w którym L
W
(Y)
jest długością wyboczeniową pręta w tej płaszczyźnie zależną od sposobu jego podparcia.
Smukłość pręta porównujemy ze smukłością graniczną i jeżeli pręt pracuje w zakresie sprężystym to siłę
krytyczną wyznaczamy ze wzoru
P
KR
=
2
⋅E⋅I
Y
L
W
Y
2
(377)
lub jeżeli pracuje w zakresie sprężysto-plastycznym to normalne naprężenie krytyczne wyznaczamy ze wzoru
KR
=
PL
−
PL
−
SP
GR
⋅
Y
.
(378)
Następnie wyznaczamy siłę krytyczną ze wzoru (364). Jako siłę krytyczną przyjmujemy mniejszą z
wartości obliczonych dla obu płaszczyzn.
L
P
a
δ
L
a
Przed przyłożeniem
siły osiowej
Po przyłożeniu
siły osiowej
Rys. 112. Przemieszczenia pręta ściskanego osiowo ze wstępną imperfekcją.
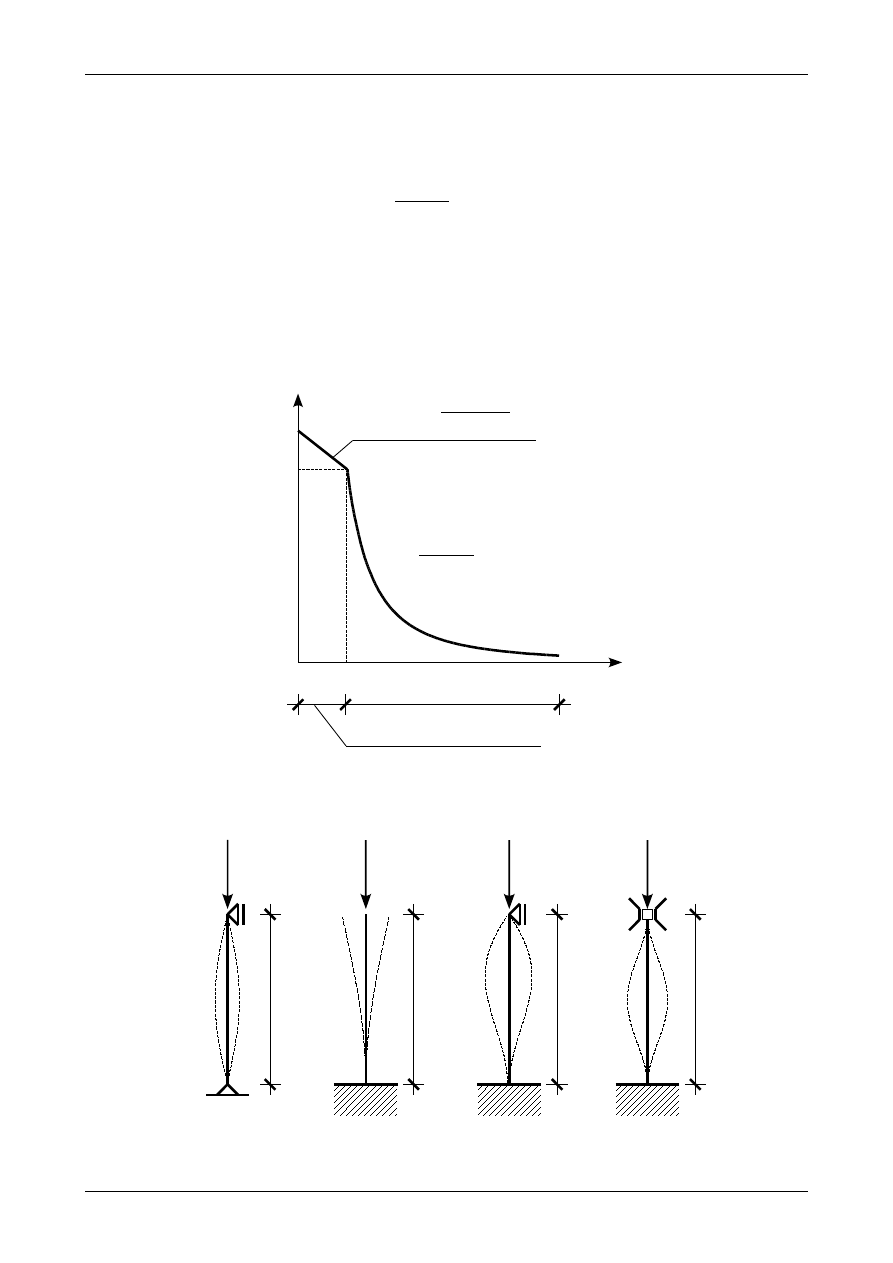
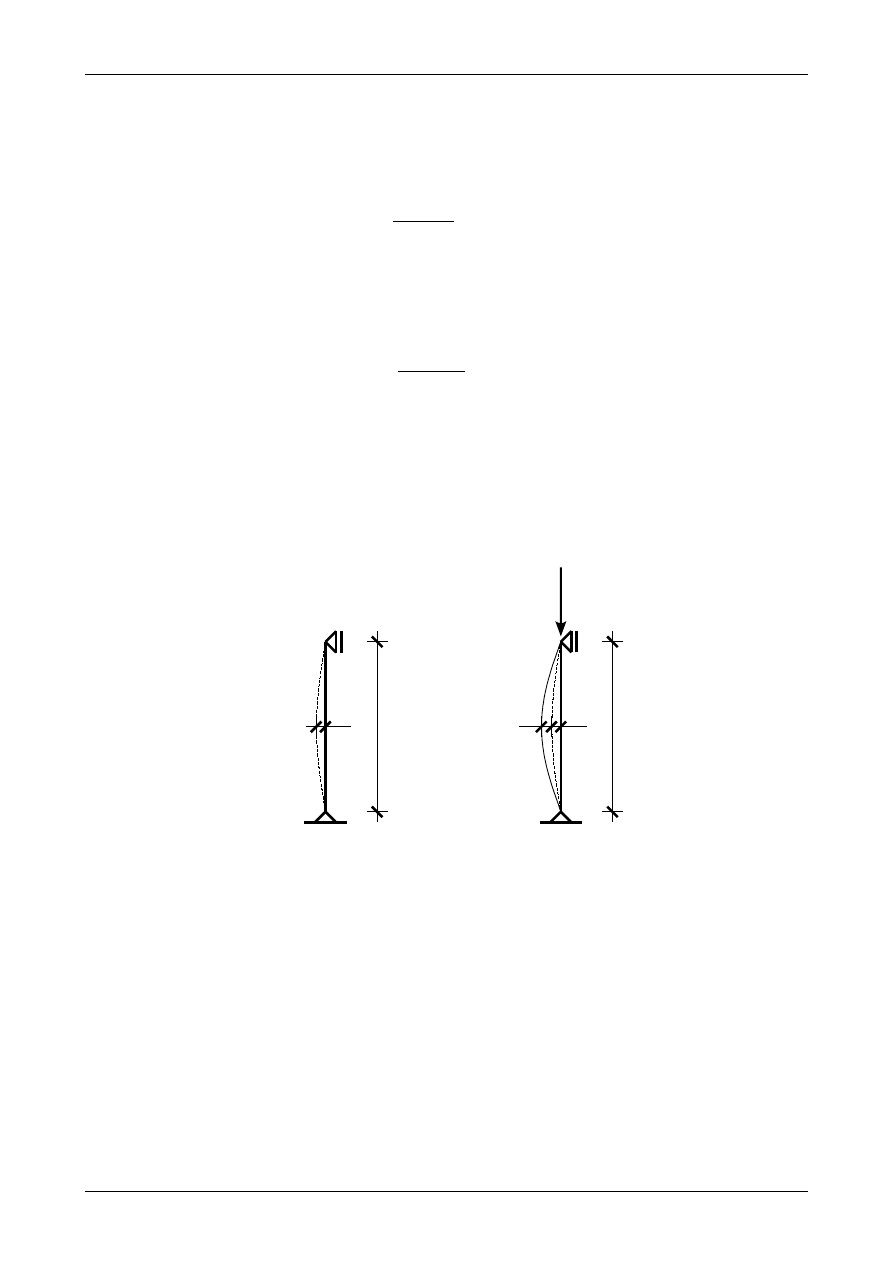
Siłę krytyczną dla pręta osiowo ściskanego wyznacza się doświadczalne metodą Southwella. Metoda ta
jest ograniczona tylko do prętów, które pracują w zakresie sprężystym. Metoda ta polega na pomiarze ugięcia
punktu znajdującego się w środku pręta. Rysunek 112 przedstawia pręt, który posiada już wstępne ugięcie
nazywane wstępną imperfekcją o wielkości a. Poprzez przyłożenie siły osiowej P środek pręta przemieści się
o wielkość ugięcia
δ
. Znając wielkości siły P oraz odpowiadające im przemieszczenia
δ
możemy wyznaczyć
siłę krytyczną dla pręta zaznaczając punkty doświadczalne w układzie współrzędnych, w którym na osi
odciętych zaznaczamy iloraz przemieszczenia
δ
przez siłę osiową P natomiast na osi rzędnych zaznaczamy
przemieszczenia
δ
. Punkty te będą tworzyć linię prostą pokazaną na rysunku 113. Krzyżykami zostały
zaznaczone punkty doświadczalne. Okazuje się, że prosta ta przecina oś rzędnych w punkcie, który odpowiada
wstępnej imperfekcji a. Natomiast
tg
=P
KR
.
(379)
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
38
P
+
+
+
+
+
+
+
=
P
KR
⋅
P
−
a
a
α
Rys. 113. Interpretacja wykresy otrzymanego metodą Southwella.
25 Tensometria elektrooporowa
Tensometrem elektrooporowym nazywa się czujnik, który zmienia swoją rezystancję wraz ze zmianą
swoich wymiarów, wykorzystywany do zmiany wielkości nieelektrycznej (odkształcenia) na elektryczną jaką
jest rezystancja. Stosuje się go do wyznaczania odkształceń różnego rodzaju materiałów budowlanych jak na
przykład beton i skały naturalne, metale, drewno, gips. Znając wielkość odkształcenia oraz wykorzystując
związki fizyczne możemy określić stan naprężenia panujący na powierzchni badanego elementu. Jak więc
widać za pomocą tensometrów możemy określić tylko składowe płaskiego stanu naprężenia na
powierzchni elementu.
Opór elektryczny przewodnika w formie drutu można wyrazić za pomocą wzoru
R
=⋅
l
A
,
(380)
w którym l oznacza długość przewodnika, A oznacza jego pole powierzchni natomiast
ρ
oznacza opór
właściwy materiału, z którego wykonano przewodnik. W celu wyznaczenia odkształceń stosuje się wzór
R
R
=K⋅
,
(381)
w którym
∆
R oznacza zmianę rezystancji pod wpływem zmiany długości tensometru, R oznacza rezystancję
początkową,
ε
oznacza odkształcenie, któremu uległ badany element. We wzorze (381) K oznacza stałą
nazywaną stałą tensoczułości, która jest wielkością charakterystyczną dla danego tensometru
elektrooporowego.
Dr inż. Janusz Dębiński
BZZ
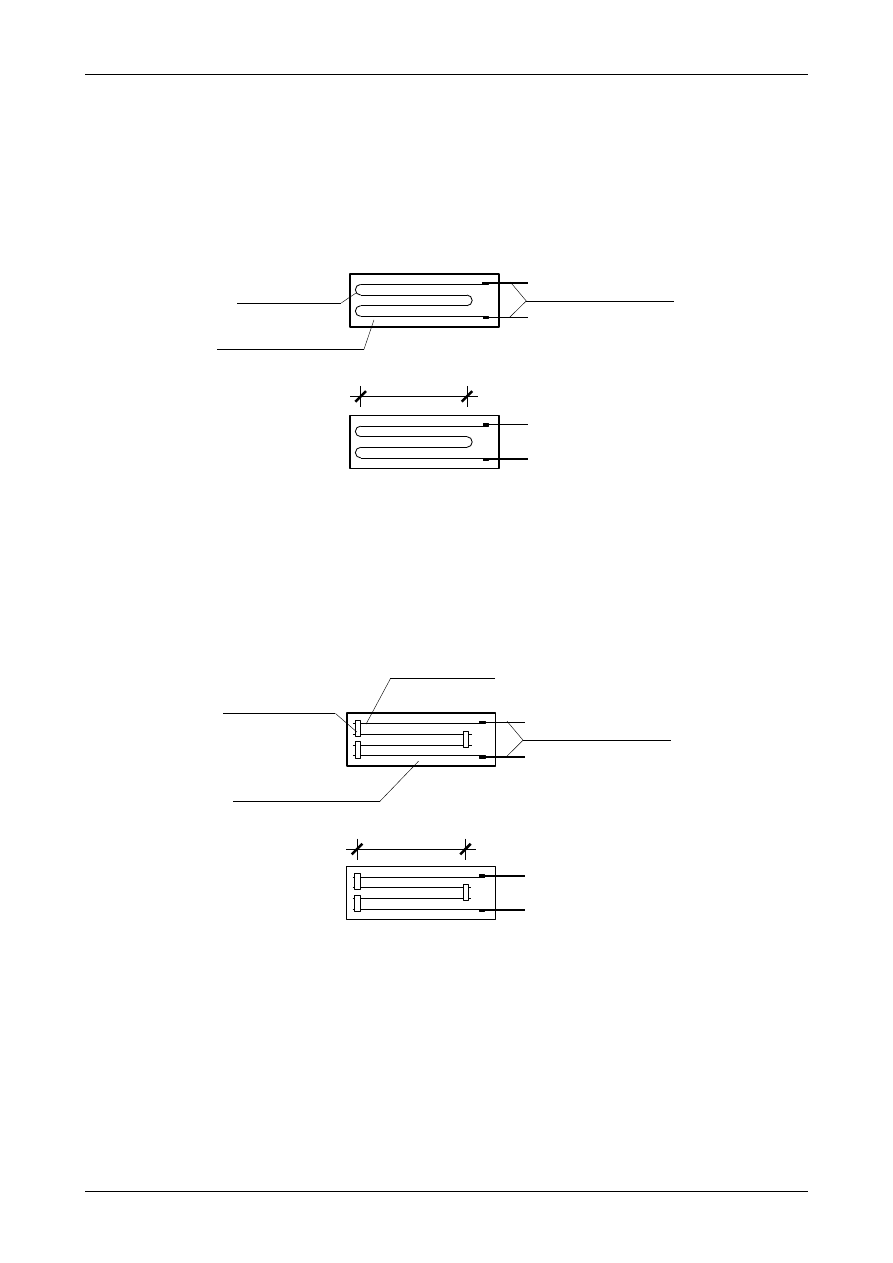
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
39
Pierwszym rodzajem tensometru elektrooporowego jest tensometr wężykowy. Składa się on z szeregu
równoległych drucików o grubości około 0,025 mm uformowanych w postaci wielokrotnego wężyka. Drucik
ten jest naklejony specjalnym klejem na cienki papier lub folię. Dopływ prądu odbywa się za pomocą
grubszych drutów doprowadzających. Całość jest od góry przykryta naklejonym paskiem papieru lub folii
mającym na celu ochronę tensometru przed wpływem czynników zewnętrznych. Tensometr taki nakleja się na
odpowiednio spreparowaną powierzchnię badanego elementu. Schemat tensometru wężykowego oraz jego
długość pomiarową (L) nazywaną bazą tensometru przedstawia rysunek 114.
drut pomiarowy
podstawa tensometru
druty doprowadzające
L
Rys. 114. Tensometr wężykowy.
Drugim rodzajem tensometru elektrooporowego jest tensometr kratowy. Budowa tego tensometru
przypomina tensometr wężykowy. Różnica występuje w budowie drucików pomiarowych. W tensometrze
kratowym są to pojedyncze druciki, które są połączone nalutowanymi lub napawanymi, znacznie grubszymi,
odcinkami taśmy metalowej. Schemat tego tensometru oraz jego bazę przedstawia rysunek 115.
drut pomiarowy
podstawa tensometru
druty doprowadzające
taśma metalowa
L
Rys. 115. Tensometr kratowy.
Tensometr kratowy eliminuje główną wadę tensometrów wężykowych, w których to zastosowanie jednego
rodzaju drucika powodowało, że tensometr ten mierzył także odkształcenia w kierunku poprzecznym do
głównego kierunku pomiaru. W tensometrze kratowym poprzeczne elementy są znacznie grubsze niż drucik
pomiarowy i zmiany oporu tego elementu spowodowane jego odkształceniem są mniejsze niż błąd pomiarowy.
Przedstawione w poprzednim punkcie tensometry wężykowe i kratowe używane są aktualnie coraz rzadziej.
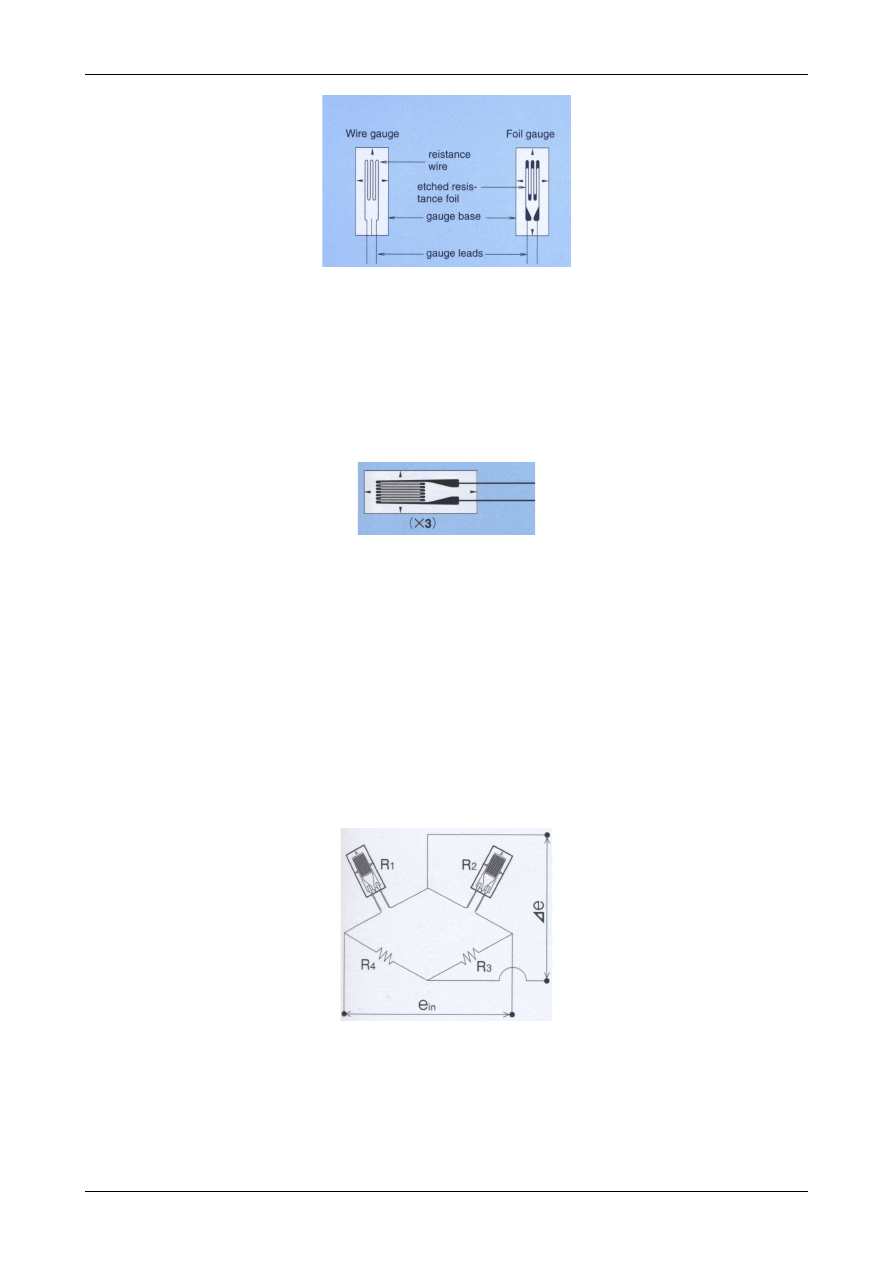
Najczęstszą grupą tensometrów stosowanych obecnie są tensometry foliowe. Rysunek 116 przedstawia
porównanie budowy tensometry wężykowego (wire gauge) i tensometru foliowego (foil gauge).
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
40
Rys. 116. Porównanie tensometru wężykowego i foliowego.
W obu typach tensometrów mamy warstwę folii jako podłoże (gauge base). W tensometrze wężykowym do
pomiaru służy drucik (resistance wire) natomiast w tensometrze foliowym do pomiaru służy warstwa
wytrawionej folii przewodzącej (etched resistance foil). Oba typy tensometrów łączy się z aparaturą
pomiarową za pomocą drutów doprowadzających (gauge leads). Na rysunku 117 przedstawiony jest
przykładowy tensometr foliowy.
Rys. 117. Przykładowy tensometr foliowy.
Zasada pomiaru odkształceń za pomocą tensometrów elektrooporowych polega na pomiarze zmian rezystancji
(oporu). Ponieważ mierzone odkształcenia są wielkościami bardzo małymi to zmiany rezystancji będą także
bardzo małe. Dlatego bezpośredni pomiar oporu jest w tym przypadku nieprzydatny. Do pomiaru bardzo
małych zmian rezystancji stosuje się mostek Wheatstone'a. Do dwóch punktów zostaje przyłożone napięcie
e
in
natomiast między innymi dwoma punktami następuje pomiar zmian napięcia
∆
e. Aby skompensować
zmiany temperatury należy zamiast opornika R
2
włączyć tensometr nazywany tensometrem
kompensacyjnym. Tensometr kompensacyjny musi się znajdować na nieobciążonej części konstrukcji, na
której dokonywany jest pomiar. Tensometr pomiarowy i kompensacyjny będą się w taki sam sposób
odkształcały w zależności od zmian temperatury. Układ pomiarowy z tensometrem kompensacyjnym
przedstawia rysunek 118.
Rys. 118. Mostek Wheatstone'a z tensometrem kompensacyjnym.
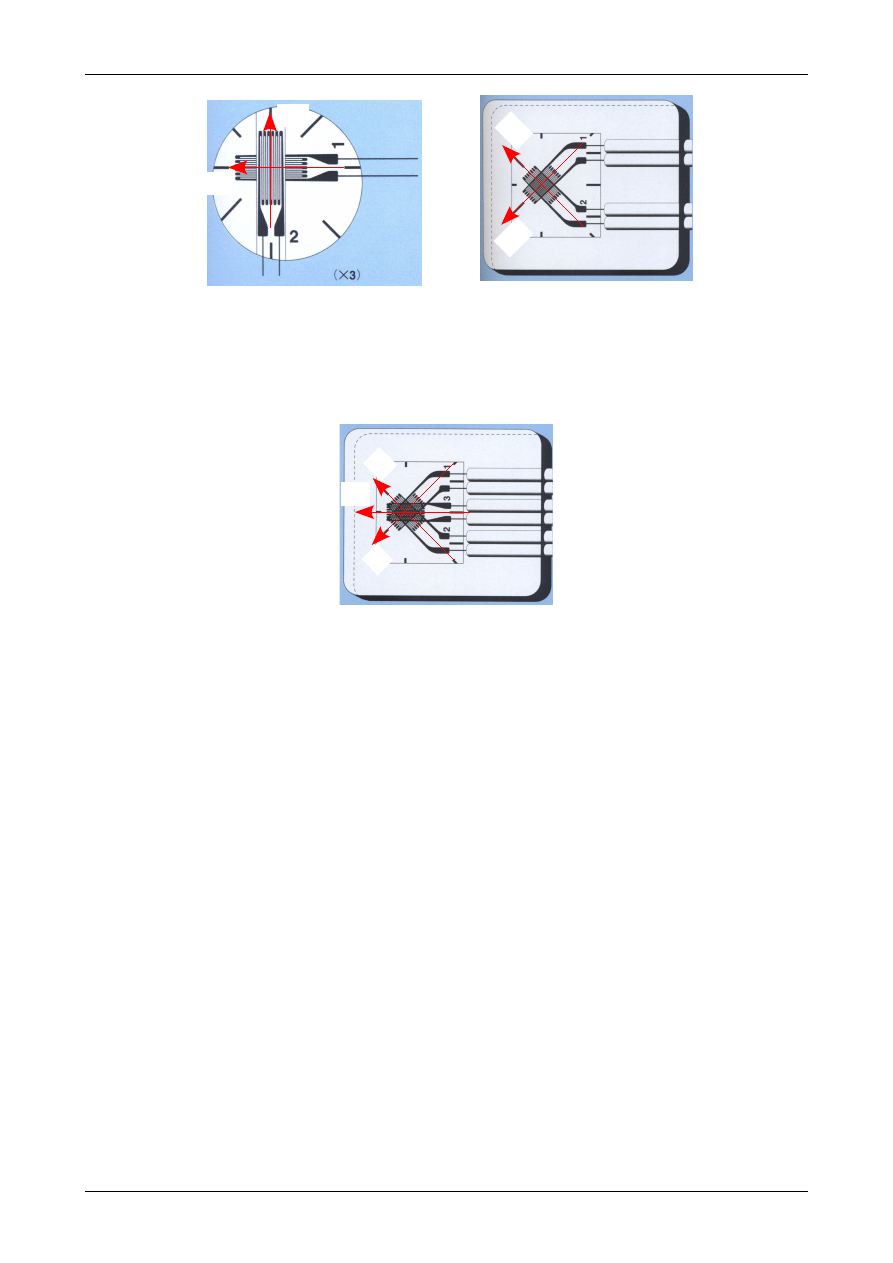
Aby móc mierzyć odkształcenia w kilku kierunkach jednocześnie należy zastosować rozety tensometryczne.
Jeżeli znamy kierunki odkształceń głównych zastosujemy rozetę prostokątną składającą się z dwóch
tensometrów, z których każdy będzie mierzył jedno z odkształceń głównych. Rozety takie przedstawia rysunek
119.
Dr inż. Janusz Dębiński
BZZ
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
41
Xgl
Ygl
Xgl
Ygl
Rys. 119. Rozety tensometryczne prostokątne.
Jeżeli nie znamy kierunków odkształceń głównych to musimy zmierzyć odkształcenia w trzech kierunkach. Do
tego celu służy rozeta tensometryczna przedstawiona na rysunku 120.
I
II
III
Rys. 120. Rozeta tensometryczna do pomiaru odkształceń w trzech kierunkach.
26 Elastooptyka
Jako elastooptyka rozumiemy badania pozwalające na określenie rozkładu naprężeń w konstrukcjach,
których modele zostały wykonane z materiału optycznie czynnego. Pod pojęciem materiału czynnego
rozumiemy materiał, który ulega zjawisku dwójłomności wymuszonej. Zjawisko to jest związane z
zastosowaniem światła spolaryzowanego, dla którego drgania fali elektromagnetycznej odbywają się tylko w
jednej płaszczyźnie. Jeżeli światło spolaryzowane przepuścimy przez obciążony materiał wykazujący
dwójłomność wymuszoną to spolaryzowany promień rozdzieli się na dwa promienie, które mają różne
prędkości i drgające w płaszczyznach pokrywających się z kierunkami naprężeń głównych.
Przy tej metodzie obserwujemy dwa rodzaje linii. Pierwszą z nich są izochromy, które łączą punkty, w których
różnica naprężeń głównych ma wartość stałą. Parametrem charakteryzującym izochromę jest rząd izochromy.
Jest nim liczba naturalna od jeden do wartości wynikającej ze stanu naprężenia panującego w modelu.
Równanie izochromy ma postać
1
−
2
=K⋅m
,
(382)
w którym
σ
1
i
σ
2
są naprężeniami głównymi, m jest rzędem izochromy natomiast K jest stałą elastooptyczną
charakterystyczną dla materiału, z którego wykonany jest model. Rysunek 121 przedstawia przebieg izochrom
w modelu belki swobodnie podpartej obciążonej siłą skupioną w środku rozpiętości.
Drugim rodzajem linii są izokliny, które łączą punkty, w których naprężenia główne są nachylone pod tym
samym kątem. Parametrem charakteryzującym izoklinę jest parametr izokliny, który jest równy kątowi
nachylenia naprężeń głównych. Rysunek 122 przedstawia izoklinę o parametrze 20
o
w belce swobodnie
podpartej obciązonej siłą skupioną w środku.
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
42
m=1
m=2
m=3
m=4
m=1
m=2
m=3
m=4
Rys. 121. Przebieg izochrom w modelu belki swobodnie podpartej.
Rys. 122. Izoklina o parametrze 20
0
.
Znając przebieg izochrom i izoklin jesteśmy w stanie określić stan naprężenia w modelu konstrukcji a
następnie stosując podobieństwo modelowe możemy określić stan naprężenia w rzeczywistej konstrukcji.
27 Młotek Schmidta
Jest to najczęściej wykorzystywaną metodą nieniszczącego badania betonu. Pozwala ona na określenie
wytrzymałości betonu na ściskanie na podstawie pomiaru twardości powierzchniowej warstwy betonu
(grubości od 3 do 10 cm).
Wytrzymałość jest miarodajna, jeśli grubość elementu nie przekracza:
1. 20 cm – przy dostępie jednostronnym,
2. 40 cm – przy dostępie dwustronnym,
60 cm – przy dostępie co najmniej z trzech stron.
Typy młotków Schmidta:
1. N – średni (normalny),
2. M – ciężki (masywny),
3. L – lekki,
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
43
4. P – wahadłowy.
Przykładowe młotki przedstawiają rysunki 123 i 124.
Rys. 123. Młotek Schmidta.
Rys. 124. Wahadłowy młotek Schmidta.
Sposób przeprowadzenia pomiaru składa się z następujących czynności
1. młotek ustawić prostopadle do badanej powierzchni i powoli naciskać,
2. nacisk powoduje cofnięcie się masy uderzeniowej i naciągnięcie sprężyny uderzeniowej. (Cofnięcie się
masy powoduje automatyczne zwolnienie i uderzenie w trzpień. Po uderzeniu masa odskakuje na
pewien odcinek, rejestrowany za pomocą wskaźnika),
3. odczyt na skali - liczba odbicia L,
4. następnie z odpowiedniej skali w zależności od liczby pokazanej na skali wyznaczyć wytrzymałość
betonu.
Dr inż. Janusz Dębiński
BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚC 3
44
Badanie należy przeprowadzać co najmniej w 12 miejscach w elemencie wykonanym z jednej partii betonu. W
elementach prefabrykowanych dopuszcza się 6 miejsc. W każdym badanym miejscu należy wykonać
przynajmniej 5 odczytów.
Dr inż. Janusz Dębiński
BZZ
Document Outline
- 21 Pręty zginane i ścinane
- 22 Mimośrodowe działanie siły
- 23 Ugięcia
- 24 Stateczność
- 25 Tensometria elektrooporowa
- 26 Elastooptyka
- 27 Młotek Schmidta
Wyszukiwarka
Podobne podstrony:
podstawy teorii part one bzz v1 07 02 06
podstawy teorii part two bzz v1 07 02 06
podstawy teorii part one bzz v1 07 02 06
Wyniki kolokwium ze statystyki matematycznej i teorii estymacji z dn 07.02.13
07 Rozdział 06 Wiadomości podstawowe z teorii funkcji zmiennej rzeczywistej
07 Rozdział 06 Wiadomości podstawowe z teorii funkcji zmiennej rzeczywistej
PODSTAWY TEORII ORGANIZACJI I ZARZĄDZANIA Konwersatorium 1
podstawy teorii przedsiębiorstwa zaoczni
Podstawy Teorii Okretow Pytania nr 4 (20) id 368475
07-02 PAM-Dostęp do Waszego Makro-Ducha i do Waszej Świadomości, ezoteryka
podstawy teorii i diagnozy logopedycznej
Podstawy teorii przeżywalności
racjonalista Dwa spojrzenia na jednostkę w systemie totalitarnym, I rok Politologia, Podstawy Teorii
Pluralizacja kultury i rozwój audiowizualności, Podstawy teorii kultury
więcej podobnych podstron