POLITECHNIKA GDAŃSKA

WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI

KATEDRA ENERGOELEKTRONIKI I MASZYN ELEKTRYCZNYCH

LABORATORIUM

M A S Z Y N Y E L E K T R Y C Z N E

ĆWICZENIE (MI)

MASZYNY INDUKCYJNE/ASYNCHRONICZNE TRÓJFAZOWE

BADANIE CHARAKTERYSTYK:

BIEGU JAŁOWEGO i ZWARCIA

Materiały pomocnicze

Kierunek Elektrotechnika
Studia stacjonarne 1-szego stopnia
semestr 3

Opracował

Mieczysław Ronkowski

Grzegorz

Kostro

Michał Michna

Gdańsk 2011-2012

M. Ronkowski, G. Kostro, M. Michna:

2

ĆWICZENIE (MI)

MASZYNY INDUKCYJNE/ASYNCHRONICZNE TRÓJFAZOWE
BADANIE CHARAKTERYSTYK: BIEGU JAŁOWEGO i ZWARCIA

Program ćwiczenia

• Pomiar rezystancji uzwojeń.
• Pomiar charakterystyki biegu jałowego.
• Pomiar charakterystyki stanu zwarcia (wirnik nieruchomy).

1.

TEORIA

1.1. Budowa, działanie i model fizyczny maszyny indukcyjnej

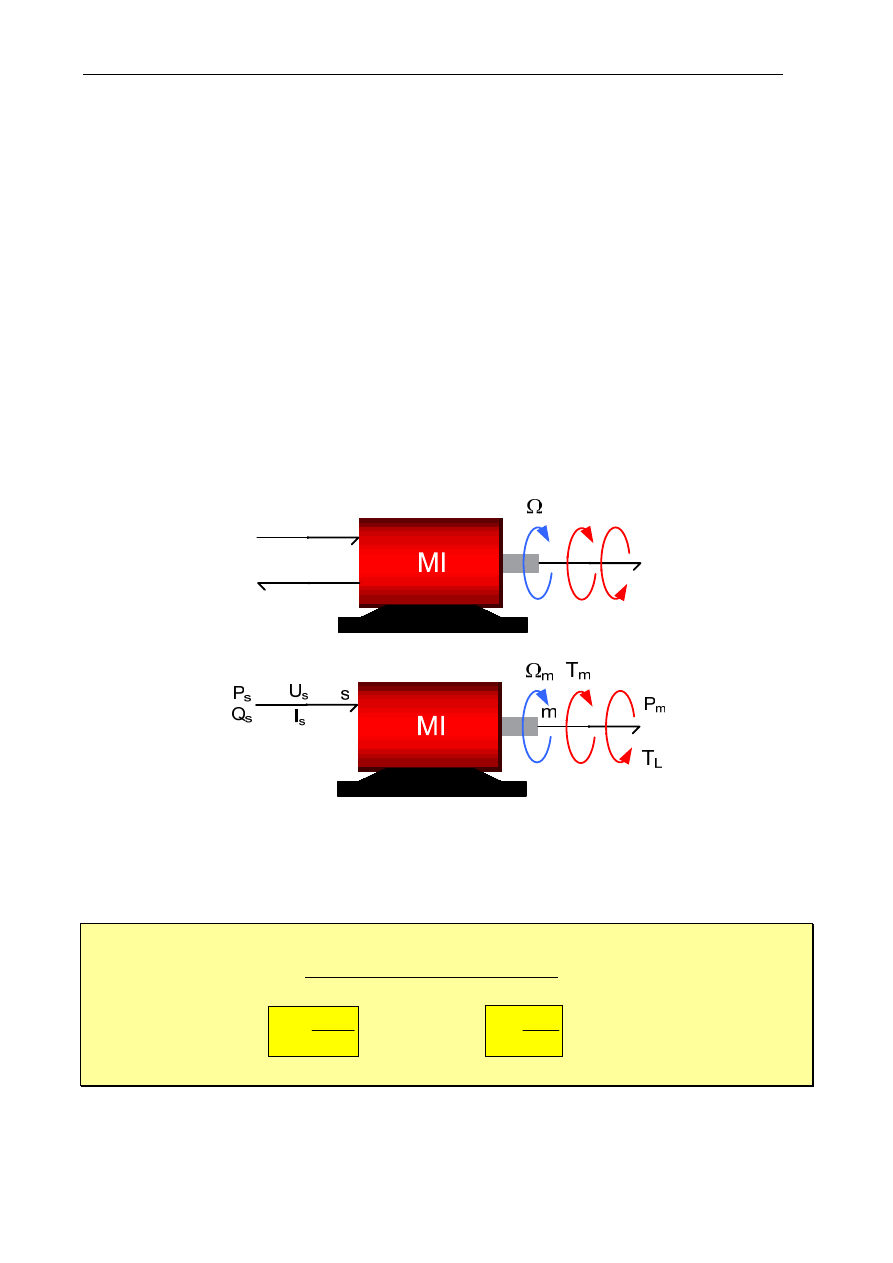
Maszyna indukcyjna/asynchroniczna (MI) jest przetwornikiem elektromechanicznym (rys. 1.1) o

trzech wrotach, które fizycznie reprezentują: „wejścia elektryczne” – zaciski uzwojenia stojana „s”;
„wyjścia/wejścia elektryczne” – zaciski uzwojenia wirnika „r”; „wyjście/wejście mechaniczne” – koniec
wału (sprzęgło) „m”. Moc elektryczna (dostarczana) P

s

i moc mechaniczna (odbierana) P

m

ulegają

przemianie elektromechanicznej za pośrednictwem pola magnetycznego. Energia pola magnetycznego jest
energią wewnętrzną maszyny, gdyż przetwornik nie ma możliwości wymiany tej energii z otoczeniem.

a)

T

m

m

P

s

P

r

P

m

s

r

m

Q

s

Q

r

T

L

U

s

I

s

U

s

I

s

b)

Rys. 1.1. Maszyna indukcyjna/asynchroniczna (strzałkowanie dla pracy silnikowej):

a) trójwrotowy przetwornik elektromechaniczny z wirnikiem pierścieniowym

b) dwuwrotowy przetwornik elektromechaniczny z wirnikiem klatkowym

wrota (zaciski) obwodu stojana „s” – dopływ energii elektrycznej przetwarzanej ma energię mechaniczną, wrota

obwodu wirnika „r” – odpływ energii do odbiornika lub sieci zasilającej,

wrota układu (obwodu) mechanicznego „m” – odpływ energii mechanicznej

Uwaga:

Działanie maszyny indukcyjnej/asynchronicznej oparte jest na wykorzystaniu idei pola o wirującym
strumieniu magnetycznym, wzbudzanym metodą elektromagnetyczną.

Prędkość wirowania pola wzbudnika/induktora określona jest wzorem:

p

f

e

s

2

π

Ω

=

[rad/s]

lub

p

f

n

e

s

60

=

[obr/min]

gdzie: f

e

– częstotliwość napięcia zasilania silnika, p – liczba par biegunów.

Budowę i podstawowe elementy MI przedstawiono na rys. 1.2. Maszyna składa się z następujących
elementów czynnych: stojana (rdzeń i uzwojenie 3-fazowe); wirnika (rdzeń i uzwojenie klatkowe lub
uzwojenie pierścieniowe – uzwojenie 3-fazowe połączone z pierścieniami ślizgowymi); wału. Stojan pełni
funkcję wzbudnika-induktora – prądy płynące w uzwojeniu stojana wzbudzają pole o wirującym strumieniu

Ćwiczenie: Maszyny indukcyjne trójfazowe

3

magnetycznym, który indukuje SEM w uzwojeniu wirnika. Natomiast wirniki pełni, w pewnym sensie,
funkcję twornika – indukowana w uzwojeniu wirnika SEM wymusza przepływ prądu, który oddziaływując z
polem stojana generuje moment elektromagnetyczny.

a) silnik indukcyjny klatkowy

b) uzwojenie wirnika – klatkowe (bez rdzenia)

c) uzwojenie wirnika – pierścieniowe (z rdzeniem)

d) tabliczka znamionowa silnika klatkowego

e) fabryczna tabliczka zaciskowa 3-fazowego

uzwojenia stojana połączonego w trójkąt (

Δ)

f) laboratoryjna tabliczka zaciskowa 3-fazowego

uzwojenia stojana połączonego w trójkąt (

Δ)

Rys. 1.2. Budowa i podstawowe elementy maszyny indukcyjnej/asynchronicznej

(produkcja firmy INDUKTA/CANTONI)

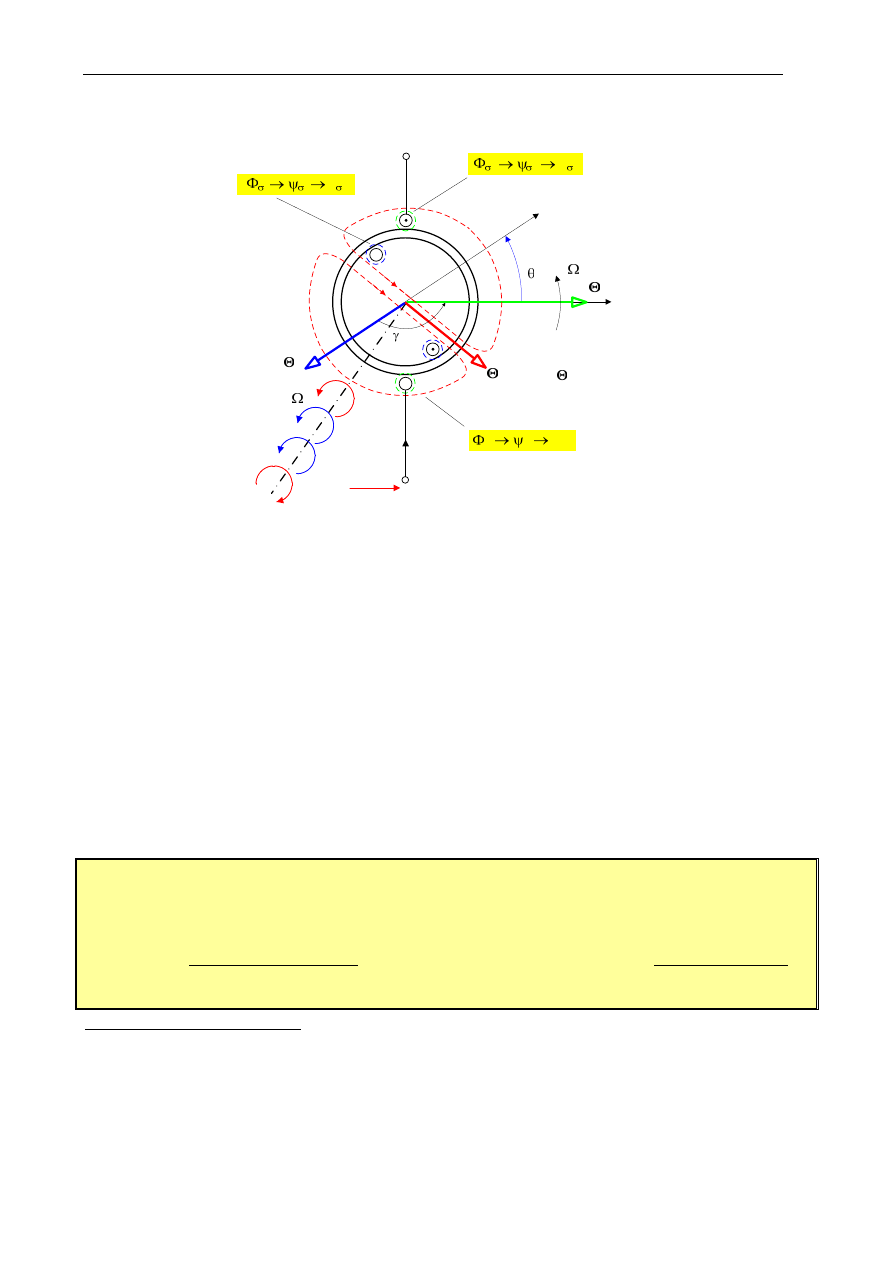
Na podstawowy model fizyczny silnika indukcyjnego pierścieniowego — pokazany na rys. 1.3 —

składają się: a) elementy czynne: wzbudnik-induktor (stojan), twornik (wirnik), wał; b) wielkości (zmienne)
fizyczne: napięcia fazowe U

s

na zaciskach uzwojeń, prądy fazowe I

s

oraz I

r

płynące w uzwojeniach, wirujący

z prędkością

Ω

s

strumień magnesujący (główny)

Φ

m

, strumienie rozproszenia uzwojeń

Φ

σ

s

oraz

Φ

σ

r

, moment

elektromagnetyczny (wewnętrzny) T

e

, moment obrotowy (zewnętrzny) T

m

, prędkość kątowa wirnika

Ω

m

,

moment obciążenia T

L

, straty w żelazie

Δ

P

Fe

, straty w uzwojeniach

Δ

P

Cus

oraz

Δ

P

Cur

, straty mechaniczne

(tarcia, wentylacyjne)

Δ

P

m

.

M. Ronkowski, G. Kostro, M. Michna:

4

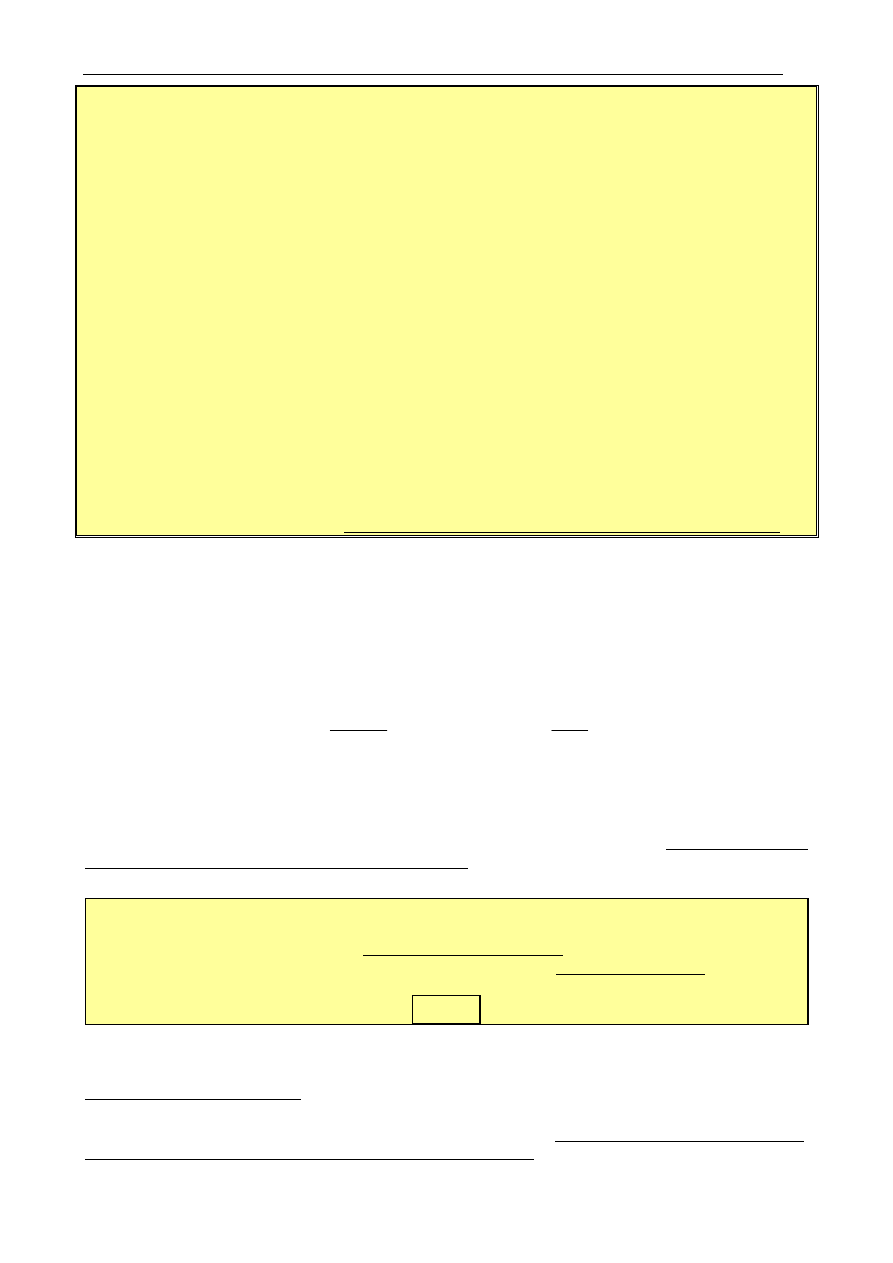
Aby zachować czytelność rysunku rys. 1.3, układ uzwojeń fazowych (pasm) stojana i wirnika

zaznaczono szkicowo tylko dla jednej fazy obwodami as-as' oraz ar-ar', przy czym litery as, ar oznaczają
umowne początki tych uzwojeń, a litery as', ar' — umowne końce

1)

.

as'

as

r

oś fazy as

oś fazy ar

s

s

L

s

ar

ar'

m

m

L

ms

r

r

L

r

T

e

T

L

m

s

+

+

i

as

u

as

+

_

s

m

r

0

lub

T

m

Rys. 1.3. Podstawowy model fizyczny wielofazowego silnika indukcyjnego pierścieniowego (liczba par biegunów p = 1)

Symetryczne prądy trójfazowe, płynące w uzwojeniach stojana, wytwarzają odpowiednio fazowe

(osiowe) przepływy pulsujące (siły magnetomotoryczne), które są skierowane zgodnie z osiami
magnetycznymi tych uzwojeń: np. oś magnetyczna as dla przepływu uzwojenia stojana as - as’. Osie
magnetyczne pozostałych faz są odpowiednio przesunięte w przestrzeni o kąt 2

π/3p (p - liczba par

biegunów).

Sumowanie geometryczne osiowych przepływów pulsujących stojana wywołuje w efekcie wirującą w

przestrzeni falę przepływu. Pierwsza harmoniczna tej fali – odwzorowana wektorem (fazorem
przestrzennym)

Θ

s

– wiruje w przestrzeni względem obserwatora na stojanie z prędkością kątową

Ω

s

= 2

π

f

e

/p (f

e

– częstotliwość napięcia zasilania uzwojeń stojana). Prędkość ta nazywaną jest zwykle prędkością

synchroniczną.

Wirujący przepływ stojana

Θ

s

wzbudza wirujący strumień, który przecinając przewody (pręty)

uzwojenia wirnika, indukuje w nich przemienne SEM rotacji, które wymuszają przy zamkniętym uzwojeniu
wirnika prądy fazowe. Prądy wirnika wytwarzają odpowiednio fazowe (osiowe) przepływy pulsujące.

Analogicznie jak w stojanie, sumowanie geometryczne osiowych przepływów pulsujących wirnika

wywołuje w efekcie wirującą w przestrzeni falę przepływu. Pierwszą harmoniczną tej fali odwzorowuje
wektor (fazor przestrzenny)

Θ

r

, wirujący z prędkością

Ω

s

= 2

π

f

e

względem obserwatora na stojanie.

Uwaga:

Interakcja wirujących pól magnetycznych stojana i wirnika, wzbudzanych przepływami

Θ

s

oraz

Θ

r

, generuje

moment elektromagnetyczny T

e

, który wymusza ruch obrotowy wirnika.

Należy zauważyć, że interakcja obu pól wynika z tendencji układu elektromagnetycznego stojana i wirnika
do wzbudzenia ekstremalnego strumienia, innymi słowy z tendencji do zgromadzenia ekstremalnej energii w
układzie (zasada minimalnej pracy – minimalnego działania).
Zatem wektory reprezentujące przepływy

Θ

s

oraz

Θ

r

będą dążyły do wzajemnego złożenia (pokrycia) się.

1) Zarówno uzwojenia stojana jak i wirnika są równomiernie rozmieszczone w żłobkach.

Uzwojenia stojana MI stanowią: trzy fazy (pasma) — osie magnetyczne poszczególnych faz są odpowiednio
względem siebie przesunięte w przestrzeni o kąt 120

0

(dla MI o liczbie par biegunów p>1 kąt wynosi 120

o

/p).

Analogicznie jest dla uzwojenia wirnika w wykonaniu pierścieniowym. W przypadku uzwojenia wirnika w
wykonaniu pierścieniowym liczba faz jest równa liczbie prętów klatki.
W opisie modelu MI, ze względów dydaktycznych, zastoswano oznaczenia: as-as’, bs-bs’, cs-cs’ dla stojana, ar-
ar’, br-br’, cr-cr’ dla wirnika, zamiast znormalizowanych: 1U1-1U2, 1V1-1V2, 1W1-1W2 dla stojana, 2U1-2U2,
2V1-2V2, 2W1-2W2 dla wirnika. Oznaczenia znormalizowane zastosowano na schematach układów pomiarowych.

Ćwiczenie: Maszyny indukcyjne trójfazowe

5

Możliwy jest tylko obrót wektora przepływu wirnika

Θ

r

w kierunku zgodnym z założonym na rys. 1.3

dodatnim zwrotem prędkości kątowej wirnika

Ω

m

(dla przyjętej konwencji odbiornikowej strzałkowania,

oznacza to zgodny zwrot momentu i prędkości – odpowiada to pracy silnikowej).

Przepływ wirnika

Θ

r

wiruje w przestrzeni względem obserwatora na wirniku z prędkością kątową równą

różnicy prędkości (

Ω

s

-

Ω

m

) — nazywaną zwykle bezwzględną prędkością poślizgu; natomiast względem

obserwatora na stojanie wiruję z prędkością kątową równą sumie prędkości: (

Ω

s

-

Ω

m

) +

Ω

m

=

Ω

s

.

To znaczy, że do prędkości poślizgu (

Ω

s

-

Ω

m

) należy dodać prędkość unoszenia przepływu wirnika

Θ

r

,

równą prędkości mechanicznej wirnika

Ω

m

.

Zatem przepływ wirnika

Θ

r

wiruje w przestrzeni względem obserwatora na stojanie z prędkością

kątową równą prędkości

Ω

s

.

Dla stanu ustalonego (brak składowych swobodnych) pracy silnika oznacza to, że przepływy stojana
Θ

s

i wirnika

Θ

r

, wirują synchronicznie

2)

.

W efekcie przepływy stojana

Θ

s

i wirnika

Θ

r

tworzą wspólny (wypadkowy) przepływ – nazywany zwykle

przepływem magnesującym, określonym sumą geometryczną:

Θ

s

+

Θ

r

=

Θ

m

(1.1)

Przepływ

Θ

s

wiruje z prędkością

Ω

s

(przy prędkości wirnika

Ω

m

≠ Ω

s

) i wzbudza strumień magnesujący

(główny)

Φ

m

.

Ze względu na ruch asynchroniczny strumienia

Φ

m

oraz rdzenia wirnika, maszyny indukcyjne nazywane są

także maszynami asynchronicznymi. Jest to zasadnicza cecha maszyn indukcyjnych/asynchronicznych.

Moment elektromagnetyczny T

e

zależy od kąta

γ (zwanego kątem momentu) między przepływami Θ

s

oraz

Θ

r

. Na rys. 1.3 pokazano schematycznie wzajemne, przestrzenne położenie kątowe osi fazy as-as’

uzwojenia stojana względem osi fazy ar-ar’ uzwojenia wirnika. Położenie to odpowiada chwili czasowej dla
której wartości prądów tych faz osiągają jednocześnie wartości maksymalne. Oznacza to, zgodnie z teorią
pola wirującego, że położenie wektorów wirujących przepływów stojana

Θ

s

i wirnika

Θ

r

jest zgodne z

osiami magnetycznymi fazy as-as’ i fazy ar-ar’.

W teorii maszyn indukcyjnych bezwzględną wartość prędkości poślizgu (

Ω

s

-

Ω

m

) odnosi się do

prędkości wirującego pola stojana, którą nazywa się poślizgiem względnym, albo po prostu poślizgiem:

s

s

m

s

=

−

Ω Ω

Ω

lub

s

ns n

ns

=

−

(1.2)

gdzie: n

s

oraz n – odpowiednio prędkość synchroniczna pola stojana i wirnika (mechaniczna) w

obr/min.

Tworzenie wspólnego przepływu magnesującego jest zjawiskiem analogicznym do magnesowania

transformatora (opisanego w ćw. Badanie transformatora), tzn. powstawania prądu magnesującego
wynikającego z sumy geometrycznej przepływu uzwojenia pierwotnego i wtórnego (uwaga: w przypadku
transformatora są to przepływy nieruchome w przestrzeni). Analogię tą wykorzystuje się w budowie modelu
obwodowego (schematu zastępczego) maszyny indukcyjnej.

Uwaga:
Analogia między transformatorem i MI dotyczy tylko tworzenia wspólnego przepływu magnesującego. W
transformatorze prąd pierwotny i wtórny mają jednakową częstotliwość. Natomiast w MI, przy stałej
częstotliwości prądu stojana (pierwotnego), prąd wirnika (wtórny) ma częstotliwość zmienną, która zależy
od prędkości poślizgu (obciążenia).

e

r

f

s

f

=

2)

Jest to podstawowy warunek generacji momentu o stałym kierunku i zwrocie — momentu o średniej wartości różnej

od zera. Zgodnie z zasadą pracy (prawem sterowania) maszyn elektrycznych: maszyna elektryczna jest układem dwóch
pól magnetycznych o osiach nieruchomych względem siebie w przestrzeni. Poszczególne typy maszyn elektrycznych
różnią się tylko sposobem sterowania położeniem tych pól.

M. Ronkowski, G. Kostro, M. Michna:

6

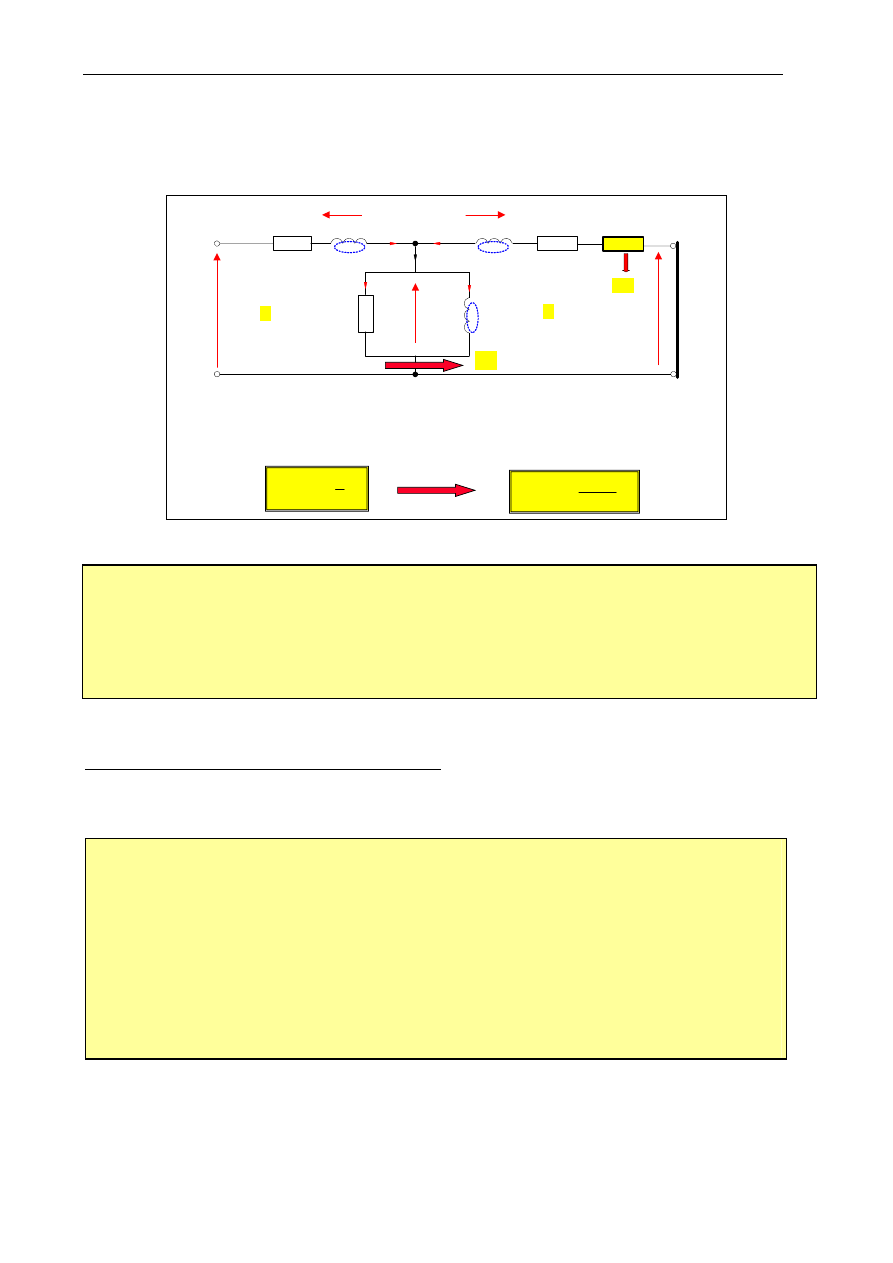
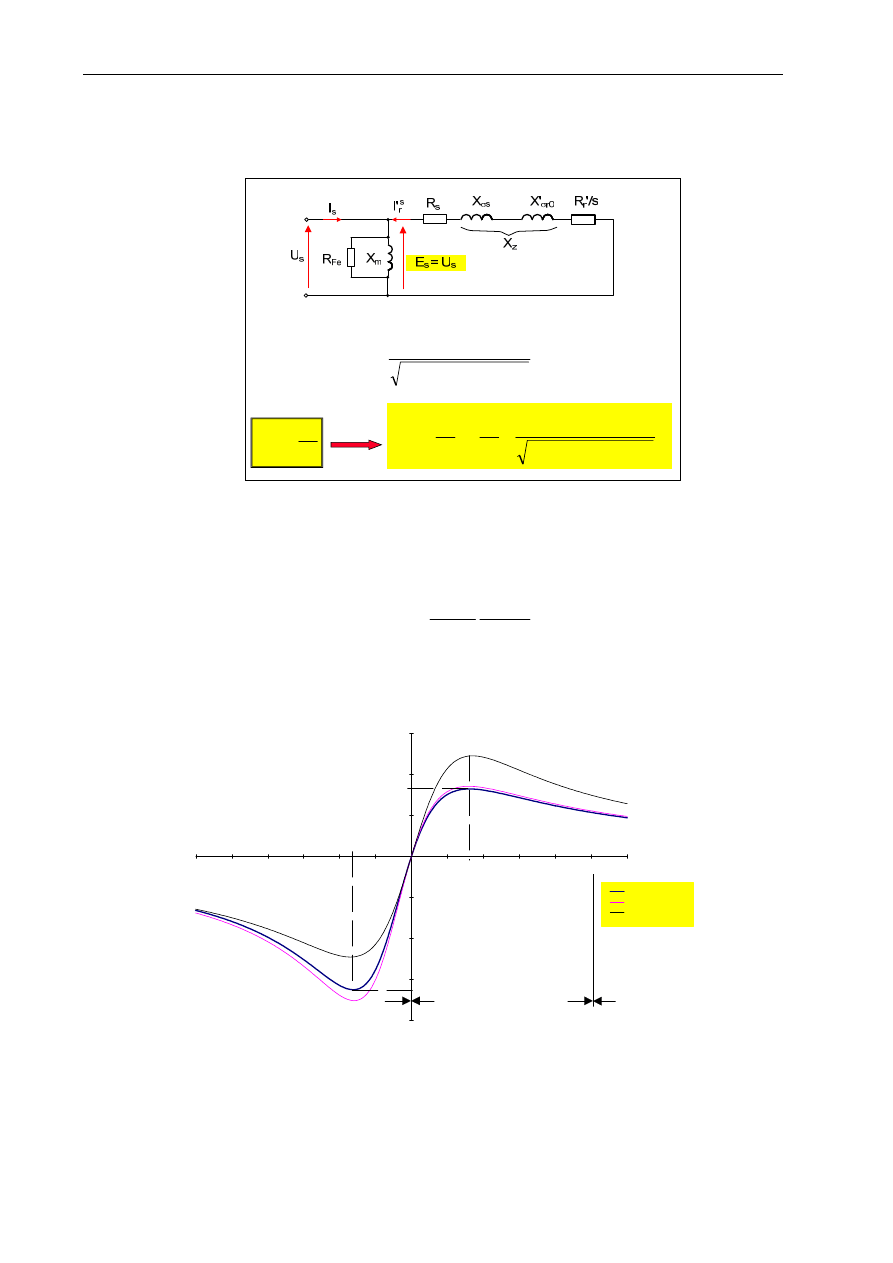
1.2. Model obwodowy (schemat zastępczy) maszyny indukcyjnej

Model obwodowy (schemat zastępczy) silnika indukcyjnego – przedstawiony na rys. 1.4 – opracowano

na podstawie modelu fizycznego silnika (rys. 1.3). Model ten jest podstawą do analizy dowolnego stanu
pracy silnika indukcyjnego.

I

m

E

s

U'

2

= 0

U

s

I

0

I

0cz

R

Fe

X

m

I

s

I'

r

R'

r

R

s

X

σs

X'

σr0

Φ'

σr

Φ

σs

Φ

m

E

σs

E’

σr0

R

m

= R'

r

(1-s)/s

E’

r0

P

m

s

s

f

e

f

e

Analogiem modelu obwodowego MI jest model obwodowy

Analogiem modelu obwodowego MI jest model obwodowy

transformatora obci

transformatora obci

ąż

ąż

onego rezystancj

onego rezystancj

ą

ą

:

:

R

R

’

’

r

r

(1

(1

-

-

s)/s

s)/s

2

)

1

(

r

r

r

m

I

s

s

R

m

P

′

−

′

=

Moc pola wiruj

Moc pola wiruj

ą

ą

cego

cego

P

P

e

e

i mechaniczna P

i mechaniczna P

m

m

wytwarzana przez MI pracuj

wytwarzana przez MI pracuj

ą

ą

c

c

ą

ą

jako silnik:

jako silnik:

2

1

r

r

r

e

I

s

R

m

P

′

′

=

P

P

e

e

Rys. 1.4. Podstawowy model obwodowy (schemat zastępczy) wielofazowego silnika indukcyjnego

Uwaga:
Aby

posłużyć się modelem obwodowym transformatora, do opisu właściwości ruchowych MI,

należy częstotliwość prądów wirnika s f

e

transformować do częstotliwości prądów stojana f

e

.

Efektem transformacji jest pojawienie się rezystancji

s

s

R

R

r

m

/

)

(

−

′

=

′

1

.

Moc

wydzielająca się na rezystancji

s

s

R

R

r

m

/

)

(

−

′

=

′

1

jest analogiem mocy mechanicznej

wytwarzanej przez silnik.

Przedstawiony model — nazywany zwykle modelem o konturze „T” — odpowiada silnikowi

indukcyjnemu o uzwojeniu wirnika sprowadzonym (zredukowanym) zarówno do przekładni

ϑ

i

= 1

jaki i

transformowanym do częstotliwości prądów stojana. Topologia i elementy modelu wynikają z rozważań
fizycznych dotyczących biegu jałowego, stanu obciążenia i stanu zwarcia silnika indukcyjnego. Z kolei
wartości parametrów modelu wyznacza się na podstawie wyników dwóch prób: biegu jałowego i stanu
zwarcia — opisanych w p. 2.3 oraz 2.5 niniejszego ćwiczenia.

Parametru modelu obwodowego silnika indukcyjnego:

rezystancja R

Fe

i reaktancja X

m

są wielkościami nieliniowymi

zależnymi od wartości strumienia głównego i rodzaju blachy rdzenia

pozostałe parametry modelu obwodowego w zakresie prądów znamionowych

można przyjąć jako stałe.

Uwaga: W przypadku wartości prądów silnika w stanie rozruch [I

sr

> (5 ÷ 7) I

sn

] drogi przepływu

strumieni rozproszenia ulegają nasyceniu – wartości reaktancji rozproszenia ulegają zmniejszeniu.

W przypadku silnika klatkowego z klatką rozruchową lub głębokimi żłobkami należy uwzględnić

zjawisko wypierania prądu – wartości reaktancji i rezystancji uzwojenia ulegają zmianie wraz ze zmianą

poślizgu.

Ćwiczenie: Maszyny indukcyjne trójfazowe

7

1.3. Charakterystyka mechaniczna maszyny indukcyjnej

Model obwodowy SI na rys. 1.4, przy założeniu U

s

≅ E

s

, można przekształcić do modelu obwodowego

o konturze „Γ” (rys. 1.5).

2

2

z

r

s

s

s

r

X

s

R

R

U

I

+

′

+

≅

)

/

(

'

2

2

2

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

+

′

≅

z

r

s

s

r

s

e

e

X

s

R

R

U

s

R

m

p

T

)

/

(

1

'

ω

e

e

e

P

p

T

ω

=

OBLICZANIE PRĄDU WIRNIKA I MOMENTU ELEKTROMAGNETYCZNEGO

Rys. 1.5. Model obwodowy (schemat zastępczy) wielofazowego silnika indukcyjnego o konturze „

Γ”

Przyjmując kolejne uproszczenie: R

s

≅ 0 równanie momentu elektromagnetycznego (na rys. 1.5) można

uprościć do postaci:

2

2

2

k

k

z

e

s

s

e

s

s

s

s

X

U

pm

T

+

≅

ω

(1.3)

gdzie,

/

z

r

k

X

R

s

′

=

jest tzw. poślizgiem krytycznym – poślizgiem dla którego moment

elektromagnetyczny osiąga wartość maksymalną. Przykładowy wykres charakterystyki mechanicznej SI,
wykreślonej wg równania (1.3), przedstawiono rys. 1.6.

-80

-60

-40

-20

0

20

40

60

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

1.2

model "T"
model " "
model " " R = 0

SILNIK

PRĄDNICA

HAMULEC

s

k+

s

k-

emx

+T

T

e

s [-]

[Nm]

Γ

Γ

emx

-T

s

Rys. 1.6. Przykładowa charakterystyka mechaniczna wielofazowego silnika indukcyjnego – charakterystyki wykreślone

na podstawie modelu obwodowego o konturze „T”, „

Γ”oraz „Γ” przy założeniu R

s

= 0 (wg równania (1.3))

M. Ronkowski, G. Kostro, M. Michna:

8

2.

BADANIA

2.1. Oględziny zewnętrzne

Należy dokonać oględzin badanego silnika indukcyjnego oraz urządzeń wchodzących w skład układu

pomiarowego. Ustalić i sprawdzić urządzenie do zahamowania wirnika. Dokładnie przeczytać i zanotować
dane zawarte na tabliczce znamionowej badanego silnika indukcyjnego (przykład na rys. 2.1) i maszyny
pomocniczej oraz ustalić układy połączeń uzwojeń.

Rys. 2.1. Tabliczka znamionowa silnika indukcyjnego klatkowego

(Producent INDUKTA/CANTONI)

Tablica 2.1
Dane znamionowe badanej maszyny indukcyjnej

Lp.

Dane znamionowe

Jednostka Wartość

1 nazwę lub znak producenta

2 nazwę i typ

3 numer

fabryczny

4 rok

wykonania

5 moc

znamionowa

kW

6 znamionowe

napięcia stojana

V

7 znamionowy

prąd stojana

A

8 znamionowy

współczynnik mocy

-

9 układ połączeń uzwojeń stojana

-

10 układ połączeń uzwojeń wirnika

10 znamionowe

napięcie wirnika

V

11 znamionowy

prąd wirnika

A

znamionowa

częstotliwość Hz

12 znamionowa

prędkość obrotowa

obr/min

13 klasa

izolacji

14 rodzaj

pracy

15 stopień ochrony

2.2. Pomiar rezystancji uzwojeń

Zasady pomiaru rezystancji uzwojeń.
• Pomiar rezystancji uzwojeń stojana wykonać za pomocą mostka lub metodą techniczną.
• Pomiar rezystancji uzwojeń wirnika silnika pierścieniowego wykonać metodą techniczną (ze

względu na obecność w obwodzie rezystancji przejścia szczotka-pierścień ślizgowy).

• Dobrać odpowiednie zakresy mierników do pomiaru metodą techniczną.
• Pomiar rezystancji uzwojeń metodą techniczną wykonać dla trzech prądów z zakresu

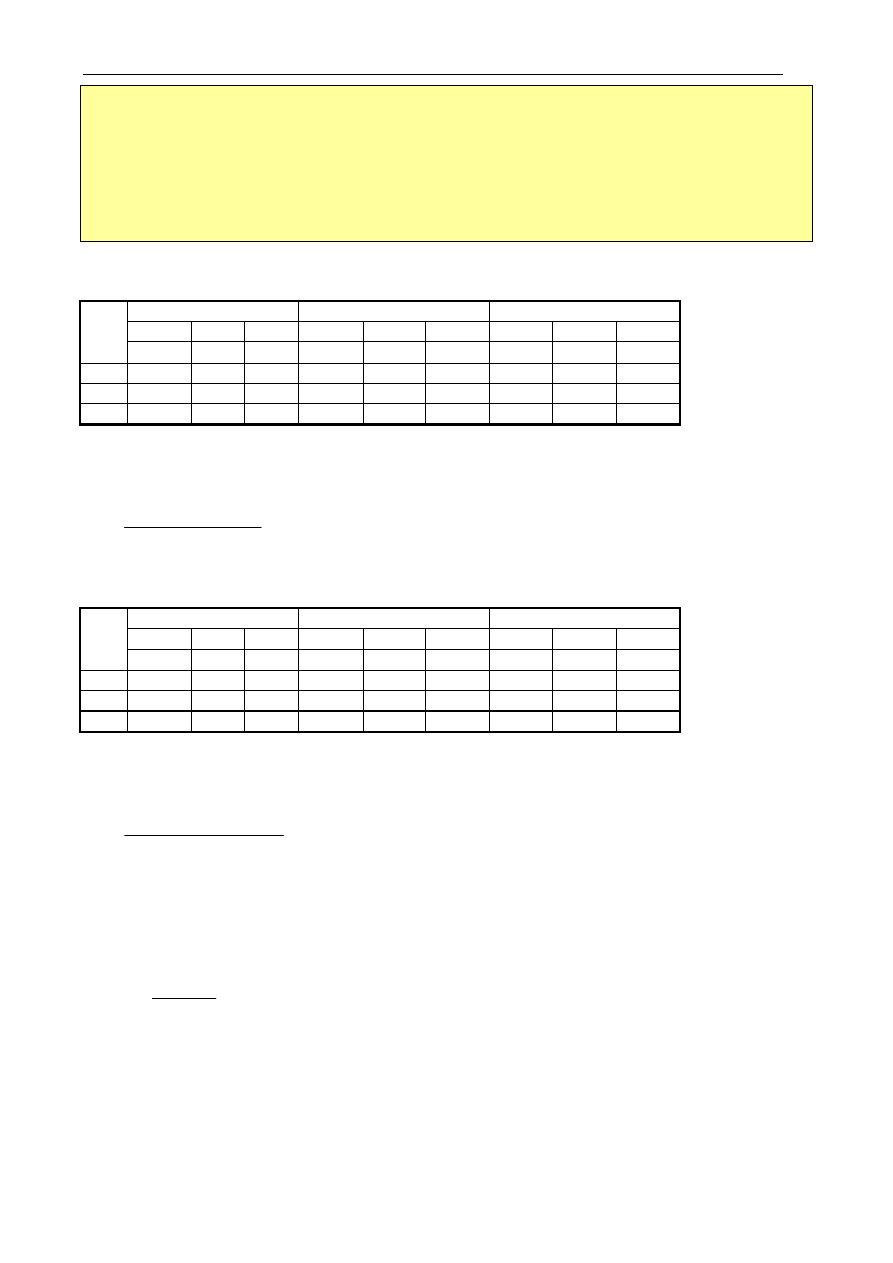
Ćwiczenie: Maszyny indukcyjne trójfazowe

9

5÷30% prądu znamionowego (w celu zmniejszenia zjawiska nagrzewania uzwojeń w wyniku

pomiaru).

• Narysować schematy połączeń uzwojeń.
• Odczytać temperaturę otoczenia t

o

(przy szybkich pomiarach można przyjąć,

że pomierzone wartości rezystancji dotyczą temperatury uzwojeń równej temperaturze

otoczenia).

• Wyniki pomiarów zanotować w tabelach 2.2a i 2.2b.

Tablica 2.2a
Pomiar rezystancji uzwojenia stojana – kolejnych faz (uzwojenie rozłączone)

Zaciski 1U1-1U2

Zaciski 1V1-1V2

Zaciski 1W1-1W2

Lp. U I R

sU

U I R

sV

U I R

sW

V A

Ω

V A

Ω

V A

Ω

τ

x

= .........

o

C

Obliczamy wartości średnie rezystancji dla kolejnych faz uzwojenia stojana, a następnie wartość średnią
rezystancji fazowej uzwojenia stojana

3

sWśr

sVśr

sUśr

s

R

R

R

R

+

+

=

(2.1)

Tablica 2.2b
Pomiar rezystancji uzwojenia wirnika – kolejno między fazami (połączenie Y)

Zaciski 2U-2V

Zaciski 2U-2W

Zaciski 2V-2W

Lp. U I R

rUV

U I R

rUW

U I R

rVW

V A

Ω

V A

Ω

V A

Ω

τ

x

= .........

o

C

Obliczamy wartości średnie dla kolejnych rezystancji „międzyfazowych” wirnika, a następnie wartość
średnią rezystancji fazowej uzwojenia wirnika

3

rVWśr

rUWśr

rUVśr

r

R

R

R

R

+

+

=

(2.2)

W praktyce wartości rezystancji R

s

oraz R

r

we wzorach (2.1) i (2.2) — pomierzone w

temperaturze

τ

x

— przelicza się do umownej temperatury odniesienia

τ

o

(przyjmuje się wartość 20

°C) wg. zależności (2.3) i (2.4).

W przypadku uzwojenia wykonanego z miedzi stosuje się następujący wzór przeliczeniowy:

x

o

R

R

x

o

τ

τ

τ

τ

+

=

235

235

+

[

Ω] (2.3)

gdzie:

τ

x

− temperatura uzwojenia w czasie pomiaru [°C],

R

τo

− rezystancja uzwojenia sprowadzona do temperatury τ

o

,

R

τ

x

− rezystancja uzwojenia pomierzona w temperaturze τ

x

.

Jeżeli uzwojenie wykonane jest z aluminium, to do przeliczenia wartości rezystancji do
temperatury odniesienia

τ

o

stosuje się zależność:

M. Ronkowski, G. Kostro, M. Michna:

10

x

o

R

R

x

o

τ

τ

τ

τ

+

=

225

225

+

[

Ω] (2.4)

2.3. . Próba biegu jałowego
• Podstawy próby biegu jałowego

Próbę biegu jałowego wykonuje się w celu wyznaczenia tzw. strat stałych dla późniejszego

określenia sprawności silnika. Przy badaniach pełnych analiza kształtu charakterystyki biegu
jałowego, tj. strat, prądów składowych i współczynnika mocy (rys.2.2.), pozwala na wyciągnięcie
szeregu wniosków o jakości wykonania maszyny.

I [A]

0

U[V]

I

0

I

m

cos??

?

?P [W]

cos??

?

?P

0

I

0cz

Rys. 2.2. Charakterystyki biegu jałowego

Dlatego też próbę biegu jałowego przeprowadza się zasilając nieobciążony silnik napięciem

regulowanym w zakresie wartości około 1,2

− 0,2 U

N

. Przy biegu jałowym, tj. przy momencie na

wale T

L

= 0, prędkość kątowa silnika nie zależy od napięcia i jest praktycznie równa prędkości

synchronicznej:

[obr/min]

p

f

n

e

s

60

=

(2.5)

Moc pobierana przez silnik przy biegu jałowym P

0

praktycznie pokrywa następujące straty:

Cus

m

Fe

P

P

P

P

Δ

Δ

Δ

+

+

≈

0

(2.6)

gdzie,

ΔP

Fe

− straty w rdzeniu (żelazie),

ΔP

m

− straty mechaniczne,

ΔP

Cus

− straty w uzwojeniu stojana.

Straty mechaniczne składają się ze strat tarcia w łożyskach, strat tarcia szczotek (w silnikach

pierścieniowych bez urządzenia do podnoszenia szczotek), strat tarcia części wirujących w
powietrzu oraz strat wentylacyjnych. Wszystkie te straty zależą od prędkości kątowej silnika, a
więc przy próbie biegu jałowego mają praktycznie wartość stałą. Straty w żelazie składają się ze
strat na prądy wirowe, strat na histerezę oraz strat dodatkowych w stojanie. Straty te są
proporcjonalne do kwadratu indukcji, a tym samym do kwadratu napięcia (analogicznie jak w
transformatorze).

Stratami jałowymi

nazywamy sumę strat mechanicznych i strat w żelazie stojana. Oznacza to:

moc pobrana z sieci przy biegu jałowym

− zmniejszona o straty w uzwojeniu stojana:

P

o

Fe

m

Cus

o

P

P

P

P

Δ

Δ

Δ

Δ

+

=

−

=

(2.7)

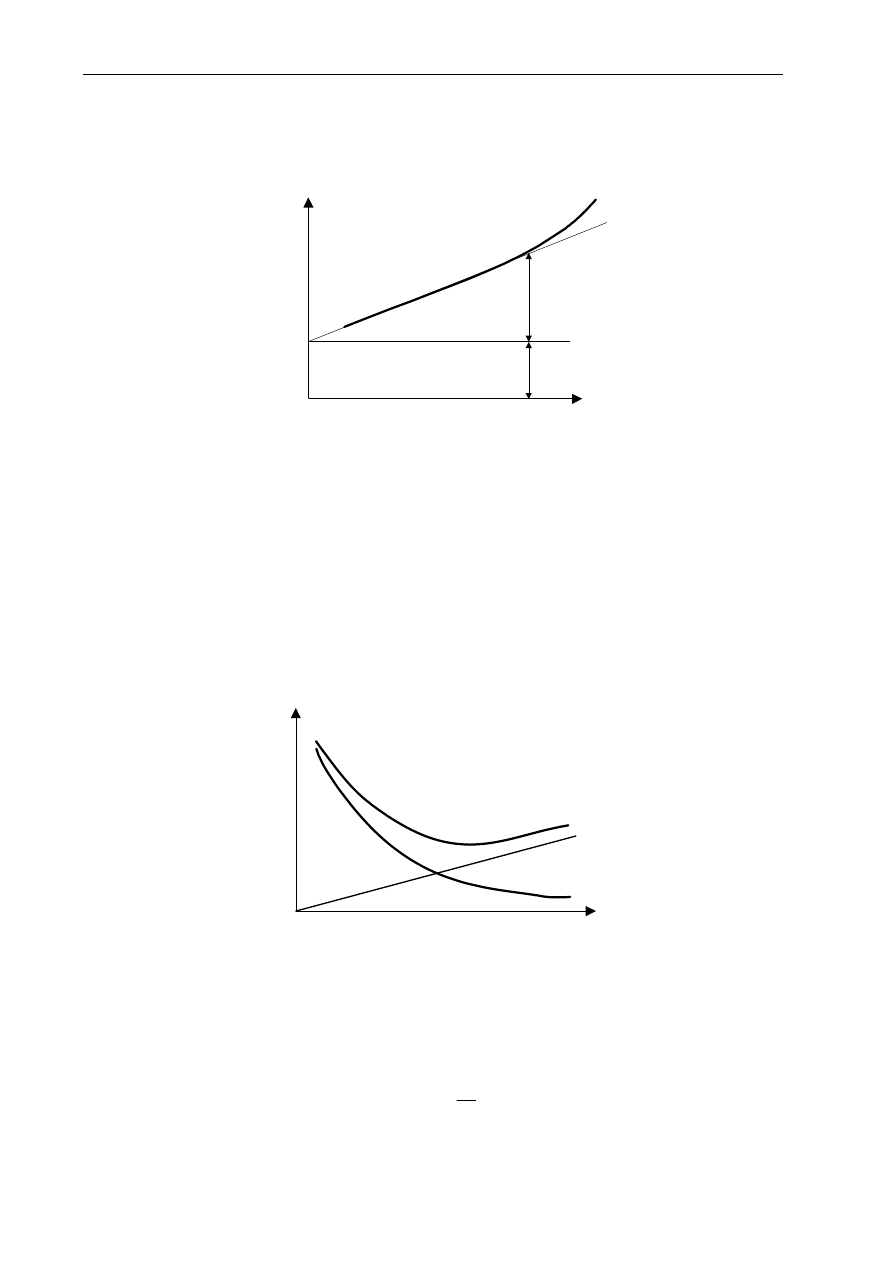
Ćwiczenie: Maszyny indukcyjne trójfazowe

11

Zatem straty jałowe wykreślone w funkcji napięcia zasilania stojana

ΔP

k

k

o

≈

+

1

2

U

2

przedstawiają parabolę przesuniętą o wartość stałą odpowiadającą stratom mechanicznym. Jeżeli
więc straty te przedstawić w funkcji kwadratu napięcia, uzyska się linię prostą, której ekstrapolacja
w kierunku osi rzędnych odetnie wielkość strat mechanicznych (rys.2.3.).

0

ΔP

0

[W]

U

2

[V

2

]

ΔP

Fe

ΔP

m

Rys. 2.3. Rozdział strat biegu jałowego

Przy większych nasyceniach obwodu magnetycznego zależność strat od napięcia jest wyższego
rzędu niż kwadratowa i dlatego charakterystyka strat jałowych przechodzi z przebiegu
prostoliniowego w paraboliczny.

Składowa czynna prądu biegu jałowego:

I

ocz

= I

om

+ I

Fe

przy czym składowa I

om

wynika z wartości strat mechanicznych, zaś składowa I

Fe

ze strat w żelazie

(

rys. 2.4.).

0

Ι

[A]

U

[V]

I

ocz

I

om

I

Fe

Rys. 2.4. Zależność składowych czynnych prądu biegu jałowego silnika od napięcia

Przy bardzo małym napięciu w silniku dominują straty mechaniczne, które, jak powiedziano

wyżej, można przyjąć jako stałe

ΔP

m

= k

1

.

Zatem zależność

I

k

U

om

=

1

przedstawia hiperbolę.
Straty

w

żelazie są proporcjonalne do kwadratu napięcia

ΔP

Fe

= k

2

U

2

,

M. Ronkowski, G. Kostro, M. Michna:

12

Zatem wyrażenie

I

k

U

k U

Fe

=

=

2

2

U

2

przedstawia zależność liniową.

Prąd biegu jałowego silnika jest sumą geometryczną składowych czynnej i biernej (magnesowania):

2

2

m

ocz

o

I

I

I

+

=

Współczynnik mocy biegu jałowego określa się:

cos

o

ϕ =

I

I

ocz

o

Przy bardzo niskich napięciach dominuje składowa czynna, a więc cos

ϕ

o

może przyjmować

wartości bliskie 1. Natomiast przy wzroście napięcia zaczyna dominować składowa bierna –
wartość cos

ϕ

o

maleje do około 0,1.

•Przebieg próby biegu jałowego
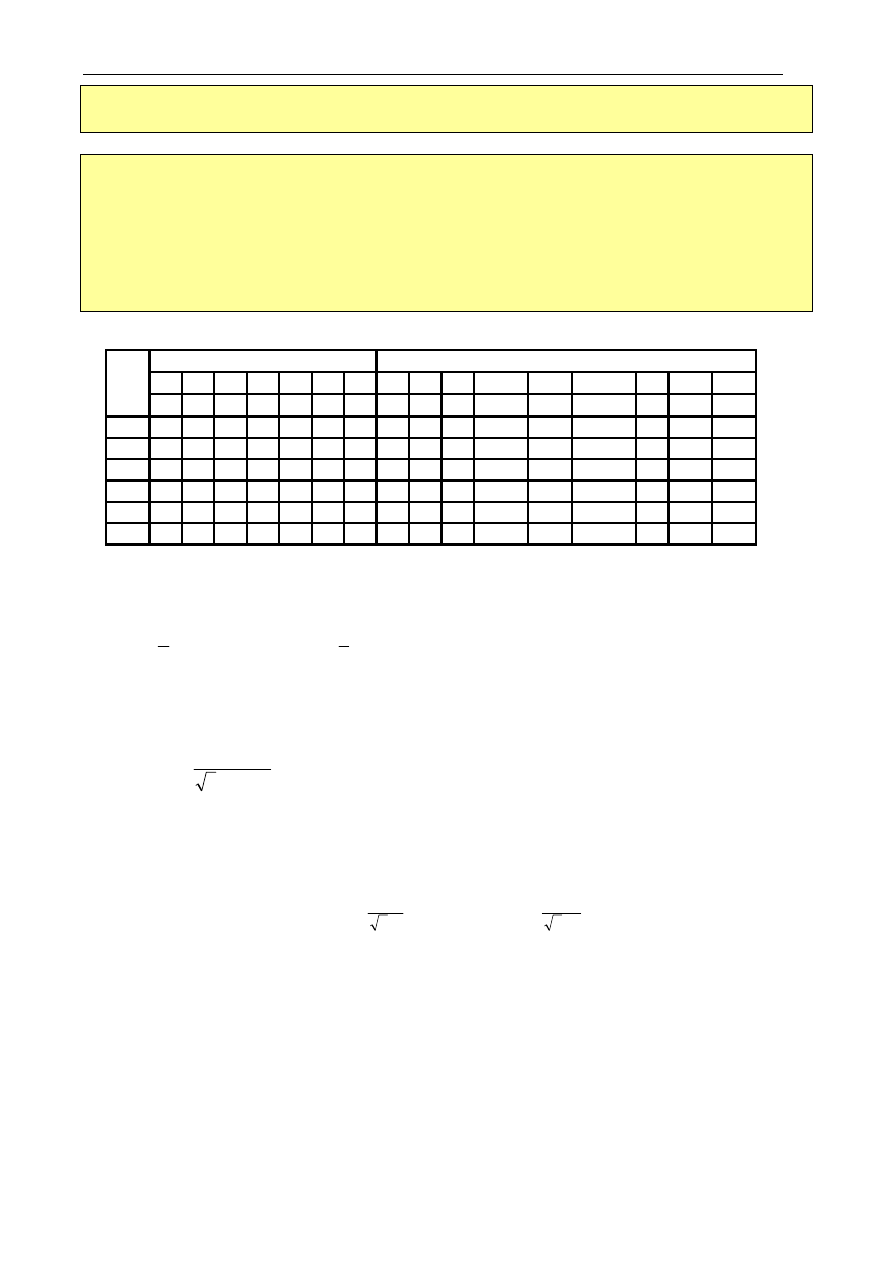
Schemat układu połączeń silnika do próby biegu jałowego przedstawiono na rys. 2.5.

Uwaga:
Należy zewrzeć zaciski uzwojenia wirnika bez podłączania dodatkowych przyrządów pomiarowych

(na pierścieniach ślizgowych - w przypadku silników ze szczotkami unoszonymi, natomiast w przypadku
silnika ze stale przylegającymi szczotkami – bezpośrednio na zaciskach wirnika).

2U

2V

2W

R

S

T

A

I

r

I’
I’’

I’’’

U’

P’

P’’

U’’

Rys. 2.5. Schemat połączeń do próby biegu jałowego silnika indukcyjnego pierścieniowego

Uwagi ogólne do wykonania próby stanu jałowego:

• Ponieważ w laboratorium dokonuje się rozruchu silnika ze źródła o regulowanym napięciu

(autotransformator lub regulator indukcyjny) zaczynając od najniższego napięcia, więc w tym
przypadku opornik rozruchowy w obwodzie wirnika jest zbyteczny.

• Należy sprawdzić, czy źródło zasilania jest ustawione na minimum napięcia i zewrzeć

pierścienie uzwojenia wirnika.

• Pomimo płynnego zwiększania napięcia rozruchowi silnika towarzyszy prąd rozruchowy,

którego wartość znacznie przewyższa prąd znamionowy silnika. Dlatego celem ograniczenia
przepływu prądu rozruchowego przez ustroje pomiarowe amperomierza i watomierza należy je
zewrzeć lub rozruchu dokonywać przy wyjętym wtyku przełącznika PW.

• Po ustaleniu się prędkości kątowej silnika rozewrzeć amperomierz (lub wtyk umieścić w

gnieździe przełącznika PW) i w trakcie dalszego zwiększania napięcia kontrolować wartość
prądu pobieranego przez silnik.

Ćwiczenie: Maszyny indukcyjne trójfazowe

13

• W przypadku ujemnego wychylenia wskazówki watomierza należy zmienić kierunek przepływu

prądu przez cewkę watomierza poprzez odwrotne umieszczenie wtyku przełącznika PW.

W czasie pomiarów należy:

• Zmieniać napięcie zasilające uzwojenie stojana w granicach od około 1,2 U

N

do wartości, przy

której prąd biegu jałowego zaczyna ponownie wzrastać, tj. do (0,2 - 0,25) U

N

lub prędkość

kątowa zaczyna się zmniejszać.

• Notować w tablicy 2.3. dwa napięcia międzyprzewodowe U

A

, U

B

.

• Notować w tablicy 2.3. trzy prądy fazowe stojana: I

A

, I

B

, I

C.

• Notować w tablicy 2.3. wskazania watomierza mierzącego moc w układzie Arona: P

α

, P

β

.

• Odczyty wykonać dla 6-8 punktów pomiarowych.

Tablica 2.3. Próba biegu jałowego silnika indukcyjnego

Wartości pomierzone

Wartości obliczone

Lp. U’ U” I” I” I’” P’ P”

U

s

I

o

P

o

ΔP

Cuo

ΔP

o

cos

ϕ

o

I

m

I

ocz

U

2

V A W V A W W V A W

W W

−

A A V

2

Opracowanie wyników próby biegu jałowego

W czasie wykonywanych pomiarów napięcia i prądy poszczególnych faz mogą się różnić między sobą. Ich
wartości średnie, podane w tablicy 2.3, należy obliczyć wg. następujących wzorów:

(

)

(

)

P

P

I

I

I

U

U

U

s

′′

+

′

=

′′′

+

′′

+

′

=

′′

+

′

=

o

o

P

I

3

1

2

1

Wartości pozostałych wielkości w tablicy 2.3 obliczamy wg. następujących wzorów:

2

3

o

s

Cuo

I

R

P

=

Δ

−

straty w uzwojeniu stojana;

Cuso

o

P

P

Δ

Δ

−

=

o

P

− pomierzone straty jałowe;

o

s

o

I

U

P

⋅

⋅

=

3

o

cos

ϕ

− współczynnik mocy przy biegu jałowym;

I

ocz

= I

o

cos

ϕ

o

− składowa czynna prądu biegu jałowego;

I

m

= I

o

sin

ϕ

o

− składowa magnesująca prądu biegu jałowego.

Na podstawie wyników uzyskanych z próby biegu jałowego należy wyznaczyć parametry gałęzi
poprzecznej schematu zastępczego silnika indukcyjnego (rys. 1.4).

Fe

s

m

s

I

U

Fe

I

U

m

X

3

3

R

≅

≅

M. Ronkowski, G. Kostro, M. Michna:

14

Wartości parametrów schematu zastępczego badanej maszyny wynoszą:

X

m

R

Fe

[

Ω] [Ω]

Uwaga:

W szczególności wyznaczyć wartości parametrów odpowiadające napięciu znamionowemu

stojana.

2.4. Pomiar przekładni napięciowej

Przekładnia napięciowa, której pomiaru dokonuje się przy otwartym obwodzie wirnika, jest

stosunkiem fazowych sił elektromotorycznych/napięć na zaciskach uzwojeń stojan i wirnika:

k

z

k

ur

r

us

u

rf

sf

s

r

s

U

U

z

E

E

≈

=

=

ϑ

(2.8)

Przebieg pomiaru przekładni
Dokonać modyfikacji schematu połączeń z rys. 2.5. poprzez rozwarcie zacisków uzwojenia

wirnika i podłączenie do nich trzech woltomierzy (lub jednego woltomierza przy założeniu
symetrii).

W czasie pomiaru przekładni napięciowej należy:

• Przy otwartym obwodzie pierścieni ślizgowych i nieruchomym wirniku (czasami wirnik obraca

się pod wpływem indukujących się prądów wirowych na powierzchni żelaza wirnika) podnieść
napięcie do wartości znamionowej.

• Dokonać pomiaru przekładni dla dwóch nieznacznie różniących się wartości napięcia.

Wyniki pomiarów notować w tablicy 2.4.

Tablica 2.4. Pomiar przekładni napięciowej

Stojan

Wirnik

Lp. U

sUV

U

sWV

U

s

U

sf

U

rUV

U

rVW

U

rWU

U

r

U

rf

ϑ

u

V V V V V V V V V

−

Opracowanie wyników przekładni napięciowej

Przy obliczeniach przekładni napięciowej należy uwzględnić następujące zależności:

3

/

s

sf

U

U

=

− napięcie fazowe przy połączeniu w gwiazdę;

U

rUV

U

rVW

U

rWU

− wartości napięcia na pierścieniach uzyskane z pomiaru; jeżeli
wszystkie napięcia są w przybliżeniu jednakowe to wirnik ma
uzwojenie 3

−fazowe i wówczas:

3

3

1

rWU

rVW

rUV

rf

U

U

U

U

+

+

=

Ćwiczenie: Maszyny indukcyjne trójfazowe

15

Jeżeli natomiast

rWU

rVW

rUV

U

U

U

′

≈

′

≈

′

2

2

, oznacza to, że wirnik ma uzwojenie 2

−fazowe,

a zatem

(

)

WU

r

VW

r

rf

U

U

U

+

=

2

1

rf

sf

u

U

U

=

ϑ

− przekładnia napięciowa.

2.5. Próba zwarcia i pomiar przekładni prądowej
• Podstawy próby zwarcia
Próbę zwarcia wykonuje się w celu wyznaczenia wartości prądu zwarcia (rozruchowego)
przy napięciu znamionowym oraz wyznaczenia strat zmiennych dla późniejszego określenia
sprawności.

Próbę zwarcia wykonuje się zasilając silnik ze źródła o regulowanym napięciu. Wirnik silnika

jest zahamowany (zablokowany). Jeżeli wartość prądu i mocy zależą od położenia wirnika
względem stojana, wirnik powinien być obracany w kierunku przeciwnym do kierunku wirowania
pola z prędkością kilkudziesięciu obrotów na minutę.

W silniku z uzwojonym wirnikiem należy zewrzeć pierścienie. Przeprowadzając próbę zwarcia

należy podnosić napięcie zasilające aż do uzyskania przegięcia charakterystyki prądowej (rys. 2.6.).

I

z

[A]

0

U

z

[V]

I

z

cos

ϕ

z

P

z

[W]

cos

ϕ

z

P

z

U'

z

Rys. 2.6. Charakterystyki zwarcia

Próbę tę należy przeprowadzić szybko i sprawnie, gdyż moc zwarcia prawie w całości jest

zużywana na nagrzewanie silnika, szczególnie uzwojeń. Brak chłodzenia silnika powoduje szybki i
znaczny wzrost temperatury, który może uszkodzić izolację. Przy próbie zwarcia nie występują
straty mechaniczne, ponieważ wirnik jest zahamowany. Straty w żelazie są pomijalnie małe,
ponieważ na zaciskach silnika jest stosunkowo niskie napięcie. Moc pobierana z sieci równa się
stratom w uzwojeniach stojana i wirnika (zamieniona na ciepło)

− jest więc proporcjonalna do

kwadratu prądu:

(

)

dod

rf

r

sf

s

z

P

I

R

I

R

P

Δ

+

′

′

+

=

2

2

3

Prąd jest w przybliżeniu proporcjonalny do napięcia, stąd charakterystyka P

z

= f(U

z

) ma

przebieg paraboliczny.

Charakterystyka prądu zwarcia I

z

= f(U

z

) w początkowej części jest linią prostą, a w miarę

wzrostu napięcia

− poprzez łagodne zagięcie − przechodzi w prostą o większym kącie nachylenia.

W początkowej fazie główna część spadku napięcia magnetycznego na drodze strumienia
rozproszenia występuje w żłobku. Przy dalszym wzroście prądu zwarcia następuje nasycenie
zębów, wskutek czego charakterystyka zagina się, by po nasyceniu znów przejść w linię prostą.

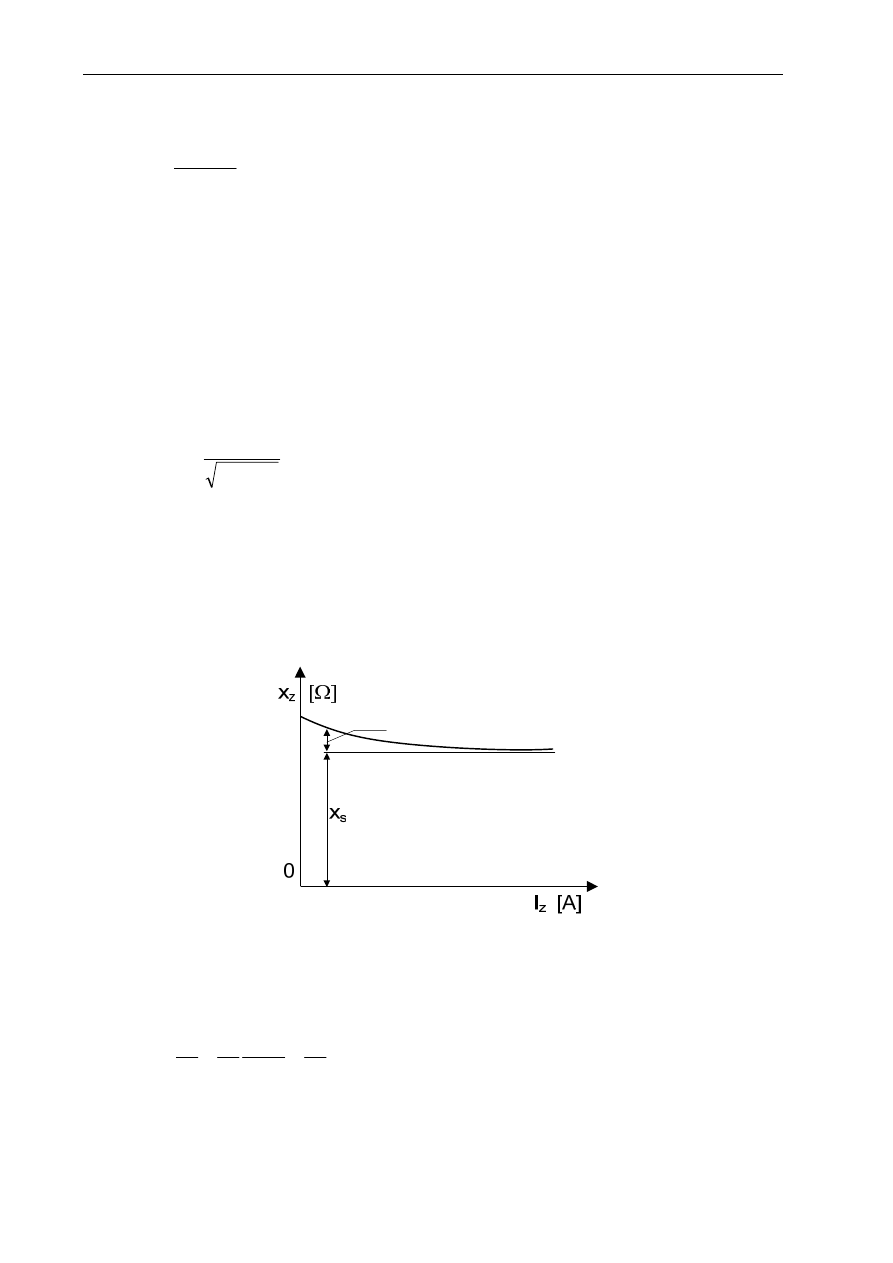
M. Ronkowski, G. Kostro, M. Michna:

16

Jeżeli z próby zwarcia uzyska się część charakterystyki ponad zagięciem, wówczas można obliczyć
prąd zwarcia przy napięciu znamionowym z zależności:

[A]

I

k

z

z

z

z

N

I

U

U

U

U

′

−

′

−

=

(2.9)

gdzie:

I

k

− prąd zwarcia przy napięciu znamionowym,

U

sN

− napięcie znamionowe,

U

z

− napięcie, przy którym w uzwojeniu płynie prąd I

z

,

′

U

z

− wartość napięcia wyznaczona graficznie na rys.2.6 - przez wykreślenie stycznej

do charakterystyki prądu zwarcia w jej górnej części.

Jak wspomniano, w stanie zwarcia strumienie rozproszenia przebiegają głównie przez

powietrze, a więc na drodze o stałym oporze magnetycznym. Reaktancja zwarciowe jest więc w
przybliżeniu stała, jeżeli pominąć wpływ nasycenia w zębach. Miarą słuszności tego założenia
może być zależność cos

ϕ

z

= f (U

z

) (rys.2.6). Jeśli nasycenie nie występuje, to reaktancja

rozproszenia jest faktycznie stała i wtedy

2

2

z

z

z

X

R

R

+

=

z

cos

ϕ

(2.10)

tzn. nie zależy od wartości prądu zwarcia. W tych warunkach charakterystyka cos

ϕ

z

= f(U

z

)

przedstawia linię prostą równoległą do osi odciętych. Ze wzrostem nasycenia reaktancja zwarcia
jednak maleje i charakterystyka cos

ϕ

z

= f(U

z

) odbiega od linii prostej (rys. 2.6.). Można więc

przyjąć, że reaktancja X

z

składa się z dwóch skłądowych:

X

s

− stałej, niezależnej od nasycenia,

X

ν

− zmiennej,

zależnej od nasycenia w zębach.

Sposób rozkładu reaktancja X

z

na składowe ilustruje rys. 2.7.

ν

X

Rys. 2.7. Rozkład reaktancji zwarcia X

z

na składowe

• Podstawy pomiaru przekładni prądowej
Pomiar przekładni prądowej dokonuje się przy pierścieniach zwartych poprzez amperomierze przy
czym:

u

r

s

s

s

r

s

sf

rf

I

m

m

z

z

m

m

I

I

ϑ

ϑ

=

=

=

ur

us

k

k

(2.11)

Ponieważ zarówno siły elektromotoryczne jak i prądy są wartościami odnoszącymi się do jednej
fazy, stąd rezystancja wirnika, sprowadzona do fazy stojana:

Ćwiczenie: Maszyny indukcyjne trójfazowe

17

2

u

r

s

r

m

m

R

ϑ

R

r

=

′

(2.12)

Analogicznie przelicza się reaktancję oraz impedancję obwodu wirnika.

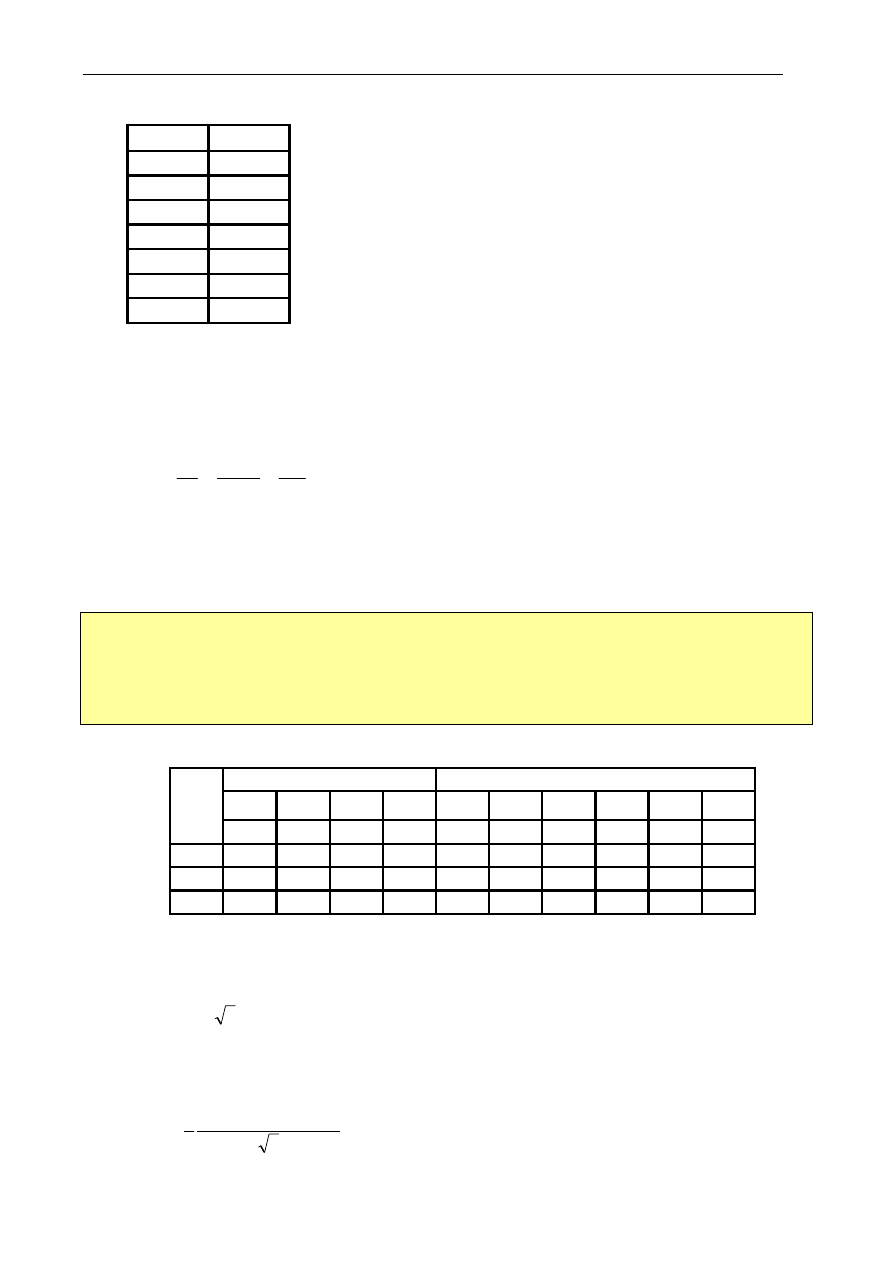
Przebieg próby zwarcia i pomiaru przekładni prądowej

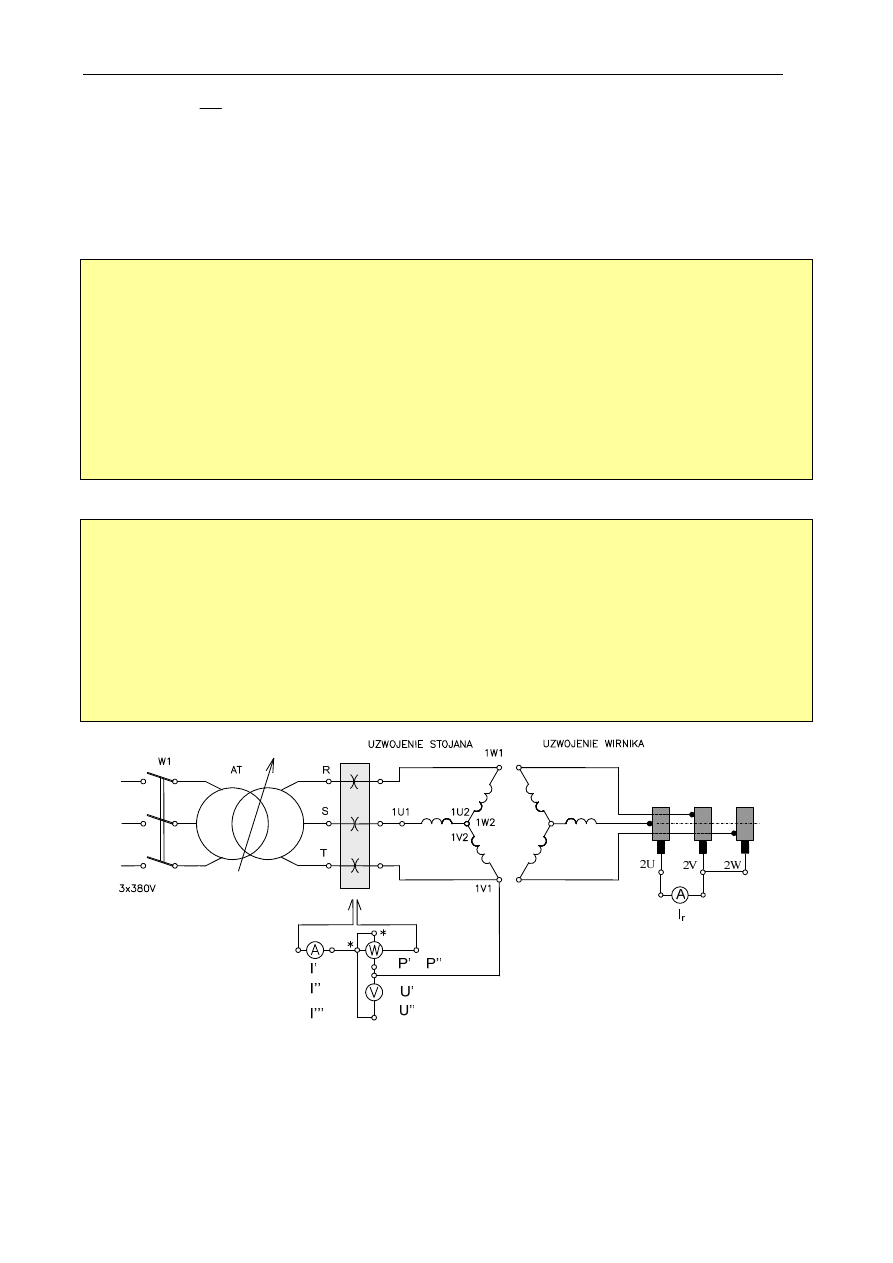
Przy próbie zwarcia zaciski uzwojenia wirnika należy zewrzeć za pomocą trzech amperomierzy

(rys. 2.8). Dogodne jest połączenie próby zwarcia z pomiarem przekładni prądowej.

Uwagi ogólne do próby zwarcia i pomiaru przekładni prądowej:

• Zakresy przyrządów pomiarowych należy dobrać do największych wartości wielkości

występujących przy tej próbie: prąd stojana i wirnika równy 1,5 prądu znamionowego, napięcie
do 60% napięcia znamionowego.

• Należy sprawdzić, czy źródło zasilania jest ustawione na minimum napięcia.
• Wirnik badanego silnika zahamować za pomocą hamulca mechanicznego.
• Próbę zwarcia należy wykonywać możliwie szybko, a w czasie przerw w pomiarach należy

wyłączać zasilanie silnika. Pozwoli to ograniczyć niekorzystny ze względu na dokładność próby
wzrost temperatury uzwojeń.

• W przypadku ujemnego wychylenia wskazówki watomierza należy zmienić kierunek przepływu

prądu przez cewkę watomierza poprzez odwrotne umieszczenie wtyku przełącznika PW.

W czasie pomiarów należy:

• Włączyć badany silnik do sieci przy napięciu możliwie bliskim wartości 0 V.
• Napięcie zasilania zwiększać tak, aby prąd stojana zmieniał się w granicach
I

z

= (0,1

− 1,0) I

N

.

• Notować w tablicy 2.5. dwa napięcia międzyprzewodowe: U

A

, U

B

.

• Notować w tablicy 2.5. trzy prądy fazowe stojana: I

A

, I

B

, I

C.

• Notować w tablicy 2.5. wskazania watomierza mierzącego moc w układzie Arona: P

α

, P

β

.

• Notować w tablicy 2.5. dwa prądy wirnika: I

rA

, I

rB

, I

rC

.(przy założeniu symetrii wystarczy

pomiar prądu w jednej z faz wirnika).

• Odczyty wykonać dla 5-6 punktów pomiarowych.

Rys. 2.8. Schemat połączeń do próby stanu zwarcia silnika indukcyjnego pierścieniowego

M. Ronkowski, G. Kostro, M. Michna:

18

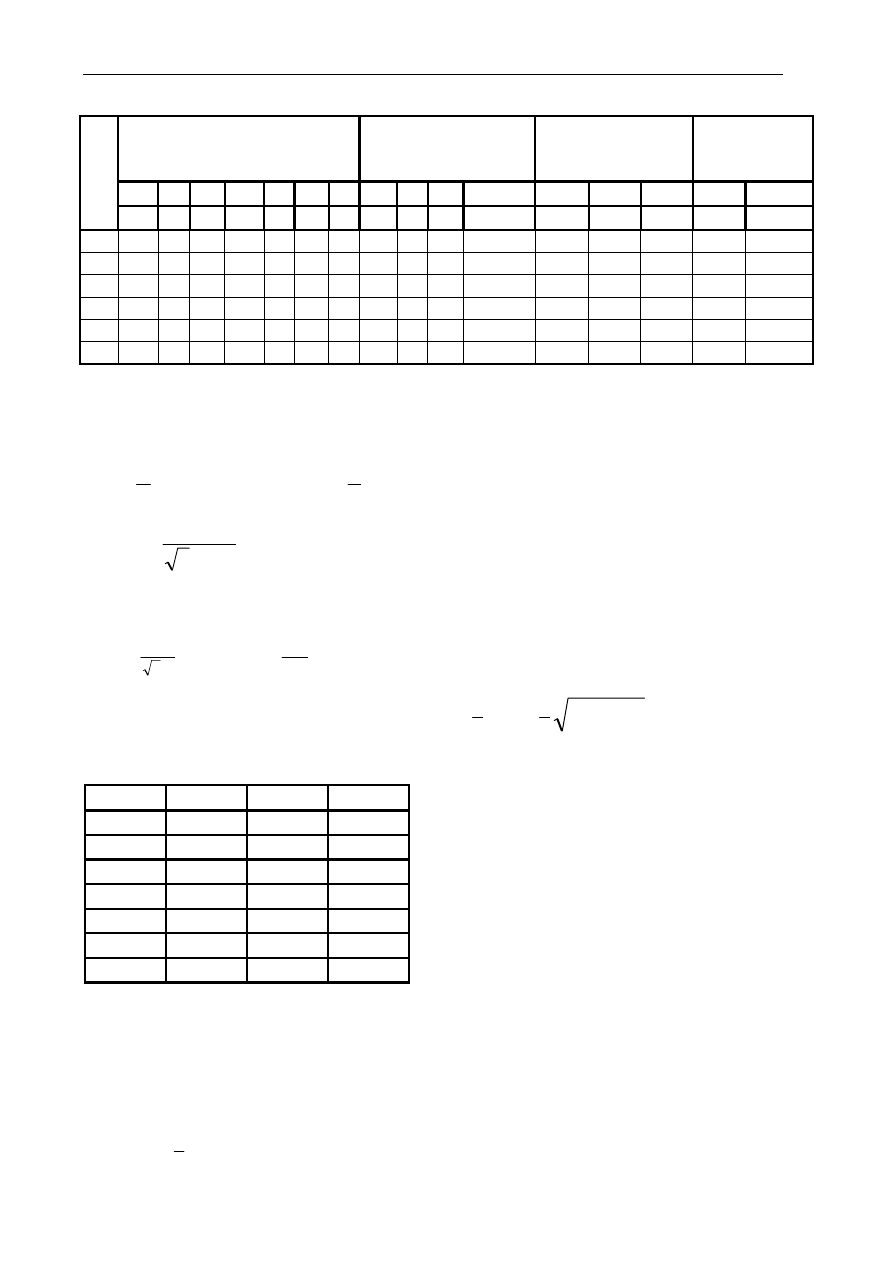
Tablica 2.5. Próba zwarcia i pomiar przekładni prądowej

Wartości pomierzone stojana Wartości obliczone -

próba zwarcia

Wartości pomierz.

wirnika

Wart. oblicz.-

przekład.

prądowa

Lp. U

s

’ I

s

’

P

’

U

s

”

I

s

”

P

”

I

s

”’

U

z

I

z

P

z

cos

ϕ

z

I

rU

I

rV

I

rW

I

r

ϑ

I

V A W V A W A V A W

−

A A A A

Opracowanie wyników próby zwarcia
W czasie wykonywanych pomiarów napięcia i prądy poszczególnych faz mogą się różnić między
sobą. Ich wartości średnie podane w tablicy 2.5. należy obliczyć wg następujących wzorów:

P

P

P

I

I

I

I

U

U

U

z

s

s

s

z

s

s

z

′′

+

′

=

′′′

+

′′

+

′

=

′′

+

′

)

(

)

(

=

3

1

2

1

z

z

z

z

I

U

P

3

cos

=

φ

Wyznaczenie parametrów gałęzi podłużnej schematu zastępczego silnika indukcyjnego

R

-

=

R

s

z

r

I

P

z

I

U

z

R

R

Z

z

z

z

z

′

=

=

2

3

3

Reaktancje rozproszeniowe:

2

2

2

1

2

1

z

z

z

r

s

R

Z

X

X

X

−

=

=

′

≅

σ

σ

Parametry schematu zastępczego

X

σs

X'

σr

R

s

R'

r

[

Ω] [Ω] [Ω] [Ω]

Uwaga:

W szczególności wyznaczyć wartości parametrów odpowiadające prądowi znamionowemu

stojana.
Opracowanie wyników pomiaru przekładni prądowej

W czasie wykonywanych pomiarów napięcia i prądy poszczególnych faz mogą się różnić między
sobą. Ich wartości średnie należy obliczyć wg. następujących wzorów (tablica 2.5):

(

)

s

s

s

s

I

I

I

I

′′′

+

′′

+

′

=

3

1

przy połączeniu uzwojeń w gwiazdę,

Ćwiczenie: Maszyny indukcyjne trójfazowe

19

(

)

s

s

s

s

I

I

I

I

′′′

+

′′

+

′

=

3

3

1

przy połączeniu uzwojeń w trójkąt,

I

r

= (I

rU

+ I

rV

+ I

rW

),

s

r

I

I

I

=

ϑ

.

2.6. Zadania

1. Obliczyć parametry schematu zastępczego badanej maszyny indukcyjnej.

Uwaga:

narysować model obwodowy i nanieść wartości parametrów odpowiadające napięciu i

prądowi znamionowego silnika.

2. Wykreślić charakterystykę strat jałowych

ΔP

o

= f (U

2

), i wyznaczyć straty przy napięciu

znamionowym:

ΔP

m

= . . . . . . . . . . [W]

ΔP

Fe

= . . . . . . . . . . [W]

Odnieść ich wartości do mocy znamionowej badanego silnika. Przeanalizować uzyskane wyniki.

3. Podać uzyskane wartości rezystancji uzwojeń, przekładnię napięciową i przekładnię prądową.

W oparciu o te wielkości narysować schemat połączeń wirnika badanego silnika.

4. Wykreślić charakterystyki zwarcia P

z

, cos

ϕ

z

, I

z

= f (U

z

). Przeprowadzić analizę oraz wyciągnąć

wnioski z ich przebiegu i wartości.

Dla

prądu znamionowego silnika porównaj wartości mocy P

Z

ze stratami w uzwojeniach

silnika, wyznaczonymi w oparciu o pomierzone wartości rezystancji:

ΔP

Cus

=

[W]

ΔP

Cur

=

[W].

Odnieść ich wartości do mocy znamionowej badanego silnika. Przeanalizować uzyskane
wyniki.
5. Obliczyć sprawność znamionową silnika w oparciu o pomierzone straty.
6. Wyznaczyć wg zależności (1.3) charakterystykę mechaniczną (moment obrotowy w funkcji

poślizgu) badanego silnika dla wyznaczonych wartości parametrów modelu obwodowego.
Wyznaczyć wartość momentu dla poślizgu znamionowego i porównać z wartością momentu
znamionowego badanego silnika (

)

/

/(

60

2

N

N

N

n

P

T

π

=

. Uzasadnić występujące różnice wartości.

2.7. Pytania kontrolne

Pytania ze znajomości teorii i zagadnień dotyczących sprawozdania

1. Podać rodzaje budowy silników indukcyjnych. Wymienić elementy stojana i wirnika silnika

indukcyjnego.

2. Opisać zasadę działania silnika indukcyjnego w ujęciu ciągu logicznego przyczyna - skutek.
3. Narysować podstawowy (elementarny) model fizyczny (układ dwóch przepływów) silnika

indukcyjnego. Wykazać analitycznie, wprowadzając dwóch obserwatorów mierzących prędkość
kątową pola wirującego wirnika, że w stanie pracy ustalonej silnika układ dwóch przepływów jest
nieruchomy względem siebie). Jakie są tego konsekwencje?

4. Opisać obraz fizyczny (składowe strumieni) i model obwodowy (schemat zastępczy) silnika

indukcyjnego dla biegu jałowego.

5. Opisać obraz fizyczny (składowe strumieni) i model obwodowy (schemat zastępczy) silnika

indukcyjnego w stanie zwarcia.

6. Narysować modele silnika indukcyjnego : fizyczny (składowe strumieni) i obwodowy (schemat

zastępczy). Podać i wyjaśnić wzajemne relacje między wielkościami modelu fizycznego a zmiennymi i
parametrami modelu obwodowego (schematu zastępczego).

7. Podać i wyjaśnić analogie modelu obwodowego (schematu zastępczego) silnika indukcyjnego i

transformatora.

8. Narysować model obwodowy (schemat zastępczy) silnika indukcyjnego, nazwać tworzące go elementy

i dokonać interpretacji fizycznej tych elementów.

M. Ronkowski, G. Kostro, M. Michna:

20

9. Podać, nazwać i objaśnić podstawowe wielkości charakterystyczne i zależności dotyczące silników

indukcyjnych (I

o

,

Φ

m

,

Φ

σ1

Φ

σ2

, E

s

, E

r

,

ϑ

I

,

ϑ

u

, I

z

, U

z

,

ΔP

Fe

,

ΔP

Cu

,

ΔP

o

,

ΔP

m

).

10. Na podstawie jakich prób wyznacza się parametry modelu obwodowego (schematu zastępczego)

silnika indukcyjnego? Podać zależności między wynikami tych prób i parametrami modelu
obwodowego.

11. Podać charakterystyki biegu jałowego badanego silnika indukcyjnego i uzasadnić fizycznie oraz

analitycznie ich kształt.

12. Podać charakterystyki zwarcia badanego silnika indukcyjnego i uzasadnić fizycznie oraz analitycznie

ich kształt.

13. Podać wykresy wartości parametrów modelu obwodowego (schematu zastępczego) badanego silnika

indukcyjnego w funkcji napięcia zasilania U

s

: oddzielnie dla gałęzi magnesującej (podłużnej) i gałęzi

zwarciowej (poprzecznej) schematu. Uzasadnić fizycznie oraz analitycznie ich kształt.

Pytania z przygotowania praktycznego do ćwiczenia

1. Podać najważniejsze dane tabliczki znamionowej silnika indukcyjnego.
2. Co to są uzwojenia stojana i wirnika, wielkości pierwotne i wtórne, silnika indukcyjnego?
3. Wymienić podstawowe metody rozruchu silnika indukcyjnego (klatkowego, pierścieniowego).
4. Wymienić podstawowe próby silnika indukcyjnego i jakie wielkości fizyczne na podstawie wyników

tych prób się wyznacza.

5. Podać orientacyjne wartości procentowe dla silników indukcyjnych:

• spadku napięcia na rezystancji zwarcia,
• prądu biegu jałowego,
• napięcia zwarcia,
• strat w żelazie, w miedzi uzwojeń i mechanicznych, a także relacje między ich wartościami,
• sprawności.

6. Podać definicję przekładni (napięciowej, prądowej) silnika indukcyjnego pierścieniowego. Dlaczego

należy wyznaczyć obie przekładnie silnika?

7. Jak należy dobrać zakresy woltomierza, amperomierza i watomierza do pomiarów biegu jałowego

silnika? Podać czy pomiary należy wykonać z poprawnie mierzonym prądem czy napięciem?

8. Jak należy dobrać zakresy woltomierza, amperomierza i watomierza do pomiarów stanu zwarcia silnika?

Podać czy pomiary należy wykonać z poprawnie mierzonym prądem czy napięciem?

9.

Wymienić podstawowe charakterystyki silnika indukcyjnego (dotyczące tematyki ćwiczenia),
wymieniając współrzędne oraz wielkości jakie należy utrzymywać stałe

.

10. Literatura

[1]

Latek W.: Zarys maszyn elektrycznych. WNT, W-wa 1974.

[2]

Latek W.: Badania maszyn elektrycznych w przemyśle. WNT, W-wa 1979.

[3]

Manitius Z.: Maszyny asynchroniczne. Skrypt. Wyd . Pol. Gdańskiej, Gdańsk 1977.

[4]

Plamitzer A.: Maszyny elektryczne. Wyd. 7. WNT, W-wa 1992.

[5]

Praca zbiorowa (red. Manitius Z.): Laboratorium maszyn elektrycznych. Skrypt. Wyd.2. Wyd. Pol.

Gdańskiej, Gdańsk 1990.

[6]

Rafalski W., Ronkowski M., Zadania z maszyn elektrycznych, Cz. I: Transformatory i maszyny

asynchroniczne, wyd. 4, Wyd. Politechniki Gdańskiej, 1994.

[7]

Roszczyk S.: Teoria maszyn elektrycznych. WNT, W-wa 1979.

[8]

Ronkowski M.: Maszyny elektryczne. Szkice do wykładów. PG 2011/2012.

http://www.eia.pg.gda.pl/e-mechatronika/

[9]

Staszewski P., Urbański W.: Zagadnienia obliczeniowe w eksploatacji maszyn elektrycznych,

Warszawa, Oficyna Wydawnicza Politechniki Warszawskiej 2009.

[10]

PN-IEC 34-1:1997

Maszyny elektryczne wirujące. Ogólne wymagania i badania

:

http://www.pkn.pl/