POLITECHNIKA GDA

Ń

SKA

WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI

KATEDRA ENERGOELEKTRONIKI I MASZYN ELEKTRYCZNYCH

L AB O R AT O R I U M

M AS Z Y N Y E L E K T R Y C Z N E

Ć

WICZENIE (TR)

TRANSFORMATORY

TRANSFORMATOR TRÓJFAZOWY

BADANIE CHARAKTERYSTYK

Materiały pomocnicze

Kierunek Elektrotechnika
Studia stacjonarne 1-szego stopnia
semestr 3

Opracowali

Mieczysław Ronkowski

Grzegorz Kostro

Michał Michna

Gda

ń

sk 2012-2013

M. Ronkowski, G. Kostro, M. Michna

:

1

ĆWICZENIE (TR)

TRANSFORMATORY

BADANIE CHARAKTERYSTYK
TRANSFORMATORA TRÓJFAZOWEGO

Program i cel ćwiczenia

1.

TEORIA.....................................................................................................................................................1

2.

BADANIA .................................................................................................................................................5

2.1.

Oględziny zewnętrzne.......................................................................................................................6

2.2.

Pomiar rezystancji uzwojeń ..............................................................................................................6

2.3.

Badanie przekładni............................................................................................................................8

2.4.

Próba stanu jałowego: badanie charakterystyk stanu jałowego......................................................10

2.5.

Próba stanu zwarcia: badanie charakterystyk zwarcia....................................................................13

2.6.

Wyznaczenie sprawności transformatora metodą strat poszczególnych ........................................17

2.7.

Wyznaczenie zmiany napięcia ........................................................................................................18

3.

ZADANIA ...............................................................................................................................................19

4.

PYTANIA KONTROLNE ......................................................................................................................20

5.

LITERATURA POMOCNICZA .............................................................................................................21

1.

TEORIA

Budowa, działanie, model fizyczny i model obwodowy transformatora

Podstawowy opis teorii transformatora (TR) zawiera rozdz. 4 e-skryptu: Ronkowski M., Michna M.,

Kostro G., Kutt F.: Maszyny elektryczne wokół nas: zastosowanie, budowa, modelowanie, charakterystyki,
projektowanie. Wyd. PG, Gdańsk, 2011.

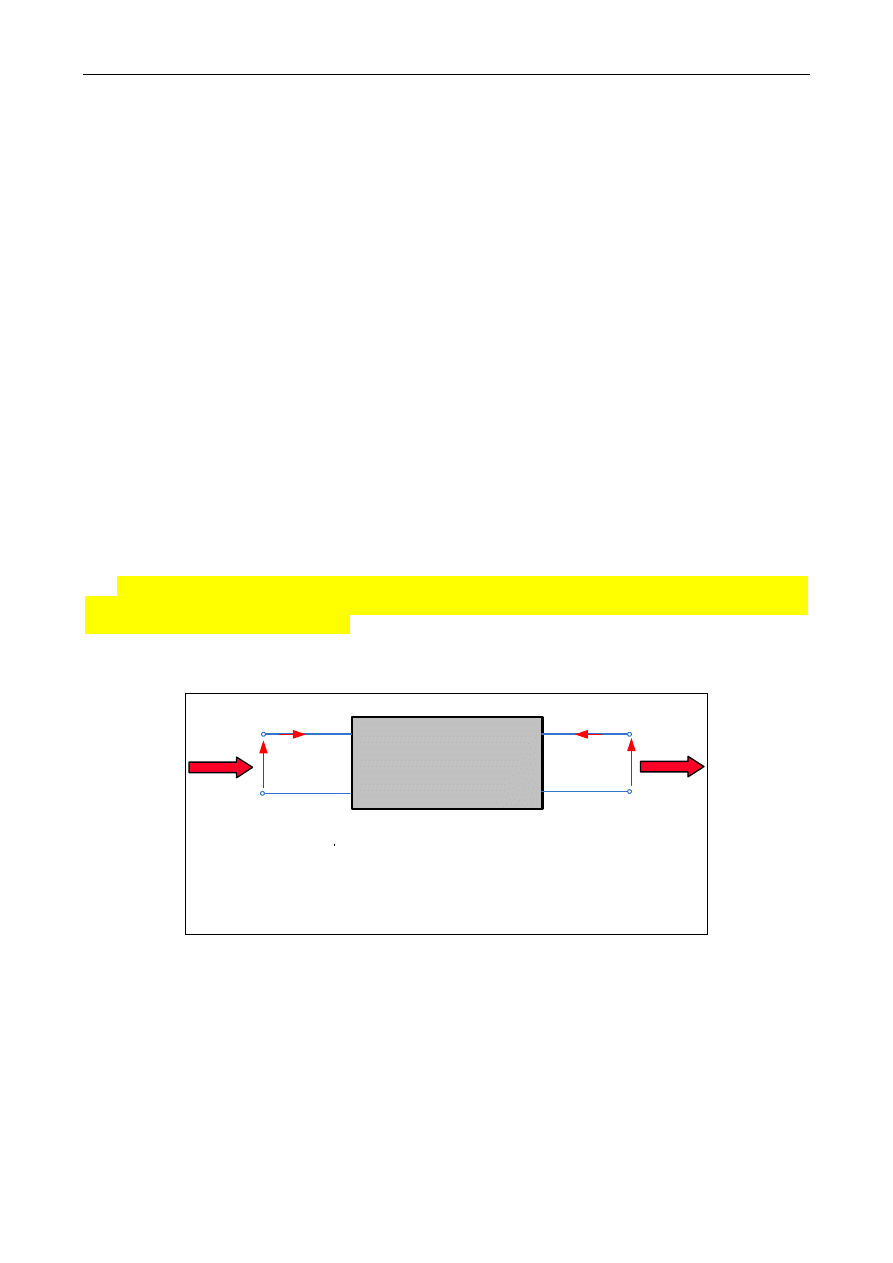
TR 1-fazowy jest przetwornikiem elektromagnetycznym (rys. 1.1a) o dwóch wrotach (parach

zacisków), które fizycznie reprezentują: zaciski uzwojenia pierwotnego „1” (zasilanego) i zaciski uzwojenia
wtórnego „2” (obciążonego).

U

1

I

1

TRANSFORMATOR

U

2

I

2

S

1

S

2

S

1

> 0

S

2

< 0

1

1'

2

2'

I

1

> 0

I

2

> 0

1 – umowny pocz

ą

tek uzwojenia pierwotnego

1' – umowny pocz

ą

tek uzwojenia pierwotnego

2 – umowny pocz

ą

tek uzwojenia wtórnego

2' – umowny pocz

ą

tek uzwojenia wtórnego

Pr

ą

d pierwotny o warto

ś

ci dodatniej (I

1

> 0) dopływa do umownego pocz

ą

tku uzwojenia

pierwotnego „1", a wypływa - z umownego ko

ń

ca uzwojenia pierwotnego „ 1'".

Pr

ą

d pierwotny o warto

ś

ci dodatniej (I

2

> 0) dopływa do umownego pocz

ą

tku uzwojenia

wtórnego „2", a wypływa - z umownego ko

ń

ca uzwojenia wtórnego„2'".

Rys. 1.1a. Transformator 1-fazowy – dwuwrotowy przetwornik elektromagnetyczny:

wrota (zaciski) obwodu pierwotnego „1” – dopływ mocy elektrycznej S

1

przetwarzanej ma moc

elektryczną S

2

, wrota (zaciski) obwodu wtórnego „2” – odpływ mocy elektrycznej S

2

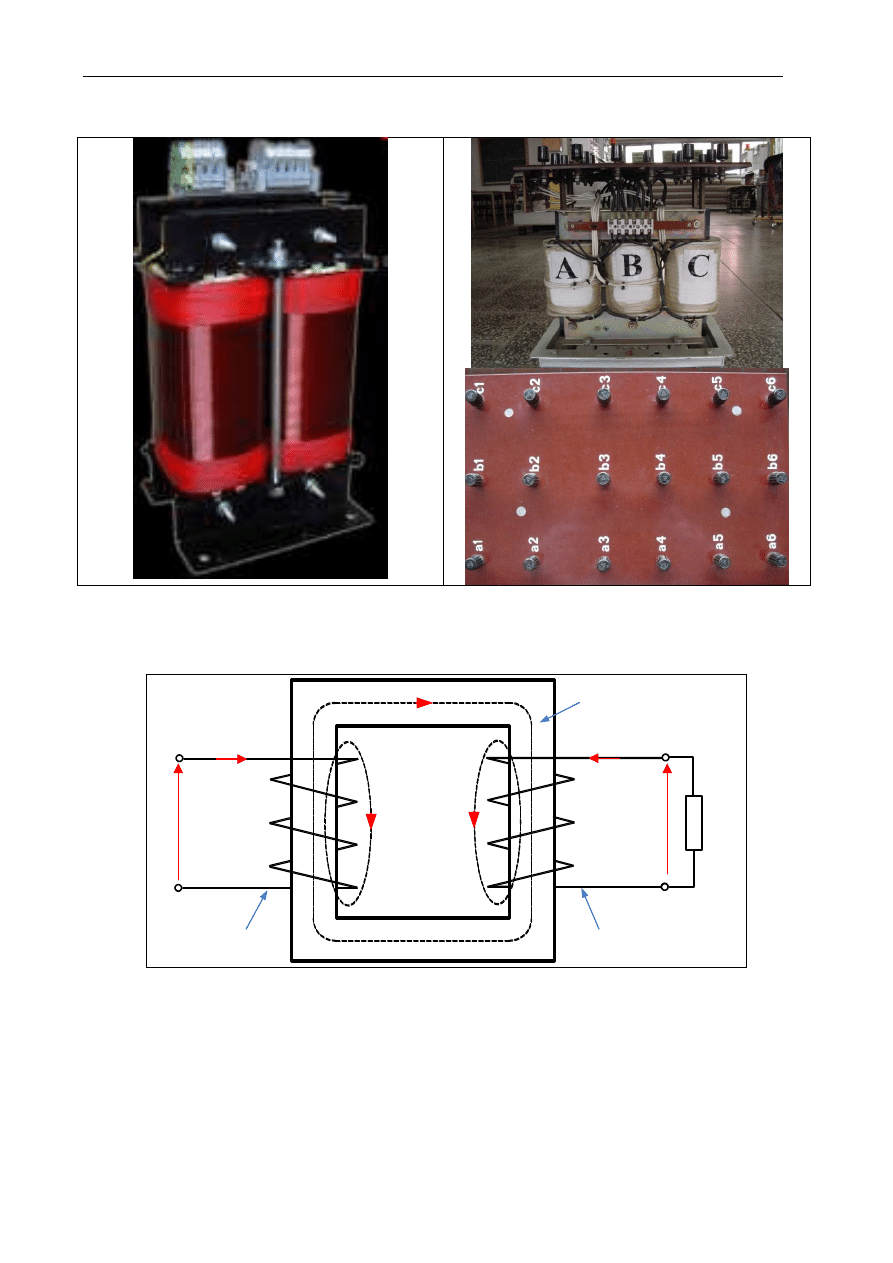
Budowę i podstawowe elementy TR 1-fazowego i 3-fazowego przedstawiono na rys. 1.1b. TR składa

się z następujących elementów czynnych: rdzenia (obwodu magnetycznego), uzwojenia pierwotnego i
uzwojenia wtórnego (obwodów elektrycznych). Np.. TR jednofazowe typu AS2 (rys. 1.1b) posiadają
uzwojenia nawinięte na karkasie lub klatce izolacyjnej, oddzielone warstwą materiału izolacyjnego,
umieszczone na dwukolumnowym rdzeniu składanym z blach transformatorowych i impregnowane
termoutwardzalną żywicą zabezpieczającą przed korozją i wilgocią. Uzwojenia strony pierwotnej i wtórnej
są wyprowadzone na zaciski śrubowe.

Na podstawowy model fizyczny TR (rozważane są zjawiska fizyczne zachodzące w TR – istotne dla

analizowanego stanu pracy) — pokazany na rys. 1.2a — składają się: elementy czynne: rdzeń, uzwojenia

2

Ćwiczenie: Transformator trójfazowy

pierwotne i wtórne; oraz zmienne fizyczne: napięcia na zaciskach uzwojeń, prądy płynące w uzwojeniach,
strumień magnetyczny główny, strumienie rozproszenia uzwojeń, straty w żelazie i straty w miedzi uzwojeń.

Rys. 1.1b. Budowa i elementy transformatów 1-fazowego (typu AS2) i 3-fazowego (Lab. ME)

Producent transformator typu AS2 – AS ELEKTROTECHNIK (http://www.as-elektrotechnik.pl/index3.php)

U

2

U

1

∆

P

Fe

z

1

z

I

1

I

2

Z

ob

Φ

σ

2

Φ

σ1

Φ

m

∆

P

Cu2

∆

P

Cu1

1

1'

2'

2

Rys.1.2a. Podstawowy model fizyczny transformatora jednofazowego w stanie obciążenia: rdzeń; cewki

uzwojeń pierwotnego i wtórnego; rozpływ strumienia głównego

Φ

m

oraz strumieni rozproszenia

Φ

σ

1

i

Φ

σ

2

; straty w żelazie

∆

P

Fe

; straty w miedzi uzwojeń

∆

P

Cu1

oraz

∆

P

Cu2

Wyróżnia się trzy podstawowe stany pracy TR: stan jałowy, stan obciążenia i stan zwarcia. Stan

obciążenia TR jest stanem pośrednim między dwoma stanami krańcowymi — stanem jałowym a stanem
zwarcia.

Stan jałowy transformatora — stan, w którym uzwojenie pierwotne zasilane jest napięciem

przemiennym U

1

, a uzwojenie wtórnego jest otwarte. Prąd płynący w uzwojeniu pierwotnym TR nazywa się

M. Ronkowski, G. Kostro, M. Michna

:

3

prądem jałowym I

o

a jego dwie składowe: składową czynną I

0cz

i bierną (magnesującą) I

m

. Wartości

prądu jałowego zwykle wyraża się w procentach prądu znamionowego I

N

TR:

[%]

100

I

o%

N

o

I

I

=

(1.1)

W TR energetycznych (mocy) wartość znamionowa prąd stanu jałowego

zawiera się w zakresie (1

−

10)% prądu znamionowego.

Zasada: im większa moc, tym na ogół mniejszy prąd stanu jałowego.

Przemienny przepływ

θ

1

= I

o

z

1

wzbudza strumień, w którym wyróżnia się

strumień magnesujący

(główny)

Φ

m

— strumień sprzężony z obydwoma uzwojeniami — oraz

strumień rozproszenia

Φ

σ

1

—

strumień sprzężony tylko z uzwojeniem własnym (zasilanym).

Efektem sprzężenia przemiennego strumienia głównego

Φ

m

z uzwojeniami jest indukowanie w nich

SEM:

44

,

4

E

1

1

f

z

m

Φ

=

44

,

4

E

2

2

f

z

m

Φ

=

E

20

2

U

=

(1.2)

gdzie: z

1

, z

2

−

liczba zwojów odpowiednio uzwojenia pierwotnego i wtórnego,

f

−

częstotliwość napięcia zasilania U

1

.

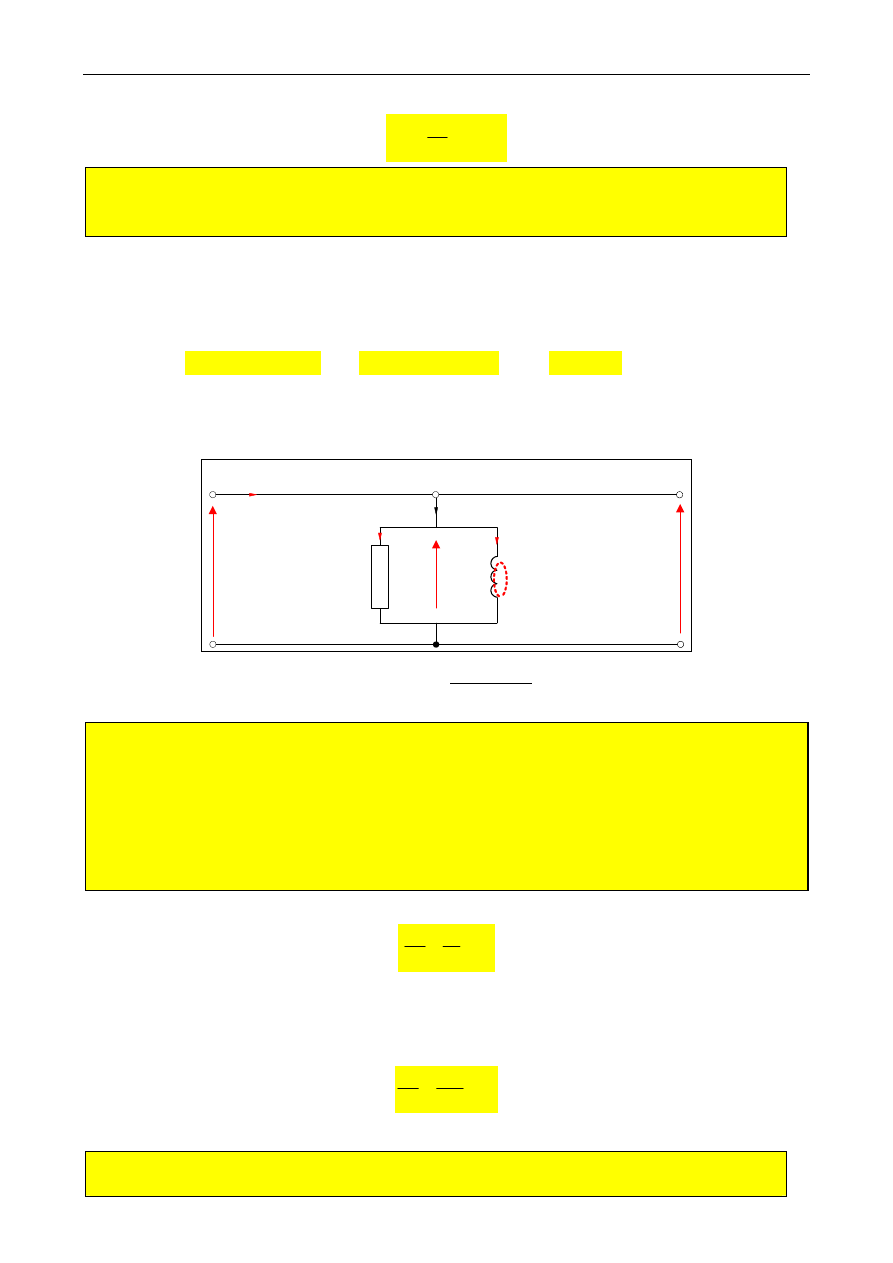
Model obwodowy (schemat zastępczy) TR 1-fazowego w stanie jałowym przedstawiono na rys.

1.2b.

I

m

E

1

U'

20

U

1

I

0

I

0cz

R

Fe

X

m

I

0

Φ

m

E’

2

Rys.1.2b. Model obwodowy (schemat zastępczy) uproszczony transformatora w stanie jałowym.

Uzwojenie wtórne o liczbie zwojów z

2

przezwojono(zredukowano) do liczby zwojów z’

2

= z

1

Właściwości TR w stanie jałowym określone są głównie przez

strumień magnesujący (główny)

Φ

m

i stratami rdzenia magnetycznego

∆

P

Fe

.

Właściwości te odwzorowuje się wielkościami obwodowymi:

X

m

−

reaktancją magnesująca modelującą strumień główny TR, tzn. E

1

= I

m

X

m

,

R

Fe

−

rezystancją modelującą straty w żelazie (jałowe)

∆

P

Fe

TR, tzn.

∆

P

Fe

= m I

0cz

E

1

.

Uwaga: TR w stanie jałowym jest obiektem nieliniowym, ze względu na zachodzące zjawisko nasycenia

obwodu magnetycznego strumienia magnesującego – skutek zasilanie napięciem U

1

= U

1N

.

Dzieląc stronami zależności (1.2) stronami otrzymuje się charakterystyczną wielkość:

z

z

z

ϑ

=

=

2

1

2

1

E

E

(1.3)

którą nazywa się

przekładnią zwojową

z

ϑ

TR.

Dla TR jednofazowego napięcie na jego zaciskach wtórnych w stanie jałowym U

20

jest równe SEM E

2

.

Biorąc pod uwagę, że SEM E

1

jest w przybliżeniu równa napięciu pierwotnemu U

1

(pomijamy spadki

napięcia R

1

I

0

oraz X

σ

1

I

0

) można napisać:

u

U

U

ϑ

=

≈

20

1

2

1

E

E

(1.4)

Stosunek U

1

/U

20

nazywa się

przekładnią napięciową

ϑ

u

TR.

W TR jednofazowym przekładnia napięciowa odpowiada praktycznie stosunkowi liczby zwojów —

zgodnie z zależnością (1.4).

4

Ćwiczenie: Transformator trójfazowy

W TR trójfazowym należy uwzględnić jeszcze współczynnik liczbowy wynikający z zastosowanego

skojarzenia uzwojeń

(patrz p. 1.4. ćwiczenia 1).

Stan obciążenia transformatora — stan, w którym uzwojenie wtórne jest zamknięte przez impedancję

Z

ob

i w uzwojeniu tym płynie prąd I

2

— prąd wymuszony przez SEM E

2

.

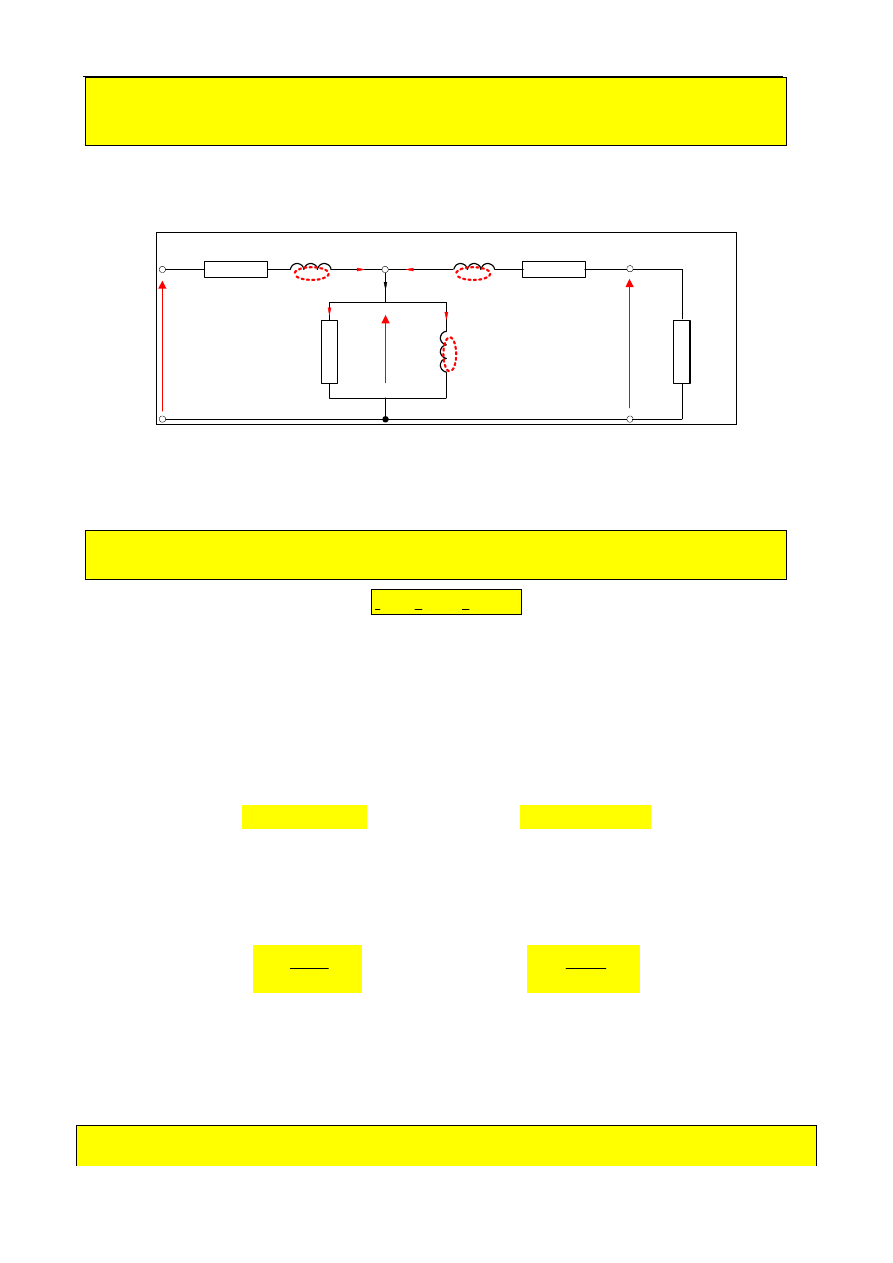
Model obwodowy (schemat zastępczy) TR 1-fazowego w stanie obciążenia przedstawiono na rys.1.2c.

I

m

E

1

U'

2

U

1

I

0

I

0cz

R

Fe

X

m

I

1

I'

2

R'

2

R

1

X

σ1

X'

σ2

Z'

ob

Φ

'

σ

2

Φ

σ1

Φ

m

E’

2

Rys.1.2c. Model obwodowy (schemat zastępczy) transformatora w stanie obciążenia

W TR obciążonym strumień główny

Φ

m

powstaje przez współdziałanie przepływów obu uzwojeń:

przepływu pierwotnego I

1

z

1

i przepływu wtórnego I

2

z

2

.

W zakresie obciążeń znamionowych transformatora suma (geometryczna) przepływów obu

uzwojeń jest równa przepływowi stanu jałowego — moduł ma stałą wartość.

[A]

I

1

2

2

1

1

z

I

z

I

z

o

=

+

(1.5)

Powyższe równanie —

równanie równowagi przepływów (podstawowe równanie transformatora) —

wynika z podstawowej zasady pracy transformatora — tendencji do wzbudzenia ekstremalnego strumienia,
innymi słowy tendencji do zmagazynowania ekstremalnego energii w polu magnetycznym transformatora.

Efektem działania przepływu wtórnego I

2

z

2

jest wzbudzenie strumienia rozproszenia uzwojenia

wtórnego

Φ

σ

2

(strumień sprzężony tylko z uzwojeniem wtórnym), a na skutek wzrostu prądu pierwotnego I

1

zwiększa się strumień rozproszenia uzwojenia pierwotnego

Φ

σ

1

. Strumienie rozproszenia

Φ

σ

1

i

Φ

σ

2

indukują

odpowiednio w uzwojeniu pierwotnym i wtórnym SEM E

σ

1

oraz E

σ

2

, które można odwzorować za pomocą

wielkości obwodowych — spadku napięcia na

reaktancji rozproszenia uzwojenia pierwotnego X

σ

1

oraz

wtórnego X

σ

2

:

[V]

E

1

1

1

I

X

σ

σ

=

[V]

E

2

2

2

I

X

σ

σ

=

(1.6)

Ponadto prądy w obu uzwojeniach transformatora powodują spadki napięcia na rezystancjach uzwojenia
pierwotnego R

1

oraz wtórnego R

2

.

Istotny wpływ na właściwości transformatora w stanie obciążenia mają straty w miedzi uzwojenia

pierwotnego

∆

P

Cu1

i wtórnego

∆

P

Cu2

— nazywane także

stratami obciążeniowymi. Za ich miarę można

przyjąć wielkości obwodowe — rezystancje uzwojeń — zdefiniowane następująco:

]

[

R

2

1

1

1

Ω

∆

=

I

m

P

Cu

]

[

m

R

2

2

2

2

Ω

∆

=

I

P

Cu

(1.7)

gdzie, m

−

liczba faz transformatora.

Model obwodowy (schemat zastępczy) TR — przedstawiony na rys.1.2c — jest podstawą analizy TR w

stanie obciążenia. Model ten odpowiada TR zredukowanemu (sprowadzonemu) do przekładni

1

====

z

ϑ

.

Topologia i elementy modelu wynikają z podanych wyżej rozważań zjawisk fizycznych (przyjętego modelu
fizycznego na rys.1.2a) dotyczących stanu jałowego i stanu obciążenia TR.

Parametry modelu obwodowego

TR (rys. 1.2c):

rezystancja R

Fe

i reaktancja X

m

są wielkościami nieliniowymi

M. Ronkowski, G. Kostro, M. Michna

:

5

zależnymi od wartości strumienia głównego i rodzaju blachy rdzenia

pozostałe parametry modelu obwodowego

można przyjąć jako stałe (liniowe).

Stan zwarcia pomiarowego transformatora (lub krótko stan zwarcia TR) — stan TR, w którym

strona wtórna jest zwarta (U

2

= 0), zaś uzwojenie pierwotne jest zasilane odpowiednio obniżonym

napięciem, tzn. takim, które wymusza w obu uzwojeniach prądy o wartościach znamionowych.

Wartość napięcia, jakie należy przyłożyć do zacisków pierwotnych TR

przy zwartym uzwojeniu wtórnym

celem wymuszenia w obu jego uzwojeniach przepływu prądów znamionowych I

1N

oraz I

2N

nazywa się napięciem zwarcia.

Napięcia zwarcia jest ważnym parametrem TR — podanym na tabliczce znamionowej, określanym

zwykle w procentach napięcia znamionowego, wg następującej zależności:

[%]

100

U

Z

%

100

U

1N

z

1

1

1

z%

⋅

=

⋅

=

N

N

z

I

U

U

(1.8)

gdzie:

U

z%

−

napięcie zwarcia procentowe,

U

1z

−

napięcie zwarcia (fazowe) mierzone w woltach,

U

1N

−

napięcie znamionowe (fazowe),

I

1N

−

prąd znamionowy (fazowy),

Z

z

−

impedancja zwarcia transformatora.

Dla normalnych TR energetycznych napięcie zwarcia zawiera się w zakresie

(3

−

15)% napięcia znamionowego.

Zasada: im większa moc, tym na ogół większe napięcie zwarcia.

W stanie zwarcia transformatora, ze względu znacznie obniżony poziom strumienia magnesującego

(zasilanie napięciem zwarcia U

1z

<< U

1N

), wartość prądu jałowego w bilansie przepływów jest pomijalnie

mała:

[A]

0

I

2

2

1

1N

≈

+

z

I

z

N

lub

I

2

2

1

1N

z

I

z

N

−

≈

(1.9)

Stąd dla modułów mamy:

[A]

1

2

1

2

2

1

z

N

N

N

I

z

z

I

I

ϑ

=

≈

lub

[A]

1

2

2

z

N

N

I

I

ϑ

=

′

(1.10)

a zredukowane wartości rezystancji i reaktancji rozproszenia w tym obwodzie wyznaczają zależności:

2

2

2

R

R

z

ϑ

=

′

2

2

2

σ

σ

ϑ

X

X

z

=

′

(1.12)

Właściwości transformatora w stanie zwarcia określone są głównie przez

strumienie rozproszenia uzwojenia pierwotnego

Φ

σ

1

i wtórnego

Φ

σ

2

oraz stratami w miedzi

∆

P

Cu1

oraz

∆

P

Cu2

zależnymi od wymiarów i rozmieszczenia uzwojeń.

Właściwości te odwzorowuje się wielkościami obwodowymi:

R

z

= R

1

+ R’

2

−

rezystancja zwarcia transformatora,

X

z

= X

σ

1

+ X’

σ

2

−

reaktancja zwarcia transformatora,

z

z

z

X

j

R

Z

+

=

−

impedancja zwarcia transformatora.

Uwaga: Wstanie zwarcia TR jest obiektem liniowym, ze względu znacznie obniżony poziom

strumienia magnesującego (zasilanie napięciem zwarcia U

1z

<< U

1N

). Stąd zarówno zjawisko nasycenia

obwodu magnetycznego jak i straty w rdzeniu (żelazie) są pomijalnie małe. Ponadto, część obwodu
magnetycznego strumieni rozproszenia zamyka się przez powietrze, stąd strumienie rozproszenia zależą
linowo od odpowiednich prądów uzwojeń. Zatem model obwodowy TR w stanie zwarcia otrzymujemy
przez uproszczenie modelu obwodowego TR dla stanu obciążenia (rys. 1.2c) – usuwamy w nim gałąź
magnesującą.

Wartości parametrów modelu obwodowego

TR (rys. 1.2c) wyznacza się na podstawie wyników

dwóch prób:

stanu jałowego i stanu zwarcia — opisanych w p. 1.5 oraz 1.6 niniejszego ćwiczenia.

6

Ćwiczenie: Transformator trójfazowy

2.

BADANIA

2.1.

Oględziny zewnętrzne

Należy dokonać oględzin zewnętrznych badanego transformatora i urządzeń wchodzących w skład

układu pomiarowego. Przede wszystkim należy dokładnie przeczytać i wynotować dane zawarte w

tabliczce

znamionowej transformatora.
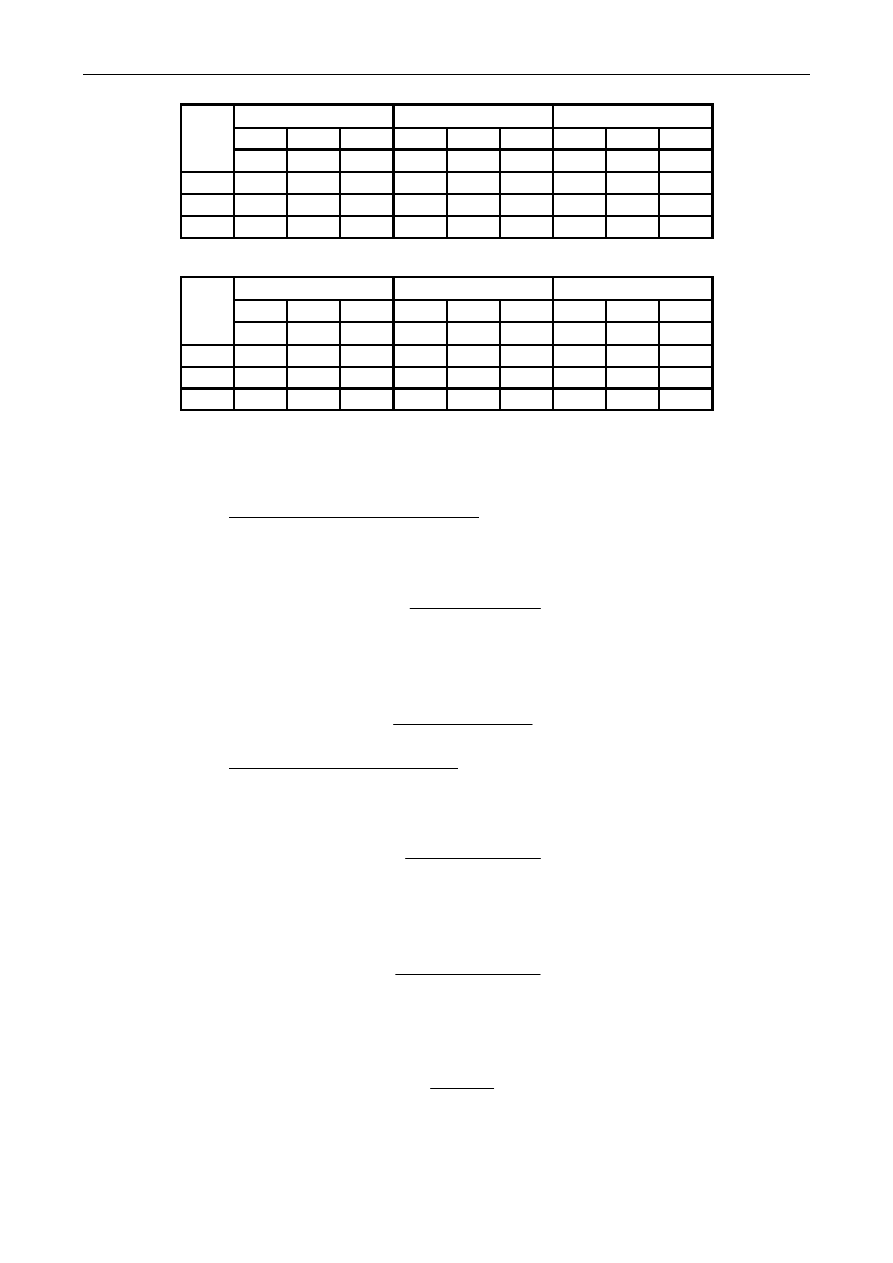
Tabliczka znamionowa transformatora (tabl. 1.1) najczęściej zawiera następujące dane (wg. PN/E-06040):

Tablica 1.1

Lp.

Dane znamionowe transformatora

Jednostka

Wartość

1

nazwę lub znak wytwórcy

-

2

nazwę i typ wyrobu

-

3

numer fabryczny

-

4

rok wykonania

-

5

liczba faz

-

6

częstotliwość znamionowa

Hz

7

moc znamionowa

kVA

8

napięcia znamionowe (U

g

/U

d

)

V

/

9

prądy znamionowe (I

g

/I

d

)

A

/

10

zmierzone napięcie zwarcia

%

11

zmierzone straty jałowe

W

12

zmierzone straty w stanie zwarcia

W

13

symbol znamionowego rodzaju pracy

-

14

symbol grupy połączeń uzwojeń

-

Uwaga !

Przez cały czas ćwiczenia należy pamiętać wartości prądów znamionowych transformatora. Wartości

tych nie powinno się niepotrzebnie przekraczać.

Należy spisać dane znamionowe użytych przyrządów pomiarowych

(woltomierzy, amperomierzy, watomierzy).

2.2.

Pomiar rezystancji uzwojeń

♦

Przebieg pomiaru rezystancji uzwojeń.

Zasady pomiaru rezystancji uzwojeń.

•

Pomiar wykonać metodą techniczną, uwzględniając układ połączeń uzwojeń transformatora.

•

Dobrać odpowiednie zakresy mierników:
amperomierza — podstawą doboru są prądy znamionowe transformatora;
woltomierza — podstawą doboru są procentowe napięcie zwarcia i procentowa sprawność
transformatora.

•

Pomiar rezystancji uzwojeń transformatora wykonać dla trzech wartości prądu.

•

Wyniki pomiarów należy notować w tablicy 1.2a
(dotyczy bezpośredniego pomiaru rezystancji fazowych uzwojeń transformatora).

•

Należy zanotować temperaturę otoczenia

τ

x

(przy szybkim pomiarze można przyjąć, że pomierzone wartości rezystancji dotyczą temperatury
równej temperaturze otoczenia).

M. Ronkowski, G. Kostro, M. Michna

:

7

Tablica 1.2a

Zaciski a1

−

a2

Zaciski b1

−

b2

Zaciski c1

−

c2

Lp.

U

I

R

1a

U

I

R

1b

U

I

R

1c

V

A

Ω

V

A

Ω

V

A

Ω

Tablica 1.2b

Zaciski a3

−

a6

Zaciski b3

−

b6

Zaciski c3

−

c6

Lp.

U

I

R

2a

U

I

R

2b

U

I

R

2c

V

A

Ω

V

A

Ω

V

A

Ω

τ

x

= . . . . .

o

C

♦

Opracowanie wyników pomiaru rezystancji uzwojeń.

Wartości średnie rezystancji uzwojeń (rezystancji fazowych) należy obliczyć wg. podanej niżej

procedury.

Wartość średnia rezystancji fazowej strony pierwotnej R

1

:

•

obliczyć dla trzech pomierzonych spadków napięć U oraz prądów I odpowiadające im wartości
rezystancji uzwojenia „a1-a2” strony pierwotnej — oznaczone kolejno symbolami R

1a1

, R

1a2

, R

1a3

;

•

następnie obliczyć wartość średnią rezystancji uzwojenia „a1-a2” wg. zależności:

3

3

1

2

1

1

1

a

a

a

1aśr

R

R

R

R

+

+

=

(1.13)

•

analogicznie obliczyć wartości średnie rezystancji R

1Bśr

oraz R

1Cśr

— odpowiadające uzwojeniu „B1-

B2” oraz „C1-C2” strony pierwotnej;

•

następnie wyznaczyć wartość średnią rezystancji fazowej strony pierwotnej:

R

R

R

R

cśr

bśr

aśr

1

3

1

1

1

+

+

=

(1.14)

Wartość średnia rezystancji fazowej strony wtórnej R

2

:

•

obliczyć dla trzech pomierzonych spadków napięć U oraz prądów I odpowiadające im wartości
rezystancji uzwojenia „a3-a6” strony wtórnej — oznaczone kolejno symbolami R

2a1

, R

2a2

, R

2a3

;

•

następnie obliczyć wartość średnią rezystancji uzwojenia „a1-a6” wg. zależności:

3

3

2

2

2

1

2

a

a

a

2aśr

R

R

R

R

+

+

=

(1.15)

•

analogicznie obliczyć wartości średnie rezystancji R

2bśr

oraz R

2cśr

— odpowiadające uzwojeniu „b3-

b6” oraz „c3-c6” strony wtórnej;

•

następnie wyznaczyć wartość średnią rezystancji fazowej strony wtórnej:

3

2

2

2

cśr

bśr

aśr

2

R

R

R

R

+

+

=

(1.16)

Wyniki obliczeń rezystancji uzwojeń badanego transformatora zestawić w odpowiedniej tabeli.

W praktyce wartości rezystancji R

1

oraz R

2

we wzorach (1.14) i (1.16) — pomierzone w temperaturze

τ

x

— przelicza się do umownej temperatury odniesienia

τ

o

(temperatury pracy) wg. zależności:

R

[ ]

τ

τ

τ
τ

o

x

o

x

R

=

+
+

235

235

Ω

(1.17)

gdzie:

R

τ

x

−

wartość rezystancji pomierzona w temperaturze

τ

x

,

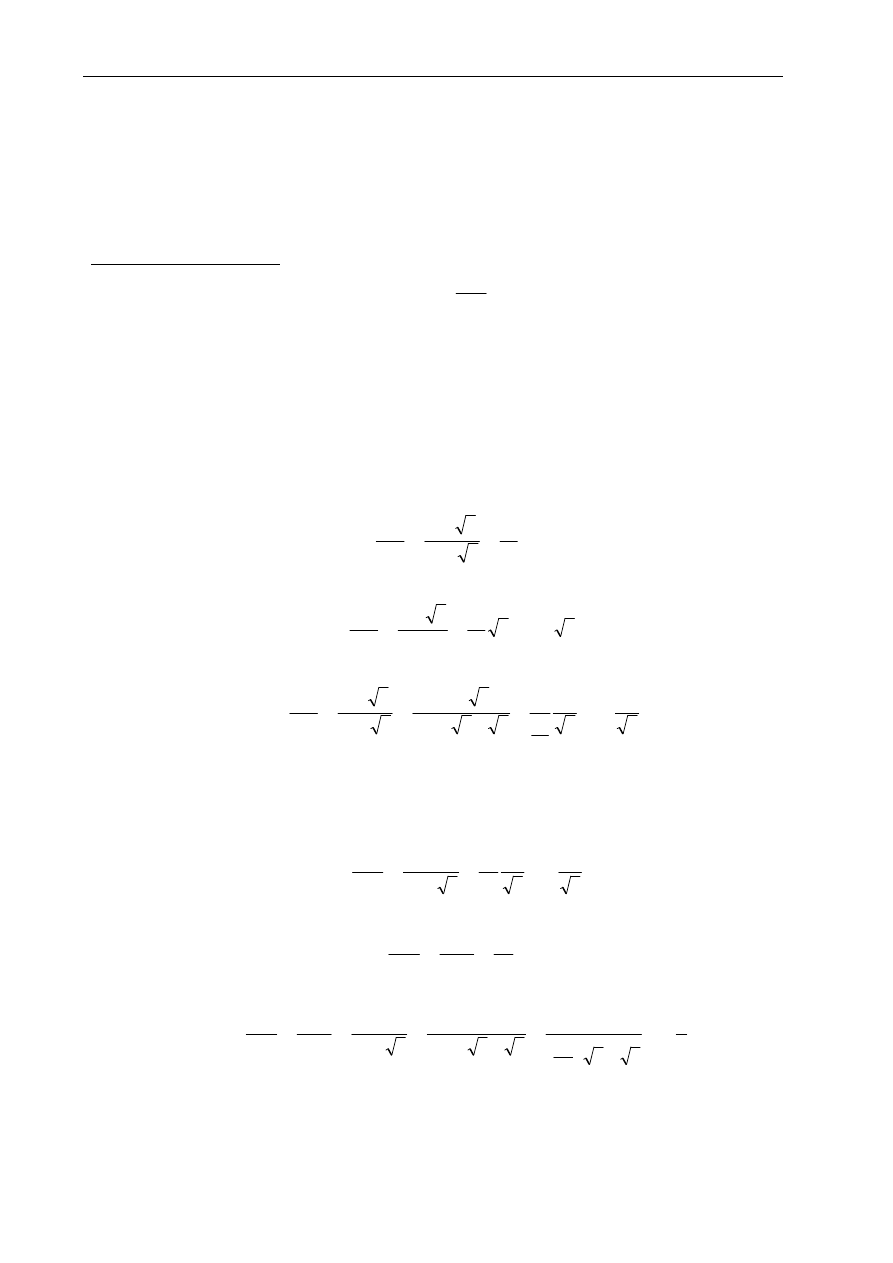
8

Ćwiczenie: Transformator trójfazowy

τ

o

−

temperatura odniesienia, np. dla klasy izolacji A, E, B wynosi 75

o

C, a dla klasy izolacji F, H

wynosi 115

o

C.

Należy przeliczyć wg. podanej wyżej zależności wartości średnie rezystancji fazowych R

1

oraz R

2

do

temperatura odniesienia

τ

o

odpowiadające klasie izolacji badanego transformatora.

2.3.

Badanie przekładni

♦

Definicja przekładni.

Zgodnie z normą PN /E-06040 przekładnia transformatora trójfazowego jest równa stosunkowi

(wartość większa od jedności) napięć międzyprzewodowych, odpowiednio górnego i dolnego napięcia:

u

ϑ =

U

U

g

do

(1.18)

Znajomość przekładni transformatora jest niezbędna przy analizie jego pracy samodzielnej i równoległej.
Pozwala ona określić napięcia strony wtórnej przy zadanych napięciach strony pierwotnej oraz przeliczać
parametry schematu zastępczego, dane dla jednej strony, na stronę drugą.

Przekładnie napięciowa

ϑ

u

transformatora trójfazowego, w związku z różnymi kombinacjami połączeń

jego uzwojeń, różni się na ogół od przekładni zwojowej

z

ϑ

. Poniżej podano zależności między tymi

przekładniami dla różnych układów połączeń. W zależnościach tych symbole U

1

i U

2o

oznaczają napięcia

międzyprzewodowe stanu jałowego, a U

1f

i U

2fo

odpowiednie napięcia fazowe.

1. Układy z uzwojeniem pierwotnym połączonym w gwiazdę:

•

układy Yy

u

z

fo

f

o

z

z

U

U

U

U

ϑ

ϑ

====

≈≈≈≈

====

====

2

1

2

1

2

1

3

3

(1.19)

•

układ Yd

u

3

3

3

2

1

2

1

2

1

⋅⋅⋅⋅

====

≈≈≈≈

====

====

z

fo

f

o

z

z

U

U

U

U

ϑ

ϑ

(1.20)

•

układ Yz

3

2

3

1

2

3

3

3

3

3

2

1

2

1

2

1

2

1

z

x

fo

f

fo

f

o

z

z

U

U

U

U

U

U

ϑ

ϑ

====

≈≈≈≈

⋅⋅⋅⋅

⋅⋅⋅⋅

====

====

====

)

(

u

(1.21)

gdzie:

U

fo

x
2

−

napięcie połowy zwojów fazy wtórnej.

2. Układy z uzwojeniem pierwotnym połączonym w trójkąt:

−

układ Dy

ϑ

ϑ

u

=

=

≈

=

U

U

U

U

z

z

o

f

fo

1

2

1

2

1

2

3

1

3

1

3

(1.22)

•

Układ Dd

ϑ

ϑ

u

=

=

≈

=

U

U

U

U

z

z

o

f

fo

1

2

1

2

1

2

(1.23)

•

Układ Dz

ϑ

ϑ

u

=

=

=

=

⋅

≈

⋅

⋅

=

U

U

U

U

U

U

U

U

z

z

o

f

fo

f

fo

f

fo

x

1

2

1

2

1

2

1

2

1

2

3

3

3

2

3

3

2

3

(

)

(

)

(1.24)

♦

Przebieg pomiaru przekładni.

Pojęciem ścisłym jest pojęcie przekładni zwojowej. Natomiast pojęcie przekładni napięciowej jest

związane z uproszczeniem (dopuszczalnym w praktyce), wynikającym z pominięcia spadków napięć: w
uzwojeniu pierwotnym (od przepływu prądu jałowego) i w uzwojeniu wtórnym (od przepływu prądu
pobieranego przez woltomierz) w czasie pomiaru napięć na zaciskach transformatora. Zatem, celem

M. Ronkowski, G. Kostro, M. Michna

:

9

ograniczenia błędu pomiarowego, pomiary przekładni napięciowej należy wykonać w zakresie
prostoliniowej części charakterystyki magnesowania rdzenia transformatora, a więc przy obniżonym
napięciu.

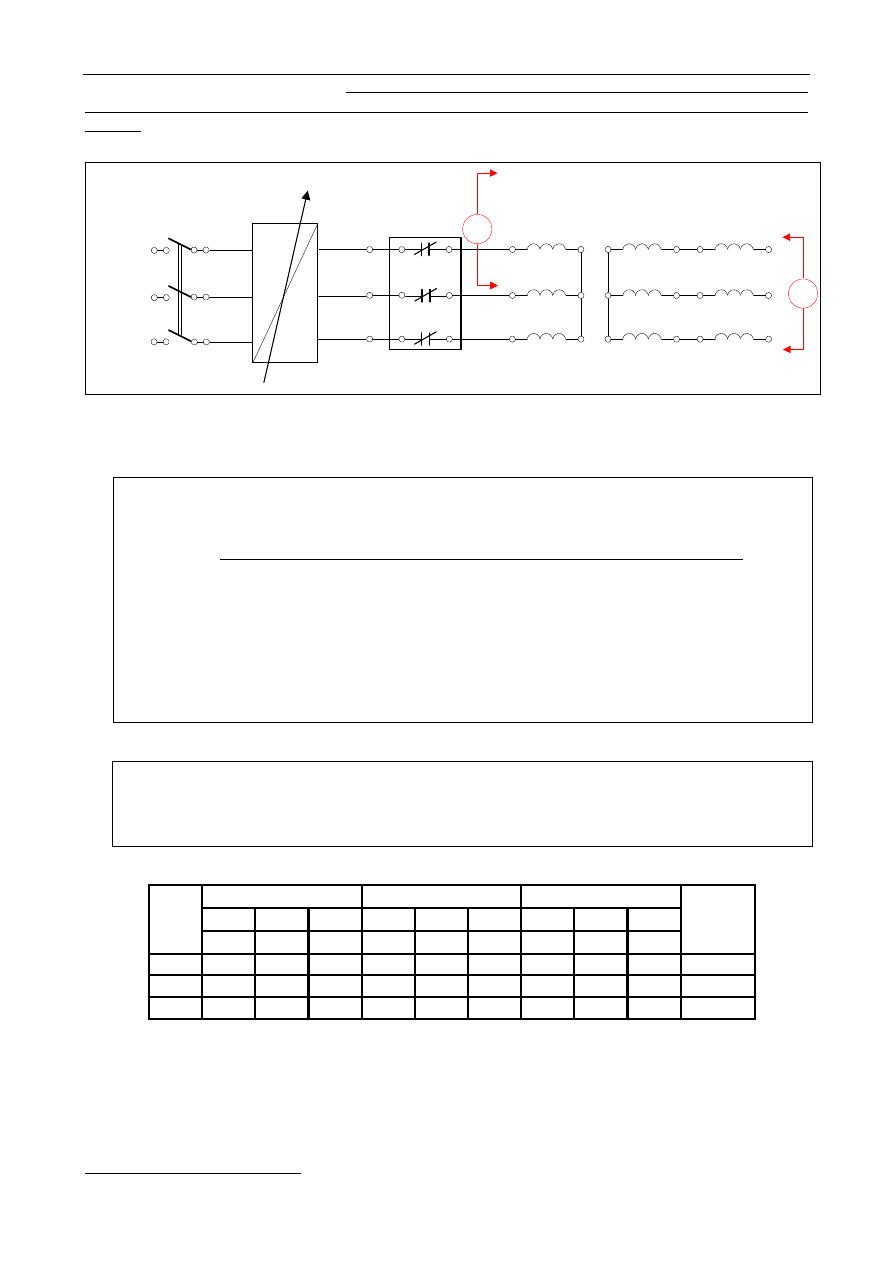
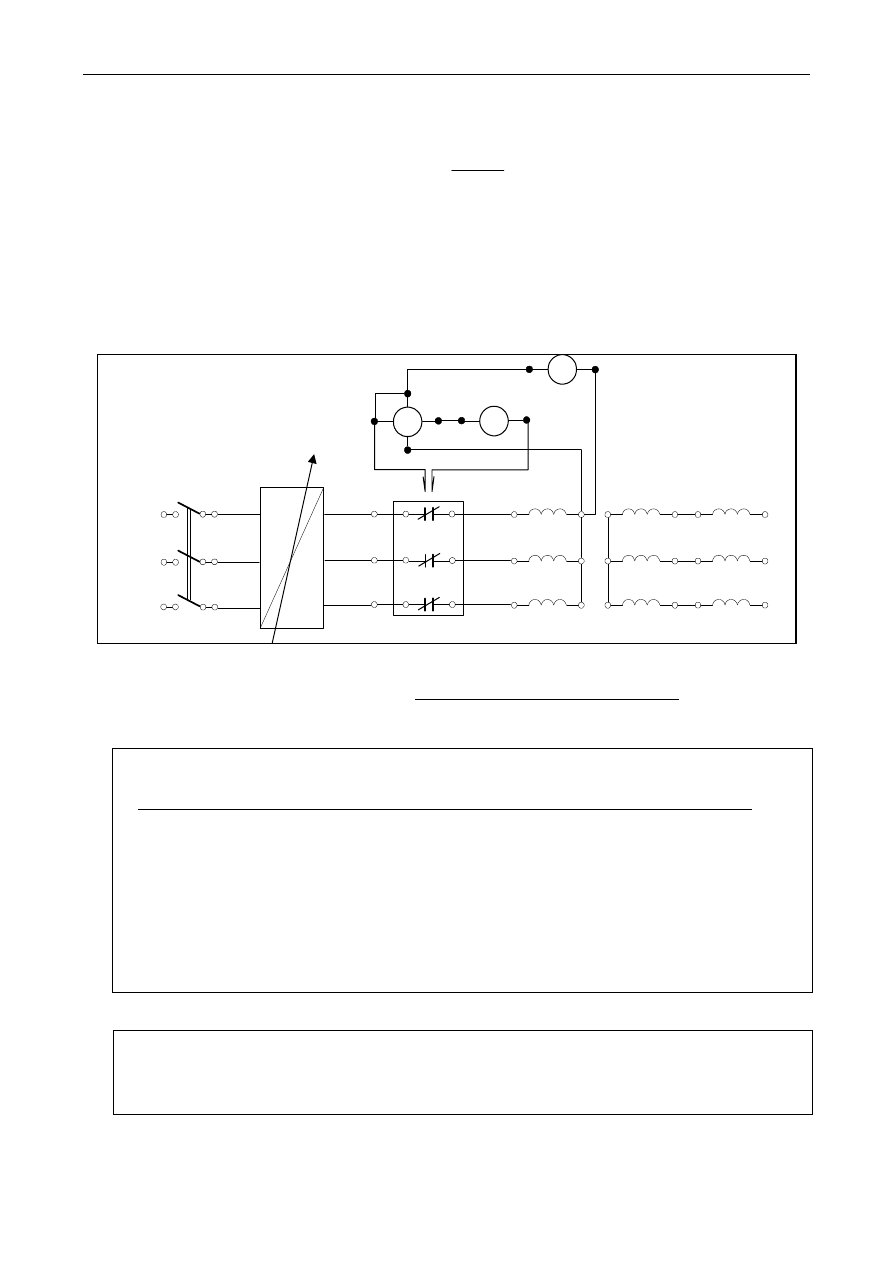
Schemat układu pomiarowego dla układu połączeń Yy przedstawiony jest na rys. 1.3.

1)

a6

b6

PW

V

V

~3 X 380 V

RN

R

S

T

a1

a3

a4 a5

b3

b4 b5

c3

c4 c5

c6

a2

b1

b2

c1

c2

Uwaga: mierzymy napięcia przewodowe

Rys. 1.3. Schemat dla pomiaru przekładni transformatora: RN

−

regulator napięcia; PW - przełącznik

watomierzowy

Uwagi ogólne do pomiaru przekładni transformatora.

•

Transformator powinien być zasilany napięciem trójfazowym, możliwie symetrycznym, po stronie
górnego napięcia.

•

Pomiar przekładni należy wykonać metodą woltomierzową.

•

Ze względu na dopuszczalny błąd pomiaru ± 0,5% należy zastosować woltomierz klasy 0,2 o
stosunkowo dużej wartości rezystancji wewnętrznej.

•

Wg. normy PN/E-06040 pomiary należy przeprowadzić dla wszystkich par uzwojeń.

•

Woltomierze należy przyłączyć bezpośrednio do zacisków transformatora.

•

Celem zmniejszenia uchybu, spowodowanego niesymetrią napięć, należy włączyć woltomierze
między zaciski oznakowane tymi samymi literkami po stronie pierwotnej i wtórnej, np. pary
zacisków oznakowane „a1-b1/a6-b6” itp.

•

Pomiary przekładni należy wykonać dla co najmniej dwu różnych układów połączeń uzwojeń (dla
celów porównawczych) — podanych przez prowadzącego ćwiczenia.

W czasie pomiarów należy:

•

Zmieniać wartość napięcia zasilania za pomocą regulator napięcia RN.

•

Celem zmniejszenia uchybu przypadkowego, przeprowadzić pomiary dla trzech wartości napięcia,
zawartych w przedziale od 0,1 do około 0,7 napięcia znamionowego.

•

Wyniki pomiarów notować w tablicy 1.3.

Tablica 1.3

a1

−

b1/a6

−

b6

b1

−

c1/b6

−

c6

c1

−

a1/c6

−

a6

Lp.

U

1

U

2o

ϑ

uab

U

1

U

2o

ϑ

ubc

U

1

U

2o

ϑ

uca

Układ

V

V

−

V

V

−

V

V

−

połącz.

♦

Opracowanie wyników pomiaru przekładni

Wartość średnią przekładni napięciowej należy obliczyć wg. podanej niżej procedury.

•

obliczyć dla trzech pomierzonych napięć U

1

oraz U

2o

odpowiadające im kolejne wartości przekładni

pary uzwojeń „a1

−

b1/a6

−

b6” wg zależności:

1)

Oznaczenia końców uzwojenia pierwotnego i wtórnego nie są zgodne z normą PN/E-81003.

10

Ćwiczenie: Transformator trójfazowy

o

uab

U

U

2

1

=

ϑ

(1.25)

oznaczone kolejno symbolami

ϑ

uab1

,

ϑ

uab2

,

ϑ

uab3

;

•

następnie obliczyć wartość średnią przekładni pary uzwojeń „a1

−

b1/a6

−

b6”:

3

uab

uab

uab

uabśr

3

2

1

ϑ

+

ϑ

+

ϑ

=

ϑ

(1.26)

•

analogicznie obliczyć wartości średnie przekładni pary uzwojeń „b1

−

c1/b6

−

c6” oraz „c1

−

a1/c6

−

a6”

— oznaczone kolejno symbolami

ϑ

ubcśr

,

ϑ

ucaśr

•

następnie wyznaczyć wartość średnią przekładni napięciowej transformatora:

3

ucaśr

ubcśr

uabśr

u

ϑ

+

ϑ

+

ϑ

=

ϑ

(1.27)

2.4.

Próba stanu jałowego: badanie charakterystyk stanu jałowego

♦

Podstawy próby stanu jałowego

Cel podstawowy próby stanu jałowego transformatora: pomiary wartości strat jałowych i prądu

jałowego przy napięciu znamionowym.

Próba stanu jałowego polega na zasilaniu transformatora z dowolnej strony i pomiarze pobieranego

przez transformator prądu i mocy. W czasie pomiaru uzwojenie wtórne transformatora jest otwarte.

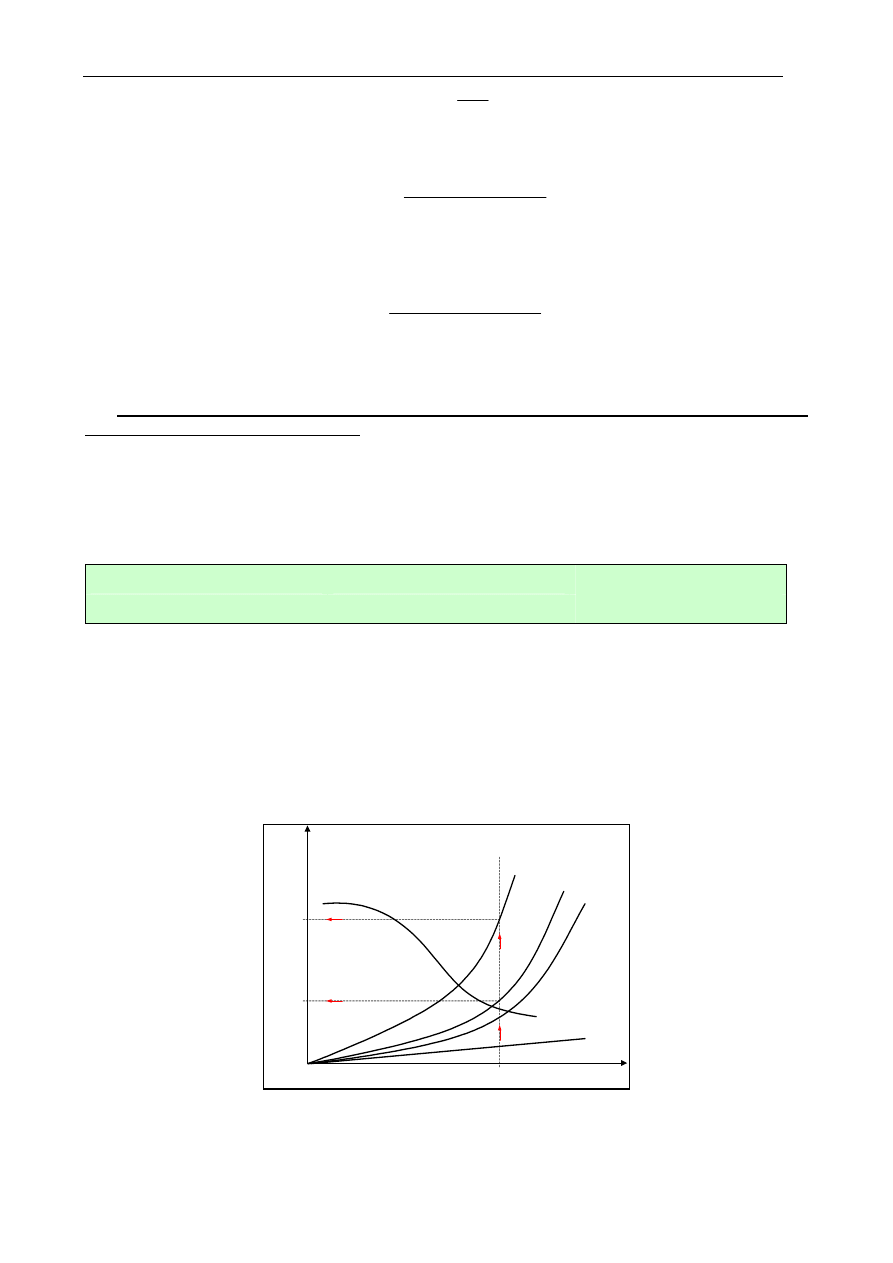
Charakterystyki stanu jałowego (rys. 1.4) przedstawiają zależności prądu jałowego I

o

oraz mocy

czynnej P

o

, pobieranych przez transformator, i współczynnika mocy cos

ϕ

o

od napięcia zasilania U

1

o

przebiegu sinusoidalnym i stałej częstotliwości f, przy nieobciążonym (otwartym) uzwojeniu wtórnym (I

2

=

0):

I

o

= f (U

1

)

P

o

= f (U

1

)

cos

ϕ

o

= f (U

1

)

przy:

f = const

I

2

= 0

Na podstawie charakterystyk stanu jałowego transformatora, wyznaczonych pomiarowo, określa się

straty jałowe

∆

P

Fe

— straty w żelazie rdzenia (potrzebne do wyznaczenia sprawności) i parametry schematu

zastępczego stanu jałowego (patrz: p.1.1 ćwiczenia 1).

Moc P

o

pobierana przez transformator w stanie jałowym zamienia się, praktycznie, całkowicie na straty

w żelazie. Z kolei straty w żelazie są w przybliżeniu proporcjonalne do kwadratu indukcji B, czyli w
przybliżeniu także do kwadratu przyłożonego napięcia U

1

(dopuszczalne jest pominięcie spadku napięć na

uzwojeniu w stanie jałowym). Zatem moc P

o

może być z jednej strony wyrażona jako:

P

[W]

o

≈

=

≈

≈

∆

P

f U

c B

c U

Fe

(

)

1

1

2

2

1

2

(1.28)

U

1

[V]

0

P

0

[W]

I

m

I

0

I

0cz

[A]

P

0

I

0

I

m

I

0cz

cos

ϕ

0

cos

ϕ

0

U

1N

I

0N

P

0N

Rys. 1.4. Charakterystyki stanu jałowego transformatora

z drugiej strony przez wyrażenie:

P

[W]

o

=

m U I

ocz

1

(1.29)

M. Ronkowski, G. Kostro, M. Michna

:

11

gdzie składowa czynna prądu jałowego I

ocz

jest proporcjonalna do napięcia U

1

:

I

[A]

ocz

= ⋅

≈

I

c U

o

o

cos

ϕ

3

1

(1.30)

przy czym współczynnik mocy stanu jałowego:

cos

o

ϕ =

P

m U I

o

o

1

(1.31)

Natomiast prąd magnesujący I

m

rośnie wg. odwróconej krzywej magnesowania B = B(H), co oznacza szybki

jego wzrost w zakresie dużych wartości indukcji (dla wartości napięcia U

1

zbliżonych do wartości

znamionowej U

N

). Wyjaśnia to malejący przebieg krzywej

cos

ϕ

o

= f (U

1

) na rys. 1.4. W zakresie małych wartości napięcia współczynnik mocy cos

ϕ

o

osiąga wartość

maksymalną — wynika to z zagięcia krzywej magnesowania.

♦

Przebieg próby stanu jałowego

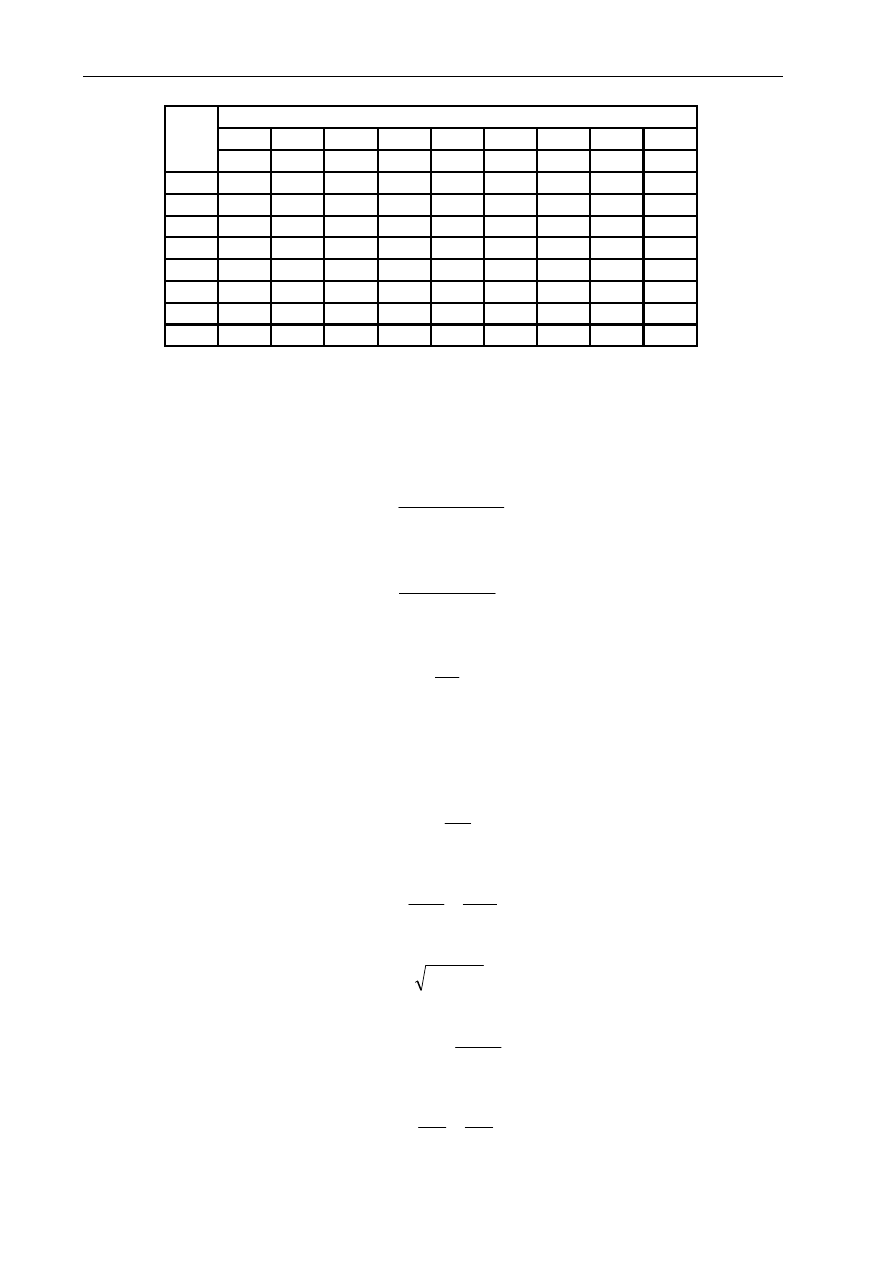
Schemat układu pomiarowego przedstawiony jest na rys. 1.5.

PW

~

3

X

3

8

0

V

RN

R

S

T

W

*

*

A

V

a1

a3

a4 a5

b3

b4 b5

c3

c4 c5

c6

a2

b1

b2

c1

c2

a6

b6

Rys. 1.5. Schemat połączeń do próby stanu jałowego transformatora: RN

−

regulator napięcia; PW -

przełącznik watomierzowy (układ z poprawnie mierzonym prądem !)

Uwagi ogólne do próby stanu jałowego.

•

Podstawą doboru zakresu pomiarowego amperomierza i watomierza są procentowe wartości prądu
jałowego badanego transformatora.

•

Woltomierz, amperomierz i watomierz połączyć w układzie z poprawnie mierzonym prądem.

•

Celem ograniczenia prądu włączania transformatora należy go załączać przy znacznie obniżonym
napięciu.

•

Przy włączaniu transformatora na pełne napięcie (znamionowe) cewki prądowe watomierzy i cewki
amperomierzy należy zewrzeć.

•

Ze względu na niesymetrię prądów jałowych (efekt niesymetrii magnetycznej rdzenia), moc
pobieraną przez transformator należy mierzyć w trzech fazach lub w układzie Arona.

•

Dla jednej z faz wychylenie watomierza może być ujemne, szczególnie w zakresie napięć
znamionowych, należy zmienić kierunek wychylenia watomierza przełącznikiem PW, a do bilansu
mocy pobieranej przez transformator wskazanie to należy brać ze znakiem ujemnym.

W czasie pomiarów należy:

•

Regulatorem napięcia RN zmieniać wartości napięcia zasilającego transformator w zakresie od
wartości bliskich zera do wartości 1,05 U

N

napięcia znamionowego (w tym dla napięcia

znamionowego).

•

Wyniki zanotować w tablicy 1.4a.

12

Ćwiczenie: Transformator trójfazowy

Tablica 1.4a

Wielkości pomierzone

Lp.

U

a

U

b

U

c

I

oa

I

ob

I

oc

P

oa

P

ob

P

oc

V

V

V

A

A

A

W

W

W

1

2

3

4

5

6

7

8

♦

Opracowanie wyników próby stanu jałowego

W czasie wykonywanych pomiarów napięcia i prądy poszczególnych faz mogą się różnić między sobą. Ich
wartości średnie, podane w tablicy 1.4a, należy obliczyć – wg. podanych poniżej zależności – i zestawić w
tablicy 1.4b.

•

Napięcie zasilania:

[A]

3

U

U

U

U

c

b

a

1

++++

++++

====

(1.32)

•

prąd stanu jałowego:

[A]

3

I

I

I

I

oc

ob

oa

o

+

+

=

(1.33a)

•

znamionowy prąd stanu jałowego (dla napięcia U

1

= U

1N

):

%

100

I

I

I

N

oN

oN%

====

(1.33b)

•

sumaryczną moc pobieraną przez transformator:

[V]

P

P

P

P

oc

ob

oa

o

++++

++++

====

(1.34a)

•

znamionowe starty jałowe (dla napięcia U

1

= U

1N

)

100

S

P

P

N

oN

oN%

====

(1.34b)

•

składową czynną prądu stanu jałowego:

[A]

U

P

E

P

I

o

Fe

ocz

1

1

3

3

≈

∆

=

(1.36)

•

prąd magnesujący

I

[A]

m

o

ocz

I

I

=

−

2

2

(1.37)

•

współczynnik mocy stanu jałowego

cos

o

ϕ =

P

U I

o

o

3

1

(1.38)

•

rezystancję modelującą straty w żelazie

]

[

I

U

I

E

R

ocz

ocz

Fe

Ω

≈

=

1

1

(1.39)

•

reaktancję magnesującą

M. Ronkowski, G. Kostro, M. Michna

:

13

]

[

I

U

I

E

X

m

m

m

Ω

≈

=

1

1

(1.40)

Uwaga: Zależności (1.36), (1.38), (1.39) i (1.40) obowiązują przy założeniu, że uzwojenie pierwotne
połączone jest w gwiazdę (Y), a pomierzone napięcia i prądy są wielkościami fazowymi

.

Tablica 1.4b

Wielkości obliczone

Lp.

U

1

I

o

P

o

∆

P

Fe

cos

ϕ

o

I

m

I

ocz

X

m

R

Fe

V

A

W

W

−

A

A

Ω

Ω

1

2

3

4

5

6

7

8

2.5.

Próba stanu zwarcia: badanie charakterystyk zwarcia

♦

Podstawy próby stanu zwarcia

Cel podstawowy próby stanu zwarcia transformatora – pomiary wartości strat w uzwojeniach

(miedzi) i napięcia zwarcia dla prądu znamionowego.

Próba stanu zwarcia transformatora polega na zasilaniu transformatora z dowolnej strony i pomiarze

pobieranego przez transformator prądu I

z

i mocy P

z

oraz napięcia zasilania. W czasie próby uzwojenie

wtórne jest zwarte.
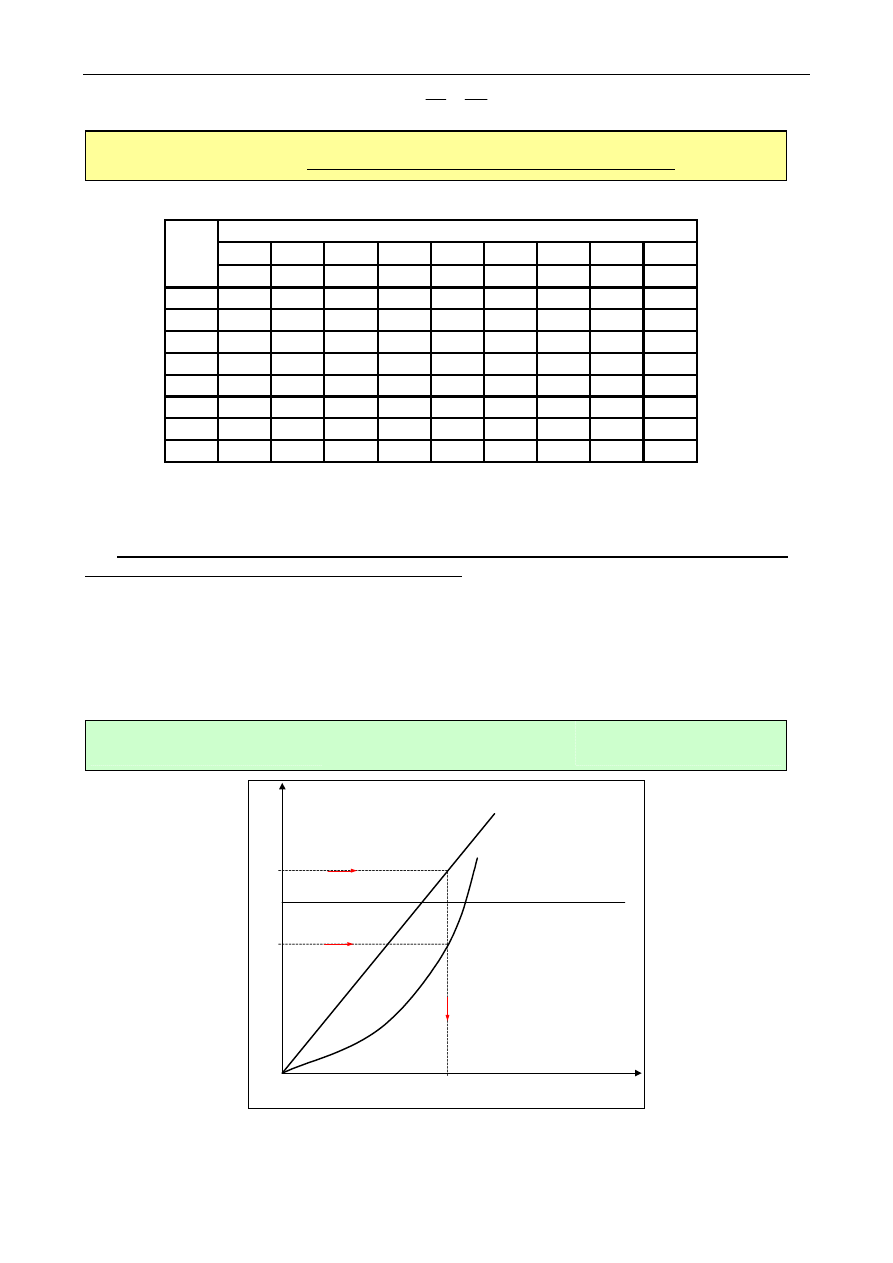
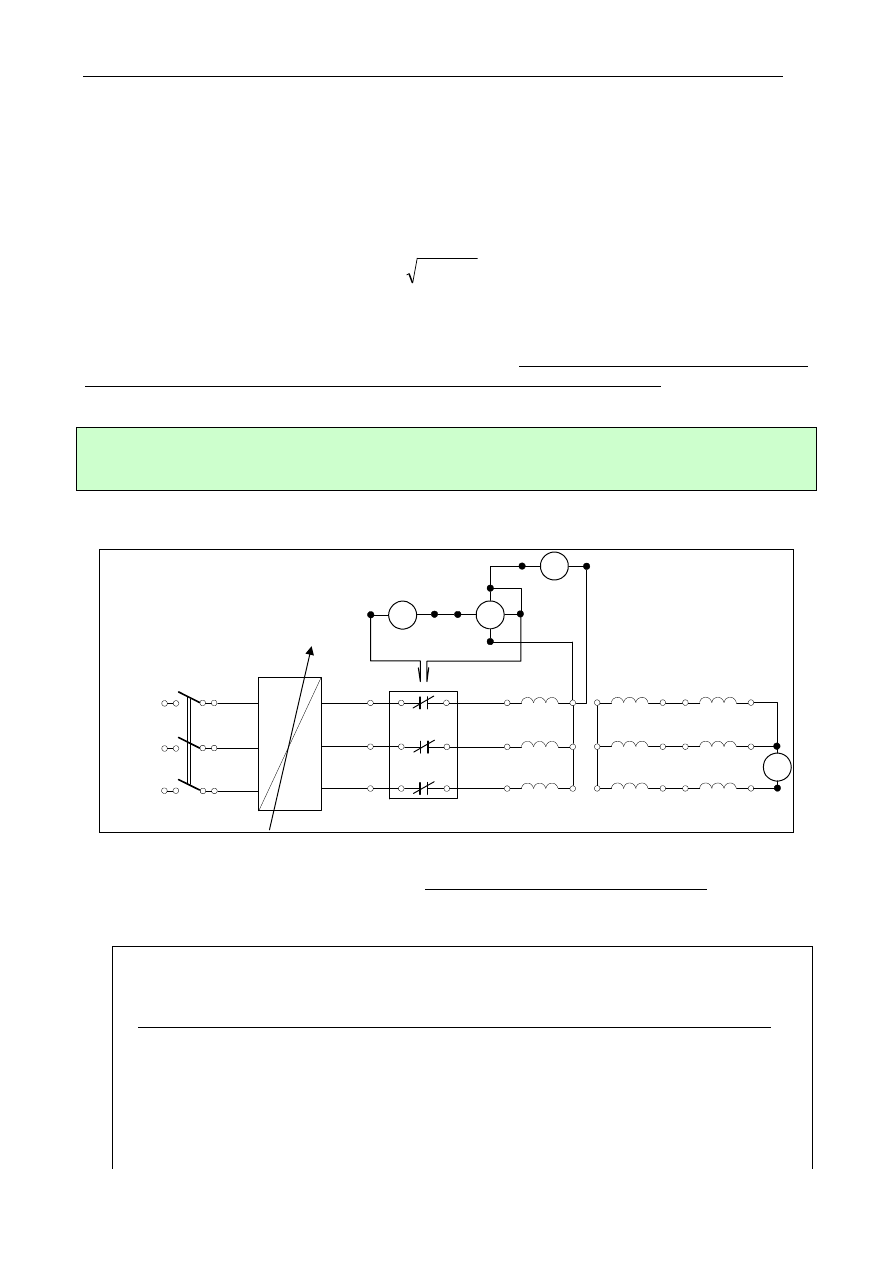
Charakterystyki zwarcia (rys. 1.6) przedstawiają zależności prądu zwarcia I

z

, mocy zwarcia P

z

,

pobieranych przez transformator, i współczynnika mocy cos

ϕ

z

od napięcia zasilania U

1

o przebiegu

sinusoidalnym i stałej częstotliwości f, przy zwartym uzwojeniu wtórnym (U

2

= 0):

I

z

= f (U

1

)

P

z

= f (U

1

)

cos

ϕ

z

= f (U

1

)

przy:

f = const

U

2

= 0

U

1

[V]

0

P

z

[W]

I

z

[A]

P

z

I

z

cos

ϕ

z

cos

ϕ

z

I

N

U

zN

P

zN

Rys. 1.6. Charakterystyki zwarcia transformatora

14

Ćwiczenie: Transformator trójfazowy

Na podstawie charakterystyk zwarcia, wyznaczonych z pomiarów, określa się wartość strat w miedzi

uzwojeń (podstawa do wyznaczenia sprawności) i napięcia zwarcia, a także parametry schematu
zastępczego stanu zwarcia (patrz: p.1.1 ćwiczenia 1).

W stanie zwarcia pomiarowego, kiedy napięcie przyłożone do uzwojenia jest znacznie mniejsze od

znamionowego, można pominąć prąd magnesujący i straty w żelazie. Można więc przyjąć, że moc pobierana
w tych warunkach przez transformator zamienia się prawie całkowicie na straty w miedzi uzwojeń:

P

I

= I R

z

≈

≈

+

∆

P

R

R

Cu

z

z

z

3

3

2

1

2

2

(

)

'

(1.41)

a dla obwodu napięcia zwarcia zachodzi relacja:

U

= I Z

z

≈

+

I

R

X

z

z

z

z

z

2

2

(1.42)

Rezystancja zwarcia R

z

zmienia się w wąskich granicach pod wpływem zmian temperatury uzwojeń.

Jednak zmiany te można pominąć, gdy próba trwa krótko.

Z kolei reaktancja zwarcia X

z

odpowiada strumieniowi rozproszenia, który na znacznej części swej

drogi przebiega w ośrodku niemagnetycznym (powietrze, olej): charakteryzuje się on stałą przenikalnością
magnetyczną – obwód magnetyczny strumienia rozproszenia jest liniowy/nienasycony. Ponieważ o wartości
reluktancji drogi strumienia rozproszenia decyduje ośrodek niemagnetyczny, więc reaktancja zwarcia X

z

nie

zależy od prądu zwarcia – jest liniowa (utrzymuje wartość stałą).
Z powyższych rozważań wynika: impedancja zwarcia transformatora jest stała i nie zależy od poziomu
prądu zwarcia; paraboliczny przebieg zależności P

z

= f (U

1

); stałą wartość cos

ϕ

z

= f (U

1

) i prostoliniowy

przebieg zależności I

z

= f (U

1

) (podanych na rys. 1.6).

♦

Przebieg próby stanu zwarcia

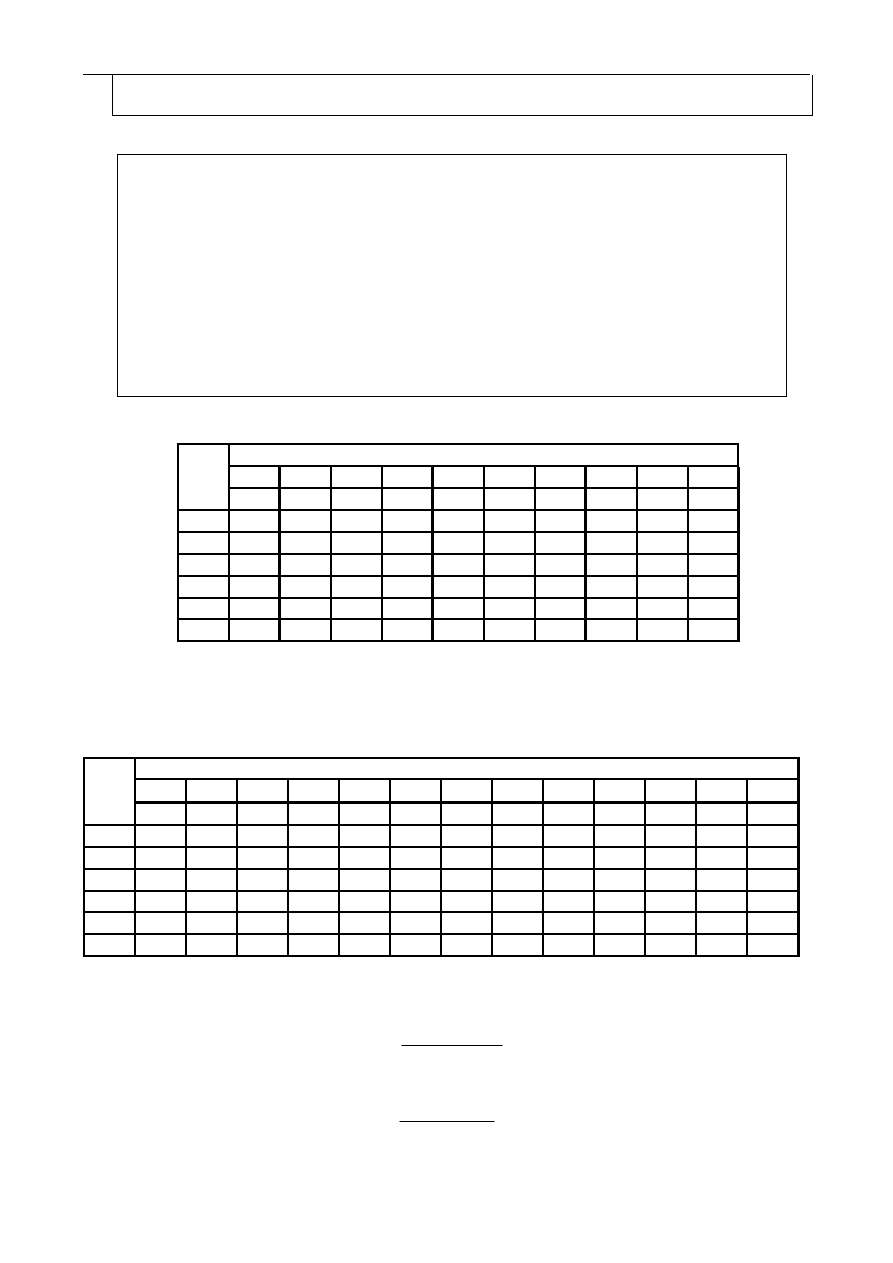
Schemat układu pomiarowego przedstawiono na rys.1.7.

a1

a2

b1

b2

c1

c2

PW

~

3

X

3

8

0

V

RN

R

S

T

a3

a4 a5

a6

b3

b4 b5

b6

c3

c4 c5

c6

A

W

*

*

A

V

Rys. 1.7. Schemat połączeń do próby zwarcia transformatora:

RN

−

regulator napięcia;

PW - przełącznik watomierzowy (układ z poprawnie mierzonym napięciem !)

Uwagi ogólne do próby stanu zwarcia.

•

Podstawą doboru zakresu pomiarowego woltomierza, amperomierza i watomierza (ewentualnie
przekładnika prądowego) są wartości prądów znamionowych i procentowe wartości napięcia
zwarcia badanego transformatora.

•

Woltomierz, amperomierz i watomierz połączyć w układzie z poprawnie mierzonym napięciem.

•

Przy włączaniu transformatora na napięcie zasilające (wartości winna być zbliżona do zera) cewki
prądowe watomierza należy zewrzeć.

•

Ze względu na ewentualną niesymetrię prądów zwarciowych (efekt niesymetrii napięć zasilających,
impedancji zwarcia), moc pobieraną przez transformator należy mierzyć w trzech fazach lub w
układzie Arona.

•

Wychylenie watomierza dla jednej z faz w układzie Arona może być ujemne (dla wartości
współczynnika mocy cos

ϕ

z

< 0,5): należy zmienić kierunek wychylenia watomierza przełącznikiem

M. Ronkowski, G. Kostro, M. Michna

:

15

PW, a do bilansu mocy pobieranej przez transformator wskazanie to należy brać ze znakiem
ujemnym.

W czasie pomiarów należy:

•

Uzwojenie wtórne transformatora należy zewrzeć odpowiednio grubym przewodem o przekroju
miedzi większym od przekroju miedzi jego uzwojenia.

•

Regulatorem napięcia RN zmieniać wartość napięcia zasilającego od wartości przy której prąd
zwarcia osiąga wartości około 1,2 I

N

, do wartości zbliżonej do zera.

•

Wykonać pomiary dla prądu znamionowego transformatora.

•

Wykonać pomiar mocy pobieranej przez transformator w układzie Arona z wykorzystaniem
przełącznika watomierzowego PW.

•

Pomiary wykonać możliwie szybko, aby ograniczyć nagrzewanie transformatora.

•

Wyznaczyć temperaturę uzwojeń na początku

τ

p

i na końcu

τ

k

pomiarów charakterystyk zwarcia

(pierwszy pomiar należy wykonać przy prądzie największym, a następny pomiar przy prądzie
najmniejszym — wtedy temperatury uzwojeń zmieniają się w niewielkich granicach).

•

Wyniki pomiarów zestawić w tablicy 1.5a.

Tablica 1.5a

Wielkości pomierzone

Lp.

U

a

U

b

U

c

I

za

I

zb

I

zc

P

za

P

zb

P

zc

I

z2

V

V

V

A

A

A

W

W

W

A

1

2

3

4

5

6

τ

p

= . . . . .

o

C

τ

k

= . . . . .

o

C

♦

Opracowanie wyników próby stanu zwarcia

Tablica 1.5b

Wielkości obliczone

Lp.

U

1

I

z

P

z

cos

ϕ

z

∆

P

Cup

∆

P

Cud

R

z

X

z

R

1

R’

2

R

2

X

σ

1

X’

σ

2

V

A

W

−

W

W

Ω

Ω

Ω

Ω

Ω

Ω

Ω

1

2

3

4

5

6

W czasie pomiarów napięcia i prądy poszczególnych faz mogą się różnić między sobą. Ich wartości

średnie, podane w tablicy 1.5a, należy obliczyć wg. następujących zależności:

•

napięcie zasilania:

[V]

3

U

U

U

U

c

b

a

1

+

+

=

(1.43)

•

prąd zwarcia:

[A]

3

I

I

I

I

zc

zb

za

z

+

+

=

(1.44a)

•

znamionowe napięcie zwarcia (wartość prądu I

z

= I

N

):

16

Ćwiczenie: Transformator trójfazowy

%

100

U

U

U

N

zN

zN%

====

(1.44b)

•

moc zwarcia pobierana przez transformator:

[W]

P

+

P

+

P

P

zc

zb

za

z

=

(1.45a)

•

znamionowa moc zwarcia (wartość prądu I

z

= I

N

):

100

S

P

P

N

zN

zN%

====

(1.45b)

•

współczynnik mocy w stanie zwarcia transformatora:

cos

z

ϕ =

P

U I

z

z

3

1

(1.46)

•

straty podstawowe w miedzi uzwojeń dla temperatury

τ

(wydzielające się w uzwojeniach przy

równomiernym przepływie prądu przez cały przekrój przewodu):

((((

))))

[W]

P

Cup

τ

τ

ϑ

2

2

1

2

3

R

R

I

z

z

++++

====

∆∆∆∆

(1.47)

przy czym rezystancje fazowe uzwojeń strony pierwotnej R

1

τ

i wtórnej R

2

τ

odpowiadające temperaturze

τ

obliczamy z zależności:

R

[ ]

1

1

235

235

τ

τ

τ

=

+

+

R

x

Ω

(1.48)

R

[ ]

2

2

235

235

τ

τ

τ

=

+

+

R

x

Ω

(1.49)

τ τ

τ

τ

=

ś

r

=

+

p

k

2

(1.50)

τ

−

temperatura przy której wykonano pomiary strat,

τ

x

−

temperatura pomiaru wartości rezystancji R

1

oraz R

2

(patrz p. 1.3 ćwiczenia 1),

ϑ

z

−

przekładnia zwojowa transformatora.

•

straty dodatkowe w miedzi uzwojeń dla temperatury

τ

(wywołane prądami wirowymi wewnątrz

przewodów):

∆

∆

P

[W]

Cud

≈

−

P

P

z

Cup

(1.51)

•

impedancja zwarcia transformatora:

Z

U

I

z

z

=

1

(1.52)

•

rezystancja zwarcia transformatora:

R

Z

z

z

=

cos

z

ϕ

(1.53)

•

reaktancja zwarcia transformatora:

X

Z

z

z

=

sin

z

ϕ

(1.54)

•

rezystancja uzwojenia strony pierwotnej transformatora:

R

R

z

1

1
2

≈

(1.55)

•

zredukowana rezystancja uzwojenia strony wtórnej transformatora:

′ ≈

R

R

z

2

1
2

(1.56)

•

realna rezystancja uzwojenia strony wtórnej transformatora:

2

2

z

R

R

ϑ

′′′′

====

2

(1.57)

•

reaktancja rozproszenia uzwojenia strony pierwotnej transformatora:

M. Ronkowski, G. Kostro, M. Michna

:

17

X

X

z

σ

1

1
2

≈

(1.58)

•

reaktancja rozproszenia uzwojenia strony wtórnej transformatora:

′ ≈

X

X

z

σ

2

1
2

2

2

z

X

X

ϑ

σ

σ

′′′′

====

2

(1.59)

•

procentowe napięcie zwarcia transformatora:

100

3

1

1

/

zN%

N

N

z

U

I

Z

U

====

(1.60)

Uwag: Zależności (1.46), (1.52) obowiązują dla połączenia uzwojenia pierwotnego

w gwiazdę (Y), a pomierzone napięcia i prądy są wielkościami fazowymi.

W praktyce wartości strat w uzwojeniach — pomierzone w temperaturze

τ

— przelicza się do umownej

temperatury odniesienia

τ

o

(temperatury pracy – stanu nagrzania transformatora). Przeliczenia strat w

uzwojeniach należy wykonać oddzielnie dla strat podstawowych i dodatkowych, ponieważ ze wzrostem
temperatury pierwsze z nich rosną, natomiast drugie maleją. Straty podstawowe przelicza się do temperatury
odniesienia

τ

o

wg. zależności:

∆

∆

P

[W]

Cup o

τ

τ

τ

τ

=

+

+

P

Cup

o

235

235

(1.61)

∆

∆

P

[W]

Cud o

τ

τ

τ

τ

=

+

+

P

Cud

o

235

235

(1.62)

gdzie, temperatura odniesienia

τ

o

, np. dla klasy izolacji A, E, B wynosi 75

o

C, a dla klasy izolacji F, H

wynosi 115

o

C.

Wyniki powyższych obliczeń zestawić w tablicy 1.5b.

2.6.

Wyznaczenie sprawności transformatora metodą strat poszczególnych

♦

Definicja sprawności

Sprawność transformatora określa jego własności energetyczne. Można ją określić jako stosunek mocy

czynnej oddanej P

2

do mocy czynnej pobranej P

1

przez transformator:

η

=

P

P

[%]

2

1

⋅

100

Sprawność znamionową określa się przy znamionowych parametrach pracy, współczynniku mocy cos

ϕ

2

=

1, znamionowej wydajności urządzeń pomocniczych i przy temperaturze uzwojeń 75

o

C (348,2

o

K).

Sprawność transformatora jest na ogół duża – największa ze sprawności wszystkich urządzeń

elektrycznych – osiąga wartości do 99%.

♦

Wyznaczenie sprawności

W praktyce, sprawności transformatora wyznacza się metodą strat poszczególnych. Metoda ta polega

na określeniu strat w transformatorze w warunkach znamionowych.

Sprawność zgodnie z definicją wynosi:

η = −

+

∑

∑

1

2

∆

∆

P

P

P

(1.63)

przy czym

∆

∆

∆

P = P

[W]

Fe

+

∑

P

Cu

(1.64)

gdzie:

∆

P

∑

−

sumaryczne straty mocy czynnej w transformatorze,

∆

P

Fe

−

straty w żelazie rdzenia,

∆

P

Cu

−

straty w miedzi (uzwojeniach),

P

2

−

moc czynna wydawana przez transformator.

18

Ćwiczenie: Transformator trójfazowy

Straty w żelazie rdzenia należą do kategorii strat jałowych (stałych), a straty w miedzi do kategorii strat

obciążeniowych (zmiennych).

Podstawą do określenia strat w zależnościach (1.63) i (1.64) są wyniki próby stanu jałowego i stanu

zwarcia transformatora (patrz p. 1.5 i 1.6 ćwiczenia 1).

Straty w żelazie wyznacza się na podstawie charakterystyki stanu jałowego, natomiast straty w miedzi

wg. wzoru:

∆

∆

P

[W]

Cu

= α

2

P

CuN

(1.65)

przy czym:

∆

P

CuN

−

znamionowe straty w miedzi w stanie nagrzanym transformatora,

α =

I

I

N

2

2

−

stosunek obciążenia faktycznego do znamionowego.

Moc czynną P

2

wyznacza się z zależności:

P

S

[W]

2

N

2

= ⋅

⋅

α

ϕ

cos

(1.66)

gdzie:

S

N

−

moc znamionowa transformatora,

cos

ϕ

2

−

współczynnik mocy odbioru.

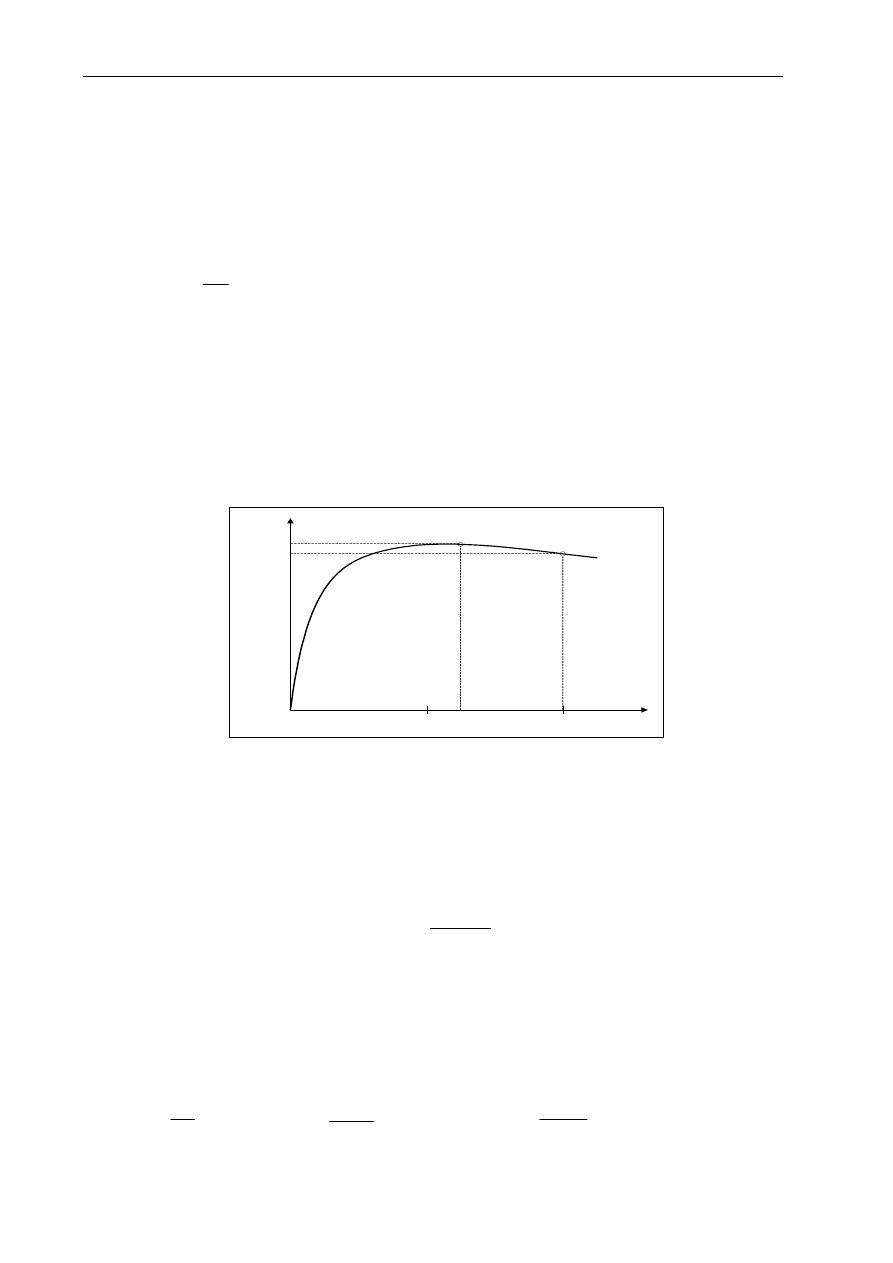
Sprawność maksymalna transformatora występuje przy takim obciążeniu, przy którym straty w

uzwojeniach równe są stratom w żelazie.

Typową charakterystykę sprawności transformatora przy stałym współczynniku mocy, przedstawiono

na rys. 1.8.

I

2

/I

2 N

0

η [% ]

0 ,5

1 ,0

η

m a x

η

N

Rys.1.8. Charakterystyka sprawności transformatora dla cos

ϕ

2

= 0,8 ind.

2.7.

Wyznaczenie zmiany napięcia

♦

Definicja zmiany napięcia

Zmiana napięcia wyraża spadek wtórnego napięcia transformatora przy przejściu od stanu jałowego do

stanu obciążenia przy określonym współczynniku mocy, niezmienionym napięciu pierwotnym i
niezmienionej częstotliwości. Zmianę tę określa się w procentach napięcia znamionowego:

100

U

2

2

2

%

o

o

U

U

U

−

=

∆

(1.67)

gdzie:

U

2o

−

napięcie wtórne w stanie jałowym,

U

2

−

napięcie wtórne przy obciążeniu.

♦

Wyznaczenie zmiany napięcia

Wartość procentową zmiany napięcia oblicza się z zależności przybliżonej:

[%]

)

sin

cos

(

U

2

%

2

%

%

ϕ

ϕ

α

X

R

U

U

±

≈

∆

(1.68)

gdzie:

α =

I

I

N

1

1

100

1

1

R%

fN

N

z

U

I

R

U

=

U

X

U

z

N

fN

X%

I

=

1

1

100

(1.69)

I

1

, I

1N

−

prądy fazowe: obciążenia i znamionowy strony pierwotnej,

U

1fN

−

fazowe napięcie znamionowe strony pierwotnej,

M. Ronkowski, G. Kostro, M. Michna

:

19

U

R%

−

wartość procentowa spadku napicia na rezystancji zwarcia,

U

X%

−

wartość procentowa spadku napicia na reaktancji zwarcia.

Największa wartość zmiany napięcia transformatora

równa jest procentowemu napięciu zwarcia transformatora.

Zależność zmiany napięcia transformatora o napięciu zwarcia 6% od charakteru obciążenia przedstawia

rys. 1.9.

1

0

2

6

∆

U

%max

∆

U

%

[%]

4

0,5

-2

-4

-6

0

ind.

cos

ϕ

2

0,5

0

poj.

Rys. 1.9. Charakterystyka zmiany napięcia transformatora o napięciu zwarcia U

z%

= 6%

3.

ZADANIA

1.

Dla badanego transformatora przy założeniu jednakowej przekładni zwojowej

z

ϑ

i dwóch różnych

układów połączeń uzwojeń wyznaczyć wartości przekładni napięciowej. Następnie sprawdzić czy
wartości te spełniają zależności (1.19) do (1.24) oraz wyjaśnić ewentualne różnice.

2.

Wykreślić charakterystyki stanu jałowego transformatora (por. rys. 1.4 ćwiczenia) i uzasadnić fizycznie
oraz analitycznie ich kształt.

3.

Wykreślić charakterystyki zwarcia badanego transformatora (por. rys. 1.6 ćwiczenia) i uzasadnić
fizycznie oraz analitycznie ich kształt.

4.

Wyznaczyć wartości procentowe: prądu stanu jałowego (także składowe), strat w żelazie i współczynnik
mocy stanu jałowego, badanego transformatora dla warunków znamionowych.

5.

Wyznaczyć wartości procentowe: napięcia zwarcia (także składowe), straty mocy w miedzi uzwojeń (z
podziałem na straty podstawowe i dodatkowe) i współczynnik mocy stanu zwarcia, badanego
transformatora dla warunków znamionowych (uwzględnić temperaturę odniesienia dla klasy izolacji
transformatora).

6.

Oblicz znamionowe straty w żelazie i w miedzi (wartości w [W] i [%]) badanego transformatora.
Porównaj wartości obu strat – wyjaśnij występujące różnice między ich wartościami.

7.

Obliczyć ustalony prąd zwarcia badanego transformatora zasilanego napięciem znamionowym
(zastosować dwie metody obliczeń – w oparciu o impedancję zwarcia Z

z

i napięcie zwarcia U

z%

).

8.

Narysować i wyznaczyć parametry (przeliczone na stronę górnego napięcia) modelu obwodowego
(schematu zastępczego) badanego transformatora dla warunków znamionowych. Wartości parametrów
wyrazić zarówno w jednostkach bezwzględnych jak i względnych (procentach).

9.

Sporządzić wykresy wartości parametrów modelu obwodowego badanego transformatora w funkcji
napięcia zasilania U

1

: oddzielnie dla gałęzi magnesującej (podłużnej) i gałęzi zwarciowej (poprzecznej)

schematu. Uzasadnić fizycznie oraz analitycznie ich kształt.

10.

Sporządzić wykresy fazorowe badanego transformatora dla stanu jałowego.

11.

Sporządzić wykresy fazorowe badanego transformatora dla stanu zwarcia.

12.

Sporządzić wykres fazorowy badanego transformatora w stanie obciążenia, przy współczynniku mocy
cos

ϕ

2

= 0,8 ind. Transformator zasilany jest napięciem znamionowym i obciążony prądem

znamionowym.

13.

Sporządzić wykres fazorowy badanego transformatora w stanie obciążenia, przy współczynniku mocy
cos

ϕ

2

= 0,8 poj. Transformator zasilany jest napięciem znamionowym i obciążony prądem

znamionowym.

20

Ćwiczenie: Transformator trójfazowy

14.

Sporządzić wykres krzywej zmiany napięcia badanego transformatora w funkcji współczynnika mocy
cos

ϕ

2

((((

))))

2

/

2

/

2

π

ϕ

π

≤≤≤≤

≤≤≤≤

−−−−

(por. rys. 1.9 ćwiczenia). Warunki zasilania i obciążenia jak w zada. 11.

Uzasadnić fizycznie wpływ charakteru obciążenia (cos

ϕ

2

) na wartość zmiany napięcia.

15.

Wyznaczyć znamionową wartość zmiany napięcia badanego transformatora dla wartości współczynnika
mocy cos

ϕ

2

= 0,8 ind.

16.

Wyznaczyć znamionową wartość zmiany napięcia badanego transformatora dla wartości współczynnika
mocy cos

ϕ

2

= 0,8 poj.

17.

Sporządzić wykres krzywej sprawności badanego transformatora (por. rys. 1.8 ćwiczenia) dla
znamionowych warunków zasilania i współczynnika mocy cos

ϕ

2

= 0,8 ind. Uzasadnić wpływ

charakteru obciążenia (cos

ϕ

2

) na charakter krzywej sprawności.

18.

Dla badanego transformatora wyznaczyć wartość sprawności maksymalnej i znamionowej (dla cos

ϕ

2

=

1) przy znamionowych warunkach zasilania. Uzasadnić dlaczego transformatory buduje się przy
założeniu maksymalnej sprawności dla obciążeń I

2

< I

2N

.

4.

PYTANIA KONTROLNE

Pytania dotyczące budowy i teorii transformatora.

1.

Podać rodzaje budowy transformatorów. Naszkicować rdzeń i uzwojenia, nazwać i podać funkcje
podstawowych elementów transformatora.

2.

Co to są wielkości pierwotne i wtórne, dolne i górne transformatora?

3.

Podać definicję przekładni transformatora.

4.

Podać różnicę między transformatorem idealnym a rzeczywistym.

5.

Naszkicować rdzeń i uzwojenia i wyjaśnić zasadę działania transformatora. Podać jakie zjawiska są
podstawą jego budowy i działania.

6.

Dla stanu jałowego narysować modele transformatora: fizyczny i obwodowy (schemat zastępczy). Podać
i wyjaśnić wzajemne relacje między wielkościami fizycznymi a zmiennymi i parametrami modelu
obwodowego.

7.

Dla stanu obciążenia narysować modele transformatora: fizyczny i obwodowy (schemat zastępczy).
Podać i wyjaśnić wzajemne relacje między wielkościami fizycznymi a zmiennymi i parametrami modelu
obwodowego.

8.

Dla stanu zwarcia narysować modele transformatora: fizyczny i obwodowy (schemat zastępczy). Podać i
wyjaśnić wzajemne relacje między wielkościami fizycznymi a zmiennymi i parametrami modelu
obwodowego.

9.

Podać i objaśnić podstawowe wielkości charakterystyczne i zależności dotyczące transformatorów (I

o

,

Φ

m

,

Φ

σ

1

Φ

σ

2

, E

1

, E

2

,

z

ϑ

,

ϑ

u

, I

z

, U

z

,

∆

P

Fe

,

∆

P

Cu

).

10.

Podać definicję sprawności transformatora. Od czego zależy jej wartość. Kiedy wystąpi sprawność
maksymalna transformatora?

11.

Podać definicję zmienności napięcia transformatora. Od czego zależy jej wartość. Kiedy wystąpi
maksymalna zmienności napięcia transformatora?

Pytania dotyczące przygotowania praktycznego do ćwiczenia

1.

Podać najważniejsze dane tabliczki znamionowej transformatora.

2.

Podać orientacyjne wartości procentowe dla transformatorów:

•

spadku napięcia na rezystancji zwarcia,

•

prądu stanu jałowego,

•

napięcia zwarcia,

•

strat w rdzeniu (żelazie) i w uzwojeniach (miedzi) i relacje między ich wartościami,

•

sprawności.

3.

Wymienić podstawowe próby transformatora. Jakie wielkości eksploatacyjne transformatora wyznacza
się na podstawie wyników tych prób

4.

Dane są wartości wielkości znamionowych transformatora. Dobrać zakresy woltomierza, amperomierza i
watomierza do pomiarów stanu jałowego transformatora.

5.

Dane są wartości wielkości znamionowych transformatora. Dobrać zakresy woltomierza, amperomierza i
watomierza do pomiarów stanu zwarcia transformatora.

6.

Na podstawie jakich prób wyznacza się parametry modelu obwodowego transformatora? Podać
zależności między wynikami tych prób i parametrami modelu obwodowego transformatora.

M. Ronkowski, G. Kostro, M. Michna

:

21

7.

Wymienić i narysować podstawowe charakterystyki transformatora, podając współrzędne oraz wielkości
jakie należy utrzymywać stałe.

8.

Z jaką dokładnością (wymagana klasa dokładności mierników) i dlaczego należy wyznaczyć przekładnię
transformatora?

5.

LITERATURA POMOCNICZA

1.

Fitzgerald A.E, Kingsley Ch. (Jr.), Umans S. D.: Electric Machinery. 6th ed. McGraw-Hill, New

York, 2003.

2.

Latek W.: Zarys maszyn elektrycznych. WNT, W-wa 1974.

3.

Latek W. : Badanie maszyn elektrycznych w przemyśle. WNT, W-wa 1979.

4.

Manitius Z.: Transformatory (skrypt). Wyd. Pol. Gd., Gdańsk 1977.

5.

Manitius Z.: Maszyny elektryczne. Cz. I. Wyd. Pol. Gd. Gdańsk 1982.

6.

Matulewicz W.: Maszyny elektryczne. Podstawy. Wydawnictwo PG 2003.

7.

Plamitzer A.: Maszyny elektryczne. Wyd. 7. WNT, W-wa 1992.

8.

Praca zbiorowa (red. Manitius Z.): Laboratorium maszyn elektrycznych. Wyd. Pol. Gd., Gdańsk

1990.

9.

Rafalski W., Ronkowski M., Zadania z maszyn elektrycznych, Cz. I: Transformatory i maszyny

asynchroniczne, skrypt, wyd. 4, Wyd. Politechniki Gdańskiej, 1994.

10.

Ronkowski M., Michna M., Kostro G., Kutt F.: Maszyny elektryczne wokół nas: zastosowanie,

budowa, modelowanie, charakterystyki, projektowanie. (e-skrypt). Wyd. PG, Gdańsk, 2011.

http://pbc.gda.pl/dlibra/docmetadata?id=16401&from=&dirids=1&ver_id=&lp=2&QI

=

11.

Roszczyk S.: Teoria maszyn elektrycznych. WNT, W-wa 1979.

12.

Staszewski P., Urbański W.: Zagadnienia obliczeniowe w eksploatacji maszyn elektrycznych.

Oficyna Wyd. Politechniki Warszawskiej, Warszawa, 2009.

Ważniejsze Normy

1.

PN-EN 60076-1:2002 Transformatory. Wymagania ogólne.

2.

PN-E-81003:1996 Transformatory. Oznaczenia zacisków i zaczepów uzwojeń, rozmieszczenie

zacisków.

Ważniejsze adresy internetowe producentów/dystrybutorów

1

ABB Sp. z o.o., http://www.abb.pl/ProductGuide/

2

ABB, www.abb.com/transformers

3

AREYA T&D Sp. z o.o. Zakład Transformatorów, www.areva-td.pl

4

AS ELEKTROTECHNIK, http://www.as-elektrotechnik.pl/index3.php

5

Fabryka Transformatorów w Żychlinie Sp. z o.o,

http://www.ftz.pl

6

Noratel Sp. z o.o,

www.noratel.pl