MECHANIKA PŁYNÓW 2

MECHANIKA PŁYNÓW 2

Wykład Nr 5

ZAGADNIENIE TRZECH ZBIORNIKÓW

Uwaga! Niektóre slajdy są w kolorze.

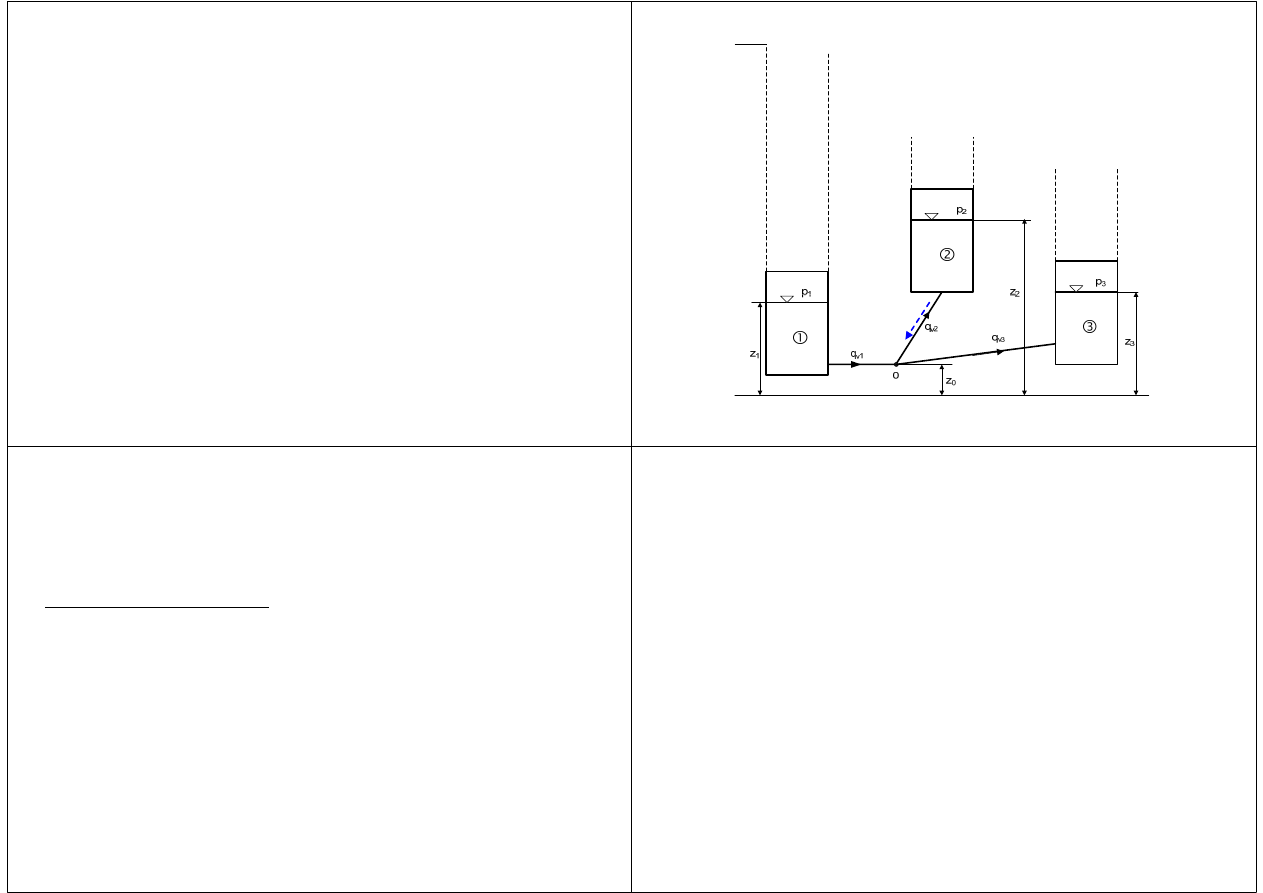
Rys.1. Schemat układu połączenia 3 zbiorników z liniami energii

Wysokości rozporządzalne w poszczególnych zbiornikach wynoszą

1

e

=

2

e

=

3

e

=

Przyjmujemy taką numerację zbiorników, aby spełniony był warunek

(1)

Przyjmujemy taką numerację zbiorników, aby spełniony był warunek

1

2

3

e

e

e

Możliwe są następujące przypadki przepływu:
A – zbiornik 1 zasila zbiornik 2 i 3
(zbiornik 1 jest zasilający, zbiornik 2 i 3 są zasilane),

(2)

(zbiornik 1 jest zasilający, zbiornik 2 i 3 są zasilane),
B – zbiornik 1 i 2 zasilają zbiornik 3
(zbiornik 1 i 1 są zasilające, zbiornik, a zbiornik 3 jest zasilany),
C- zbiornik 1 zasila zbiornik 3, a dopływ do zbiornika 2 jest równy
zero (zbiornik 1 jest zasilany, zbiornik 2 jest tzw. zbiornikiem
wyrównawczym (kompensacyjnym), zbiornik 3 jest zasilany)

Energia rozporządzalna w węźle e

0

wynosi:

0

( )

v

e q

=

- patrząc od strony zbiornika 1 (zasilającego)

(3)

- patrząc od strony zbiornika 3 (zasilanego)

0

( )

v

e q

=

Zbiornik 2 może być zasilający lub zasilany.

(4)

Jaki warunek musi być spełniony aby zbiornik 2 był zasilający
lub zasilany?

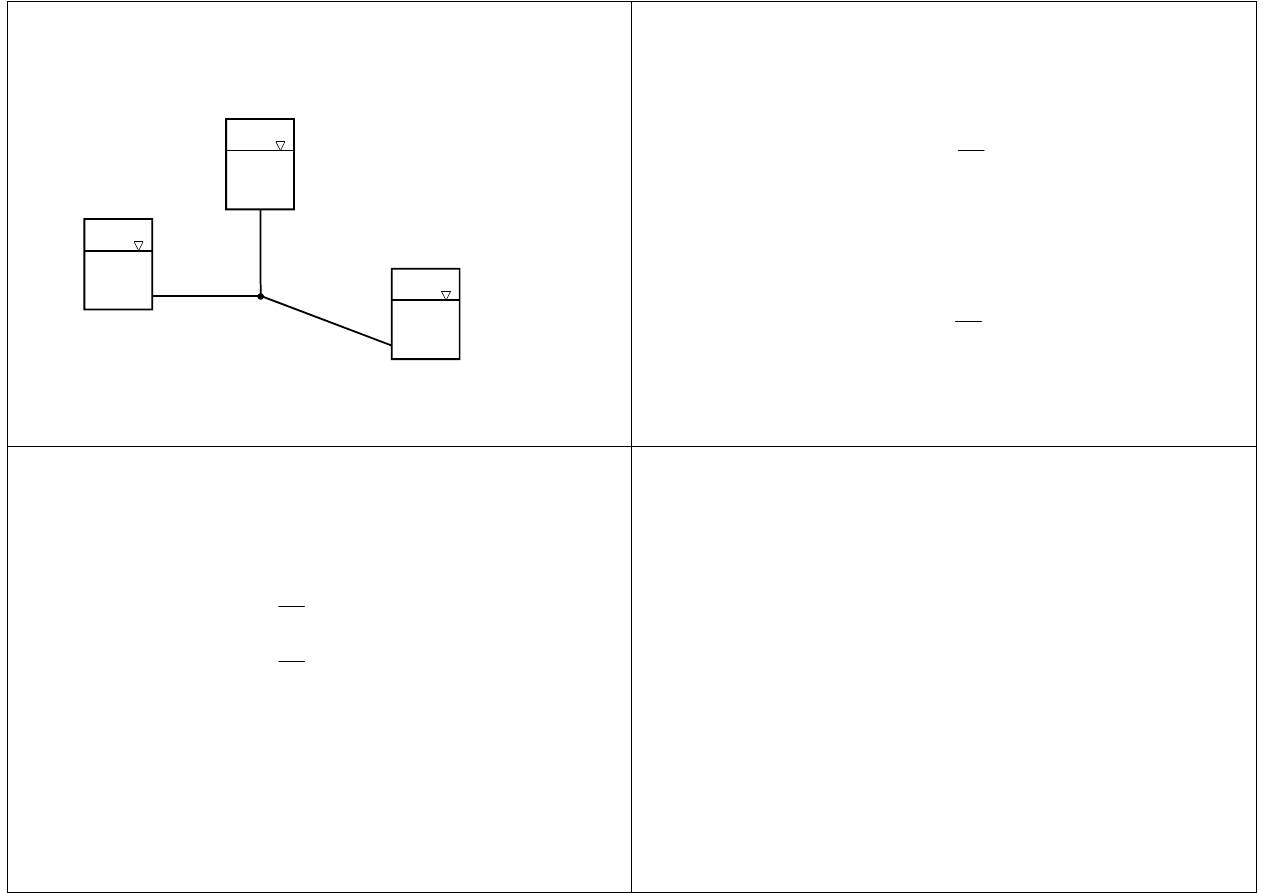
X

Zatem energia rozporządzalna w węźle e

0

patrząc od strony

zbiornika 2 wynosi:

- jeśli zbiornik 2 jest zasilający

2

2

X

p

e

z

ρ

+

(5)

0

( )

v

e q

=

2

X

e

z

g

ρ

+

- jeśli zbiornik 2 jest zasilany

(6)

0

( )

v

e q

=

2

2

X

p

e

z

g

ρ

+

(7)

(8)

Pozostaje wyznaczenie energii rozporządzalnej e

X

tzn. energii w

węźle przy odłączonym zbiorniku 2.
Energia ta może zostać wyznaczona rozwiązując zagadnienie
przepływu pomiędzy dwoma zbiornikami czyli rozwiązując układ
równań utworzony z charakterystyk przepływu zbiornika 1 i 3.

*

2

1

p

e

z

R q



=

+ −

*

2

1

1

1

*

2

3

3

3

X

vX

X

vX

p

e

z

R q

g

p

e

z

R q

g

ρ

ρ



=

+ −









=

+ +



Rozwiązaniem układu równań jest

(9)

vX

X

q

e

=

=

(11)

(10)

Znając trzy równania przepływu zbiornik-przewód (3,4, 6 lub 8)
możemy wykreślić charakterystyki.

Należy zauważyć, że jeśli zbiornik jest zasilający to równaniach
przepływu występuje znak (-), natomiast jeśli zbiornik jest zasilany

przepływu występuje znak (-), natomiast jeśli zbiornik jest zasilany
znak (+).

Obrazem charakterystyk przepływu są parabole symetryczne
względem osi odciętych, a ramionach zwróconych w górę lub w dół
(w zależności od znaku) oraz pochyleniu zależnym od oporności
hydraulicznej przewodu.

hydraulicznej przewodu.

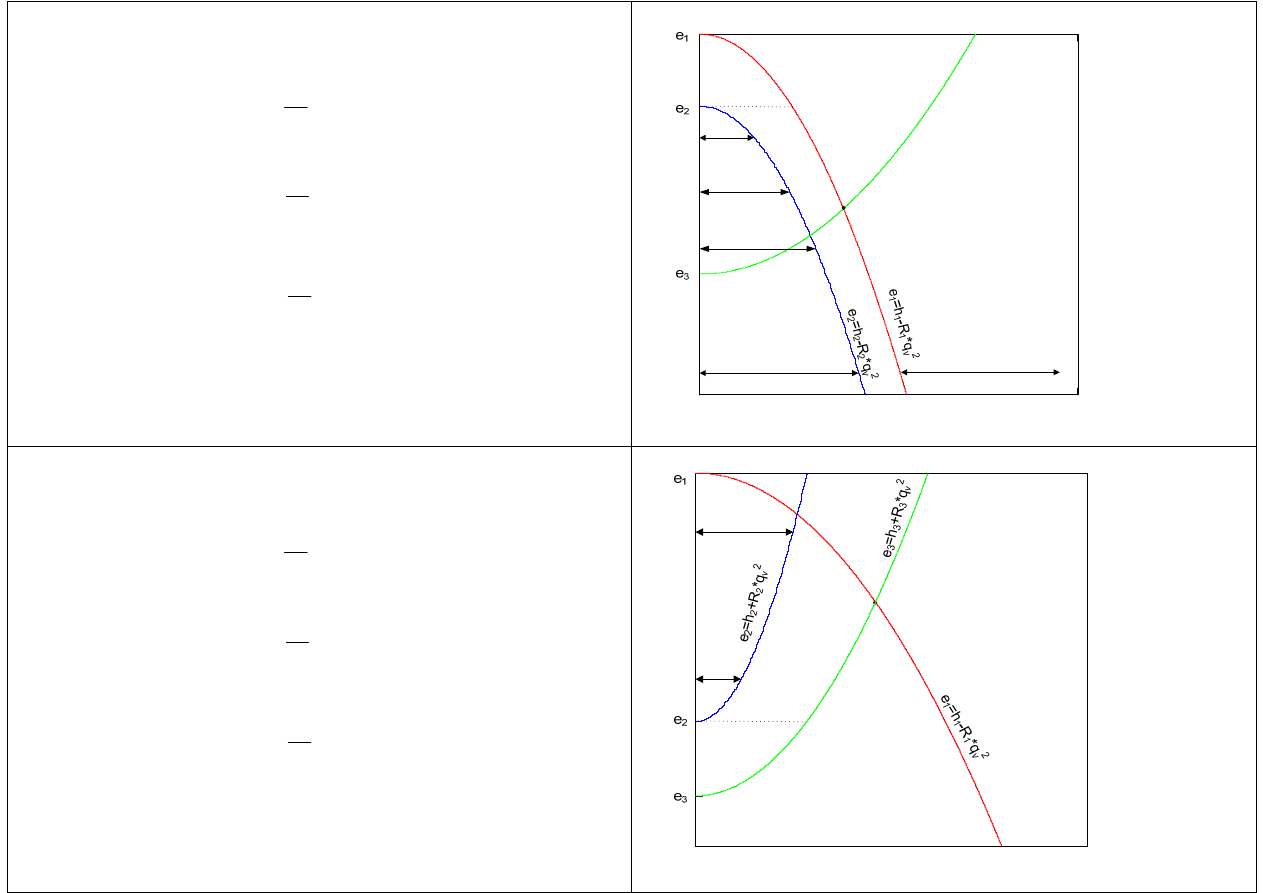
Rozwiązanie graficzne przypadku 1

Zbiornik 1 jest zasilający (ZAWSZE)

*

2

1

0

1

1

( )

v

v

p

e q

z

R q

g

ρ

=

+ −

Zbiornik 2 jest zasilający

*

2

3

( )

p

e q

z

R q

=

+ +

Zbiornik 2 jest zasilający

*

2

2

0

2

2

( )

v

v

p

e q

z

R q

g

ρ

=

+ −

Zbiornik 3 jest zasilany (ZAWSZE)

*

2

3

0

3

3

( )

v

v

e q

z

R q

g

ρ

=

+ +

Bilans strumieni objętości ma postać

(12)

e

3

=

h

3

+

R

3

*q

v

2

2

X

e

h

<

→

zbiornik 2 jest
zasilający

Rozwiązanie graficzne przypadku 2

Zbiornik 1 jest zasilający (ZAWSZE)

*

2

1

0

1

1

( )

v

v

p

e q

z

R q

g

ρ

=

+ −

Zbiornik 2 jest zasilany

*

2

3

( )

p

e q

z

R q

=

+ +

Zbiornik 2 jest zasilany

*

2

2

0

2

2

( )

v

v

p

e q

z

R q

g

ρ

=

+ +

Zbiornik 3 jest zasilany (ZAWSZE)

*

2

3

0

3

3

( )

v

v

e q

z

R q

g

ρ

=

+ +

Bilans strumieni objętości ma postać

(12)

2

X

e

h

>

→

zbiornik 2 jest
zasilany

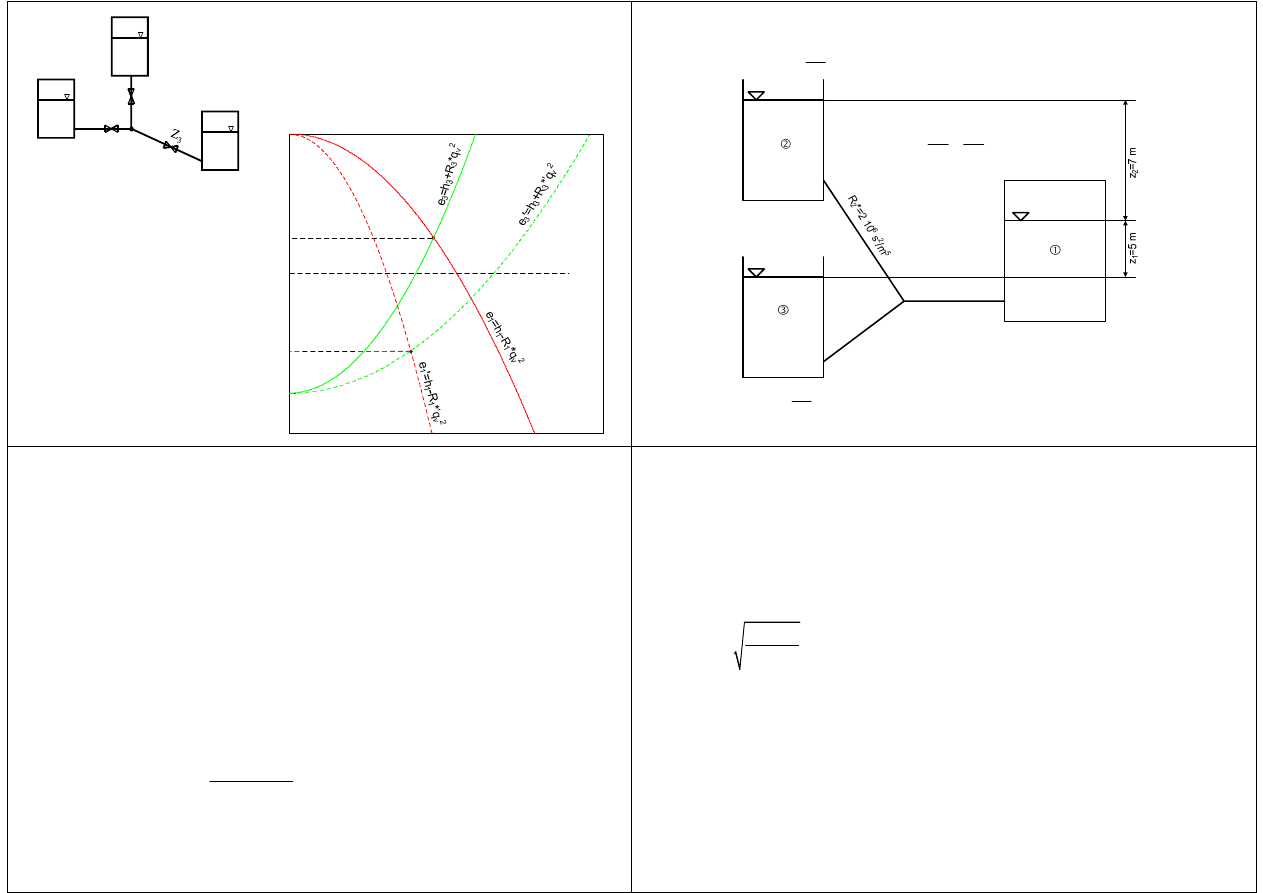
Regulacja trzech zbiorników

e

1

Z

2

Z

1

e

2

e

X

’

X’

X’ – zb.2 zasilany

X” – zb.2 zasilający

e

3

e

X

”

X”

Przykład:

p

b

1

1

b

n

p

p

h

z

g

g

ρ

ρ

−

=

+ =

2

1

2

b

p

h

z

z

g

ρ

−

= + =

p

b

p

n

=100kPa

1

1

g

g

ρ

ρ

R

1

*=6 10

6

s

2

/m

5

3

b

p

h

g

ρ

−

=

R

1

6 10 s /m

R

3

*=

10

6

s

2

/m

5

1) Numeracja zbiorników zgodnie z warunkiem

1

2

3

e

e

e

> >

2) Charakterystyka przewodów 1 i 3

1

3

e

e

=

=

3) Określenie rodzaju 2 zbiornika

3) Określenie rodzaju 2 zbiornika

*

*

1 3

3 1

*

*

1

3

X

R e

R e

e

R

R

+

=

=

+

ponieważ

X

e

=

to zbiornik 2 jest zasilający czyli charakterystyka przewodu 2

2

e

=

Natomiast strumień objętości q

vX

1

3

*

*

1

3

vX

e

e

q

R

R

−

=

=

+

Zatem, charakterystyki przepływu wykreślone zostaną w zakresie
przepływów od 0 do 4 dm

3

/s (punkt X znajdzie się wówczas

przepływów od 0 do 4 dm /s (punkt X znajdzie się wówczas
mniej więcej na środku wykresu).

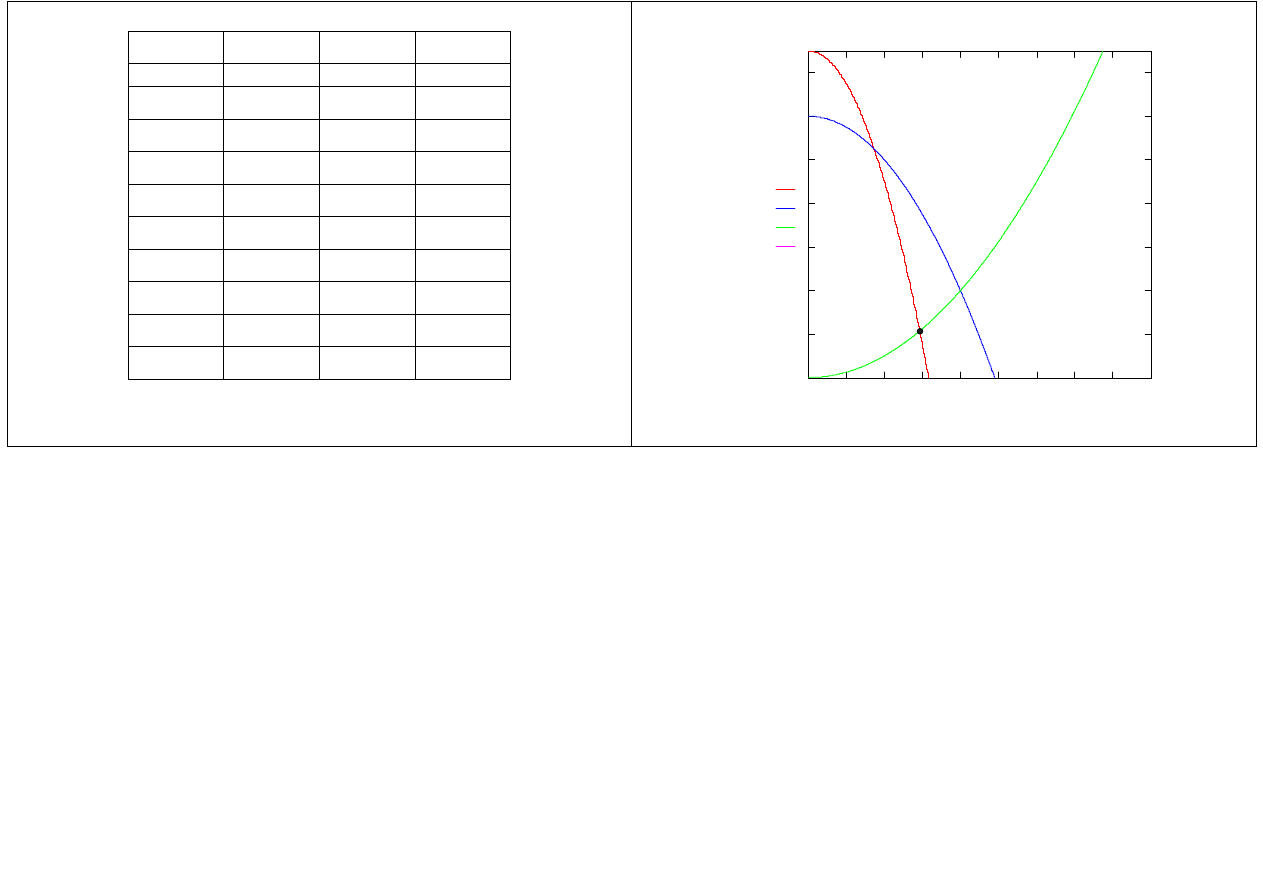
q

v

dm3/s

m

m

m

0

15,0

12,0

0

0,5

13,5

11,5

0,25

6

2

1

15 6 10

v

e

q

= − ⋅

6

2

3

10

v

e

q

=

6

2

2

12 2 10

v

e

q

= − ⋅

1

9,0

10,0

1,0

1,5

1,5

7,5

2,25

2

-9,0

4,0

4,0

2,5

―

-0,5

6,25

3

―

―

9,0

3

―

―

9,0

3,5

―

―

12,25

4

―

―

16,0

4) Wykreślenie charakterystyk i rozwiązanie graficzne

12

14

e, m

4

6

8

10

6

2

2

12 2 10

v

e

q

= − ⋅

6

2

1

15 6 10

v

e

q

= − ⋅

6

2

3

10

v

e

q

=

1

2

e

e

+

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

0

2

4

3

,

/

v

q

dm

s