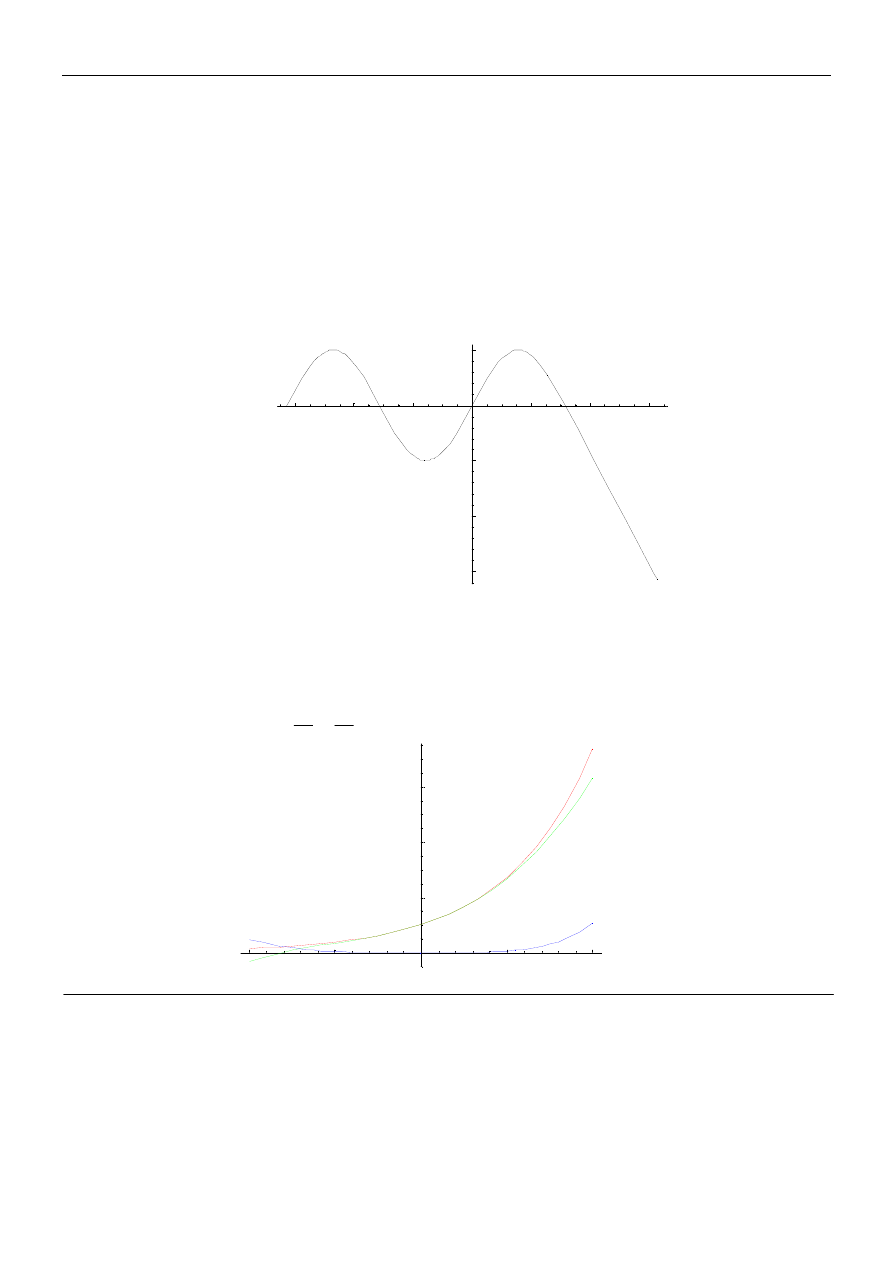
Metody numeryczne - ćwiczenia nr 1
1. Napisz komendę powodującą wypisanie na ekranie kwadratów liczb nieparzystych mniejszych od
10, wykorzystując instrukcje:
a) Do,
b) While,
c) For.
2. Zdefiniuj funkcję luc[n_] obliczającą n – ty wyraz ciągu Lucasa, w którym
2
1
−
−
+
=
n
n
n
f
f
f
oraz
.
1
,
2
1
0
=
=
f
f
Oblicz
.
15
f
Przedstaw graficznie 15 pierwszych wyrazów tego ciągu.
3. Rozwiąż poprzednie zadanie, wykorzystując procedurę Module.
4. Używając instrukcji Which zdefiniuj funkcję, której wykres widzisz poniżej i narysuj taki wykres
(widoczny łuk jest fragmentem sinusoidy).
-6
-4
-2
2
4
6
-3
-2
-1
1
5. Jak obliczyć, korzystając jedynie z działań arytmetycznych, przybliżoną wartość funkcji
x
e
x
f
≈
)
(
dla dowolnych x rzeczywistych? Na wykresie przedstawić otrzymaną funkcję
),
(x
f
x
e oraz
).
(x
f
e
x
−
Napisać odpowiednią procedurę w wyniku, której otrzymamy np.:
1
+
x
+
x
2
2
+
x
3
6
-2
-1
1
2
2
4
6
Do[expr, {i, imax}] -
oblicza expr ze zmienną i od wartości 1 do imax (z krokiem 1)
Do[expr, {i, imin, imax, di}] -
z krokiem di
While[war, treść] -
wykonuje treść, dopóki war jest spełniony
For[start, test, instr, treść] - zaczynając od wartości start, powtarza wykonanie
treść i instr aż test ma wartość fałsz
Which[test
1
, value
1
, test
2
, value
2
, … ] -
oblicza wartość logiczną test
i
i zwraca
wartość value
i
, dla której po raz pierwszy wystąpiła równość test
i
= True.

Metody numeryczne - ćwiczenia nr 2
1. Obliczyć numerycznie i porównać z dokładnymi wartościami (o ile to jest możliwe):
a)
,
1
1
1
2
∏
∞
=
+
n
n
b)
,
1
1
2
∑
∞
=
n
n
c)
,
)
!
(
2
)
1
(
0
2
2
∑
∞
=
−
n
n
n
n
k
dla
30
=
k
(użyć opcji NSumTerms, której wartość domyślna to 15),
d)
∫
1
0
))
(
tg
cos(
1
dx
x
(narysować wykres rozpatrywanej funkcji).
2.
Korzystając z funkcji
FindRoot
rozwiązać podane równania oraz układ równań. Punkt
0
x (dla
układu
)
,
(
0
0
y
x
) odczytać z odpowiedniego wykresu.
a)
,
0
)
sin(
2
=
x
b)
,
0
2
=
−
x
e
x
c)
=
+
−
=
+
,
0
,
1
2
2
y
xe
y
x
x
(do narysowania wykresu użyć funkcji
ContourPlot
).
3.
Korzystając
z
polecenia
FindMinimum
wyznaczyć
minimum
lokalne
funkcji
).
cos
(sin
)
,
(
2
2
10
2
2
y
x
e
y
x
f
y
x
+
=
−
−
Punkt
)
,
(
0
0
y
x
odczytać z odpowiedniego wykresu.
4.
Stosując podany niżej algorytm obliczania pierwiastka n - tego stopnia wyznaczyć
3 oraz
3
5
(zastosować funkcje
NestList i FixedPoint
).
Działanie algorytmu:
1.
Jako pierwsze przybliżenie liczby
n
A
przyjmujemy dowolną liczbę
,
0
x
np.
A
x =
0
.
2.
Za kolejne przybliżenie przyjmujemy:
.
)
1
(
1
1
1
+
−
=
−
+
n
k
k
k
x
A
x
n
n
x
3.
Powtarzamy punkt 2 tak długo, aż otrzymamy wymaganą dokładność przybliżenia.
5.
Napisać procedurę
pierwiastek[A_,n_,k_],
na podstawie, której obliczymy dowolny
pierwiastek, korzystając z algorytmu opisanego wyżej (
k
– ilość iteracji).

Metody numeryczne - ćwiczenia nr 3
1.
Obliczyć wartość całek
∫
=
=
−
1
0
1
,...,
2
,
1
,
k
dx
e
x
I
x
k
k
stosując wzór rekurencyjny
.
1
,
/
1
1
1
−
−
=
=
k
k
kI
I
e
I
Wykonać obliczenia dla k = 1, 2, …, 20.
Otrzymane wyniki porównać z dokładną wartością i przedstawić w postaci tabeli np.:
k
całka
iteracje
1
0.3678794412
0.367879
2
0.2642411177
0.264241
3
0.2072766470
0.207277
4
0.1708934119
0.170893
5
0.1455329406
0.145533
6
0.1268023566
0.126802
7
0.1123835041
0.112384
8
0.1009319674
0.100932
9
0.09161229299
0.0916123
10
0.08387707010
0.0838771
………..………………………………….
2.
Zastosuj dwa algorytmy obliczania wartości funkcji
.
cos
1
)
(
2
x
x
x
f
−
=
Pierwszy według podanego
wzoru, a drugi zmodyfikowany:
,
2
/
)
2
/
sin(
x
x
w =
.
2
1
ww
y =
Wykonaj obliczenia dla
,
10
123
.
1
1
−
⋅
=
x
…,
.
10
123
.
1
10
−
⋅
=
x
Utwórz wykres rozpatrywanej funkcji dla
)
2
,
2
(−
∈
x
.
Wyniki obliczeń przedstaw w postaci tabeli, np.:
x
Algorytm I
Algorytm II
0.11230000
0.49947475
0.49947475
0.01123000
0.49999475
0.49999475
0.00112300
0.49999995
0.49999995
……………………………………………………………..
3.
Zastosuj następujący algorytm obliczania przybliżonej wartości pochodnej
:
)
(c
f ′
.
)
(
)
(
)
(
h
c
f
h
c
f
c
f
−
+
≈
′
Wykonaj obliczenia dla różnych wartości parametru h (np.: h = 0.1, …,
)
10
1
.
0
20
−
⋅
i funkcji f (np.
dla
2
)
(
x
x
f
=
i c = 1.1). Porównaj z dokładną wartością pochodnej, wyznaczając błąd względny.
Otrzymane wyniki przedstaw w postaci tabeli, np.:
h
wartość ilorazu rożnicowego
bład wzgledny
0.10000000
2.30000000
0.04545455
0.01000000
2.21000000
0.00454545
0.00100000
2.20100000
0.00045455
0.00010000
2.20010000
0.00004545
0.00001000
2.20001000
4.54546350
×
10
−
6
1.00000000
×
10
−
6
2.20000100
4.54463230
×
10
−
7
……………………………………………………………………………………….

Metody numeryczne - ćwiczenia nr 4
1.
Napisać funkcję
w[lst_]
wyznaczającą
wielomian interpolacyjny Lagrange’a dla dowolnej
listy punktów
lst = {{x
1
,y
1
}, …,
{x
n
,y
n
}}, a następnie znaleźć taki, wielomian, który
w punktach
a.
{-2, 1, 2, 4} przyjmuje wartości {3, 1, -3, 8},
b.
{1, 3, 4, 6} przyjmuje wartości {-3, 0, 30, 132}.
Wyniki porównać z wynikami działania procedury
Fit.
Podać interpretację geometryczną.
2.
Znaleźć wielomian interpolacyjny Lagrange’a dla funkcji określonej tablicą wartości
(wykorzystać funkcję
w[lst]
):
x
1
2
5
f(x)
1
4
10
Następnie wyznaczyć wartość f(3). Podać interpretację geometryczną.
3.
Sporządzić tablicę różnic dla funkcji, która w punktach {0.1, 0.2, 0.3, 0.4, 0.5} przyjmuje wartości
{1.4, 1.56, 1.76, 2, 2.28} np.:
Znaleźć wielomian interpolacyjny Newtona dla różnic progresywnych i wstecznych. Zdefiniować
odpowiednie funkcje. Porównać z wynikami działania procedury
Interpolation.
Podać
interpretację geometryczną.
4.
Dane ilości sprzedanych sztuk towaru x w latach 1996-2004 przedstawione są w tabeli. Oszacuj za
pomocą wielomianu interpolacyjnego Newtona (wykorzystaj funkcje z poprzedniego zadania),
jaka była wysokość sprzedaży w 2003 roku.
x
1996 1998 2000 2002 2004
y
40
43
48
52
58
5.
Znaleźć wielomian interpolacyjny Newtona i Lagrange’a dla funkcji
x
x
f
cos
)
(
=
.
∑
∏
=
≠
=
−
−
=
n
j
n
j
i
i
i
j
i
j
n
x
x
x
x
y
x
L
0
,
0
)
(
)
(
)
(
- wzór interpolacyjny Lagrange’a,
)
)...(
)(
(
!
...
)
)(
(
!
2
)
(
)
(
1
1
0
0
1
0
2
0
2
0
0
0
)
(
−
−
−
−
∆
+
+
−
−
∆
+
−
∆
+
=
n
n
n
I
n
x
x
x
x
x
x
h
n
y
x
x
x
x
h
y
x
x
h
y
y
x
N
- pierwszy wzór interpolacyjny Newtona,
)
)...(
)(
(
!
...
)
)(
(
!
2
)
(
1
1
0
1
2
2
2
1
)
(
x
x
x
x
x
x
h
n
y
x
x
x
x
h
y
x
x
h
y
y
N
n
n
n
n
n
n
n
n
n
n
II
n
−
−
−
∆
+
+
−
−
∆
+
−
∆
+
=
−
−
−
−
- drugi wzór interpolacyjny Newtona.
Metody numeryczne - ćwiczenia nr 5
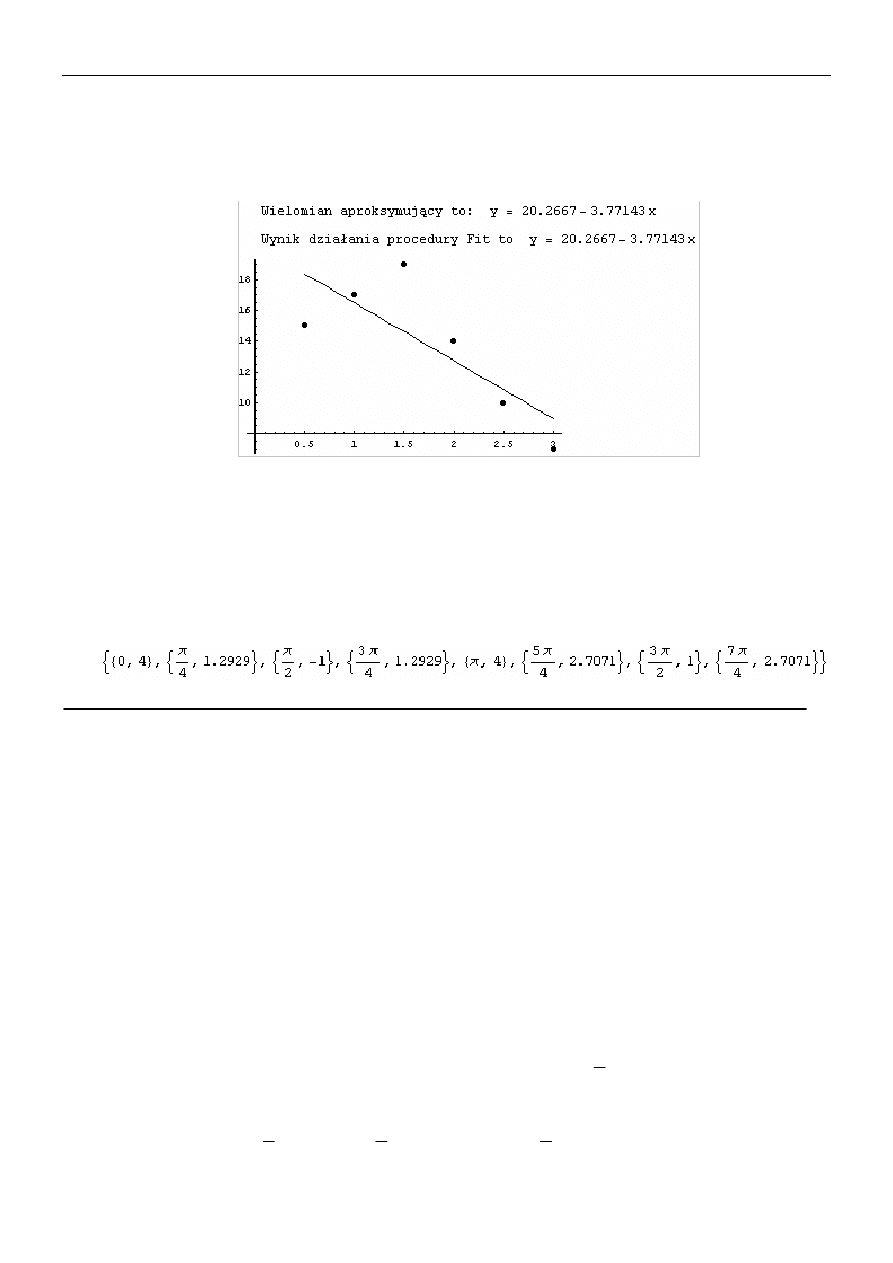
1.
Napisać procedurę
aprok[X_, Y_]
realizującą aproksymację wielomianem stopnia
pierwszego, w wyniku, której otrzymamy (procedurę wywołano z następującymi parametrami
X = {0.5, 1, 1.5, 2, 2.5, 3}, Y = {15, 17, 19, 14, 10, 7}):
aprok[X,Y]
Wykonać obliczenia dla innych danych np.: X = {1, 3, 4, 6, 8, 9, 11, 14}, Y ={1, 2, 4, 4, 5, 7, 8, 9}.
2.
Napisać procedurę
aprok2[X_, Y_]
realizującą aproksymację wielomianem stopnia
trzeciego. Zastosować do danych z poprzedniego zadania.
3.
Napisać procedurę
aprok3[X_, Y_, m_]
realizującą aproksymację wielomianami
trygonometrycznymi (m – stopień wielomianu trygonometrycznego). Zastosować do
następujących danych:
Współczynniki aproksymującej funkcji wielomianowej
n
n
x
a
x
a
x
a
x
a
a
y
+
+
+
+
+
=
...
3
3
2
2
1
0
wyznaczamy z następującego układu:
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
=
=
=
+
=
+
=
=
=
+
=
=
=
=
=
=
=
=
+
+
+
+
=
+
+
+
+
=
+
+
+
+
n
i
i
n
i
n
n
i
n
i
n
i
n
i
n
i
n
i
n
i
n
i
n
i
i
i
n
n
i
n
i
n
i
i
n
i
i
n
i
i
n
i
i
n
n
i
n
i
n
i
i
n
i
i
y
x
a
x
a
x
a
x
a
x
y
x
a
x
a
x
a
x
a
x
y
a
x
a
x
a
x
na
1
1
2
2
1
2
1
1
1
0
1
1
1
1
2
1
3
1
1
2
0
1
1
1
2
1
2
1
1
0
.
...
..........
..........
..........
..........
..........
..........
..........
..........
..........
..........
,
...
,
...
Trygonometryczne przybliżenie funkcji
)
(x
f
to:
,
2
),
sin
cos
(
)
(
1
0
n
m
jx
b
jx
a
a
x
f
j
m
j
j
<
+
+
≈
∑
=
gdzie
∑
∑
∑
=
=
=
=
=
=
n
j
j
j
j
n
j
j
j
j
n
j
j
jx
y
n
b
jx
y
n
a
y
n
a
1
1
1
0
.
sin
2
,
cos
2
,
1

Metody numeryczne - ćwiczenia nr 6
1.
Stosując funkcje
NestList
oraz
FixedPoint
z opcją
SameTest->(Abs[#1-
#2]<10^-3&)
znaleźć pierwiastek równania
0
2
1
sin
=
−
x
x
metodą Newtona w przedziale
[π/2, π]. Zdefiniować odpowiednie funkcje, sprawdzić założenia. Porównać uzyskany wynik
z wynikiem otrzymanym za pomocą polecenia
FindRoot
2.
Napisać procedurę
bi[f_,a_,b_,eps_]
rozwiązywania równań
0
)
(
=
x
f
metodą bisekcji.
Wyznaczyć pierwiastki poniższych równań w przedziale [0, 1.6] z błędem
eps
mniejszym od
0.02. Porównać uzyskane wyniki z wynikami otrzymanymi za pomocą polecenia
FindRoot
a)
x
x
x
ln
cos =
,
b)
0
2
=
−
− x
e
x
,
c)
x
e
x
−
=
−
1
2
.
3.
Napisać procedurę
sie[f_,a_,b_,eps_]
rozwiązywania równań
0
)
(
=
x
f
metodą
siecznych. Wyznaczyć przybliżone pierwiastki poniższych równań z dokładnością do
.
10
5
−
Narysować wykresy odpowiednich funkcji w zadanym przedziale:
a)
0
2
=
−
− x
x
,
],
1
,
0
[
∈
x
b)
0
6
cos
2
2
=
−
+
+
−
x
e
x
x
,
],
2
,
1
[
∈
x
c)
,
0
2
3
2
=
−
+
−
x
x
e
x
].
1
,
0
[
∈
x
Algorytm metody Newtona:
a)
)
(x
f
musi być ciągła i określona w rozpatrywanym przedziale
[
]
b
a,
,
)
(
' x
f
musi być różna od
zera w
[
]
b
a,
,
b)
wybieramy punkt startowy
0
x z przedziału
[
]
b
a,
,
c)
kolejne przybliżenia obliczmy ze wzoru
,...
2
,
1
,
)
(
)
(
1
=
′
−
=
+
n
x
f
x
f
x
x
n
n
n
n
Algorytm metody bisekcji:
a)
sprawdzamy, czy
0
)
(
)
(
<
b
f
a
f
,
b)
dzielimy przedział [a ,b] na połowę punktem
,
2
/
)
(
1
b
a
x
+
=
c)
jeżeli
0
)
(
1
=
x
f
, to
x
1
jest pierwiastkiem równania i koniec iteracji,
d)
gdy
0
)
(
1
≠
x
f
, to wybieramy jeden z przedziałów
[
]
1
,
x
a
lub
[
]
b
x ,
1
, w którym funkcja zmienia
znak,
e)
powtarzamy b), c) i d) dopóki nie otrzymamy żądanej dokładności
ε
(tj. gdy długość aktualnego
przedziału jest nie większa od
ε
).
Algorytm metody siecznych:
a)
sprawdzamy, czy
0
)
(
)
(
<
b
f
a
f
,
b)
jeśli zachodzi a), to
,
,
1
0
b
x
a
x
=
=
c)
dopóki nie jest spełnione kryterium zakończenia (stopu), np.
ε
<
−
−1
n
n
x
x
, gdzie
ε
jest zadaną
dokładnością, lub
ε
<
)
(
n
x
f
, lub przekroczenie liczby iteracji to wykonujemy:
,...
2
,
1
,
)
(
)
(
)
)(
(
1
1
1
=
−
−
−
=
−
−
+
n
x
f
x
f
x
x
x
f
x
x
n
n
n
n
n
n
n
Metody numeryczne - ćwiczenia nr 7
1.
Napisać procedurę
sturm[w_, n_]
w wyniku,
której otrzymamy
n
wyrazów ciągu Sturma
dla dowolnego wielomianu
w(x)
(wykorzystać polecenie
PolynomialRemainder[p, q,
x]
,
które wyznacza resztę z dzielenia wielomianu
)
(x
p
przez
)
(x
q
).
2.
Zastosować twierdzenie Sturma do określenia liczby pierwiastków rzeczywistych następujących
wielomianów (wykorzystać funkcję z poprzedniego zadania):
a)
,
5
5
2
)
(
2
3
+
−
−
=
x
x
x
x
f
b)
,
4
10
3
2
)
(
2
3
4
−
+
−
−
=
x
x
x
x
x
g
c)
.
1
)
(
2
3
−
−
+
=
x
x
x
x
h
Za pomocą polecenia
NSolve
sprawdzić poprawność obliczeń. Narysować wykres.
3.
Napisać procedurę
four[w_, n_]
w wyniku,
której otrzymamy
n
wyrazów ciągu Fouriera
dla dowolnego wielomianu
w(x)
.
4.
Wyznaczyć, przy pomocy twierdzenia Fouriera, liczbę zer rzeczywistych wielomianów:
a)
,
5
5
2
)
(
2
3
+
−
−
=
x
x
x
x
f
(porównać wynik z wynikiem zadania 2 a)),
b)
.
1
4
3
2
)
(
2
3
4
−
+
−
−
=
x
x
x
x
x
g
Za pomocą polecenia
NSolve
sprawdzić poprawność obliczeń. Narysować wykres.
Ciąg Sturma:
),
(
)
(
0
x
f
x
f
=
),
(
'
)
(
1
x
f
x
f
=
)
(
2
x
f
jest resztą z dzielenia
)
(
0
x
f
przez
)
(
1
x
f
wziętą ze znakiem przeciwnym,
)
(
3
x
f
jest resztą z dzielenia
)
(
1
x
f
przez
)
(
2
x
f
wziętą ze znakiem przeciwnym, itd.
Zakładamy, że
0
)
(
1
=
+
x
f
p
, a
)
(x
f
p
jest ostatnią resztą różną od zera czyli jest największym wspólnym
podzielnikiem dla wielomianu
)
(
0
x
f
i jego pochodnej
).
(
1
x
f
Jeżeli ten największy wspólny podzielnik jest liczbą
rzeczywistą różna od zera, oznacza to, że wielomian
)
(
0
x
f
nie ma zer wielokrotnych, gdy natomiast jest to
wielomian stopnia k, oznacza to, że jego miejsce zerowe jest (k+1)-krotnym zerem wielomianu
)
(
0
x
f
.
Twierdzenie Sturma. Jeżeli ciąg (f
i
(x)), i = 0,1,..., p, jest ciągiem Sturma na przedziale (a, b)
i
0
)
(
)
(
0
0
≠
b
f
a
f
, to liczba różnych zer rzeczywistych wielomianu
)
(
0
x
f
leżących w tym przedziale jest
równa N(a) - N(b), gdzie N(x) to ilość zmian znaku w ciągu Sturma w punkcie x.
Twierdzenie Fouriera. Jeżeli
)
(x
f
jest wielomianem stopnia n określonym w przedziale
)
,
( b
a
i
0
)
(
)
(
≠
b
f
a
f
, to liczba zer wielomianu
)
(x
f
w tym przedziale jest równa
)
(
)
(
b
M
a
M
−
, gdzie
)
(
0
x
M
oznacza liczbę zmian znaku w ciągu
,
,...
0
)),
(
(
)
(
n
k
x
f
k
=
dla
.
0
x
x =

Metody numeryczne - ćwiczenia nr 8
1.
Znaleźć minima lokalne w otoczeniu punktów odczytanych z wykresu funkcji
x
x
x
x
x
f
15
23
9
)
(
2
3
4
−
+
−
=
. Czy funkcja ta posiada maksimum?
2.
Wyznaczyć minimum funkcji
x
x
g
=
)
(
w przedziale
]
4
,
4
[−
za pomocą metody połowienia
(opracować odpowiednią procedurę
pol[f_,x1_,x2_,eps_]
). Sprawdzić nieskuteczność
polecenia
FindMinimum
.
3.
Za pomocą metody Johnsona wyznaczyć minimum lokalne funkcji
.
1
9
6
)
(
2
−
+
−
=
x
x
x
x
f
4.
Napisać procedurę
zloty[f_,x1_,x2_,eps_]
w wyniku, której otrzymamy minimum
funkcji
f
metodą złotego podziału. Korzystając z tej procedury wyznaczyć minimum funkcji
.
2
sin
)
(
2
x
x
x
f
=
Porównać otrzymany wynik z uzyskanym za pomocą polecenia
FindMinimum
.
FindMinimum[f,{x,x
0
}]
znajduje lokalne minimum dla f w otoczeniu punktu
0
x
x =
.
Algorytm metody połowienia
:
a)
Jeśli
eps
a
b
2
<
−
, to
2
b
a
t
+
=
i wypisujemy t (koniec procedury), w przeciwnym przypadku
b)
wybieramy punkty podziału:
,
,
,
4
3
4
1
)
(
3
2
1
2
1
)
(
2
4
1
4
3
)
(
1
b
a
t
b
a
t
b
a
t
i
i
i
+
=
+
=
+
=
c)
jeśli
),
(
)
(
2
1
t
f
t
f
≤
to
2
t
b =
, w przeciwnym przypadku
jeśli
),
(
)
(
3
2
t
f
t
f
≤
to
1
t
a =
i
3
t
b =
, a w przeciwnym przypadku
,
2
t
a =
d)
i
= i + 1, powtarzamy punkty a) do c).
Algorytm metody Johnsona
:
n
F
- n-ta liczba Fibonacciego -
.
,
1
2
1
1
0
−
−
+
=
=
=
n
n
n
F
F
F
F
F
Wybieramy n takie, że
.
1
n
eps
a
b
n
F
F
≤
<
−
−
a)
Określamy
a
a
b
F
F
t
i
n
i
n
i
+
−
=
+
−
−
−
)
(
1
1
)
(
1
,
a
a
b
F
F
t
i
n
i
n
i
+
−
=
+
−
−
)
(
1
)
(
2
,
b)
i
= 1, jeśli
),
(
)
(
)
(
2
)
(
1
i
i
t
f
t
f
≤
to a pozostaje bez zmiany,
)
(
2
i
t
b =
, w przeciwnym przypadku
,
)
(
1
i
t
a =
b - bez zmiany,
c)
punkty a), b) powtarzamy do
,
2
−
= n
i
d)
wypisujemy
.
2
min
b
a
x
+
=
Algorytm metody złotego podziału
:
a)
Obliczamy
2
1
5 −
=
τ
,
),
)(
1
(
)
(
1
a
b
a
t
i
−
−
+
=
τ
),
)(
1
(
)
(
2
a
b
b
t
i
−
−
−
=
τ
b)
jeśli
),
(
)
(
)
(
2
)
(
1
i
i
t
f
t
f
>
to
)
(
1
i
t
a =
, b pozostaje bez zmiany,
,
)
(
2
)
1
(
1
i
i
t
t
=
+
),
)(
1
(
)
1
(
2
a
b
b
t
i
−
−
−
=
+
τ
c)
w przeciwnym przypadku a - bez zmiany,
,
)
(
2
i
t
b =
,
)
(
1
)
1
(
2
i
i
t
t
=
+
),
)(
1
(
)
1
(
1
a
b
a
t
i
−
−
+
=
+
τ
d)
jeśli
ε
2
≤
− a
b
-koniec procedury, wypisujemy
2
min
b
a
x
+
=
, w przeciwnym przypadku
e)
powtarzamy punkty b) do d).

Metody numeryczne - ćwiczenia nr 9
1.
Metodą kolejnych przybliżeń rozwiązać układ równań liniowych (zastosować funkcje
NestList
oraz FixedPoint):
=
+
+
=
+
+
−
=
−
+
.
0
.
7
0
.
2
3
.
0
4
.
0
,
3
.
8
2
.
0
0
.
4
3
.
0
,
9
.
1
3
.
0
4
.
0
0
.
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Wyniki obliczeń przedstawić w postaci tablicy, np.:
x1
x2
x3
1
0.
0.
0.
2
0.95
2.075
3.5
3
1.06
1.97125
2.99875
2.
Metodą eliminacji Gaussa rozwiązać układ równań liniowych
=
−
+
=
+
−
=
−
+
.
8
.
7
6
.
5
4
.
3
2
.
1
,
0
.
9
8
.
7
6
.
5
4
.
3
,
2
.
3
4
.
5
6
.
7
8
.
9
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Wykorzystać poniższą procedurę (po uzupełnieniu):
Rozwiązanie porównać z rozwiązaniem uzyskanym za pomocą polecenia
LinearSolve.
Algorytm eliminacji Gaussa:
a)
przyjmujemy
,
)
1
(
ij
ij
a
a
=
,
)
1
(
i
i
b
b
=
),
,...,
1
,
(
n
j
i
=
b)
dla
1
,...,
1
−
=
n
k
oraz dla
n
k
i
,...,
1
+
=
obliczamy
a.
,
/
)
(
)
(
k
kk
k
ik
ik
a
a
l =
b.
dla
n
k
j
,...,
1
+
=
obliczmy
,
)
(
)
(
)
1
(
k
kj
ik
k
ij
k
ij
a
l
a
a
−
=
+
c.
,
)
(
)
(
)
1
(
k
k
ik
k
i
k
i
b
l
b
b
−
=
+
c)
obliczamy
,
/
)
(
)
(
n
nn
n
n
n
a
b
x =
dla
1
,...,
1
−
= n
i
obliczamy
.
/
1
)
(
)
(
)
(
−
=
∑
+
=
n
i
j
i
ii
j
i
ij
i
i
i
a
x
a
b
x
Metody numeryczne - ćwiczenia nr 10
1.
Metodą iteracji prostej (zastosować funkcje
NestList
i
FixedPoint
) oraz metodą Newtona
rozwiązać następujący układ równań:
−
=
+
=
.
4
2
cos
,
4
2
sin
y
x
y
y
x
x
Podać interpretację geometryczną (wykorzystać funkcję
ContourPlo
t).
2.
Układ równań
+
+
=
+
+
=
)
(
tg
5
.
0
),
3
(
1
2
2
2
2
y
e
h
y
x
e
h
x
x
x
y
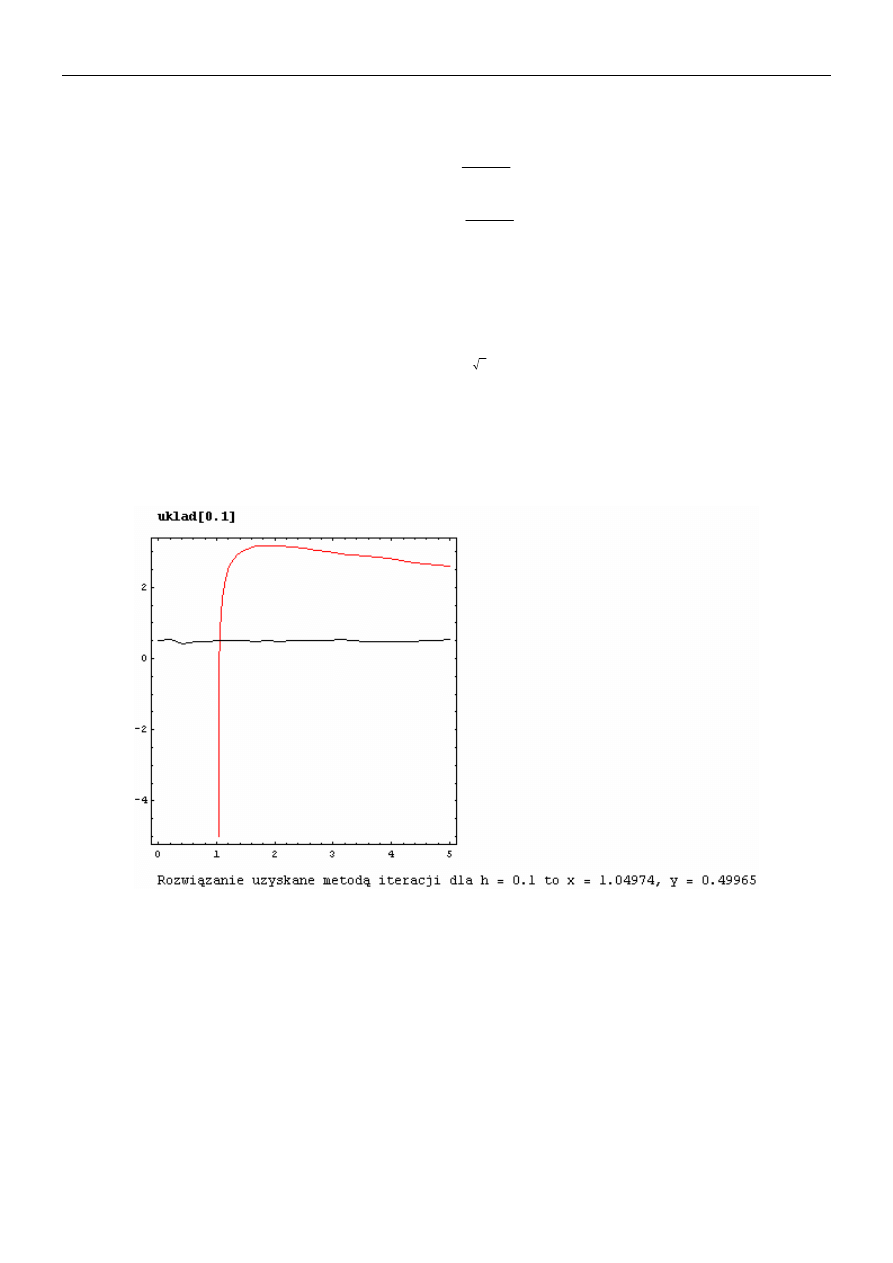
można dla małych h, rozwiązać iteracyjnie. Napisać procedurę
układ[h_]
w wyniku, której
otrzymamy (przyjąć
,
1
0
=
x
)
5
.
0
0
=
y
:
Metody numeryczne - ćwiczenia nr 11
1.
Zdefiniować funkcje
calka1[a_,b_,n_]
,
calka2[a_,b_,n_]
i
calka3[a_,b_,n_]
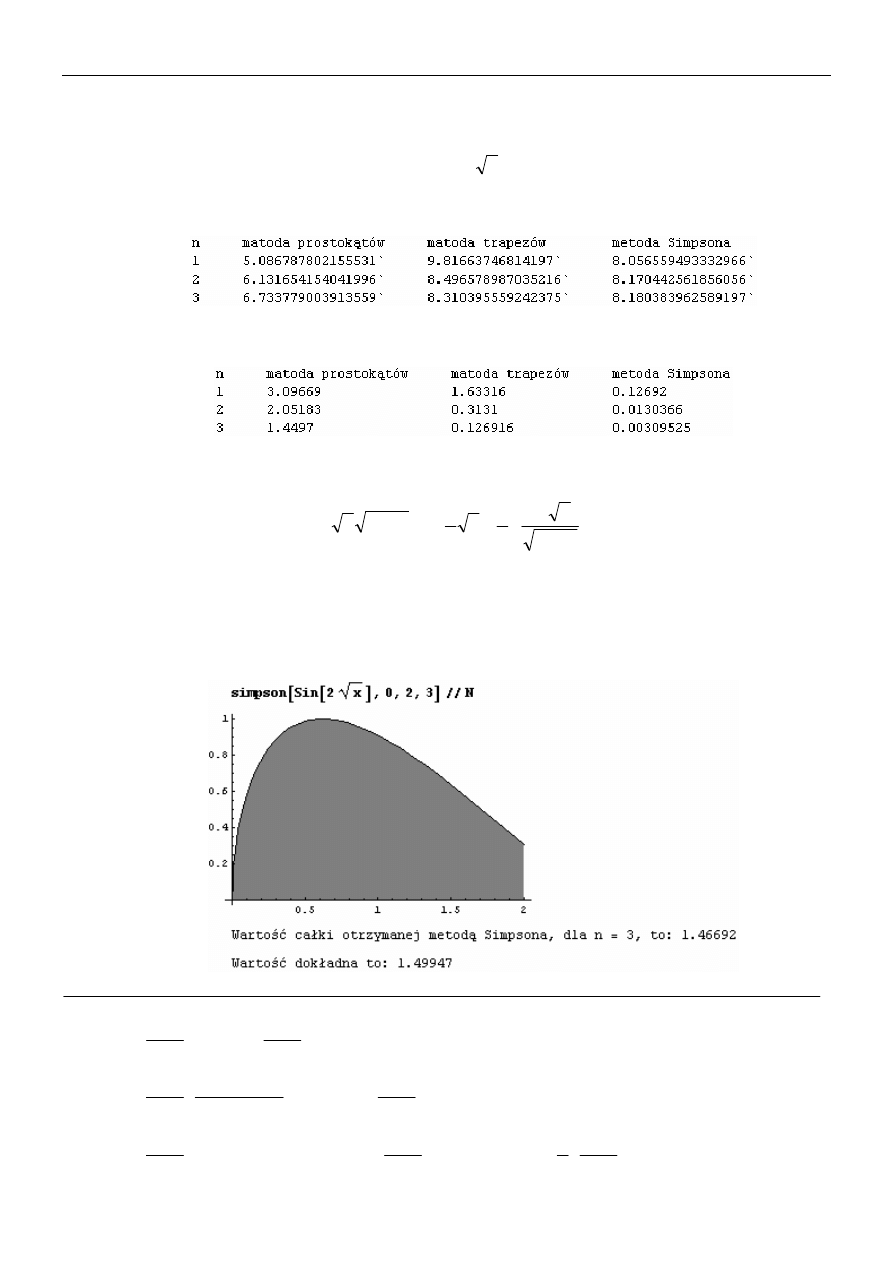
wyznaczające odpowiednio całki metodą prostokątów, metodą trapezów i metodą Simpsona.
Obliczyć trzema metodami całkę:
∫
+
6
1
)
2
sin(
2
(
dx
x
dla n = 1, …, 20. Wyniki przedstawić w postaci tabeli:
…..………………..……………………………………………………………..
Otrzymane wyniki porównać z dokładną wartością i różnice przedstawić w postaci tabeli np.:
……….…..……………………………………………………………..
2.
Za pomocą wzoru Simpsona obliczyć oddzielnie lewą i prawa stronę poniższej równości
otrzymanej przez całkowanie przez części:
.
1
3
4
2
3
2
1
1
0
4
4
1
0
4
dx
x
x
x
dx
x
x
∫
∫
+
−
=
+
Otrzymane wyniki porównać z dokładnymi wartościami.
3.
Napisać procedurę
simpson[f_,a_,b_,n_]
w wyniku, której otrzymamy wartość dowolnej
całki obliczoną metodą Simpsona, wartość dokładną rozpatrywanej całki oraz interpretację
geometryczną np.:
∑
∫
=
−
+
−
≈
n
i
b
a
n
a
b
i
a
f
n
a
b
dx
x
f
1
)
(
-
wzór prostokątów
−
+
+
+
−
≈
∑
∫
−
=
1
1
2
)
(
)
(
)
(
n
i
b
a
n
a
b
i
a
f
b
f
a
f
n
a
b
dx
x
f
-
wzór trapezów
−
−
+
+
−
+
+
+
−
≈
∑
∑
∫
=
−
=
n
i
n
i
b
a
n
a
b
i
a
f
n
a
b
i
a
f
b
f
a
f
n
a
b
dx
x
f
1
1
1
2
1
4
2
)
(
)
(
6
)
(
- wzór Simpsona

Metody numeryczne - ćwiczenia nr 12
1.
Korzystając z funkcji
ChebyshevT[n,x]
utworzyć wykres przedstawiający wielomiany
Czebyszewa dla n = 1, 2, …, 5 oraz
).
1
,
1
(−
∈
x
2.
Wyznaczyć wartości węzłów (zera wielomianów Czebyszewa) i współczynników
k
A
kwadratur Gaussa – Czebyszewa dla n = 2, 3, …, 8. Otrzymane wyniki przedstawić w postaci
tabeli np.:
3.
Obliczyć następujące całki za pomocą kwadratur Gaussa – Czebyszewa (zdefiniować
odpowiednią funkcję
calka[n_]
):
a)
dx
x
x
∫
−
−
1
1
2
1
(wykonać obliczenia dla n = 2, 3, …, 20),
b)
dx
x
e
x
∫
−
−
1
1
2
1
(wykonać obliczenia dla n = 2, 3, …, 10).
Otrzymane wyniki porównać z dokładną wartością i przedstawić w postaci tabeli np. dla punkt a):
…….…………………………………
4.
Napisać procedurę
chebyszew[f_,n_]
w wyniku, której otrzymamy np.:
( )
∑
∫
=
−
≈
−
n
k
k
k
x
f
A
dx
x
x
f
1
2
1
1
1
1
)
(
- wzór kwadratur Gaussa – Czebyszewa,
gdzie
n
A
k
π
=
- współczynniki tych kwadratur,
−
=
π
n
k
x
k
2
1
2
cos
- węzły.
Wyszukiwarka
Podobne podstrony:
Laboratorium metod numerycznych Nieznany
Laboratorium metod numerycznych Nieznany
cwiczenie9 id 125928 Nieznany
cwiczenia23 id 124959 Nieznany
cwiczenia 4 2 id 124428 Nieznany
Fizjologia Cwiczenia 3 id 17436 Nieznany
5 Najlepszych Metod Notowania i Nieznany
cwiczenie 4 2 id 125411 Nieznany
cwiczenie 9 id 125104 Nieznany
Cwiczenia w szkicowaniu czesc4 Nieznany
Cwiczenia 5 id 124444 Nieznany
opis cwiczenia id 336864 Nieznany
cwiczenie 5 id 101060 Nieznany
Cwiczenie 3 id 125305 Nieznany
CWICZENIE 6 2 id 99618 Nieznany
cwiczenie 5 id 125447 Nieznany
Cwiczenie 6 id 125101 Nieznany
więcej podobnych podstron