Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

1

Ćwiczenie 8.

Joystick force-feedback

Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

2

Wstęp.

W skład stanowiska laboratoryjnego wchodzi:

–

komputer   PC   z  oprogramowaniem   Matlab/Simulink  pozwalający  na  wykonanie  pomiarów   oraz   realizację 

algorytmu sterowania,

–

joystick Logitech Force 3D Pro będący obiektem sterowania,

–

joystick Logitech Extreme 3D Pro służący jako źródło sygnału zadanego.

Joystick Logitech Force 3D Pro posiada funkcję siłowego sprzężenia zwrotnego (force feedback) – pozwala on 

nie tylko na pomiar położenia rękojeści, ale może także wywierać pewną siłę – wystarczającą do poruszania swobodną 

rękojeścią w dwóch wymiarach.

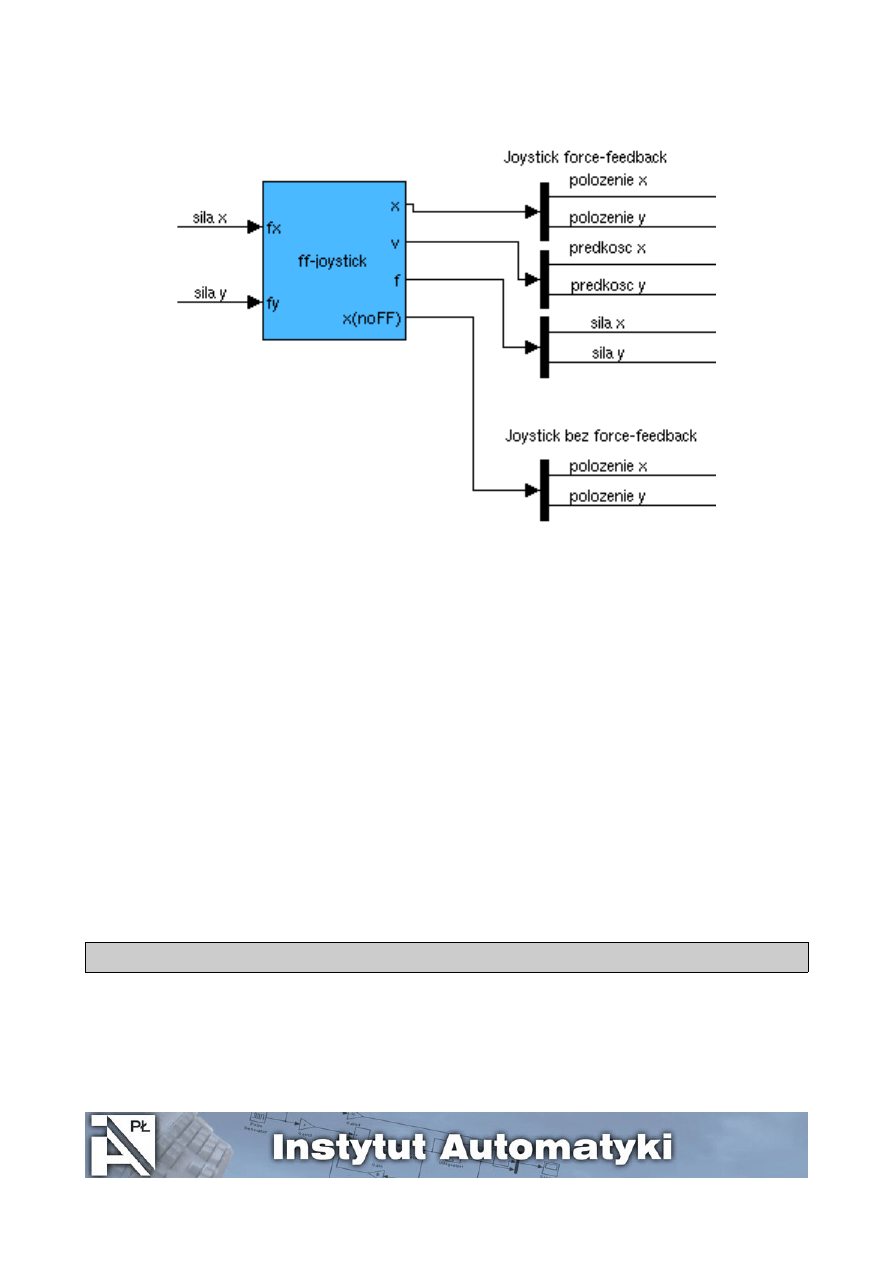
Współpracę z joystickem z poziomu Simulinka umożliwia blok ff-joystick pokazany na rysunku 2. Sygnałami 

wejściowymi dla bloku są wartość siły w osi x oraz siły w osi y. Sygnały wyjściowe to położenie joysticka (port 

oznaczony jako „x”), prędkość („v”) i wywierana siła („f”) oraz położenie drugiego joysticka (bez sprzężenia siłowego, 

port oznaczony jako "x(noFF)"). Sygnały te zawierają dwie współrzędne – dla osi x i y. Przyjęto, że oś x odpowiada 

wychyleniom w lewo/prawo, oś y – wychyleniom do przodu/do tyłu. Aby rozdzielić sygnał na dwie współrzędne należy 

skorzystać z bloku demux (położenia wykorzystywanych bloków w bibliotece Simulinka podano na końcu instrukcji), 

co pokazano na rysunku.

Rysunek 1. Stanowisko laboratoryjne. Po prawej joystick z force-feedback

Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

3

Rysunek 2. Blok ff-joystick oraz sygnały wejściowe i wyjściowe

Zakresy wartości poszczególnych sygnałów wynoszą:

–

dla   położenia   –   wartości   całkowite   od   -1000   do   +1000,   co   odpowiada   wychyleniu   o   około   15   stopni 

odpowiednio w lewo i prawo / do przodu i do tyłu,

–

dla sił w obu osiach – wartości całkowite od -10000 do +10000,

–

prędkość   obliczana   jest   przy   pomocy   filtru   Golay'a-Savitzky'ego   i   przyjmuje   wartości   z   zakresu 

± 1.6 ⋅ 10

4.

.

Uwaga. Działanie algorytmu w Simulinku zawierającego blok ff-joystick jest spowolnione w taki sposób, by 

czas symulacji odpowiadał czasowi rzeczywistemu. Komunikacja z joystickiem wykonywana jest co 1/100 sekundy, 

stąd w parametrach symulacji (menu Simulation, polecenie Configuration parameters) należy wybrać Type: Fixed-step 

oraz Fixed-step size: sampletime. (zmienna sampletime powinna zostać zdefiniowana w Matlabie przed uruchomieniem 

bloku ff-joystick, wartość: 0.01).

Blok   ff-joystick   komunikuje   się   z   joystickiem   korzystając   z   dodatkowego   programu   ff-const   (skrót   na 

pulpicie). Program ten należy uruchomić i pozostawić działający w tle przez cały czas wykonywania ćwiczenia.

Po uruchomieniu Matlaba należy w linii wpisać polecenie:

start_joy

Zadanie 0. Zapoznać się z działaniem stanowiska laboratoryjnego:

–

uruchomić program ff-const,

–

uruchomić Matlab i Simulink (w Matlabie wpisać polecenie Simulink),

Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

4

–

utworzyć nowy model (w oknie Simulinka: File > New > Model),

–

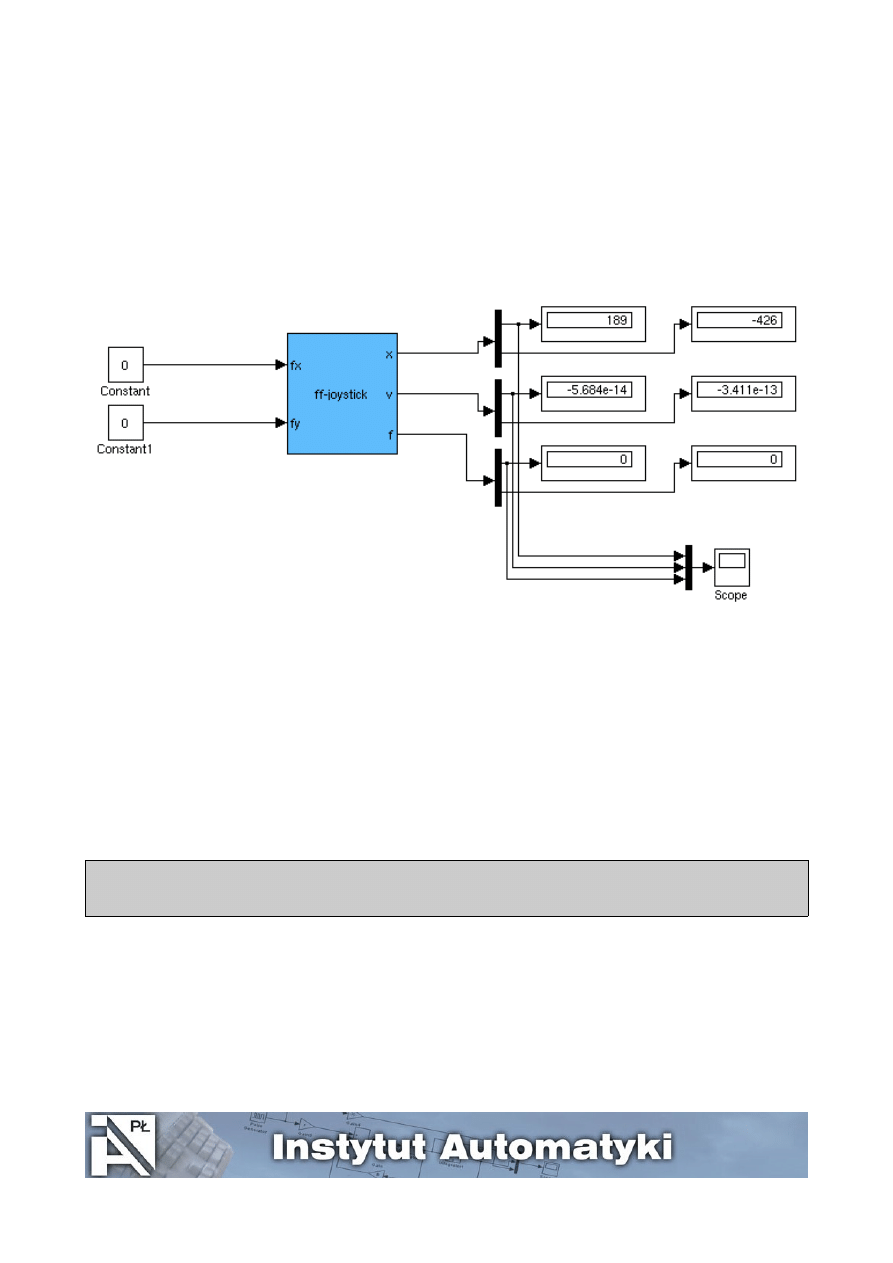
z odpowiednich bloków złożyć schemat pokazany na rysunku 3,

–

ustawić parametry symulacji zgodnie z informacjami podanymi powyżej, wpisać czas zakończenia symulacji 

(Stop time) jako inf,

–

uruchomić symulację, zbadać zakresy uzyskiwanych wartości oraz możliwości zadania siły (zmienić wartość 

w bloku Constant lub Contant1 na różną od zera, np. 2000).

Zadanie 1. Wyznaczenie odpowiedzi skokowej obiektu.

–

zmodyfikować schemat z poprzedniego zadania, tak by zadawana w osi x siła zmieniała się skokowo od 

wartości zero do wybranej wartości z zakresu 0-10000,

–

schemat uzupełnić o blok To Workspace (w ustawieniach bloku wybrać rodzaj danych: Structure with time),

–

ustawić joystick w położeniu zerowym (lub bliskim zera) w obu osiach,

–

uruchomić symulację i zatrzymać po skoku,

–

w Matlabie wykreślić przebieg siły i położenia joysticka w osi x w funkcji czasu:

plot( odp.time, odp.signals.values(:,1), 'r', odp.time, 

odp.signals.values(:,2), 'b' )

–

sprawdzić jak zależy kształt uzyskiwanej odpowiedzi od amplitudy skoku?

Zadanie 2. Wyznaczanie charakterystyki statycznej.

Pomiary z siłą zadawaną ręcznie:

–

zbudować   schemat   edytorze   Simulink   pozwalający   na   zadawanie   dowolnej   siły   i   wykorzystać   go   do 

wyznaczenia 10-20 punktów charakterystyki statycznej joysticka (dla jednej osi)

Rysunek 3.Schemat Simulinka do Zadania 0

Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

5

–

punkty wpisać do Matlaba jako macierz i wykreślić poleceniem plot

Automatyczne wyznaczanie charakterystyki:

–

zbudować schemat Simulinka, w którym generowany jest sygnał prostokątny (okres 2s, wypełnienie 50%) o 

rosnącej   amplitudzie,   np.   200,   400,   600,   itd.   (Można   skorzystać   np.   z   bloków   Ramp,   Quantizer,   Pulse 

Generator oraz Product)

–

wygenerowany sygnał podać jako siłę w osi x joysticka

–

zarejestrować w Matlabie zadawaną siłę oraz uzyskiwaną pozycję joysticka (blok To Workspace – zmienić 

nazwę zmiennej z "simout" na "pomiar", rodzaj zmiennej: Structure with time)

–

skorzystać z pliku steady_char do uzyskania punktów charakterystyki statycznej:

[sU,sY] =steady_char( pomiar.signals.values(:,1), pomiar.signals.values(:,2) )

–

powtórzyć pomiary dla ujemnych wartości siły

Zadanie 3. Wyznaczanie charakterystyki częstotliwościowej.

–

schemat z poprzedniego zadania zmodyfikować tak by zadawana była siła o przebiegu sinusoidalnym

–

ustalić wartość amplitudy, która zapewnia jak najmniej zniekształcony sygnał na wyjściu

–

po   wykonaniu   pomiaru   skorzystać   z   pliku   sin_analyz   do   wyznaczenia   amplitudy   (ampl),   przesunięcia 

fazowego (phi) i okresu (period) sygnału wyjściowego:

[ampl,   phi,   period]   =   sin_analyz(   pomiar.time,   pomiar.signals.values(:,1), 

pomiar.signals.values(:,2) );

–

pomiary wykonać dla różnych częstotliwości – pamiętając, że próbkowanie jest z okresem 10ms

–

wykreślić charakterystyki:

–

logarytmiczną amplitudową i fazową (Bodego),

–

amplitudowo-fazową (Nyquista)

–

uwaga:   w  celu  poprawienia   dokładności   działania   programu   sin_analyz   można   usunąć   początkową   część 

zmierzonego przebiegu, np.: (usuwa początkowe 3 sekundy z pomiaru typu Structure with time)

pomiar = przytnij( pomiar, 3 );

Zadanie 4. Wyznaczanie prędkości

–

zbudować układ pozwalający na obserwowanie prędkości joysticka obliczanej przy pomocy:

a) bloku Derivative z biblioteki Continuous

b) bloku Discrete Derivative z biblioteki Discrete (tylko Matlab >6.5)

c) bloku o transmitancji: 

Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

6

G

 s=

sT

1sT / N 

 

(1)

d) filtru Golaya-Savitzkiego (wyjście v bloku ff-joystick)

–

sprawdzić działanie poszczególnych metod w zależności od parametrów

–

wybrać metodę do dalszych badań – wybór uzasadnić

Zadanie 5. Dobór parametrów regulatora PID przy pomocy metody Zieglera-Nicholsa

–

zbudować  układ, w którym  szeregowe połączenie  regulatora PID oraz  bloku ff-joystick obwiedzione jest 

sprzężeniem zwrotnym zawierającym blok Unit Delay (biblioteka Discrete, należy pamiętać o zmienieniu 

wartości Sample time w ustawieniach bloku). Jako wartość zadaną należy podać zero. Regulator PID należy 

zbudować   jako   równoległe   połączenie   elementu   proporcjonalnego   (wzmocnienie   Kp),   różniczkującego 

(prędkość   poprzez   blok   Gain   o   wzmocnieniu   Kp*Td)   i   całkującego   (wzmocnienie   Kp/Ti).   Można   także 

skorzystać z bloku PID controller (with Approximate Derivative) jeśli jest dostępny (prędkość wyznaczana jest 

wówczas metodą c). Uwaga: w gotowym blok PID występuje interakcja, a parametry transmitancji to Kp, Ki i 

Kd – nastawy uzyskane w sposób opisany poniżej należy odpowiednio przeliczyć! 

–

wyznaczyć minimalną wartość wzmocnienia K

c

, przy której występują w układzie drgania nietłumione (uwaga 

– do powstania drgań w układzie konieczne jest wcześniejsze wytrącenie go ze stanu równowagi)

–

wyznaczyć przybliżony okres drgań T

c

–

sprawdzić działanie regulatorów (zgodnie z Z-N):

–

P: K

p

 = 0.5*K

c

–

PI: K

p

 = 0.45*K

c

, T

i

 = T

c 

/ 1.2

–

PID: K

p

=0.6*K

c

; T

i

=T

c 

/ 2; T

d

 = T

c 

/ 8

–

sprawdzić działanie układu regulacji dla różnych przebiegów (wartości i kształtów) sygnału zadanego

–

zbadać zachowanie układu regulacji w przypadku wystąpienia długotrwałego zakłócenia:

–

odchylić joystick do położenia skrajnego i natychmiast puścić, obserwować przebiegi przejściowe

–

odchylić   joystick   do   położenia   skrajnego   i   puścić   po   trzech   sekundach,   obserwować   przebiegi 

przejściowe. Z czego wynika zachowanie układu? 

–

wykreślić sygnały wyjściowe poszczególnych części regulatora PID

–

w   elemencie   całkującym   wprowadzić   ograniczenie   wartości   (upper   i   lower   saturation   limit), 

sprawdzić działanie układu w zależności od poziomu ograniczenia

–

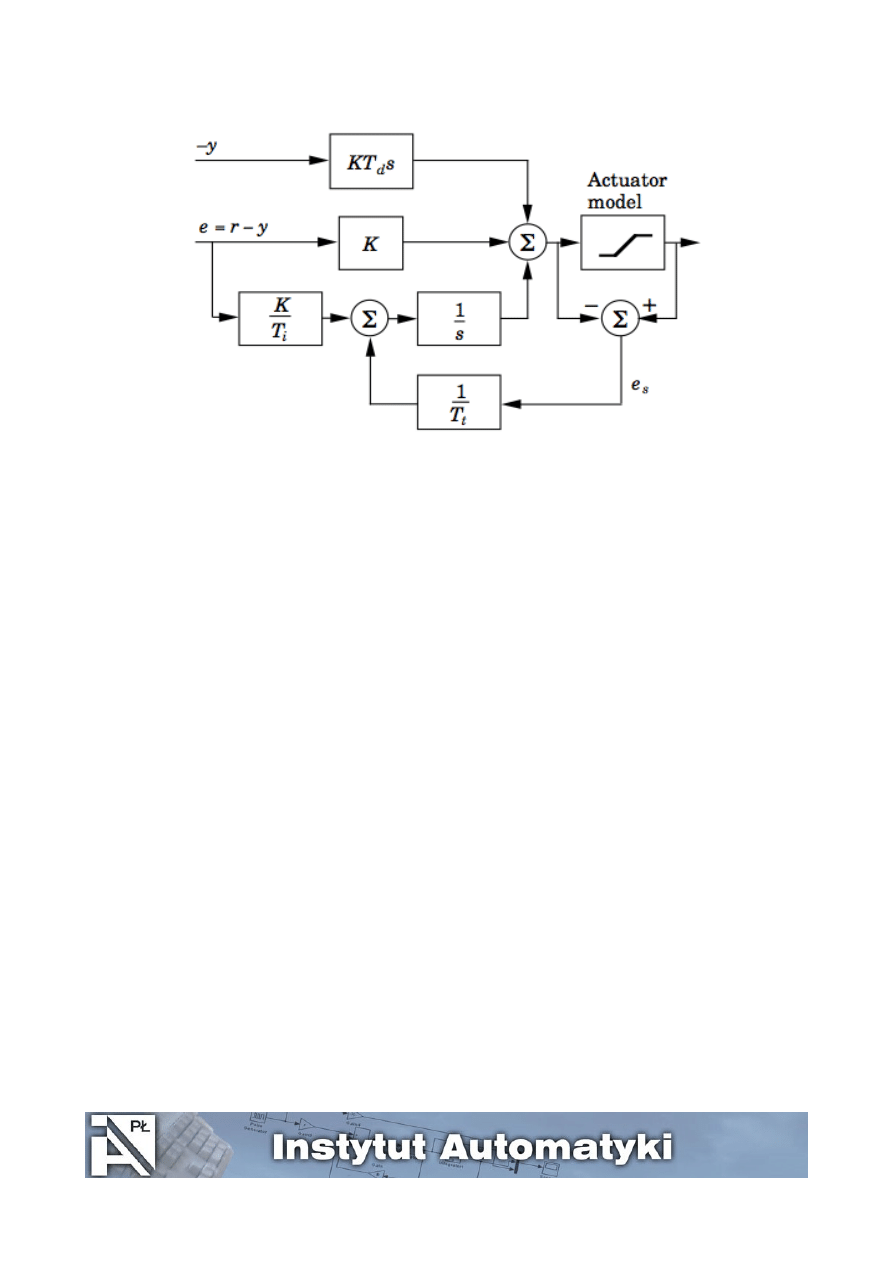
zamiast ograniczenia wartości integratora wprowadzić tzw. Anty Windup wg schematu pokazanego 

na rysunku 4 (jako blok "Actuator model" zastosować blok Saturation z biblioteki Discontinuities). 

Instrukcja do ćwiczenia nr 8 z Laboratorium Automatyki

7

Zadanie 6. Ruch w obu osiach

–

przeprowadzić strojenie regulatora dla ruchu w osi y

–

zbudować schemat zawierający układy regulacji dla obu osi, jako źródło sygnału zadanego podać położenie 

drugiego joysticka.

Bloki Simulinka wykorzystywane w ćwiczeniu:

–

Step, Ramp, Pulse Generator -Simulink > Sources >

–

Constant – Simulink > Sources >

–

Sum, Product – Simulink > Math >

–

Mux, Demux – Simulink > Signal routing >

–

ff-joystick – Force Feedback Joystick >

–

Integrator, Derivative – Simulink > Continuous >

–

Transfer Fcn – Simulink > Continuous >

–

PID Controller (with Approximate Derivative) – Simulink Extras > Additional linear >

–

Saturation, Quantizer – Simulink > Nonlinear >

–

To Workspace, Scope, Display – Simulink > Sinks >

–

Gain – Simulink > Math >

Rysunek  4.   Schemat   układu   z   regulatorem   PID   i   anty-windup.   Wartość   stałej   T

t

  to   0.5T

i

  dla 

regulatora PI oraz sqrt(T

i

T

d

) dla PID