Logistyka 6/2013

2

Logistyka - nauka

Andrzej Banachowicz

1

, Grzegorz Banachowicz

2

Wstęp

We współczesnym świecie pojęcie fuzji danych

nabiera nowego znaczenia. Wieloźródłowość danych,
bądź niewystarczająca liczba danych sprawiają, że
opis interesującego nas wycinka rzeczywistości na
satysfakcjonującym odbiorcę poziomie stał się o wiele
trudniejszy.

W odniesieniu do końca dwudziestego wieku

i początku obecnego, mamy do czynienia z dynamicz-
nym procesem integracji informacji nawigacyjnej oraz
szeroko pojętej globalizacji danych i ich źródeł . Roz-
powszechnienie globalnego systemu nawigacji, który
znalazł zastosowanie w nawigacji morskiej, lotniczej
(również kosmicznej) i lądowej, okazał się na tyle
uniwersalny, że jego praktyczne wykorzystanie jest
niemal nieograniczone. Wystarczy nadmienić, iż
w geodezji, geologii czy leśnictwie i budownictwie
określenie dokładnej pozycji jest pierwszorzędne.
Wszystko to nie byłoby możliwe bez odpowiedniego
poziomu technologicznego współczesnych systemów
nawigacyjnych i informatycznych. Wysoka dokładność
określania pozycji za pomocą systemów satelitarnych
ora automatyzacja systemów nawigacji zliczeniowej
(ang. DR – dead reckoning) stawia duże wymagania
w stosunku do przetwarzania danych nawigacyjnych.

Często przyjmuje się, że obróbka danych pomia-

rowych ma na celu wyłącznie ich optymalne przetwo-
rzenie z punktu widzenia eliminacji zakłóceń (minima-
lizacji błędów określanych wielkości). Z tego względu
najczęściej wykorzystywana jest estymacja danych
nawigacyjnych, względnie parametrów rozkładów
zakłóceń

tych

danych.

Błędy

nadmiarowe

i systematyczne staramy się eliminować na etapie ob-
róbki pierwotnej. Jednakże, rzeczywistość nie zawsze
sprzyja takim założeniom, co dawniej uwidaczniane
było podczas tzw. testów pomiarów, a obecnie jako
sprawdzenie wiarygodności (integrity) urządzenia lub
systemu nawigacyjnego.

1

dr hab. inż. Andrzej Banachowicz, Zachodniopomorski Uniwersytet

Technologiczny w Szczecinie

2

mgr inż. Grzegorz Banachowicz, Policealna Szkoła Morska w Szczeci-

nie, Towarzystwo Krzewienia Wiedzy o Morzu

W artykule przedstawiono zagadnienia budowy

różnych modeli nawigacji zintegrowanej drogą doboru
odpowiedniej struktury filtru Kalmana – modelu stanu
i modelu pomiarów.

Filtr Kalmana

Metody filtracji Kalmanowskiej można stosować

na różnych poziomach obróbki informacji nawigacyj-
nej. Poczynając od obróbki pierwotnej – estymacji
błędów pomiarów nawigacyjnych (na poziomie
pomiaru wielkości fizycznych takich jak: faza, czas,
amplituda itd.), a kończąc na estymacji współrzędnych
pozycji oraz innych parametrów nawigacyjnych
(wielkości geometrycznych). W każdym z tych
przypadków

posługujemy

się

takim

samym

algorytmem obliczeniowym. Ze względu na to, że
współcześnie posługujemy się cyfrowymi układami
pomiarowo-obliczeniowymi, to istotę tego algorytmu
przedstawimy na przykładzie dyskretnego losowego
układu dynamicznego. Opisują go dwa poniższe
równania [Anderson, 1979], [Balakrishnan, 1984]:

• równanie stanu (model strukturalny)

,

(1)

• równanie pomiarów (model pomiarowy)

,

(2)

gdzie:
- n-wymiarowy wektor stanu,

- r-wymiarowy wektor zakłóceń stanu,

- m-wymiarowy wektor pomiarów,

- p-wymiarowy wektor zakłóceń pomiarów

(szum pomiarowy),

- n×n-wymiarowa macierz przejścia,

- m×n-wymiarowa macierz pomiarów,

r ≤ n, p ≤ m.

Fuzja pomiarów nawigacyjnych GPS/I S/DR

Logistyka - nauka

Logistyka 6/2013

3

Ponadto dla wektorów zakłóceń w i v zakła-

damy, że są to szumy gaussowskie (o rozkładzie nor-
malnym), o zerowym wektorze średnim i są wzajemnie
nieskorelowane.

Równanie stanu opisuje zmiany (trend) intere-

sującego nas wektora, a model pomiarów podaje zależ-
ność funkcyjną pomiarów od tego wektora. Rozwiąza-
niem układu równań (1), (2), przy uwzględnieniu ogra-
niczeń nałożonych na wektory zakłóceń, jest filtr Kal-
mana. Estymację wektora stanu w filtrze możemy
przedstawić za pomocą poniższego schematu:

• prognoza wektora stanu

,

(3)

gdzie wartość prognozowana wektora stanu,

wartość estymowana wektora stanu,

• macierz kowariancji prognozowanego wektora sta-

nu

,

(4)

gdzie Q macierz kowariancji zakłóceń stanu (wekto-

ra w),

• proces innowacji

,

(5)

• macierz kowariancji procesu innowacji

,

(6)

gdzie R macierz kowariancji zakłóceń pomiarów

(wektora v),

• macierz wzmocnienia filtru

,

(7)

• ocena (estymata) wektora stanu z filtracji po wyko-

naniu pomiaru

,

(8)

• macierz kowariancji estymowanego wektora stanu

(9)

Jak już wcześniej wspomniano algorytm

obliczeniowy pozostaje ten sam, ale w konkretnych
zastosowaniach będziemy mieli różne postacie
i wymiary poszczególnych wektorów oraz macierzy.
Poniżej przedstawiamy warianty rozwiązania nawigacji
zintegrowanej oparte o różne modele strukturalne
i pomiarowe.

Przyjmując konkretny model nawigacji zinte-

growanej musimy określić dwa równania: model struk-
turalny oraz model pomiarowy. Model strukturalny
zdeterminowany jest przyjętym przez nas modelem
procesu nawigacyjnego. Proces ten jest określony po-
przez składowe wektora stanu oraz jego ewolucję (ma-
cierz A). Wektor stanu dobieramy w zależności od
tego, jakie parametry chcemy estymować, tj. końcowe
parametry nawigacyjne lub też ich błędy (składowe
systematyczne w postaci poprawek). Ponadto musimy
już z góry uwzględnić to, czy dysponujemy możliwo-
ścią wykonywania pomiarów wielkości fizycznych
pozostających w związku funkcyjnym z estymowany-
mi parametrami. Wynika z tego, że przy projektowaniu
modelu strukturalnego musimy mieć co najmniej przy-
bliżony obraz modelu pomiarowego. I w praktyce kon-
struowania zintegrowanych systemów nawigacyjnych
tak postępujemy. Przyjmujemy wstępną koncepcję
określającą jakie wielkości chcemy estymować
i sprawdzamy, czy istnieją odpowiednie możliwości
pomiarowe.

Model

pomiarowy

(równanie

2)

opisuje

zależność pomiarów od wektora stanu. W przypadku
deterministycznego obliczania współrzędnych pozycji
(bez

uwzględniania

zakłóceń

losowych

stanu

i pomiarów) lub estymacji metodą najmniejszych
kwadratów zależność tą ujmujemy za pomocą
macierzy Jacobiego (macierzy gradientów powierzchni
pozycyjnych) [Banachowicz, 1991]. Powyższe rozwa-
żania zilustrujmy na przykładzie dwóch modeli
nawigacji. W pierwszym wykorzystujemy pomiary
nawigacji zliczeniowej (DR), satelitarnego systemu
nawigacyjnego

oraz

naziemnego

systemu

radionawigacyjnego. W drugim modelu zastosowano
tylko jeden system pozycyjny (GPS lub DGPS) oraz
dwa układy nawigacji zliczeniowej – log-żyrokompas
i nawigację inercjalną (ang. INS – inertial navigation
system) [Banachowicz, 2001].

Fuzja pomiarów DR/GPS

W tym przypadku dysponujemy pomiarami sate-

litarnego systemu nawigacyjnego (GPS, GLONASS,
DGPS, DGLONASS), naziemnego systemu radiona-
wigacyjnego (LORAN lub radionawigacyjny system
bliskiego zasięgu) oraz pomiarami z logu i żyrokompa-
su. W nawigacji morskiej jako elementy wektora stanu
przyjmujemy przede wszystkim współrzędne pozycji
(

oraz ich pochodne, np. składowe wektora pręd-

kości, wektora przyspieszeń itd. Załóżmy, że wielko-

Logistyka 6/2013

4

Logistyka - nauka

ściami estymowanymi będą następujące parametry:
współrzędne pozycji (

), rzuty wektora prędkości

względem dna na południk i równoleżnik (

), błąd

systematyczny kąta drogi względem dna –

)

(ang. COG – Course Over Ground) oraz błąd systema-
tyczny szybkości względem dna – (

) (ang. SOG

– Speed Over Ground). Przy tych założeniach wektor
stanu będzie miał postać:

.

(10)

Jak pamiętamy model strukturalny tworzy równanie
stanu (wzór 1). Dlatego musimy określić także
strukturę macierzy przejścia A. Przyjmijmy ją
w następującej postaci:

,

(11)

gdzie:

(12)

(13)

– szerokość geograficzna,

– długość geograficzna,

a – duża półoś elipsoidy ziemskiej,
e – pierwszy mimośród elipsoidy ziemskiej,

– współczynniki zamiany miary kątowej na

liniową na elipsoidzie odniesienia, odpowiednio na
południku i równoleżniku.

Składowe prędkości średniej

i

mogą być

obliczane jako prędkość wypadkowa z ciągu pozycji

systemu radionawigacyjnego. Dla pomiarów synchro-
nicznych zazwyczaj przyjmujemy w uproszczeniu, że

t

i

= 1 sekunda – jest to zazwyczaj stosowane w przy-

padku pomiarów synchronicznych, taktowanych z od-
biornika GPS.

Elementem uzupełniającym model strukturalny

jest macierz kowariancji wektora zakłóceń stanu Q.
Poszczególne elementy tej macierzy określają rozkłady
apriori

zakłóceń

estymowanych

wielkości.

Interpretacja tej macierzy z punktu widzenia praktyki
nawigacyjnej jest następująca – elementy jej
wyznaczają przedziały ufności, w których mogą
znajdować się estymowane parametry nawigacyjne. Na
przykład elementy (1,1) i (2,2) macierzy Q wyznaczają
przedział

myszkowania

statku,

ściślej

mówiąc

określają zakłócenia ruchu po szerokości i długości
geograficznej. Dla wektora stanu zdefiniowanego
wzorem (10) macierz Q może przyjąć postać:

,

(14)

gdzie:

– zakłócenie ruchu statku po szerokości geogra-

ficznej,

– zakłócenie ruchu statku po długości geograficznej,

,

(15)

,

(16)

,

(17)

COG – Course Over Ground,

SOG – Speed Over Ground,

Logistyka - nauka

Logistyka 6/2013

5

– błąd pomiaru COG,

– błąd pomiaru SOG,

– błąd określenia poprawki

,

– błąd określenia poprawki

.

Równania (10) – (17) określają model

strukturalny procesu nawigacji, gdy estymowanymi
wielkościami są współrzędne pozycji, składowe
wektora prędkości względem dna oraz poprawki – kąta
drogi względem dna, prędkości względem dna.

Jako wielkości mierzone w modelu pomiaro-

wym przyjmijmy następujące parametry: współrzędne
pozycji systemu DGPS

, naziemnego

systemu radionawigacyjnego

, kąt drogi

względem dna (COG) i szybkość względem dna
(SOG). Elementy wektora pomiarów będą więc nastę-
pujące:

.

(18)

Macierz pomiarów będzie macierzą Jacobiego,

która po obliczeniu poszczególnych pochodnych cząst-
kowych i odpowiednim uporządkowaniu otrzyma
następującą postać:

,

(19)

Uzupełnieniem modelu pomiarowego jest ma-

cierz kowariancji zakłóceń pomiarów (wektora pomia-
rów).

Ponieważ niektóre wielkości mierzone nie są ze

sobą skorelowane – np. pomiary DGPS i radionawiga-
cyjny system naziemny, to macierz ta uprości się. Jeśli
przyjmiemy konkretne wartości poszczególnych wa-
riancji i kowariancji występujących w tej macierzy, to
otrzymamy:

, (20)

Model ten został zastosowany w nawigacyjnym

systemie stabilizacji pozycji okrętu ratowniczego.
W algorytmie

i

oprogramowaniu

przyjęliśmy

następujące parametry błędów pomiarów:

• system DGPS:

m,

m, współ-

rzędne są nieskorelowane; badania przeprowadzo-
no na Zalewie Szczecińskim i Zatoce Pomorskiej;

• radionawigacyjny

system

naziemny

AD-2:

m,

m,

m

2

(kowa-

riancja); badania przeprowadzono na Zatoce Gdań-
skiej;

• kąt drogi względem dna:

;

• prędkość względem dna:

węzła.

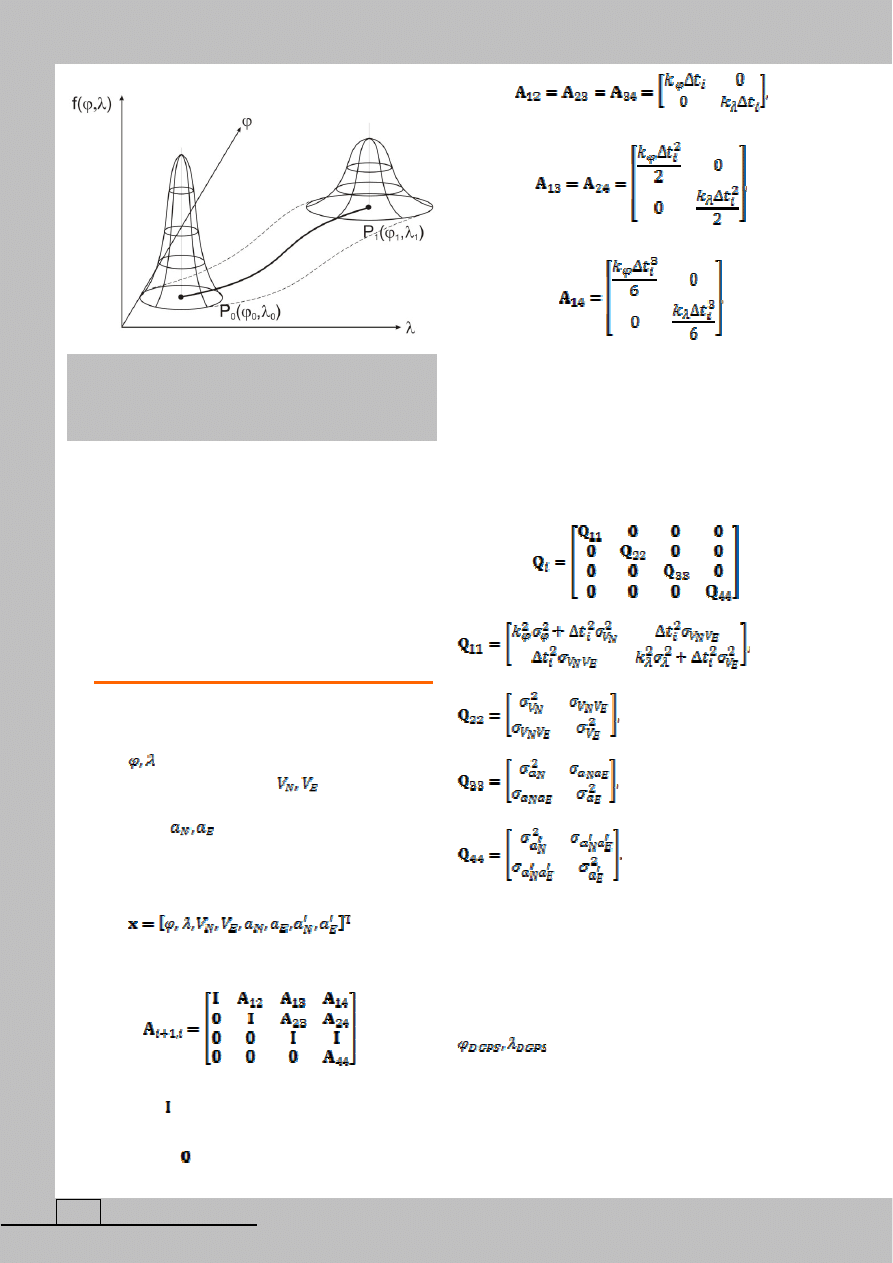
Narastanie błędów zliczenia (ich przyrostowy

charakter) ilustruje poniższy rysunek (rys. 1).

a)

Logistyka 6/2013

6

Logistyka - nauka

b)

Jak widzimy, wyraźnie dokładność pozycji zli-

czonej „rozmywa” się, co oznacza wzrost elementów
macierzy kowariancji pozycji zliczonej (widmo nisko-
częstotliwościowe zakłóceń pomiarów). Fakt ten zmu-
sza do stosowania korekcji zewnętrznej pozycji, tj.
wykorzystania systemów pozycyjnych, o innym wid-
mie błędów (wysokoczęstotliwościowym).

Fuzja pomiarów I S/DR/GPS

Innym

rozwiązaniem

jest

sytuacja,

gdy

wielkościami

estymowanymi

będą:

współrzędne

pozycji (

), rzuty wektora prędkości względem dna

na południk i równoleżnik (

), rzuty wektora

przyspieszenia

względem

dna

na

południk

i równoleżnik (

) oraz rzuty pochodnych wektora

przyspieszenia

względem

dna

na

południk

i równoleżnik (a’ , a’

E

). W przypadku tym wektor

stanu będzie posiadał następujące elementy:

, (21)

Zaś macierz przejścia A będzie określona następująco:

,

(22)

– macierz jednostkowa,

– macierz zerowa,

W tym przypadku ewolucja stanu jest określona

przez pochodne wyższych rzędów poszczególnych
estymowanych parametrów nawigacyjnych. Macierz
kowariancji zakłóceń stanu również otrzyma postać
dostosowaną do elementów nowego wektora stanu.
Tak więc będziemy mieli (macierz diagonalną):

,

(23)

Macierze kowariancji zakłóceń stanu (14) i (23)

różnią się tylko tymi elementami, które odpowiadają
różnym elementom odpowiadającym im wektorom
stanu.

W tym modelu za wielkości mierzone przyjmij-

my:

współrzędne

pozycji

systemu

DGPS

), składowe prędkości względem połu-

dnika i równoleżnika z nawigacji zliczeniowej (V , V

E

),

składowe przyspieszenia względem południka i równo-
leżnika z przetwornika inercjalnego (a , a

E

). Przy tych

założeniach wektor pomiarów będzie wyglądał nastę-
pująco:

Rys. 1. Przyrostowy charakter dokładności pozycji
zliczonej: a) trajektoria obiektu nawigacji na płasz-
czyźnie, b) wizualizacja przestrzenna rozkładu nor-
malnego pozycji obiektu.
Źródło: opracowanie własne.

Logistyka - nauka

Logistyka 6/2013

7

(24)

Macierz pomiarów, podobnie jak i wyżej, będzie

macierzą Jacobiego. Obliczmy poszczególne pochodne
cząstkowe i uporządkujemy. Otrzymamy wówczas
następującą bardzo prostą postać macierzy C:

,

(25)

Otrzymaliśmy macierz blokową, co znacznie

upraszcza obliczenia i w dużym stopniu zmniejsza
błędy numeryczne.

Macierz kowariancji zakłóceń pomiarów (wekto-

ra pomiarów), po uwzględnieniu braku korelacji oraz
dokładności poszczególnych pomiarów, będzie wyglą-
dała następująco:

,

(26)

W tym przypadku przyjęliśmy następujące war-

tości wariancji i kowariancji poszczególnych pomia-
rów:

• system DGPS:

m,

m, współ-

rzędne są nieskorelowane; badania przeprowadzo-
no na Zalewie Szczecińskim i Zatoce Pomorskiej;

• radionawigacyjny

system

naziemny

AD-2:

m,

m,

m

2

(kowa-

riancja); badania przeprowadzono na Zatoce
Gdańskiej;

• składowych prędkości:

;

• składowych przyspieszeń:

m/s

2

.

Ze względu na lepsze uwzględnienie dynamiki

statku, model ten ma istotną przewagę nad modelem
pierwszym. Okazuje się, że dla prędkości bliskich zeru
oraz pracujących sterach aktywnych, log Dopplerowski
charakteryzuje się dużymi błędami pomiarowymi.
Wtedy koniecznością, pomimo dość wysokiej ceny
przetwornika inercjalnego, jest stosowanie modelu
INS/GPS [Banachowicz, Bober, 1999].

Wykorzystując powyższy model nawigacji zin-

tegrowanej oraz zebrane podczas prób morskich dane
z urządzeń nawigacyjnych posłużyły do implementacji
w algorytmie obróbki informacji nawigacyjnej. Prze-
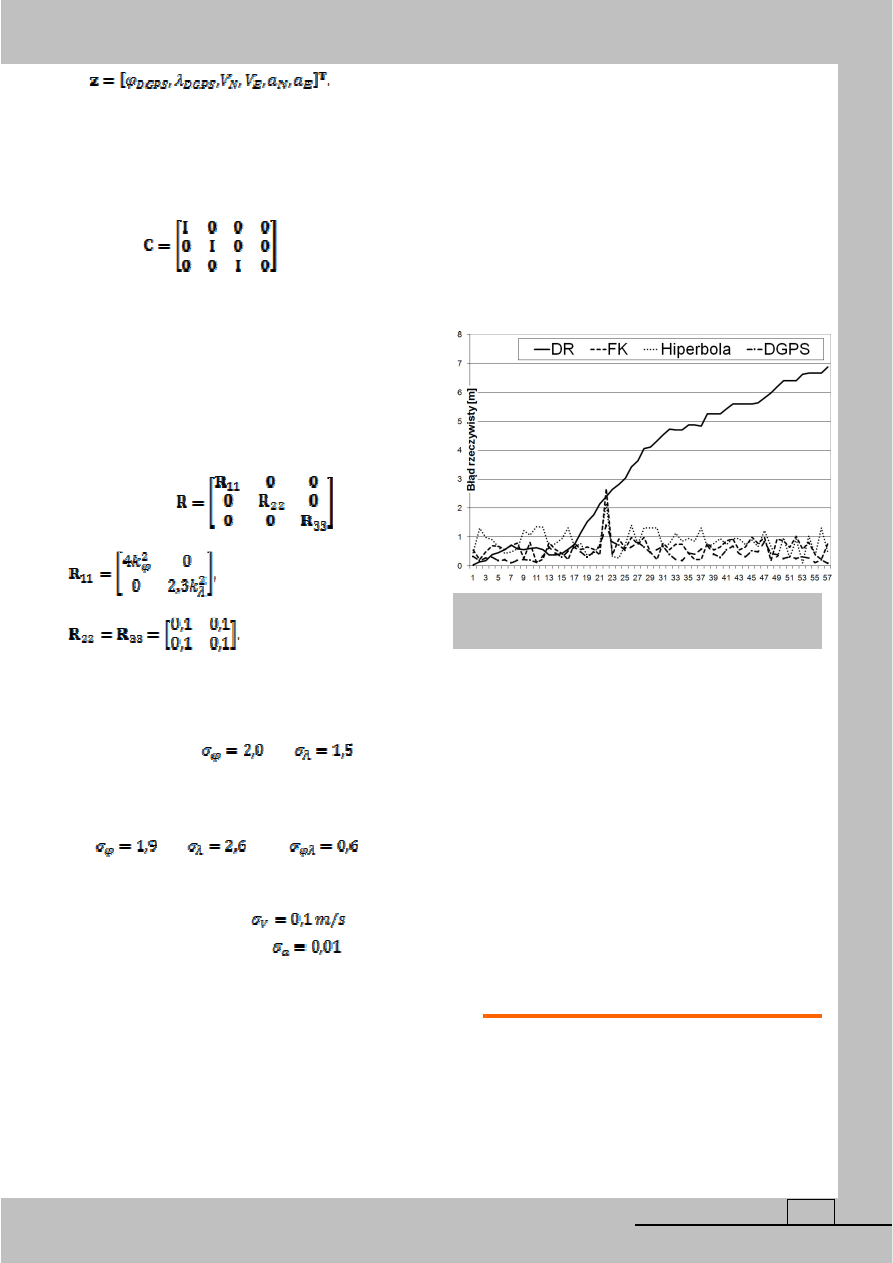
prowadzono również badania symulacyjne. Poniższy
rysunek (rys. 2) ukazuje przebieg błędów średnich
kołowych poszczególnych pozycji: DR – nawigacji
zliczeniowej, FK – pozycji zintegrowanej po fuzji da-
nych, Hiperbola – pozycja obserwowana z naziemnego
systemu fazowego Jemiołuszka (hiperbolicznego) oraz
DGPS – pozycja satelitarna.

Symulacje wykonano w przedziale jednej minu-

ty. Ze względu na błąd systematyczny występujący
w pomiarach logu elektromagnetycznego, błąd pozycji
zliczonej wyraźnie narasta wraz z czasem. Po tym cza-
sie wzrasta o 7 metrów (w stosunku do pozycji po-
przedniej). W tym czasie błędy rzeczywiste systemów
pozycyjnych (Jemiołuszka i DGPS) są porównywalne
i wahają się w przedziale od kilkudziesięciu centyme-
trów do 2 – 3 metrów (są niezależne od czasu prowa-
dzenia nawigacji). Natomiast średni błąd kołowy pozy-
cji zintegrowanej (FK) jest 2 – 3 razy mniejszy niż
poszczególnych systemów składowych.

Wnioski

Przedstawione powyżej modele procesu nawiga-

cyjnego nie wyczerpują wszystkich możliwych roz-
wiązań. W zasadzie można podać przykładów prawie
tyle samo, ile będzie stawianych wymagań w stosunku
do zbioru estymowanych parametrów nawigacyjnych
oraz możliwości pomiarowych. Należy wyraźnie pod-
kreślić, że postać tych modeli decyduje w dużym stop-

Rys. 2. Błędy rzeczywiste współrzędnych pozycji w
funkcji czasu.
Źródło: opracowanie własne.

Logistyka 6/2013

8

Logistyka - nauka

niu o sukcesie lub porażce opracowywanego filtru.
Dotyczy to przede wszystkim poprawnego, adekwat-
nego do rzeczywistości określenia elementów poszcze-
gólnych macierzy – przejścia A, pomiarów C oraz
macierzy kowariancji Q i R. W przypadku macierzy
kowariancji najistotniejszy jest stosunek odpowied-
nich elementów względem siebie. Przyjęte zbyt duże
błędy zakłóceń stanu powodują, że filtr staje się
„sztywny” i za mocno nadąża za pomiarami [Bana-
chowicz, 1995]. Efektem tego jest to, że nie są odfil-
trowywane błędy pomiarów. Gdy z kolei przyjmiemy
zbyt małe wartości zakłóceń stanu, wtedy filtr zacznie
odrzucać pomiary zbyt mocno różniące się od ich pro-
gnoz. Szczególnie ważne jest to w rzeczywistych sytu-
acjach pomiarowych, gdy występuje niezgodność po-
między pomiarami z różnych urządzeń i systemów
nawigacyjnych oraz przy niskiej wiarygodności mier-
ników oraz wyników pomiarów [Banachowicz, Bober,
1997], [Banachowicz, Bober, 1999]. Nie można rów-
nież zapominać o problemie synchronizacji skal czasu
poszczególnych mierników, długości cykli pomiaro-
wych oraz przedziałach dyskretyzacji. Ponieważ pre-
cyzja pomiarów obecnie jest bardzo duża, a prędkości
nawigujących obiektów też, to założenie o jednocze-
sności pomiarów często jest fikcją. Może więc zdarzyć
się, że wartość pomiaru będzie dużo różniła się od jego
prognozy. Jest to błąd systematyczny skali czasu, po
prostu następuje równoległe przesunięcie ciągu pomia-
rów względem ciągu prognoz. Innym zagadnieniem
jest stabilność numeryczna obliczeń. Zapis macierzo-
wo-wektorowy jest bardzo wygodny i dobrze interpre-
towalny. Gotowe biblioteki procedur i podprogramów
również znakomicie ułatwiają tworzenie aplikacji.
Jednakże powoduje to rozbudowywanie się algoryt-
mów, co pociąga za sobą kumulowanie się błędów
numerycznych i spowolnienie wykonywanych obli-
czeń.

Rozszerzeniem techniki filtracji Kalmanowskiej

są filtry cząsteczkowe [Ristic, 2004], w których wyko-
rzystywana jest symulacja Monte Carlo. Filtry te są
suboptymalne, ale szczególnie przydatne w przypad-
kach szybko manewrujących obiektów (silnie nieli-
niowych równań stanu i pomiarów).

Streszczenie

W artykule przedstawiono fuzję danych nawiga-

cyjnych uzyskanych z różnych sensorów. Zastosowano
rozszerzony filtr Kalmana budując odpowiednie mode-
le stanu i pomiarów procesu nawigacji. Ogólny algo-

rytm filtru Kalmana umożliwia budowanie różnych
modeli fuzji danych w nawigacji zintegrowanej. Po-
stać konkretnego modelu jest zdeterminowana możli-
wościami pomiarowymi parametrów nawigacyjnych
oraz założoną postacią wektora stanu.

Abstract

GPS/I S/DR

avigational

Data

Fusion

The article presents multi-sensor navigational data
fusion. Extended Kalman’s filter was used to build
proper models of navigational process (both states and
measurements).
The general Kalman’s filter algorithm allows to build
different data model fusions in integrated navigation.
The given model form depends on navigational meas-
urements parameters possibilities and established state
vector form.

Literatura

1. Anderson B.D.O., Moore J.B., Optimal filtering,

Prentice-Hall, 1979 New Jersey.

2. Balakrishnan A.V., Kalman Filtering Theory, Op-

timization Software, 1984 New York.

3. Banachowicz A., Geometria liniowego modelu

nawigacji parametrycznej, „Zeszyty Naukowe
AMW”, 1991, 109A. (monografia)

4. Banachowicz A., Wykorzystanie filtru Kalmana w

pomiarach skalarnych parametrów nawigacyjnych,
„Prace Wydziału Nawigacyjnego WSM w Gdyni”,
1995, Zeszyt 1, 116 – 125.

5. Banachowicz A., Bober R., Metodyka obróbki sy-

gnałów z urządzeń nawigacyjnych dla potrzeb sys-
tem nawigacji zintegrowanej, WSM, 1997 Szcze-
cin. (raport naukowy)

6. Banachowicz A., Bober R., System zintegrowanej

nawigacji na okręty ORP „Piast” i ORP „Lech”,
WSM, 1999 Szczecin. (raport naukowy)

7. Banachowicz A., Variants of Structural and Meas-

urement Models of an Integrated avigational Sys-
tem, „Annual of Navigation”, 2001, No 3, 5 – 18.

8. Ristic B., Arulampalm S., Gordon N., Beyond the

Kalman Filter. Participle Filters for Tracking Ap-
plications, Artech House, 2004 Boston.