Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
1
MIESZANINY GAZÓW DOSKONAŁYCH
W technice często spotyka się mieszaniny (roztwory) gazów, czego przykładem jest
powietrze zawierające wiele gazów jednorodnych. Innym bardzo typowym rodzajem mieszaniny
gazów są spaliny otrzymane po spaleniu paliwa.
Gazy mają tę charakterystyczną właściwość, że mieszają się zawsze ze sobą w dowolnych
proporcjach wskutek dyfuzji, przy czym po dostatecznie długim czasie ustala się stan
równowagi, w którym skład mieszaniny jest jednorodny w całej masie gazu.
Roztwór gazów doskonałych można traktować jako jednorodny gaz doskonały, jeśli do
równań stanu wprowadzi się zastępczą stałą gazową R
m
oraz określi zastępczą masę molową
M
μm
i zastępczą pojemność cieplną.
SKŁAD MIESZANINY
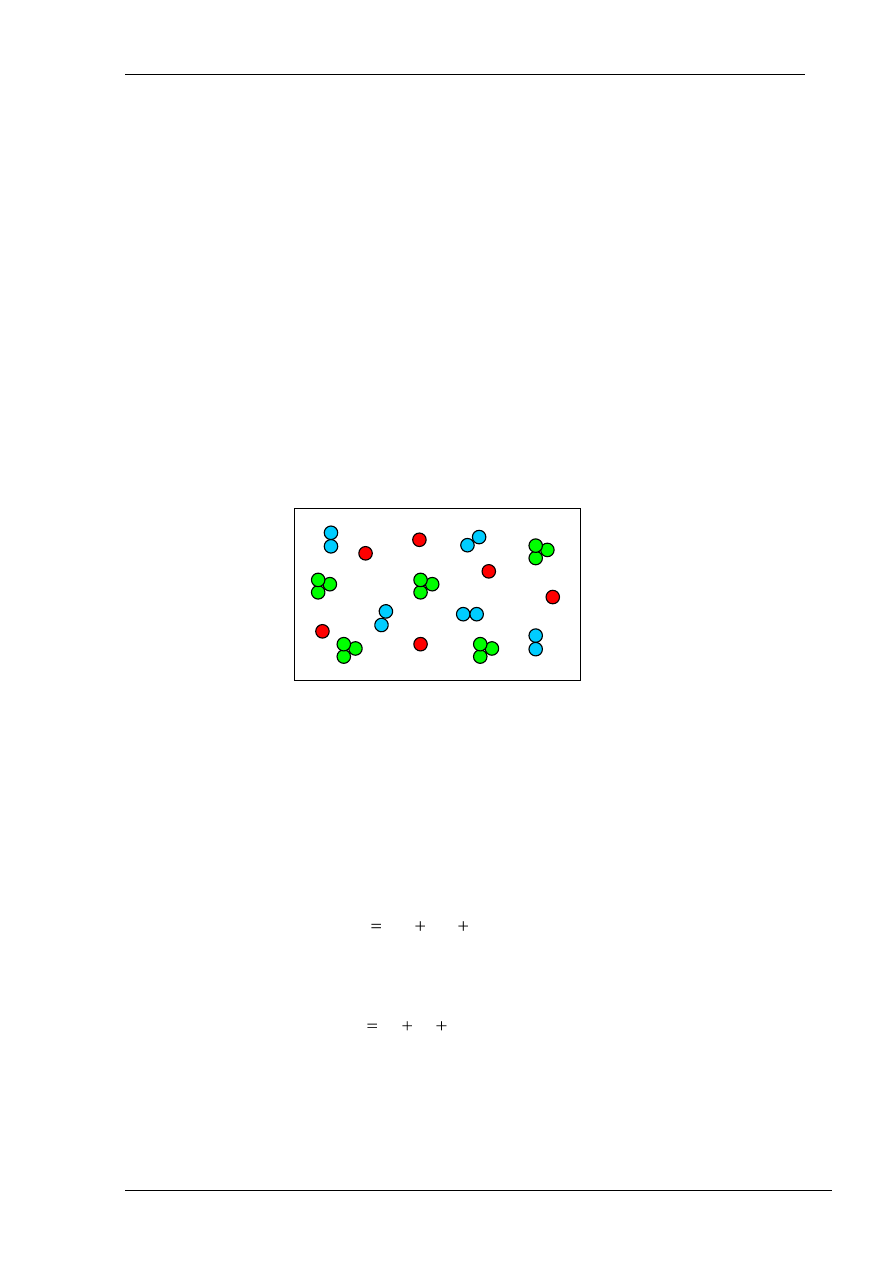
Rys. 1. Przykład mieszaniny gazów
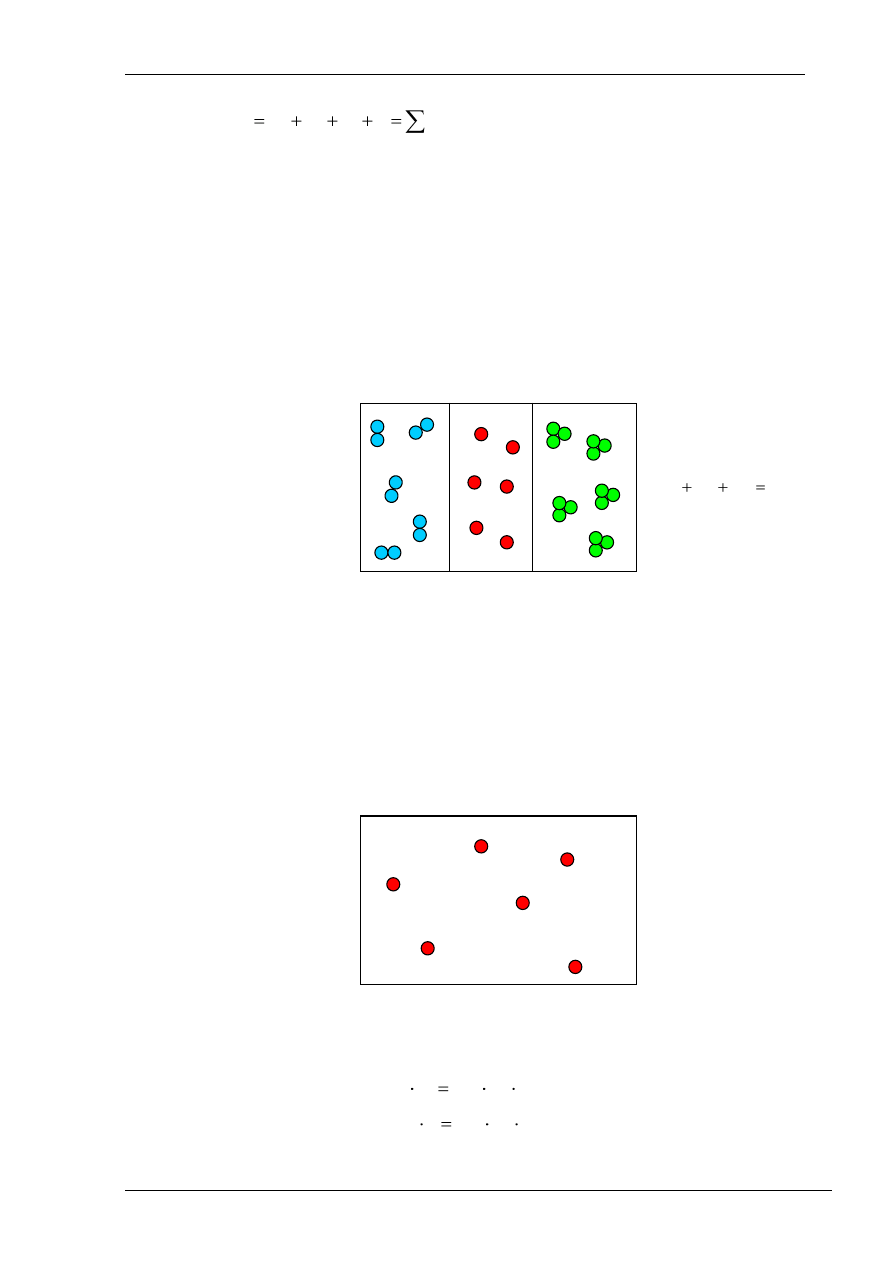
W zbiorniku (rys. 1.) znajduje się mieszanina (roztwór) kilku gazów doskonałych (np.
1-atomowy gaz A -, 2-atomowy gaz B, 3-atomowy gaz C). Objętość zbiornika wynosi V [m
3
],
ciśnienie gazu w zbiorniku wynosi p [Pa], a temperatura T [K]. Masa mieszaniny wynosi M
m
[kg].
Masa mieszaniny M
m
jest sumą mas tworzących ją gazów, a więc:
C
B
A
m
M
M
M
M
Ilość cząstek gazu w mieszaninie jest sumą cząstek tworzących ją gazów, a zatem liczba
kilomoli mieszaniny będzie również sumą liczb kilomoli tworzących ją gazów:
C
B
A
m
n
n
n
n
Skład mieszaniny określa się za pomocą udziałów masowych (kilogramowych,
gramowych), kilomolowych (molowych) lub objętościowych.
p, T, V
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
2
Udział masowy g
i
jest to stosunek masy danego składnika mieszaniny do masy mieszaniny.
1
g
M
M
g
i
i
m
i
i
gdzie: M
i
– masa danego składnika mieszaniny (i = A, B, C,.....),
M
m
– masa mieszaniny (roztworu).
Udział molowy z
i
jest to stosunek liczby kilomoli danego składnika do liczby kilomoli
mieszaniny.
i
i
m
i
i
1
z
n
n
z
gdzie: n
i
– liczba kilomoli danego składnika mieszaniny,
n
m
– liczba kilomoli mieszaniny.
Udział objętościowy
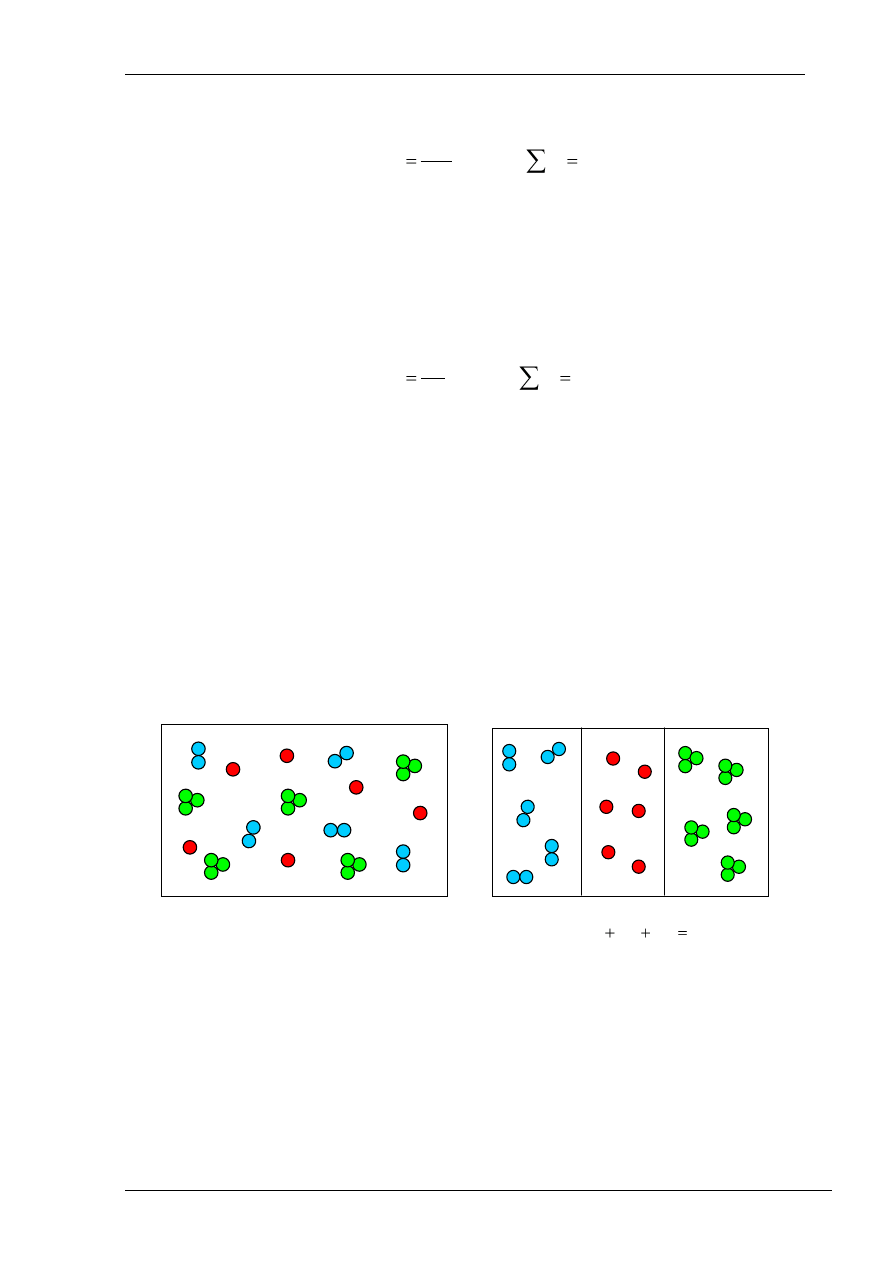
Wyobraźmy sobie, że cząsteczki gazów tworzących roztwór (rys. 2a.), zostały
w zbiorniku rozdzielone tak, że każdy gaz zajmuje pewną objętość zbiornika, ale ciśnienie
i temperatura każdego gazu są takie same jak ciśnienie i temperatura roztworu (rys. 2b).
a)
b)
Rys. 2. Mieszanina gazów – a), gazy rozdzielone - b)
W zbiorniku panuje nadal ciśnienie p i temperatura T, zbiornik nadal ma objętość V. Masa gazów
w zbiorniku nadal wynosi M
m
. Każdy gaz tworzący roztwór zajmuje pewną część zbiornika
o objętości V
i
,w której również panuje ciśnienie p i temperatura T.
Można zatem napisać:
p, T
V
A
,
M
A
p, T
V
B
,
M
B
p, T
p, T
p, T
V
B
V
A
V
C
V
C
V
B
V
A
V
p, T, V
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
3
....
V
V
V
V
C
B
A
Stosunek objętości każdego składnika do objętości roztworu jest nazywany udziałem
objętościowym.
i
i
i
i
1
r
V
V
r
Powyższa zależność tylko wtedy jest prawdziwa, gdy zarówno objętości V
i
jak i objętość V
są wyznaczone przy tym samym ciśnieniu i w tej samej temperaturze.
W przypadku gazów doskonałych udział objętościowy jest identyczny z udziałem kilomolowym
(molowym):
i
i
z
r
n
n
n
n
V
V
i
m
i
i
i
m
i
- objętości kilomolowe gazów doskonałych w tej samej temperaturze i przy tym
samym ciśnieniu są jednakowe (wynika z prawa Avogadra).
PARAMETRY MIESZANINY
Masa mieszaniny:
...
C
B
A
m
M
M
M
M
Liczba kilomoli mieszaniny:
.....
C
B
A
m
n
n
n
n
Objętość mieszaniny:
....
V
V
V
V
C
B
A
- pod warunkiem, że wszystkie
objętości są wyznaczone przy tym samym ciśnieniu i przy tej samej temperaturze (rys. 2.).
Indywidualna stała gazowa mieszaniny:
Napiszemy równania stanu gazu dla każdego gazu zajmującego osobną objętość (rys. 2.b.):
gaz A:
T
R
n
T
R
M
V
p
A
A
A
A
gaz B:
T
R
n
T
R
M
V
p
B
B
B
B
(1)
gaz C:
T
R
n
T
R
M
V
p
C
C
C
C
Dodajemy pierwszą i drugą kolumnę wszystkich równań:
T
)
R
M
R
M
R
M
(
V
V
V
p
C
C
B
B
A
A
C
B
A
Uwzględniając w powyższym równaniu:
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
4
m
i
i
m
i
i
M
g
M
M
M
g
oraz
....
V
V
V
V
C
B
A
otrzymamy:
T
R
M
T
R
g
R
g
R
g
M
V
p
m
m
C
C
B
B
A
A
m
)
(
gdzie:
C
C
B
B
A
A
m
R
g
R
g
R
g
R
- indywidualna stała gazowa mieszaniny (można ją
również wyznaczyć z zależności (5)),
a zatem równanie stanu mieszaniny można zapisać następująco:
T
R
M
V
p
m
m
(2)
Dodając pierwszą i trzecią kolumnę równań (1) otrzymamy:
T
R
)
n
n
n
(
V
V
V
p
C
B
A
C
B
A
gdzie:
....
V
V
V
V
C
B
A
- objętość mieszaniny.
....
C
B
A
m
n
n
n
n
- liczba kilomoli mieszaniny,
a zatem równanie stanu mieszaniny można zapisać również następująco:
T
R
n
V
p
m
(3)
lub
T
R
p
m
(4)
Zapis równania stanu gazu dla mieszaniny w postaci (2), (3) i (4) niczym nie różni się od zapisu
równania stanu gazu dla pojedynczego gazu. Różni je sposób wyznaczania indywidualnej stałej
gazowej, masy, objętości i liczby kilomoli.
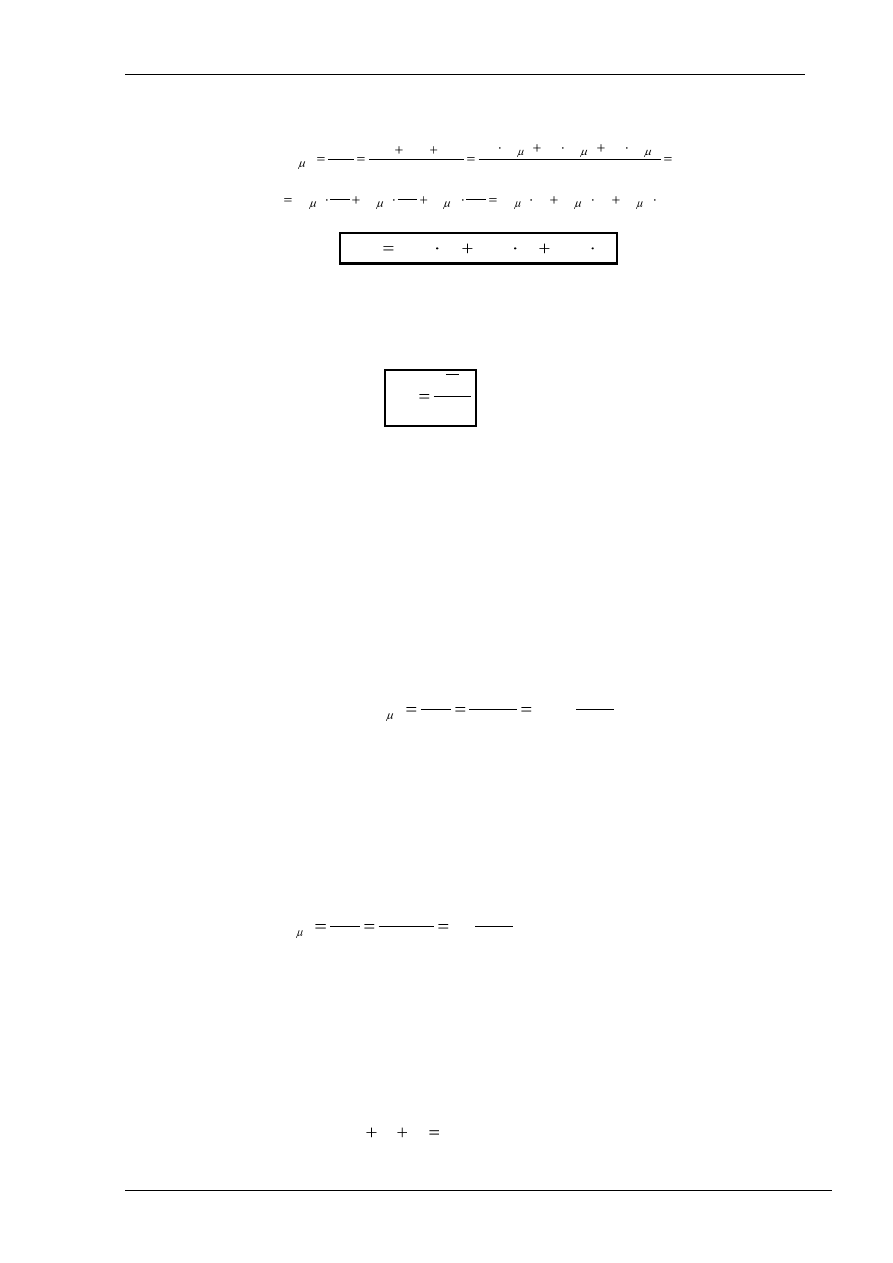
Objętość właściwa mieszaniny:
C
C
B
B
A
A
m
C
C
m
B
B
m
A
A
m
C
C
B
B
A
A
m
C
B
A
m
m
g
g
g
M
M
M
M
M
M
M
M
M
M
M
V
V
V
M
V
C
C
B
B
A
A
m
g
υ
g
υ
g
υ
υ
Gęstość mieszaniny:
C
C
B
B
A
A
C
C
B
B
A
A
C
C
B
B
A
A
C
B
A
m
m
r
r
r
V
V
V
V
V
V
V
V
V
V
V
M
M
M
V
M
C
C
B
B
A
A
m
r
ρ
r
ρ
r
ρ
ρ
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
5
Masa kilomolowa mieszaniny:
C
C
B
B
A
A
m
C
C
m
B
B
m
A
A
m
C
C
B
B
A
A
m
C
B
A
m
m
m
r
M
r
M
r
M
n
n
M
n
n
M
n
n
M
n
M
n
M
n
M
n
n
M
M
M
n
M
M
C
μC
B
μB
A
μA
μm
r
M
r
M
r
M
M
Masę kilomolową mieszaniny można również wyznaczyć z zależności (6).
Znając masę kilomolową mieszaniny można indywidualną stałą gazową wyznaczyć
również z zależności:
μm
m
M
R
R
(5)
Masę kilomolową mieszaniny można również wyznaczyć znając liczbę cząsteczek
poszczególnych gazów i ich masy albo liczby kilomoli gazów i ich masy kilomolowe.
Przykład:
Skład mieszaniny jest następujący: 1 kmol He, 1 kmol H
2
, 1 kmol CO
2
. Masy kilomolowe
tych gazów wynoszą odpowiednio: M
μHe
= 4 kg/kmol, M
μH
2
= 2 kg/kmol, M
μCO
2
= 44 kg/kmol,
a ich masy wynoszą: M
He
= 4 kg, M
H
2
= 2 kg, M
CO
2
= 44 kg.
Liczba kilomoli mieszaniny wynosi zatem n
m
= 3 kmol, a masa mieszaniny - M
m
= 50 kg. Masa
kilomolowa mieszaniny wynosi:
kmol
kg
kmol
kg
n
M
M
m
m
m
66
,
16
3
50
.
Te same gazy mogą tworzyć mieszaninę o zupełnie innej masie kilomolowej – zależy to od
ilości każdego gazu w mieszaninie, czyli od składu mieszaniny.
Niech mieszaninę tworzą te same gazy, tylko w innych ilościach: 1,2 kmol He, 1,3 kmol H
2
,
0,5 kmol CO
2
. Ich masy wynoszą: M
He
= 4,8 kg, M
H
2
= 2,6 kg, M
CO
2
= 22 kg. Liczba kilomoli
mieszaniny wynosi zatem n
m
= 3 kmol, a masa mieszaniny - M
m
= 29,4 kg. Masa kilomolowa
mieszaniny wynosi:
kmol
kg
kmol
kg
n
M
M
m
m
m
8
,
9
3
4
,
29
.
A zatem: masa kilomolowa mieszaniny zależy od składu mieszaniny - ilości każdego
z tworzących ją gazów, a nie tylko od ich rodzaju.
Inny sposób wyznaczenia masy kilomolowej mieszaniny:
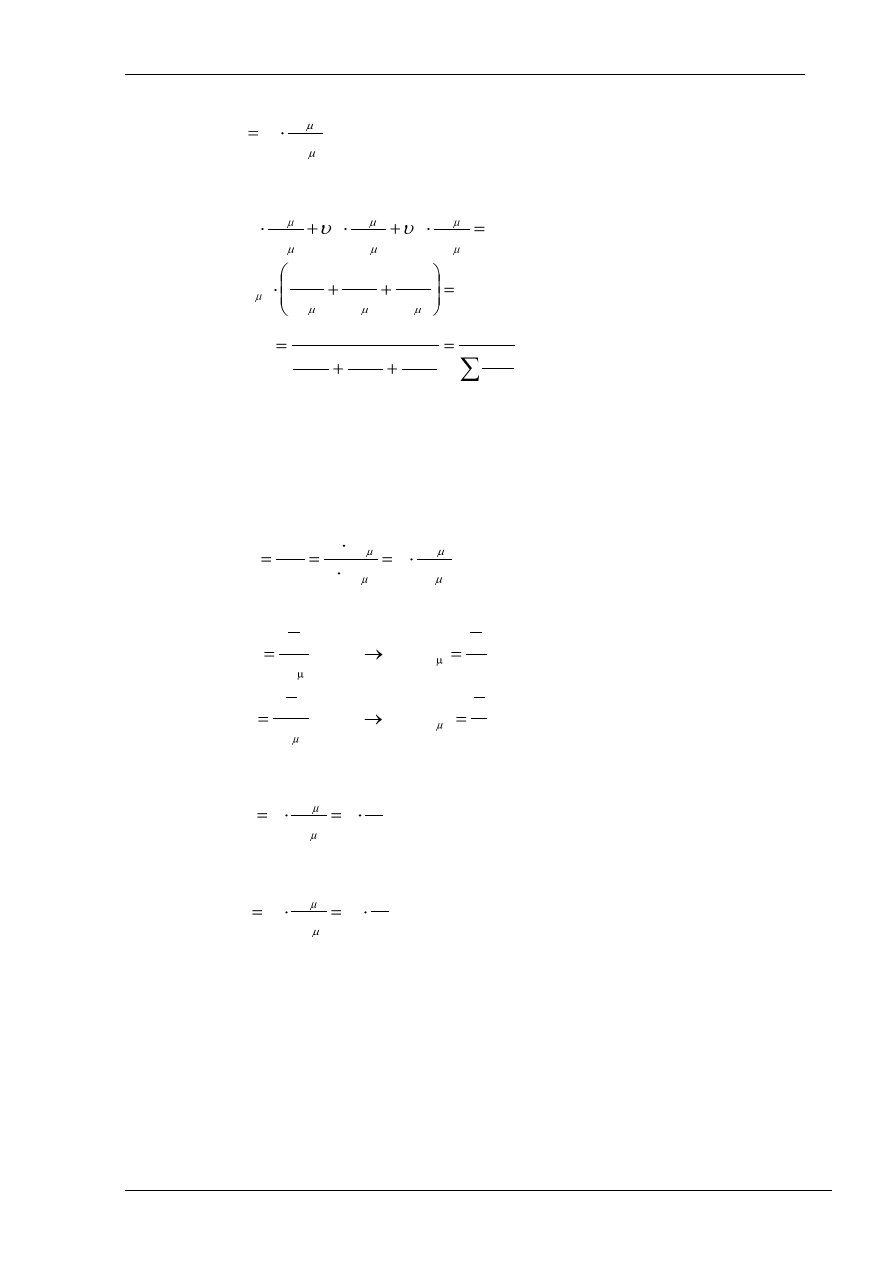
Korzystając z zależności pomiędzy udziałami, można masę kilomolową wyznaczyć następująco:
1
r
r
r
C
B
A
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
6
podstawiając:
i
m
i
i
M
M
g
r
otrzymuje się:
i
μi
i
μC
C
μB
B
μA
A
μm
M
g
1
M
g
M
g
M
g
1
M
1
1
C
C
B
B
A
A
m
C
m
C
B
m
B
A
m
A
M
g
M
g
M
g
M
M
M
M
M
M
M
g
ZALEŻNOŚCI POMIĘDZY UDZIAŁAMI
Wystarczy określić tylko zależności pomiędzy udziałami masowymi a kilomolowymi,
jako że udziały kilomolowe i objętościowe są sobie równe.
m
i
i
m
i
i
m
i
i
M
M
r
M
n
M
n
M
M
g
Podstawiając do powyższego równania:
i
i
i
i
R
R
M
M
R
R
R
R
M
M
R
R
m
m
otrzymuje się:
i
i
m
i
i
i
R
R
r
M
M
r
g
albo:
R
R
g
M
M
g
r
i
i
i
m
i
i
PRAWO DALTONA
Każdy z gazów tworzących mieszaninę można traktować tak, jakby sam zajmował całą
objętość mieszaniny przy takiej samej temperaturze jak temperatura mieszaniny, a ciśnienie
jakie wtedy wywierałby jest ciśnieniem udziałowym p
i
. Suma ciśnień udziałowych jest równa
ciśnieniu mieszaniny p.
(6)
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
7
i
i
C
B
A
p
...
p
p
p
p
Zależność na ciśnienie udziałowe można otrzymać przeprowadzając następujące
rozumowanie: Niech mieszaninę tworzą gazy A, B i C. Mieszanina znajduje się w zbiorniku
o objętości V. W zbiorniku panuje ciśnienie p i temperatura T (rys. 2a): Rozważymy dwa
przypadki:
-przypadek I:
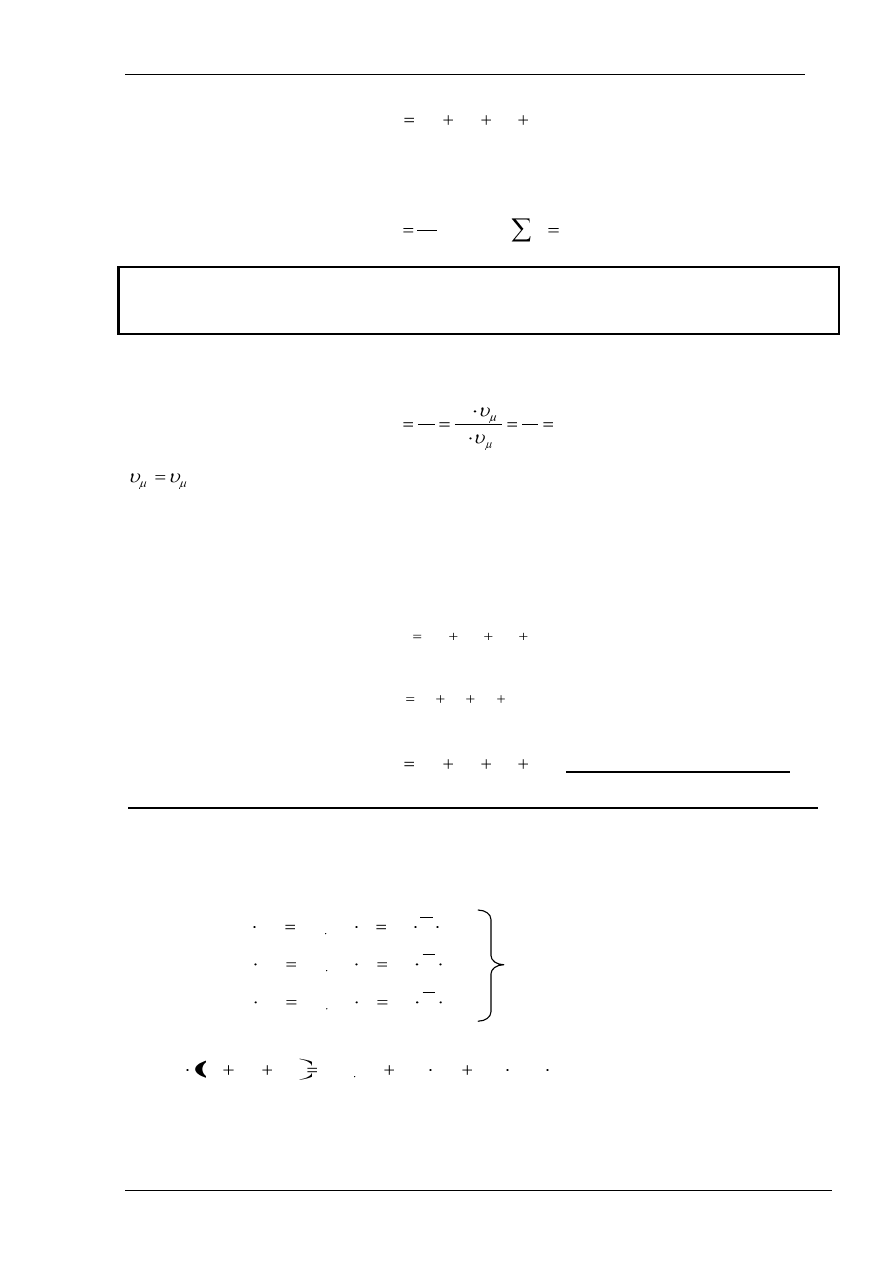
Wyobraźmy sobie, że każdy gaz zajmuje w tym zbiorniku osobną część, którą oznaczymy
V
A
, V
B
, V
C
i że w każdej części panuje ciśnienie p i temperatura T (rys. 2.b.).
Rys. 3. Układ zawierający kilka gazów przed zmieszaniem
- przypadek II:
Teraz wyobraźmy sobie, że ze zbiornika został usunięty gaz B i C. Całą objętość zbiornika
zajmuje teraz gaz A, a zatem gaz A zajmuje objętość V, jego temperatura wynosi nadal T, jego
masa nie uległa zmianie, a zatem musi ulec zmianie ciśnienie, które teraz wynosi p
A
. Ciśnienie
p
A
jest nazywane ciśnieniem udziałowym.
Rys. 3. Układ zawierający tylko gaz A
Napiszemy równanie stanu gazu A dla obydwu przypadków:
przypadek I:
T
R
M
V
p
A
A
A
przypadek II:
T
R
M
V
p
A
A
A
Przypadek
I
V
B
V
A
V
C
V
C
V
B
V
A
V
p, T
p, T
p, T
Przypadek
II
T
V
p
A
,
,
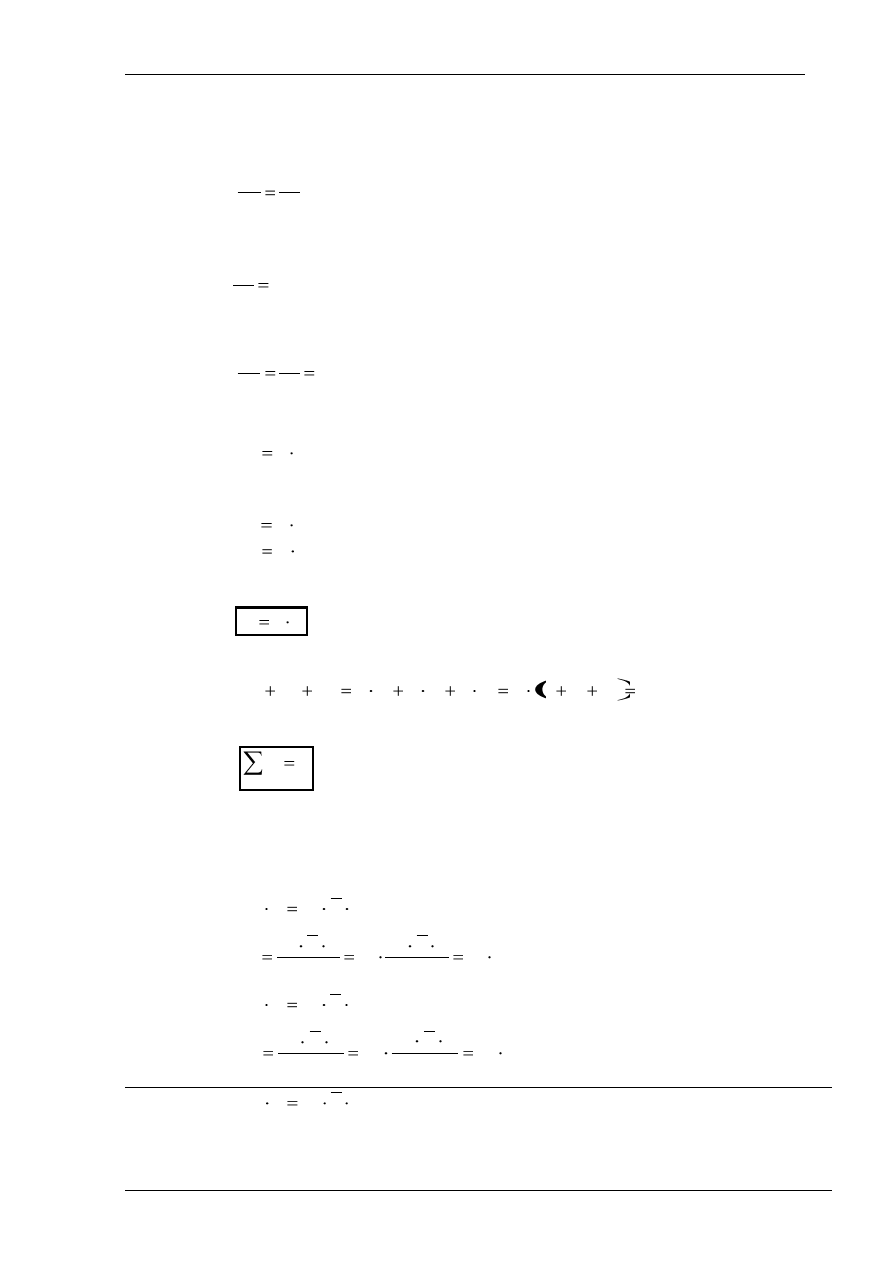
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
8
Równanie dla przypadku II jest nazywane udziałowym równaniem stanu gazu.
Po podzieleniu obydwu równań stronami, otrzymamy:
A
A
V
V
p
p
Wiedząc, że:
A
A
r
V
V
otrzymamy:
A
A
A
r
V
V
p
p
skąd wyznaczymy ciśnienie udziałowe gazu A:
A
A
r
p
p
Powtarzając rozumowanie dla gazów dla gazów B i C otrzymamy zależności:
C
C
r
p
p
Ogólny zapis ciśnienia udziałowego jest zatem następujący:
i
i
r
p
p
Suma ciśnień udziałowych wynosi:
p
r
r
r
p
r
p
r
p
r
p
p
p
p
C
B
A
C
B
A
C
B
A
A zatem:
i
i
p
p
Zależność na ciśnienie udziałowe gazu można również wyznaczyć bezpośrednio
z równania udziałowego stanu gazu, czyli z równania dla przypadku II, w następującej postaci:
- gaz A:
T
R
n
V
p
A
A
p
z
V
T
R
n
z
V
T
R
n
p
A
m
A
A
A
- gaz B:
T
R
n
V
p
B
B
p
z
V
T
R
n
z
V
T
R
n
p
B
m
B
B
B
- gaz C:
T
R
n
V
p
C
C
B
B
r
p
p
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
9
p
z
V
T
R
n
z
V
T
R
n
p
C
m
C
C
C
Suma ciśnień udziałowych wynosi:
p
z
z
z
p
z
p
z
p
z
p
p
p
p
C
B
A
C
B
A
C
B
A
MIESZANINY – ZADANIA (WAT)
1. Spaliny mają skład objętościowy: r
CO
2
=0,12, r
CO
=0,01, r
O
2
=0,075
,
r
N
2
=0,795
.
Obliczyć
gęstość spalin w normalnych warunkach fizycznych oraz udziały masowe
poszczególnych składników.
Odp.: ρ
N
= 1,35 kg/m
3
, g
CO
2
= 0,1714
,
g
CO
= 0,0093
,
g
O
2
= 0,0794
,
g
N
2
= 0,7366
2. Gaz miejski ma skład objętościowy: r
H
2
=0,5, r
CH
4
=0,19, r
CO
=0,18, r
C
2
H
4
=0,02, r
CO
2
=0,05,
r
N
2
=0,06. Obliczyć masę kilomolową, stałą gazową, gęstość gazu w normalnych
warunkach fizycznych oraz ciśnienie udziałowe przy ciśnieniu całkowitym gazu p=1bar.
Odp.: M
μ
= 13,52 kg/kmol , R = 615 J/(kg
.
K) , ρ
N
= 0,603 kg/m
3
, p
H
2
= 0,5 bar ,
p
CH
4
= 0,19 bar , p
CO
= 0,18 bar , p
C
2
H
4
= 0,02 bar , p
CO
2
= 0,05 bar , p
N
2
= 0,06 bar
3. W palniku gazowym spala się 1 część objętościowa gazu miejskiego z 1,5 części
objętościowej powietrza. Stała gazowa gazu miejskiego R
g
=615 J/(kg
.
K), stała gazowa
powietrza R
p
=287 J/(kg
.
K). Obliczyć udziały objętościowe i masowe składników, stałą
gazową mieszaniny oraz gęstość przy 20 C i ciśnieniu 1013 hPa.
Odp.:r
g
= 0,4 , r
p
= 0,6 , g
g
= 0,2372 , g
p
= 0,7624, R
m
= 364,7 J/(kg
.
K) , ρ
= 0,948 kg/m
3
4. Obliczyć stałą gazową mieszaniny gazów składającą się z 1 kmola gazu generatorowego
i 1,8 kmola powietrza oraz ciśnienia udziałowe w normalnych warunkach fizycznych.
Gęstość gazu generatorowego w normalnych warunkach fizycznych wynosi 1,19 kg/m
3
,
a powietrza 1,29 kg/m
3
.
Odp.: R
m
= 297 J/(kg
.
K) , p
p
= 65142 Pa , p
g
= 36183 Pa
5. Gaz generatorowy ma następujący skład objętościowy: r
H
2
=0,07, r
CH
4
=0,02, r
CO
=0,276,
r
CO
2
=0,048, r
N
2
=0,586. Obliczyć masę kilomolową, udziały masowe, stałą gazową oraz
gęstość i ciśnienie udziałowe przy temperaturze 15 C i ciśnieniu 0,1 MPa.
Odp.: M
μ
= 26,7 kg/kmol , g
H
2
=0,0052, g
CH
4
=0,012, g
CO
=0,2894, g
CO
2
=0,0791,
g
N
2
=0,6145 , R
m
= 311,4 J/(kg
.
K), ρ
m
= 1,11 kg/m
3
, p
H
2
= 0,07 bar , p
CH
4
= 0,02 bar ,
p
CO
= 0,276 bar , p
CO
2
= 0,048 bar , p
N
2
= 0,586 bar
6. W zbiorniku o pojemności 125 m
3
znajduje się gaz koksowniczy przy ciśnieniu 5 bar
i temperaturze 18 C. Skład molowy gazu jest następujący: z
H
2
=0,46, z
CH
4
=0,32,
z
CO
=0,15, z
N
2
=0,07. Po zużyciu pewnej ilości gazu jego ciśnienie zmalało do 2 bar,
a temperatura obniżyła się do 12 C. Obliczyć masę zużytego gazu koksowniczego.
Odp.:∆M = 186,3 kg
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
10
7. Określić skład masowy mieszaniny dwutlenku węgla i azotu, jeśli wiadomo, że ciśnienie
udziałowe dwutlenku węgla p
CO
2
=
1,2 bar, a ciśnienie roztworu p=3 bar. Ile wynosi stała
gazowa tej mieszaniny?
Odp.: g
CO
2
=0,511, g
N
2
=0,488 , R
m
= 241,7 J/(kg
.
K)
8. Gaz miejski o składzie objętościowym: : r
H
2
=0,48, r
CH
4
=0,35, r
C
2
H
2
=0,17 zmieszano
z powietrzem w proporcji 1 kg gazu na 13,7 kg powietrza. Obliczyć masę kilomolową
powstałej mieszaniny oraz udziały objętościowe gazu miejskiego i powietrza. Przyjąć
następujący skład objętościowy powietrza: z
O
2
=0,21, z
N
2
=0,79.
Odp.: M
μm
= 26 kg/kmol, r
g
= 0,14 , r
p
= 0,84
9. Mieszanina gazów składa się z 2 kmol dwutlenku węgla, 2 kmol tlenu i 4 kmol azotu.
Określić udziały objętościowe i masowe składników, stałą gazową i masę kilomolową
mieszaniny.
Odp.: r
CO
2
=0,25 , r
O
2
=0,25 , r
N
2
=0,5 , g
CO
2
=0,3333 , g
O
2
=0,2424 , g
N
2
=0,4242,
R
m
= 252 J/(kg
.
K), M
μm
= 33 kg/kmol
10. Spaliny silnika tłokowego mają następujący skład objętościowy: r
CO
2
=0,13, r
O
2
=0,06,
r
CO
=0,01, reszta azot. Określić skład masowy spalin, masę kilomolową i stałą gazową.
Odp.: g
CO
2
=0,1886 , g
O
2
=0,0633 , g
CO
=0,0092 , g
N
2
=0,7388
11. Do cylindra silnika gazowego jest doprowadzana mieszanina gazów składająca się z 20
części masowych powietrza i jednej części gazu koksowniczego. Obliczyć gęstość
i objętość właściwą mieszaniny w warunkach normalnych fizycznych, a także ciśnienie
udziałowe powietrza i gazu koksowniczego. Dla gazu koksowniczego przyjąć M
μ
=11,5
kg/kmol, ρ=0,515 kg/m
3
, dla powietrza M
μ
=28,84 kg/kmol, ρ=1,293 kg/m
3
.
Odp.: ρ
Nm
= 1,202 kg/m
3
, v
Nm
= 0,832 m
3
/kg, p
p
= 89976,6 Pa, p
g
= 11348,4 Pa
12. Mieszanina gazów ma następujący skład masowy: g
CO2
=0,12, g
O2
=0,08, g
N2
=0,8. Do
jakiego ciśnienia należy sprężyć tę mieszaninę znajdującą się w normalnych warunkach
fizycznych, aby jej gęstość wynosiła 1,6 kg/m
3
?
Odp.: p =122740 Pa
13. Mieszanina 10 [kg] tlenu i 15 kg azotu znajduje się pod ciśnieniem 3 bar i w
temperaturze t=27 C. Obliczyć udziały molowe i ciśnienie składnikowe, masę
kilomolową, stałą gazową mieszaniny oraz gęstość.
Odp.: r
O
2
= 0,368 , r
N
2
= 0,632 , p
O
2
= 1,104 bar, p
N
2
= 1,896 bar, M
μm
= 29,47 kg/kmol,
R
m
= 282 J/(kg
.
K), ρ
m
= 3,55 kg/m
3
14. Gaz świetlny o składzie z
H2
=0,5, z
CH4
=0,34, z
C2H2
=0,16 zmieszano z powietrzem
w stosunku 1 kg gazu na 12,5 kg powietrza. Obliczyć udziały kilomolowe gazu
świetlnego i powietrza oraz masę kilomolową mieszaniny. Skład objętościowy
powietrza: z
O
2
=0,21, z
N
2
=0,79.
Odp.: r
g
= 0,1783 , r
p
= 0,8217 , M
μm
= 25,6 kg/kmol
15. Mieszanina gazów składa się z wodoru i tlenku węgla. Udział masowy wodoru
g
H2
=0,0667. Obliczyć stałą gazową mieszaniny i jej objętość właściwą w normalnych
warunkach fizycznych.
Odp.: R
m
= 554,5 J/(kg
.
K), v
Nm
= 1,49 m
3
/kg
Mieszaniny gazów doskonałych
Opracowanie: Ewa Fudalej-Kostrzewa
11
16. Mieszanina wodoru i metanu CH
4
ma objętość V= 67,2 m
3
, ciśnienie p=0,98 bar,
temperaturę t=15 C oraz masę m=8,94 kg. Obliczyć stałą gazową mieszaniny, udziały
masowe i molowe oraz ciśnienia składnikowe.
Odp.: R
m
=2558 J/(kg
.
K), g
H2
=0,5604, g
CH4
=0,4396, r
H2
=0,91, r
CH4
=0,09, p
H2
=0,892
bar, p
CH4
=0,088 bar
17. Mieszanina azotu i wodoru ma gęstość ρ=0,28 kg/m
3
przy ciśnieniu p=1,4 bar
i temperaturze t=570 C. Ile kilomoli azotu i kilomoli wodoru należy ze sobą zmieszać,
aby otrzymać 3 kg tej mieszaniny?
Odp.: n
H2
=0,115 kmol, n
N2
=0,099 kmol
18. W zbiorniku o pojemności V=2 m
3
znajduje się m
p
= 5kg powietrza o temperaturze
t=40 C. Do zbiornika wtłoczono m
CO
2
=2[kg] dwutlenku węgla. Obliczyć udziały masowe
i objętościowe obydwu składników oraz ciśnienie po wtłoczeniu dwutlenku węgla, jeśli
temperatura nie zmieniła się. Stała gazowa powietrza: R=287 J/(kg
.
K).
Odp.: g
p
=0,714 , g
CO
2
=0,286 , r
p
=0,791 , r
CO
2
=0,209 ,p = 2,84 bar
19. W butli o pojemności V = 0,1m
3
znajduje się powietrze pod ciśnieniem p
p
=2 bar
i w temperaturze t = 20 C. Ile trzeba wtłoczyć do butli azotu, aby ciśnienie wzrosło do
p = 10 bar przy tej samej temperaturze?
Odp.: M
N
2
= 0,92 kg
20. Mieszanina gazów składająca się 1,5 kg azotu N
2
i 2 kg dwutlenku węgla CO
2
znajduje
się w cylindrze z ruchomym tłokiem pod ciśnieniem p
1
=10 bar i w temperaturze t
1
=50 C.
Obliczyć zmianę objętości mieszaniny po zmianie tych parametrów do p
2
=4 bar i
t
2
=230 C.
Odp.: ∆V =0,849 m
3