Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 1
Zadane jest prawo ruchu w zmiennych Lagrange’a
=
=
≥ 0
gdzie, X, Y oznaczają współrzędne materialne dla t = 0.
Wyznaczyć opis ruchu w zmiennych Eulera. Znaleźć linię prądu. Pokazać, że ruch jest ustalony.
Rozwiązanie
Prędkość we współrzędnych Lagrange’a oblicza się jako:
⃗ ( ,
,
)
=
⃗( ,
,
)
=
⃗
−
−
⃗
, ≥ 0
Funkcja odwrotna do funkcji (
,
) daje prawo ruchu w zmiennych Eulera:
=
=
≥ 0
Po podstawieniu wyrażenia na X i Y do wzoru na prędkość w zmiennych Lagrange’a otrzyma się pole
prędkości w zmiennych Eulera (przestrzennych):
⃗
=
⃗
−
⃗
Równanie linii prądu znajdujemy po scałkowaniu równania:
=
stąd
ln| | = − ln| | +
A więc równanie linii prądu ma postać wzoru:
=
Ponieważ prędkość wyrażona w zmiennych Eulera nie zależy w sposób jawny od czasu
= 0, więc
ruch jest ustalony. Równanie określające tor cząstki, zadane dwzorowaniem
⃗
, musi być identyczne z
równaniem linii prądu. Rzeczywiście, po wyeliminowaniu z równań
=
,
=
, czasu t,
otrzymuje się:
=
=
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 2
Zadane jest prawo ruchu w zmiennych Lagrange’a:
=
+ (
− 1)
= (
−
) +
=
gdzie (X,Y,Z) – współrzędne materialne
Sprawdzić, czy jakobian J dla zadanego prawa ruchu jest różny od zera. Znaleźć prawo ruchu w
zmiennych Eulera.
Rozwiązanie:
Sprawdzamy czy jakobian jest różny od zera:
=
=
0
− 1
0
1
−
0
0
1
=
≠ 0
Po prostych przekształceniach można znaleźć funkcję odwrotną:
=
+ (
− 1)
=
− (
−
)
=
Zwróćmy uwagę, że przy obu sposobach opisu prawa ruch dla t = 0 otrzymujemy x = X, y = Y, z = Z.
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 3
Zadane jest prawo ruchu:
=
=
+
=
a) Znaleźć prawo ruchu we współrzędnych Eulera.
b) Określić prędkość i przyspieszenie cząstki we współrzędnych Lagrange’a i Eulera.
c) Dla danego pola prędkości zadane jest pole temperatury T = Axy. Obliczyć pochodną
substancjalną dT/dt.
Rozwiązanie:
a) Odwzorowanie odwrotne, dające opis w zmiennych Eulera, równa się:
=
=
−
=
b) Prędkość i przyspieszenie we współrzędnych Lagrange’a
⃗( , , , ) =
⃗
= ⃗ + 2
⃗ +
⃗
⃗ =
= 2
⃗
Prędkość i przyspieszenie we współrzędnych Eulera otrzymujemy po podstawieniu za X = x.
⃗( , , , ) = 2
⃗
⃗( , , , ) = 2
⃗
c) Pochodna substancjalna temperatury równa się:
=
+
+
= 2
= 2
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 4
Zadane jest prawo ruchu:
=
+
=
+
=
=
= 1/2
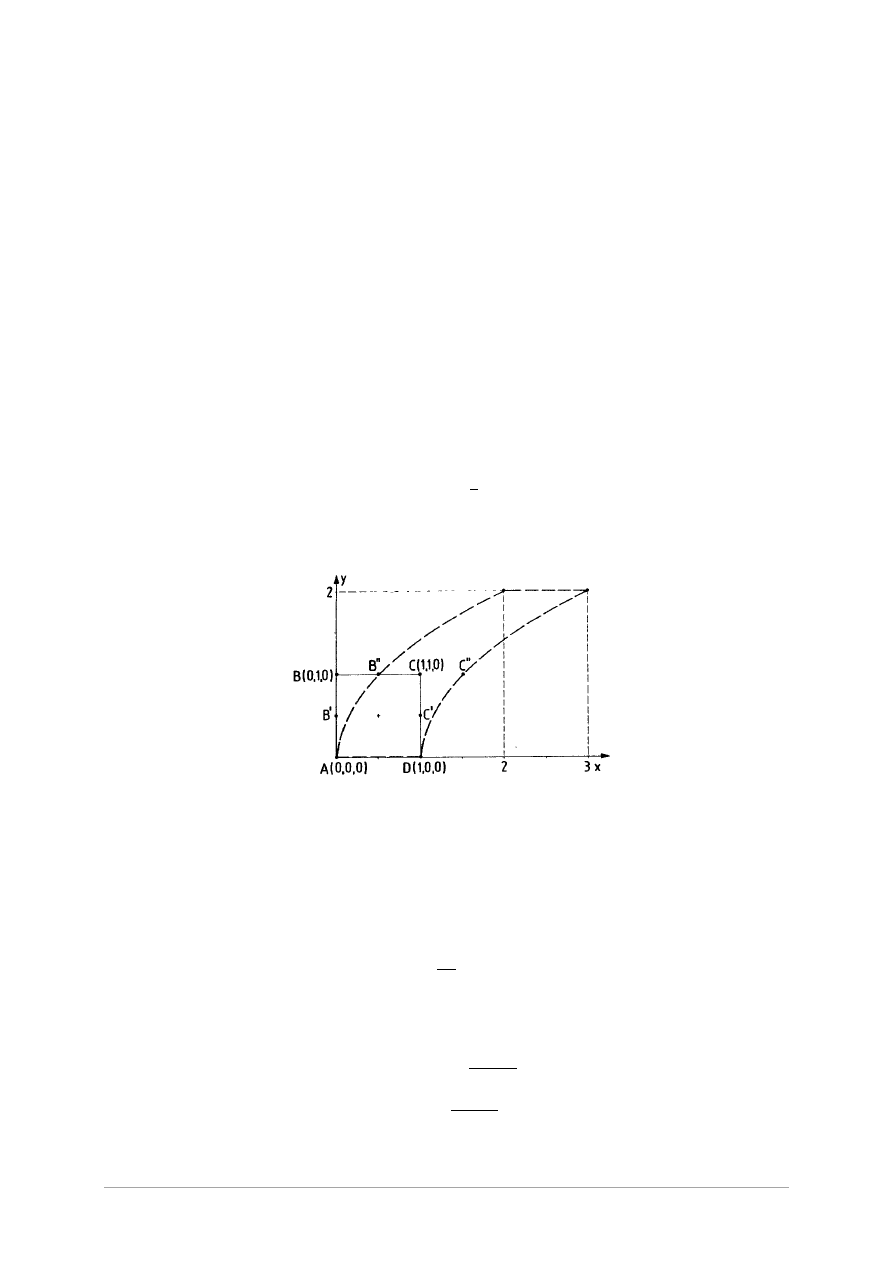
a) W chwili t = 0 wierzchołki kwadratu ABCD mają współrzędne A(0,0,0), B(0,1,0), C(1,1,0),
D(1,0,0). Określić położenie A, B,C,D w chwili t = 2 i naszkicować nowy kształt czworokąąta.
b) Określić prędkość i przyspieszenie we współrzędnych materialnych i przestrzennych.
Rozwiązanie:
a) Obliczamy przemieszczenie każdego wierzchołka kwadratu według zadanego prawa ruchu
(rysynek poniżej). Wierzchołek A(0,0,0) i D(1,0,0) nie zmieni swojego położenia, a więc linia
materialna AD przez cały czas ruchu nie będzie ulegała zmianie, wierzchołek C(1,1,0)
przejdzie do punktu:
=
+
=
1
2
∙ 1 ∙ 4 + 1 = 3
=
+
= 2
= 0
Wierzchołek B(0,1,0) przejdzie do punktu x = 2, y = 2. Boki nowego czworokąta nie będą jednak już
odcinkami prostych. Obliczmy jak przeniosą się środki boków AB i CD. B’(0,1/2,0) oraz C’(1,1/2,0). B’
przejdzie do B’’ o współrzędnych (1/2,1,0), a punkt C do punktu C’’ o współrzędnych (1,5,1,0).
Przybliżony kształt nowego czworokąta zaznaczono linią przerywaną.
b) Prędkość i przyspieszenie we spółrzędnych Lagrange’a:
⃗( , , , ) =
⃗
= 2
⃗ +
⃗
⃗ = 2
⃗
Opis ruchu w zmiennych Eulera dany jest wzorami:
=
−
+ 1
=
+ 1
=
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 5
Zadane jest pole prędkości:
= 0
= (
−
)
= (
−
)
A i B są pewnymi stałymi. Wyznaczyć gradient prędkości gradient prędkości, tensor deformacji oraz
wirowość w punkcie P(1,0,3) w chwili t = 0.
Rozwiązanie:
( ⃗) =
⎝
⎜
⎜
⎜
⎛
⎠
⎟
⎟
⎟
⎞
=
0
0
0
−2z
−
2
−
W punkcie P(1,0,3) i czasie t = 0 tensor ma wartość:
( ⃗) =
0
0
0
0
−6
−3
0
−
Tensor deformacji obliczamy z wzoru:
=
1
2
( ⃗) +
( ⃗)
=
1
2
0
0
0
0
−6
−3
0
−
+
1
2
0
0
−3
0
0
0 −6
−
=
0
0
−1,5
0
−3
−1,5 −3
−
Tensor wirowości obliczamy z następującego wzoru:
Ω =
1
2
( ⃗) −
( ⃗)
=
0
0
1,5
0
0
−3
−1,5
3
0
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 6
Znaleźć równanie linii wirowych dla pola prędkości:
⃗ = (
−
)⃗ + (
−
)⃗ + (
−
) ⃗
Rozwiązanie:
Wektor wirowości ⃗
=
( ⃗) ma składowe:
⃗ = × ⃗ =
−
−
−
= 2 ⃗ + 2 ⃗ + 2 ⃗
Linie wirowe, czyli linie styczne w każdym punkcie do kierunku pola wirowego, wyznaczamy z układu
równań różniczkowych:
2
=
2
=
2
czyli
=
=
=
stąd
=
+
=
+
=
+
gdzie K
1
, K
2
, K
3
są stałymi całkowania.
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 7
Wykazać, że pole prędkości z zad. 6 odpowiada ruchowi ciała szczytowego (tensor deformacji D=0).
Rozwiązanie:
Zapszmy gradient prędkości w postaci macierzowej:
( ⃗) =
0
−
0
−
−
0
Jak widać macierz
( ⃗) jest asymetryczna. Część symetryczna macierzy
( ⃗) , zwana
tensorem deformacji D, jest tożsamościowo równa zeru (D=0).
Zadanie 8
Dane jest następujące pole prędkości dla cieczy nieściśliwej:
= ( − 2)
= −
=
Określić stałą k tak aby spełnione było równanie ciągłości.
Rozwiązanie:
Dla cieczy nieściśliwej
( ⃗) = 0, a więc:
+
+
= − +
= 0
stąd
= 1
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 9
Wykazać, że jeśli F jest polem przekroju poprzecznego strugi, to równanie ciągłości ma postać:
+
(
) = 0
gdzie
oznacza pochodną wzdłuż osi strugi.
Rozwiązanie:
Rozpatrzmy dwa przekroje strugi oddalone od siebie o ds które wycinają ze strugi objętość kontrolną
V = A ds. Korzystając z zasady zachowania masy można dla objętości V ułożyć następujący bilans
masy:
(masa wypływająca z V) - (masa dopływająca do V) + (zmiana masy w V) = 0
Masa cieczy dopływającej do objętości V równa się:
∙
a odpływająca:
+
+
+
Zmiana masy wewnątrz objętości kontrolnej jest równa:
Pomijając w wyrażeniu na masę wypływającą z objętości kontrolnej człony zawierające nieskończenie
małe wyższego rzędu (ds
2
dt), otrzymujemy:
+
+
+
= 0
Równanie to można przekształcić do postaci:
+
(
)
= 0
Dla przepływu ustalonego (
= 0) równanie ciągłości przybiera formę:
=
=
Q
m
– strumień masy
Kinematyka płynów - zadania
Notatki w Internecie | Podstawy mechaniki płynów – materiały do ćwiczeń
Zadanie 10
Ciecz wiruje w ten sposób, że cząstki poruszają się stale po tych samych okręgach z jednakową
prędkością kątową ω. Jakie równanie musi spełniać gęstość płynu ρ?
Rozwiązanie:
Podczas ruchu płynu, gęstość płynu musi spełniać równanie ciągłości:
+
∙
( ⃗) = 0
Z warunków zadania wynika, że składowe prędkości tego ruchu wynoszą:
= − ∙
= − ∙ ∙
= − ∙
=
∙
=
∙ ∙
=
∙
gdzie: v = ωr – moduł wektora prędkości
Dywergencja prędkości:
( ⃗) =
+
+
= − +
= 0
Płyn jest więc nieściśliwy, (
= 0), czyli:
−
∙ ∙
+
∙
∙
= 0
Z warunków zadania wynika, że prędkość jest funkcją tylko promienia r i istnieje tylko składowa
obwodowa v
φ
= ωr. Korzystnie jest więc przedstawić równanie ciągłości we współrzędnych
cylindrycznych, które to równanie we współrzędnych (r, φ, z) ma postać:
+
1
∙
(
)
+
1
∙
(
)
+
(
)
= 0
ponieważ:
= 0
= 0
= ∙
więc:
+
( ∙ )
= 0