


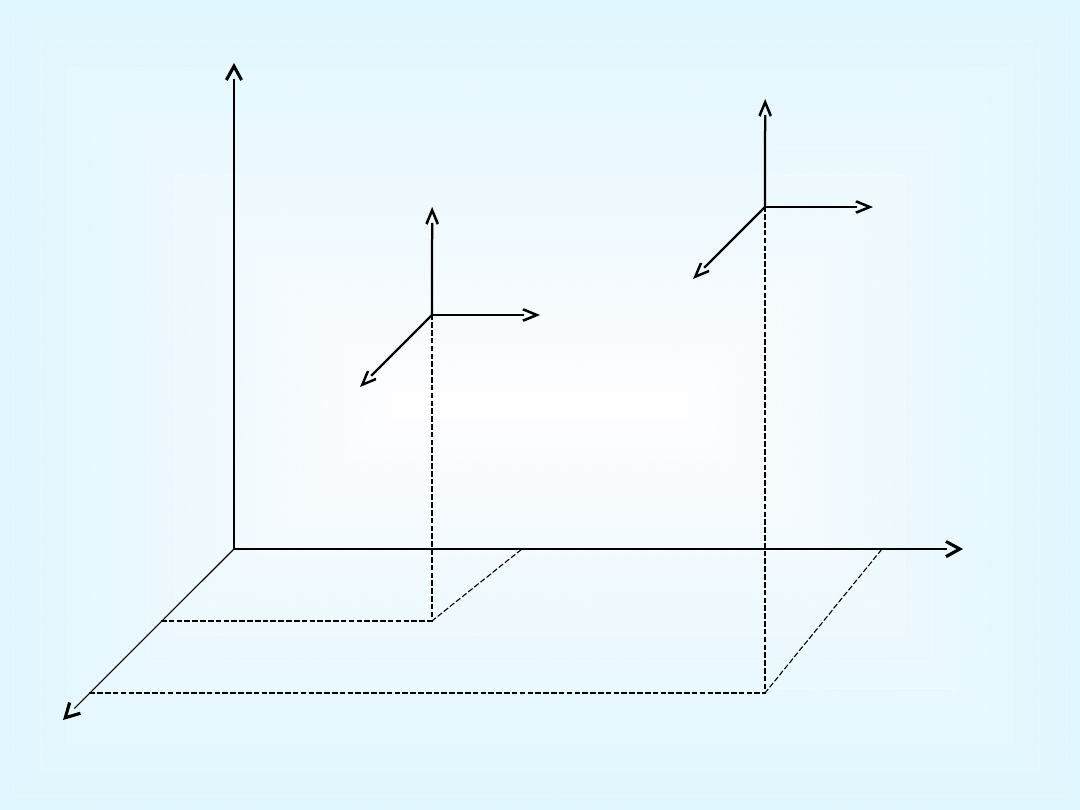
Metoda Lagrange’a – badanie ruchu
wybranej cząstki płynu
.
)
,
,
,
(
,
)
,
,
,
(
,
)
,
,
,
(
t
Z
Y
X
z
z
t
Z
Y
X
y
y
t
Z
Y
X
x
x
.
,
,
t
z
V
t
y
V
t
x
V
z
y
x
.
,
,
2
2
2
2
2
2
t
z
t
V
w
t
y
t
V
w
t
x
t
V
w
z
z
y
y
x
x
x
z
0
0
x
V
0
z
V
0
y
V
1
y
V
1
z
V
1
x
V
0
x
0
z
0
y
1
x
1
z
1
y
y
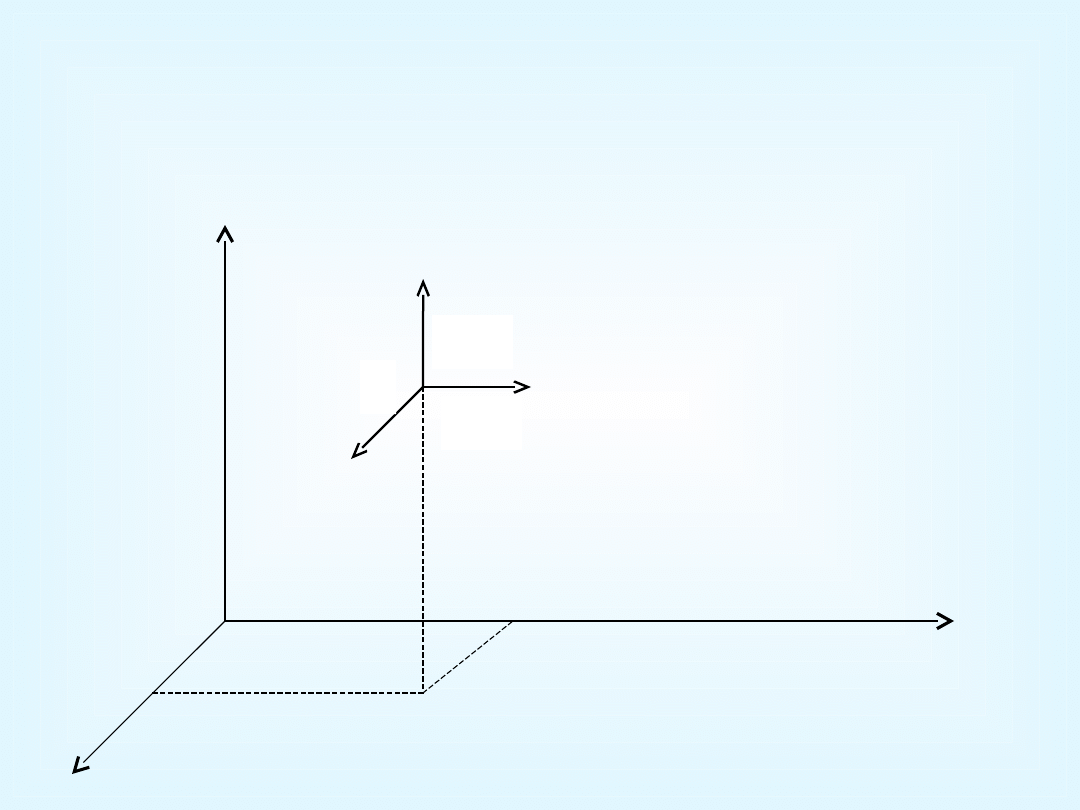
Metoda Eulera
x
z
0
0
x
V
0
z
V
0
y
V
x
z
y
1
y
V
1
z
V
1
x
V
)
,
,
(
z
y
x
H
H
)
,
,
,
(
t
z
y
x
H
H
Badanie ruchu płynu w określonych punktach przestrzeni:
y

Pojęcia związane z ruchem płynu
Obszar płynny – wyodrębniona masa płynu, którą tworzą wciąż te
same elementy
płynu.
Obszar kontrolny – wyodrębniona masa płynu którą tworzą wciąż
te same punkty przestrzenne, natomiast znajdują się w niej, w miarę
upływu czasu, coraz to inne elementy płynu.
Powierzchnia płynna – powierzchnia zamknięta, ograniczająca
obszar płynny.
Powierzchnia kontrolna – powierzchnia zamknięta, ograniczająca
obszar kontrolny.


Linia prądu
Niech będzie dane pole wektora prędkości płynu:
.
)
,
,
,
(
)
,
,
,
(
)
,
,
,
(
t
z
y
x
V
z
d
t
z
y
x
V
y
d
t
z
y
x
V
x
d
z
y
x
.
]
,
,
[
,
)
,
,
,
(
z
y
x
V
V
V
t
z
y
x
V
V
V
Linie tego pola wektorowego (styczne w każdym swym punkcie do
wektora pola) nazywają się liniami prądu.
Oznaczając element linii prądu przez
,
]
,
,
[
z
d
y
d
x
d
d
s
równanie linii prądu możemy napisać w postaci iloczynu
wektorowego
0
s
V
d
lub też w postaci równoważnej
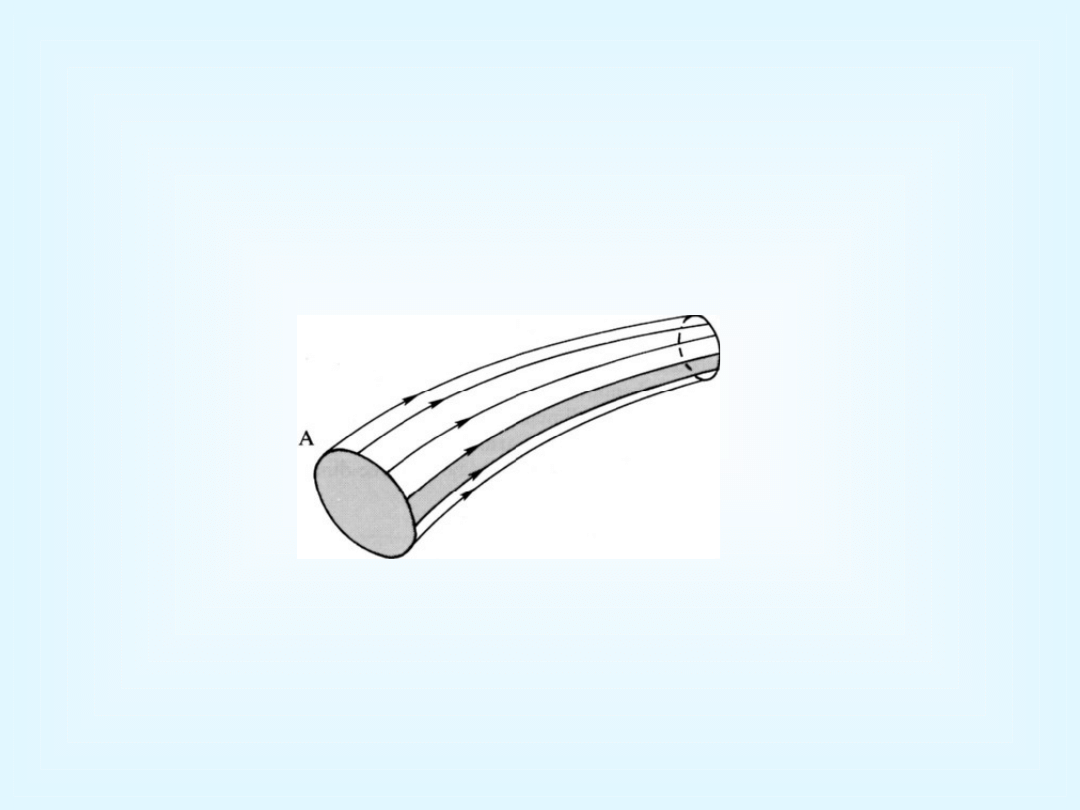
Powierzchnia i rurka prądu
Powierzchnia prądu – powierzchnia utworzona z linii prądu,
przecinających dowolną linię, nie będącą linią prądu.
Rurka prądu – powierzchnia utworzona z linii prądu,
przecinających dowolną linię zamkniętą, nie będącą linią prądu.

Tor elementu płynu
Linia, po której porusza się pojedynczy element płynu. Jest ona
graficzną reprezentacją matematycznego opisu ruchu w zmiennych
Lagrange’a.
.
t
d
V
z
d
V
y
d
V
x
d
z
y
x
Oznaczając element toru przez
]
,
,
[
z
d
y
d
x
d
d
s
otrzymujemy równanie różniczkowe toru
,
)
,
,
,
(
t
d
t
z
y
x
d
V
s
albo po przekształceniu


Przyspieszenie elementu płynu, traktowanego jako punkt, jest
pochodną prędkości elementu względem czasu, wyraża się zatem
wzorem:
.
)
,
,
,
(
t
d
t
z
y
x
dV
w
Różniczka zupełna prędkości jest określona
następująco:
.
t
d
t
z
d
z
y
d
y
x
d
x
d
V
V
V
V
V
Przyspieszenie elementu płynu można zapisać w postaci:
.
z
V
y
V
x
V
t
z
y
x
V
V
V
V
w
V
d
t
z
y
x
,
,
,
V
V

Przy zastosowaniu operatora Hamiltona
z
y
x
k
j
i
przyspieszenie można zapisać w postaci
,
V
V
V
V
w
t
t
d
d
gdzie
.
z
V
y
V
x
V
z
y
x
V
dt
dV
pochodna
substancjalna prędkości – określa zmiany
zachodzące
w poruszającym się, ale wciąż tym samym elemencie płynu
t
V
pochodna
lokalna – określa zmiany zachodzące z upływem
czasu w stałym
punkcie przestrzeni
V
V
pochodna
konwekcyjna – określa zmiany prędkości
związane z samym
tylko przesunięciem elementu płynu w inne położenie

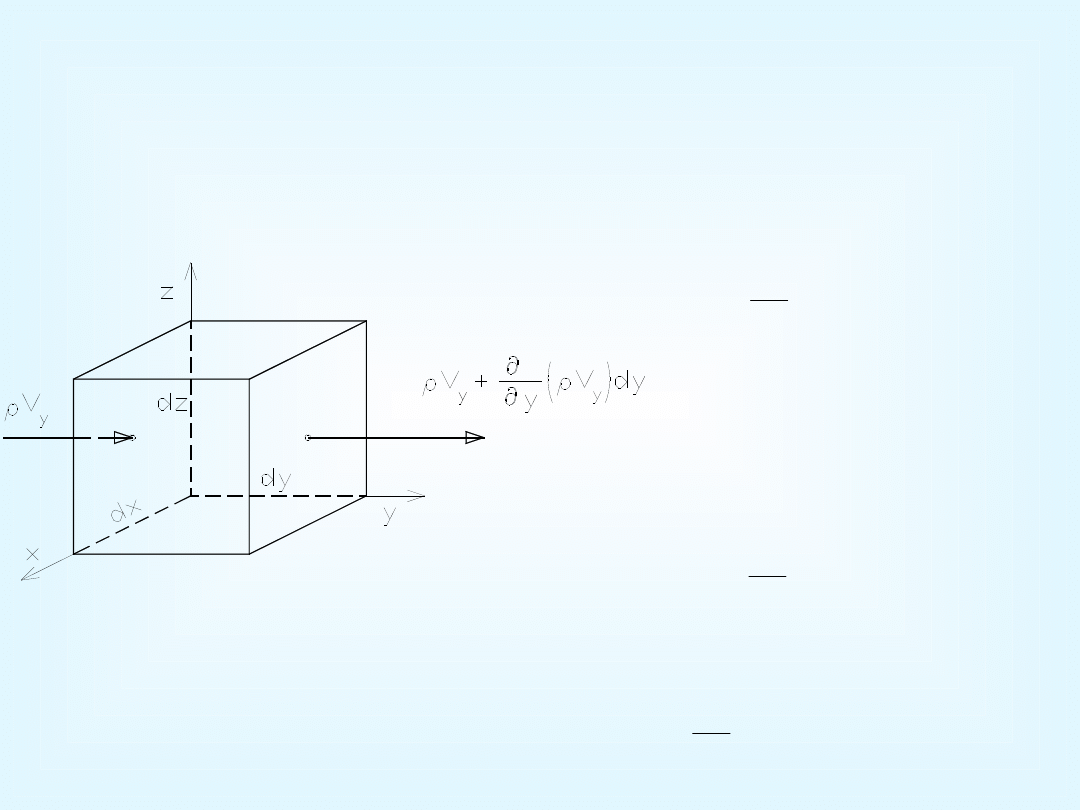
Ruch płynu został określony za pomocą pola prędkości i pola
gęstości płynu:
]
,
,
[
,
)
,
,
,
(
z
y
x
V
V
V
t
z
y
x
V
V
V
.
)
,
,
,
(
t
z
y
x
Zmiana masy płynu
wynikająca ze zmiany jego
gęstości wynosi
t
d
z
d
y
d
x
d
t
– masa
wpływająca
,
t
d
z
d
x
d
V
y
.
t
d
z
d
x
d
y
d
V
y
V
y
y
Różnica masy wpływającej i
wypływającej:
.
t
d
z
d
y
d
x
d
V
y
y
– masa
wypływająca

Porównując zmiany masy na wszystkich ściankach otrzymamy
różniczkowe równanie ciągłości przepływu
.
0
z
y
x
V
z
V
y
V
x
t
Forma wektorowa
.
0
div
ρ
V
t
Formy uproszczone:
;
0
0
div
t
V
( ciecz )
.
)
const.
(
0
div
V
( ruch stacjonarny )
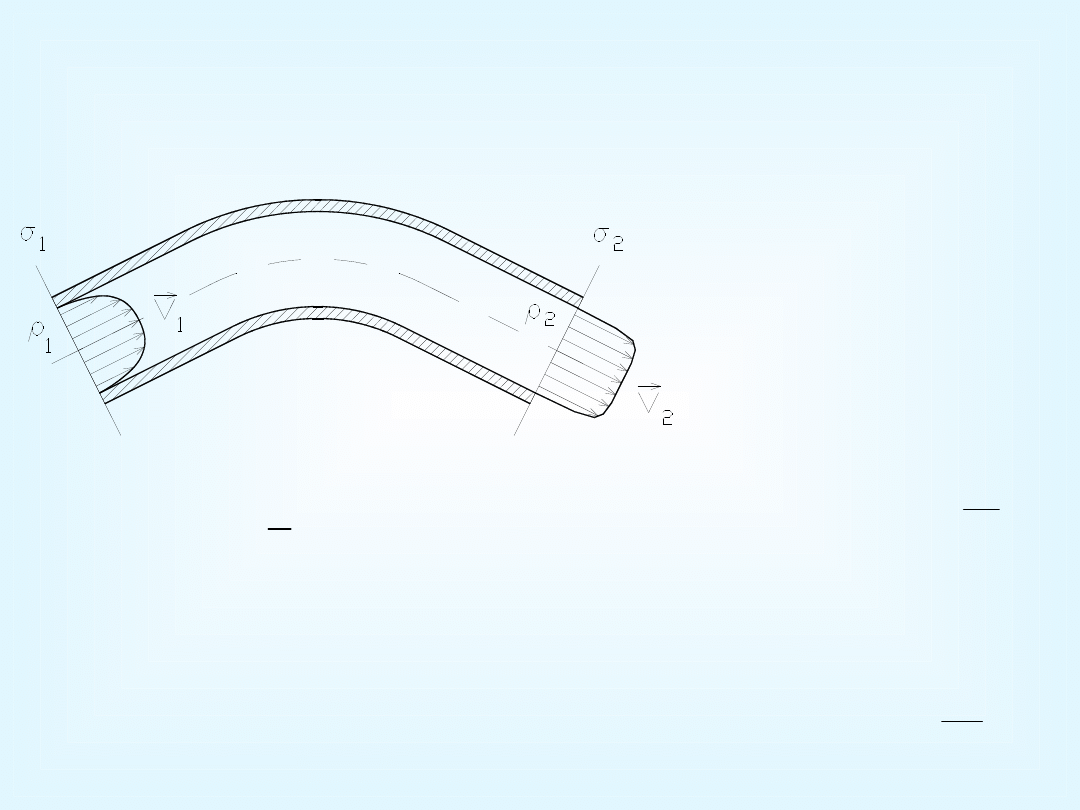
Stacjonarny przepływ jednowymiarowy
Rozważamy ruch przez kanał ograniczony ściankami kontrolnymi
σ
1
i
σ
2
Prędkość
średnia
,
1
śr
d
V
V
n
masa płynu zawarta
wewnątrz kanału musi
być stała
;
)
(
)
(
śr
2
2
2
śr
1
1
1
V
V
Wydatek
masowy
s
kg
.
const
śr
V
m
Wydatek
objętościowy
s
m
const.
3
śr
V
Q
V
- strumień masy,
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
Wyszukiwarka
Podobne podstrony:
3 Elementy kinematyki płynów 3
3 Elementy kinematyki plynow
3 Elementy kinematyki płynów 5
Wędrychowicz,mechanika płynów, Kinematyka płynów
3 Elementy kinematyki płynów
kinematyka plynow zadania
14 Elementy kinematyki i dynamiki
Elementy statyki i dynamiki płynów
W2-Ruch elementu płynu, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr
Wyk 02 Pneumatyczne elementy
Elementy prawa prawo administracyjne
7 Mikro i makro elementy naszej diety
Wykład 4 Elementarne zagadnienia kwantowe
więcej podobnych podstron