Mechanika ogólna

Mechanika ogólna

1

1

Wykład

Wykład nr

nr 14

14

Elementy

Elementy kinematyki i dynamiki

kinematyki i dynamiki

Kinematyka

Kinematyka





Dział

Dział mechaniki

mechaniki zajmujący się

zajmujący się

matematycznym opisem układów

matematycznym opisem układów

mechanicznych oraz badaniem

mechanicznych oraz badaniem

geometrycznych właściwości ich ruchu,

geometrycznych właściwości ich ruchu,

geometrycznych właściwości ich ruchu,

geometrycznych właściwości ich ruchu,

bez wnikania w związek między

bez wnikania w związek między

ruchem, a siłami go powodującymi.

ruchem, a siłami go powodującymi.





Ruch

Ruch ciała

ciała –– zmiana położenia w

zmiana położenia w

przestrzeni, względem innego ciała,

przestrzeni, względem innego ciała,

które traktujemy jako nieruchome.

które traktujemy jako nieruchome.

2

2

Podstawowe pojęcia

Podstawowe pojęcia





Przestrzeń i czas;

Przestrzeń i czas;

–– Współrzędne;

Współrzędne;

–– Tor ruchu;

Tor ruchu;





Ruch postępowy:

Ruch postępowy:





Ruch postępowy:

Ruch postępowy:

–– Prędkość;

Prędkość;

–– Przyspieszenie;

Przyspieszenie;





Ruch obrotowy:

Ruch obrotowy:

–– Prędkość kątowa;

Prędkość kątowa;

–– Przyspieszenie kątowe.

Przyspieszenie kątowe.

3

3

Równania ruchu

Równania ruchu





Wektor wodzący poruszającego się

Wektor wodzący poruszającego się

punktu:

punktu:

Funkcje skalarne opisujące ruch punktu:

Funkcje skalarne opisujące ruch punktu:

 

t



r

r





Funkcje skalarne opisujące ruch punktu:

Funkcje skalarne opisujące ruch punktu:

4

4

 

x

x t



 

y

y t



 

z

z t



x

y

z







r

i

j

k

x

y

z

x

y

z

i

j

k

 

t

r

P

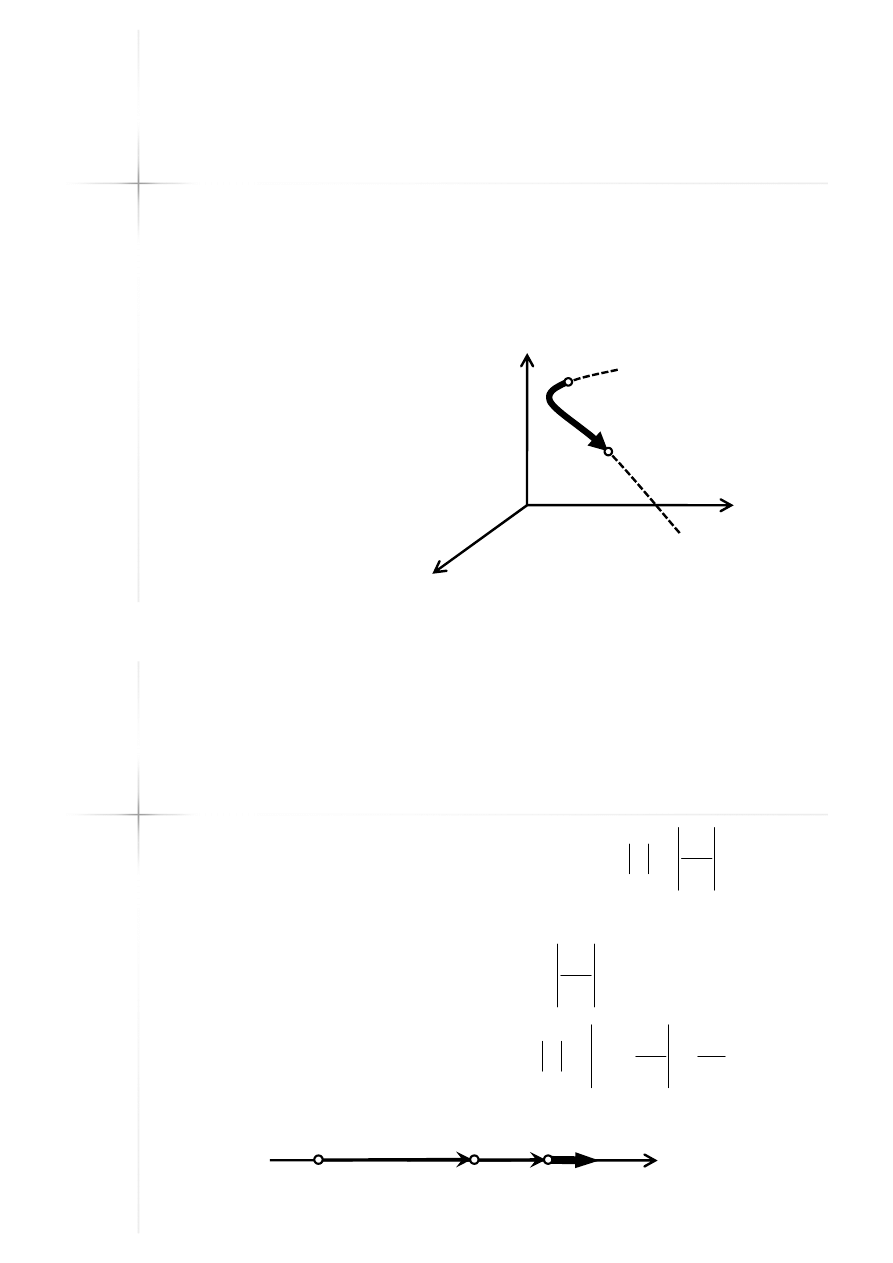
Równanie ruchu po torze

Równanie ruchu po torze

(równanie drogi)

(równanie drogi)





Równanie opisujące ruch punktu P,

Równanie opisujące ruch punktu P,

gdy znany jest tor ruchu względem

gdy znany jest tor ruchu względem

nieruchomego położenia

nieruchomego położenia

nieruchomego położenia

nieruchomego położenia

początkowego P

początkowego P

00

::

5

5

x

y

z

P

 

s

s t



0

P

 

s t

Prędkość w ruchu

Prędkość w ruchu

prostoliniowym

prostoliniowym





W ruchu jednostajnym:

W ruchu jednostajnym:





W dowolnym ruchu prostoliniowym:

W dowolnym ruchu prostoliniowym:

x

v

t









v

x



–– Prędkość średnia:

Prędkość średnia:

–– Prędkość chwilowa:

Prędkość chwilowa:

6

6

sr

x

v

t







0

lim

t

x

dx

v

t

dt















v

x

x

x



0

P

1

P

2

P

v

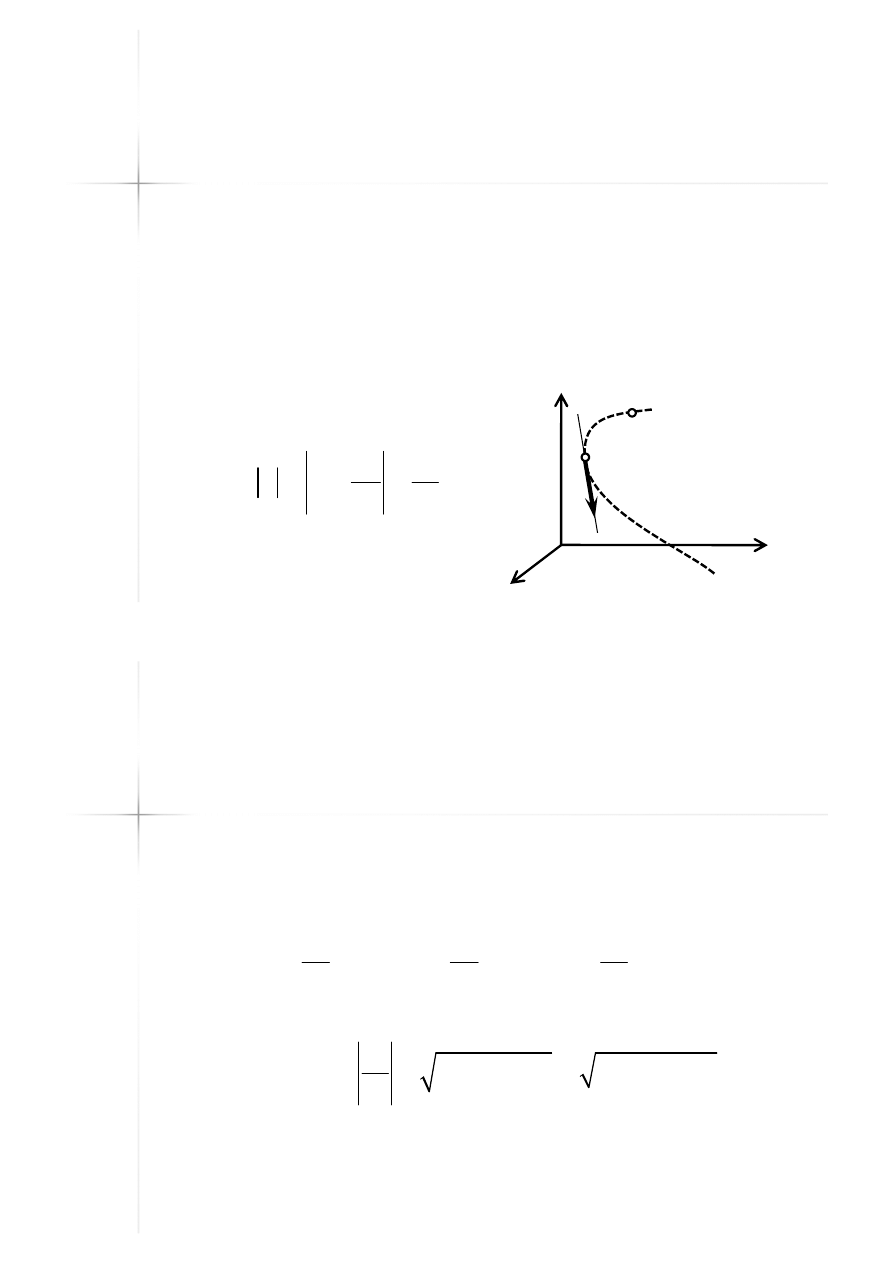
Prędkość w ruchu

Prędkość w ruchu

krzywoliniowym

krzywoliniowym

(1)

(1)





Prędkość punktu:

Prędkość punktu:

–– Wektor o module równym wartości

Wektor o module równym wartości

bezwzględnej pochodnej drogi po czasie,

bezwzględnej pochodnej drogi po czasie,

bezwzględnej pochodnej drogi po czasie,

bezwzględnej pochodnej drogi po czasie,

skierowany wzdłuż stycznej do toru ruchu

skierowany wzdłuż stycznej do toru ruchu

i o zwrocie w kierunku ruchu w danej

i o zwrocie w kierunku ruchu w danej

chwili.

chwili.

7

7

0

lim

t

s

ds

v

t

dt















v

x

y

z

P

0

P

v

Prędkość w ruchu

Prędkość w ruchu

krzywoliniowym

krzywoliniowym

(2)

(2)





Składowe prędkości w układzie

Składowe prędkości w układzie

współrzędnych równe są pochodnym po

współrzędnych równe są pochodnym po

czasie odpowiednich współrzędnych:

czasie odpowiednich współrzędnych:

dx

v

x



 

dy

v

y



 

dz

v

z



 





Moduł prędkości (wartość liczbowa):

Moduł prędkości (wartość liczbowa):





Rzut prędkości punktu na oś układu

Rzut prędkości punktu na oś układu

współrzędnych równy jest prędkości z

współrzędnych równy jest prędkości z

jaką porusza się rzut punktu wzdłuż osi.

jaką porusza się rzut punktu wzdłuż osi.

8

8

x

dx

v

x

dt



 

y

dy

v

y

dt



 

z

dz

v

z

dt



 

2

2

2

2

2

2

x

y

z

ds

v

v

v

v

x

y

z

dt





















Prędkość w ruchu

Prędkość w ruchu

krzywoliniowym

krzywoliniowym

(3)

(3)





W układzie współrzędnych

W układzie współrzędnych

prostokątnych rzuty prędkości punktu

prostokątnych rzuty prędkości punktu

są prędkościami rzutów wektora

są prędkościami rzutów wektora

są prędkościami rzutów wektora

są prędkościami rzutów wektora

wodzącego

wodzącego rr..





Prędkość punktu równa jest pochodnej

Prędkość punktu równa jest pochodnej

geometrycznej względem czasu

geometrycznej względem czasu

promienia wodzącego tego punktu:

promienia wodzącego tego punktu:

9

9

 

d

d ds

ds

t

dt

ds dt

dt









r

r

v

r

t



Przyspieszenie punktu

Przyspieszenie punktu





Pierwsza pochodna prędkości

Pierwsza pochodna prędkości

względem czasu:

względem czasu:

2

2

d

d

dt

dt



 



v

r

a

v

r









Składowe w układzie kartezjańskim

Składowe w układzie kartezjańskim

można wyrazić jako drugie pochodne

można wyrazić jako drugie pochodne

współrzędnych:

współrzędnych:

10

10

dt

dt

x

a

x

 

y

a

y

 

z

a

z

 

2

2

2

2

2

2

x

y

z

a

a

a

a

x

y

z



















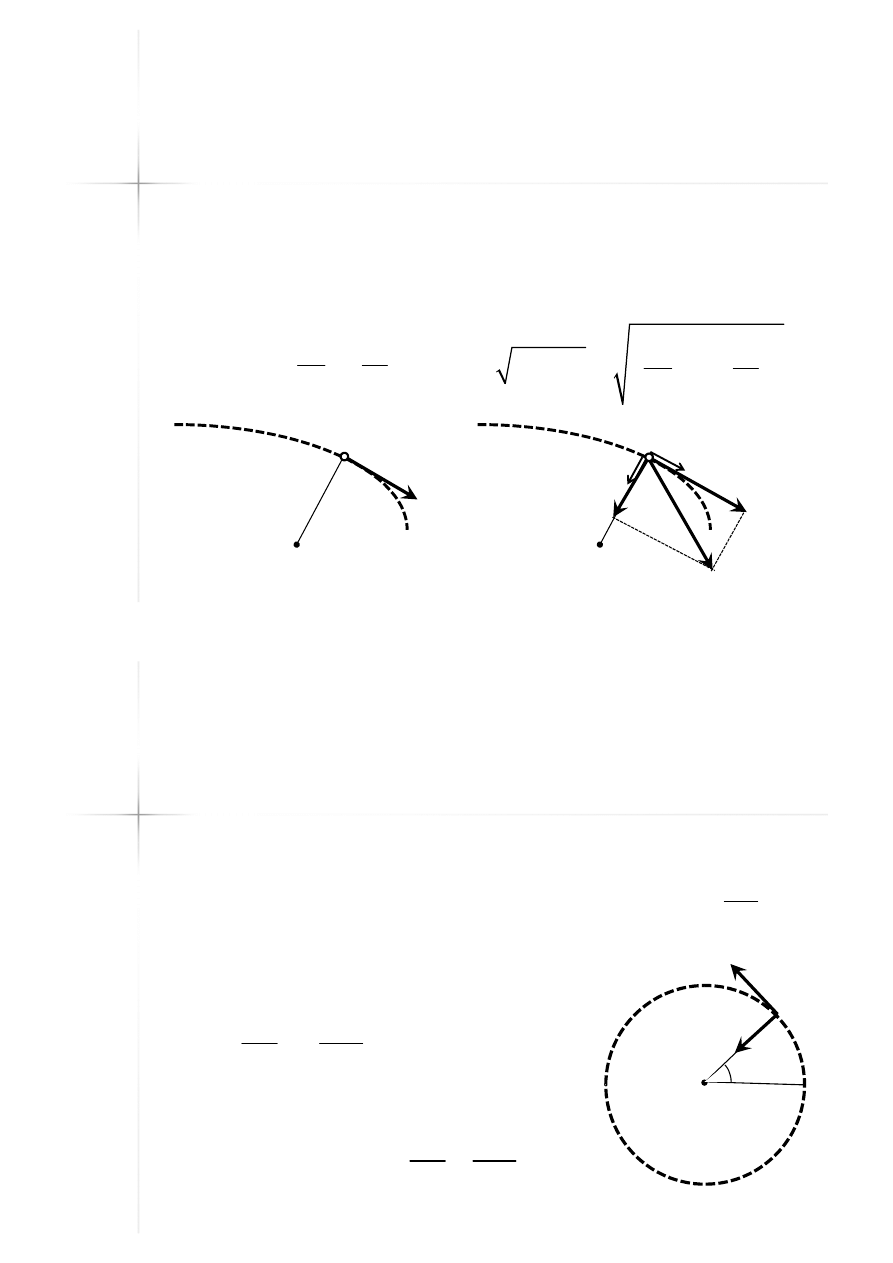
Przyspieszenie styczne i

Przyspieszenie styczne i

normalne do toru ruchu

normalne do toru ruchu





Całkowite przyspieszenie punktu jest

Całkowite przyspieszenie punktu jest

równe sumie składowych

równe sumie składowych –– stycznej i

stycznej i

normalnej do toru ruchu:

normalnej do toru ruchu:

normalnej do toru ruchu:

normalnej do toru ruchu:

11

11

2

t

n

dv

v

dt



 





a

a

a

t

n

2

2

2

2

2

t

n

dv

v

a

a

a

dt

















  













0



0



v

t

n

t

a

n

a

a

P

P

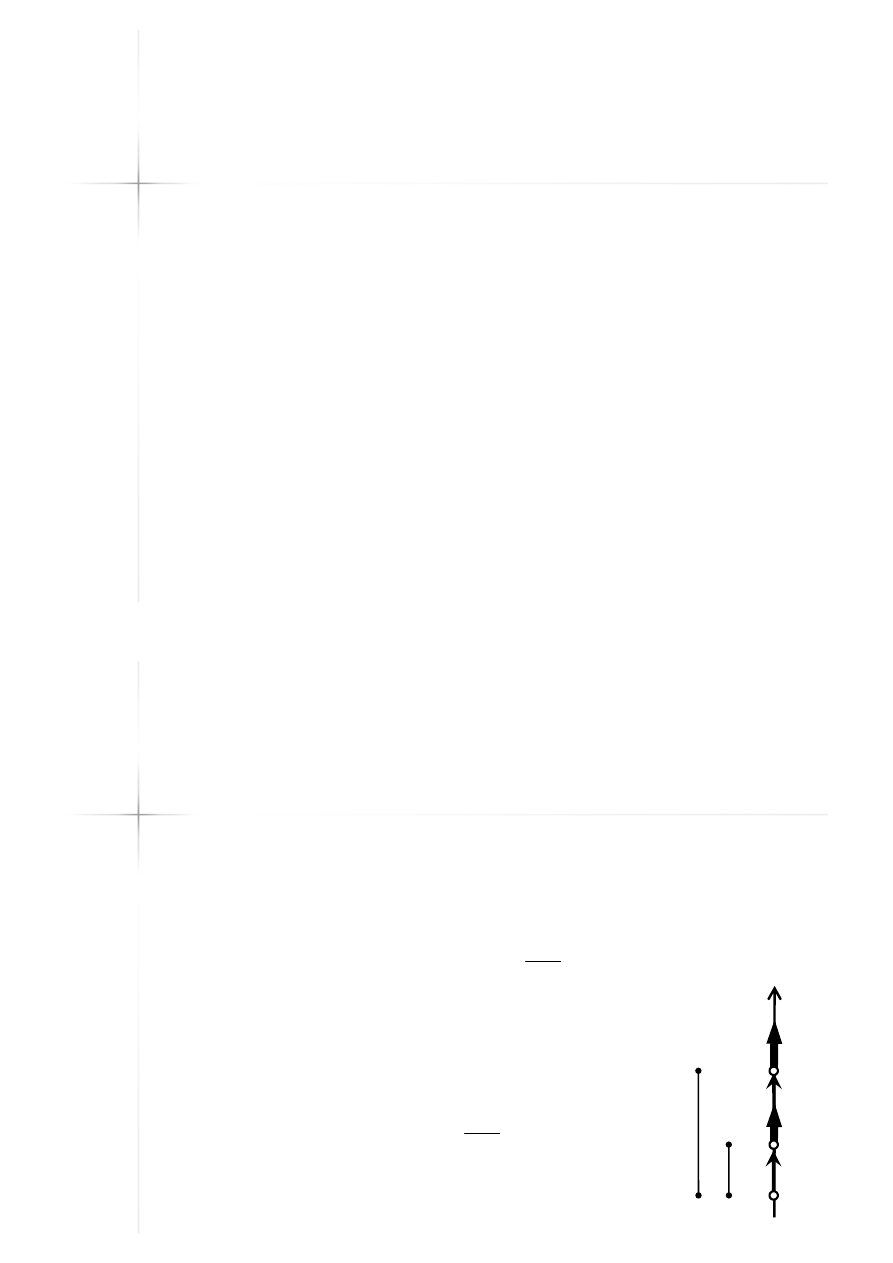
Składowe przyspieszenia

Składowe przyspieszenia

w ruchu po torze kołowym

w ruchu po torze kołowym





Prędkość w zależności od prędkości

Prędkość w zależności od prędkości

kątowej:

kątowej:





Promień krzywizny:

Promień krzywizny:

v

r





d

dt







r









Promień krzywizny:

Promień krzywizny:





Składowe przyspieszenia:

Składowe przyspieszenia:





Przyspieszenie kątowe:

Przyspieszenie kątowe:

12

12

2

2

t

d

d

a

r

r

dt

dt









0

r

t

a

n

a

r





2

n

a

r





t

a

r





2

2

d

d

dt

dt













Szczególne przypadki ruchu

Szczególne przypadki ruchu





Ruch jednostajnie przyspieszony

Ruch jednostajnie przyspieszony

prostoliniowy;

prostoliniowy;





Ruch harmoniczny;

Ruch harmoniczny;





Ruch harmoniczny;

Ruch harmoniczny;





Ruch krzywoliniowy ze stałym

Ruch krzywoliniowy ze stałym

przyspieszeniem.

przyspieszeniem.

13

13

Ruch jednostajnie

Ruch jednostajnie

przyspieszony prostoliniowy

przyspieszony prostoliniowy





Ruch po prostej ze stałym co do wartości

Ruch po prostej ze stałym co do wartości

i kierunku przyspieszeniem:

i kierunku przyspieszeniem:





Prędkość:

Prędkość:





Położenie punktu:

Położenie punktu:

x

a

x

a

const

  



1

x

v

x

at

C

 





2

at

x

C t

C











Położenie punktu:

Położenie punktu:





Warunki brzegowe:

Warunki brzegowe:





Stałe całkowania:

Stałe całkowania:





Równanie ruchu:

Równanie ruchu:





Równanie prędkości:

Równanie prędkości:

14

14

1

2

2

at

x

C t

C







0

(

0)

x t

x





0

(

0)

x

x

v t

v





1

0 x

C

v



2

0

C

x



2

0

0

2

x

at

x

v t

x







 

0 x

v t

at

v





x

0

x

0

P

P

v

0

0

v

 

x t

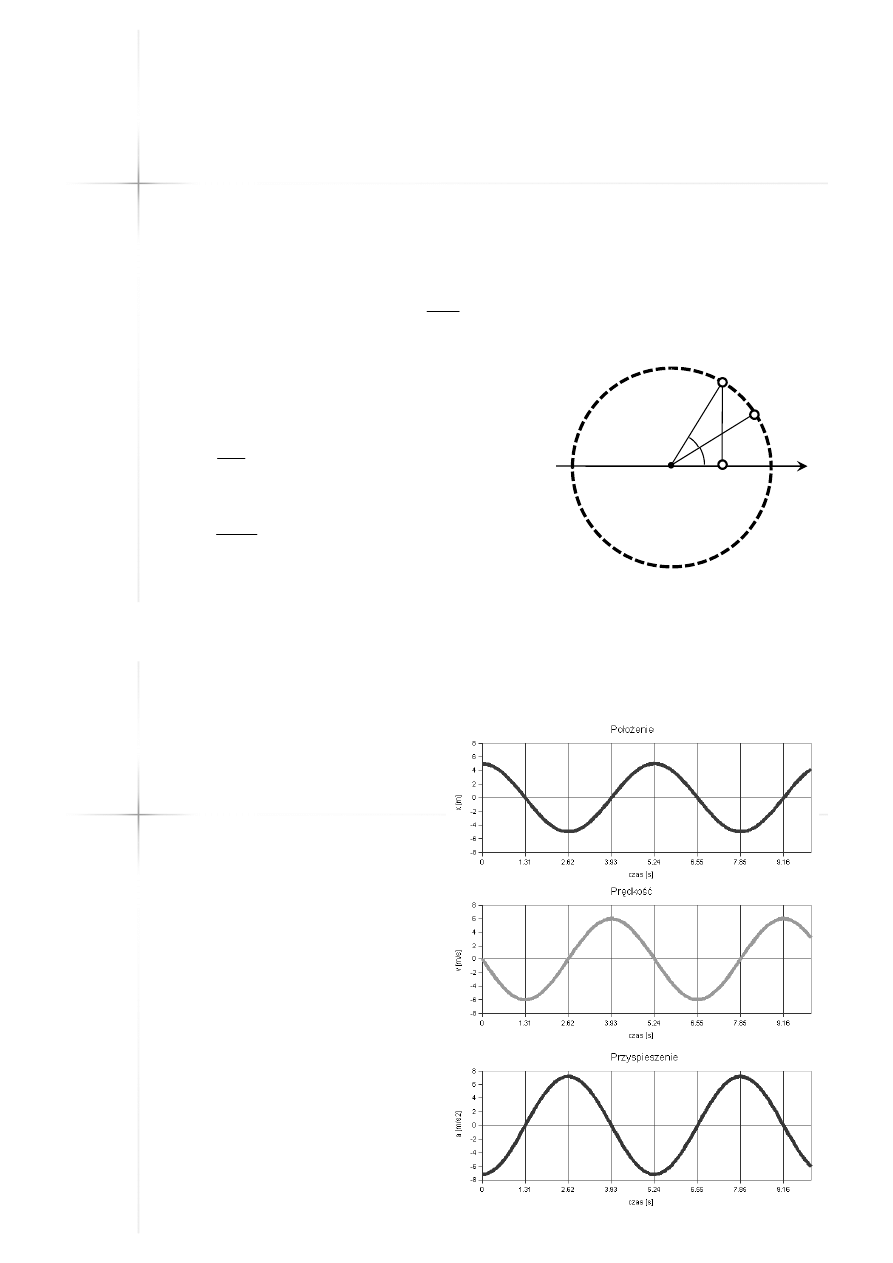
Ruch harmoniczny

Ruch harmoniczny





Punkt

Punkt P

P poruszający się jednostajnie

poruszający się jednostajnie

po okręgu o promieniu

po okręgu o promieniu rr::

2

T







t

 







Ruch rzutu punktu

Ruch rzutu punktu P

P po osi

po osi xx::

15

15

0

r

0





0

P

P

x

P









0

0

cos

cos

x

r

r

t

 

 









T





t

 







0

sin

dx

v

r

t

dt



 



 







2

2

2

0

2

cos

d x

a

r

t

x

dt



 





 



 

Ruch

Ruch

harmoniczny

harmoniczny





Wykresy

Wykresy

położenia,

położenia,

prędkości

prędkości

prędkości

prędkości

i przyspieszenia:

i przyspieszenia:

16

16

Ruch ciała sztywnego

Ruch ciała sztywnego





Ciało sztywne

Ciało sztywne –– układ punktów

układ punktów

materialnych, których wzajemne

materialnych, których wzajemne

odległości pozostają niezmienne.

odległości pozostają niezmienne.

odległości pozostają niezmienne.

odległości pozostają niezmienne.





Ruch postępowy;

Ruch postępowy;





Ruch obrotowy;

Ruch obrotowy;





Złożenie ruchów:

Złożenie ruchów:

–– Ruch płaski;

Ruch płaski;

–– Ruch kulisty.

Ruch kulisty.

17

17

Ruch postępowy ciała

Ruch postępowy ciała

sztywnego

sztywnego





W ruchu

W ruchu postępowym

postępowym prędkości i

prędkości i

przyspieszenia wszystkich punktów

przyspieszenia wszystkich punktów

ciała są jednakowe. Punkty ciała

ciała są jednakowe. Punkty ciała

ciała są jednakowe. Punkty ciała

ciała są jednakowe. Punkty ciała

poruszają się po jednakowych

poruszają się po jednakowych

równolegle przesuniętych torach.

równolegle przesuniętych torach.

18

18

A

B

C

A

B

C

A

B

C





v

v

v

A

B

C





p

p

p

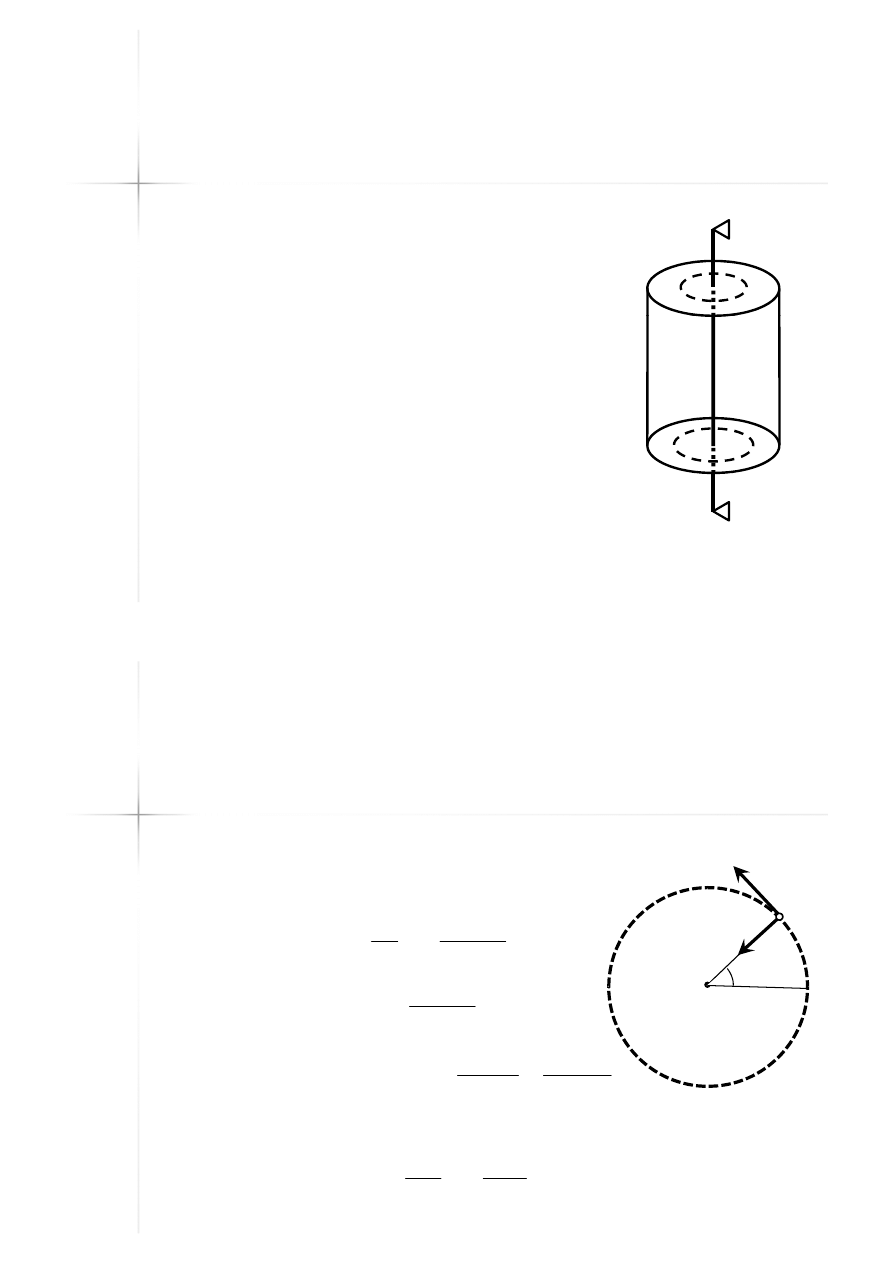
Ruch obrotowy ciała

Ruch obrotowy ciała

sztywnego

sztywnego





Ruch

Ruch obrotowy

obrotowy wokół

wokół

nieruchomej osi obrotu

nieruchomej osi obrotu

(środka obrotu w ruchu

(środka obrotu w ruchu

płaskim).

płaskim).

płaskim).

płaskim).





Torami punktów ciała są

Torami punktów ciała są

okręgi w płaszczyznach

okręgi w płaszczyznach

prostopadłych do osi

prostopadłych do osi

obrotu i środkach leżących

obrotu i środkach leżących

na tej osi.

na tej osi.

19

19

Ruch obrotowy ciała

Ruch obrotowy ciała

sztywnego

sztywnego





Równanie ruchu obrotowego ciała sztywnego:

Równanie ruchu obrotowego ciała sztywnego:





Prędkość

Prędkość

liniowa:

liniowa:

t

a

a

 

s

r

t





 

 

d

t

ds

v

r

r

t

dt

dt











liniowa:

liniowa:





Prędkość

Prędkość

kątowa:

kątowa:





Przyspieszenie

Przyspieszenie

kątowe:

kątowe:





Składowe przyspieszenia

Składowe przyspieszenia

liniowego:

liniowego:

20

20

0

r

n

a

 

v

r

r

t

dt

dt









 

 

d

t

t

dt







 

 

 

2

2

d

t

d

t

t

dt

dt











2

2

t

d

d

a

r

r

r

dt

dt













2

n

a

r







Dynamika

Dynamika





Dział

Dział mechaniki

mechaniki zajmujący się

zajmujący się

badaniem związków między ruchem

badaniem związków między ruchem

punktów materialnych i ciał sztywnych

punktów materialnych i ciał sztywnych

punktów materialnych i ciał sztywnych

punktów materialnych i ciał sztywnych

oraz sił go wywołujących.

oraz sił go wywołujących.





Dynamika bada zależności między

Dynamika bada zależności między

takimi wielkościami jak: siła,

takimi wielkościami jak: siła,

przyspieszenie, prędkość, pęd, kręt,

przyspieszenie, prędkość, pęd, kręt,

praca, energia itd.

praca, energia itd.

21

21

Pierwsza zasada

Pierwsza zasada

dynamiki Newtona

dynamiki Newtona





Prawo bezwładności

Prawo bezwładności::

–– Z punktu widzenia dynamiki jest wszystko

Z punktu widzenia dynamiki jest wszystko

jedno, czy ciało się porusza ruchem

jedno, czy ciało się porusza ruchem

jedno, czy ciało się porusza ruchem

jedno, czy ciało się porusza ruchem

jednostajnym prostoliniowym, czy jest w

jednostajnym prostoliniowym, czy jest w

spoczynku.

spoczynku.

–– W obu przypadkach siły działające na

W obu przypadkach siły działające na

ciało są w równowadze.

ciało są w równowadze.

–– Można zawsze założyć istnienie

Można zawsze założyć istnienie

nieruchomego układu odniesienia.

nieruchomego układu odniesienia.

22

22

Druga zasada dynamiki

Druga zasada dynamiki

Newtona

Newtona





Pod działaniem stałej siły punkt materialny

Pod działaniem stałej siły punkt materialny

porusza się ruchem jednostajnie

porusza się ruchem jednostajnie

przyspieszonym po linii prostej.

przyspieszonym po linii prostej.
Przyspieszenie z jakim porusza się punkt

Przyspieszenie z jakim porusza się punkt





Przyspieszenie z jakim porusza się punkt

Przyspieszenie z jakim porusza się punkt

jest wprost proporcjonalne do działającej

jest wprost proporcjonalne do działającej

siły (wypadkowej układu sił), a odwrotnie

siły (wypadkowej układu sił), a odwrotnie

proporcjonalne do masy ciała.

proporcjonalne do masy ciała.

23

23

m



P

a

P

a

m

Trzecia zasada dynamiki

Trzecia zasada dynamiki

Newtona

Newtona





Siły wzajemnego oddziaływania dwóch

Siły wzajemnego oddziaływania dwóch

punktów materialnych równoważą się,

punktów materialnych równoważą się,

tj. mają jednakowe moduły i kierunki,

tj. mają jednakowe moduły i kierunki,

tj. mają jednakowe moduły i kierunki,

tj. mają jednakowe moduły i kierunki,

zaś zwroty przeciwne.

zaś zwroty przeciwne.

24

24

P

1

P

2

2

1

P

P



2

1

P

P





Zasada superpozycji

Zasada superpozycji





Efekt działania kilku wpływów na ciało

Efekt działania kilku wpływów na ciało

można wyrazić jako sumę efektów ich

można wyrazić jako sumę efektów ich

działania.

działania.
Przyspieszenie z jakim porusza się ciało

Przyspieszenie z jakim porusza się ciało





Przyspieszenie z jakim porusza się ciało

Przyspieszenie z jakim porusza się ciało

pod wpływem układu sił (siły

pod wpływem układu sił (siły

wypadkowej) może zostać obliczone

wypadkowej) może zostać obliczone

jako suma przyspieszeń powodowanych

jako suma przyspieszeń powodowanych

przez każdą z sił składowych.

przez każdą z sił składowych.

25

25

1

2

...

...

n

n

m

m

m

m





 





 



1

2

a

a

a

a

P

P

P

P

Prawo grawitacji

Prawo grawitacji





Dwa ciała działają na siebie wzajemnie

Dwa ciała działają na siebie wzajemnie

jednakowymi co do wartości i

jednakowymi co do wartości i

przeciwnie zwróconymi siłami o wartości

przeciwnie zwróconymi siłami o wartości

przeciwnie zwróconymi siłami o wartości

przeciwnie zwróconymi siłami o wartości

odwrotnie proporcjonalnej do kwadratu

odwrotnie proporcjonalnej do kwadratu

odległości między ich środkami i wprost

odległości między ich środkami i wprost

proporcjonalnej do iloczynu mas tych

proporcjonalnej do iloczynu mas tych

ciał.

ciał.

26

26

1

2

2

m m

r





P

G

Równania ruchu punktu

Równania ruchu punktu

materialnego

materialnego





Dynamiczne równanie różniczkowe ruchu

Dynamiczne równanie różniczkowe ruchu

punktu materialnego:

punktu materialnego:

d

d

m

m

m



     





r

r

a

P







Dynamiczne różniczkowe równania ruchu

Dynamiczne różniczkowe równania ruchu

we współrzędnych prostokątnych:

we współrzędnych prostokątnych:

27

27

m

m

m

dt

dt

    









r

a

P



x

ix

i

m x

m a

P

  







z

iz

i

m z

m a

P

  







y

iy

i

m y

m a

P

  







Skalarne równania ruchu

Skalarne równania ruchu





Rzutowanie przyspieszenia na osie

Rzutowanie przyspieszenia na osie

normalną, styczną i binormalną:

normalną, styczną i binormalną:

2

v

m a

m

P









dv

m a

m

P

 









Wektor przyspieszenia całkowitego leży

Wektor przyspieszenia całkowitego leży

na płaszczyźnie ściśle stycznej do toru.

na płaszczyźnie ściśle stycznej do toru.

28

28

n

in

i

v

m a

m

P











t

it

i

dv

m a

m

P

dt

 





b

ib

i

m a

P







0

b

a



Pierwsze i drugie zadanie

Pierwsze i drugie zadanie

dynamiki

dynamiki





Pierwsze zadanie dynamiki:

Pierwsze zadanie dynamiki:

–– Dana jest masa i równania ruchu punktu

Dana jest masa i równania ruchu punktu

materialnego, należy wyznaczyć siły

materialnego, należy wyznaczyć siły

materialnego, należy wyznaczyć siły

materialnego, należy wyznaczyć siły

działające na ten punkt;

działające na ten punkt;





Drugie zadanie dynamiki:

Drugie zadanie dynamiki:

–– Dana jest masa i siły działające na punkt

Dana jest masa i siły działające na punkt

materialny, należy wyznaczyć równania

materialny, należy wyznaczyć równania

ruchu tego punktu.

ruchu tego punktu.

29

29

Pierwsze zadanie

Pierwsze zadanie

dynamiki

dynamiki





Równanie ruchu:

Równanie ruchu:





Składowe wypadkowej we współrzędnych

Składowe wypadkowej we współrzędnych

prostokątnych:

prostokątnych:

m

m

   

a

r

P



Składowe wypadkowej we współrzędnych

Składowe wypadkowej we współrzędnych

prostokątnych:

prostokątnych:





Wartość i kierunek wypadkowej:

Wartość i kierunek wypadkowej:

30

30

x

P

mx

 

y

P

my

 

x

P

mz

 

2

2

2

x

y

z

P

P

P

P







 

cos

,

x

P

P



P i



 

cos

,

y

P

P



P j







cos

,

z

P

P



P k



Drugie zadanie dynamiki

Drugie zadanie dynamiki





Ruch punktu pod działaniem siły:

Ruch punktu pod działaniem siły:

–– Stałej co do wartości i kierunku;

Stałej co do wartości i kierunku;

const



P

–– Zależnej od czasu;

Zależnej od czasu;

–– Zależnej od prędkości;

Zależnej od prędkości;

–– Zależnej od położenia.

Zależnej od położenia.

31

31

 

t



P

P

 

v



P

P

 

x



P

P

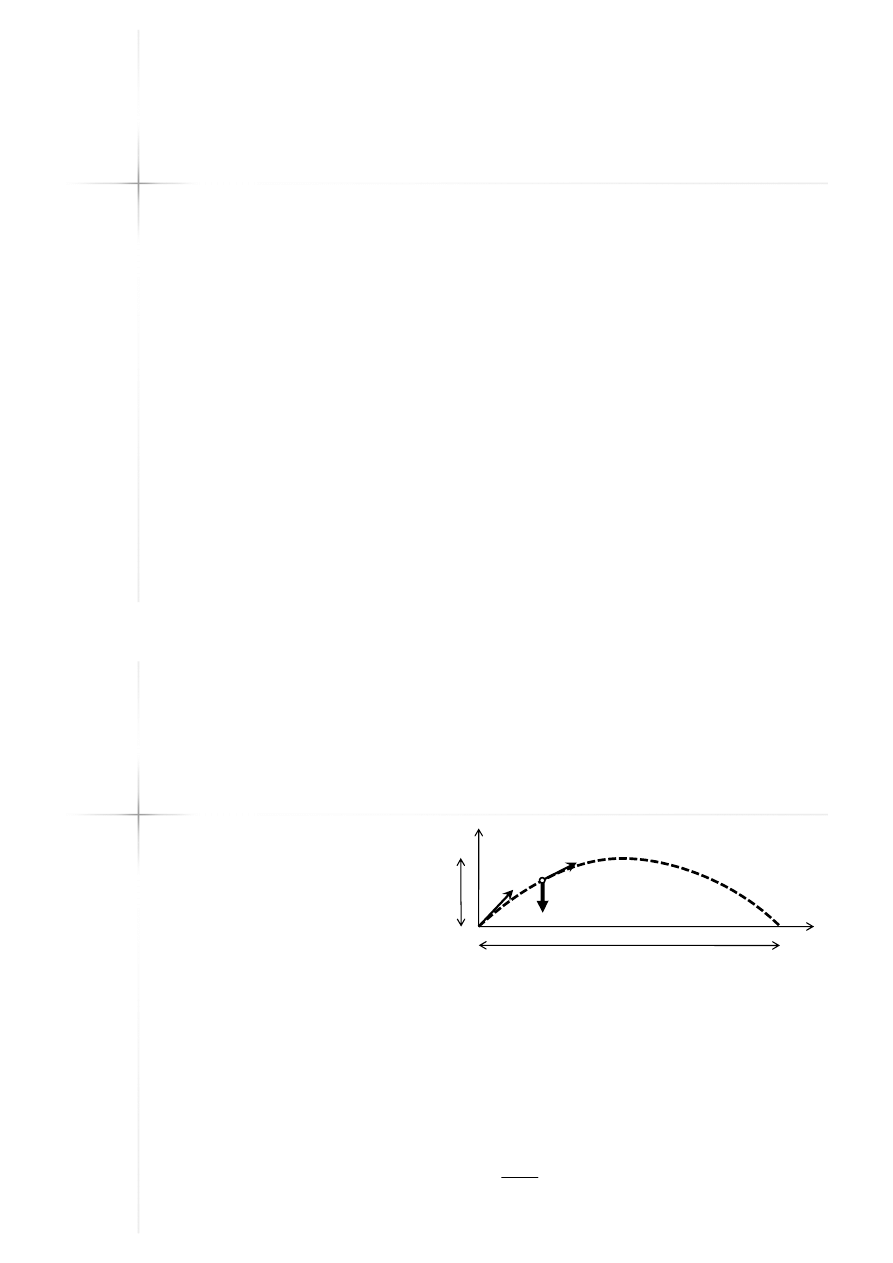
Ruch pod działaniem

Ruch pod działaniem

stałej siły

stałej siły

(1)

(1)





Rzut ukośny:

Rzut ukośny:





Równania ruchu:

Równania ruchu:

0

v

0

mx





my

mg

 



mg

v

max

x

max

y





Składowe przyspieszeń:

Składowe przyspieszeń:





Składowe prędkości:

Składowe prędkości:





Równania ruchu:

Równania ruchu:

32

32

 

2

y

v

t

gt

C

  

 

1

3

x t

C t

C





0

mx





my

mg

 



0

x

a



y

a

g

 

1

x

v

C



 

2

2

4

2

gt

y t

C t

C

 





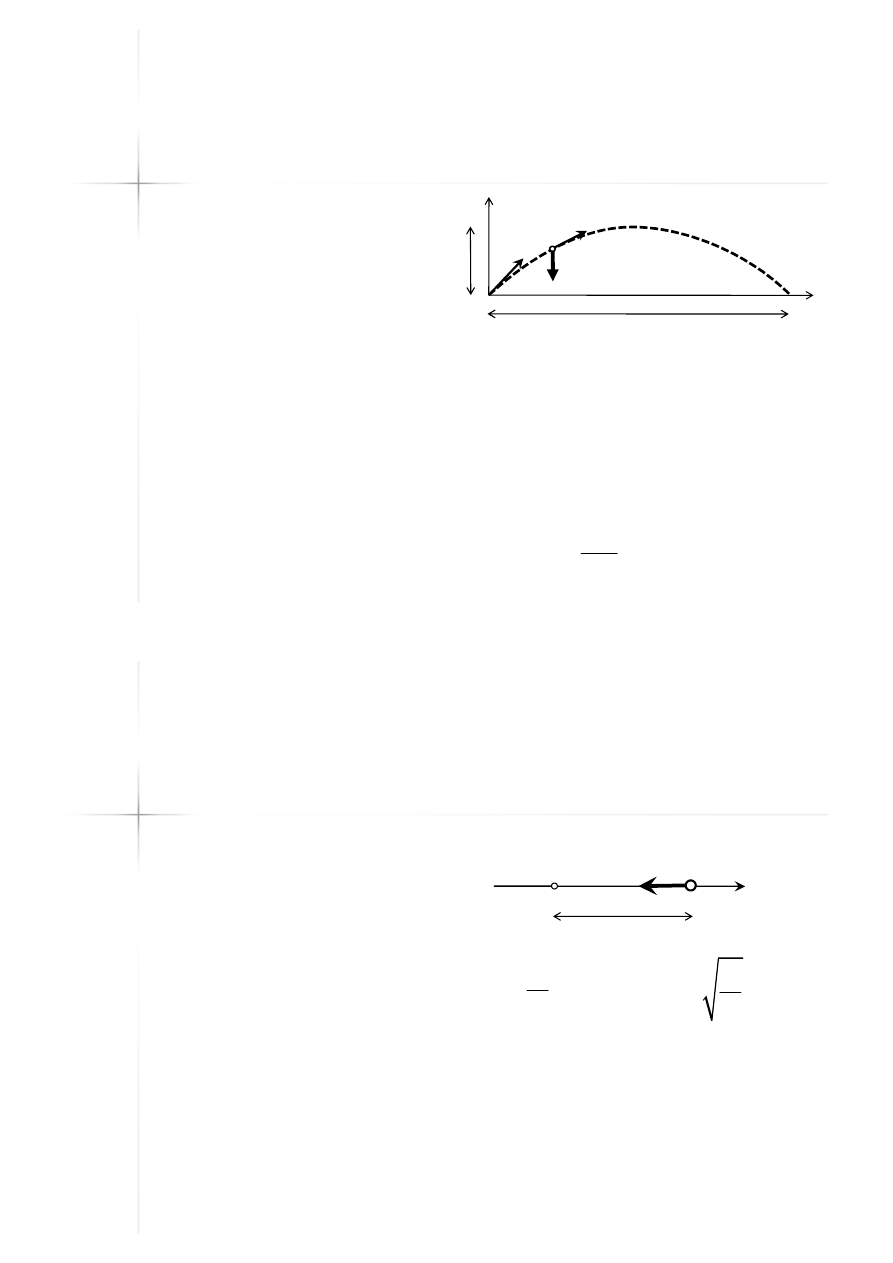
Ruch pod działaniem

Ruch pod działaniem

stałej siły

stałej siły

(2)

(2)





Warunki brzegowe:

Warunki brzegowe:

0

0

(

0)

cos

x

x

v t

v

v









0

0

(

0)

sin

y

y

v t

v

v









(

0)

0

x t





(

0)

0

y t





0

v

mg

v

max

y

max

x





Stałe całkowania:

Stałe całkowania:





Równania prędkości:

Równania prędkości:





Równania ruchu

Równania ruchu

33

33

1

0

cos

C

v





 

0

sin

v t

gt

v



  

(

0)

0

x t





(

0)

0

y t





2

0

sin

C

v





3

0

C



4

0

C



0

cos

x

v

v





 

0

cos

x t

v t





 

2

0

sin

2

gt

y t

v t



 



Ruch pod działaniem siły

Ruch pod działaniem siły

zależnej od położenia

zależnej od położenia





Drgania liniowe:

Drgania liniowe:





Różniczkowe

Różniczkowe

równanie ruchu:

równanie ruchu:

0

x

P

m

x

równanie ruchu:

równanie ruchu:





Rozwiązanie ogólne:

Rozwiązanie ogólne:

(Równanie ruchu harmonicznego prostego)

(Równanie ruchu harmonicznego prostego)

34

34

x

x

P

ma

mx

kx





 



0

k

x

x

m







k

m





1

2

sin

cos

x

C

t

C

t













0

sin

x

a

t

 





1

0

cos

C

a





2

0

sin

C

a





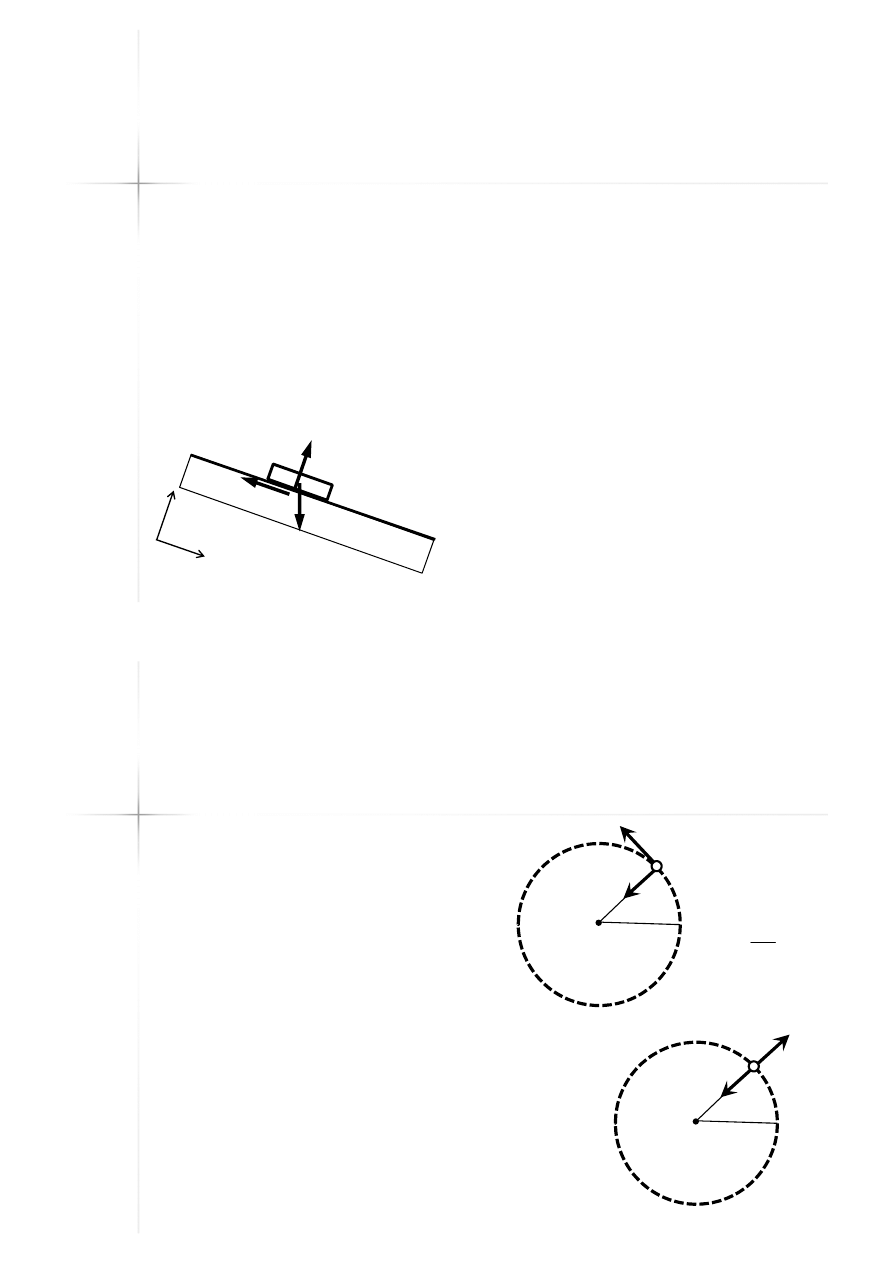
Ruch nieswobodnego

Ruch nieswobodnego

punktu materialnego

punktu materialnego





W przypadku, gdy warunki zewnętrzne

W przypadku, gdy warunki zewnętrzne

ograniczają swobodę ruchu, w

ograniczają swobodę ruchu, w

równaniu ruchu należy uwzględnić

równaniu ruchu należy uwzględnić

równaniu ruchu należy uwzględnić

równaniu ruchu należy uwzględnić

także siły bierne (reakcje więzów):

także siły bierne (reakcje więzów):

35

35

m

m



 

a

r

P

R



X

Y

N

m



G

g





T

N

x

x

m





a

P

0

y

y

m







a

P

Siła bezwładności

Siła bezwładności





Równanie ruchu:

Równanie ruchu:





Siła bezwładności

Siła bezwładności

((d’Alemberta

d’Alemberta):

):

m



P

a

0

m





P

a

0

r

v

n

a

0

t

a



const



v

2

n

v

a

r



m

((d’Alemberta

d’Alemberta):

):





Zasada

Zasada d’Alemberta

d’Alemberta::

–– Siły rzeczywiste działające na

Siły rzeczywiste działające na

punkt materialny równoważą

punkt materialny równoważą

się z siłą bezwładności tego

się z siłą bezwładności tego

punktu.

punktu.

36

36

m

 

B

a

0

 

P

B

0

r

P

n

a

r



m

B