MO

2. Ćwiczenie projektowe numer 2 – przykład 5

1

2. Ćwiczenie projektowe numer 2 – przykład 5

2.1. Ćwiczenie projektowe numer 2

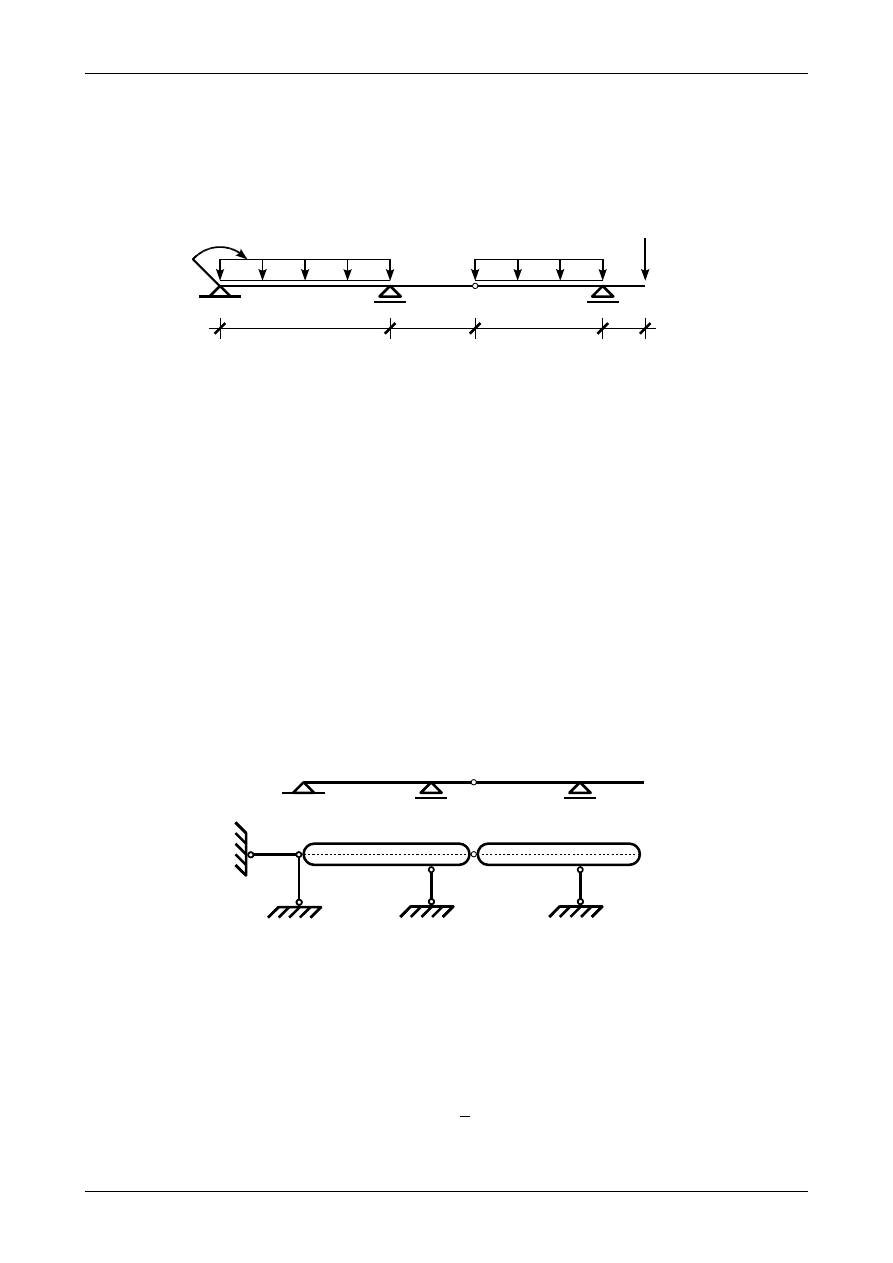
Narysować wykresy siły poprzecznej oraz momentu zginającego dla belki złożonej przedstawionej na 

rysunku 2.1.

A

B

C

D

E

8,0 kN∙m

16,0 kN/m

24,0 kN/m

12,0 kN

4,0

2,0

3,0

1,0

[m]

Rys. 2.1. Belka złożona

2.2. Analiza kinematyczna belki złożonej

Rysunek 2.2 przedstawia belkę złożoną taktowaną jako układ tarcz sztywnych. Warunek konieczny 

geometrycznej niezmienności ma postać

3

⋅

2

=

4

⋅

1



2

.

Warunek ten został spełniony. Tarcza sztywna numer I połączona jest z tarczą podporową za pomocą trzech 
prętów podporowych numer 1, 2 i 3, których kierunki nie przecinają się w jednym punkcie. Został więc 
spełniony warunek dostateczny geometrycznej niezmienności dla tej tarczy sztywnej. Jest więc ona geomet-
rycznie niezmienna i stanowi tarczę podporową dla tarczy sztywnej numer II. Tarcza sztywna numer II jest 
połączona z tarczą podporową  za pomocą przegubu rzeczywistego C oraz pręta podporowego numer  4. 
Przegub rzeczywisty C nie leży na kierunku pręta podporowego numer 4. Został więc spełniony warunek 
dostateczny   geometrycznej   niezmienności.   Można   stwierdzić,   że   belka   złożona   jest   geometrycznie   nie-
zmienna i statycznie wyznaczalna. 

4

1

2

3

C

I

II

A

B

C

D

E

Rys. 2.2. Belka złożona jako płaski układ tarcz sztywnych

2.3. Wyznaczenie reakcji podporowych

Rysunek 2.3 przedstawia założone zwroty reakcji podporowych. Wszystkie poziome reakcje wynoszą 

zero. Pionowa reakcja na podporze D ma wartość



M

C



CE



=−

V

D

⋅

3,024,0⋅3,0⋅

1

2

⋅

3,012,0⋅4,0=0

V

D

=

52,0 kN

.

Dr inż. Janusz Dębiński

BNS-I-Kalisz

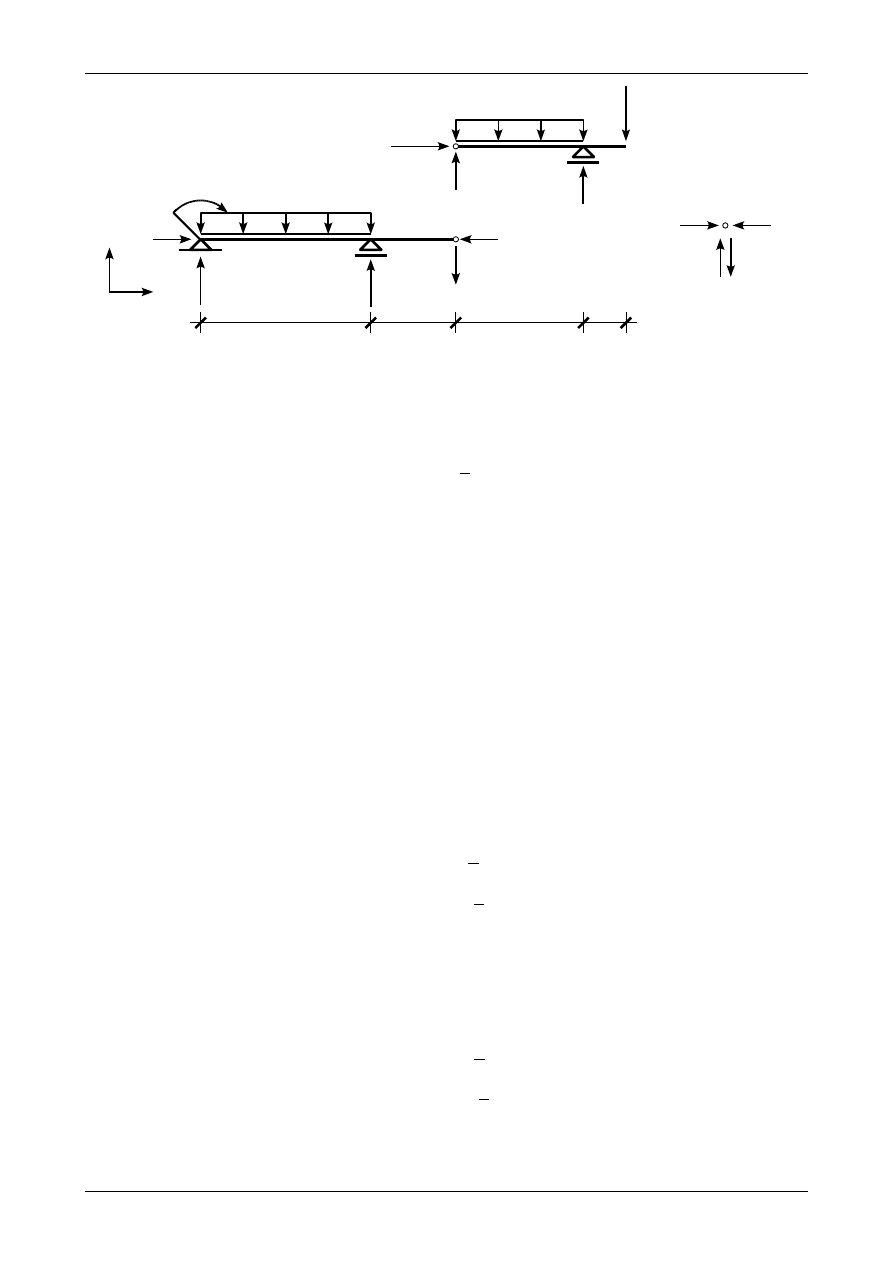
MO

2. Ćwiczenie projektowe numer 2 – przykład 5

2

A

B

C

8,0 kN∙m

16,0 kN/m

4,0

2,0

3,0

1,0

C

D

E

24,0 kN/m

12,0 kN

H

A

V

A

V

B

V

C

(AC)

H

C

(AC)

V

C

(CE)

H

C

(CE)

V

D

[m]

X

Y

C

V

C

(CE)

H

C

(CE)

H

C

(AC)

V

C

(AC)

Rys. 2.3. Założone zwroty reakcji podporowych

Pionowa reakcja na podporze C działająca na pręt CE ma wartość



M

D



CE



=

V

C



CE



⋅

3,0−24,0⋅3,0⋅

1

2

⋅

3,012,0⋅1,0=0

V

C



CE



=

32,0 kN

.

Sprawdzenie obliczeń



Y



CE



=

V

C



CE





V

D

−

24,0⋅3,0−12,0=32,052,0−84,0=0

.

Pionowa reakcja na podporze C działająca na pręt AC ma wartość

V

C



AC



=

32,0 kN

.

Pionowa reakcja na podporze A ma wartość



M

B



AC



=

V

A

⋅

4,08,0−16,0⋅4,0⋅

1
2

⋅

4,0V

C



AC



⋅

2,0=0

V

A

⋅

4,08,0−16,0⋅4,0⋅

1
2

⋅

4,032,0⋅2,0=0

V

A

=

14,0 kN

.

Pionowa reakcja na podporze B ma wartość



M

A



AC



=−

V

B

⋅

4,08,016,0⋅4,0⋅

1

2

⋅

4,0V

C



AC



⋅

6,0=0

−

V

B

⋅

4,08,016,0⋅4,0⋅

1

2

⋅

4,032,0⋅6,0=0

V

B

=

82,0 kN

.

Dr inż. Janusz Dębiński

BNS-I-Kalisz

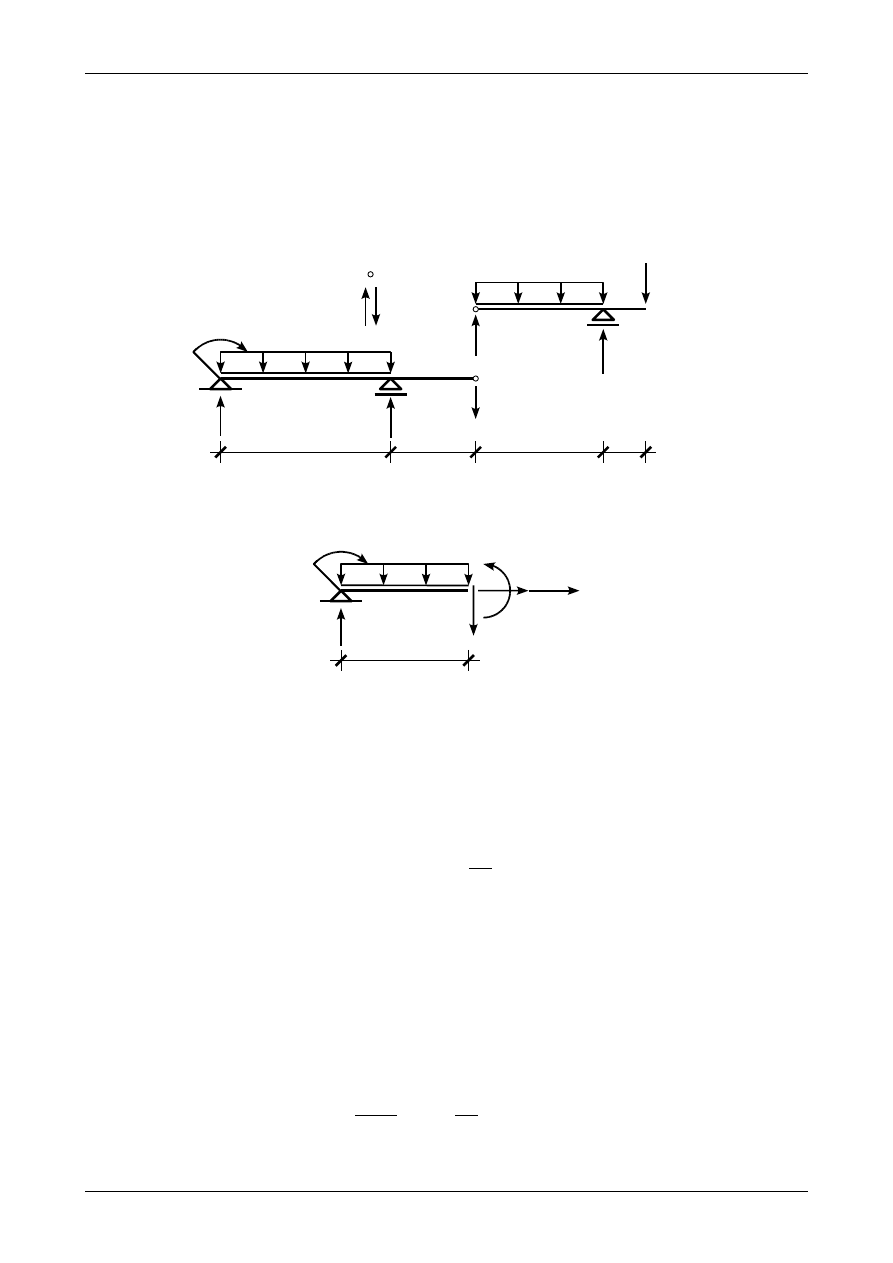
MO

2. Ćwiczenie projektowe numer 2 – przykład 5

3

Sprawdzenie obliczeń



Y



AC



=

V

A



V

B

−

V

C



AC



−

16,0⋅4,0=14,082,0−32,0−64,0=0

.

Rysunek 2.4 przedstawia prawidłowe wartości i zwroty reakcji podporowych.

A

B

C

8,0 kN∙m

16,0 kN/m

4,0

2,0

3,0

1,0

C

D

E

24,0 kN/m

12,0 kN

[m]

52,0 kN

32,0 kN

32,0 kN

82,0 kN

14,0 kN

C

32,0 kN

32,0 kN

Rys. 2.4. Prawidłowe wartości i zwroty reakcji podporowych

N(x)

T(x)

M(x)

A

8,0 kN∙m

16,0 kN/m

x

14,0 kN

X

Rys. 2.5. Siły przekrojowe w przedziale AB

2.4. Siły przekrojowe w przedziale AB

Rysunek   2.5  przedstawia   równowagę   odciętej   części   belki   w  przedziale   AB.   Funkcja   obciążenia 

ciągłego ma postać

q



x



=

16,0

kN

m

.

Funkcja siły poprzecznej ma postać

T



x



=

14,0−16,0⋅x

.

Równanie różniczkowe równowagi ma postać

dT



x



dx

=−

16,0

kN

m

=−

q



x



.

Dr inż. Janusz Dębiński

BNS-I-Kalisz

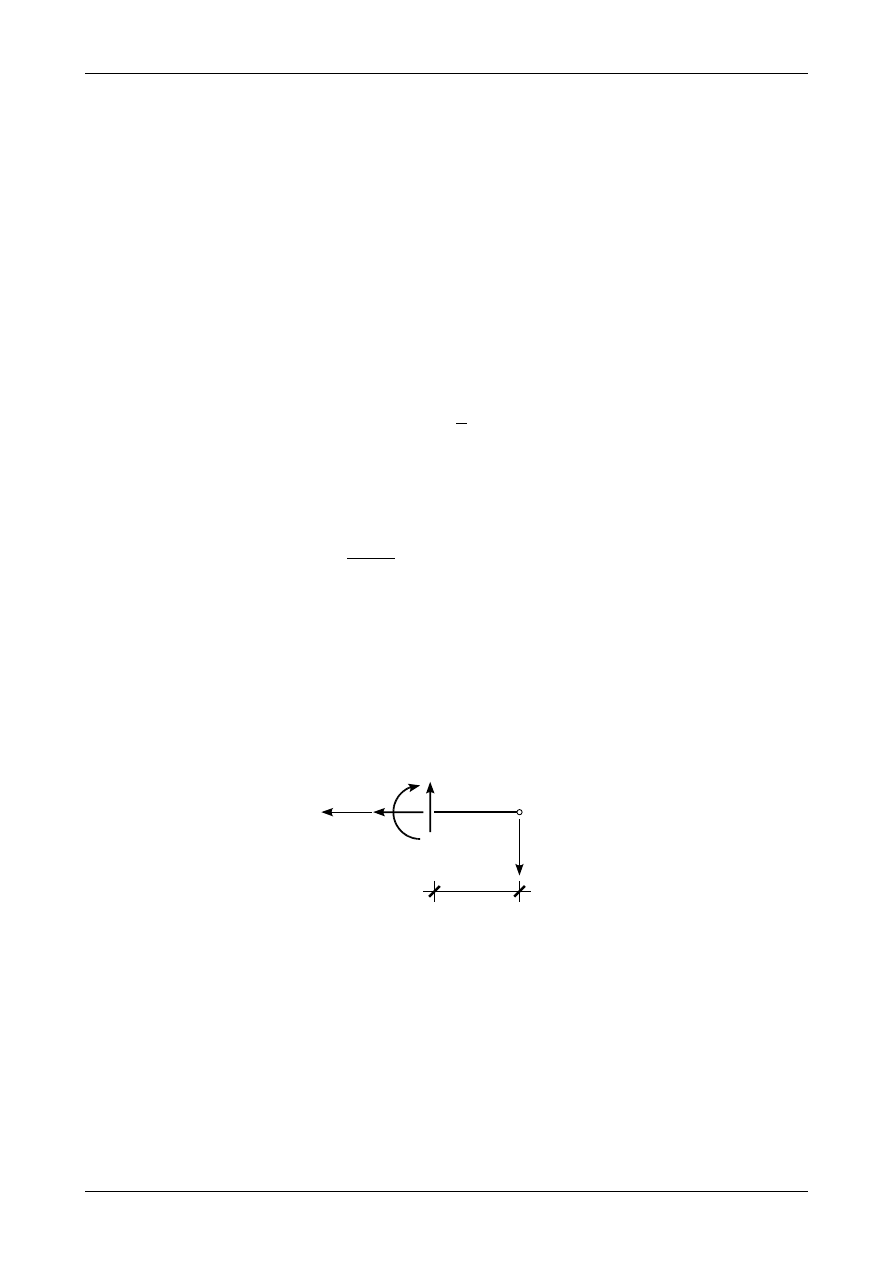
MO

2. Ćwiczenie projektowe numer 2 – przykład 5

4

Wartości siły poprzecznej w punktach charakterystycznych wynoszą

T



0,0



=

14,0 kN

T



4,0



=

14,0−16,0⋅4,0=−50,0 kN

.

Miejsce zerowe funkcji siły poprzecznej znajduje się w punkcie

14,0−16,0⋅x

0

=

0

x

0

=

0,875 m

.

Funkcja momentu zginającego ma postać

M



x



=

14,0⋅x8,0−16,0⋅x⋅

x

2

=−

8,0⋅x

2



14,0⋅x8,0

.

Równanie różniczkowe równowagi ma postać

dM



x



dx

=

14,0−16,0⋅x=T



x



.

Wartości momentu zginającego w punktach charakterystycznych wynoszą

M



0,0



=

8,0kN⋅m

M



0,875



=−

8,0⋅0,875

2



14,0⋅0,8758,0=14,13 kN⋅m

M



4,0



=−

8,0⋅4,0

2



14,0⋅4,08,0=−64,0 kN⋅m

.

N(x)

T(x)

M(x)

C

x

32,0 kN

X

Rys. 2.6. Siły przekrojowe w przedziale BC

2.5. Siły przekrojowe w przedziale BC

Rysunek 2.6 przedstawia równowagę odciętej części belki w przedziale BC. Funkcja siły poprzecznej 

ma postać

T



x



=

32,0 kN

.

Funkcja momentu zginającego ma postać

Dr inż. Janusz Dębiński

BNS-I-Kalisz

MO

2. Ćwiczenie projektowe numer 2 – przykład 5

5

M



x



=−

32,0⋅x

.

Równanie różniczkowe równowagi ma postać

dM



x



dx

=−

32,0 kN=−T



x



.

Wartości momentu zginającego w punktach charakterystycznych wynoszą

M



0,0



=

0,0kN⋅m

M



2,0



=−

32,0⋅2,0=−64,0 kN⋅m

.

2.6. Siły przekrojowe w przedziale CD

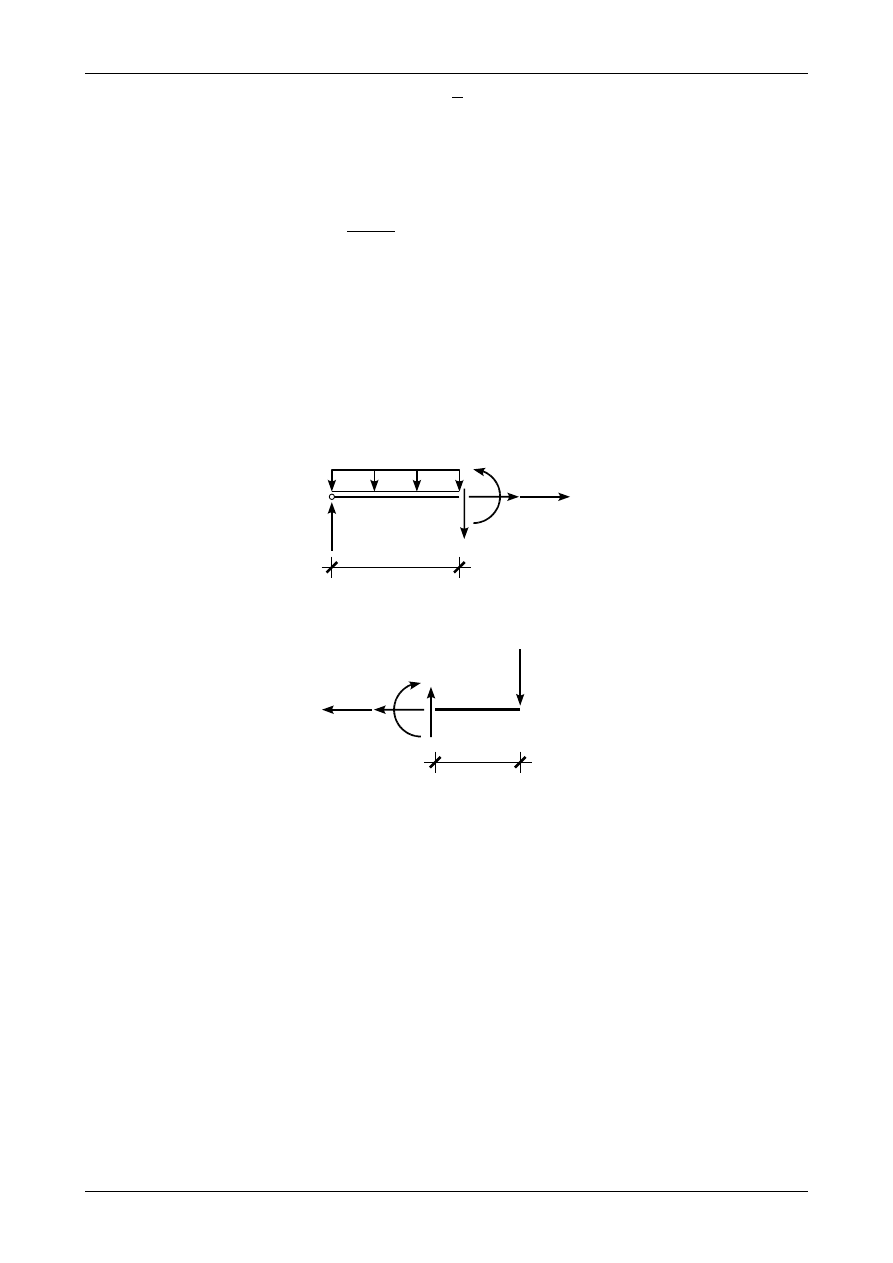
Rysunek   2.7  przedstawia   równowagę   odciętej   części   belki   w  przedziale   CD.   Funkcja   obciążenia 

ciągłego ma postać

q



x



=

24,0

kN

m

.

Funkcja siły poprzecznej ma postać

T



x



=

32,0−24,0⋅x

.

Równanie różniczkowe równowagi ma postać

dT



x



dx

=−

24,0

kN

m

=−

q



x



.

Wartości siły poprzecznej w punktach charakterystycznych wynoszą

T



0,0



=

32,0 kN

T



4,0



=

32,0−24,0⋅3,0=−40,0 kN

.

Miejsce zerowe funkcji siły poprzecznej znajduje się w punkcie

32,0−24,0⋅x

0

=

0

x

0

=

1,333 m

.

Funkcja momentu zginającego ma postać

Dr inż. Janusz Dębiński

BNS-I-Kalisz

MO

2. Ćwiczenie projektowe numer 2 – przykład 5

6

M



x



=

32,0⋅x−24,0⋅x⋅

x
2

=−

12,0⋅x

2



32,0⋅x

.

Równanie różniczkowe równowagi ma postać

dM



x



dx

=

32,0−24,0⋅x=T



x



.

Wartości momentu zginającego w punktach charakterystycznych wynoszą

M



0,0



=

0,0 kN⋅m

M



1,333



=−

12,0⋅1,333

2



32,0⋅1,333=21,33 kN⋅m

M



3,0



=−

12,0⋅3,0

2



32,0⋅3,0=−12,0 kN⋅m

.

x

C

24,0 kN/m

32,0 kN

N(x)

T(x)

M(x)

X

Rys. 2.7. Siły przekrojowe w przedziale CD

N(x)

T(x)

M(x)

E

x

12,0 kN

X

Rys. 2.8. Siły przekrojowe w przedziale DE

2.7. Siły przekrojowe w przedziale DE

Rysunek 2.8 przedstawia równowagę odciętej części belki w przedziale DE. Funkcja siły poprzecznej 

ma postać

T



x



=

12,0 kN

.

Funkcja momentu zginającego ma postać

M



x



=−

12,0⋅x

.

Równanie różniczkowe równowagi ma postać

Dr inż. Janusz Dębiński

BNS-I-Kalisz

MO

2. Ćwiczenie projektowe numer 2 – przykład 5

7

dM



x



dx

=−

12,0 kN=−T



x



.

Wartości momentu zginającego w punktach charakterystycznych wynoszą

M



0,0



=

0,0kN⋅m

M



1,0



=−

12,0⋅1,0=−12,0 kN⋅m

.

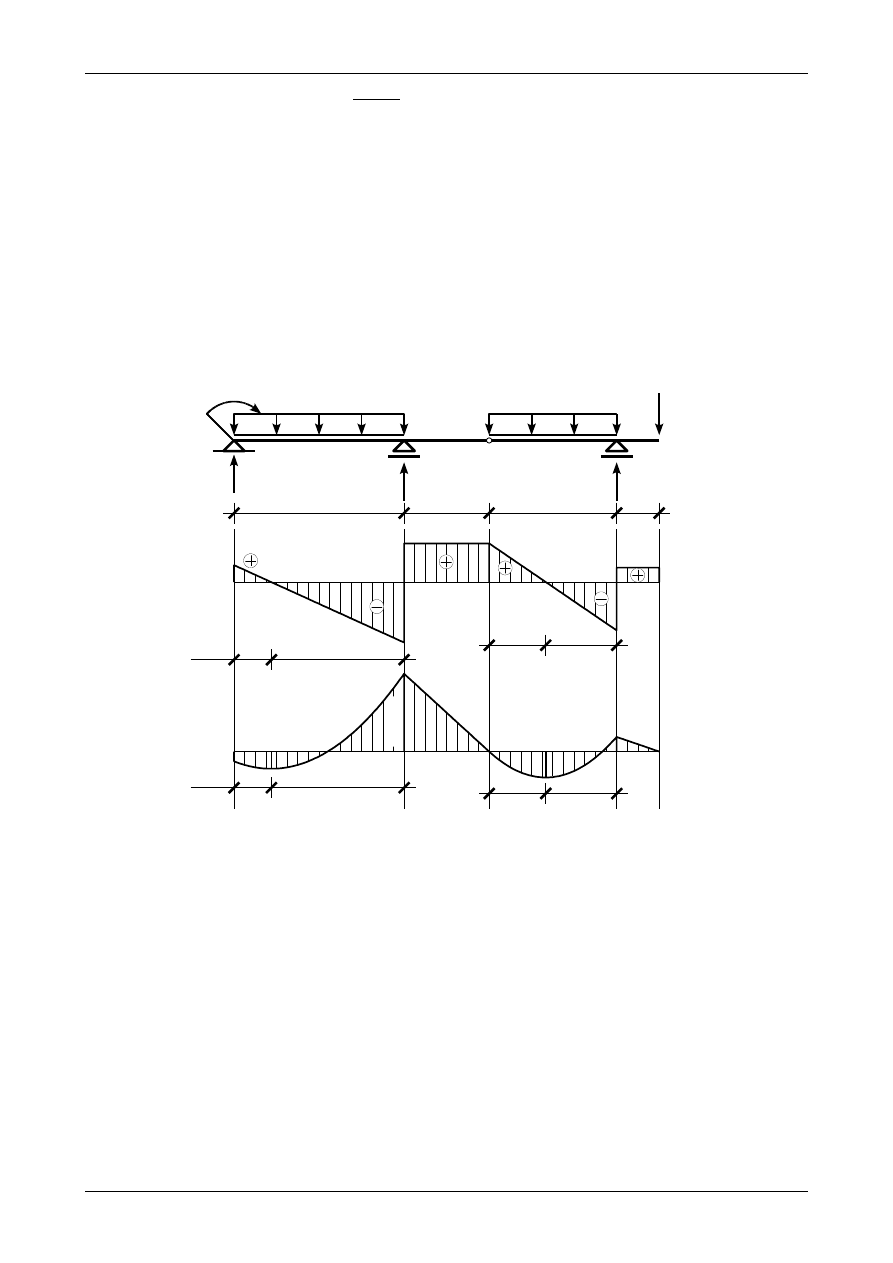
2.8. Wykresy sił przekrojowych w belce złożonej

Rysunek 2.9 przedstawia wykresy siły poprzecznej oraz momentu zginającego w belce złożonej. 

A

B

C

D

E

8,0 kN∙m

16,0 kN/m

24,0 kN/m

12,0 kN

4,0

2,0

3,0

1,0

[m]

14,0 kN

82,0 kN

52,0 kN

T(x) [kN]

M(x) [kN∙m]

14

,0

50

,0

32,0

40

,0

12,0

8,

0

0,

0

0,

0

1

2,

0

0,875

3,125

0,875

3,125

1,333

1,667

1,333

1,667

14

,1

3

2

1,

3

3

64

,0

Rys. 2.9. Wykresy sił przekrojowych w belce złożonej

Dr inż. Janusz Dębiński

BNS-I-Kalisz