Politechnika Rzeszowska
Katedra Metrologii i Systemów Diagnostycznych
Metrologia – laboratorium
Grupa
Data
Nr ćwiczenia
Opracowanie danych pomiarowych
Working out of measurement data
7
Student
……………………………
Ocena
I. Cel
ćwiczenia.
Celem
ćwiczenia jest poznanie zasad statystycznego opracowania serii niezależnych wyników
pomiarów oraz podstawowych problemów metrologicznych występujących podczas pomiarów
w warunkach istnienia zakłóceń losowych.
II. Zagadnienia.
1. Rozkłady prawdopodobieństwa zmiennej losowej: jednostajny, normalny (Gaussa), Studenta.
2. Parametry
rozkładów zmiennej losowej: wartość oczekiwana, wariancja, odchylenie standardowe
wartości oczekiwanej.
3. Estymatory parametrów rozkładów zmiennej losowej: średnia arytmetyczna, wariancja
eksperymentalna, odchylenie standardowe eksperymentalne średniej arytmetycznej.
III. Literatura.
1.
Chwaleba A.: Metrologia elektryczna, Warszawa: WNT, 2010.
2. Tumański S.: Technika pomiarowa, Warszawa: WNT, 2007.
3. Parchański J.: Miernictwo elektryczne i elektroniczne, Warszawa: WSiP, 1997.
4.
Taylor J. R.: Wstęp do analizy błędu pomiarowego. Warszawa: PWN, 1999.
5. Wyrażanie niepewności pomiaru – Przewodnik. Warszawa: Wyd. GUM, 1999.
IV. Efekty
kształcenia.
Po
zakończeniu ćwiczenia 7 student:
- definiuje menzurand
- szkicuje schemat układu pomiarowego
- przygotowuje multimetr cyfrowy do pomiarów
- odczytuje wskazanie przyrządu cyfrowego
- oblicza estymatory wartości oczekiwanej oraz odchylenia standardowego
- wyznacza graniczne wartości błędu przypadkowego
- wyznacza graniczne wartości błędu instrumentalnego
- zapisuje i interpretuje wynik pomiaru
- szacuje wartość mocy wydzielanej w badanym rezystorze
- wykonuje proste obliczenia w notacji inżynierskiej
Wykaz używanych przyrządów i ich podstawowe parametry metrologiczne.
Przyrząd Zakresy
Dokładność Inne
parametry
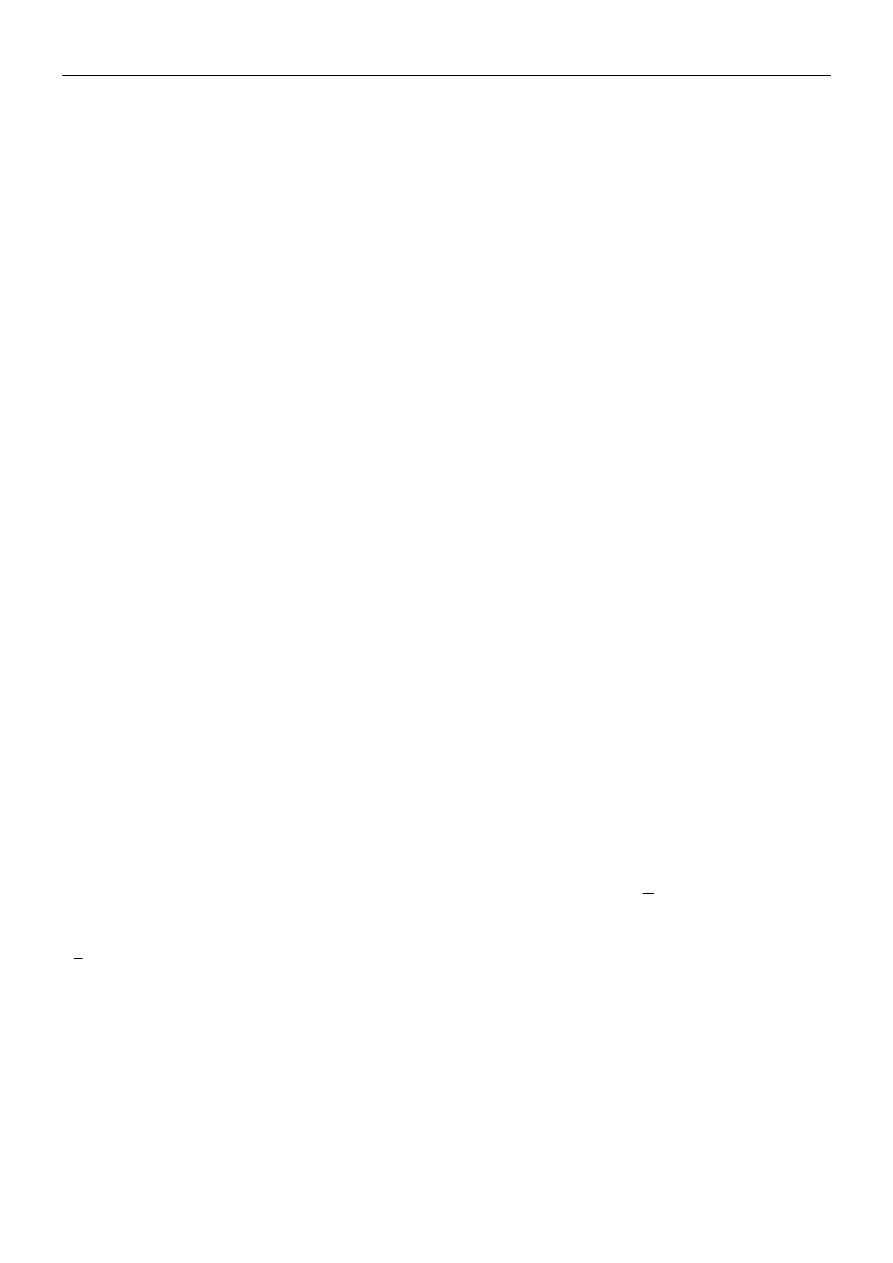
Katedra Metrologii i Systemów Diagnostycznych
Metrologia – laboratorium. EN-DI-1, r. ak. 2012/13
ćw. 7 / str. 2
V. Program
ćwiczenia.
1. Zadanie
pomiarowe.
Obiektem badanym (DUT) jest rezystor. Poznać wartość rezystancji R opornika w stanie
bezprądowym (I = 0), pozyskując informację o przedmiocie poznania za pomocą omomierza cyfrowego –
metodą bezpośrednią. Pomiar odbywa się w warunkach istnienia zakłóceń losowych, objawiających się
rozrzutem kolejnych wskazywanych wartości rezystancji.
W celu zasymulowania oddziaływania zakłóceń na badany opornik, pomiary wykonuje się dla n
rezystorów z tej samej partii produkcyjnej, przyjmując i-te wskazanie jako kolejną wartość R
i
. Przyjmuje
się, że n-elementowa próba rezystorów wybrana jest z populacji o normalnym rozkładzie rezystancji.
Oszacować wartość mocy P wydzielanej na obiekcie badanym i zastanowić się, czy prąd
pomiarowy I omomierza nie powoduje efektu samopodgrzewania się badanego opornika.
2. Schemat
układu pomiarowego (zaznaczyć: co widzę, co mierzę, co chcę poznać).
Rys. 1. Pomiar wartości rezystancji R omomierzem cyfrowym w warunkach zakłóceń losowych.
Wybrana funkcja pomiarowa multimetru:
Menzurand: przedmiotem poznania jest
Czy występują błędy o charakterze losowym?
TAK / NIE
Model matematyczny pojedynczego wyniku pomiaru:
∑
−
−
−
=
met
instr
rand
∆
∆
∆
i
R
R
3.
Wyniki pomiarów i obliczeń.
Obliczenia
należy wykonać wykorzystując program-projekt Statystyka (działa w środowisku
Windows tylko w wersji 32-bitowej). Podczas wprowadzania danych zaobserwować tworzenie się
histogramu (rozkładu wskazywanych wartości). Do tabeli zapisywać: wartość współczynnika
rozszerzenia
p
t dla rozkładu Studenta, wartość średnią arytmetyczną R , wartości odchylenia
standardowego eksperymentalnego: pojedynczego wskazania
R
s
oraz średniej arytmetycznej wskazań
R
s . Przed rozpoczęciem i po zakończeniu pomiarów sprawdzić, czy rezystancja przewodów ma wpływ
na wartość wskazywanej rezystancji. Jeżeli tak, należy skorygować obliczoną wartość średnią.
WSKAZANIE
Zakres pomiarowy omomierza:
=
n
R
Czy przy zwartych zaciskach wyświetlacz wskazuje zero?
TAK / NIE
Wartości wskazywanych rezystancji:
R
1
,
R
2
, ...,
R
i
, ...
Rozdzielczość pomiaru rezystancji:
=
RES
Liczba cyfr znaczących wskazania:
Katedra Metrologii i Systemów Diagnostycznych
Metrologia – laboratorium. EN-DI-1, r. ak. 2012/13
ćw. 7 / str. 3
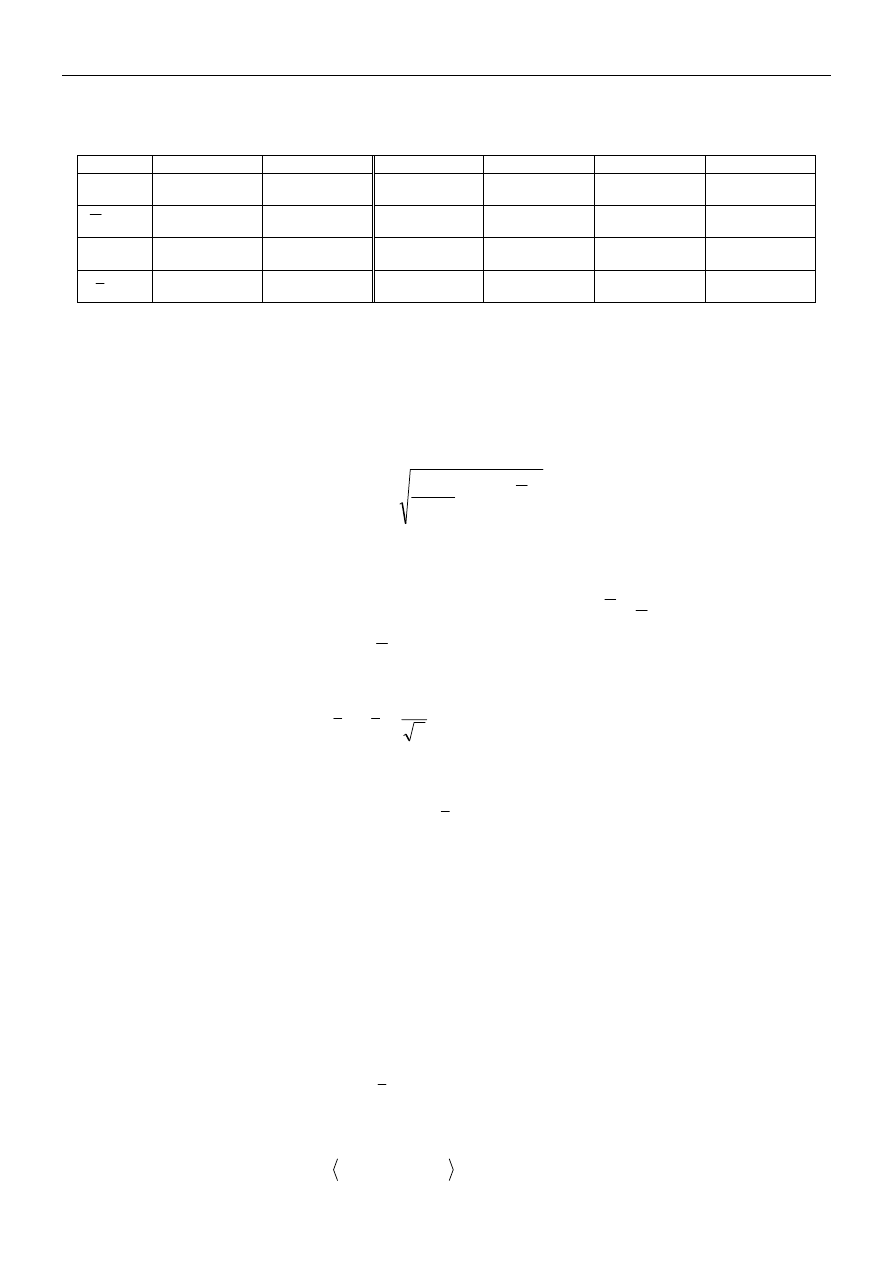
Tabela 1. Wartości: współczynnika rozszerzenia dla rozkładu Studenta (dla prawdopodobieństwa rozszerzenia
p = 0,9973), średniej arytmetycznej, odchylenia standardowego pojedynczego wskazania oraz średniej arytmetycznej
wskazań – w funkcji liczności próby n.
n
5 10 20 30 40 50
p
t
R ,
R
s
,
R
s ,
BŁĄD PRZYPADKOWY
Przypadek 1
Estymator wartości oczekiwanej – pojedyncze wskazanie:
=
≈
i
R
R
wsk
Błąd przypadkowy pomiaru:
wsk
rand
R
R
i
−
=
∆
* Estymator odchylenia standardowego błędu dla pojedynczego wskazania:
(
)
(
)
=
−
−
=
≈
∑
=
n
i
i
R
R
R
R
n
s
1
2
1
1
σ
Przypadek 2
Estymator wartości oczekiwanej – średnia arytmetyczna wskazań:
=
=
≈
∑
=
n
i
i
R
n
R
R
1
1
wsk
Błąd przypadkowy pomiaru:
wsk
rand
R
R
−
=
∆
* Estymator odchylenia standardowego błędu dla średniej arytmetycznej wskazań:
=
=
≈
n
s
s
R
R
R
σ
Odchylenie standardowe eksperymentalne błędu dla średniej arytmetycznej nazywane jest niepewnością
standardową wyznaczoną metodą typu A (
R
s
u
=
A
).
Charakter rozkładu błędów przypadkowych (w populacji błędów): normalny (?)
Ze względu na fakt, iż odchylenie standardowe
R
σ rozkładu błędów nie jest znane, normalny rozkład
błędów reprezentowany jest w dalszych obliczeniach przez rozkład Studenta.
* Maksymalna (
p > 0,99) wartość błędu przypadkowego pojedynczego pomiaru:
=
⋅
±
=
R
p
s
t
max
∆
* Maksymalna (
p > 0,99) wartość błędu przypadkowego wartości średniej:
=
⋅
±
=
R
p
s
t
max
∆
Przedział wartości błędu przypadkowego dla pojedynczego pomiaru / dla wartości średniej:
∈
+
−
∈
rand
max
max
rand
;
∆
∆
∆
∆
,
Katedra Metrologii i Systemów Diagnostycznych
Metrologia – laboratorium. EN-DI-1, r. ak. 2012/13
ćw. 7 / str. 4
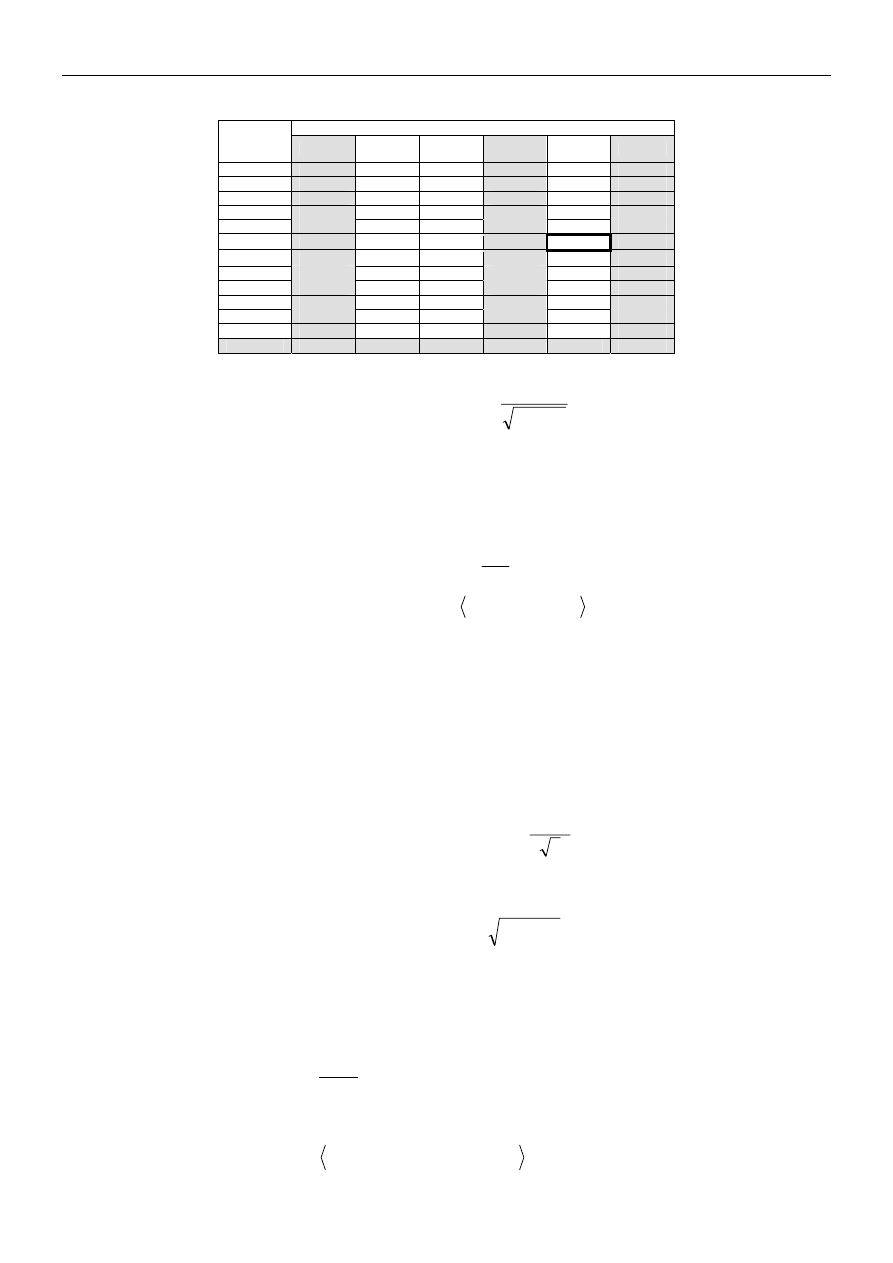
Tabela 2. Wybrane współczynniki rozszerzenia t
p
dla różnych prawdopodobieństw rozszerzenia p i liczności próby n.
Prawdopodobieństwo rozszerzenia p
Liczba
pomiarów
n
0,6827 0,90 0,95 0,9545 0,99 0,9973
2
1,84 6,31 12,71
13,97 63,66 235,8
3
1,32 2,92 4,30 4,53 9,92 19,21
4
1,20 2,35 3,18 3,31 5,84 9,22
5
1,14 2,13 2,78 2,87 4,60 6,62
10
1,06 1,83 2,26 2,32 3,25 4,09
15 1,04 1,76 2,14 2,20
2,98
3,64
20
1,03 1,73 2,09 2,14 2,86 3,45
25
1,02 1,71 2,06 2,11 2,80 3,33
30
1,02 1,70 2,04 2,09 2,76 3,27
40
1,01 1,69 2,02 2,07 2,72 3,20
50
1,01 1,68 2,01 2,05 2,68 3,16
100
1,00 1,66 1,98 2,02 2,63 3,08
∞ 1,00
1,64
1,96
2,00
2,58
3,00
* Względna niepewność wyznaczenia
max
∆
:
(
)
(
)
=
−
=
1
2
1
max
n
U
∆
rel
BŁĄD SYSTEMATYCZNY INSTRUMENTALNY
Błąd instrumentalny pomiaru:
m
wsk
instr
R
R
−
=
∆
Deklaracja dokładności omomierza:
=
+ dgt
rdg
%
k
m
* Wartość MDB pomiaru rezystancji:
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
±
=
RES
k
R
m
MPE
wsk
100
Przedział wartości błędu instrumentalnego:
∈
+
−
∈
instr
instr
;
∆
∆
,
MPE
MPE
Charakter rozkładu błędów systematycznych (w populacji błędów, w granicach
±MPE): prostokątny (?)
Traktując błąd systematyczny instrumentalny jako zmienną losową, która może przyjmować dowolną
wartość w granicach
±MPE z jednakowym prawdopodobieństwem, można obliczyć wartość odchylenia
standardowego błędu, tzw. niepewność standardową wyznaczoną metodą typu B.
* Niepewność standardowa wyznaczona metodą typu B:
=
⋅
≈
=
MPE
MPE
u
6
,
0
3
B
GRANICZNA WARTOŚĆ BŁĘDU POMIARU
* Niepewność standardowa złożona (Combined):
=
+
=
2
B
A
C
u
u
u
2
Wynikowy rozkład błędów:
płasko-normalny
Ze względu na brak informacji o kształcie wypadkowego rozkładu błędów przypadkowych
i systematycznych, będącego efektem złożenia rozkładu normalnego (Studenta) z rozkładem
jednostajnym, nie jest możliwe łatwe wyznaczenie niepewności rozszerzonej
p
U dla założonego
prawdopodobieństwa rozszerzenia p = 0,99, w celu wyznaczenia przedziału rozszerzenia.
Niepewność rozszerzona
:
C
99
0
99
0
u
k
U
,
,
⋅
=
Przedział rozszerzenia
:
99
0
wsk
99
0
wsk
m
;
,
,
U
R
U
R
R
+
−
∈
Katedra Metrologii i Systemów Diagnostycznych
Metrologia – laboratorium. EN-DI-1, r. ak. 2012/13
ćw. 7 / str. 5
Graniczna wartość błędu pomiaru rezystancji – wyznaczona metodą najgorszego rozłożenia (WDM –
W
orst Distribution Method):
(
)
=
+
±
=
MPE
max
gr
∆
∆
Która ze składowych błędu jest dominująca?
składowa losowa / składowa instrumentalna
Przedział wartości błędu pomiaru:
∈
+
−
∈
∆
∆
∆
∆
,
gr
gr
;
Przedział wartości mierzonej rezystancji:
∈
+
−
∈
m
gr
wsk
gr
wsk
m
R
R
R
R
,
;
∆
∆
BŁĄD SYSTEMATYCZNY METODY POMIAROWEJ
Błąd metody pomiaru rezystancji:
R
R
−
=
m
met
∆
Wartość prądu w obwodzie omomierza:
=
I
* Oszacowana wartość mocy wydzielanej w oporniku:
=
⋅
=
2
wsk
I
R
P
Czy moc wydzielona w oporniku może spowodować zmianę wartości menzurandu? Czy konieczne jest
wprowadzenie poprawki ze względu na błąd metody pomiarowej?
Wynik pomiaru
:
∈
+
=
R
p
R
R
,
met
m
Interpretacja metrologiczna wyniku pomiaru:
Przedział wartości
〈 ; 〉 ...... obejmuje
punkt
R, będący prawdziwą wartością zdefiniowanego menzurandu, z prawdopodobieństwem bliskim
jedności.
{
}
{
}
1
......
;
1
;
≈
∈
≈
∈
R
R
R
R
Pr
,
Pr
g
d
Naszkicować sytuację pomiarową, uwzględniając R
i
, R
wsk
, R
m
, R.
VI. Podsumowanie.
..... , .....