Przekształcenia geometryczne 2D

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Przekształcenia geometryczne 2D

Przekształcenia 2D (przekształcenia na płaszczyźnie)

•

przesunięcie równoległe (translacja)

Elementy grafiki komputerowej

•

skalowanie

•

obrót (rotacja)

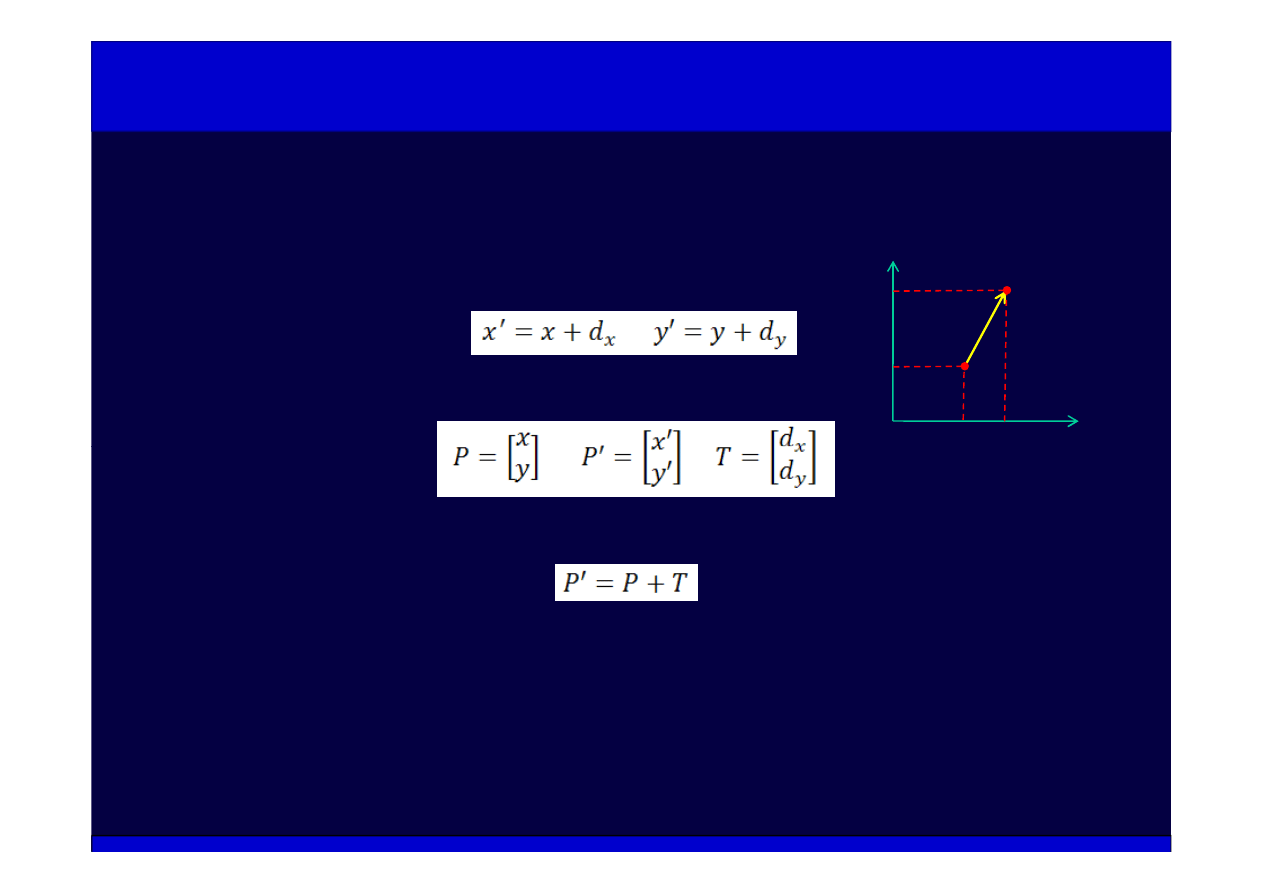
Przesunięcie równoległe

Współrzędne przesuniętego punktu

P

’ zdefiniowane są jako:

Definiujemy 3 wektory (macierze kolumnowe)

Przekształcenia geometryczne 2D

x

y

P(x, y)

P’(x’, y’)

Elementy grafiki komputerowej

W zapisie macierzowym mamy

Uwaga: powyższe równanie stosuje się do każdego punktu obiektu. Efekt: czasochłonne obliczenia!
W praktyce np. dla odcinków przesuwamy tylko ich końce i wyświetlamy odcinek łączący nowe końce.

x

Skalowanie względem początku układu współrzędnych

Współrzędne przeskalowanego punktu

P

’ zdefiniowane są jako:

W zapisie macierzowym mamy

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Gdzie

S

jest macierzą skalowania

Jeżeli

s

x

i

s

y

< 1 (>1), to po przeskalowaniu punkt znajduje się bliżej (dalej) początku układu

współrzędnych

Jeżeli

s

x

=

s

y

(

s

x

≠

s

y

), to skalowanie nazywamy jednorodnym (niejednorodnym)

Skalowanie względem dowolnego punktu – kroki: 1. przesunięcie do początku układu, 2. skalowanie,
3. przesunięcie do pozycji wyjściowej

Obrót o zadany kąt wokół początku układu współrzędnych

Współrzędne nowego punktu

P

’ zdefiniowane są jako:

W zapisie macierzowym mamy

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Gdzie

R

jest macierzą obrotu

Kąty dodatnie mierzone są w kierunku przeciwnym do ruchu wskazówek zegara (od osi x do osi y).
Dla kątów ujemnych (mierzonych zgodnie z ruchem wskazówek zegara) w równaniach stosuje się
tożsamości:

Obrót wokół dowolnego punktu – kroki: 1. przesunięcie do początku układu, 2. obrót, 3. przesunięcie
do pozycji wyjściowej

Współrzędne jednorodne i macierzowa reprezentacja przekształceń 2D

Reprezentacja macierzowa przekształceń przesunięcia, skalowania i obrotu

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Problem : jednolity zapis wszystkich trzech przekształceń (ułatwienie składania przekształceń)

Rozwiązanie: zastosowanie tzw. współrzędnych jednorodnych

Współrzędne jednorodne (1)

Punkt we współrzędnych jednorodnych reprezentowany jest przez trójkę liczb

Dwa zestawy współrzędnych jednorodnych

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Reprezentują ten sam punkt wtedy i tylko wtedy, gdy jeden jest wielokrotnością drugiego

Wniosek: każdy punkt ma wiele różnych reprezentacji we współrzędnych jednorodnych

Przynajmniej jedna ze współrzędnych jednorodnych musi być różna od zera. Reprezentacja
(0, 0, 0) jest niedopuszczalna

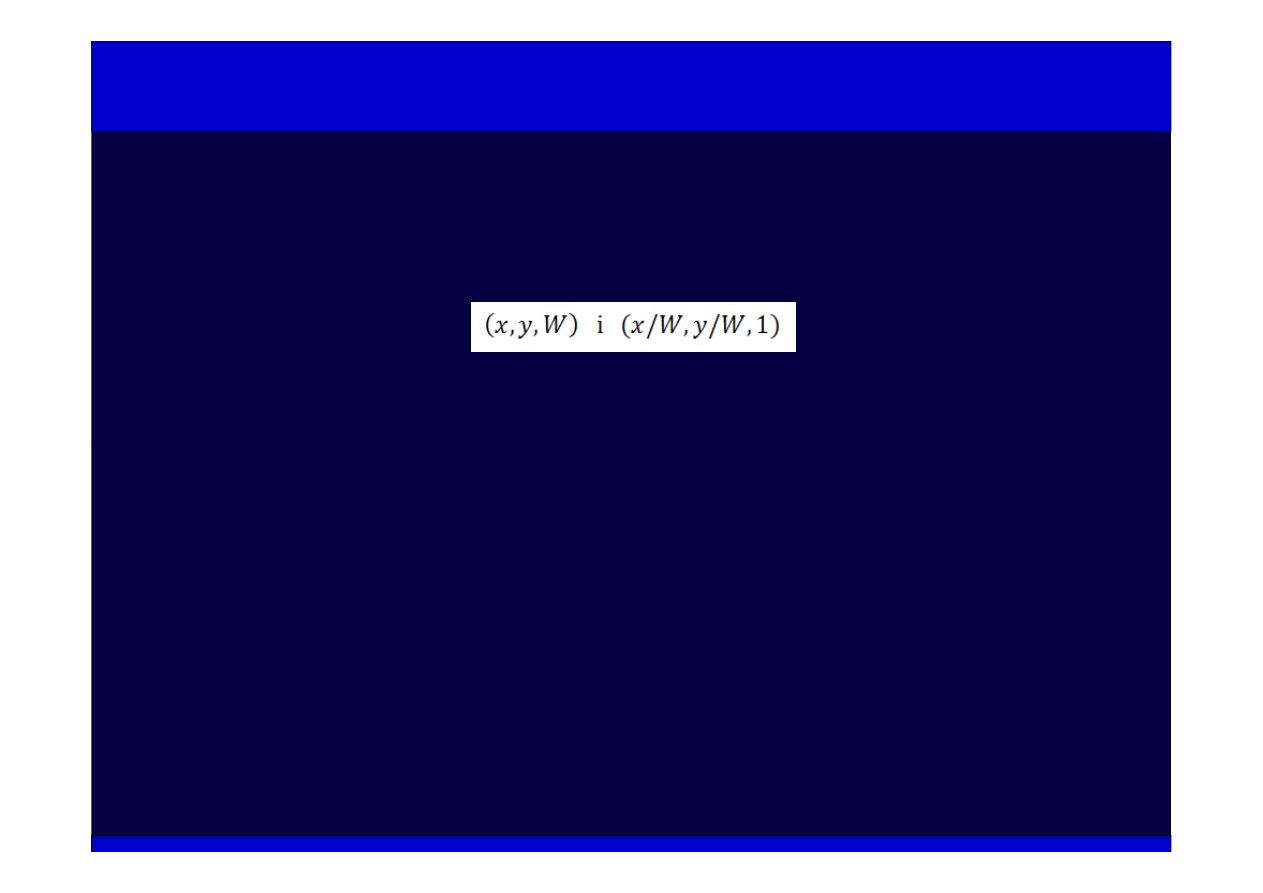
Współrzędne jednorodne (2)

Jeżeli

W

≠

0, to

reprezentują ten sam punkt, a

x

/

W

i

y

/

W

są nazywane współrzędnymi kartezjańskimi

punktu jednorodnego. Punkty dla

W

= 0 są punktami w nieskończoności

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

x

/

W y W

W

= 0

Jeżeli weźmiemy wszystkie trójki reprezentujące ten sam punkt, to jest trójki o postaci
(

t

x

,

t

y

,

t

W

);

t

≠

0, otrzymamy linię w przestrzeni trójwymiarowej

Punkty jednorodne (

x

,

y

, 1) tworzą płaszczyznę o równaniu

W

=1 w przestrzeni

(

x

,

y

,

W

)

Przekształcenie przesunięcia we współrzędnych jednorodnych

(postać macierzowa)

Zapisujemy przekształcenie przesunięcia jako

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

T

jest macierzą przekształceń o wymiarze 3x3 (macierz przesunięcia)

Składanie dwóch przesunięć

Zapisujemy to przekształcenie jako

a następnie

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Stąd mamy

Otrzymujemy macierz o podobnej strukturze do

T

(

d

x

,

d

y

)

Wniosek: składanie przesunięć jest addytywne (macierz przekształceń zawiera człony

d

x1

+

d

x2

,

d

y1

+

d

y2

)

Przekształcenie skalowania we współrzędnych jednorodnych

(postać macierzowa)

Zapisujemy przekształcenie skalowania jako

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

S

jest macierzą przekształceń o wymiarze 3x3 (macierz skalowania)

Składanie dwóch skalowań

Zapisujemy to przekształcenie jako

a następnie

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Stąd mamy

Wniosek: składanie skalowań jest multiplikatywne

Przekształcenie obrotów we współrzędnych jednorodnych

(postać macierzowa)

Zapisujemy przekształcenie obrotów jako

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

R

jest macierzą przekształceń o wymiarze 3x3 (macierz obrotów)

Można pokazać, że składanie obrotów jest addytywne, tzn.

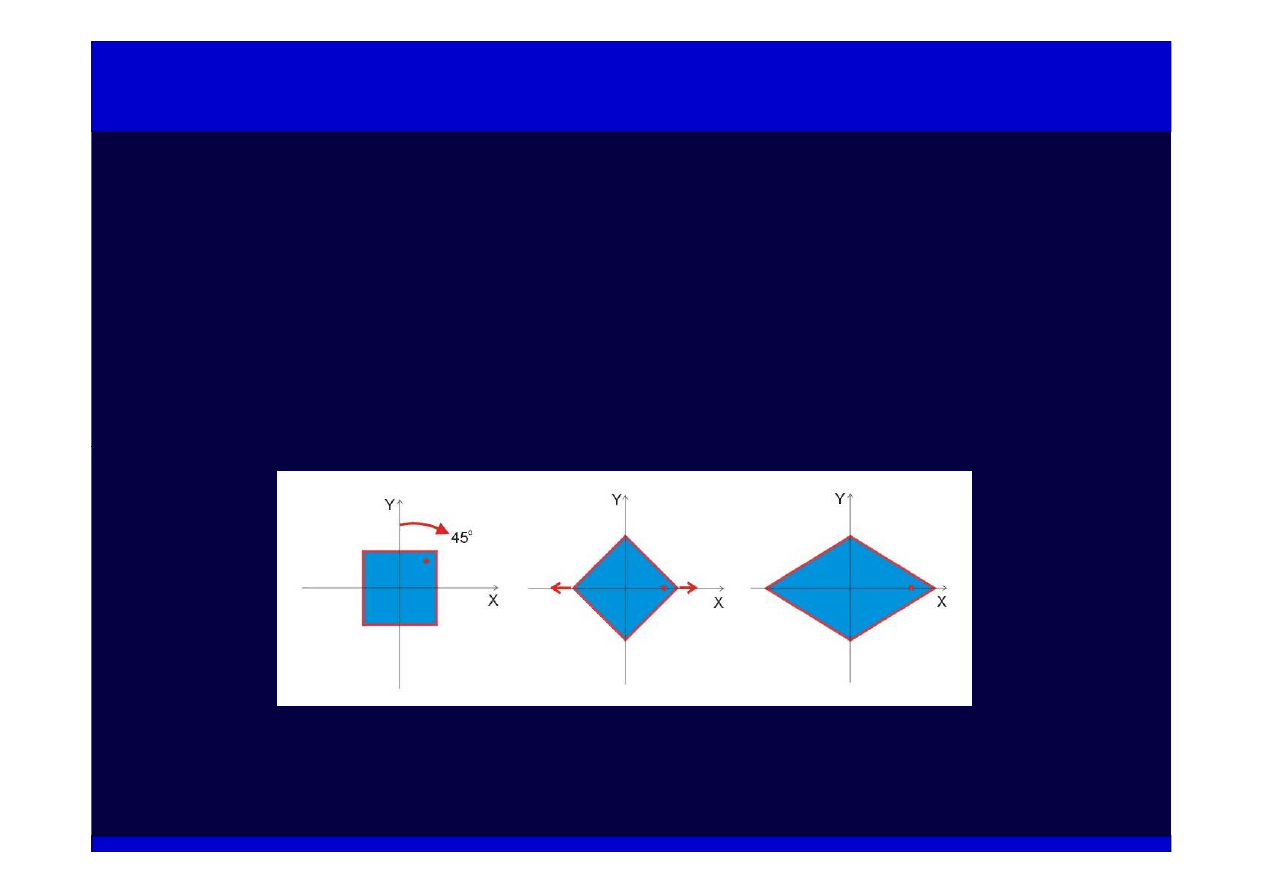
Przekształcenia afiniczne (1)

Przekształcenia opisywane iloczynem macierzy obrotu, przesunięcia i skalowania
opisują tzw. przekształcenia afiniczne

Przekształcenia afiniczne zachowują równoległość linii ale nie zachowują kątów i
długości

Przykład: składanie dwóch przekształceń

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Przykład: składanie dwóch przekształceń

obrót

skalowanie w kierunku osi X

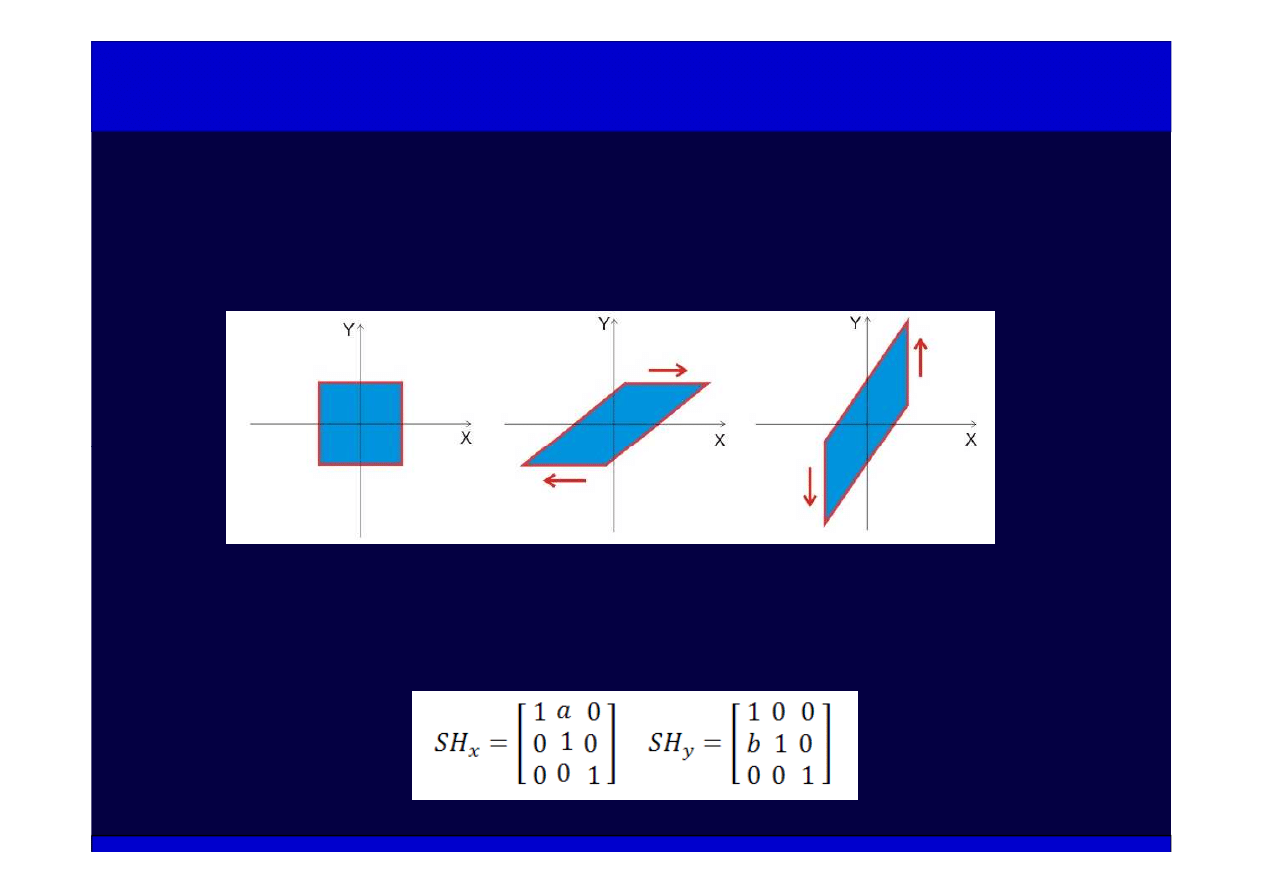
Przekształcenia afiniczne (2)

Przykład: przekształcenie pochylające

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Pochylenie wzdłuż osi X Pochylenie wzdłuż osi Y

Macierze pochylenia wzdłuż osi X oraz wzdłuż osi Y (a, b – współczynniki proporcjonalności)

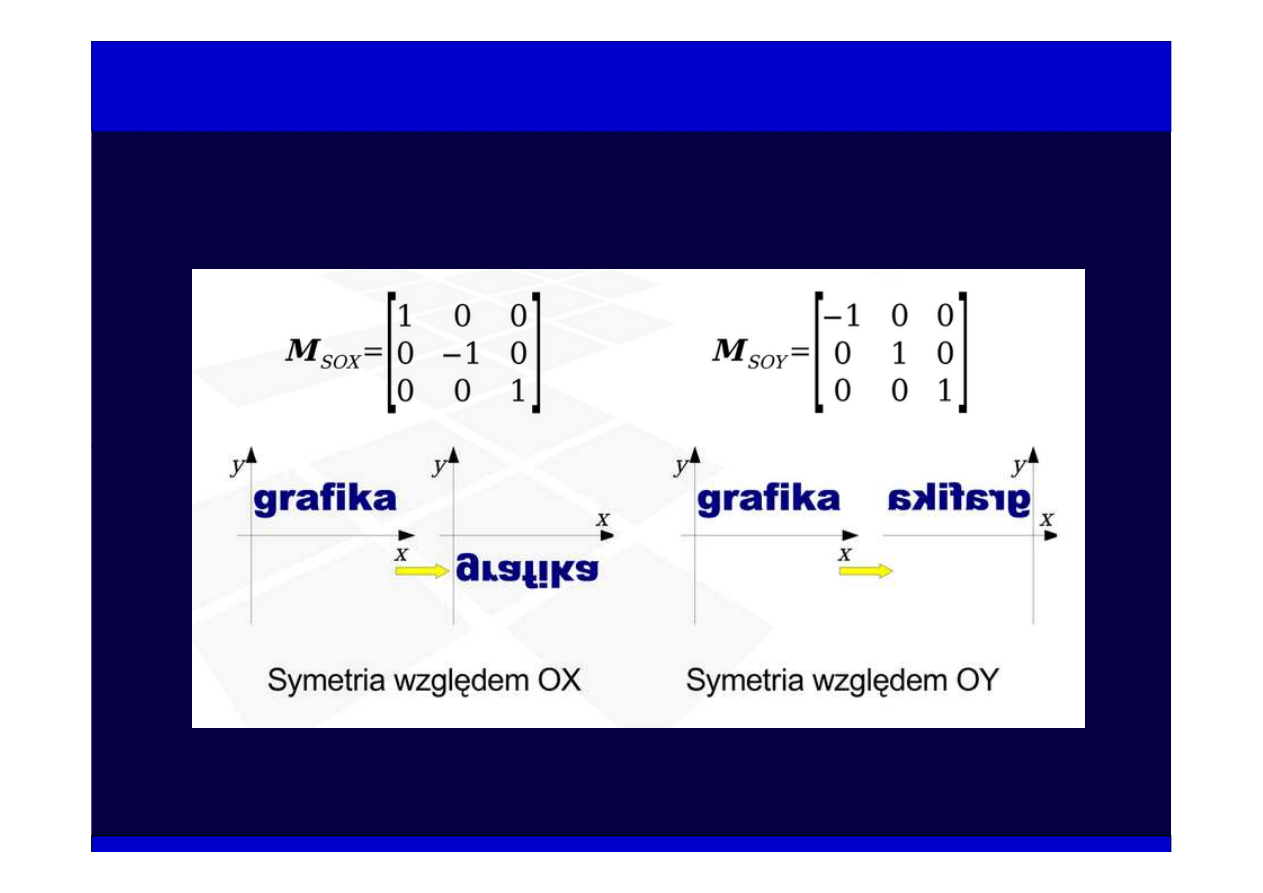
Przekształcenia geometryczne 2D

Symetrie osiowe

Elementy grafiki komputerowej

Przekształcenia geometryczne 2D

Symetria środkowa

Elementy grafiki komputerowej

Przekształcenia geometryczne 2D

Obrót wokół początku układu współrzędnych o zadany kąt

Elementy grafiki komputerowej

Przekształcenia geometryczne 2D

Przesunięcie (translacja) o wektor [T

x

, T

y

]

Elementy grafiki komputerowej

Przekształcenia geometryczne 2D

Skalowanie (przekształcenie nieizometryczne)

Elementy grafiki komputerowej

Przekształcenia geometryczne 2D

Pochylenie (przekształcenie nieizometryczne)

Elementy grafiki komputerowej

Składanie przekształceń 2D

Idea składania przekształceń: zamiast ciągu przekształceń (każde reprezentowane przez
odpowiednią macierz) stosuje się jedną macierz złożoną opisującą wszystkie przekształcenia

Przykład: obrót obiektu wokół dowolnego punktu

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Zapis przekształceń

Składanie przekształceń 2D

Przykład: skalowanie obiektu wokół dowolnego punktu

Zapis przekształceń

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

Składanie przekształceń 2D

Przykład: skalowanie, obrót i przesunięcie obiektu z punktem P1 jako środkiem obrotu i
skalowania

Przekształcenia geometryczne 2D

Elementy grafiki komputerowej

(1) (2) (3) (4)

Opis przekształceń

(4) (3) (2) (1)