Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

dysleksja

PRÓBNY

EGZAMIN MATURALNY

Z MATEMATYKI

POZIOM ROZSZERZONY

Czas pracy 180 minut

Instrukcja dla zdaj¹cego
1. SprawdŸ, czy arkusz egzaminacyjny zawiera 12 stron (zadania

1 – 10). Ewentualny brak zg³oœ przewodnicz¹cemu zespo³u
nadzoruj¹cego egzamin.

2. Rozwi¹zania zadañ i odpowiedzi zamieœæ w miejscu na to

przeznaczonym.

3. W rozwi¹zaniach zadañ przedstaw tok rozumowania prowadz¹cy

do ostatecznego wyniku.

4. Pisz czytelnie. U¿ywaj d³ugopisu/pióra tylko z czarnym

tuszem/atramentem.

5. Nie u¿ywaj korektora, a b³êdne zapisy przekreœl.
6. Pamiêtaj, ¿e zapisy w brudnopisie nie podlegaj¹ ocenie.
7. Obok ka¿dego zadania podana jest maksymalna liczba punktów,

któr¹ mo¿esz uzyskaæ za jego poprawne rozwi¹zanie.

8. Mo¿esz korzystaæ z zestawu wzorów matematycznych, cyrkla

i linijki oraz kalkulatora.

¯yczymy powodzenia!

Przed matur¹

MAJ 2011 r.

Za rozwi¹zanie

wszystkich zadañ

mo¿na otrzymaæ

³¹cznie

50 punktów

Wype³nia zdaj¹cy

przed rozpoczêciem pracy

PESEL ZDAJ¥CEGO

KOD

ZDAJ¥CEGO

Miejsce

na naklejkê

z kodem szko³y

Zadanie 1. (4 pkt)

Liczby

1

2

4

3

+ log x , log

4

4x, log

4

x w podanej kolejnoœci, dla pewnej rzeczywistej wartoœci x,

s¹ trzema kolejnymi pocz¹tkowymi wyrazami nieskoñczonego ci¹gu arytmetycznego.
Wyznacz x oraz sumê czterdziestu pocz¹tkowych wyrazów tego ci¹gu.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

2

Zadanie 2. (5 pkt)

Wyznacz wszystkie wartoœci parametru m, m

Î R, dla których równanie |

|

x

x

- -

4

= m

ma tylko jedno rozwi¹zanie.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

3

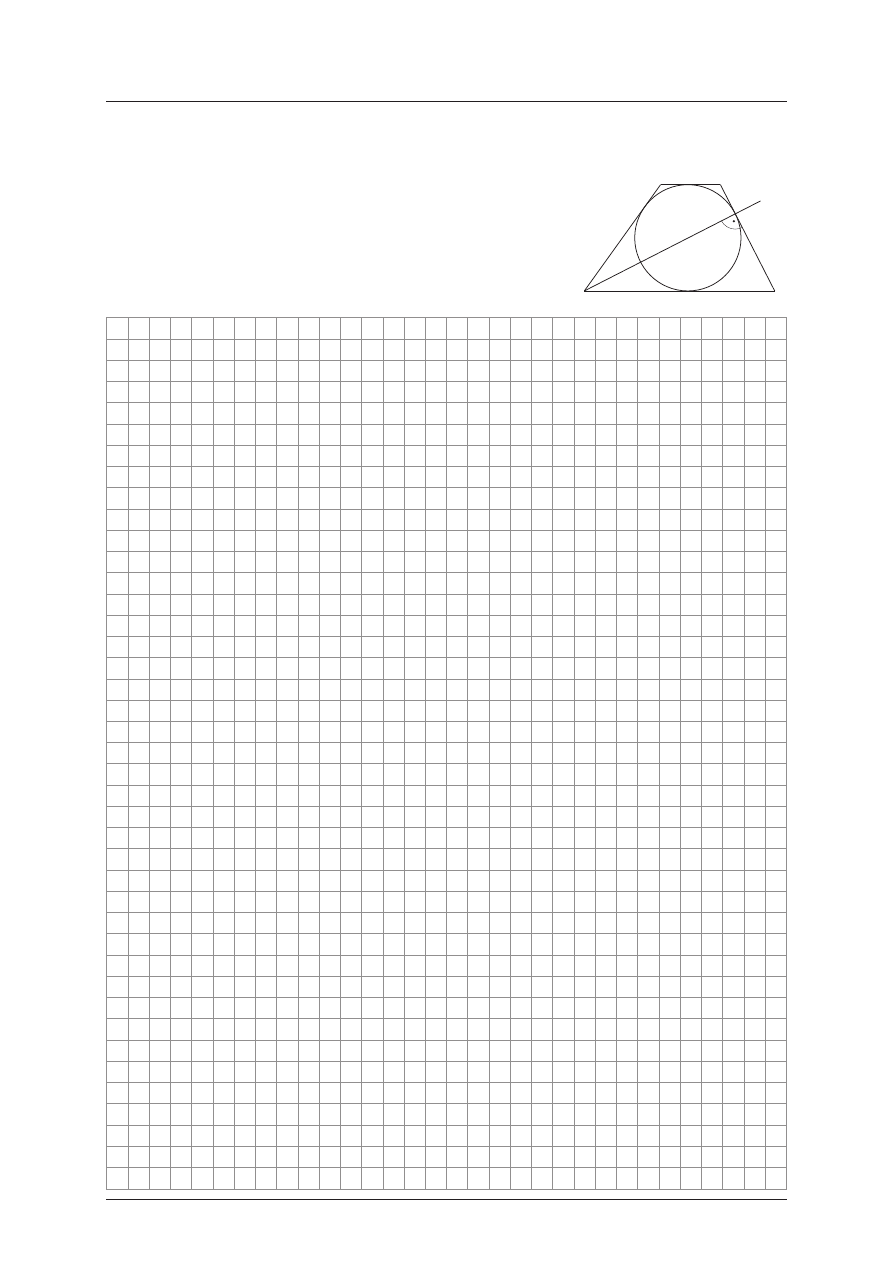
Zadanie 3. (5 pkt)

W trapez ABCD, gdzie AB || CD i |AB| > |CD|, wpisano okr¹g
(patrz rysunek obok). Dwusieczna k¹ta ostrego przy wierz-
cho³ku A jest prostopad³a do ramienia BC.
a) Wyka¿, ¿e dwusieczna k¹ta przy wierzcho³ku D jest

równoleg³a do ramienia BC.

b) Oblicz |BC| : |DC|.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

4

A

B

C

D

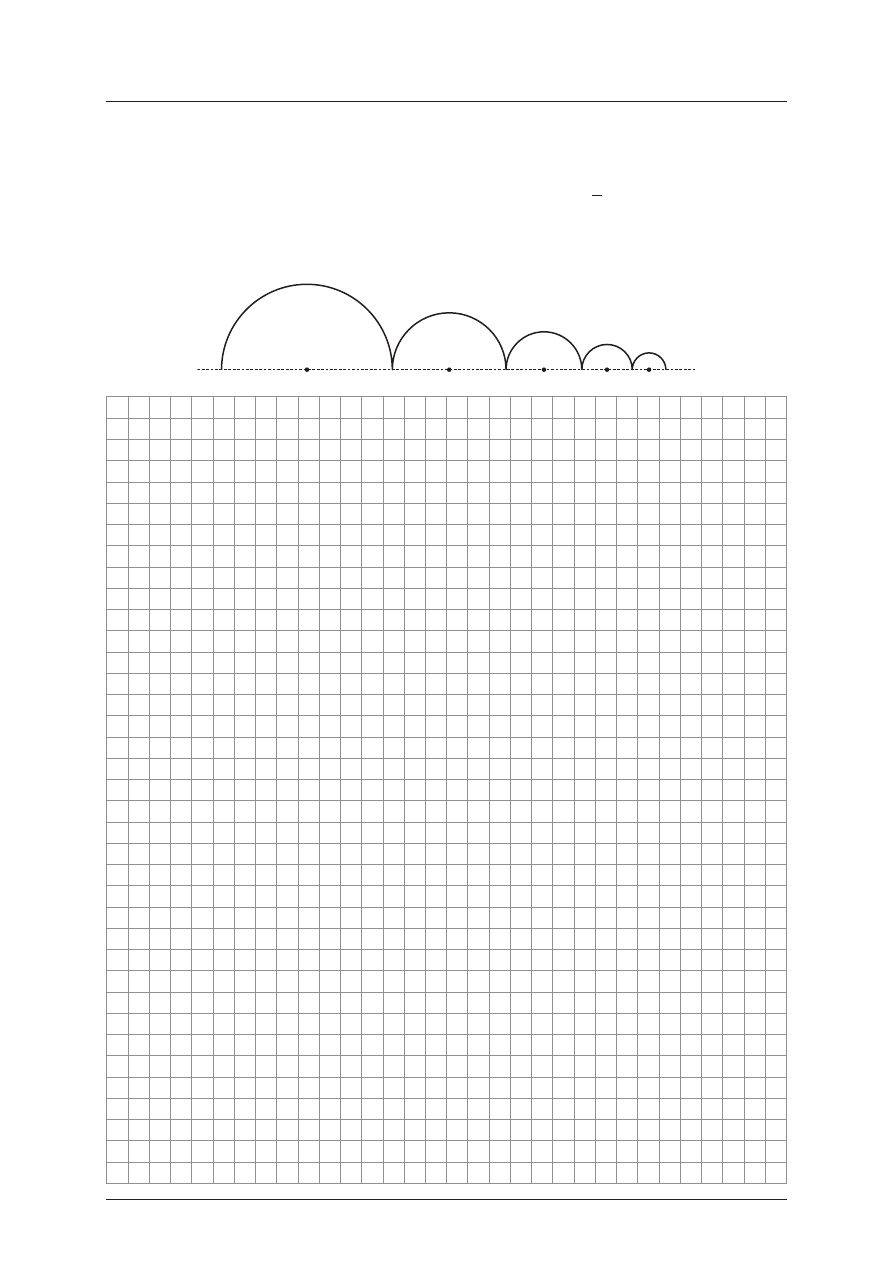
Zadanie 4. (4 pkt)

Z pó³okrêgów budujemy krzyw¹ (patrz rysunek poni¿ej). Pierwszy pó³okr¹g ma promieñ

d³ugoœci r, r > 0, a promieñ ka¿dego nastêpnego pó³okrêgu stanowi

2

3

promienia poprzedniego.

Niech n oznacza liczbê pó³okrêgów tworz¹cych tê krzyw¹. Udowodnij, ¿e dla dowolnej liczby
naturalnej dodatniej n d³ugoœæ krzywej jest mniejsza od 3

pr.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

5

Zadanie 5. (6 pkt)

Punkty przeciêcia paraboli y = x

2

– 2x – 8 z prost¹ k: 2x + y – 1 = 0 s¹ koñcami przek¹tnej rom-

bu, którego pole jest równe 30. Oblicz wspó³rzêdne wierzcho³ków tego rombu.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

6

Zadanie 6. (5 pkt)

Czworok¹t ABCD jest wpisany w okr¹g o promieniu 4 3 (patrz
rysunek obok). Przek¹tna BD czworok¹ta ma d³ugoœæ 12. Iloczyn
sinusów wszystkich k¹tów wewnêtrznych czworok¹ta jest równy

3

16

. Wiedz¹c, ¿e |

ËA| < |ËC| < |ËD|, oblicz miary k¹tów czwo-

rok¹ta ABCD.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

7

A

B

C

D

Zadanie 7. (5 pkt)

W wyniku podzielenia wielomianu W(x) przez (x + 2) otrzymujemy iloraz Q(x) i resztê 0. Jeœli
natomiast podzielimy wielomian W(x) przez (x + 1), to otrzymamy iloraz Q(x) + 2x – 3 i resztê 2.
a) Wyznacz wielomian W(x).
b) Rozwi¹¿ nierównoœæ W(x)

£ –(x + 1)(x + 2).

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

8

Zadanie 8. (4 pkt)

Ze zbioru {1, 2, 3, 4, 5, 6, 7} losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbê trzy-
cyfrow¹: pierwsza wylosowana cyfra jest cyfr¹ setek, druga – cyfr¹ dziesi¹tek, a trzecia – cyfr¹
jednoœci. Oblicz prawdopodobieñstwo zdarzenia, ¿e otrzymana liczba ma nastêpuj¹c¹ w³as-
noœæ: ró¿nica miêdzy najwiêksz¹ i najmniejsz¹ cyfr¹ tej liczby jest nie wiêksza ni¿ 3.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

9

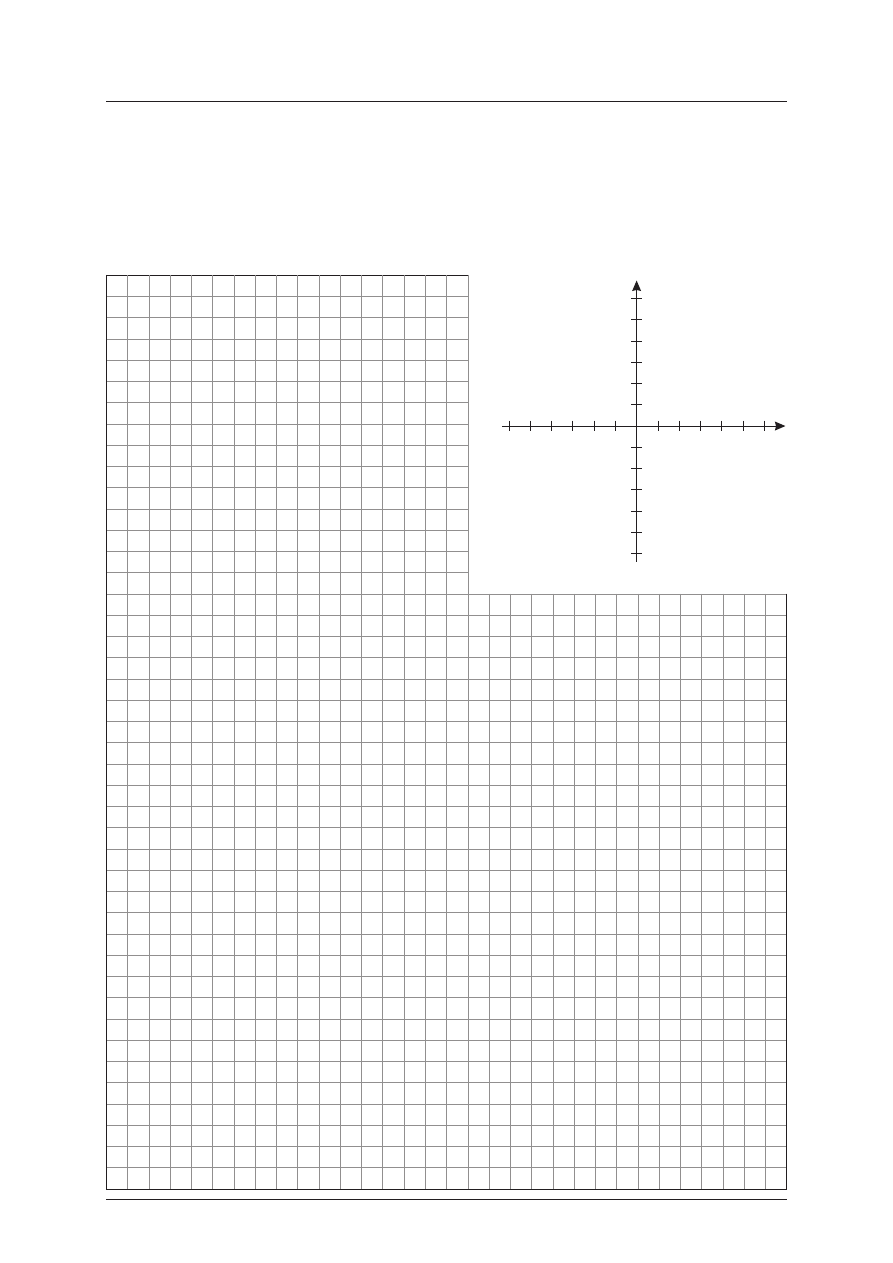
Zadanie 9. (6 pkt)

Dane jest równanie kwadratowe (m – 1)x

2

+ 2x + 3 – m = 0 z niewiadom¹ x i parametrem m.

a) ZnajdŸ wzór i dziedzinê funkcji f, która zmiennej rzeczywistej m przyporz¹dkowuje iloczyn

dwóch ró¿nych pierwiastków danego równania. Naszkicuj wykres funkcji f w prostok¹tnym
uk³adzie wspó³rzêdnych.

b) Wyka¿, ¿e do wykresu funkcji f nale¿¹ tylko trzy punkty o obu wspó³rzêdnych ca³kowitych.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

10

X

Y

0 1 2 3 4 5 6

–3 –2 –1

–1

–2

1

2

3

4

5

–4

–5

–3

–4

–6

6

–5

–6

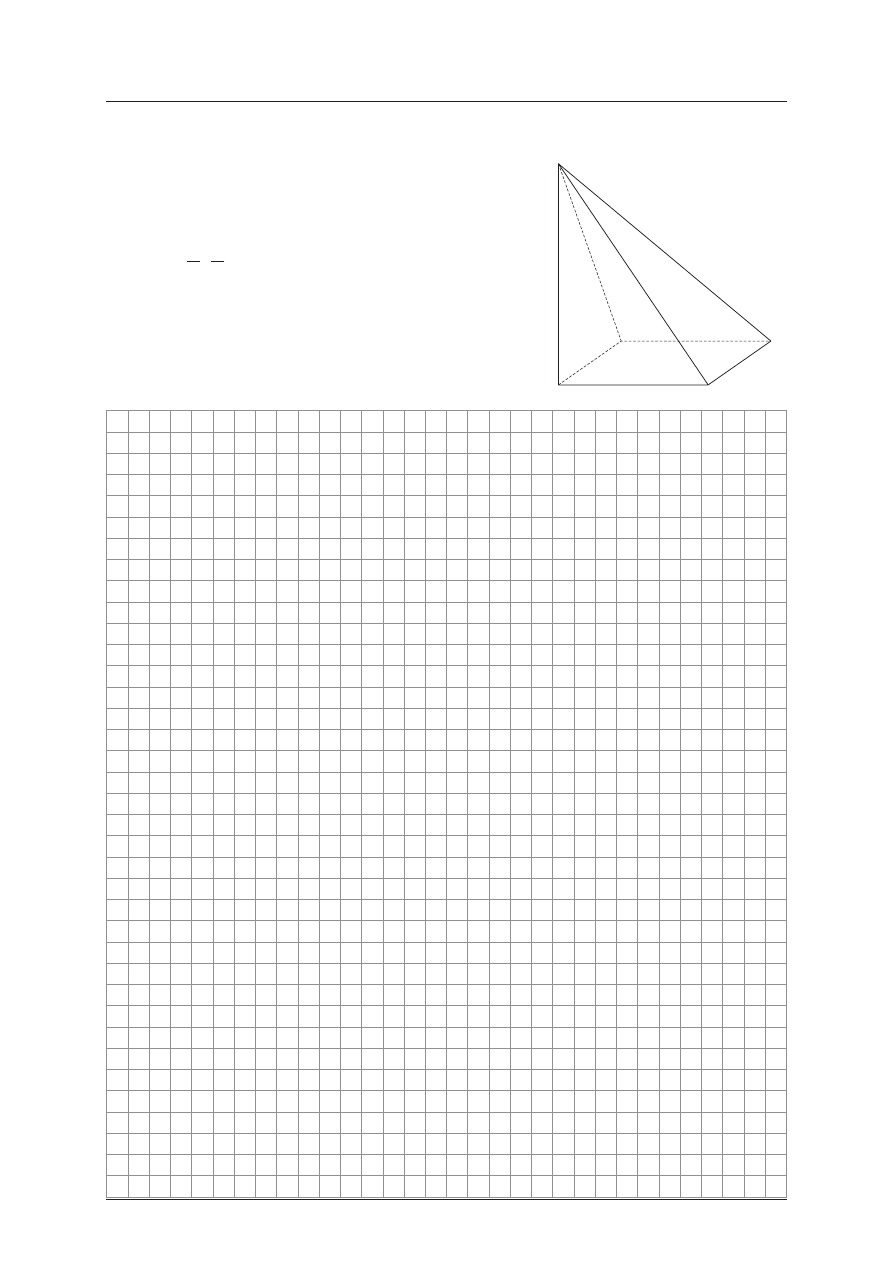
Zadanie 10. (6 pkt)

Podstaw¹ ostros³upa ABCDS jest kwadrat ABCD (patrz ry-
sunek obok). KrawêdŸ AS jest wysokoœci¹ tego ostros³upa.
Odleg³oœæ punktu B od krawêdzi CS jest równa d, a k¹t
dwuœcienny miêdzy œcianami BCS i CDS ma miarê 2

a,

gdzie

a Îæ

è

ç

ö
ø

÷

p p

4 2

,

. Oblicz:

a) odleg³oœæ punktu A od krawêdzi CS
b) wysokoœæ tego ostros³upa.

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

11

A

B

C

D

S

BRUDNOPIS

Wydawca: OFICYNA EDUKACYJNA * KRZYSZTOF PAZDRO Sp. z o.o.

Próbny egzamin maturalny z matematyki

Poziom rozszerzony

12