1. Niezwykłe właściwości dwuwymiarowego materiału grafenu. Postaci
krystaliczne węgla, sieć krystaliczna grafenu.

Grafen:
- jest niemal całkowicie przezroczysty
- niezwykle wytrzymały i lekki, a dodatkowo elastyczny

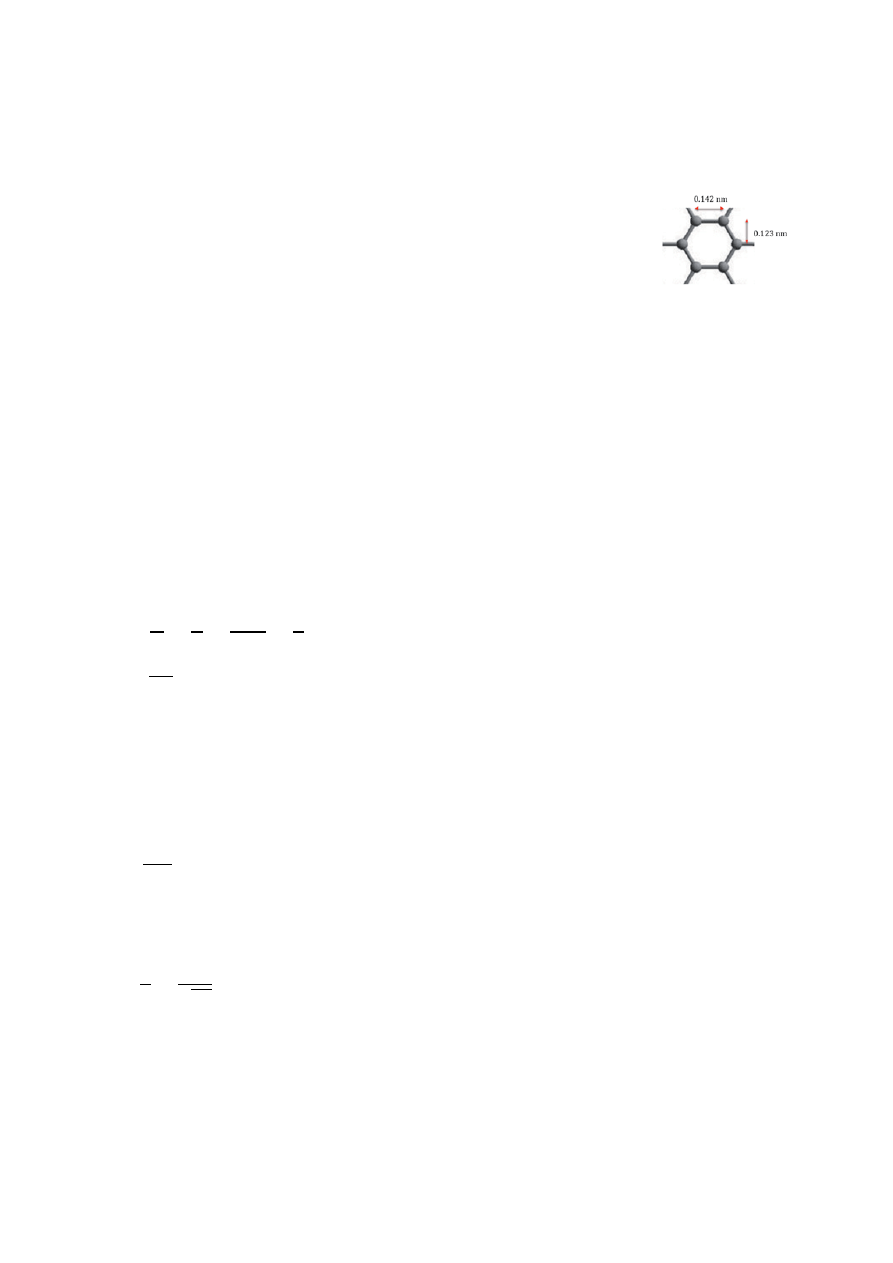
Sieć krystaliczna grafenu to płaska siatka atomów węgla połączonych ze
sobą w sześciokątne oczka. Wiązania mają długość ok. 0,142 nm.

Postaci krystaliczne węgla:
- grafit – układ warstw grafenu, silne wiązania w warstwach, słabe między warstwami
- diament – każdy z atomów ma 4 sąsiadów, wiązania mocne, kowalencyjne, twardy materiał
- fulereny – wiele atomów węgla (np. 60), duże przestrzenne struktury (kula)
- grafen
- nanorurki – zwinięty grafen

8. Fale materii: zależność dyspersyjna ω(k), prędkość fazowa i grupowa,
porównanie z falami elektromagnetycznymi.

Mamy prędkość fazową i grupową (cząstka opisana przez paczkę falową) cząstki:

𝑉

𝑓

=

𝜔

𝑘

=

𝐸

𝑝

=

𝑚𝑣

2

2𝑚𝑣

=

𝑣
2

𝑉

𝑔

=

𝑑𝜔

𝑑𝑘

Dyspersja to zależność prędkości fazowej fal od częstotliwości.
Gdy dyspersja zachodzi to prędkość fazowa nie jest równa prędkości grupowej.
Gdy dyspersja nie zachodzi to prędkości są równe.

Zależność dyspersyjna:

𝜔 =

ħ𝑘

2

2𝑚

Prędkość fazowa fal elektromagnetycznych jest zależna od cech ośrodka, zachodzi dyspersja.
Zależność ta ma postać:

𝑣 =

𝑐

𝑛

=

𝑐

ℇ𝜇

W mianowniku mamy względną przenikalność elektryczną i magnetyczną ośrodka.

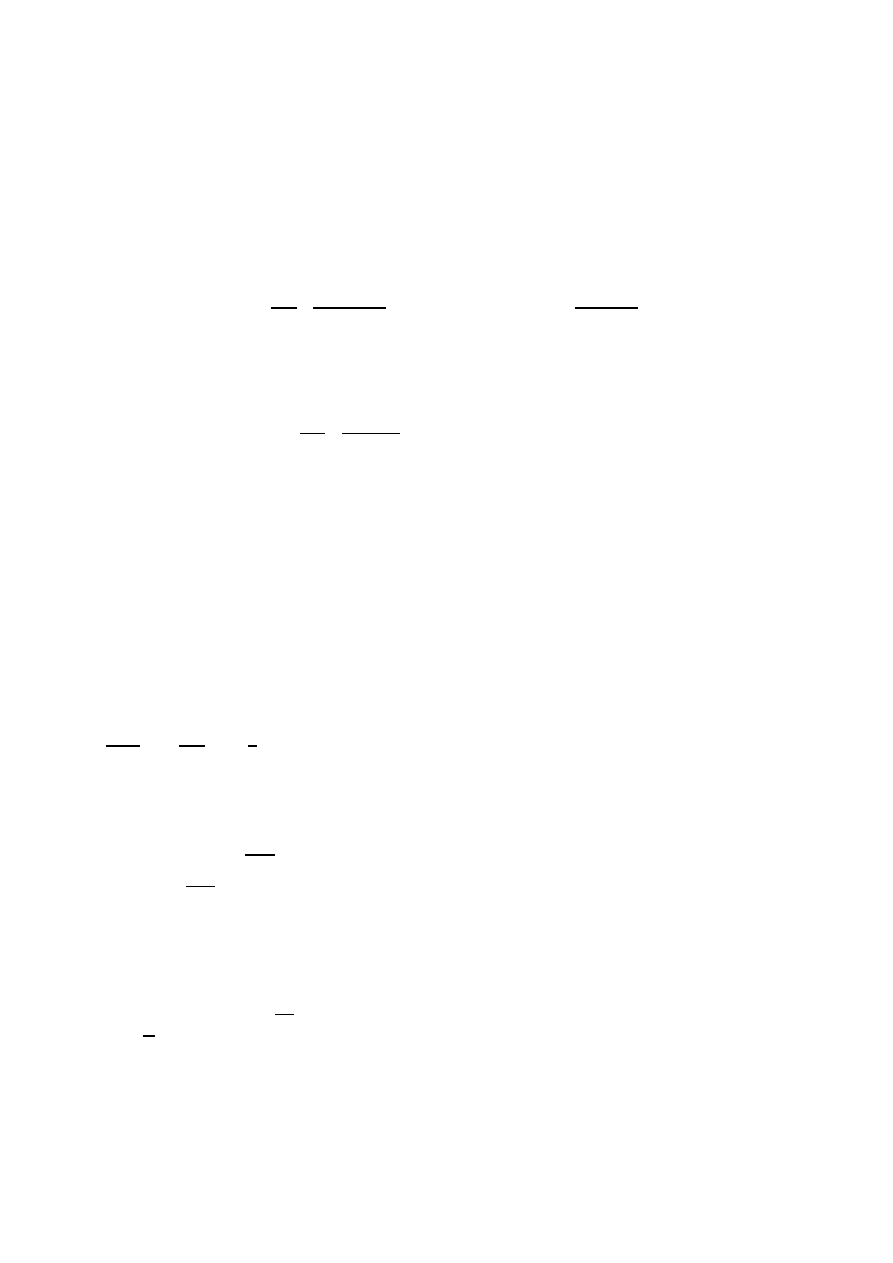
15. Rozdzielenie zmiennych przestrzennych i czasu, równ. Schrödingera
niezależne od czasu, funkcje i wartości własne energii.

Rozdzielenie zmiennych przestrzennych i czasu prowadzi do otrzymania równania
Schrödingera niezależnego od czasu.

Równanie zależne od czasu i położenia ma postać:

−

ħ

2

2𝑚

∗

𝜕

2

𝛹(𝑥, 𝑡)

𝜕𝑥

2

+ 𝑉 𝑥, 𝑡 ∗ Ψ 𝑥, 𝑡 = 𝑖ħ

𝜕𝛹(𝑥, 𝑡)

𝜕𝑡

Przyjmujemy, że Ψ(x,t) = Ψ(x)*ϕ(t), po podstawieniu do równania wyżej człon zależny od
czasu się skraca i otrzymujemy równanie niezależne od czasu:

−

ħ

2

2𝑚

∗

𝜕

2

𝛹(𝑥)

𝜕𝑥

2

+ 𝑉 𝑥 ∗ Ψ 𝑥 = 𝐸 ∗ Ψ 𝑥

Ψ 𝑥 – funkcje własne, spełniające powyższe równanie
E – wartości własne energii, które odpowiadają określonym funkcjom własnym

Ψ 𝑥

22. Równanie Schrödingera oscylatora harmonicznego, funkcja falowa
stanu podstawowego, znajdowanie kolejnych funkcji
własnych metodą rozwinięcia w szereg - wielomiany Hermite’a, poziomy
energii.

Równanie dla oscylatora ma postad:

𝑑

2

𝛹

𝑑𝑥

2

= −

2𝑚

ħ

[𝐸 −

1
2

𝑚𝜔

0

2

𝑥

2

]Ψ

W stanie podstawowym funkcja falowa ma postad:

𝛹

0

𝑥 = 𝐴 exp(−

𝛼𝑥

2

2

)

Gdzie 𝛼 =

𝑚 𝜔

0

ħ

Poza stanem podstawowym funkcje własne nie są takie proste i poszukiwane są w postaci
iloczynu funkcji w stanie podstawowym i nieznanej funkcji H(y). Argument y pojawia się dla
ułatwienia poszukiwania tych funkcji, a nowe funkcje falowe mają postad:

𝛹

𝑛

𝑦 = 𝐴

𝑛

𝐻

𝑛

exp(−

𝑦

2

2

)

y = 𝛼 ∗ 𝑥

Równanie Schroedingera możemy zapisad w innej postaci, podstawiając:

𝛽 =

2𝑚𝐸

ħ

Otrzymamy wówczas:

𝑑

2

𝛹

𝑑𝑥

2

+

𝛽
𝛼

− 𝑦

2

Ψ = 0

Podstawiając do tego równania 𝛹

𝑛

𝑦 = 𝐴

𝑛

𝐻

𝑛

exp(−

𝑦

2

2

) otrzymamy nowe równanie, z

funkcjami H(y):

𝑑

2

𝐻(𝑦)

𝑑𝑦

2

− 2𝑦

𝑑𝐻(𝑦)

𝑑𝑦

+

𝛽
𝛼

− 1 𝐻(𝑦) = 0

Jest to równanie Hermite’a, a jego rozwiązaniami są wielomiany Hermite’a. Można je
przedstawid w postaci szeregu:

𝐻 𝑦 =

𝑎

𝑖

𝑦

𝑖

∞

𝑖=0

= 𝑎

0

+ 𝑎

1

𝑦+...

Musi byd spełniony warunek, żeby funkcja H(y) nie rosła szybciej od 𝑒

𝑦 2

2

, z czego wynika:

𝛽
𝛼

= 2𝑛 + 1 ; 𝑛 = 0,1,2, …

α zależy od energii, więc pojawia się ograniczenie na energię w postaci:

𝐸

𝑛

= 𝑕𝜈(𝑛 +

1
2

)

Energia oscylatora może przyjmowad różne poziomy, od poziomu zerowego zaczynając (dla
n=0):

𝐸

0

=

1
2

𝑕𝜈

Ze wzrostem wartości n oscylator kwantowy zbliża się swoim zachowaniem do oscylatora
klasycznego.