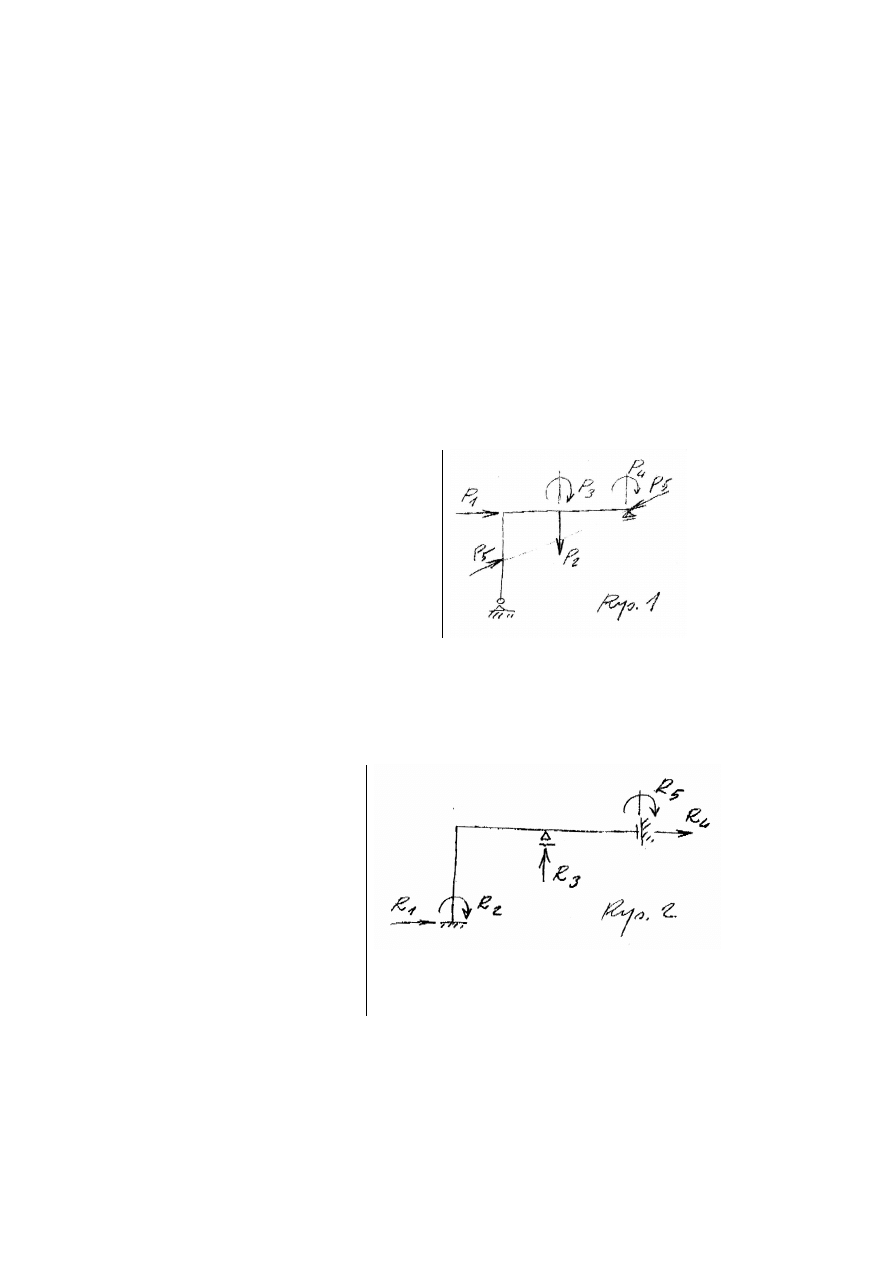
1

Tematyka egzaminu i zaliczenia wykładu z sem. 5

przedmiotu "Mechanika Budowli"

III BD, Sem. 4 i 5, r. ak. 2007/08

1. Podać różnice między układem statycznie wyznaczalnym i niewyznaczalnym oraz zalety i wady

stosowania każdego z nich.

2. Jakie główne założenia muszą być spełnione dla układów liniowo sprężystych.

3. Czy osiadanie podpór i zmiany temperatury mają wpływ na wartości sił przekrojowych w układzie

statycznie wyznaczalnym. Odpowiedź uzasadnić.

4. Na podstawie własnego przykładu PUP objaśnić zasadę superpozycji przemieszczeń. Czy obowiązuje ona w

zagadnieniach:

a) statyki

b) stateczności

c) dynamiki

5. Na przykładzie ramy podanej na Rys.1 objaśnić

zasadę wzajemności przemieszczeń

δ

i j

=

δ

j i

przez wskazanie odpowiednich przemieszczeń dla
i = ... , j = ... na wykresach deformacji ramy od

P

i

= 1 oraz od P

j

= 1 .

6. W układzie statycznie niewyznaczalnym objaśnić zasadę wzajemności reakcji r

i j

= r

j i

dla i = ... ,

j = ... dla jednostkowych przemieszczeń

∆

i

= 1,

∆

j

= 1 . Punkty i, j odpowiadają punktom przyłożenia

uogólnionych reakcji R

i

, zaznaczonych na Rys. 2. Na oddzielnych rysunkach narysować bez obliczeń

przewidywaną postać zdeformowanej ramy od przemieszczeń

∆

i

= 1,

∆

j

= 1 .

6. W układzie statycznie niewyznaczalnym

objaśnić zasadę wzajemności reakcji r

i j

= r

j i

dla i = ... ,

j = ... dla jednostkowych przemieszczeń

∆

i

= 1,

∆

j

= 1 . Punkty i, j odpowiadają

punktom przyłożenia uogólnionych
reakcji R

i

, zaznaczonych na Rys. 2. Na

oddzielnych rysunkach narysować bez
obliczeń

przewidywaną postać zdeformowanej

ramy od przemieszczeń

∆

i

= 1,

∆

j

= 1 .

8. Podać definicje stopnia statycznej niewyznaczalności i kinematycznej niewyznaczalności oraz napisać ile

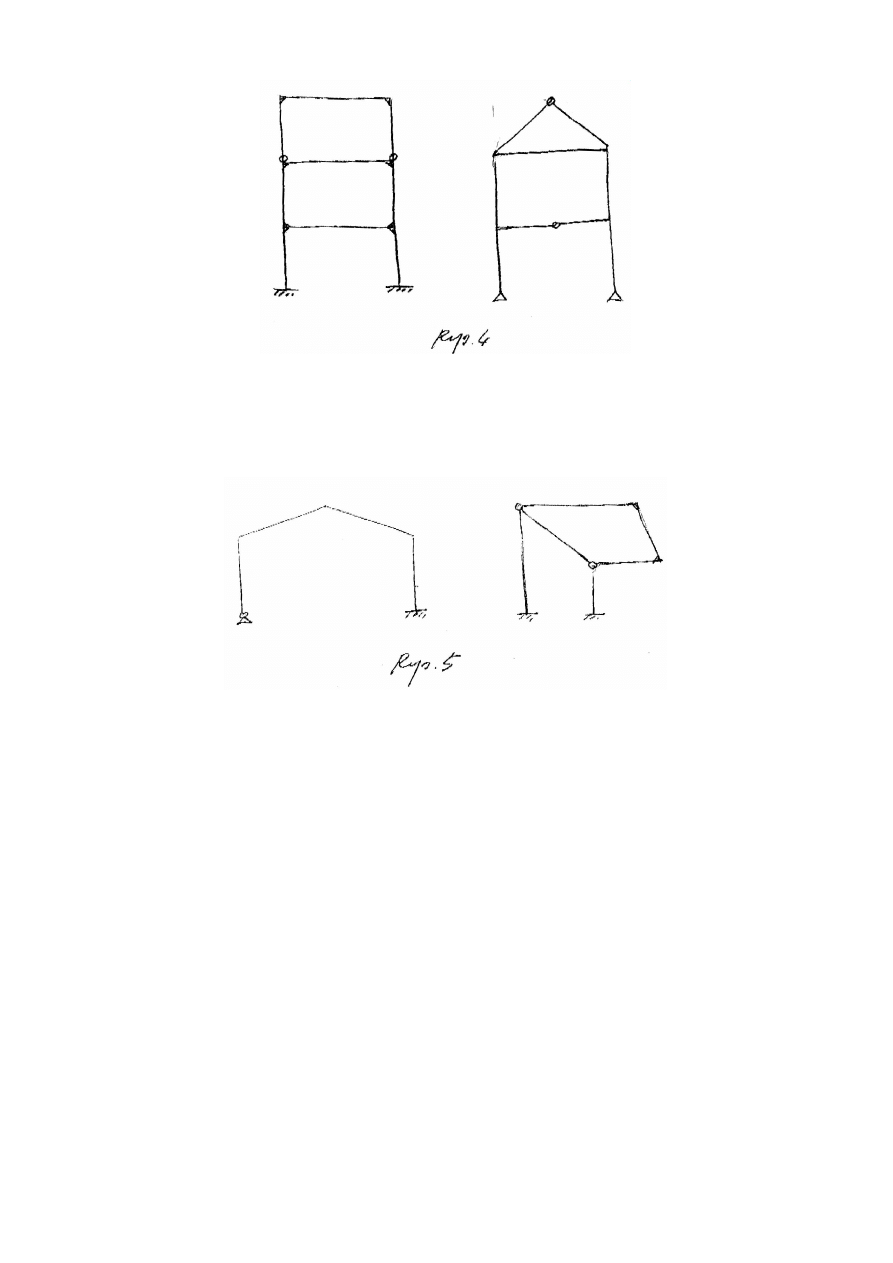
wynosi SSN i SKN dla ram podanych na Rys. 4.

2

9. Dla układu wskazanego na Rys. 4 przyjąć schematy połówkowe i podać dla nich SSN i SKN. Podać metody
(MS lub MS) i uzasadnienie ich wyboru, stosowane do analizy symetrii lub antysymetrii.

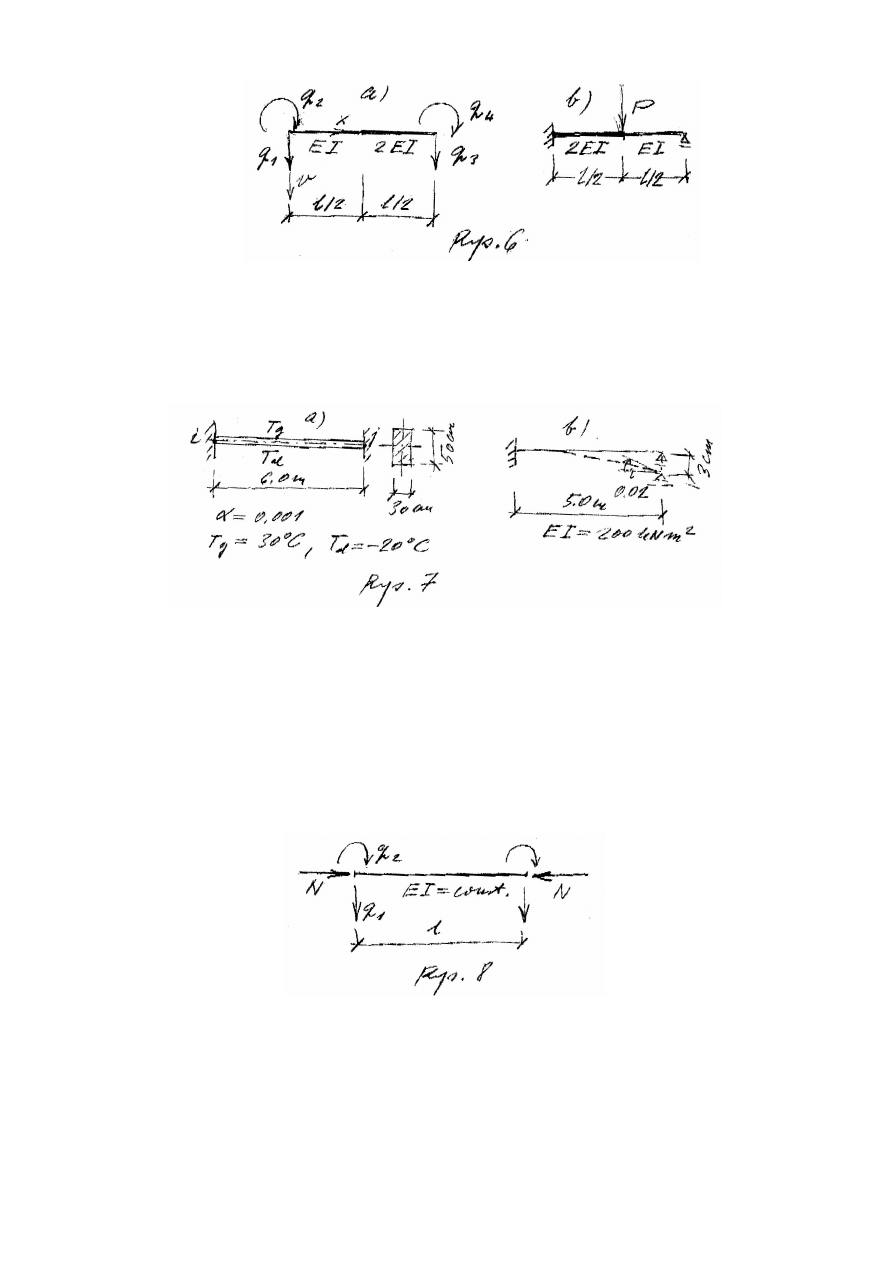
10. Określić SKN dla ram podanych na Rys. 5 i uzasadnić je przez analizę ruchu odpowiednich łańcuchów

kinematycznych.

11. Podać interpretację równania MS

0

2

3

1

2

=

∆

+

∑

δ

=

p

j

j

j

X

dla dobranego przez siebie przykładu ramy płaskiej o SSN = 3.

12. Podać interpretację równania MP

0

)

(

3

3

1

3

=

+

∑

=

R

Z

r

w

j

j

j

dla dobranej przez siebie ramy płaskiej o SKN = 3 i jednokrotnie przesuwnej dla Z

1

=

∆

1 .

13. Obliczyć sztywność k

41

elementu belkowego o skokowo zmiennym momencie bezwładności

przekroju, por. Rys. 6a, korzystając ze wzoru

k

41

=

dx

B

EI

B

l

1

)

(

4

∫

oraz wielomianowej aproksymacji linii ugięcia v

i

(x) = N

i

dx

3

14. Obliczyć wartość wstępnego momentu dla MP dla pręta jednostronnie utwierdzonego i obciążo-nego siłą

skupioną P , Rys. 6b.

15. Obliczyć wartość wstępnego momentu utwierdzenia dla pręta nierównomiernie ogrzewanego o danych jak

jak na Rys. 7a

16. Obliczyć wartość wstępnych reakcji dla pręta ze wstępnymi przemieszczeniami końców, Rys. 7b .

17. Obliczyć sztywność geometryczną

k

g

ij

dla i = ... , j = ... dla elementu belkowego pokazanego na Rys. 8,

korzystając ze wzoru

k

g

ij

=

dx

N

N

N

j

l

i

∫

)

(

i aproksymacji wielomianowej v (x) = N

i

dx

.

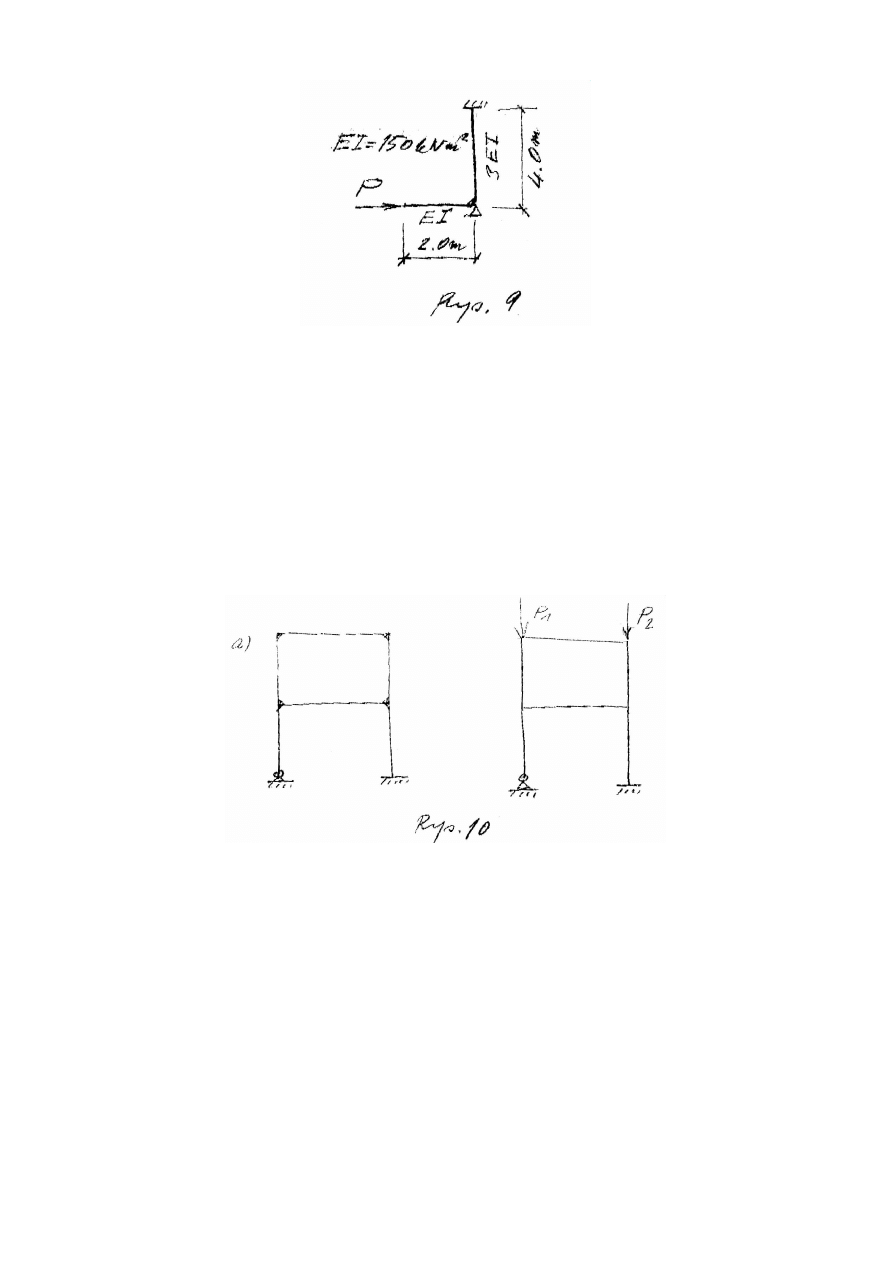
18. Obliczyć wartość obciążenia krytycznego klasyczną MP dla układu dwuprętowego, pokazanego na Rys. 9.

4

19. Na czym polega zjawisko wyboczenia PUP ? Dlaczego to zjawisko analizujemy w mechanice konstrukcji?

Zilustrować zjawisko wyboczenia, stan przedwyboczeniowy i powyboczeniowy i wpływ imperfekcji na
ś

cieżkę równowagi P - A .

20. Objaśnić interpretację rozwiązań równania stateczności (równania wiekowego) i na ścieżce równowagi
P - A zaznaczyć części stateczne i niestateczne ścieżek przed i powyboceniowych.

21. Które z założeń MP, stosowanej w teorii wyboczenia, narusza liniowość PUP? Dlaczego, pomimo tego,

rozwiązujemy liniowe równanie zagadnienia własnego?

22. Podać różnice między klasyczną MP i MES na przykładzie ramy na Rys. 10 a dla zagadnienia statyki.

Podać liczbę SS w MP i MES po uwzględnieniu warunków podparcia.

23. Podać różnice między klasyczną MP i MES na przykładzie ramy na Rys. 10 b dla zagadnienia

stateczności. Podać liczbę SS w MP i MES po uwzględnieniu warunków podparcia. Jaką dyskretyzację

(liczbę ES) należy przyjąć w MES aby uzyskać dokładność obliczenia P

kr

rzedu 1% ?

24. Na przykładzie równania ruchu oscylatora o 1SS (układ o jednej masie skupionej) objaśnić pojęcia:

1) drgania własne, jak je inicjujemy,

2) drgania własne nietłumione, jak formułujemy parę własną,

3) drgania własne z wymuszeniem harmonicznym, wpływ tłumienia, drgania nietłumione, odpowiedź
układu przed i porezonansową.

25. Drgania poprzeczne belki jednoprzęsłowej bez tłumienia, z masami skupionymi. Pary własne, postacie

drgań i ich ortogonalność.

5

26. Korzystając z równań ruchu

(

ω

2

D M

−

I ) A = 0

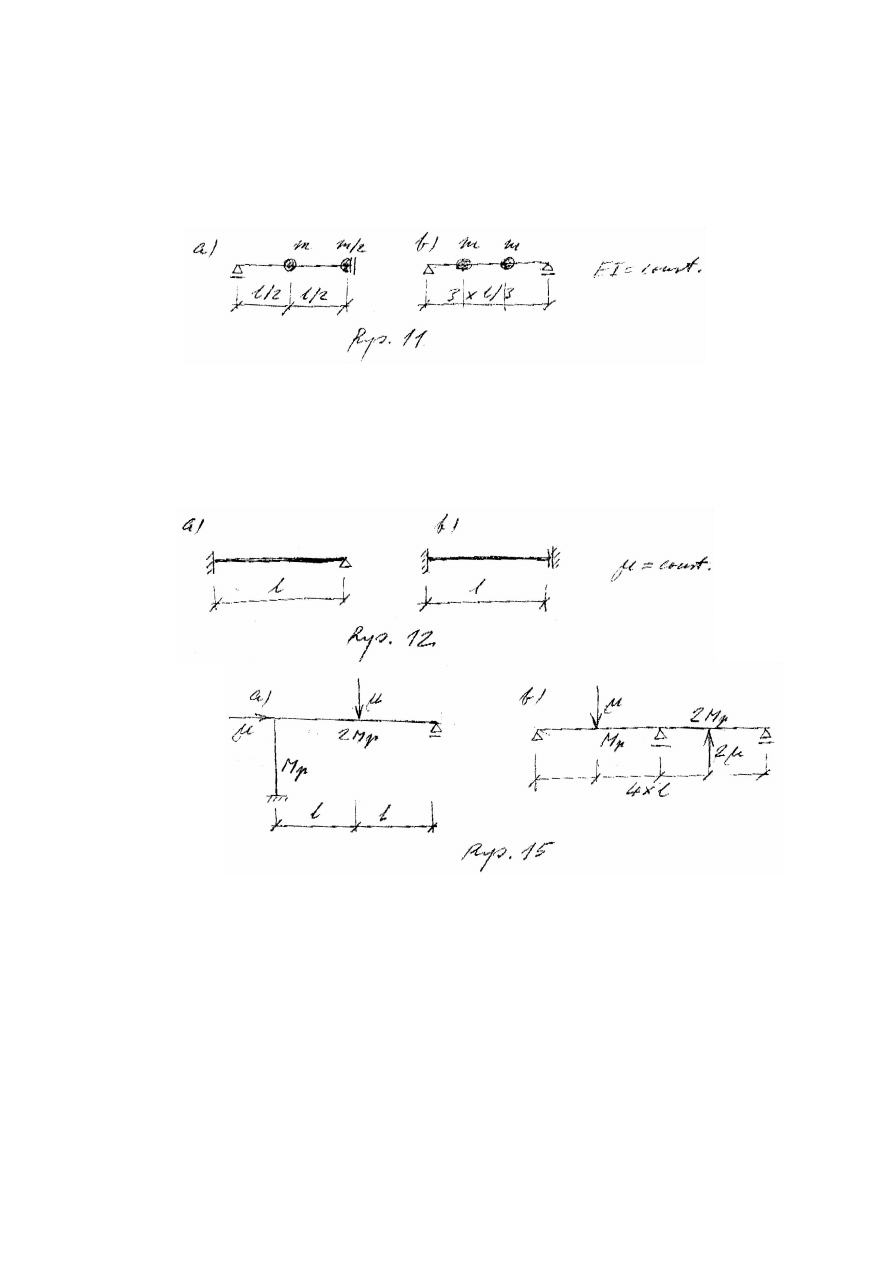
obliczyć częstości drgań belek podanych na Rys. 11. Narysować postacie drgań i sprawdzić warunek ich
ortogonalności.

27. Dla belki z Rys.11 oszacować podstawowe częstości drgań własnych korzystając ze wzoru Dunkerley’a.

28. Zakładając, że belka pokazana na Rys. 12 jest aproksymowana jednym ES obliczyć jej częstości drgań

własnych. Obliczone wartości porównać z odpowiednimi wartościami częstości modelu kontynualnego
opierając się na możliwych postaciach drgań.