
Mechanika budowli
______________________________________________________________________________________________ 1
Dynamika elementów prętowych
Literatura
[1] Ziemba S.: "Analiza drgań". PWN, Warszawa 1957.
[2] Nowacki W.: "Dynamika budowli". Arkady, Warszawa 1972.
[3] Langer J.: "Dynamika budowli". Politechnika Wrocławska, Wrocław 1980.
[4] Ciesielski R. i inni: "Mechanika budowli. Ujęcie komputerowe tom 2". Arkady, Warszawa 1992
[5] Dyląg Z., Krzemińska-Niemiec E.: "Mechanika budowli tom 4". Wydawnictwo Politechniki
Białostockiej, Białystok 1993.
[6] Stojek Z., Zylski W.: "Dynamika konstrukcji". Politechnika Rzeszowska, Rzeszów 1993
[7] Chmielewski T., Zembaty Z.: "Dynamika budowli". Politechnika Opolska, Opole 1997.
[8] Sułocki J.: "Dynamika budowli. Metody obliczeń i przykłady". Politechnika Łódzka, Łodź 1976
[9] Woroszył S.: "Przykłady i zadania z teorii drgań. Część 1 i 2". PWN, Warszawa 1976/1979.
[10] Osiński Z.: "Zbiór zadań z teorii drgań". PWN Warszawa 1989.
[11] Nizioł J.: "Podstawy drgań w maszynach". Politechnika Krakowska, Kraków 1996
[12] Skarżyński R., Labocha S.: "Elementy dynamiki budowli w zadaniach"
Politechnika Częstochowska Częstochowa 2001
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 2
1. Przedmiot, zadania i metody dynamiki budowli
Dynamika jest działem mechaniki zajmującym się ruchem układów materialnych pod
wpły-
wem działających na nie sił. W analizie dynamicznej rozpatruje się dwa rodzaje zadań:
zadanie bezpośrednie, kiedy zadane są siły, a należy określić ruch wywołany tymi siłami,
•
przy spełnieniu określonych warunków narzuconych na położenie i prędkość
początkową,
zadanie odwrotne, kiedy zadane są równania ruchu, a należy wyznaczyć siły wywołujące
•
ten ruch.
Ustroje budowlane powinny być układami geometrycznie niezmiennymi o zachowawczej
postaci
równowagi. Przedmiotem dynamiki budowli będzie w związku z tym obszar dynamiki
obejmujący naukę o ruchu ustrojów mającym zwykle charakter oscylacyjny wokół położenia
równowagi.
Ruch o takim charakterze nazywamy ruchem drgającym.
Zadaniem dynamiki budowli jest określenie odpowiedzi konstrukcji, tj. wyznaczenie
prze- mieszczeń i naprężeń, będących reakcją na oddziaływanie dowolnego obciążenia
dynamicznego. Obciążenie to może zmieniać w czasie swoją wartość, kierunek, zwrot lub
miejsce położenia. W analizie dynamicznej należy dodatkowo uwzględnić powstające
podczas ruchu siły masowe (bezwładności) i opory ruchu. Z punktu widzenia dynamiki
należy więc każdy rozpatrywany układ konstrukcyjny badać na podstawie schematu
dynamicznego ustroju. Będzie nim schemat statyczny uzupełniony o opis pola masowego
związanego z konstrukcją oraz rozkład sił dyssypatywnych (oporów ruchu) i sił
wzbudzających drgania.
Przemieszczenie punktów masowych ustroju można opisać dowolnym zbiorem
współrzęd- nych. Rozpatruje się zarówno przemieszczenia translacyjne jak i rotacyjne,
dlatego określa się ten
zbiór wspólnym mianem współrzędnych uogólnionych.
Definicja:
Liczbą d dynamicznych stopni swobody nazywa się liczbę niezależnych współrzędnych
uogólnionych, niezbędnych do jednoznacznego określenia położenia wszystkich punktów
masowych układu.
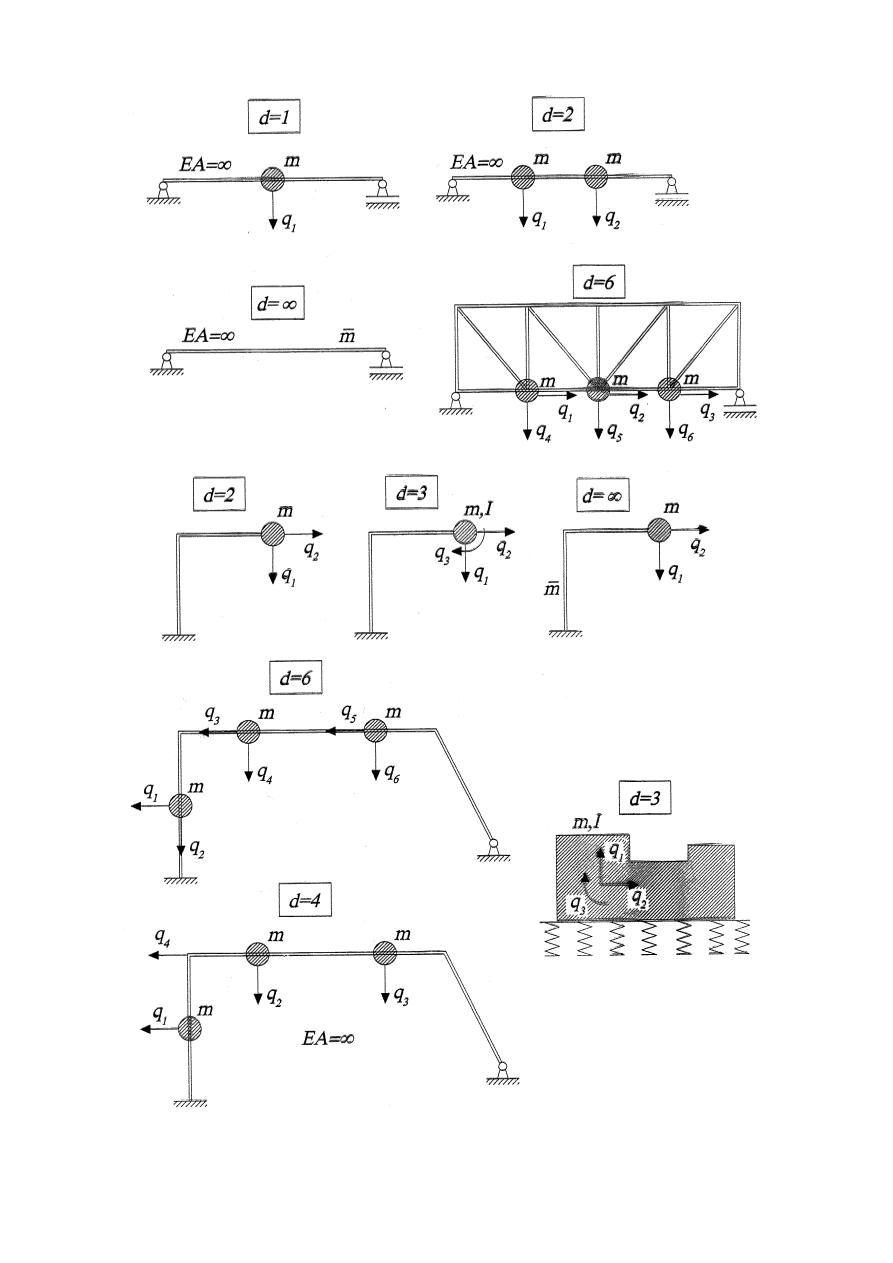
Na rysunku 1.1 przedstawiono przykłady określania dynamicznych stopni swobody. Należy
zwrócić szczególnie uwagę na znaczne uproszczenie zadań w przypadku założeń
upraszczających,
najczęściej przyjmowanych podczas obliczeń "ręcznych", ówzględniających nieskończenie
dużą
sztywność podłużną elementów ( EA=
∞)
Rodzaje obciążeń dynamicznych konstrukcji budowlanych:
Obciążenia zmienne, nieprzemieszczające się (siły bezwładności obracających się
•
niewywa- żonych części maszyn wirnikowych).
Obciążenia udarowe (uderzenia spadających swobodnie ciał, napędzanych elementów
•
młotów
i kafarów, uderzenia pocisków, uderzenia kół pojazdów na nierównościach nawierzchni).
Obciążenia impulsowe (nagłe, krótkotrwałe, szybko zanikające jak np. fale ciśnień
•
podczas wybuchów)
Obciążenia ruchome (pojazdy przemieszczające się po konstrukcji)
•
Pulsacje ciśnień cieczy lub gazu (falowanie cieczy w zbiornikach, obciążenie wiatrem)
•
Obciążenia sejsmiczne i parasejsmiczne (trzęsienia ziemi, tąpnięcia)
•
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 3
Rys. 1.1 Przykłady określania dynamicznych stopni swobody
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 4
δ
st
Q
K
=
Oznaczając wielkość przemieszczenia statycznego jako
δ
d2
Q
K
Q
K
2
2 H
⋅
Q
K
⋅
+
−
=
δ
d1
Q
K
Q
K
2
2 H
⋅
Q
K
⋅
+
+
=
Pierwiastki tego kwadratowego równania względem
δ
d
wynoszą
K
δ
d
2
⋅
2 Q
⋅ δ
d
⋅
−
2 Q
⋅ H
⋅
−
0
=
Po przekształceniu równanie powyższe przyjmuje postać
Q H
δ
d
+
(
)
⋅
K
δ
d
2
⋅
2
=
Z porównania podanych wielkości
E
s
K
δ
d
2
⋅
2
=
Energia sprężysta zgromadzona w układzie:
L
z
Q H
δ
d
+
(
)
⋅
=
Rozwiązanie:
Na podstawie zasady zachowania energii można przyjąć, iż energia kinetyczna spadającego ciała
zostanie całkowicie zamieniona na energię potencjalną odkształcenia układu. Energia kinetyczna
w chwili maksymalnego ugięcia będzie równa pracy wykonanej przez siły zewnętrzne:
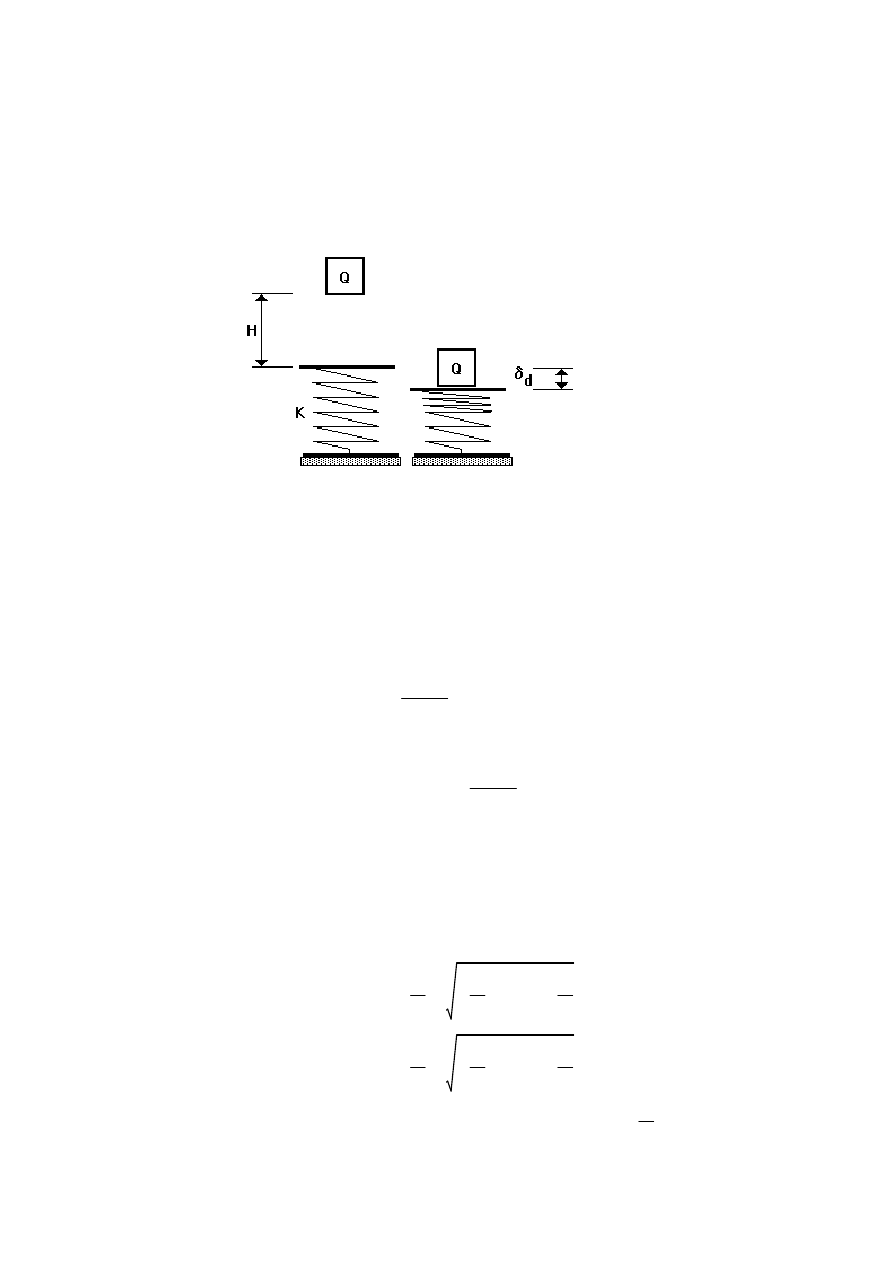
Wyznaczyć wielkość przemieszczenia dynamicznego
δ
d
przy swobodnym spadku ciężaru Q
z wyskości H. Sztywność ustroju reprezentuje stała K.
Przykład 1.1
Wpływ efektów dynamicznych na zachowanie się konstrukcji może nieco przybliżyć prosty
przykład zaczerpnięty jeszcze z przedmiotu "mechanika ogólna".
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 5
oraz zakładając zwiększenie przemieszczeń przy wpływach dynamicznych należy
uwzględnić większą wartość pierwiastka, przyjmując postać rozwiązania:
δ
d
δ
d1
=
δ
st
δ
st
2
2 H
⋅ δ
st
⋅
+
+
=
Można ją przekształcić następująco
δ
d
δ
st
1
1
2 H
⋅
δ
st
+
+
⋅
=
δ
st
β
⋅
=
Wyrażenie opisujące zależność
β
można teraz nazwać współczynnikiem dynamicznym,
wyrażającym wzrost przemieszczenia z tytułu dynamicznego oddziaływania:
β 1
1
2 H
⋅
δ
st
+
+
=
β 2
≥
Jak widać przyjmuje on znaczące wartości i nawet w przypadku zerowej wartości H
(nagłe obciążenie układu bez wysokości początkowej) osiąga wielkość 2 powodując
dwukrotne zwiększenie wartości przemieszczenia w stosunku do wilkości statycznej.
2. Kinematyka ruchu drgającego
Ruchem drgającym nazywamy taki ruch, w którym badana wielkość (współrzędna) q(t)
na przemian zbliża się i oddala od pewnej wartości przeciętnej. W dynamice budowli
taką wartość reprezentuje stan położenia równowagi statycznej (położenie obojętne).
Klasyfikacja ruchów drgających:
ze względu na przebieg w czasie
•
a) ustalone (periodyczne-okresowe),
b) nieustalone (aperiodyczne-nieokresowe),
ze względu na model reologiczny
•
a) nietłumione
b) tłumione
ze względu na model konstrukcji
•
a) dyskretne (skończona liczba stopni swobody)
b) ciągłe (nieskończona liczba stopni swobody)
ze względu na model fizyczny
•
a) liniowe
b) nieliniowe
ze względu na przyczynę drgań
•
a) swobodne
b) wymuszone
ze względu na formę przestrzenną
•
a) podłużne
b) giętne
c) skrętne
d) giętno-skrętne
e) mieszane
ze względu na na opis matematyczny funkcji wymuszającej
•
a) deterministyczne
b) niedeterministyczne (losowe)
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 6
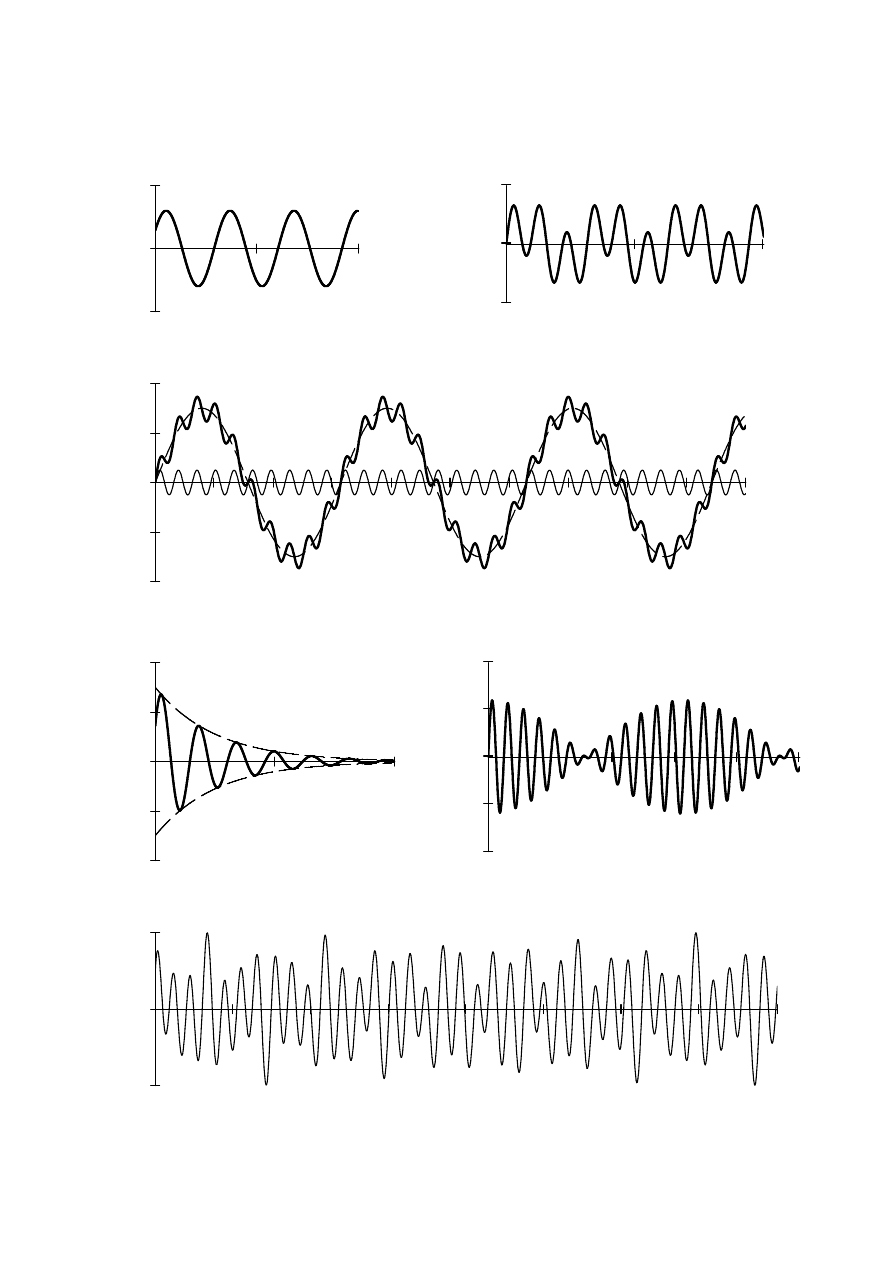
Zjawisko drgań dobrze ilustrują wykresy przedstawiające zmiany w czasie przemieszczeń lub
przyspieszeń wybranych punktów badanego układu. Przykłady wykresów ruchów drgających
zaprezentowano na rysunku 2.1.
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 7
A
1
sin
ϕ
1
( )
⋅
A
2
sin
ϕ
2
( )
⋅
+
A sin
ϕ
( )
⋅
=
(3.5)
A
1
cos
ϕ
1
( )
⋅
A
2
cos
ϕ
2
( )
⋅
+
A cos
ϕ
( )
⋅
=
Wprowadzając ponadto oznaczenia skracające zapis wielkości stałych
sin
ω t⋅ ϕ
2
+
(
)
sin
ω t⋅
( )
cos
ϕ
2
( )
⋅
sin
ϕ
2
( )
cos
ω t⋅
( )
⋅
+
=
(3.4)
sin
ω t⋅ ϕ
1
+
(
)
sin
ω t⋅
( )
cos
ϕ
1
( )
⋅
sin
ϕ
1
( )
cos
ω t⋅
( )
⋅
+
=
można zapisać
(3.3)
sin
α β
+
(
)
sin
α
( )
cos
β
( )
⋅
sin
β
( )
cos
α
( )
⋅
+
=
Wykorzystując zależność trygonometryczną
(3.2)
q t
( )
q
1
t
( )
q
2
t
( )
+
=
A
1
sin
ω t⋅ ϕ
1
+
(
)
⋅
A
2
sin
ω t⋅ ϕ
2
+
(
)
⋅
+
=
ruch złożony będzie opisywać równanie
q
2
t
( )
A
2
sin
ω t⋅ ϕ
2
+
(
)
⋅
=
(3.1)
Wśród wszystkich ruchów drgających szczególne miejsce zajmują drgania okresowe.
Drgania nazywamy okresowymi, jeżeli opisująca je funkcja q(t) jest okresowa, tj. gdy
istnieje taka dodatnia wielkość T [s], że w każdej chwili t zachodzi związek
q t
T
+
(
)
q t
( )
=
(2.1)
Najmniejsza z wielkości T, która spełnia powyższą zależność nazywana jest okresem drgań.
Część drgań zachodząca w trakcie jednego okresu nazywana jest cyklem drgań. Odwrotność
okresu (liczbę cykli w jednostce czasu) nazywa się częstością drgań (częstotliwością) f
wyrażaną w [Hz=cykl/s]
f
1
T
=
(2.2)
Największe odchylenie od położenia średniego nazywane jest amplitudą drgań A.
Najważniejszym przypadkiem szczególnym drgań okresowych są drgania harmoniczne
q t
( )
A sin
ω t⋅ ϕ
+
(
)
⋅
=
(2.3)
gdzie
ω 2 π
⋅ f⋅
=
2
π
⋅
T
=
[rad/s] jest częstością kolową (pulsacją) a
ϕ [rad] - fazą początkową
3. Synteza drgań harmonicznych
Punkt materialny lub nieodkształcalna bryła mogą wykonywać kilka ruchów harmonicznych
jednocześnie. Wypadkowy ruch tego punktu lub bryły jest superpozycją ruchów składowych.
3.1 Ruch złożony współosiowy o jednakowej częstości drgań składowych
W najprostszym przypadku, jeśli punkt wykonuje ruch złożony z dwóch składowych
o częstości
ω, amplitudach A
1
i A
2
oraz fazach początkowych
ϕ
1
i
ϕ
2
:
q
1
t
( )
A
1
sin
ω t⋅ ϕ
1
+
(
)
⋅
=
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 8
(3.14)
tan
ϕ
( )
1
n
i
A
i
sin
ϕ
i
( )
⋅
(
)
∑
=
1
n
i
A
i
cos
ϕ
i
( )
⋅
(
)
∑
=
=
(3.13)
A
1
n
i
A
i
cos
ϕ
i
( )
⋅
(
)
∑
=
2
1
n
i
A
i
sin
ϕ
i
( )
⋅
(
)
∑
=
2
+
=
Ruch wypadkowych będzie wówczas opisywać równanie (3.7) w którym:
(3.12)
q t
( )
A
1
sin
ω t⋅ ϕ
1
+
(
)
⋅
A
2
sin
ω t⋅ ϕ
2
+
(
)
⋅
+
....
+
A
n
sin
ω t⋅ ϕ
n
+
(
)
⋅
+
=
Zależność (3.9) wyznaczono po podzieleniu drugiego z równań (3.5) przez pierwsze.
Przeprowadzone rozważania będą również aktualne w przypadku, gdy równania
ruchu opisane zostaną funkcją cosinus zamiast sinus.
Rozważania powyższe można rozszerzyć na przypadek drgań będących sumą n
drgań harmonicznych:
(3.11)
cos
α β
−
(
)
cos
α
( )
cos
β
( )
⋅
sin
α
( )
sin
β
( )
⋅
+
=
oraz wykorzystanie zależności trygonometrycznej
3.10
(
)
A
1
cos
ϕ
1
( )
⋅
A
2
cos
ϕ
2
( )
⋅
+
(
)
2
A
1
sin
ϕ
1
( )
⋅
A
2
sin
ϕ
2
( )
⋅
+
(
)
2
+
A
2
=
Zależność (3.8) wyznaczono z równań (3.5) poprzez podniesienie ich obustronnie do kwadratu
i zsumowanie
(3.9)
tan
ϕ
( )
A
1
sin
ϕ
1
( )
⋅
A
2
sin
ϕ
2
( )
⋅
+
A
1
cos
ϕ
1
( )
⋅
A
2
cos
ϕ
2
( )
⋅
+
=
(3.8)
A
A
1
2
A
2
2
+
2 A
1
⋅
A
2
⋅
cos
ϕ
1
ϕ
2
−
(
)
⋅
+
=
gdzie
(3.7)
q t
( )
A sin
ω t⋅ ϕ
+
(
)
⋅
=
Ponownie korzystając z zależności (3.3) można równanie ruchu (3.6) zapisać krócej:
(3.6)
q t
( )
A sin
ω t⋅
( )
cos
ϕ
( )
⋅
sin
ϕ
( )
cos
ω t⋅
( )
⋅
+
(
)
⋅
=
wyrażenie (3.2) przyjmie postać
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 9
(3.17)
q t
( )
q
1
t
( )
q
2
t
( )
+
=
A
1
sin
2
π
⋅
T
1
t
⋅ ϕ
1
+
⋅
A
2
sin
2
π
⋅
T
2
t
⋅ ϕ
2
+
⋅
+
=
Ruch wypadkowy nie jest ruchem harmonicznym. Można jednak zapisać
T
2
2
π
⋅
ω
2
=
T
1
2
π
⋅
ω
1
=
(3.16)
Oznaczając okresy ruchów składowych jako
q
2
t
( )
A
2
sin
ω
2
t
⋅ ϕ
2
+
(
)
⋅
=
(3.15)
q
1
t
( )
A
1
sin
ω
1
t
⋅ ϕ
1
+
(
)
⋅
=
Rozważany jest ruch złożony o składowych:
3.2 Ruch złożony współosiowy o różnych częstościach drgań składowych
Skladowa 1
Skladowa 2
Ruch wypadkowy
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
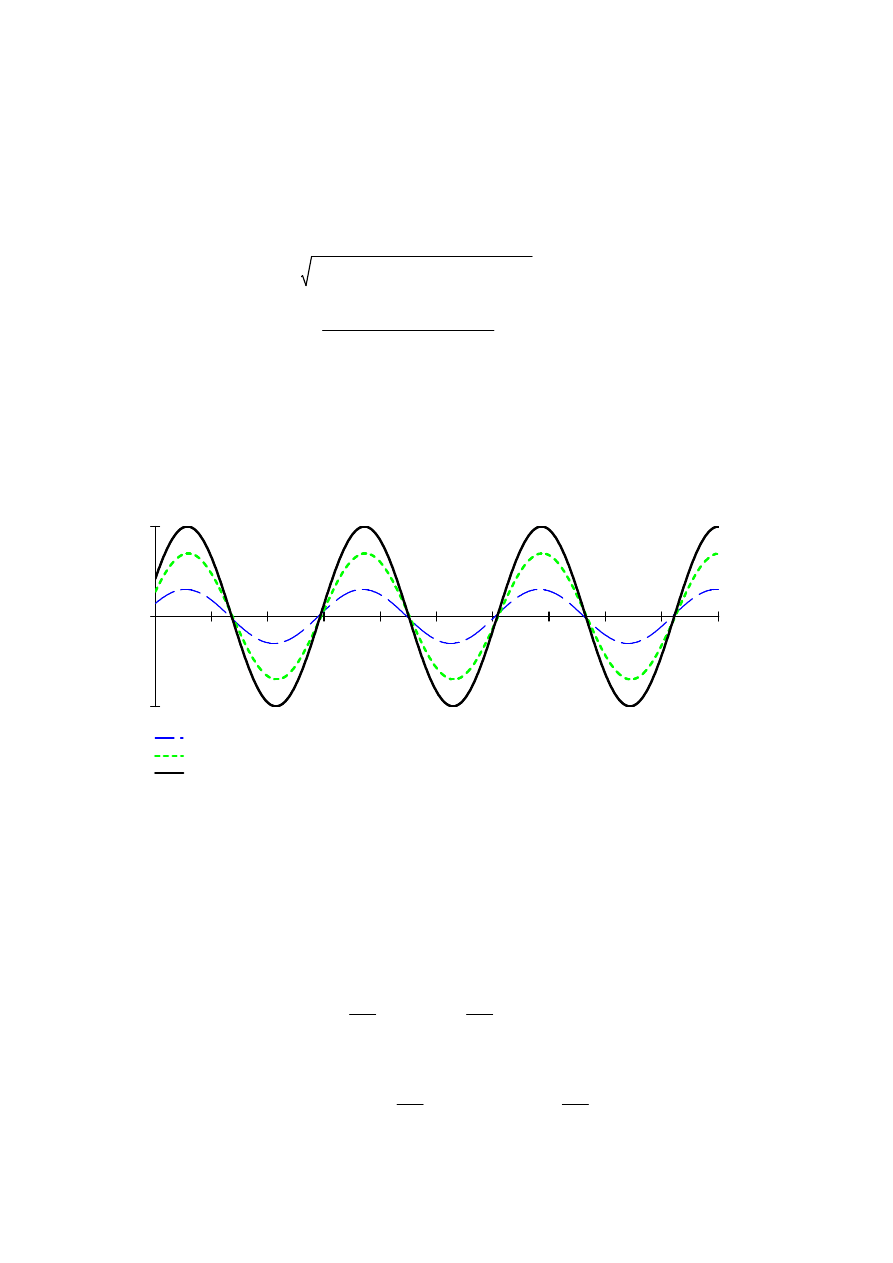
Graficzne przedstawienie rozwiązania:
q t
( )
9.99 sin 2 t
⋅ 0.43
+
(
)
⋅
=
Ruch wypadkowy opisuje zależność
ϕ 0.43
=
stąd
tan
ϕ 0.459
=
tan
ϕ
3 sin 0.5
(
)
⋅
7 sin 0.4
(
)
⋅
+
3 cos 0.5
(
)
⋅
7 cos 0.4
(
)
⋅
+
=
A
9.99
=
A
3
2
7
2
+
2 3
⋅ 7
⋅ cos 0.5 0.4
−
(
)
⋅
+
=
Amplituda i faza ruchu według zależności (3.8) i (3.9)
q
2
t
( )
7 sin 2 t
⋅ 0.4
+
(
)
=
q
1
t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
=
Wyznaczyć parametry ruchu złożonego punktu, określonego składowymi
Przykład 3.1
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 10
(3.23)
q t
( )
q
1
t
( )
q
2
t
( )
+
=
A
1
sin
ω
1
t
⋅ ϕ
1
+
(
)
⋅
A
2
sin
ω
1
∆ω
+
(
)
t
⋅ ϕ
2
+
⋅
+
=
Ruch wypadkowy opisuje funkcja
q
2
t
( )
A
2
sin
ω
1
∆ω
+
(
)
t
⋅ ϕ
2
+
⋅
=
(3.22)
q
1
t
( )
A
1
sin
ω
1
t
⋅ ϕ
1
+
(
)
⋅
=
Interesujący przypadek występuje wtedy, gdy ruch wypadkowy składa się z dwu drgań
niewspółmiernych o częstościach bardzo mało różniących się
∆ω 〈 〈 ω
1
:
(3.21)
max q t
( )
⋅
1
n
i
A
i
∑
=
≤
Jeśli przynajmniej jedna z liczb n
1
lub n
2
nie jest liczbą całkowitą, wówczas iloczyny
2
πn
1
i 2
πn
2
nie nie są wielokrotnościami 2
π i zalezność (3.20) nie jest spełniona.
Oznacza to, iż ruch wypadkowy nie jest wówczas ruchem okresowym.
Rozważania powyższe są prawdziwe również w przypadku n składowych drgań. Wykres
ruchu wypadkowego może mieć różnorodne kształty, lecz największe wychylenie nie może
przewyższyć sumy amplitud składowych:
(3.20)
A
1
sin
ω
1
t
⋅ ϕ
1
+
(
)
⋅
A
2
sin
ω
2
t
⋅ ϕ
2
+
(
)
⋅
+
q t
( )
=
=
A
1
sin
2
π
⋅
T
1
t
⋅ ϕ
1
+
2
π
⋅ n
2
⋅
+
⋅
A
2
sin
2
π
⋅
T
2
t
⋅ ϕ
2
+
2
π
⋅ n
1
⋅
+
⋅
+
=
=
A
1
sin
2
π
⋅
T
1
t
n
2
T
1
⋅
+
(
)
⋅
ϕ
1
+
⋅
A
2
sin
2
π
⋅
T
2
t
n
1
T
2
⋅
+
(
)
⋅
ϕ
2
+
⋅
+
=
q t
T
+
(
)
A
1
sin
2
π
⋅
T
1
t
T
+
(
)
⋅
ϕ
1
+
⋅
A
2
sin
2
π
⋅
T
2
t
T
+
(
)
⋅
ϕ
2
+
⋅
+
=
=
Korzystając z definicji ruchu okresowego wg zależności (2.1) można obliczyć
Okres T ruchu wypadkowego jest więc najmniejszą współną wielokrotnością okresów
ruchów składowych. Jeśli liczby n
1
i n
2
są liczbami małymi to okres T jest porównywalny
z okresami składowych. W przypadku przeciwnym może być wielokrotnie większy.
(3.19)
T
n
2
T
2
⋅
=
n
1
T
2
⋅
=
Założenie (3.18) pozwala na przyjęcie wypadkowego okresu
gdzie n
1
i n
2
są najmniejszymi z liczb naturalnych spełniającymi powyższą zależność.
T
1
T
2
n
1
n
2
=
(3.18)
Jeśli stosunek okresów składowych daje się wyrazić przez stosunek dwóch liczb
naturalnych to są one współmierne. Zachodzi wówczas związek
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 11
A
1
A
2
=
Zjawisko to nosi nazwę dudnienia i jest szczególnie wyraźne jeśli
(3.32)
τ
2
π
⋅
∆ω
=
(3.31)
A
1
A
2
−
A
≤
A
1
A
2
+
≤
Ruch wypadkowy przypomina zatem ruch harmoniczny o częstości
ω
1
, ale amplituda zmienia
w czasie swą wartość według funkcji o okresie
τ (τ >> T
1
i T
2
)
:
(3.30)
tan
ϕ tanϕ t()
=
sin
ϕ
1
( )
A
1
⋅
sin t
∆ω
⋅
( )
A
2
⋅
+
cos
ϕ
1
( )
A
1
⋅
cos t
∆ω
⋅
( )
A
2
⋅
+
=
(3.29)
A
1
2
A
2
2
+
2 A
1
⋅
A
2
⋅
cos
∆ω t⋅ ϕ
1
−
(
)
⋅
+
=
=
A
A t
( )
=
cos
ϕ
1
( )
A
1
⋅
cos t
∆ω
⋅
( )
A
2
⋅
+
(
)
2
sin
ϕ
1
( )
A
1
⋅
sin t
∆ω
⋅
( )
A
2
⋅
+
(
)
2
+
=
Mamy do czynienia z drganiami, których amplituda i faza jest funkcją czasu. Przyjmując
odpowiednio układ współrzędnych zawsze można doprowadzić do sytuacji, gdy
ϕ
2
=0.
Wyrażenia (3.27) i (3.28) upraszczają się do postaci:
(3.28)
tan
ϕ tanϕ t()
=
sin
ϕ
1
( )
A
1
⋅
sin t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
cos t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
+
(
)
A
2
⋅
+
cos
ϕ
1
( )
A
1
⋅
cos t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
sin t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
−
(
)
A
2
⋅
+
=
(3.27)
A
A t
( )
=
cos
ϕ
1
( )
A
1
⋅
cos t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
sin t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
−
(
)
A
2
⋅
+
2
sin
ϕ
1
( )
A
1
⋅
sin t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
cos t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
+
(
)
A
2
⋅
+
2
+
...
=
gdzie
(3.26)
q t
( )
A sin
ω
1
t
⋅ ϕ
+
(
)
⋅
=
otrzymuje się zależność
sin
ϕ
1
( )
A
1
⋅
sin t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
cos t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
+
(
)
A
2
⋅
+
A sin
Ω
( )
⋅
=
(3.25)
cos
ϕ
1
( )
A
1
⋅
cos t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
sin t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
−
(
)
A
2
⋅
+
A cos
Ω
( )
⋅
=
Przyjmując poniższe tożsamości
(3.24)
q t
( )
cos
ϕ
1
( )
A
1
⋅
cos t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
sin t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
−
(
)
A
2
⋅
+
sin
ω
1
t
⋅
( )
⋅
sin
ϕ
1
( )
A
1
⋅
sin t
∆ω
⋅
( )
cos
ϕ
2
( )
⋅
cos t
∆ω
⋅
( )
sin
ϕ
2
( )
⋅
+
(
)
A
2
⋅
+
cos
ω
1
t
⋅
( )
⋅
+
...
=
Korzystając z przekształceń trygonometrycznych uzyskuje się
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 12
Przykład 3.2
Wyznaczyć równanie ruchu określonego składowymi o współmiernych okresach drgań
q
1
t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
=
q
2
t
( )
7 sin 4 t
⋅ 0.04
+
(
)
=
q t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
7 sin 4 t
⋅ 0.04
+
(
)
⋅
+
=
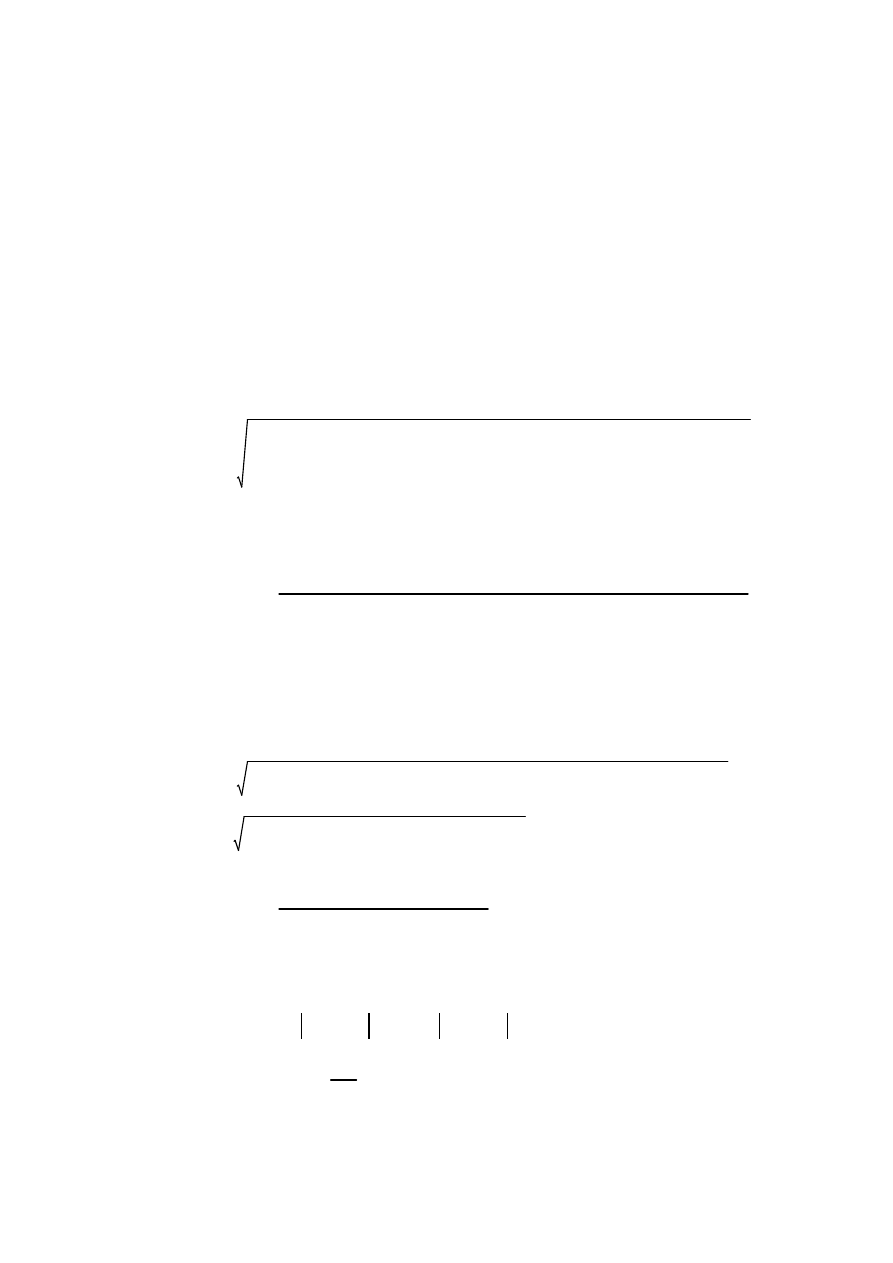
Graficzne przedstawienie rozwiązania:
Skladowa 1
Skladowa 2
Ruch wypadkowy
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Przykład 3.3
Wyznaczyć równanie ruchu określonego składowymi
q
1
t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
=
q
2
t
( )
7 sin 3.5 t
⋅ 0.04
+
(
)
=
q t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
7 sin 3.5 t
⋅ 0.04
+
(
)
⋅
+
=
Graficzne przedstawienie rozwiązania:
Skladowa 1
Skladowa 2
Ruch wypadkowy
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 13
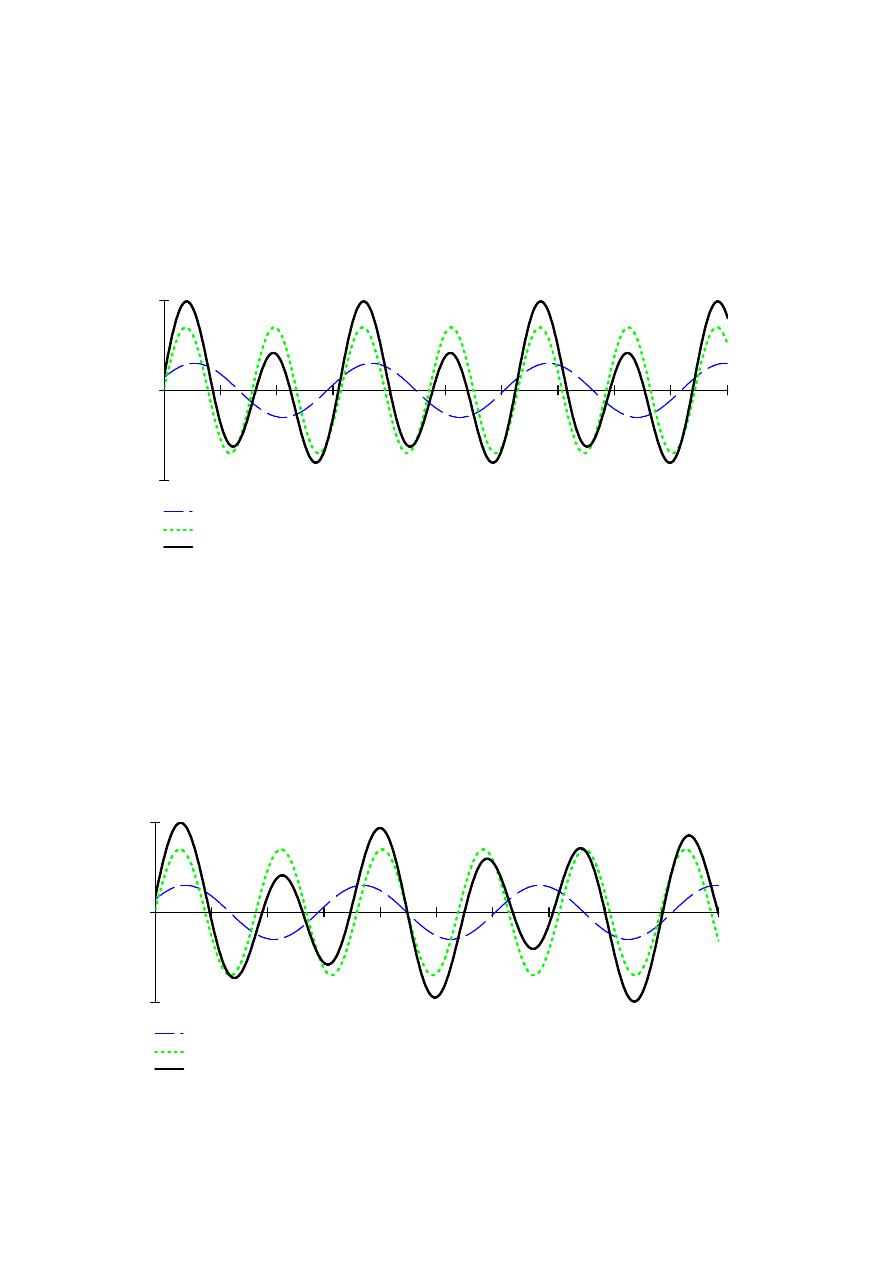
Skladowa 1
Skladowa 2
Ruch wypadkowy
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Graficzne przedstawienie rozwiązania:
q t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
0.8 sin 9.5 t
⋅ 0.04
+
(
)
⋅
+
=
q
2
t
( )
0.8 sin 9.5 t
⋅ 0.04
+
(
)
=
q
1
t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
=
ω
1
〈 〈 ω
2
oraz
A
2
〈 〈 A
1
Wyznaczyć równanie ruchu określonego składowymi gdzie
Przykład 3.5
Skladowa 1
Skladowa 2
Ruch wypadkowy
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Graficzne przedstawienie rozwiązania:
q t
( )
2 sin 2 t
⋅ 0.5
+
(
)
⋅
7 sin 9 t
⋅ 0.04
+
(
)
⋅
+
=
q
2
t
( )
7 sin 9 t
⋅ 0.04
+
(
)
=
q
1
t
( )
2 sin 2 t
⋅ 0.5
+
(
)
⋅
=
ω
1
〈 〈 ω
2
oraz
A
1
〈 〈 A
2
Wyznaczyć równanie ruchu określonego składowymi gdzie
Przykład 3.4
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 14
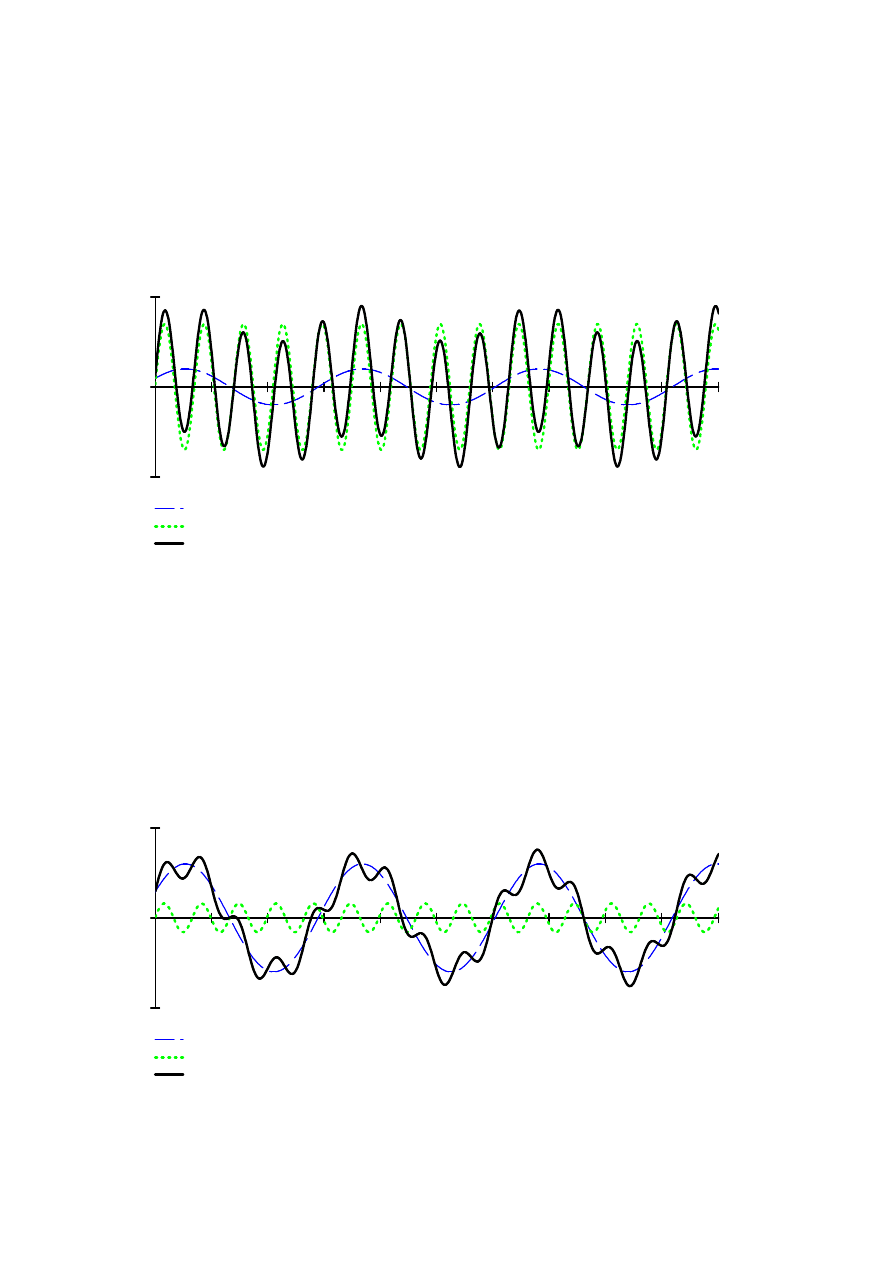
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Graficzne przedstawienie rozwiązania:
τ 4.189
=
τ
2
π
⋅
1.5
=
q t
( )
7 sin 10 t
⋅ 0.5
+
(
)
⋅
7 sin 11.5 t
⋅
(
)
⋅
+
=
T
2
0.546
=
T
2
2
π
⋅
11.5
=
q
2
t
( )
7 sin 11.5 t
⋅
(
)
=
T
1
0.628
=
T
1
2
π
⋅
10
=
q
1
t
( )
7 sin 10 t
⋅ 0.5
+
(
)
⋅
=
Wyznaczyć równanie ruchu określonego składowymi
Przykład 3.7
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
Graficzne przedstawienie rozwiązania:
τ 4.189
=
τ
2
π
⋅
1.5
=
q t
( )
2 sin 10 t
⋅ 0.5
+
(
)
⋅
8 sin 11.5 t
⋅
(
)
⋅
+
=
T
2
0.546
=
T
2
2
π
⋅
11.5
=
q
2
t
( )
8 sin 11.5 t
⋅
(
)
=
T
1
0.628
=
T
1
2
π
⋅
10
=
q
1
t
( )
2 sin 10 t
⋅ 0.5
+
(
)
⋅
=
Wyznaczyć równanie ruchu określonego składowymi
Przykład 3.6
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 15
powtórzą się liczby okresów dla obu funkcji i krzywa będąca torem zamknię się. W przeciwnym
przypadku tor punktu będzie krzywą otwartą. W zależności od stosunku amplitud, okresów i faz
początkowych tor ma postać krzywych mniej lub bardziej skomplikowanych, nazywanych
liniami lub figurami Lissajous.
(3.37)
T
n
1
T
1
⋅
n
2
T
2
⋅
+
=
to ruch wypadkowy będzie również krzywoliniowy, lecz na ogół nieokresowy. Można wykazać,
że będzie on okresowy tylko wóczas gdy częstości
ω
1
i
ω
2
są współmierne. Jeśli n
1
i n
2
będą
liczbami całkowitymi to po czasie
q
y
t
( )
A
2
sin
ω
2
t
⋅ ϕ
2
+
(
)
⋅
=
(3.36)
q
x
t
( )
A
1
sin
ω
1
t
⋅ ϕ
1
+
(
)
⋅
=
W przypadku, gdy składowe ruchu mają różne częstości
W zależności od różnicy faz równanie toru przybiera różne formy.
(3.35)
q
x
2
A
1
2
q
y
2
A
2
2
+
2
q
x
A
1
⋅
q
y
A
2
⋅
cos
ϕ
2
ϕ
1
−
(
)
⋅
−
sin
2
ϕ
2
ϕ
1
−
(
)
=
Po obustronnym podniesieniu do kwadratu i uporządkowaniu uzyskuje się równanie toru
(3.35)
q
y
t
( )
A
2
q
x
t
( )
A
1
cos
ϕ
2
ϕ
1
−
(
)
⋅
−
sin
ϕ
2
ϕ
1
−
(
)
1
q
x
t
( )
A
1
2
−
⋅
=
Następnie otrzymuje się
(3.34)
q
x
t
( )
A
1
cos
ϕ
2
ϕ
1
−
(
)
⋅
sin
ϕ
2
ϕ
1
−
(
)
1
q
x
t
( )
A
1
2
−
⋅
+
=
=
sin
ω t⋅ ϕ
1
+
(
)
cos
ϕ
2
ϕ
1
−
(
)
⋅
sin
ϕ
2
ϕ
1
−
(
)
cos
ω t⋅ ϕ
1
+
(
)
⋅
+
=
=
q
y
t
( )
A
2
sin
ω t⋅ ϕ
1
+
ϕ
2
+
ϕ
1
−
(
)
=
to ruch wypadkowy będzie ogólnie ruchem okresowym, krzywoliniowym i płaskim,
przy czym tor punktu będzie krzywą zamkniętą. Równanie ruchu otrzymuje się rugując
z równań (3.33) czas t. Uzyskuje się w ten sposób równanie krzywej stożkowej, która
na ogół będzie elipsą. W tym celu drugie z równań (3.33) przepisuje się postaci:
q
y
t
( )
A
2
sin
ω t⋅ ϕ
2
+
(
)
⋅
=
(3.33)
q
x
t
( )
A
1
sin
ω t⋅ ϕ
1
+
(
)
⋅
=
Jeśli składowe ruchu występują z jednakowymi częstościami
3.3 Ruch złożony z ruchów odbywających się w dwóch prostopadłych kierunkach
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
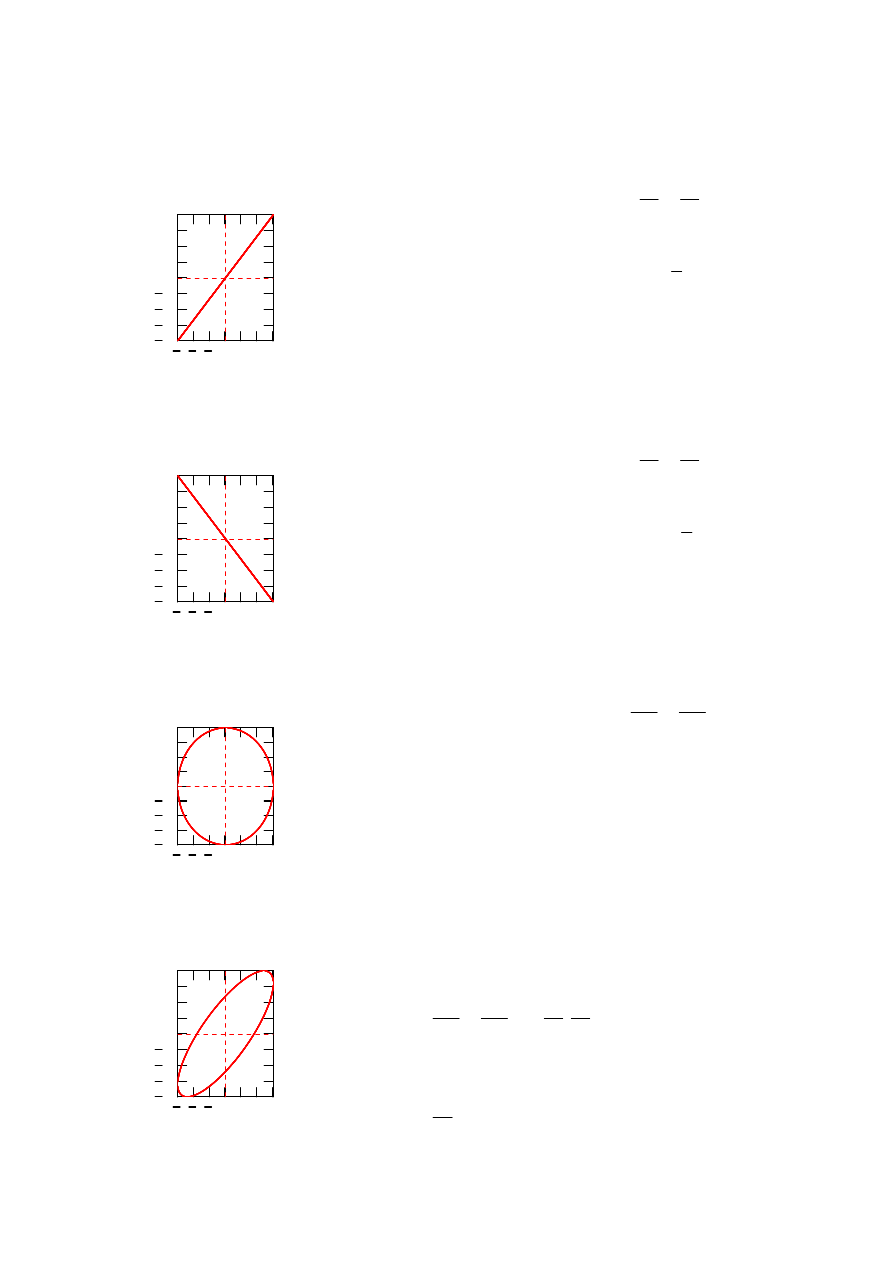
Mechanika budowli
______________________________________________________________________________________________ 16
stąd
q
y
4
3
− q
x
⋅
=
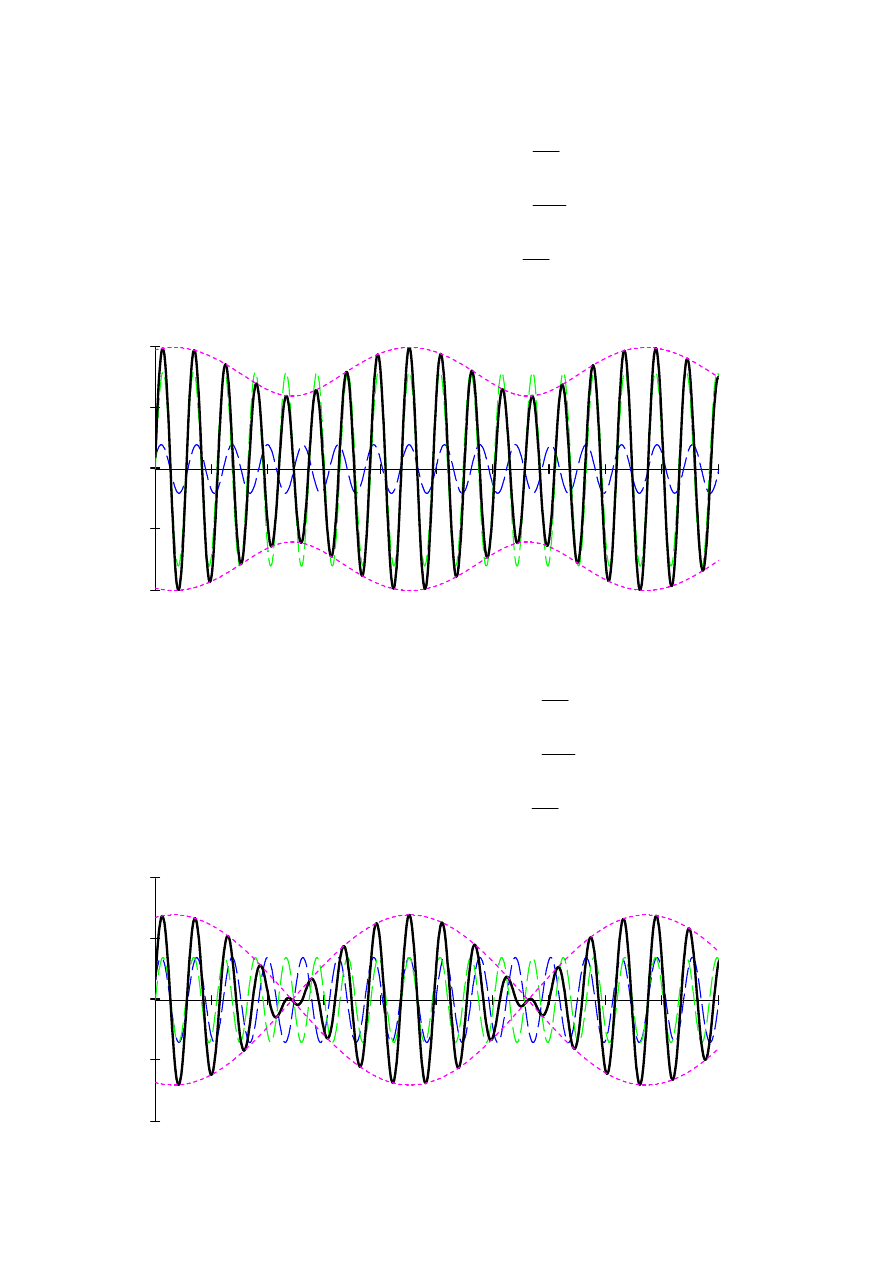
c)
q
x
t
( )
3 sin 2 t
⋅
(
)
⋅
=
różnica faz
ϕ
2
ϕ
1
−
0.5
π
=
q
y
t
( )
4 sin 2 t
⋅ 0.5π
+
(
)
=
3 2 1 0 1 2 3
4
3
2
1
0
1
2
3
4
0
0
równanie toru wg (3.35)
q
x
2
3
2
q
y
2
4
2
+
1
=
d)
q
x
t
( )
3 sin 2 t
⋅ 2.5
+
(
)
⋅
=
różnica faz
q
y
t
( )
4 sin 2 t
⋅ π
+
(
)
=
ϕ
2
ϕ
1
−
π 2.5
−
=
0.642
=
3 2 1 0 1 2 3
4
3
2
1
0
1
2
3
4
0
0
równanie toru wg (3.35)
q
x
2
3
2
q
y
2
4
2
+
2
q
x
3
⋅
q
y
4
⋅
cos 0.642
(
)
⋅
−
sin
2
0.642
(
)
=
czyli ostatecznie
16
9
q
x
2
q
y
2
+
0.133 q
x
⋅ q
y
⋅
−
5.737
=
Przykład 3.8
Wyznaczyć i zilustrować graficznie równania toru
a)
q
x
t
( )
3 sin 2 t
⋅ 0.5
+
(
)
⋅
=
różnica faz
ϕ
2
ϕ
1
−
0
=
q
y
t
( )
4 sin 2 t
⋅ 0.5
+
(
)
=
3 2 1 0 1 2 3
4
3
2
1
0
1
2
3
4
0
0
równanie toru wg (3.35)
q
x
3
q
y
4
−
2
0
=
stąd
q
y
4
3
q
x
⋅
=
b)
q
x
t
( )
3 sin 2 t
⋅ π
+
(
)
⋅
=
różnica faz
ϕ
2
ϕ
1
−
π
−
=
q
y
t
( )
4 sin 2 t
⋅
(
)
=
3 2 1 0 1 2 3
4
3
2
1
0
1
2
3
4
0
0
równanie toru wg (3.35)
q
x
3
q
y
4
+
2
0
=
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 17
0
0
0
0
q
y
t
( )
3 sin 1 t
⋅ 0.6
+
(
)
=
q
y
t
( )
3 sin 1 t
⋅
(
)
=
q
x
t
( )
3 sin 2 t
⋅ 4
+
(
)
⋅
=
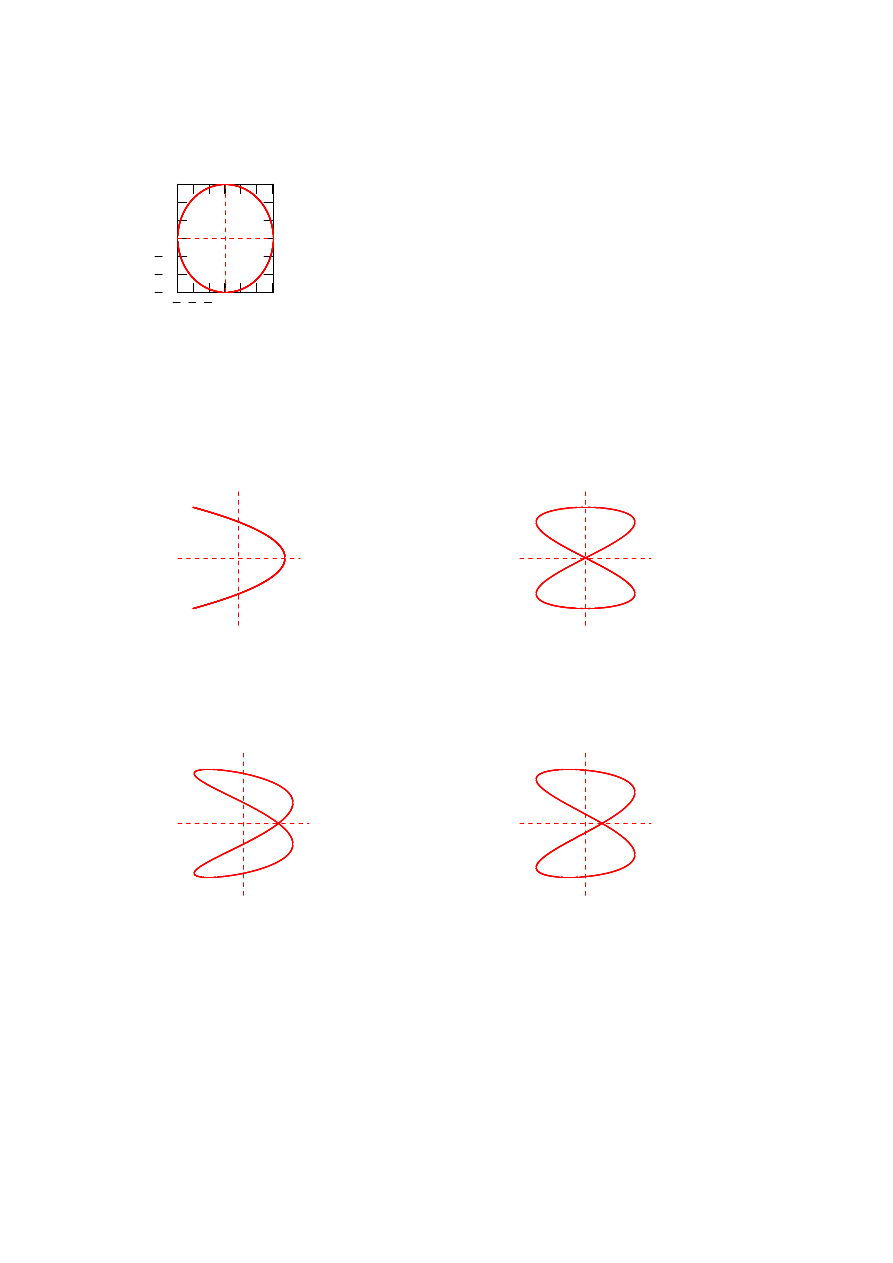
d)
q
x
t
( )
3 sin 2 t
⋅ 0.75π
+
(
)
⋅
=
c)
0
0
0
0
q
y
t
( )
3 sin 1 t
⋅
(
)
=
q
y
t
( )
3 sin 1 t
⋅
(
)
=
q
x
t
( )
3 sin 2 t
⋅
(
)
⋅
=
b)
q
x
t
( )
3 sin 2 t
⋅ 0.5π
+
(
)
⋅
=
a)
Wyznaczyć i zilustrować graficznie równania toru
Przykład 3.9
q
x
2
q
y
2
+
9
=
równanie toru wg (3.35)
3 2 1 0 1 2 3
3
2
1
0
1
2
3
0
0
ϕ
2
ϕ
1
−
0.5
− π
=
q
y
t
( )
3 sin 2 t
⋅
(
)
=
różnica faz
q
x
t
( )
3 sin 2 t
⋅ 0.5π
+
(
)
⋅
=
e)
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
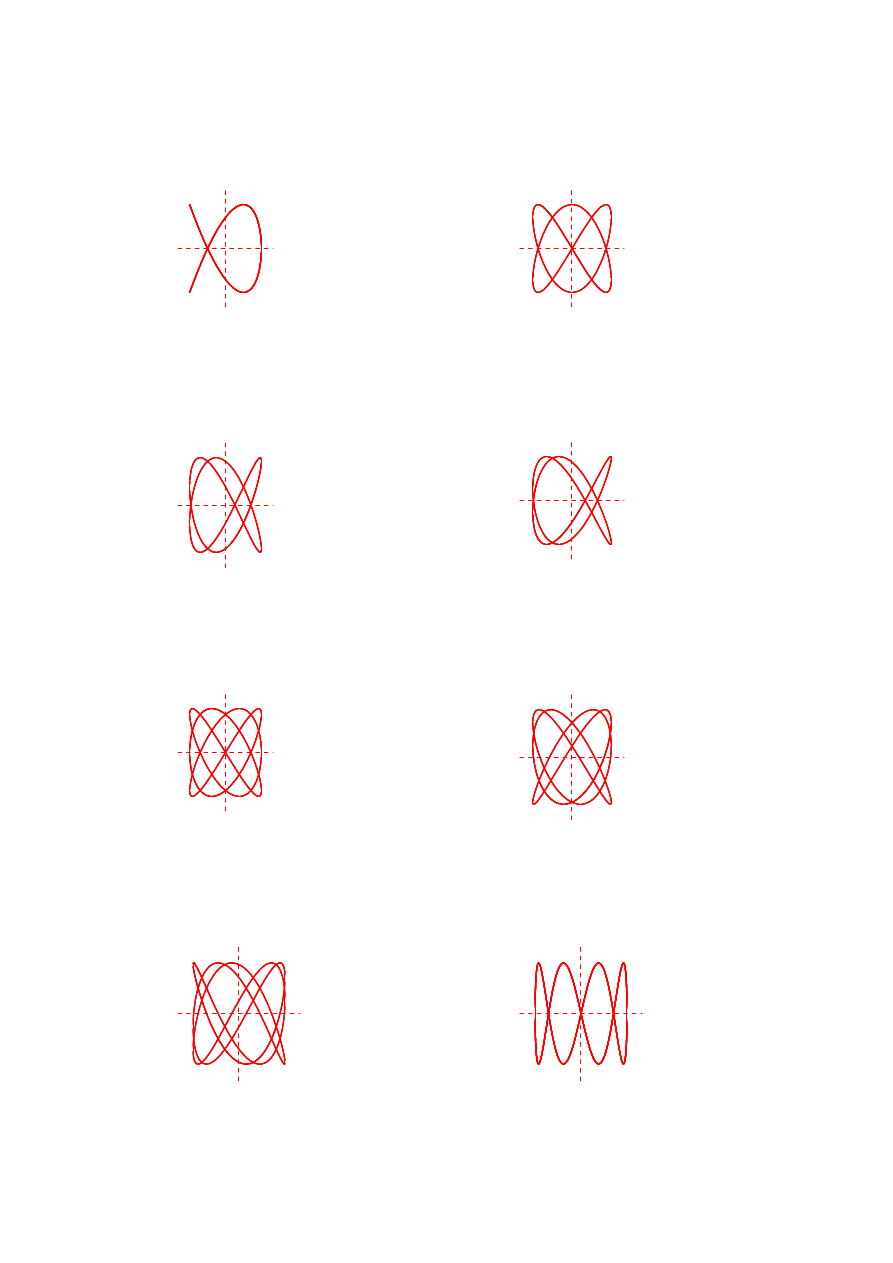
Mechanika budowli
______________________________________________________________________________________________ 18
0
0
0
0
q
y
t
( )
3 sin 12 t
⋅
(
)
=
q
y
t
( )
3 sin 5 t
⋅
(
)
=
q
x
t
( )
3 sin 3 t
⋅
(
)
⋅
=
l)
q
x
t
( )
3 sin 3 t
⋅ 0.75π
+
(
)
⋅
=
k)
0
0
0
0
q
y
t
( )
3 sin 4 t
⋅ 5
+
(
)
=
q
y
t
( )
3 sin 4 t
⋅
(
)
=
q
x
t
( )
3 sin 3 t
⋅ π
+
(
)
⋅
=
j)
q
x
t
( )
3 sin 3 t
⋅ 0.5π
+
(
)
⋅
=
i)
0
0
0
0
q
y
t
( )
3 sin 3 t
⋅ 1.8
+
(
)
=
q
y
t
( )
3 sin 3 t
⋅
(
)
=
q
x
t
( )
3 sin 2 t
⋅ 4
+
(
)
⋅
=
h)
q
x
t
( )
3 sin 2 t
⋅ 0.75π
+
(
)
⋅
=
g)
0
0
0
0
q
y
t
( )
3 sin 3 t
⋅
(
)
=
q
y
t
( )
3 sin 3 t
⋅
(
)
=
q
x
t
( )
3 sin 2 t
⋅
(
)
⋅
=
f)
q
x
t
( )
3 sin 2 t
⋅ 0.5π
+
(
)
⋅
=
e)
2005-02-28
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Wyszukiwarka
Podobne podstrony:
Mechanika Budowli Sem[1][1] VI Wyklad 04
Mechanika Budowli Sem[1][1] VI Wyklad 01
Mechanika Budowli Sem[1][1] VI Wyklad 05
Mechanika Budowli Sem[1][1] VI Wyklad 04
Konstrukcje metalowe Sem VI Wyklad 02
Konstrukcje metalowe Sem VI Wyklad 04
sem VI FŚ k-z 02, UCZELNIA ARCHIWUM, UCZELNIA ARCHIWUM WGiG, WGiG Rok III sem VI (2013-2014), sem VI
Konstrukcje metalowe Sem VI Wyklad 03
Mechanika Budowli sem 4 i5 tematy egzaminu
harmonogram CWICZ, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, matreiały na mb
Mecha- belka, Sem V, Mechanika Budowli Proj, Mechanika Budowli, Belka
wstep do zadan, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, EGZ, egzam
mechanika budowli projekt (28 02 2010 r )
MECHANIKA BUDOWLI projekt 1 , sem IV (1)
więcej podobnych podstron