
Mechanika budowli
______________________________________________________________________________________________ 53
(7.74)
q t
( )
q
o
cos
ω t⋅
( )
⋅
v
o
ω
sin
ω t⋅
( )
⋅
+
1
ω
0
t
τ
sin
ω t τ
−
( )
⋅
f
τ
( )
⋅
⌠
⌡
d
⋅
+
=
Dokonując na równaniu (7.73) odwrotnej transformacji Laplace'a znajdujemy poszukiwane
równanie ruchu
(7.73)
Q s
( )
s q
o
⋅
v
o
+
s
2
ω
2
+
F s
( )
s
2
ω
2
+
+
=
q
o
s
s
2
ω
2
+
⋅
v
o
ω
ω
s
2
ω
2
+
⋅
+
ω
s
2
ω
2
+
F s
( )
ω
⋅
+
=
Wyznaczając funkcję Q(s) uzyskujemy
(7.72)
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
ω
2
Q s
( )
⋅
+
F s
( )
=
Wykorzystując powyższe, równanie (7.69) zapisujemy jako
L
f t
( )
(
)
F s
( )
=
L
ω
2
q
⋅
( )
ω
2
Q s
( )
⋅
=
L
d
2
q t
( )
d t
2
s
2
Q s
( )
⋅
s q 0
( )
⋅
−
d q 0
( )
d t
−
=
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
=
Rozpisując poszczególne składniki, oraz wykorzystując (7.19) otrzymujemy
(7.71)
L
d
2
q
d t
2
ω
2
q
⋅
+
L
f t
( )
(
)
=
Rozwiązania równania (7.75) poszukujemy metodą transformacji Laplace'a:
wg (7.16)
ω
(7.76)
f t
( )
P t
( )
m
=
gdzie
(7.75)
d
2
q
d t
2
ω
2
q
⋅
+
f t
( )
=
Po przekształceniu do wygodniejszej postaci matematycznej będzie ono wyglądać następująco
(7.74)
m
d
2
q
d t
2
⋅
k q
⋅
+
P t
( )
=
W przypadku drgań pod wpływem sił wymuszających, przy pominięciu wpływu tłumienia
równania ruchu układu o jednym stopniu swobody opisuje równanie:
7.3 Drgania wymuszone nietłumione.
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 54
(7.77)
1
ω
0
t
τ
sin
ω t τ
−
( )
⋅
P
o
m
⋅
⌠
⌡
d
⋅
P
o
m
ω
⋅
0
t
τ
sin
ω t τ
−
( )
⋅
⌠
⌡
d
⋅
=
i trzeci wyraz równania (7.74) lub (7.75) będzie wyglądał następująco
f t
( )
P
o
m
=
wówczas
(stała siła nagle przyłożona)
P t
( )
P
o
=
const
=
Jeśli wymuszenie jest opisane funkcją
Pominięte drgania opisane pierwszymi dwoma członami rozwiązania (7.74) nazywane
są procesem przejściowym.
(7.75)
q t
( )
1
ω
0
t
τ
sin
ω t τ
−
( )
⋅
f
τ
( )
⋅
⌠
⌡
d
⋅
=
Jeśli przyjmiemy zerowe warunki początkowe lub uwzględnimy, że w praktycznych przypadkach
drgania własne będą zanikały (w rzeczywistości zawsze występuje tłumienie) zależność (7.74)
uprości się do postaci:
Ostateczna postać rozwiązania (7.74) zależy od funkcji f(
τ)
L
1
−
ω
s
2
ω
2
+
F s
( )
ω
⋅
1
ω
0
t
τ
sin
ω t τ
−
( )
⋅
f
τ
( )
⋅
⌠
⌡
d
⋅
=
otrzymujemy zależność
L
1
−
F s
( )
ω
f t
( )
ω
=
f
2
t
( )
=
L
1
−
ω
s
2
ω
2
+
sin
ω t⋅
( )
=
f
1
t
( )
=
którym odpowiadają
F
2
s
( )
F s
( )
ω
=
F
1
s
( )
ω
s
2
ω
2
+
=
W naszym przypadku
(7.75)
L
0
t
t
f
1
t
τ
−
( )
f
2
τ
( )
⋅
⌠
⌡
d
F
1
s
( ) F
2
s
( )
⋅
=
prawdziwa jest zależność
ich transformatami Laplace'a
F
1
s
( ) F
2
s
( )
,
są oryginałami, natomiast
f
1
t
( ) f
2
t
( )
,
Jeżeli
Dwa pierwsze człony rozwiązania są identyczne z równaniem (7.22) i opisują drgania
swobodne układu bez tłumienia. Człon trzeci opisuje drgania wywołane siłą f(t). W ogólnym
przypadku wypadkowe drgania nie będą okresowe. Ostatni człon uzyskano wykorzystując
twierdzenie Borela o splocie funkcji:
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 55
1
ω
0
t
τ
sin
ω t τ
−
( )
⋅
P
o
m
⋅
sin
Θ τ
⋅
( )
⋅
⌠
⌡
d
⋅
P
o
m
ω
⋅
0
t
τ
sin
ω t τ
−
( )
⋅
sin
Θ τ
⋅
( )
⋅
⌠
⌡
d
⋅
=
a następnie z zależności (7.75) otrzymujemy
(7.80)
f t
( )
P
o
m
sin
Θ t⋅
( )
⋅
=
obliczamy
P t
( )
P
o
sin
Θ t⋅
( )
⋅
=
W przypadku gdy drgania wymuszone są siłą harmoniczną
Czas t
P
rz
em
ie
sz
cz
en
ie
δ
st
2
δ
st
⋅
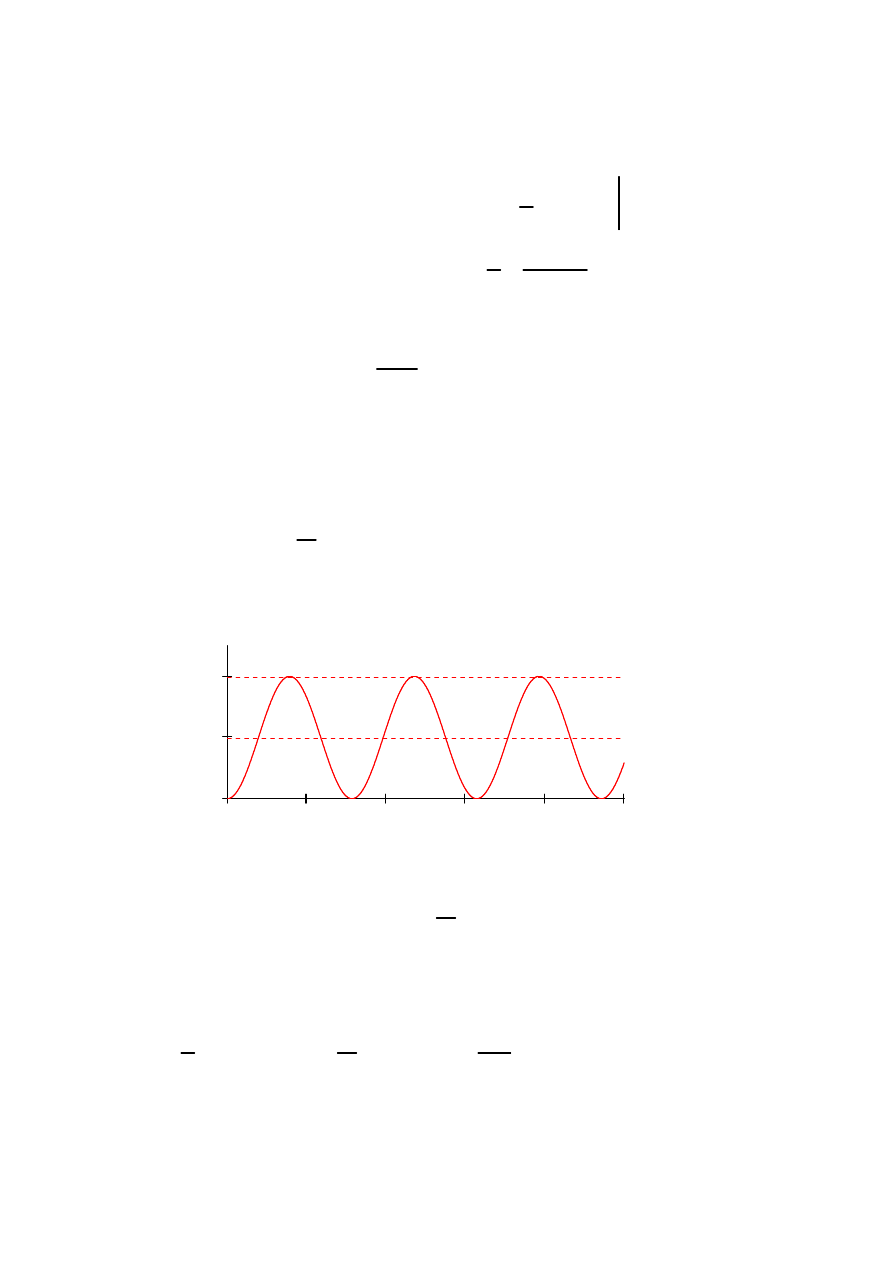
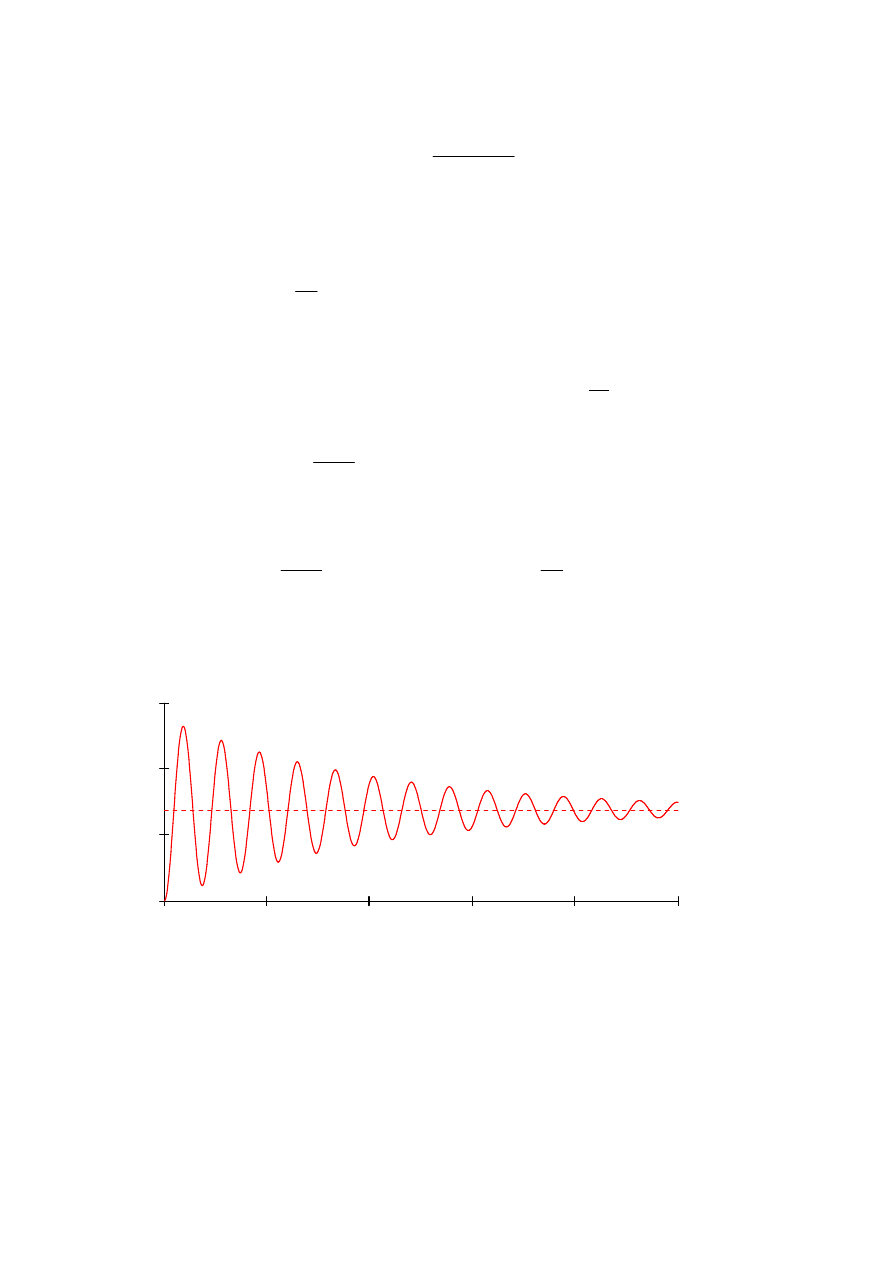
Przebieg drgań opisanych zależnością (7.78) można zilustrować przykładowym wykresem
oznacza statyczne przemieszczenie pod działaniem siły P
o
δ
st
P
o
k
=
gdzie wielkość
(7.79)
q t
( )
δ
st
1
cos
ω t⋅
( )
−
(
)
⋅
=
rozwiązanie to można przepisać jako
m
ω
2
⋅
k
=
Z uwagi na znaną zależność
(7.78)
q t
( )
P
o
m
ω
2
⋅
1
cos
ω t⋅
( )
−
(
)
⋅
=
Ostatecznie rozwiązanie (7.75) będzie wyglądać następująco:
1
ω
cos
ω t⋅
( )
ω
−
po podstawieniu granic całkowania otrzymujemy
0
t
τ
sin
ω t τ
−
( )
⋅
⌠
⌡
d
t
0
x
sin
ω x
⋅
( )
−
⌠
⌡
d
=
1
ω
cos
ω x
⋅
( )
⋅
=
0
t
i stąd
d
τ
dx
−
=
uzyskujemy
t
τ
−
x
=
podstawiając
Występująca w powyższej zależności całkę najłatwiej rozwiązać metodą zamiany zmiennych
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 56
1
Θ ω
−
ω t⋅
Θ t⋅
x
cos x
( )
⌠
⌡
d
⋅
1
Θ ω
−
sin
Θ t⋅
( )
sin
ω t⋅
( )
−
(
)
⋅
=
1
Θ ω
+
−
ω t⋅
Θ
− t⋅
x
cos x
( )
⌠
⌡
d
⋅
1
Θ ω
+
−
sin
Θ
− t⋅
(
)
sin
ω t⋅
( )
−
(
)
⋅
=
1
Θ ω
+
sin
Θ t⋅
( )
sin
ω t⋅
( )
+
(
)
⋅
=
poniższą postać całek (7.84)
po podstawieniu granic całkowania otrzymuje się
x
cos x
( )
⌠
⌡
d
sin x
( )
=
ponieważ
0
t
τ
cos
Θ ω
−
(
)
τ
⋅
ω t⋅
+
⌠
⌡
d
1
Θ ω
−
ω t⋅
Θ t⋅
x
cos x
( )
⌠
⌡
d
⋅
=
(7.84)
0
t
τ
cos
ω Θ
+
(
)
−
τ
⋅
ω t⋅
+
⌠
⌡
d
1
Θ ω
+
−
ω t⋅
Θ
− t⋅
x
cos x
( )
⌠
⌡
d
⋅
=
wówczas
d
τ
dx
Θ ω
−
=
skąd
Θ ω
−
(
)
τ
⋅
ω t⋅
+
x
=
(7.83)
d
τ
dx
Θ ω
+
−
=
skąd
ω Θ
+
(
)
−
τ
⋅
ω t⋅
+
x
=
korzystając z addytywnych własności całek oba wyrażenia całkujemy oddzielnie przez podstawienie
(7.82)
1
2
cos
ω Θ
+
(
)
−
τ
⋅
ω t⋅
+
cos
Θ ω
−
(
)
τ
⋅
ω t⋅
+
−
⋅
porządkując uzyskujemy
sin
ω t τ
−
( )
⋅
sin
Θ τ
⋅
( )
⋅
1
2
cos
ω t τ
−
( )
⋅
Θ τ
⋅
−
cos
ω t τ
−
( )
⋅
Θ τ
⋅
+
−
⋅
=
wyrażenie podcałkowe przybierze postać
(7.81)
sin
α
( )
sin
β
( )
⋅
1
2
cos
α β
−
(
)
cos
α β
+
(
)
−
(
)
⋅
=
wykorzystując zależność trygonometryczną
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 57
(7.90)
q t
( )
P
o
m
ω
2
⋅
ω
2
−
⋅
cos
ω t⋅
( )
t
⋅
1
ω
sin
ω t⋅
( )
⋅
−
⋅
=
Ostatecznie równanie (7.88) dla
Θ=ω będzie opisane funkcją
ω
Θ
cos
Θ t⋅
( )
t
⋅
1
ω
sin
ω t⋅
( )
⋅
−
2
− Θ
⋅
ω
2
lim
→
cos
ω t⋅
( )
t
⋅
1
ω
sin
ω t⋅
( )
⋅
−
2
−
ω
=
Obliczając granicę wyrażenia (7.89) otrzymujemy
(7.89)
ω
Θ
sin
Θ t⋅
( )
Θ
ω
sin
ω t⋅
( )
⋅
−
1
Θ
2
ω
2
−
lim
→
Pierwszy człon w nawiasie opiseje drgania z częstością siły wymuszające, drugi z częstością
własną. Te drugie drgania wraz z upływającym czasem będą w rzeczywistości zanikać.
Interesujący jest przypadek gdy częstość siły wymuszjącej jest równa częstości drgań własnych.
Z uwagi na nieoznaczoną wartość (7.88) dla
Θ=ω należy wyznaczyć wartość graniczną
(7.88)
q t
( )
P
o
m
ω
2
⋅
1
1
Θ
2
ω
2
−
⋅
sin
Θ t⋅
( )
Θ
ω
sin
ω t⋅
( )
⋅
−
⋅
=
Można je przepisać w następującej postaci
(7.87)
q t
( )
P
o
m
ω
⋅
ω
ω
2
Θ
2
−
sin
Θ t⋅
( )
Θ
ω
sin
ω t⋅
( )
⋅
−
⋅
⋅
=
Wykorzystując (7.86) rozwiązanie równania ruchu będzie miało postać
(7.86)
ω
ω
2
Θ
2
−
sin
Θ t⋅
( )
Θ
ω
sin
ω t⋅
( )
⋅
−
⋅
Po dokonaniu prostych przekształceń otrzymujemy
(7.85)
1
2
1
Θ ω
+
sin
Θ t⋅
( )
sin
ω t⋅
( )
+
(
)
⋅
1
Θ ω
−
sin
Θ t⋅
( )
sin
ω t⋅
( )
−
(
)
⋅
−
⋅
wykorzystując te rozwiązania można teraz zapisać wyrażenie (7.82) jako
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 58
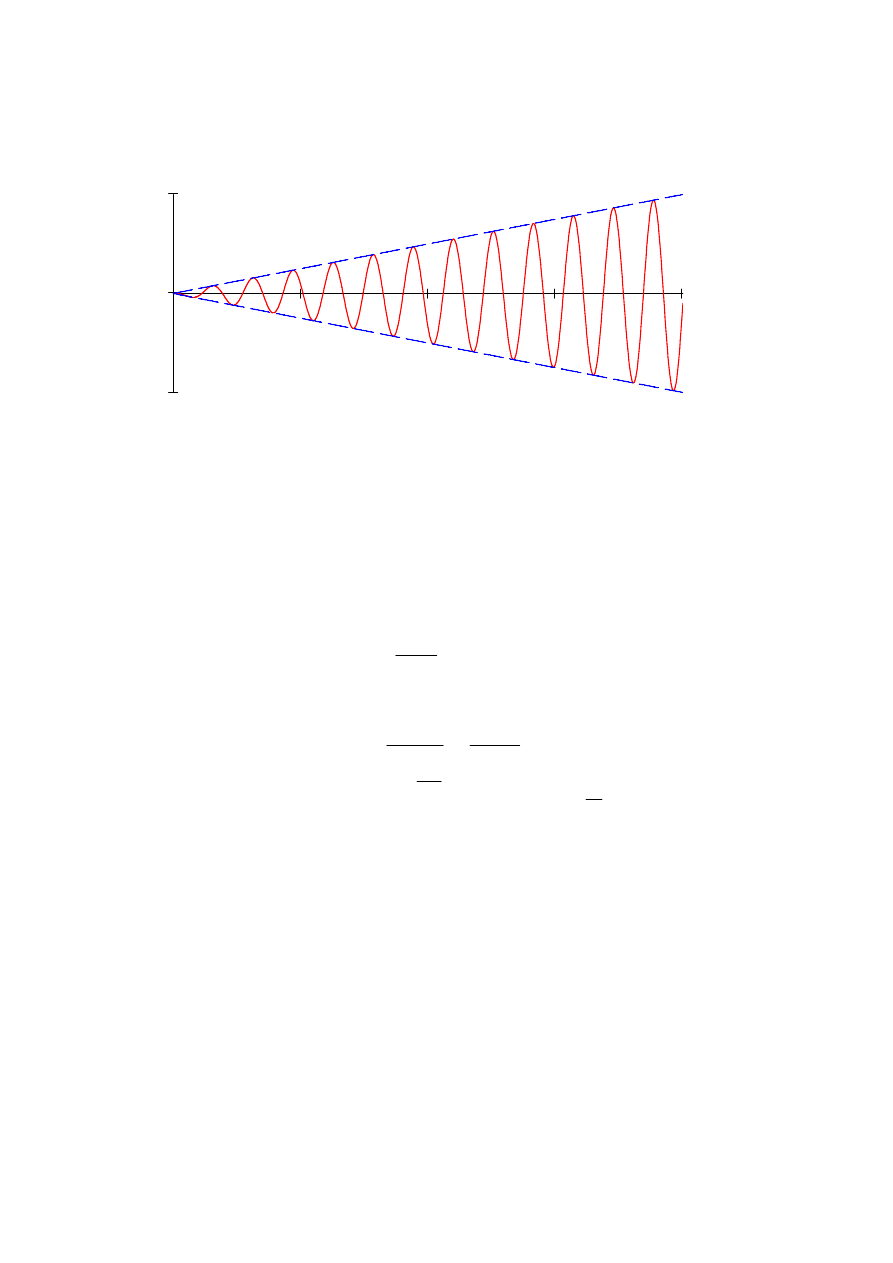
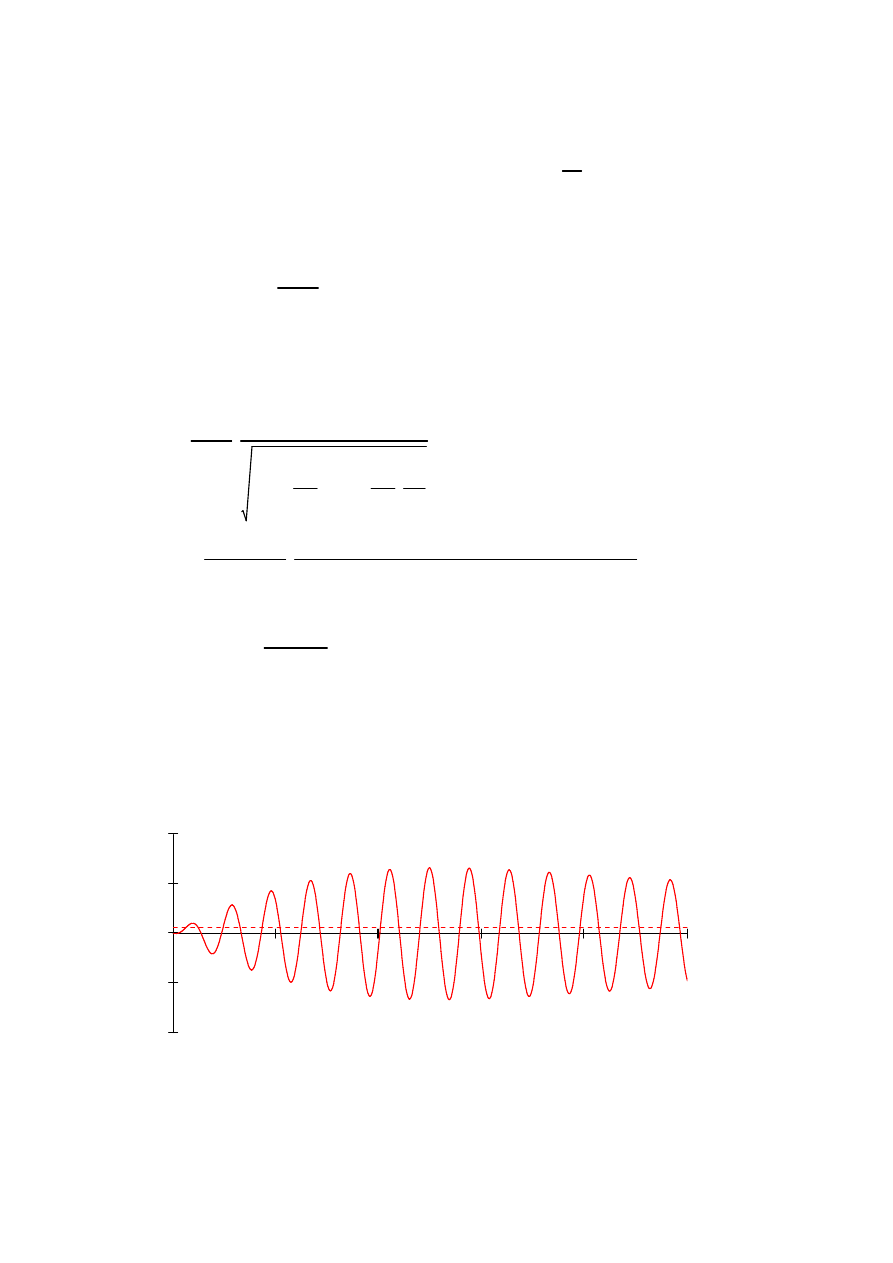
Przykładowy przebieg drgań zilustrowano na rysunku poniżej
Czas t
P
rz
em
ie
sz
cz
en
ie
Widać stąd, że drgania narastają nieograniczenie. W rzeczywistości przebieg będzie nieco inny, gdyż
przy dużych deformacjach zagadnienie przestaje być liniowe a ponadto występuje tłumienie. Niemniej
amplitudy drgań będą bardzo duże i mogą doprowadzić do zniszczenia lub uszkodzenia konstrukcji.
Wracając do wyrażenia (7.88) można w przypadku drgań wyłącznie pod wpływem siły harmonicznej
zapisać je następująco
q t
( )
δ
st
β
⋅ sin Θ t⋅
( )
⋅
=
(7.91)
gdzie
δ
st
P
o
m
ω
2
⋅
=
przemieszczenie statyczne wywołane
amplitudą siły wymuszającej
współczynnik
dynamiczny
(7.92)
β
1
1
Θ
2
ω
2
−
=
1
1
η
2
−
=
η
Θ
ω
=
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 59
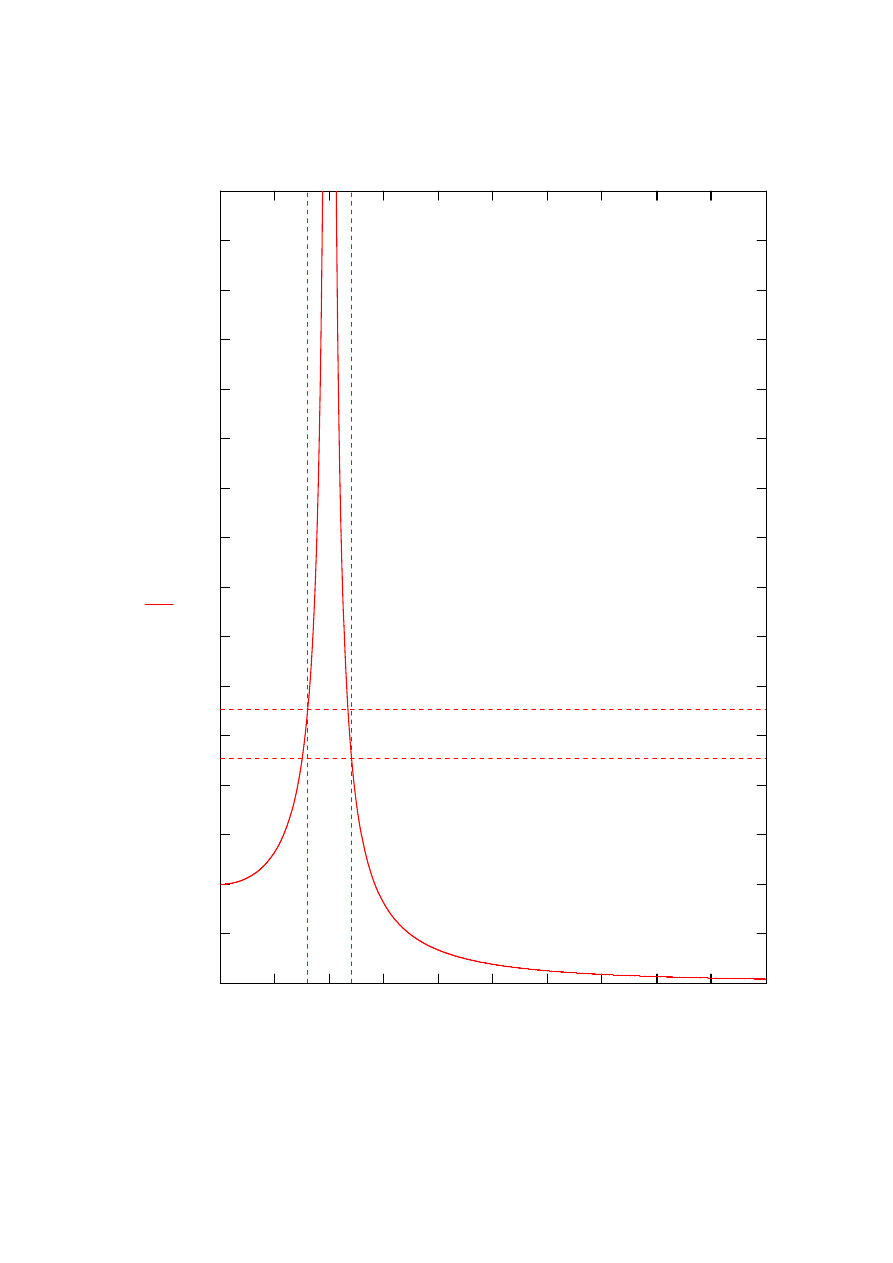
Wykres współczynnika dynamicznego przedstawiono poniżej
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
β 1.2
(
)
β 0.8
(
)
β η
( )
0.8
1.2
η
Wartości szczególne
β 0.8
(
)
2.778
=
β 1.2
(
)
2.273
=
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
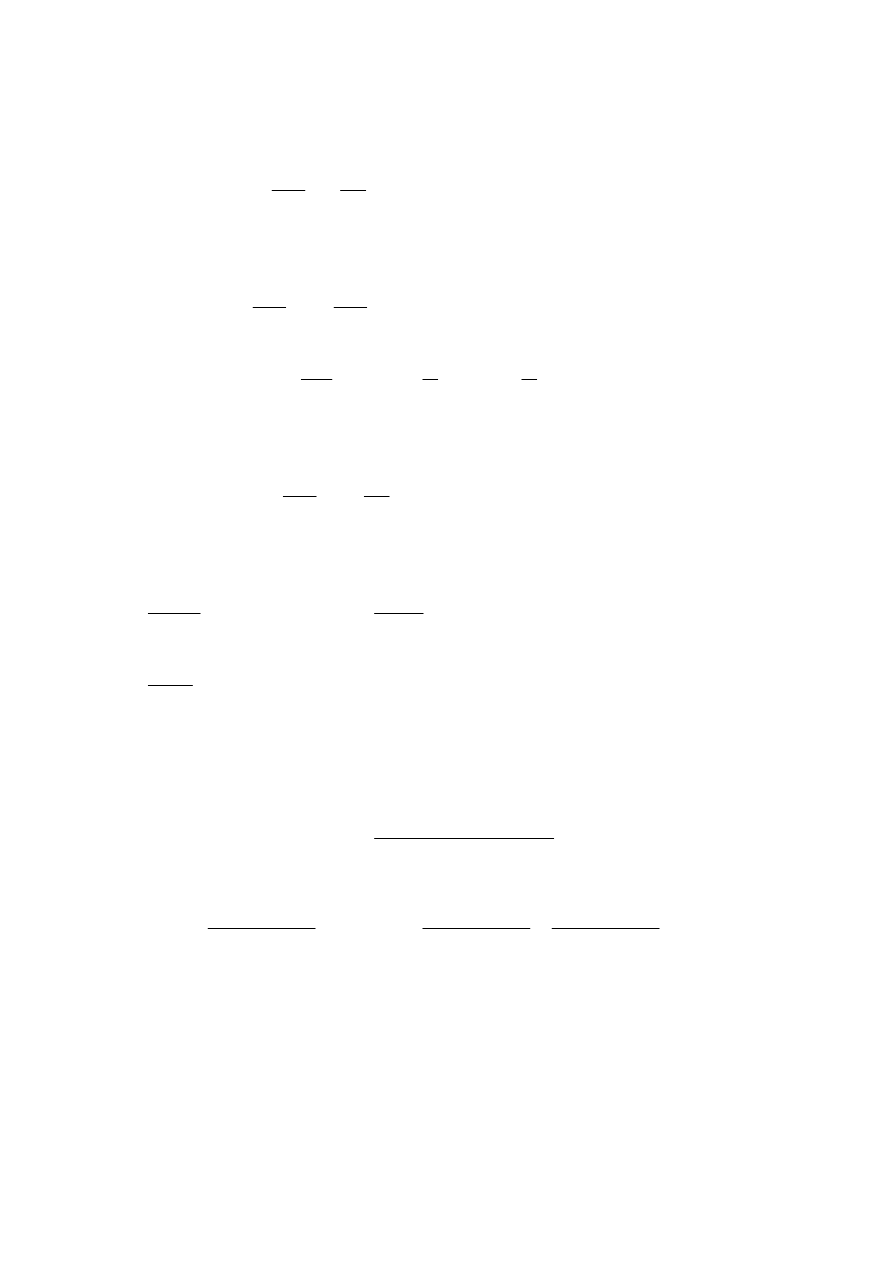
Mechanika budowli
______________________________________________________________________________________________ 60
(7.99)
q t
( )
q
o
t
( )
0
t
τ
g t
τ
−
( )
f
τ
( )
⋅
⌠
⌡
d
+
=
Dokonując na równaniu (7.98) odwrotnej transformacji Laplace'a, przy wykorzystaniu twierdzenia
o splocie funkcji, znajdujemy poszukiwane równanie ruchu
Q s
( )
q
o
s
r
+
s
2
2 r
⋅ s⋅
+
ω
2
+
⋅
r q
o
⋅
v
o
+
(
)
1
s
2
2 r
⋅ s⋅
+
ω
2
+
⋅
+
F s
( )
s
2
2 r
⋅ s⋅
+
ω
2
+
+
=
(7.98)
i dalej
(7.97)
Q s
( )
s q
o
⋅
2 r
⋅ q
o
⋅
+
v
o
+
F s
( )
+
s
2
2 r
⋅ s⋅
+
ω
2
+
=
skąd
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
2 r
⋅ s Q s
( )
⋅
q
o
−
(
)
⋅
+
ω
2
Q s
( )
⋅
+
F s
( )
=
zapisujemy równanie (7.96) jako
L
d q t
( )
⋅
d t
⋅
s Q s
( )
⋅
q 0
( )
−
=
s Q s
( )
⋅
q
o
−
=
L
d
2
q t
( )
d t
2
s
2
Q s
( )
⋅
s q 0
( )
⋅
−
d q 0
( )
d t
−
=
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
=
Korzystając z zależności (7.34) po uwzględnieniu warunków początkowych:
(7.96)
L
d
2
q
d t
2
2 r
⋅
d q
d t
⋅
+
ω
2
q
⋅
+
L
f t
( )
(
)
=
Rozwiązania równania (7.94) poszukujemy metodą tranformacji Laplace'a:
(7.95)
2 r
⋅
c
m
=
ω
2
k
m
=
f t
( )
P t
( )
m
=
gdzie
(7.94)
d
2
q
d t
2
2 r
⋅
d
2
q
d t
2
⋅
+
ω
2
q
⋅
+
f t
( )
=
Po przekształceniu do wygodniejszej postaci matematycznej będzie wyglądać
(7.93)
m
d
2
q
d t
2
⋅
c
d q
d t
⋅
+
k q
⋅
+
P t
( )
=
Równanie ruchu układu opisuje równanie:
7.4 Drgania wymuszone tłumione.
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 61
(7.102)
q t
( )
q
o
t
( )
1
ω
d
0
t
τ
e
r
− t τ
−
( )
⋅
sin
ω
d
t
τ
−
( )
⋅
⋅
f
τ
( )
⋅
⌠
⌡
d
⋅
+
=
i wówczas wyrażenie (7.99) będzie miało postać
(7.101)
g t
( )
1
ω
d
e
r
− t⋅
⋅
sin
ω
d
t
⋅
( )
⋅
=
ω
2
r
2
−
ω
d
=
W tym przypadku możemy zapisać po uwzględnieniu, że
r
2
ω
2
<
W dalszej części ograniczamy rozważania do przypadku opisującegu ruch oscylacyjny
(7.100)
Q s
( )
1
s
2
2 r
⋅ s⋅
+
ω
2
+
F s
( )
⋅
=
G s
( ) F s
( )
⋅
=
Funkcja g(t) jest reakcją układu na impuls
δ-Diraca, jest więc funkcją wpływu (funkcją Greena).
Jej tansformata G(s) jest tzw. operatorową funkcją przejścia (transmitacją). Jeśli założyć zerowe
warunki początkowe, to równanie (7.98) będzie wyglądało
L
1
−
1
s
2
2 r
⋅ s⋅
+
ω
2
+
F s
( )
⋅
L
1
−
G s
( ) F s
( )
⋅
(
)
=
0
t
τ
g t
τ
−
( )
f
τ
( )
⋅
⌠
⌡
d
=
- dla splotu funkcji
L
1
−
F s
( )
(
)
f t
( )
=
- dla drugiej funkcji
r
2
ω
2
>
dla
g t
( )
1
r
2
ω
2
−
e
r
− t⋅
⋅
sinh
r
2
ω
2
−
t
⋅
(
)
⋅
=
r
2
ω
2
=
dla
g t
( )
t e
r
− t⋅
⋅
=
↔
L
1
−
1
s
2
2 r
⋅ s⋅
+
ω
2
+
r
2
ω
2
<
dla
g t
( )
1
ω
2
r
2
−
e
r
− t⋅
⋅
sin
ω
2
r
2
− t⋅
(
)
⋅
=
- dla pierwszej funkcji
natomiast całka w wyrażeniu (7.99) reprezentująca całkę szczególną równania (7.94), określona została
na podstawie twierdzenia Borela o splocie funkcji
w zależności od proporcji r do
ω jest opisane przez
prawe strony równań (7.36), (7.37) lub (7.50); zależność ta
przedstawia całką ogólną równania (7.94)
q
o
t
( )
gdzie
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 62
Czas t
P
rz
em
ie
sz
cz
en
ie
δ
st
Przykładowy obraz drgań opisanych wzorem (7.106) przedstawiono poniżej
(7.106)
q t
( )
P
o
m
ω
2
⋅
1
e
r
− t⋅
cos
ω
d
t
⋅
( )
⋅
−
e
r
− t⋅
r
ω
d
⋅
sin
ω
d
t
⋅
( )
⋅
−
⋅
=
Po wykonaniu całkowania uzyskujemy
(7.105)
q t
( )
P
o
m
ω
d
⋅
0
t
τ
e
r
− t τ
−
( )
⋅
sin
ω
d
t
τ
−
( )
⋅
⋅
⌠
⌡
d
⋅
=
otrzymujemy
f t
( )
P
o
m
=
a stąd
P t
( )
P
o
=
const
=
Odpowiedź układu będzie teraz zależeć już tylko od postaci wymuszenia. Zakładając
(7.104)
q t
( )
1
ω
d
0
t
τ
e
r
− t τ
−
( )
⋅
sin
ω
d
t
τ
−
( )
⋅
⋅
f
τ
( )
⋅
⌠
⌡
d
⋅
=
jeśli założymy zerowe warunki początkowe, lub uwzględnimy, iż drgania opisane przez (7.103)
reprezentują zanikający proces przejściowy równanie (7.102) uprości się do postaci
(7.103)
q
o
t
( )
e
r
− t⋅
q
o
cos
ω
d
t
⋅
( )
⋅
r q
o
⋅
v
o
+
(
)
ω
d
sin
ω
d
t
⋅
( )
⋅
+
⋅
=
gdzie całka ogólna opisana jest zależnością (7.50)
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 63
Przejdziemy obecnie do rozpatrzenia przejścia sygnału sinusoidalnego, czyli funkcji wymuszenia
opisanej zależnością
P t
( )
P
o
sin
Θ t⋅
( )
⋅
=
czyli
f t
( )
P
o
m
sin
Θ t⋅
( )
⋅
=
Rozwiązane będzie teraz przedstawione równaniem
q t
( )
P
o
m
ω
d
⋅
0
t
τ
e
r
− t τ
−
( )
⋅
sin
ω
d
t
τ
−
( )
⋅
⋅
sin
Θ τ
⋅
( )
⋅
⌠
⌡
d
⋅
=
(7.107)
Po obliczeniu całki otrzymujemy wyrażenie
q t
( )
P
o
m
ω
2
⋅
sin
Θ t⋅ λ
−
(
)
1
Θ
2
ω
2
−
2
4
Θ
2
ω
2
⋅
r
2
ω
2
⋅
+
⋅
P
o
Θ
⋅ e
r
− t⋅
⋅
m
ω
d
⋅
2 r
⋅ ω
d
⋅
cos
ω
d
t
⋅
( )
⋅
sin
ω
d
t
⋅
( )
Θ
2
ω
2
−
2 r
2
⋅
+
(
)
⋅
+
ω
2
Θ
2
−
(
)
2
4
Θ
2
⋅
r
2
⋅
+
⋅
+
...
=
(7.108)
gdzie
tan
λ
2 r
⋅ Θ
⋅
ω
2
Θ
2
−
=
natomiast pozostałe oznaczenia jak poprzednio
W rozwiązaniu (7.108) pierwszy człon opisuje proces stacjonarnych drgań z częstością siły
wymuszającej, natomiast człon drugi opisuje zanikające drgania odbywające się z częstością
drgań własnych tłumionych. Po pewnym czasie drgania te zupełnie zanikają i ruch odbywa się
wyłącznie według zależności opisanej pierwszym członem. Przykładowy obraz drgań poniżej
Czas t
P
rz
em
ie
sz
cz
en
ie
δ
st
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 64
B
P
o2
m
ω
2
Θ
2
−
(
)
⋅
P
o1
m
2
⋅ r⋅ Θ
⋅
+
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
=
(7.112)
A
P
o1
m
ω
2
Θ
2
−
(
)
⋅
P
o2
m
2
⋅ r⋅ Θ
⋅
−
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
=
Rozwiązując ten układ równań względem A i B uzyskujemy
B
− Θ
2
⋅
2 r
⋅ A
⋅ Θ
⋅
−
ω
2
B
⋅
+
P
o2
m
=
(7.111)
A
− Θ
2
⋅
2 r
⋅ B
⋅ Θ
⋅
+
ω
2
A
⋅
+
P
o1
m
=
Zależność powyższa musi być spełniona dla dowolnej chwili t, muszą więc zachodzić związki
A
− Θ
2
⋅
cos
Θ t⋅
( )
⋅
B
Θ
2
⋅
sin
Θ t⋅
( )
⋅
−
(
)
2 r
⋅
A
− Θ
⋅ sin Θ t⋅
( )
⋅
B
Θ
⋅ cos Θ t⋅
( )
⋅
+
(
)
⋅
+
...
ω
2
A cos
Θ t⋅
( )
⋅
B sin
Θ t⋅
( )
⋅
+
(
)
⋅
+
...
P
o1
m
cos
Θ t⋅
( )
⋅
P
o2
m
sin
Θ t⋅
( )
⋅
+
=
Po podstawieniu do (7.110) otrzymujemy równanie
d q
d t
A
− Θ
⋅ sin Θ t⋅
( )
⋅
B
Θ
⋅ cos Θ t⋅
( )
⋅
+
=
d
2
q
⋅
d t
2
⋅
A
− Θ
2
⋅
cos
Θ t⋅
( )
⋅
B
Θ
2
⋅
sin
Θ t⋅
( )
⋅
−
=
Obliczając pochodne uzyskujemy
gdzie A,B dowolne stałe
q t
( )
A cos
Θ t⋅
( )
⋅
B sin
Θ t⋅
( )
⋅
+
=
Rozwiązanie zakładamy w postaci
(7.110)
d
2
q
d t
2
2 r
⋅
d q
d t
+
ω
2
q
⋅
+
P
o1
m
cos
Θ t⋅
( )
⋅
P
o2
m
sin
Θ t⋅
( )
⋅
+
=
Poszukujemy więc całki szczególnej równania
(7.109)
P t
( )
P
o1
cos
Θ t⋅
( )
⋅
P
o2
sin
Θ t⋅
( )
⋅
+
=
Korzystając z wyciągniętych już wniosków można uzyskać rozwiązanie dotyczące wymuszenia
harmonicznego w dowolnej postaci na drodze uproszczonej. W tym celu poszukujemy wyłącznie
stacjonarnego rozwiązania równania (7.93) pod obciążeniem w postaci
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
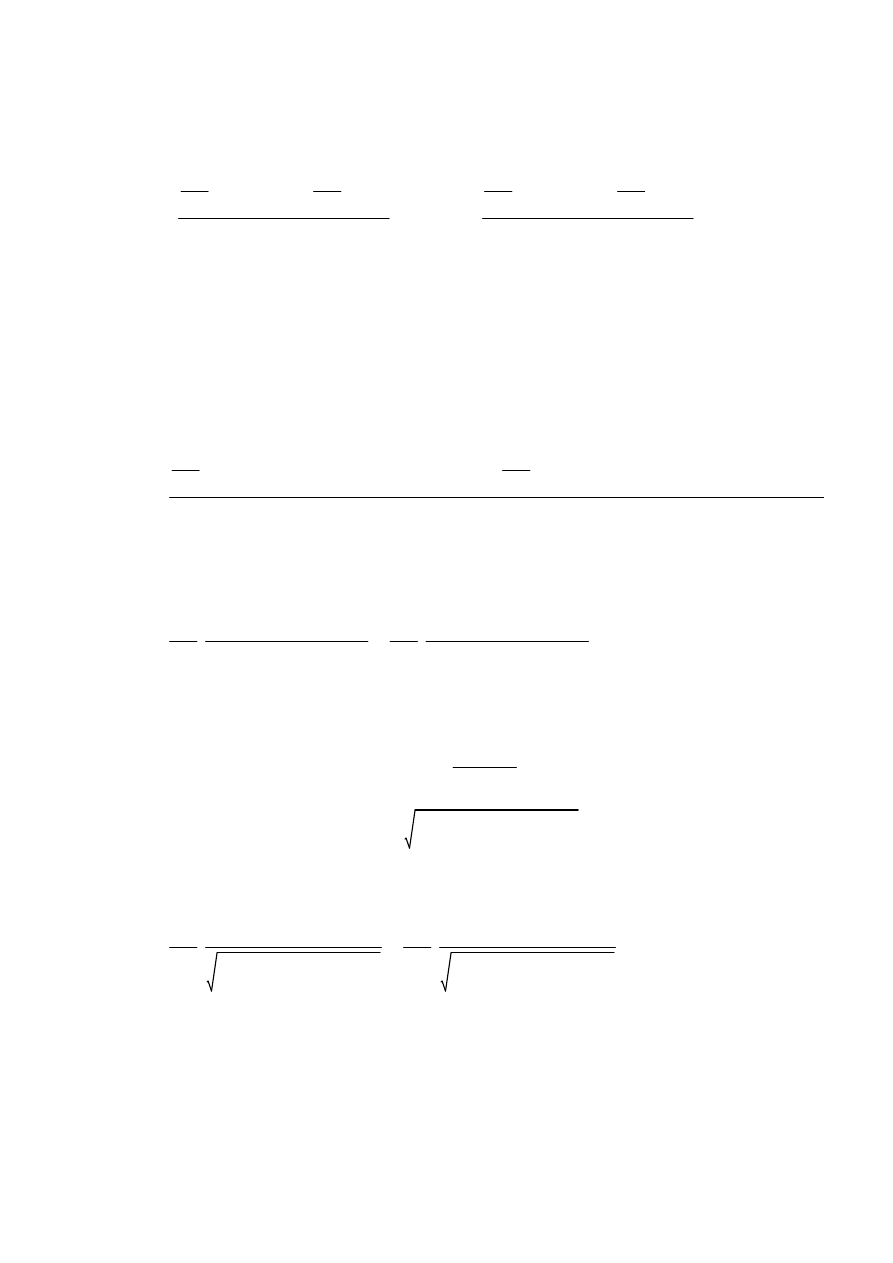
Mechanika budowli
______________________________________________________________________________________________ 65
(7.116)
q t
( )
P
o1
m
cos
Θ t⋅ λ
−
(
)
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
⋅
P
o2
m
sin
Θ t⋅ λ
−
(
)
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
⋅
+
=
Wykorzystując drugie z wyrażeń (7.115) rozwiązanie (7.114) zapiszemy w formie
C
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
=
(7.115)
tan
λ
2
Θ
⋅ r⋅
ω
2
Θ
2
−
=
Z zależności (7.113) można wyznaczyć związki między stałymi
(7.114)
q t
( )
P
o1
m
C cos
Θ t⋅ λ
−
(
)
⋅
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
⋅
P
o2
m
C sin
Θ t⋅ λ
−
(
)
⋅
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
⋅
+
=
i dalej wykorzystując znane zależności trygonometryczne jako
q t
( )
P
o1
m
C cos
λ
⋅
cos
Θ t⋅
( )
⋅
C sin
λ
⋅
sin
Θ t⋅
( )
⋅
+
(
)
⋅
P
o2
m
C
− sinλ
⋅
cos
Θ t⋅
( )
⋅
C cos
λ
⋅
sin
Θ t⋅
( )
⋅
+
(
)
⋅
+
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
=
funkcję opisującą ruch można przedstawić jako
2
Θ
⋅ r⋅ C sinλ
⋅
=
(7.113)
ω
2
Θ
2
−
C cos
λ
⋅
=
Podstawiając nowe stałe wg wzorów
q t
( )
P
o1
m
ω
2
Θ
2
−
(
)
⋅
P
o2
m
2
⋅ r⋅ Θ
⋅
−
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
cos
Θ t⋅
( )
⋅
P
o2
m
ω
2
Θ
2
−
(
)
⋅
P
o1
m
2
⋅ r⋅ Θ
⋅
+
ω
2
Θ
2
−
(
)
2
4 r
2
⋅ Θ
2
⋅
+
sin
Θ t⋅
( )
⋅
+
=
Rozwiązanie przybiera więc postać
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 66
(7.121)
współczynnik zwielokrotnienia
amplitudy - jako współczynnik
dynamiczny
β
1
1
η
2
−
(
)
2
4
ξ
2
⋅ η
2
⋅
+
=
(7.120)
δ
st2
P
o2
m
ω
2
⋅
=
δ
st1
P
o1
m
ω
2
⋅
=
gdzie
(7.119)
q t
( )
δ
st1
β
⋅ cos Θ t⋅ λ
−
(
)
⋅
δ
st2
β
⋅ sin Θ t⋅ λ
−
(
)
⋅
+
=
będzie można rozwiązanie (7.117) zapisać w skróconej formie
(7.118)
r
ω
ξ
=
oraz
Θ
ω
η
=
statycznym działaniem amplitud sił wymuszających, oraz wprowadzimy pomocnicze wielkości
przedstawiają przemieszczenia wywołane
P
o1
m
ω
2
⋅
P
o2
m
ω
2
⋅
,
Jeśli zauważymy, że wyrażenia
(7.117)
q t
( )
P
o1
m
ω
2
⋅
cos
Θ t⋅ λ
−
(
)
1
Θ
2
ω
2
−
2
4
r
2
ω
2
⋅
Θ
2
ω
2
⋅
+
⋅
P
o2
m
ω
2
⋅
sin
Θ t⋅ λ
−
(
)
1
Θ
2
ω
2
−
2
4
r
2
ω
2
⋅
Θ
2
ω
2
⋅
+
⋅
+
=
Wyciągając następnie z mianownika
ω otrzymamy
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 67
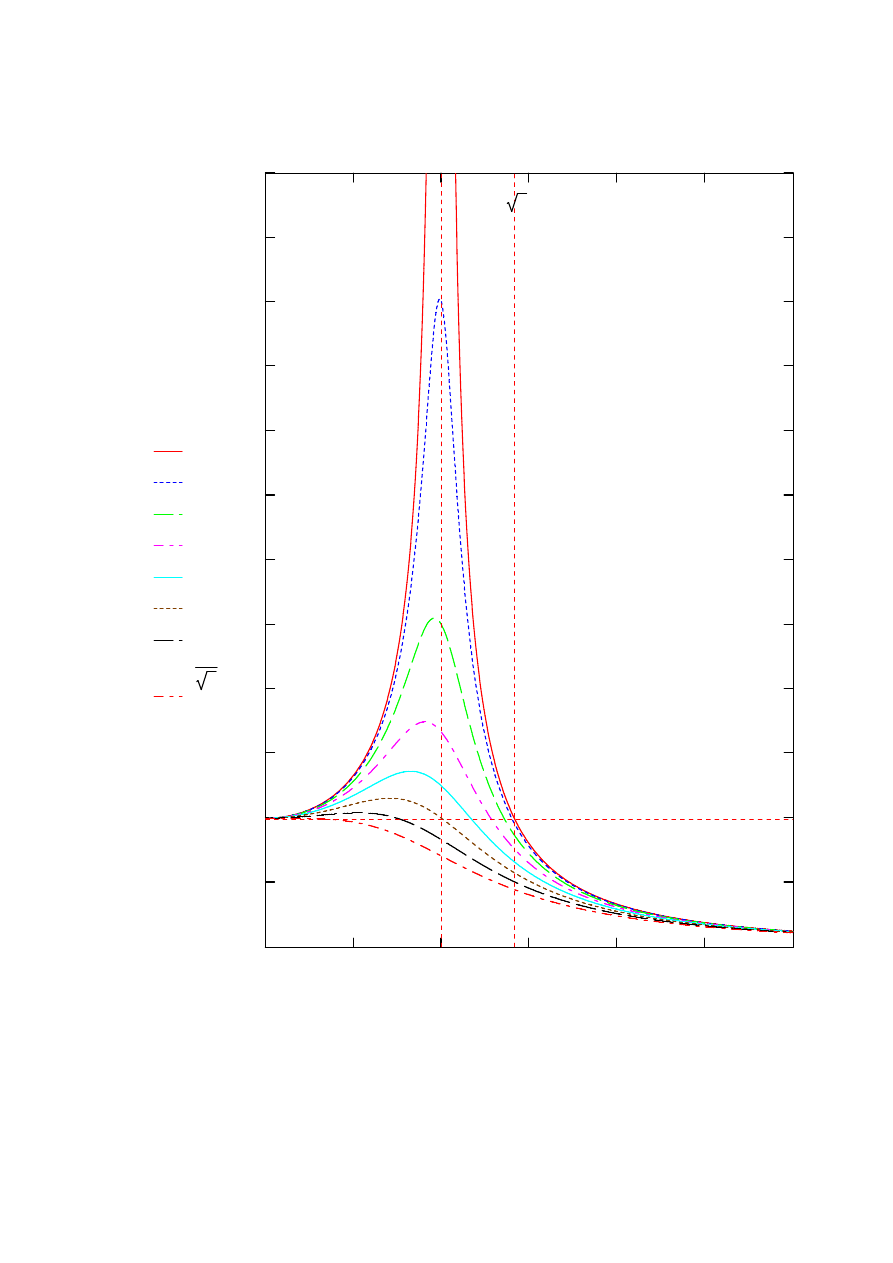
Wykres współczynnika dynamicznego przedstawiono poniżej
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
1
β η
( )
β η 0.1
,
(
)
β η 0.2
,
(
)
β η 0.3
,
(
)
β η 0.4
,
(
)
β η 0.5
,
(
)
β η 0.6
,
(
)
β η
1
2
,
1
2
η
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 68
0
0.2
0.4
0.6
0.8
0
5
10
1
2
ξ
⋅
1
ξ
2
−
⋅
ξ
Poniżej graficzny obraz zależności (7.123)
(7.123)
β
max
1
1
1
2
ξ
2
⋅
−
(
)
−
2
4
ξ
2
⋅
1
2
ξ
2
⋅
−
(
)
⋅
+
=
1
2
ξ
⋅
1
ξ
2
−
⋅
=
podstawiając tę wartość do zależności opisującej współczynnik dynamiczny uzyskujemy
(7.122)
η
1
2
ξ
2
⋅
−
=
ξ
1
2
<
dla
η
2
1
2
ξ
2
⋅
−
=
skąd znajdujemy
4
− 1 η
2
−
(
)
⋅
η
⋅
8
ξ
2
⋅ η
⋅
+
0
=
Miejsca zerowe tej funkcji znajdziemy przyrównując licznik do zera
η
1
1
η
2
−
(
)
2
4
ξ
2
⋅ η
2
⋅
+
d
d
1
−
2
1
η
2
−
(
)
2
4
ξ
2
⋅ η
2
⋅
+
3
2
⋅
4
− 1 η
2
−
(
)
⋅
η
⋅
8
ξ
2
⋅ η
⋅
+
⋅
=
Nie jest to jednak wielkość maksymalna jaką osiąga współczynnik dynamiczny. Ekstremum
wyznaczymy obliczając pochodną
1
η
β
lim
→
1
η
1
1
η
2
−
(
)
2
4
ξ
2
⋅ η
2
⋅
+
lim
→
=
1
1
1
2
−
( )
2
4
ξ
2
⋅ 1
2
⋅
+
=
1
2
ξ
⋅
=
Rezonansowa wartość współczynnika dynamicznego, czyli dla
η=1 wynosi
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 69
∆
0.06
=
- masa maszyny
m
1150 kg
⋅
=
- amplituda siły wymuszającej
P
o
25 kN
⋅
=
- częstości siły wymuszającej
Θ
1
40
rad
s
⋅
=
Θ
2
49
rad
s
⋅
=
Θ
3
60
rad
s
⋅
=
Rozwiązanie:
Moment zginający wywołany ciężarem własnym maszyny i siłą P
o
działającą statycznie (czyli
tak gdyby była siłą stałą niezależną od czasu)
M
P
o
m g
⋅
+
(
)
L
⋅
4
=
M
45.347 kNm
=
Naprężenia maksymalne w belce
σ
M
W
=
σ 116.573MPa
=
σ f
d
<
Przykład 7.13
Belka swobodnie podparta o rozpiętości 2a obciążona jest maszyną o masie m, oddziaływującą
dynamicznie na konstrukcję. Siłę P(t) zmienną w czasie opisuje zależność:
P t
( )
P
o
sin
Θ t⋅
( )
⋅
=
Układ konstrukcyjny charakteryzuje się tłumieniem opisanym logarytmicznym dekrementem
tłumienia
∆. Obliczyć współczynnik dynamiczny oraz maksymalne ugięcia i naprężenia w belce.
EI
a
q
m
P(t)
a
Pominąć wpływ masy własnej belki, ale uwzględnić różne częstości sił wymuszających.
Dane:
- parametry sztywności belki wsporczej E
205 GPa
⋅
=
I
3690 cm
4
⋅
=
- parametry wytrzymałościowe
W
389 cm
3
⋅
=
f
d
235MPa
=
- rozpiętość
a
250 cm
⋅
=
L
2 a
⋅
=
- dekrement tłumienia
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 70
r
∆ ω
⋅
4
π
2
∆
2
+
=
r
0.48 s
-1
=
Bezwymiarowy współczynnik tłumienia
ξ
r
ω
=
ξ 0.01
=
Współczynniki dynamiczne z uwzględnieniem tłumienia
β
d
oraz bez tłumienia
β
β
d1
1
1
η
1
2
−
(
)
2
4
ξ
2
⋅ η
1
2
⋅
+
=
β
d1
2.726
=
β
1
1
1
η
1
2
−
=
β
1
2.728
=
β
d2
1
1
η
2
2
−
(
)
2
4
ξ
2
⋅ η
2
2
⋅
+
=
β
d2
18.928
=
β
2
1
1
η
2
2
−
=
β
2
20.226
=
β
d3
1
1
η
3
2
−
(
)
2
4
ξ
2
⋅ η
3
2
⋅
+
=
β
d3
2.348
=
β
3
1
1
η
3
2
−
=
β
3
2.352
=
Można zauważyć iż w obszarze pozarezonansowym wpływ tłumienia jest praktycznie
niezauważalny. Wyraźne obniżenie wartości współczynnika dynamicznego występuje
tylko w obszarze bezpośredniego sąsiedztwa rezonansu.
Ugięcie belki od sił działających statycznie
q
st
P
o
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
q
st
1.249 cm
=
<
L
200
2.5 cm
=
Sztywność belki
k
48 E
⋅ I⋅
L
3
=
k
2904768
N
m
=
Częstość drgań własnych belki
ω
k
m
=
ω 50.258s
-1
=
Stosunki częstości
η
η
1
Θ
1
ω
=
η
1
0.796
=
η
2
Θ
2
ω
=
η
2
0.975
=
η
3
Θ
3
ω
=
η
3
1.194
=
Współczynnik tłumienia
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 71
L
200
2.5 cm
=
>>
L
30
16.667 cm
=
Widać z powyższego, iż w drugim przypadku, bez względu nawet na uwzględnienie tłumienia,
wartości naprężeń bardzo znacząco przekraczają nie tylko przyjętą wytrzymałość dopuszczalną
dla materiału belki, ale również dla najwyżych jakości stali budowlanych. Wartości towarzyszących
im przemieszczeń osiągnęłyby abstrakcyny poziom, przekraczający założenia analizy liniowej
σ
3
225.153 MPa
=
σ
3
P
o
β
3
⋅
m g
⋅
+
(
)
L
⋅
4 W
⋅
=
σ
d3
224.882 MPa
=
σ
d3
P
o
β
d3
⋅
m g
⋅
+
(
)
L
⋅
4 W
⋅
=
σ
2
1661.051 MPa
=
σ
2
P
o
β
2
⋅
m g
⋅
+
(
)
L
⋅
4 W
⋅
=
σ
d2
1556.799 MPa
=
σ
d2
P
o
β
d2
⋅
m g
⋅
+
(
)
L
⋅
4 W
⋅
=
σ
1
255.397 MPa
=
σ
1
P
o
β
1
⋅
m g
⋅
+
(
)
L
⋅
4 W
⋅
=
σ
d1
255.209 MPa
=
σ
d1
P
o
β
d1
⋅
m g
⋅
+
(
)
L
⋅
4 W
⋅
=
q
3
2.412 cm
=
q
3
P
o
β
3
⋅
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
q
d3
2.409 cm
=
q
d3
P
o
β
d3
⋅
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
q
2
17.796 cm
=
q
2
P
o
β
2
⋅
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
q
d2
16.679 cm
=
q
d2
P
o
β
d2
⋅
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
q
1
2.736 cm
=
q
1
P
o
β
1
⋅
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
q
d1
2.734 cm
=
q
d1
P
o
β
d1
⋅
m g
⋅
+
(
)
L
3
⋅
48 E
⋅ I⋅
=
Ugięcia i naprężenia dynamiczne dla kolejnych częstości wymuszenia
2005-03-31
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Wyszukiwarka
Podobne podstrony:
Mechanika Budowli Sem[1][1] VI Wyklad 04
Mechanika Budowli Sem[1][1] VI Wyklad 02 color
Mechanika Budowli Sem[1][1] VI Wyklad 01
Mechanika Budowli Sem[1][1] VI Wyklad 04
sem VI FŚ k-z 05, UCZELNIA ARCHIWUM, UCZELNIA ARCHIWUM WGiG, WGiG Rok III sem VI (2013-2014), sem VI
Konstrukcje metalowe Sem VI Wyklad 02
Konstrukcje metalowe Sem VI Wyklad 04
Konstrukcje metalowe Sem VI Wyklad 03
Mechanika Budowli sem 4 i5 tematy egzaminu
harmonogram CWICZ, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, matreiały na mb
Mecha- belka, Sem V, Mechanika Budowli Proj, Mechanika Budowli, Belka
wstep do zadan, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, EGZ, egzam
MECHANIKA BUDOWLI projekt 1 , sem IV (1)
więcej podobnych podstron