
Mechanika budowli
______________________________________________________________________________________________ 35
Związana zależnością (7.16) stała
ω uzyskuje dzięki (7.22) interpretację fizyczną.
(7.22)
q t
( )
v
o
ω
sin
ω t⋅
( )
⋅
q
o
cos
ω t⋅
( )
⋅
+
=
Wykorzystując zależności transformacyjne oryginał przybiera ostatecznie postać
(7.21)
Q s
( )
v
o
s q
o
⋅
+
s
2
ω
2
+
=
v
o
ω
ω
s
2
ω
2
+
⋅
q
o
s
s
2
ω
2
+
⋅
+
=
Wyznaczając z powyższego równania szukaną funkcję q(s) otrzymuje się
(7.20)
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
ω
2
Q s
( )
⋅
+
0
=
Równanie (7.17) przybiera postać
(7.19)
d q 0
( )
d t
v
o
=
q 0
( )
q
o
=
oraz przyjęciu skróconych oznaczeń dla warunków początkowych
L
d
2
q t
( )
d t
2
s
2
Q s
( )
⋅
s q 0
( )
⋅
−
d q 0
( )
d t
−
=
przy uwzględnieniu, że
(7.18)
L m
d
2
q
d t
2
⋅
k q
⋅
+
0
=
Wykonując następnie tranformację całkową Laplace'a względem funkcji q(t)
(7.17)
d
2
q
d t
2
ω
2
q
⋅
+
0
=
można je przepisać w postaci
(7.16)
ω
2
k
m
=
Wprowadzając oznaczenie
(7.15)
m
d
2
q
d t
2
⋅
k q
⋅
+
0
=
Drganiami swobodnymi nietłumionymi nazywamy proces fizyczny spowodowany wyłącznie
początkowym zaburzeniem równowagi (nałożenie warunków początkowych), przy braku
wymuszających sił zewnętrznych oraz braku sił oporów ruchu. Ruch drgający odbywa się
wówczas wyłącznie pod działaniem sił potencjalnych (sprężystości). Jeśli ponadto siły
te są liniowymi funkcjami przemieszczeń będą to drgania liniowe. Opisuje je równanie
7.1 Drgania swobodne nietłumione. Drgania własne
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 36
Matematyczne ujęcie ruchu postaci (7.15) stanowi podstawę opisu szeregu różnych drgań.
Wszystkie takie układy (o jednym stopniu swobody) nazywane są oscylatorami harmonicznymi.
Do oscylatorów harmonicznych można zaliczyć: wahadło kołowe, wahadło cykloidalne, układy
mechaniczne zawierające elementy masowe i sprężyste, układy elektryczne zawierające elementy
indukcyjne i pojemnościowe.
(7.29)
d
2
q
d t
2
ω
2
−
q
⋅
=
Z zależności (7.28) wynika, że w ruchu drgającym harmonicznym zachodzi następująca
ważna zależność:
(7.28)
d
2
q
d t
2
A
− ω
2
⋅
sin
ω t⋅ ϕ
+
(
)
⋅
=
(7.27)
d q
d t
A
ω
⋅ cos ω t⋅ ϕ
+
(
)
⋅
=
Pochodne tej funkcji wynoszą
(7.26)
q t
( )
A sin
ω t⋅ ϕ
+
(
)
⋅
=
Równanie (7.22) można przepisać także w formie uproszczonej
ϕ atan
ω q
o
⋅
v
o
=
(7.25)
A
v
o
ω
2
q
o
2
+
=
Wykorzystując zależności
Funkcja powyższa stanowi matematyczne rozwiązanie równania (7.15) i nie jest
procesem fizycznym. Opisuje jedynie pewną dyspozycję ustroju do drgań.
(7.24)
q t
( )
A sin
ω t⋅
( )
⋅
B cos
ω t⋅
( )
⋅
+
=
Stacjonarny proces harmoniczny postaci (7.22) z dowolnymi stałymi A i B, spełniający
równanie (7.15) nazywamy drganiami własnymi:
(7.23)
ω
k
m
=
Wiekość tę nazywa się częstością drgań własnych. Jest ona indywidualną cechą rozważanego
obiektu. Nie zależy od czynników zewnętrznych. Po przekształceniu (7.16) można ją w
przypadku ustroju o jednym stopniu swobody wyznaczać z zależności
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
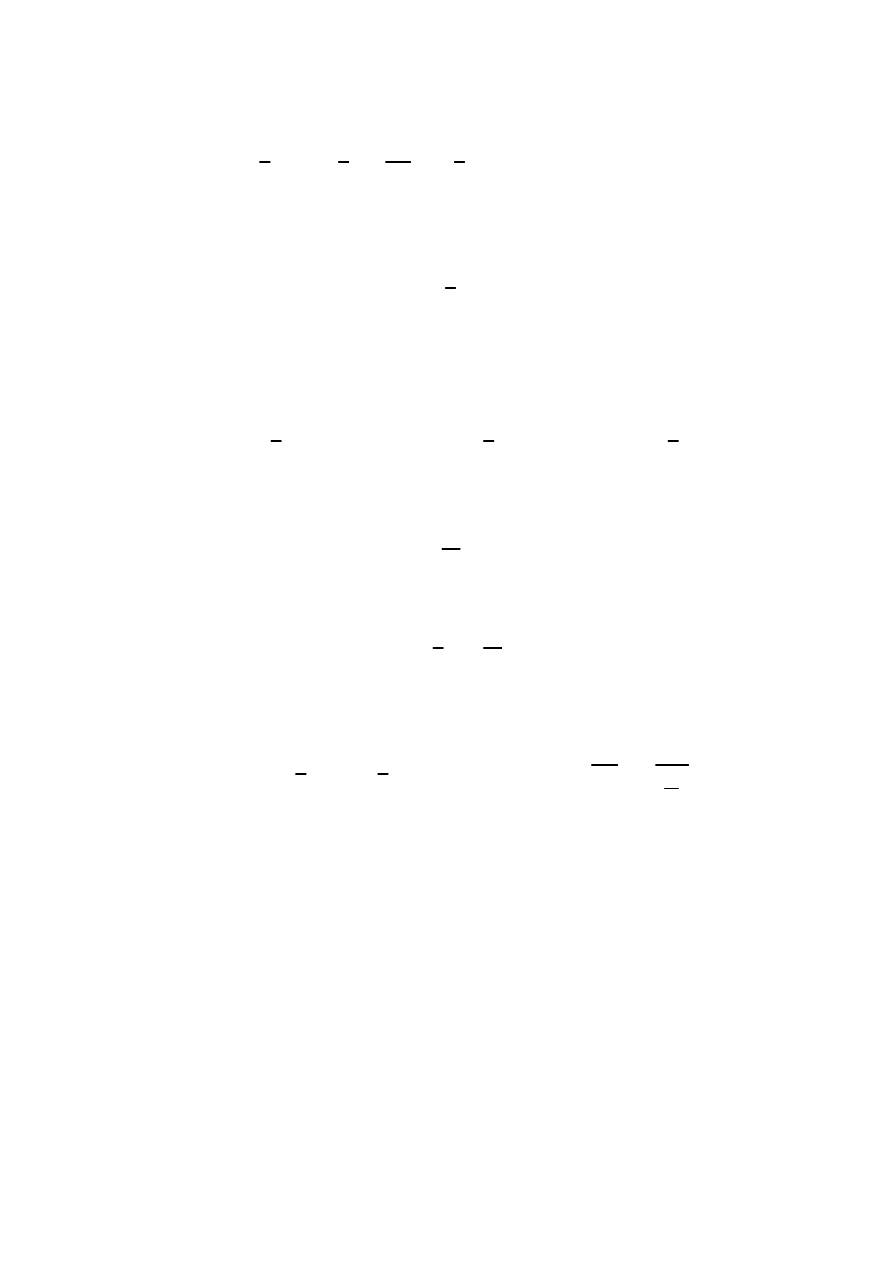
Mechanika budowli
______________________________________________________________________________________________ 37
Przez cały czas trwania ruchu harmonicznego suma energii knetycznej i potencjalnej jest stała.
Stałą wartość tej sumy określają warunki początkowe.
E
k
E
p
+
E
ko
E
po
+
=
const
=
Otrzymujemy więc prawo zachowania energii
gdyż
E
ko
E
po
+
1
2
m
⋅ v
o
2
⋅
1
2
k q
o
2
⋅
+
=
k
v
o
2
ω
2
⋅
k
v
o
2
k
m
=
m v
o
2
⋅
=
jest ona oczywiście równa sumie tych energii w chwili początkowej
E
k
E
p
+
1
2
k
⋅
v
o
ω
2
q
o
2
+
⋅
=
można sumę energii zapisać jako
A
2
v
o
ω
2
q
o
2
+
=
Ponieważ z pierwszej z zależności (7.25) wynika, że
E
k
E
p
+
1
2
m
⋅ A
2
⋅
ω
2
⋅
cos
ω t⋅ ϕ
+
(
)
2
⋅
1
2
k
⋅ A
2
⋅
sin
ω t⋅ ϕ
+
(
)
2
⋅
+
=
1
2
k A
2
⋅
=
Stała C w przypadku odniesienia enerii do położenia q=0 (położenia równowagi) będzie równa 0.
Suma obu energii wyniesie więc ostatecznie
E
p
q
k q
⋅
⌠
⌡
d
=
1
2
k
⋅ q
2
⋅
C
+
=
Energia potencjalna wynosi natomiast
E
k
1
2
m
⋅ v
2
⋅
=
1
2
m
⋅
d q
d t
2
⋅
=
1
2
m
⋅ A
2
⋅
ω
2
⋅
cos
ω t⋅ ϕ
+
(
)
2
⋅
=
Prosty oscylator harmoniczny stanowi układ zachowawczy. Jego energia kinetyczna jest równa
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 38
ω
k
b
m
=
ω 13.926s
-1
=
Sztywność zastępcza układu z podkładkami
k
z
1
1
k
1
k
b
+
=
k
z
63575.121
N
m
=
Częstość drgań własnych konstrukcji z podkładkami
ω
p
k
z
m
=
ω
p
8.405 s
-1
=
Z założeń zadania wynika, że v
o
0
=
q
o
0.02
=
równania ruchu przybierą więc postać
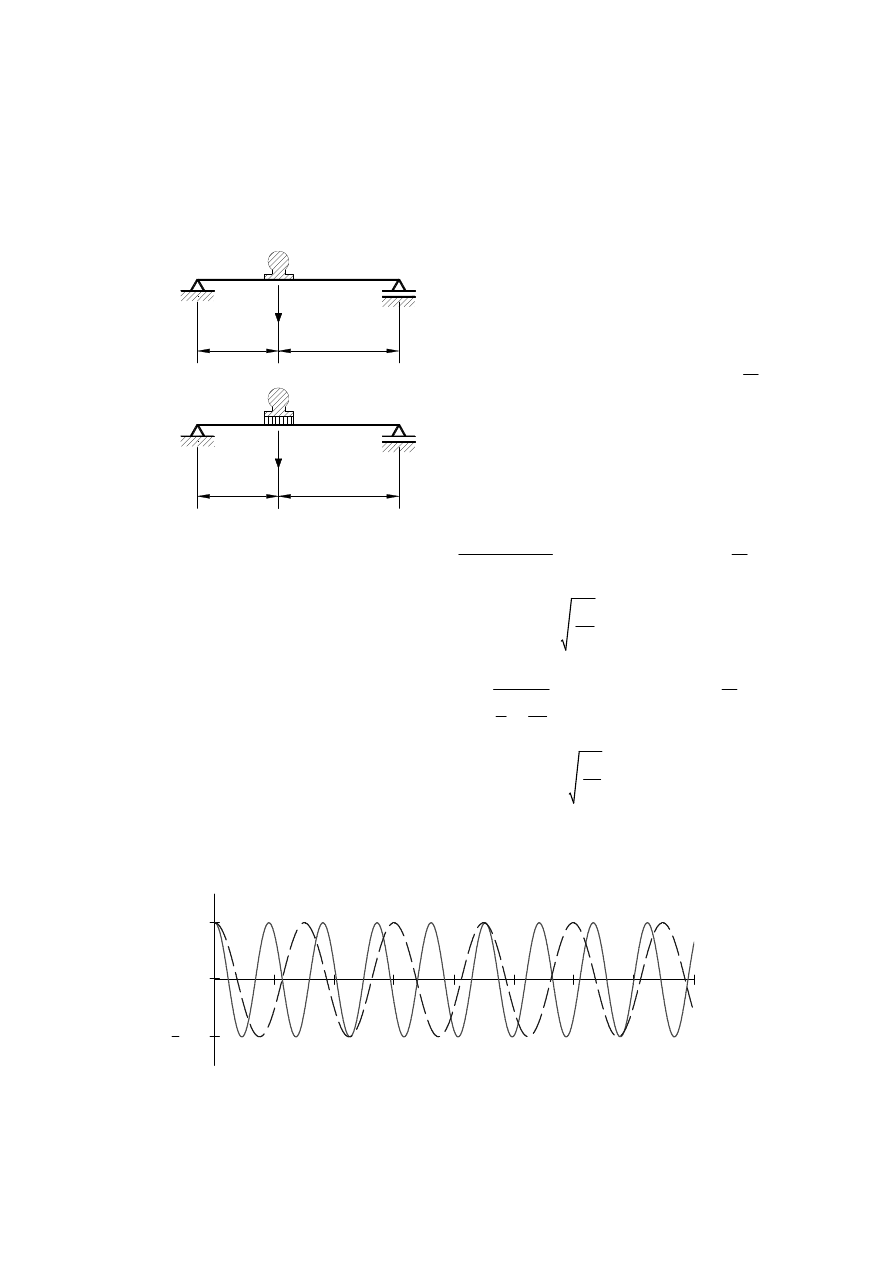
q t
( )
0.02 cos
ω t⋅
( )
⋅
=
(linia ciągła na wykresie)q t
( )
0.02 cos
ω
p
t
⋅
( )
⋅
=
(linia przerywana)
0
0.5
1
1.5
2
2.5
3
3.5
4
0.02
0.02
Czas t
P
rz
em
ie
sz
cz
en
ie
q
Przykład 7.2
Na belce ustawiono maszynę. Wyznaczyć częstość drgań własnych ustroju w przypadku
bezpośredniego zamontowania maszyny na belce oraz przy zastosowaniu podkładek o
sztywności k. Wyznaczyć równanie ruchu ustroju w obu przypadkach przy wychyleniu
maszyny (przemieszczenie w pionie zgodnie z kierunkiem q) z położenia równowagi o 2 cm.
Dane:
EI
a
q
b
m
a)
EI
b
q
a
b)
m
k
- parametry sztywności belki wsporczej
E
205 GPa
⋅
=
I
80.1 cm
4
⋅
=
- masa maszyny
m
900 kg
⋅
=
-sztywności podkładek
k
10
5
N
m
⋅
=
- wymiary geometryczne a
120 cm
⋅
=
b
280 cm
⋅
=
Rozwiązanie:
Sztywność modelowa belki
k
b
3 E
⋅ I⋅ a b
+
(
)
⋅
a
2
b
2
⋅
=
k
b
174537.628
N
m
=
Częstość drgań własnych konstrukcji bez podkładek
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 39
π d
2
⋅
8
L
⋅ ρ
⋅
d q
d t
2
⋅
π d
2
⋅
4
ρ
⋅ g
⋅ q
2
⋅
+
const
=
Z zasady zachowania energii otrzymamy
E
p
2
0
q
ξ
π d
2
⋅
4
ρ
⋅ g
⋅ ξ
⋅
⌠
⌡
d
=
π d
2
⋅
2
ρ
⋅ g
⋅
0
q
ξ
ξ
⌠
⌡
d
⋅
=
π d
2
⋅
4
ρ
⋅ g
⋅ q
2
⋅
=
Energia potencjalna związana jest z nadwyżką potencjału podniesionego słupa cieczy
ponad aktualne zwierciadło cieczy w drugim słupie. Należy zwrócić uwagę, że wyniesienie
zwierciadła o wielkość q ponad poziom równowagi powoduje różnicę wysokości o 2q.
E
k
1
2
M v
2
⋅
=
π d
2
⋅
8
L
⋅ ρ
⋅
d q
d t
2
⋅
=
Przy założeniu, iż ciecz jest nieściśliwa, jej energię kinetyczną można wyrazić wzorem
M
14.137 kg
=
M
π d
2
⋅
4
L
⋅ ρ
⋅
=
Wykorzystamy zasadę zachowania energii dla oscylatora harmonicznego. Wyrażenia
opisujące energie należy jednak zmodyfikować z uwzględnieniem specyfiki cieczy.
Całkowita masa cieczy w naczyniu
Rozwiązanie:
ρ
1000
kg
m
3
⋅
=
- gęstość cieczy
d
10 cm
⋅
=
- średnica przewodu naczynia
L
180cm
=
- całkowita długość słupa cieczy (L=a+2b)
Dane:
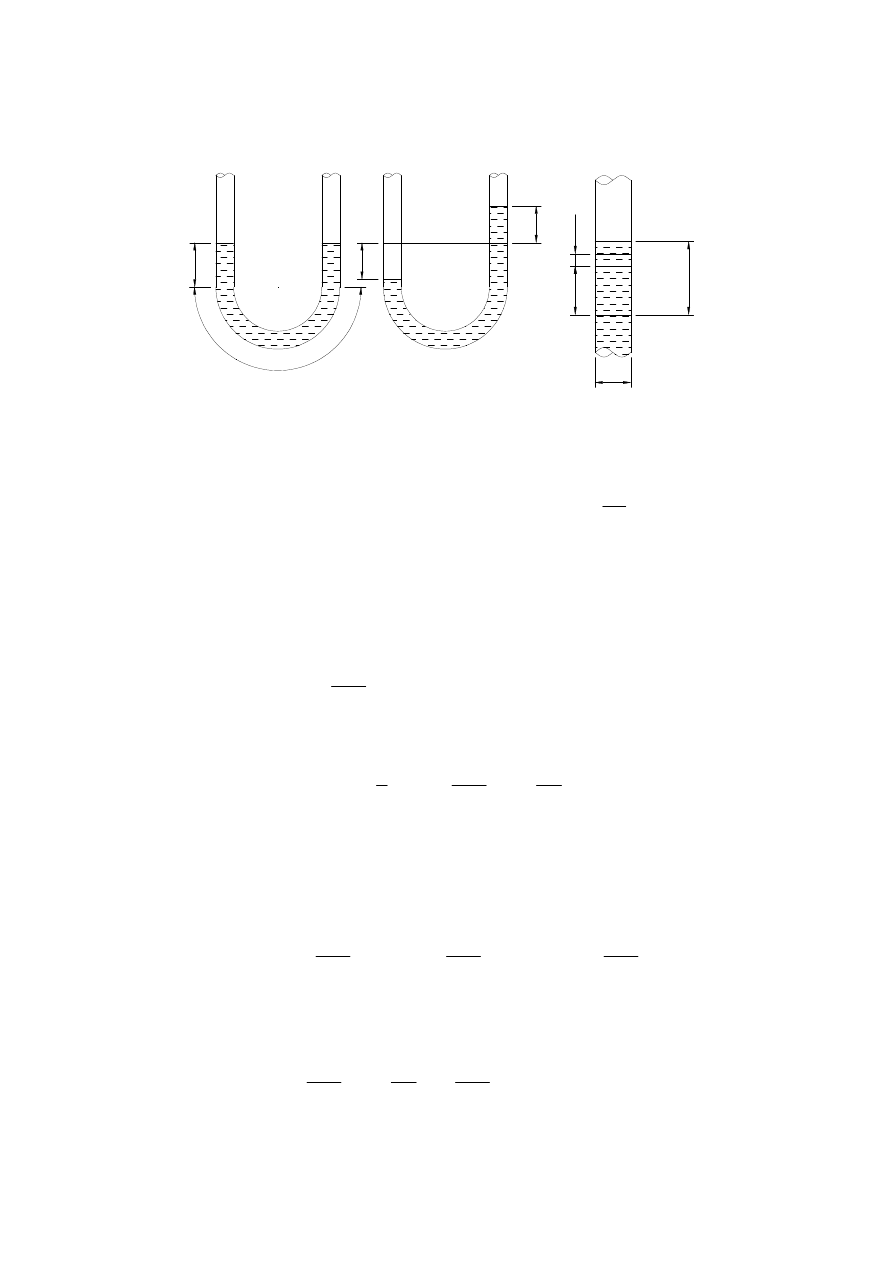
a)
b)
a
b
ξ
dξ
d
c)
q
q
q=0
q
Opisać równanie ruchu cieczy nieściśliwej w naczyniu o kształcie U-rurki
Przykład 7.3
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 40
A
33.805 cm
=
A
v
o
ω
2
q
o
2
+
=
Amplituda
T
1.903 s
=
T
2
π
ω
=
Okres drgań
0
2
4
6
8
10
50
50
Wykres tej funkcji przedstawia poniższy szkic
q t
( )
q
o
cos
2 g
⋅
L
t
⋅
⋅
v
o
ω
sin
2 g
⋅
L
t
⋅
⋅
+
=
Opis ruchu upraszcza się do postaci
v
o
1
m
s
=
q
o
15 cm
⋅
=
Stałe A i B należy obliczyć z warunków początkowych. Zakładając przykładowo
q t
( )
A sin
2 g
⋅
L
t
⋅
⋅
B cos
2 g
⋅
L
t
⋅
⋅
+
=
Zatem ostatecznie ruchu cieczy w naczyniu będzie opisywać zależność
ω 3.301s
-1
=
ω
2 g
⋅
L
=
Porównując otrzymany związek z równaniem (7.17) możemy jeszcze przyjąć podstawienie
d
2
q
d t
2
2 g
⋅
L
q
⋅
+
0
=
skąd wynika
d q
d t
d
2
q
d t
2
2 g
⋅
L
q
⋅
+
⋅
0
=
Po uporządkowaniu uzyskujemy równanie różniczkowe ruchu
π d
2
⋅
4
L
⋅ ρ
⋅
d q
d t
⋅
d
2
q
d t
2
⋅
π d
2
⋅
2
ρ
⋅ g
⋅ q
⋅
d q
d t
⋅
+
0
=
Jeśli wyrażenie to zróżniczkujemy to uzyskamy zależność
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 41
(7.35)
Q s
( )
s q
o
⋅
2 r
⋅ q
o
⋅
+
v
o
+
s
2
2 r
⋅ s⋅
+
ω
2
+
=
q
o
s
r
+
s
2
2 r
⋅ s⋅
+
ω
2
+
⋅
r q
o
⋅
v
o
+
(
)
1
s
2
2 r
⋅ s⋅
+
ω
2
+
⋅
+
=
skąd
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
2 r
⋅ s Q s
( )
⋅
q
o
−
(
)
⋅
+
ω
2
Q s
( )
⋅
+
0
=
Po podstawieniu do (7.33) otrzymujemy
L
d q t
( )
⋅
d t
⋅
s Q s
( )
⋅
q 0
( )
−
=
s Q s
( )
⋅
q
o
−
=
(7.34)
L
d
2
q t
( )
d t
2
s
2
Q s
( )
⋅
s q 0
( )
⋅
−
d q 0
( )
d t
−
=
s
2
Q s
( )
⋅
s q
o
⋅
−
v
o
−
=
Korzystając z zależności (7.19) zapisujemy
(7.33)
L
d
2
q
d t
2
2 r
⋅
d q
d t
⋅
+
ω
2
q
⋅
+
0
=
Rozwiązania równania (7.31) poszukujemy metodą tranformacji Laplace'a:
wg (7.16)
ω
(7.32)
2 r
⋅
c
m
=
gdzie
(7.31)
d
2
q
d t
2
2 r
⋅
d q
d t
⋅
+
ω
2
q
⋅
+
0
=
Po przekształceniu do wygodniejszej postaci matematycznej będzie wyglądać
(7.30)
m
d
2
q
d t
2
⋅
c
d q
d t
⋅
+
k q
⋅
+
0
=
Równanie drgań swobodnych tłumionych opisuje proces fizyczny spowodowany zaburzeniem
stanu równowagi, czyli zaistnieniem warunków początkowych (7.19). Przy uwzględniu sił
oporu tłumienia wiskotycznego równanie ruchu przybierze postać:
7.2 Drgania swobodne tłumione.
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
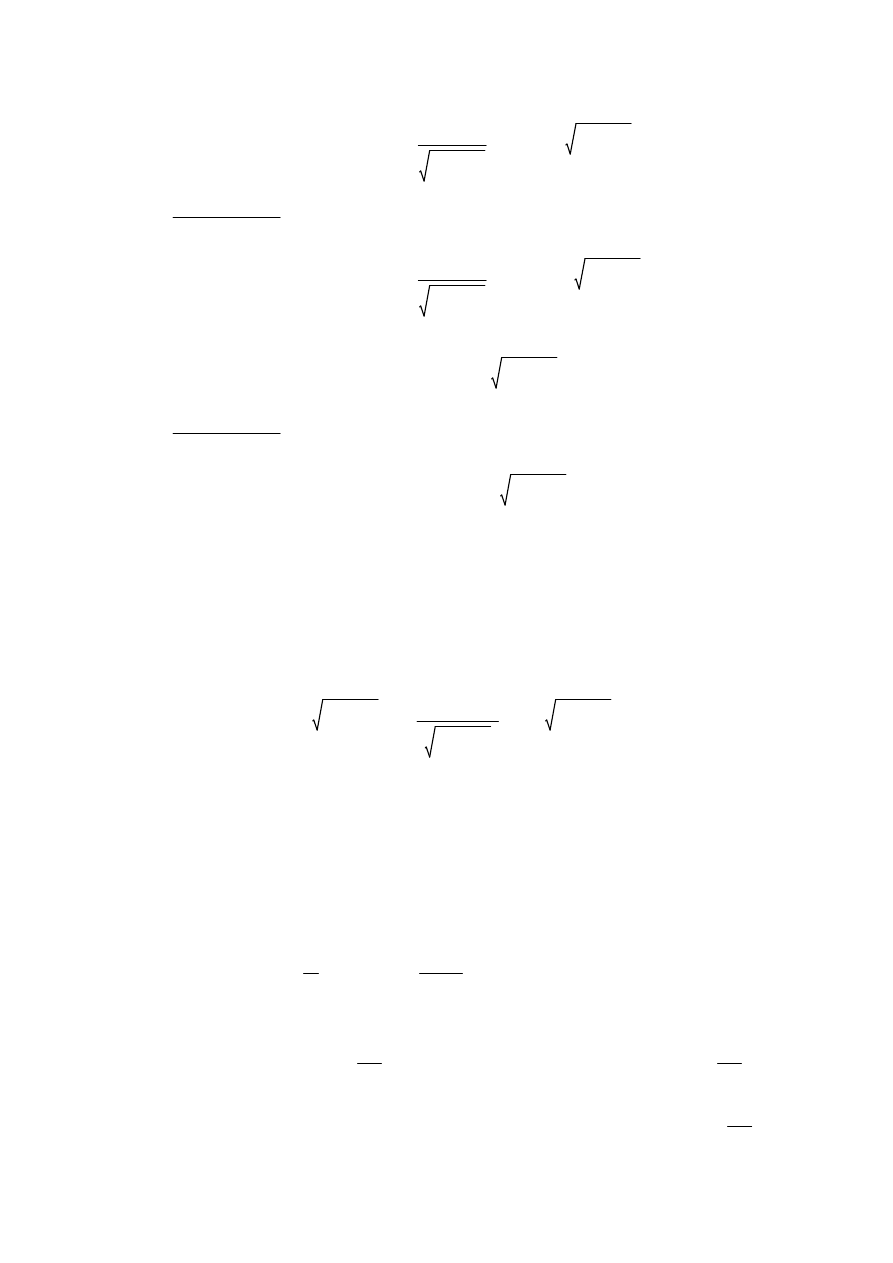
Mechanika budowli
______________________________________________________________________________________________ 42
W tym przypadku tłumienie jest tak duże, iż zachodzi zależność
r
2
ω
2
>
wówczas
q t
( )
e
r
− t⋅
q
o
cosh
r
2
ω
2
−
t
⋅
(
)
⋅
r q
o
⋅
v
o
+
(
)
r
2
ω
2
−
sinh
r
2
ω
2
−
t
⋅
(
)
⋅
+
⋅
=
(7.36)
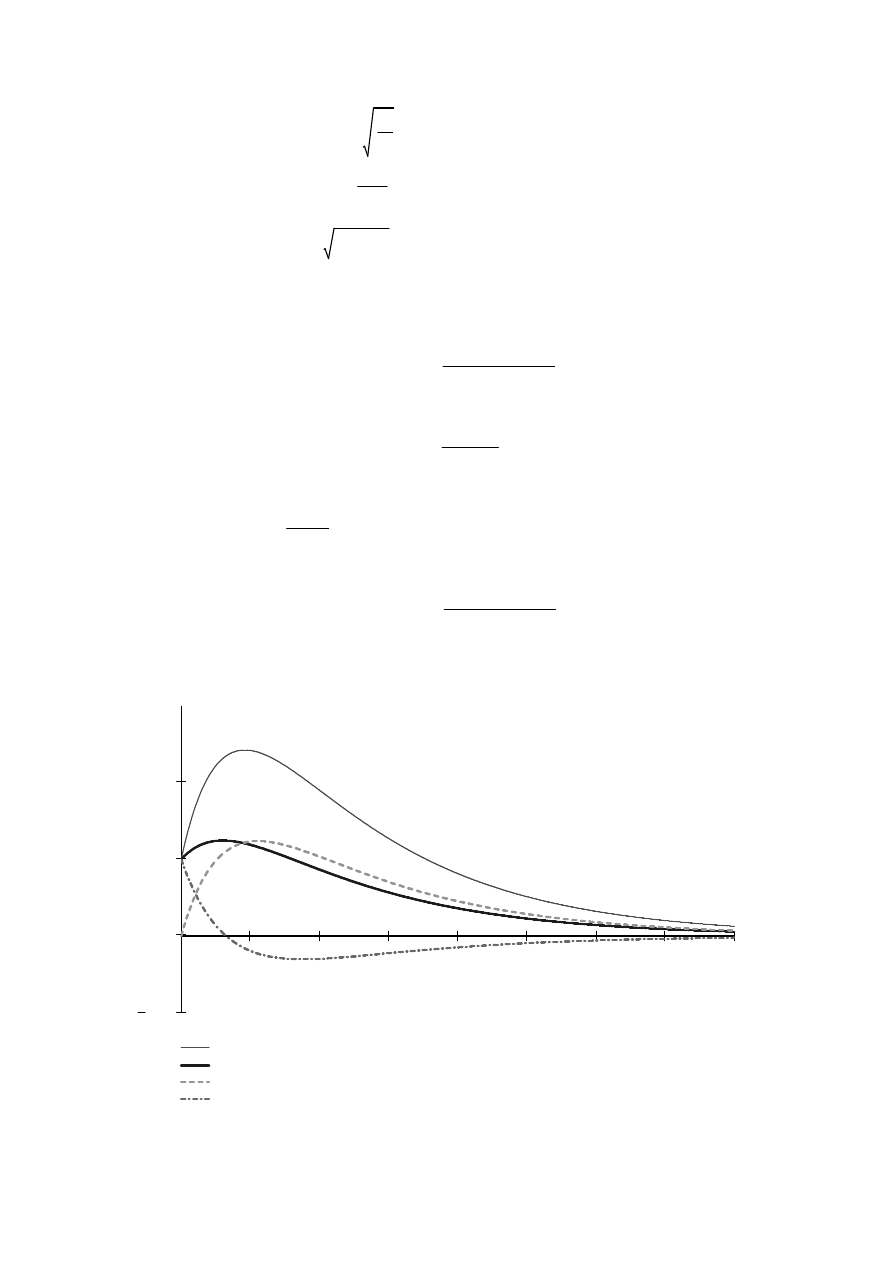
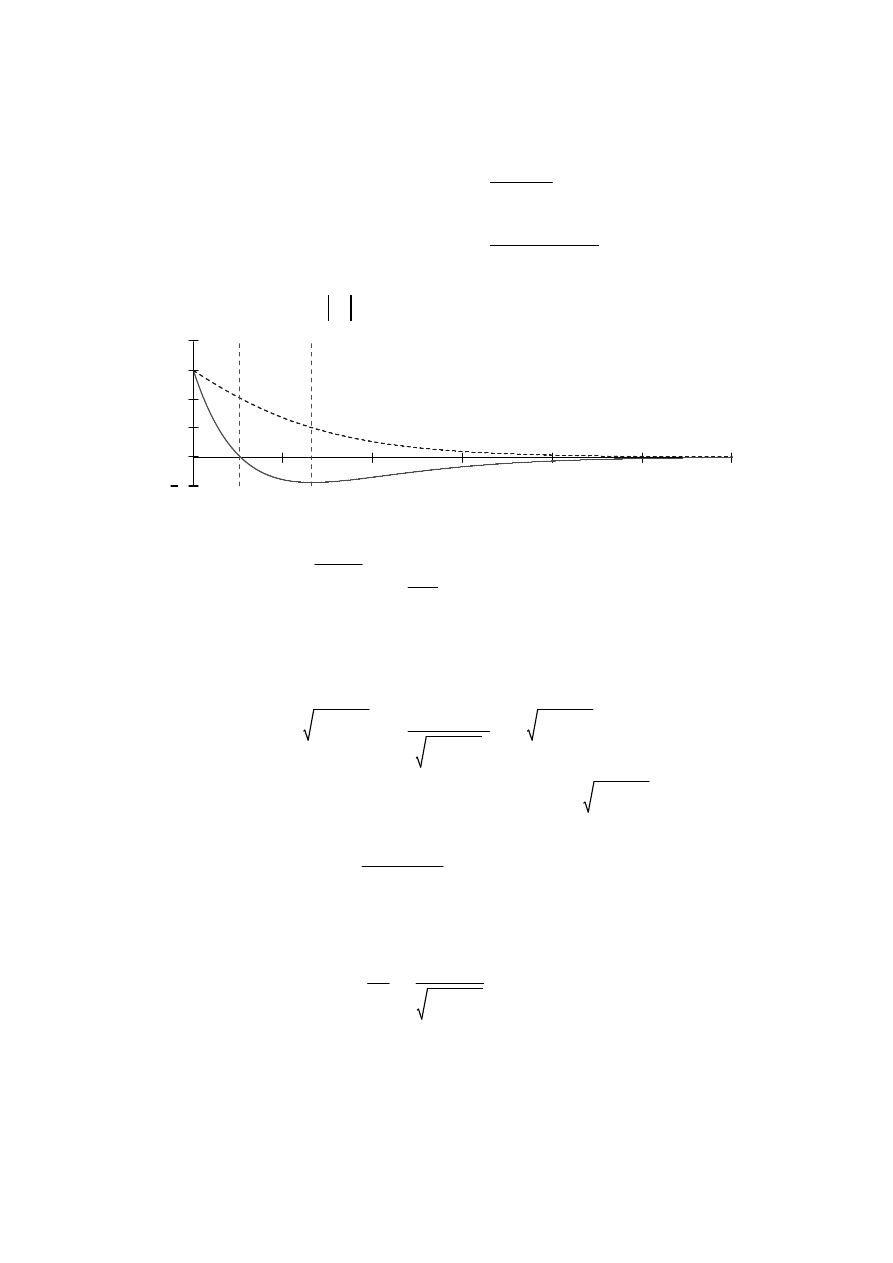
Równanie (7.36) opisuje ruch masy, który jest ruchem aperiodycznym, to znaczy nie występują
tu oscylacje. Masa jednorazowo wytrącona z położenia równowagi statycznej asymptotycznie
zmierza do tego położenia - ruch zanika z czasem. Kształt przebiegu rozwiązania (7.36) w
zależności od wartości stałych q
0
i v
0
zilustrowano w przykładach.
Przykład 7.4
Wyznaczyć równania ruchu układu o jednym stopniu swobody, scharakteryzowanego wielkościami:
m
50 kg
⋅
=
k
900
N
m
⋅
=
c
500
N sec
⋅
m
⋅
=
dla następujących wartości parametrów początkowych:
a)
q
o
5 cm
⋅
=
v
o
0.8
m
sec
⋅
=
c)
q
o
0
=
v
0
0.8
m
sec
⋅
=
b)
q
o
5 cm
⋅
=
v
o
0
=
d)
q
0
5 cm
⋅
=
v
0
0.8
−
m
sec
⋅
=
Transformację odwrotną wyznacza się korzystając z zależności
f t
( )
1
ω
2
r
2
−
e
r
− t⋅
⋅
sin
ω
2
r
2
− t⋅
(
)
⋅
=
dla
r
2
ω
2
<
F s
( )
1
s
2
2 r
⋅ s⋅
+
ω
2
+
=
↔
f t
( )
t e
r
− t⋅
⋅
=
dla
r
2
ω
2
=
f t
( )
1
r
2
ω
2
−
e
r
− t⋅
⋅
sinh
r
2
ω
2
−
t
⋅
(
)
⋅
=
dla
r
2
ω
2
>
f t
( )
e
r
− t⋅
cos
ω
2
r
2
− t⋅
(
)
⋅
=
dla
r
2
ω
2
<
F s
( )
s
r
+
s
2
2 r
⋅ s⋅
+
ω
2
+
=
↔
f t
( )
e
r
− t⋅
=
dla
r
2
ω
2
=
f t
( )
e
r
− t⋅
cosh
r
2
ω
2
−
t
⋅
(
)
⋅
=
dla
r
2
ω
2
>
Ostateczne rozwiązanie zależy więc od wielkości tłumienia. W zależności od jego wartości
wyrażonej wartością współczynnika tłumienia r, mierzonej w stosunku do wartości częstości
drgań własnych
ω rozróżnia się trzy przypadki.
Przypadek 1 - tłumienie nadkrytyczne
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 43
Rozwiązanie:
Częstość drgań własnych
ω
k
m
=
ω 4.243s
-1
=
Współczynnik tłumienia
r
c
2 m
⋅
=
r
5 s
-1
=
Wielkość pomocnicza
r
2
ω
2
−
2.646 s
-1
=
Po uwzględnieniu warunków początkowych równania ruchu typu (7.36) przybiorą postać
q
a
t
( )
e
5
− t⋅
0.05 cosh 2.646 t
⋅
(
)
⋅
10 0.05
⋅
0.8
+
(
)
2.646
sinh 2.646 t
⋅
(
)
⋅
+
⋅
=
q
b
t
( )
e
5
− t⋅
0.05 cosh 2.646 t
⋅
(
)
⋅
10 0.05
⋅
2.646
sinh 2.646 t
⋅
(
)
⋅
+
⋅
=
q
c
t
( )
e
5
− t⋅
0.8
2.646
sinh 2.646 t
⋅
(
)
⋅
⋅
=
q
d
t
( )
e
5
− t⋅
0.05 cosh 2.646 t
⋅
(
)
⋅
10 0.05
⋅
0.9
−
(
)
2.646
sinh 2.646 t
⋅
(
)
⋅
+
⋅
=
Wykresy przebiegów drgań
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0.05
0.05
0.1
Przypadek a
Przypadek b
Przypadek c
Przypadek d
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 44
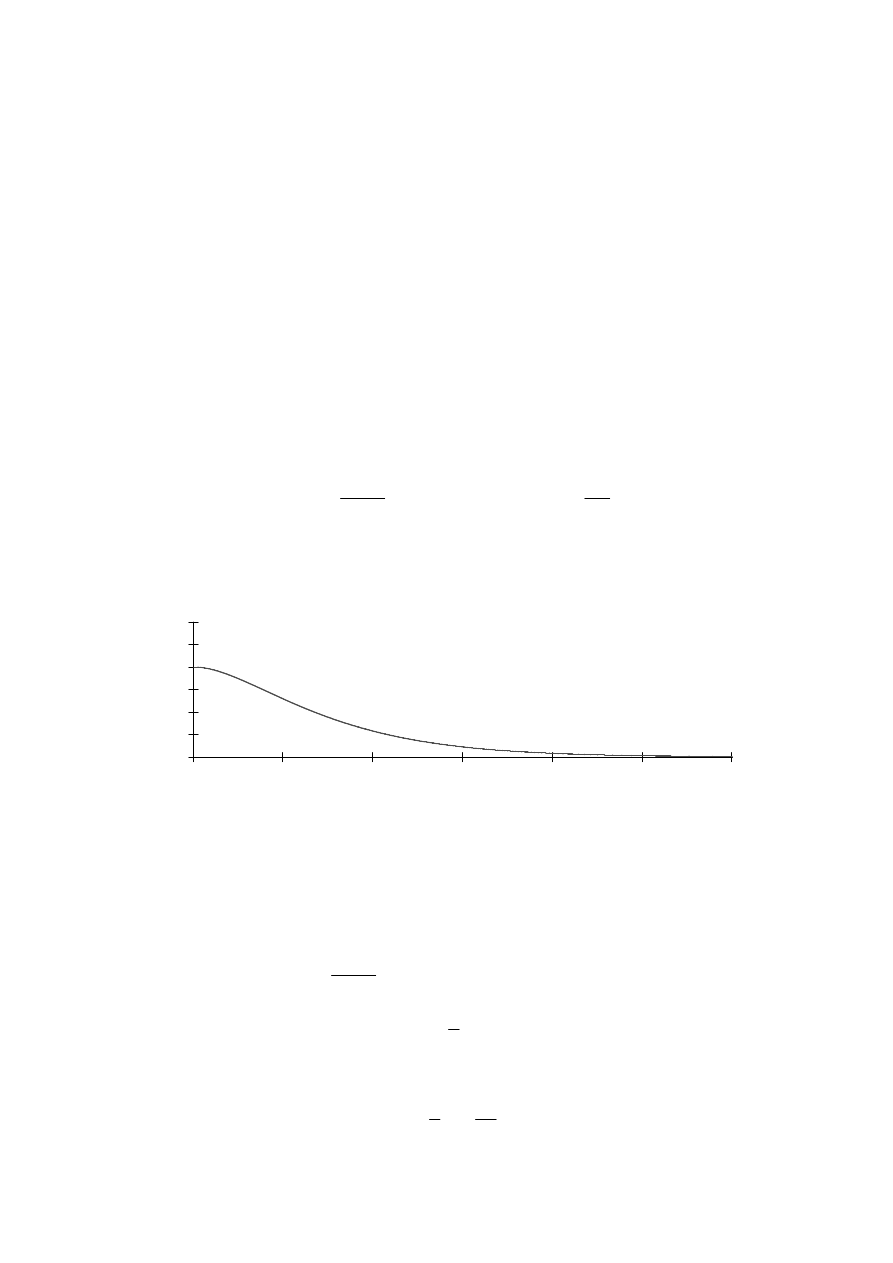
Przykład 7.5
Ilustracja przykładowego wykresu ruchu
q t
( )
2 e
5
− t⋅
⋅
1
5 t
⋅
+
(
)
⋅
=
0
0.25
0.5
0.75
1
1.25
1.5
0.5
1
1.5
2
2.5
3
Czas t
W
y
ch
y
le
n
ie
q
Dla
q
o
0
=
oraz
v
o
0
>
równanie ruchu przybiera formę
q t
( )
e
r
− t⋅
v
o
⋅ t⋅
=
(7.40)
Ciało w tym przypadku osiągnie maksymalne wychylenie w chwili, gdy prędkość stanie się równa 0
v t
( )
d q t
( )
d t
=
v
o
e
r
− t⋅
⋅
1
r t
⋅
−
(
)
⋅
=
(7.41)
v t
( )
0
=
(
)
⇔ t
1
1
r
=
(7.42)
Wartość maksymalnego wychylenia
q
max
q t
1
( )
=
q
1
r
=
v
o
r e
⋅
=
(7.43)
Przypadek 2 - tłumienie krytyczne
Tłumienie w układzie również osiąga duże wartości, współczynnik tłumienia przybiera szczególną
wartość r=
ω. W takim przypadku równanie opisujące ruch wygląda następująco:
q t
( )
e
r
− t⋅
q
o
r q
o
⋅
v
o
+
(
)
t
⋅
+
⋅
=
(7.37)
Przeanalizujemy pewne przypadki szczególne.
Dla
q
o
0
>
oraz
v
o
0
=
równanie ruchu przybiera formę
q t
( )
q
o
e
r
− t⋅
⋅
1
r t
⋅
+
(
)
⋅
=
(7.38)
Widać z niego, że zawsze będzie q(t)>0 a ponadto dlat
⇒ ∞ będzie
q t
( )
⇒ 0
Oznacza to, iż ciało wychylone z położenia równowagi i puszczone bez prędkości początkowej
będzie zdążał do położenia równawagi z prędkością ujemną stale malejącą co do wartości
bezwględnej, gdyż
v t
( )
d q t
( )
d t
=
r
2
− q
o
⋅ e
r
− t⋅
⋅
t
⋅
=
r
2
− q
o
⋅
t
e
r t
⋅
⋅
=
(7.39)
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 45
d q t
( )
⋅
d t
⋅
⇒ 0
będzie
t
⇒ ∞
ale dla
d q t
( )
d t
0
<
Widać z (7.44), że po czasie t
1
wg (7.45) będzie
(7.46)
q
max
q t
1
( )
=
e
v
o
−
r q
o
⋅
v
o
+
q
o
v
o
r
+
⋅
=
Maksymalne wychylenie
(7.45)
t
1
v
o
r
2
q
o
⋅
r v
o
⋅
+
=
Wartość zerową przyjmuje ona dla chwili
(7.44)
v t
( )
d q t
( )
d t
=
e
r
− t
v
o
t r
2
q
o
⋅
r v
o
⋅
+
(
)
⋅
−
⋅
=
równanie ruchu wg (7.37), stąd równanie opisujące prędkość
v
o
0
>
oraz
q
o
0
>
Dla
28
5 e
⋅
2.06
=
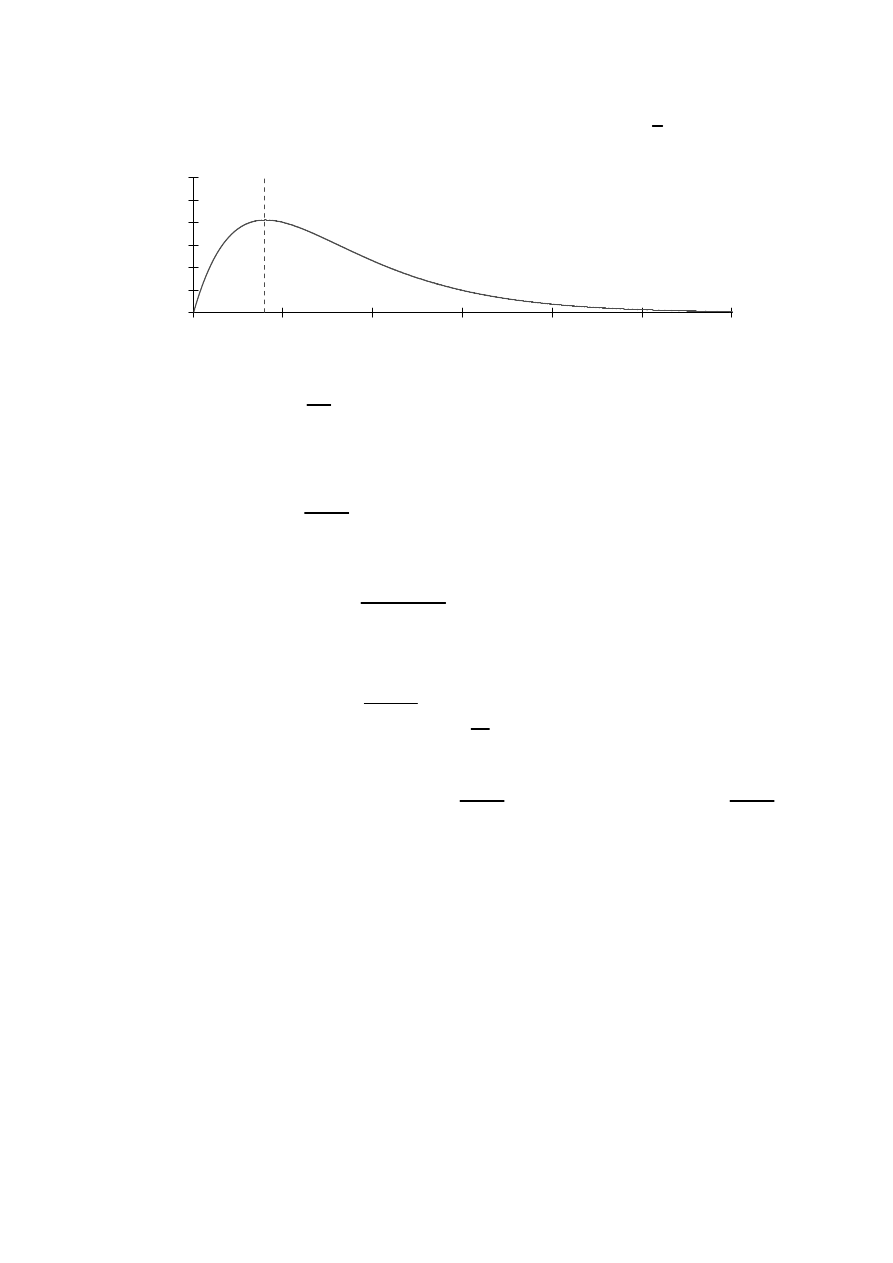
Maksymalne wychylenie
0
0.25
0.5
0.75
1
1.25
1.5
0.5
1
1.5
2
2.5
3
Czas t
W
y
ch
y
le
n
ie
q
t
1
t
1
1
5
=
q t
( )
e
5
− t⋅
28
⋅ t⋅
=
Ilustracja przykładowego wykresu ruchu
Przykład 7.6
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 46
v
o
0
<
To maksymalne wychylenie określone jest zależnością (7.46), z tym tylko że
(7.49)
t
2
v
o
r
2
q
o
⋅
r v
o
⋅
+
=
W przeciwnym przypadku położenie równowagi nie zostanie osiągnięte, ciało będzie zbliżać się do
niego asymptotycznie. Na podstawie zależności (7.44) można w przypadku dostatecznie dużej
prędkości początkowej wyznaczyć czas, po którym ciało osiągnie maksymalne wychylenie w kierunku
ujemnym
(7.48)
v
o
−
r q
o
⋅
>
czyli
r q
o
⋅
v
o
+
0
<
to musi zachodzić
t
1
0
>
Ponieważ z fizycznego punktu widzenia wymagane jest aby czas
(7.47)
v
o
0
<
gdzie
t
1
q
o
−
r q
o
⋅
v
o
+
(
)
=
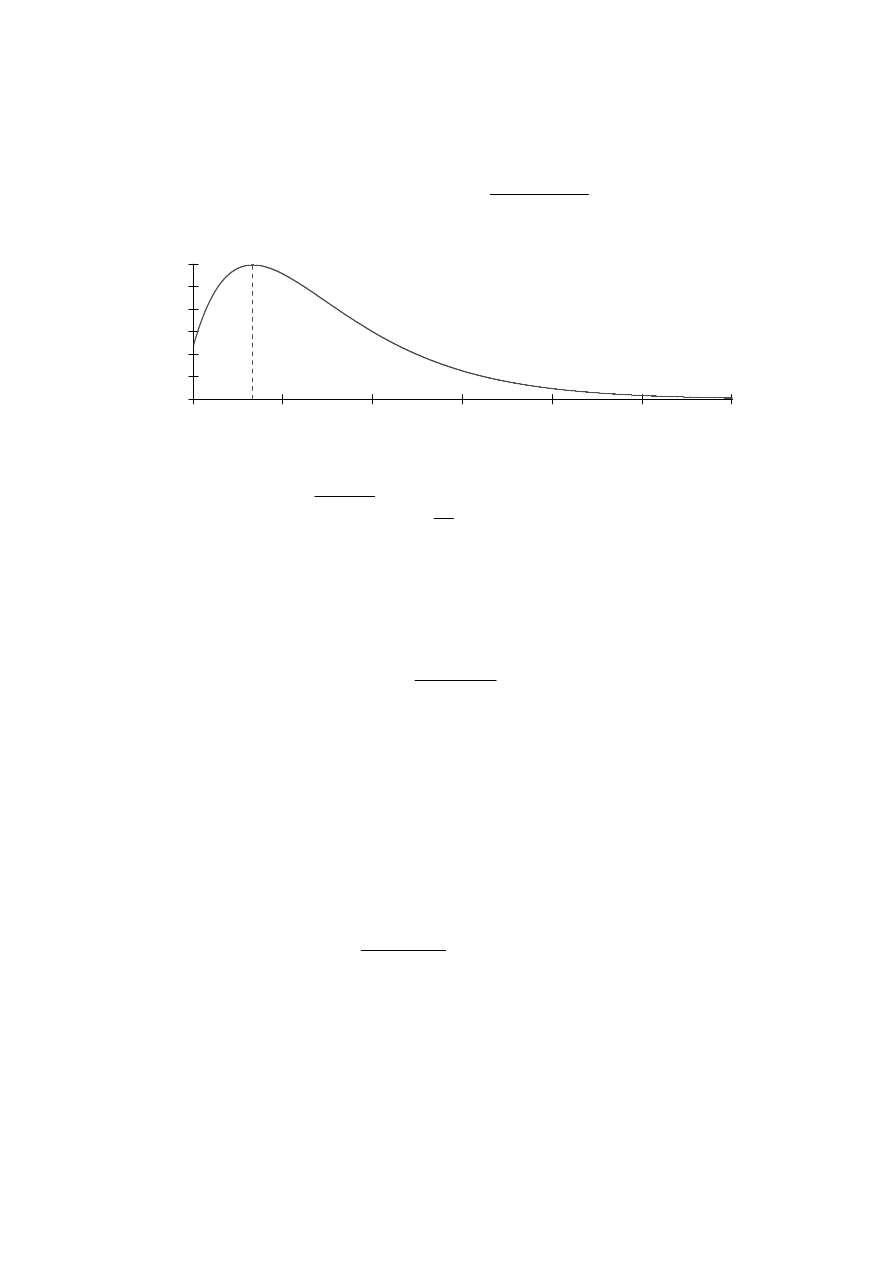
Przykład 7.7
Ilustracja przykładowego wykresu ruchu
q t
( )
e
5
− t⋅
1.2
5 1.2
⋅
28
+
(
) t
⋅
+
[
]
⋅
=
Czas osiągnięcia maksymalnego wychylenia t
1
28
5
2
1.2
⋅
5 28
⋅
+
=
t
1
0.165
=
0
0.25
0.5
0.75
1
1.25
1.5
0.5
1
1.5
2
2.5
3
Czas t
W
y
ch
y
le
n
ie
q
t
1
Maksymalne wychylenie e
28
−
5 1.2
⋅
28
+
1.2
28
5
+
⋅
2.984
=
Jeśli
q
o
0
>
oraz
v
o
0
<
możliwe są dwie postaci rozwiązania.
Ogólne rozwiązanie dane jest równaniem (7.37). Z uwagi jednak na ujemną wartość początkowej
prędkości możliwe jest osiągnięcie położenia równowagi . Występuje to w chwili t
1
gdy
q
o
r q
o
⋅
v
o
+
(
)
t
1
⋅
+
0
=
⇒
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 47
Ruch opisany równaniem (7.52) jest quasi-harmonicznym ruchem zanikającym, modulowanym
funkcją wykładniczą. Rozwiązanie ma przebieg oscylacyjny, niemniej funkcja ta nie jest funkcją
okresową w pełnym tego słowa znaczeniu. Zależność (7.52) można również zapisać w formie
zwiniętej:
(7.53)
T
d
2
π
ω
d
=
2
π
ω
2
r
2
−
=
Wielkość opisana zależnością (7.51) nazywana jest częstością drgań tłumionych. Okres tych
drgań wyniesie więc
(7.52)
q t
( )
e
r
− t⋅
q
o
cos
ω
d
t
⋅
( )
⋅
r q
o
⋅
v
o
+
(
)
ω
d
sin
ω
d
t
⋅
( )
⋅
+
⋅
=
(7.51)
ω
d
ω
2
r
2
−
=
Powyższy zapis można uprościć wprowadzając oznaczenie
(7.50)
q t
( )
e
r
− t⋅
q
o
cos
ω
2
r
2
− t⋅
(
)
⋅
r q
o
⋅
v
o
+
(
)
ω
2
r
2
−
sin
ω
2
r
2
− t⋅
(
)
⋅
+
⋅
=
wówczas ruch masy opisuje równanie
r
2
ω
2
<
W tym przypadku zachodzi zależność
Przypadek 3 - tłumienie podkrytyczne
e
38
5 3
⋅ 38
−
3
38
−
5
+
⋅
0.882
−
=
Maksymalne wychylenie
0
0.25
0.5
0.75
1
1.25
1.5
1
1
2
3
4
Czas t
W
y
ch
y
le
n
ie
q
t
1
t
2
q
2
t
( )
e
5
− t⋅
3
3 5
⋅
8
−
(
) t
⋅
+
[
]
⋅
=
v
o
r q
o
⋅
<
Wykres ruchu dla prędkości
t
2
0.33
=
t
2
38
−
5
2
3
⋅
5
38
−
(
)
⋅
+
=
Czas osiągnięcia maksymalnego wychylenia
t
1
0.13
=
t
1
3
−
5 3
⋅
38
−
=
Czas ociągnięcie położenia równowagi
q t
( )
e
5
− t⋅
3
3 5
⋅
38
−
(
) t
⋅
+
[
]
⋅
=
Ilustracja przykładowego wykresu ruchu
Przykład 7.8
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 48
Zamiast wymiarowego współczynnika tłumienia r stosowany bywa również bezwymiarowy
współczynnik tłumienia określony zależnością
(7.61)
r
≈ ∆ ω
⋅
2
π
Ze względu na to, iż w typowych ustrojach występujących w zagadnieniach mechaniki budowli
wartość logarytmicznego dekrementu tłumienia jest znacznie mniejsza od jedności wyrażenie (7.60)
może zostać uproszczone do postaci
(7.60)
r
∆ ω
⋅
4
π
2
∆
2
+
=
Wyznaczając z powyższego współczynnik r otrzymuje się
(7.59)
r
∆
T
d
=
∆ ω
d
⋅
2
π
=
∆ ω
2
r
2
−
⋅
2
π
=
Logarytmiczny dekrement tłumienia może byc więc miarą zdolności tłumienia drgań przez
konstrukcję. Nie jest on stałą materiałową, lecz wielkością związaną z ustrojem. Związany jest
ze współczynnikiem tłumienia następującymi zależnościami:
(7.58)
∆ ln
A
n
A
n
1
+
=
Jego wartość można wyznaczyć doświadczalnie, drogą pomiaru dwóch kolejnych amplitud
przemieszczeń tego samego znaku.
(7.57)
∆ ln
q t
( )
q t
T
d
+
(
)
=
ln e
r T
d
⋅
( )
=
r T
d
⋅
=
Logarytm naturany tego stosunku wychyleń nazywany jest logarytmicznym dekrementem tłumienia
(7.56)
q t
( )
q t
T
d
+
(
)
A e
r
− t⋅
⋅
sin
ω
d
t
⋅ ϕ
+
(
)
⋅
A e
r
− t T
d
+
( )
⋅
⋅
sin
ω
d
t
T
d
+
(
)
⋅
ϕ
+
⋅
=
e
r T
d
⋅
=
Rozpatrzmy stosunek dwóch kolejnych wychyleń w tę samą stronę różniących się w czasie o okres
A
− e
r
− t⋅
⋅
amp q
( )
≤
A e
r
− t⋅
⋅
≤
Amplitudy przemieszczeń będą się zawierały między liniami
(7.55)
tan
ϕ
q
o
ω
d
⋅
q
o
r
⋅ v
o
+
=
A
q
o
2
q
o
r
⋅ v
o
+
ω
d
2
+
=
gdzie
(7.54)
q t
( )
A e
r
− t⋅
⋅
sin
ω
d
t
⋅ ϕ
+
(
)
⋅
=
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
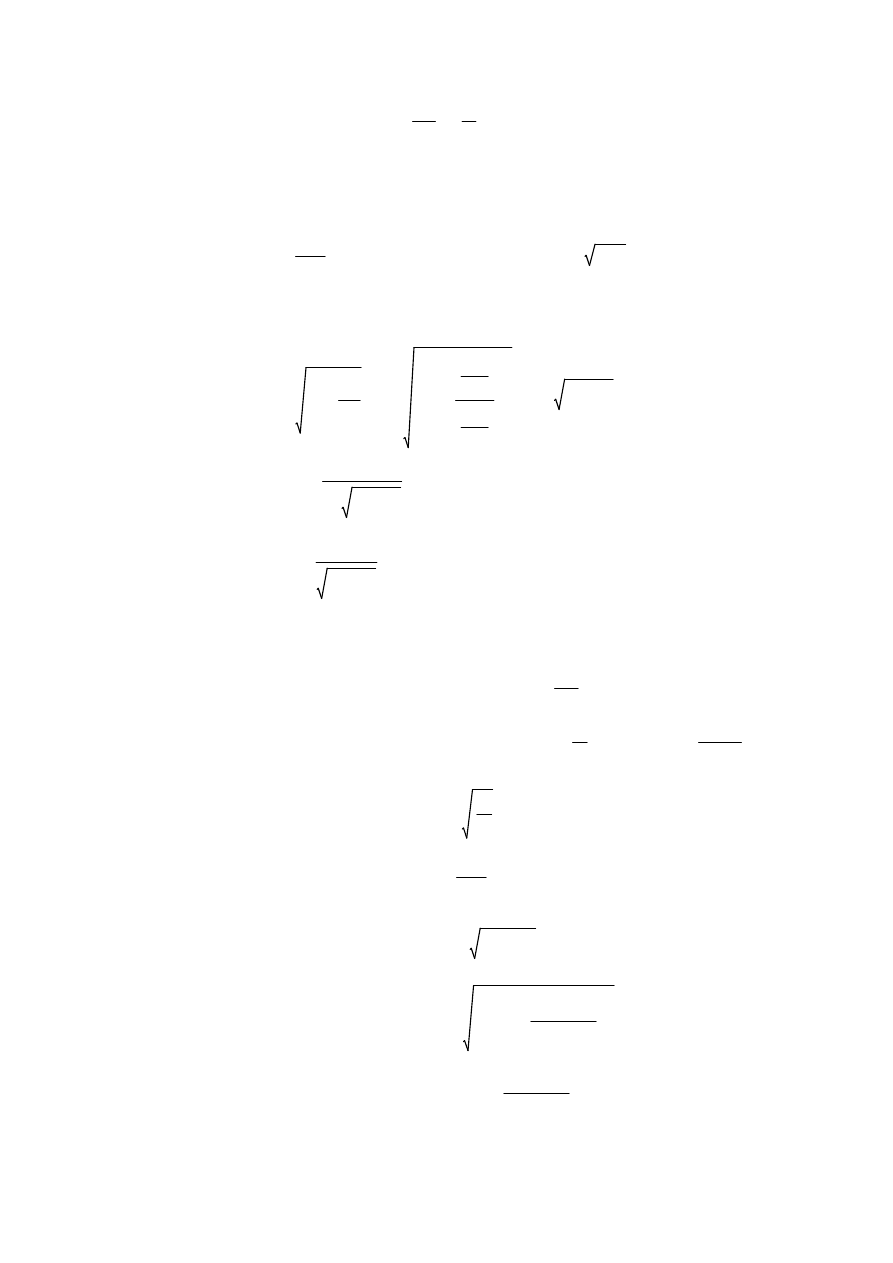
Mechanika budowli
______________________________________________________________________________________________ 49
m
80 kg
⋅
=
k
10
5
N
m
⋅
=
c
400
N sec
⋅
m
⋅
=
Rozwiązanie
Częstość drgań własych
ω
k
m
=
ω 35.355s
-1
=
Współczynnik tłumienia
r
c
2 m
⋅
=
r
2.5 s
-1
=
Częstość drgań tłumionych
ω
d
ω
2
r
2
−
=
ω
d
35.267 s
-1
=
Stałe związane z warunkami początkowymiA
q
o
2
q
o
r
⋅ v
o
+
ω
d
2
+
=
A
0.539 m
=
ϕ
atan
q
o
ω
d
⋅
q
o
r
⋅ v
o
+
=
ϕ 0.263
=
ξ
c
c
kr
=
r
ω
=
(7.62)
gdzie c
kr
jest krytycznym parametrem tłumika wiskotycznego wyznaczającym granicę między
tłumieniem nad i podkrytycznym, odpowiadający więc tłumieniu krytycznemu. Wyznacza się
go z zależności (7.32)
r
kr
c
kr
2 m
⋅
=
ω
=
stąd
c
kr
2 m
⋅ ω
⋅
=
2 k m
⋅
=
(7.63)
Za pomocą bezwymiarowego współczynnika tłumienia można opisać wszystkie parametry
tłumionego układu drgającego
ω
d
ω 1
r
2
ω
2
−
⋅
=
ω 1
c
2 m
⋅
c
kr
2 m
⋅
2
−
⋅
=
ω 1 ξ
2
−
⋅
=
(7.64)
T
d
2
π
ω 1 ξ
2
−
⋅
=
(7.65)
(7.66)
∆
ξ 2
⋅ π
1
ξ
2
−
=
Przykład 7.9
Wyznaczyć odpowiedź tłumionego układu drgającego, przy nastepujących warunkach początkowych:
q
o
14 cm
⋅
=
v
o
18
m
sec
⋅
=
Parametry charakteryzujące układ
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 50
(7.70)
A
0
A
n
A
0
A
1
A
1
A
2
⋅
A
2
A
3
⋅
....
⋅
A
n 1
−
A
n
⋅
=
stosunek pierwszej i ostatniej mierzonej amplitudy można zapisać jak niżej
(7.69)
e
∆
A
0
A
1
=
A
1
A
2
=
A
2
A
3
=
....
=
A
n 1
−
A
n
=
przekształcając równanie (7.68) otrzymujemy
są kolejnymi amplitudami wychylenia
A
0
A
1
,
A
2
,
A
3
,
....
,
A
n
,
gdzie
(7.68)
∆ ln
A
0
A
1
=
ln
A
1
A
2
=
ln
A
2
A
3
=
....
=
ln
A
n 1
−
A
n
=
Wynika to z następującego rozumowania. Stosunki kolejnych amplitud w ruchu tłumionym
wiskotycznie są jednakowe tzn. logarytmiczny dekrement tłumienia można obliczyć z każdej
z poniższych zależności:
gdzie i oraz i+n oznaczają numery amplitud różniących się o ilość n cykli.
(7.67)
∆
1
n
ln
A
i
A
i n
+
⋅
=
Dokładność wyznaczania doświadczalnego wartości parametrów charakteryzyjących tłumienie
zależy od stopnia dokładności pomiaru amplitud drgań. Jeśli tłumienie, tak jak w przypadku
ustrojów budowlanych nie jest bardzo intensywne, sąsiednie amplitudy różnią się nieznacznie.
Z tego powodu celem zwiększenia dokładności obliczeń można przy wyznaczaniu logarytmicznego
dekrementu tłumienia korzystać z poniższej zależności:
0
0.2
0.4
0.6
0.8
0.6
0.3
0.3
0.6
Czas t
P
rz
em
ie
sz
cz
en
ie
q
(t
)
q t
( )
0.539 e
2.5
−
t
⋅
⋅
sin 35.267 t
⋅ 0.263
+
(
)
⋅
=
Równanie ruchu układu
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha

Mechanika budowli
______________________________________________________________________________________________ 51
ω 57.126s
-1
=
ω
ω
d
2
r
2
+
=
Częstość drgań własnych
ω
d
57.12 s
-1
=
ω
d
2
π
⋅
T
d
=
Częstość drgań tłumionych
r
0.833 s
-1
=
r
∆
T
d
=
Współczynnik tłumienia
∆ 0.092
=
∆
ln
A
4
A
5
=
Logarytmiczny dekrement tłumienia
Rozwiązanie
Wyznaczyć parametry tłumienia układu i porównać z wartościami własnymi.
T
d
0.11 sec
⋅
=
Pomierzony okres drgań wynosi
A
5
32.3 mm
⋅
=
A
4
35.4 mm
⋅
=
Wartości kolejnych amplitud tego samego znaku wyznaczone podczas pomiarów wynoszą
Przykład 7.10
Amplituda startowa, od której zaczynamy pomiar nie musi być koniecznie faktycznie pierwszą
od początku drgań, tylko każdą dowolną. Stąd otrzymujemy wzór (7.67)
∆
1
n
ln
A
0
A
n
⋅
=
(7.73)
Stąd ostatecznie można zapisać
(7.72)
ln
A
0
A
n
n
∆
⋅
=
Na mocy równości (7.68) uzyskujemy
(7.71)
ln
A
0
A
n
ln
A
0
A
1
ln
A
1
A
2
+
ln
A
2
A
3
+
....
+
ln
A
n 1
−
A
n
+
=
Dokonując obustronnego zlogarytmowania wyrażenia (7.70), przy wykorzystaniu znanych
własności logarytmów otrzymujemy zależność
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Mechanika budowli
______________________________________________________________________________________________ 52
- dekrement tłumienia
∆
0.19
=
Rozwiązanie:
Sztywność belki
k
b
48 E
⋅ I⋅
L
3
=
k
b
240534.668
N
m
=
Częstość drgań własnych
ω
k
b
m
=
ω 17.34s
-1
=
Okres drgań własnych
T
2
π
ω
=
T
0.362 s
=
Współczynnik tłumienia
r
∆ ω
⋅
4
π
2
∆
2
+
=
r
0.524 s
-1
=
Częstość drgań tłumionych
ω
d
ω
2
r
2
−
=
ω
d
17.332 s
-1
=
Okres drgań tłumionych
T
d
2
π
ω
d
=
T
d
0.363 s
=
Przykład 7.11
Wyznaczyć logarytmiczny dekrement tłumienia jeśli podczas pomiarów w czasie 18.5 s
zarejestrowano 11 pełnych cykli drgań, a amplitudy tego samego znaku na początku i końcu
pomiaru wynosiły odpowiednio 26.3 mm i 18.5 mm.
Rozwiązanie
Okres drgań tłumionych
T
d
18.5 sec
⋅
11
=
T
d
1.682 s
=
Logarytmiczny dekrement tłumienia
∆
1
9
ln
26.3
18.5
⋅
=
∆ 0.039
=
Przykład 7.12
Na belce stalowej ustawiono maszynę. Wyznaczyć częstość i okres drgań własnych układu
oraz drgań swobodnych tłumionych określonych wartością logarytmicznego dekrementu tłumienia.
Dane:
EI
q
m
L/2
L/2
- parametry sztywności belki wsporczej
E
205 GPa
⋅
=
I
80.1 cm
4
⋅
=
- masa maszyny
m
800 kg
⋅
=
- wymiary geometryczne L
320 cm
⋅
=
2005-03-05
______________________________________________________________________________________________
Politechnika Częstochowska Katedra Mechaniki Technicznej
Dr inż.S.Labocha
Wyszukiwarka
Podobne podstrony:
Mechanika Budowli Sem[1][1] VI Wyklad 02 color
Mechanika Budowli Sem[1][1] VI Wyklad 01
Mechanika Budowli Sem[1][1] VI Wyklad 05
Konstrukcje metalowe Sem VI Wyklad 04
Konstrukcje metalowe Sem VI Wyklad 02
sem VI FŚ k-z 04, UCZELNIA ARCHIWUM, UCZELNIA ARCHIWUM WGiG, WGiG Rok III sem VI (2013-2014), sem VI
Konstrukcje metalowe Sem VI Wyklad 03
Mechanika Budowli sem 4 i5 tematy egzaminu
harmonogram CWICZ, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, matreiały na mb
Mecha- belka, Sem V, Mechanika Budowli Proj, Mechanika Budowli, Belka
wstep do zadan, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, EGZ, egzam
mechanika budowli ćwiczenia (11 04 2010 r )
MECHANIKA BUDOWLI projekt 1 , sem IV (1)
więcej podobnych podstron