Konstrukcje metalowe

______________________________________________________________________________________________ 23

gdzie A

n

- pole najmniejszego płaskiego lub łamanego przekroju netto

R

m

- wytrzymałość na rozciąganie stali

R

e

- granica plastyczności stali

(5)

A

ψ

A

≤

lecz

A

ψ

A

n

0.8 R

m

⋅

R

e

⋅

=

- dla prętów obciążonych osiowo i osłabionych otworami, w przypadku pojedynczej

ścianki (dla ścianki, blachy, pasa lub środnika belki)

Sprowadzone pole przekroju oblicza się z zależności

gdzie A

ψ

-

sprowadzone pole przekroju

(32)

N

Rt

A

ψ

f

d

⋅

=

W przypadku elementów osłabionych otworami na łączniki lub zamocowanych

mimośrodowo (kątowniki zamocowane jednym ramieniem, ceowniki zamocowane

środnikiem, teowniki półką) nośność przekroju należy wyznaczyć ze wzoru

N - siła osiowa w pręcie

N

Rt

- nośność obliczeniowa przekroju przy rozciąganiu

A - pole przekroju pręta

f

d

- wytrzymałość obliczeniowa stali

gdzie

(31)

N

N

Rt

≤

A f

d

⋅

=

Nośność elementów rozciąganych osiowo należy sprawdzać ze wzoru

Elementy rozciągane osiowo

Wybrane zagadnienia z PN-90/B-03200

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 24

dla cięgien bez wstępnego naciągu

λ 350

≤

dla prętów kratownic

λ 250

≤

Ponadto:

- dla prętów o długości rzutu większej niż 6 m należy uwzględnić zginanie wywołane

ciężarem własnym

- w przypadku obciążeń dynamicznych obowiązuje ograniczenie smukłości:

gdzie A

1

ψ

-

sprowadzone pole przekroju części przylgowej kształtownika

A

1n

-

pole przekroju netto części przylgowej kształtownika

(30)

A

ψ

A

1

ψ

=

A

1n

0.8 R

m

⋅

R

e

⋅

=

- dla prętów zamocowanych mimośrodowo na jeden łącznik

gdzie A

1

- pole przekroju części przylgowej kształtownika, brutto dla połączeń

spawanych, netto dla połączeń śrubowych i nitowych

A

2

- pole przekroju części odstającej kształtownika

(29)

A

ψ

A

1

3 A

1

⋅

3 A

1

⋅

A

2

+

A

2

⋅

+

=

- dla prętów zamocowanych mimośrodowo

A

i

ψ

wg wzoru (5)

(6)

A

ψ

i

A

i

ψ

∑

=

- dla prętów obciążonych osiowo i osłabionych otworami, w przypadku elementu

złożonego z kilku ścianek (dla całego kształtownika)

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 25

k

t

0.6k

=

Dla naprężeń stycznych

Przy projektowaniu należy sprawdzać naprężenia wg obu rodzajów naprężeń (I, II)

(wsp.pewności 1,4)

k

II

1700

kG

cm

2

⋅

=

(wsp. pewności 1,6)

k

I

1500

kG

cm

2

⋅

=

Zgodnie z PN-62/B-03200 przyjmowano dwa rodzaje naprężeń dopuszczalnych:

I rodzaj przy uwzględnianiu tylko zasadniczych obciążeń,

II rodzaj przy uwzględnianiu zasadniczych i dodatkowych obciążeń.

Przykładowo dla stali St3S

Siły wewnętrzne P i M wyznaczone dla obciążeń normowych

σ

M

W

k

≤

=

- zginanie

σ

P

β F

⋅

k

≤

=

- ściskanie

σ

P

F

n

k

≤

=

- rozciąganie

Warunki wytrzymałościowe

n

χ

1

χ

2

⋅ χ

3

⋅ ....

⋅ χ

i

⋅

=

Współczynnik pewności jest iloczynem kilku arbitralnych współczynników składowych

- współczynnik bezpieczeństwa (pewności)

n

- granica plastyczności

R

e

k

R

e

n

=

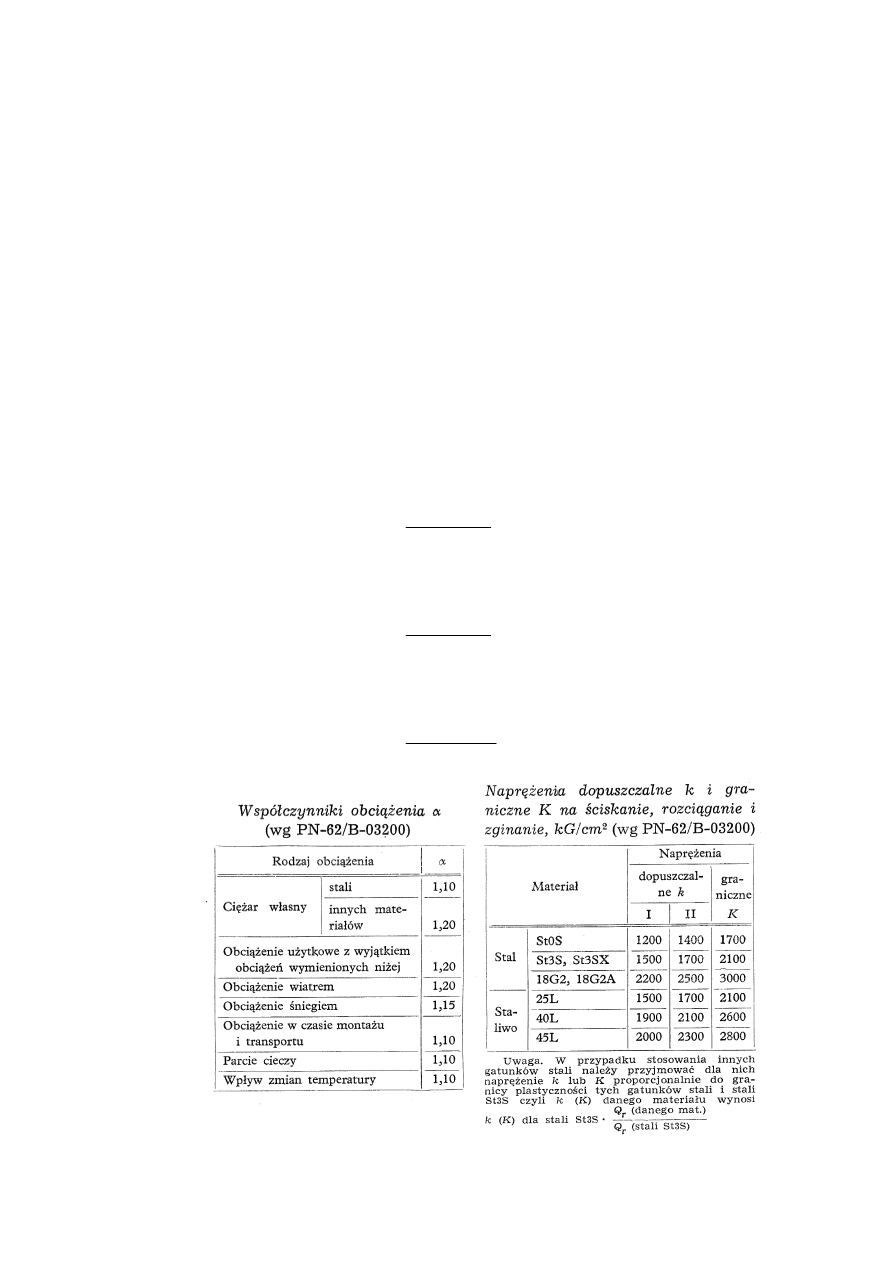
Metody wymiarowania konstrukcji metalowych

Metoda naprężeń dopuszczalnych

•

metoda deterministyczna, obciążenia i własności materiału przyjmowane są jako wielkości

określone nielosowe; kryterium zniszczenia oparte jest o największe naprężenia w elementach,

które nie może przekroczyć naprężeń dopuszczalnych k;

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 26

Metoda naprężeń granicznych

•

metoda uwzględnia specyfikę różnych rodzajów obciążeń; kryterium wyczerpania nośności

zależy od sposobu obciążenia:

- przy rozciąganiu z chwilą wystąpienia na całym polu przekroju naprężenia na granicy plastyczności,

- przy ściskaniu jak wyżej lub z chwilą utraty stateczności,

- przy zginaniu z chwilą wystąpienia we włóknach skrajnych naprężeń na granicy plastyczności

lub utraty stateczności strefy ściskanej.

Naprężenia graniczne

K

κ R

e

⋅

=

κ 1

<

Warunki wtrzymałościowe

- rozciąganie

σ

i

α

i

P

i

⋅

( )

∑

F

n

K

≤

=

- ściskanie

σ

i

α

i

P

i

⋅

( )

∑

β F

⋅

K

≤

=

- zginanie

σ

i

α

i

M

i

⋅

(

)

∑

W

K

≤

=

α - współczynniki obciążenia

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 27

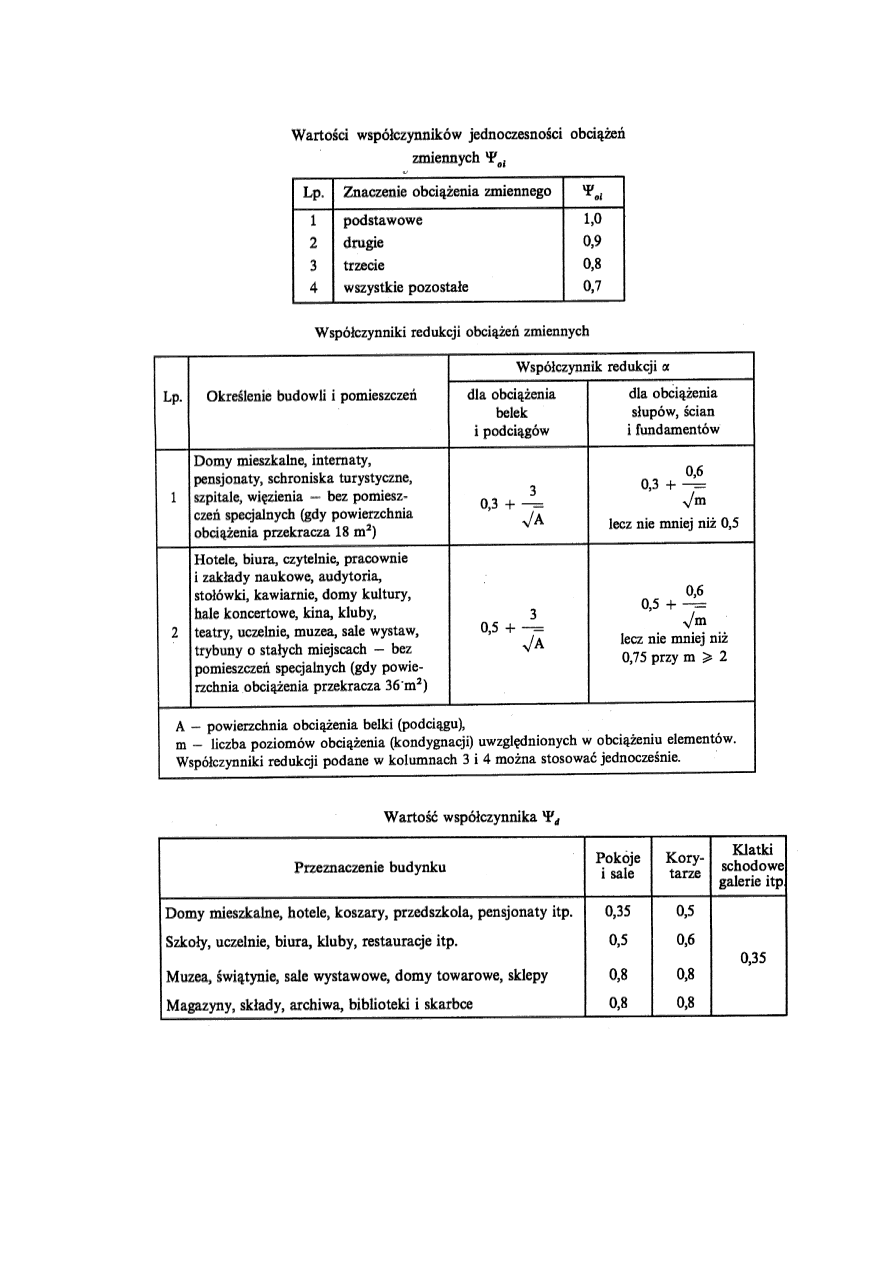
Kombinacje obciążeń - zestawienie schematów i wartości obciążeń działających na konstrukcję:

F

a

G

d

Q

d

γ

f

G

k

⋅

=

,

γ

f

Q

k

⋅

,

G

k

Q

k

,

Parametry obciążenia

- obciążenia charakterystyczne (stałe i zmienne)

- obciążenia obliczeniowe

- obciążenia wyjątkowe

Współczynniki uzupełniające:

- współczynnik jednoczesności obciążeń

ψ

ο

,

- współczynnik redukcji obciążeń

α,

- współczynnik konsekwencji zniszczenia

γ

n

,

- współczynnik dynamiczny

β,

- współczynnik części długotrwałej obciążenia zmiennego

ψ

d

.

f

d

f

yk

γ

s

=

Parametry wytrzymałościowe:

- wytrzymałość charakterystyczna f

yk

,

- wytrzymalość obliczeniowa f

d

N

d

....

γ

n

,

γ

f

,

(

)

N

Rd

....

γ

s

,

( )

≤

Warunek bezpieczeństwa

- współczynnik materiałowy

γ

s

- współczynnik obciążeń

γ

f

- współczynnik konsekwencji zniszczenia

γ

n

Wprowadzono trzy częściowe współczynniki bezpieczeństwa:

Metoda stanów granicznych

•

Metoda wiąże się z granicą tolerancji dla niekorzystnych losowych odchyleń nośności i wymiarów

elementów od wartości oczekiwanej. Odchyleniem losowym nazywane jest takie odchyleniem,

któremu można przypisać określone prawdopodobieństwo. Metoda korzysta więc z metod

probabilistycznych.

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 28

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 29

Stany graniczne

I stan graniczny: nośności (zniszczenia)

•

- utrata stateczności sprężystej lub sprężysto-plastycznej,

- narastanie odkształceń trwałych i przekształcenie konstrukcji w mechanizm

- uszkodzenie (pęknięcia) uniemożliwiające normalną eksploatację,

- utrata równowagi ogólnej lub częściowej konstrukcji.

Kombinacje obciążeń:

- podstawowa

i

G

k

i

γ

f

i

⋅

( )

∑

i

Q

k

i

γ

f

i

⋅ Ψ

o

i

⋅

(

)

∑

+

- wyjątkowa

i

G

k

i

γ

f

i

⋅

( )

∑

0.8

i

Q

k

i

γ

f

i

⋅

( )

∑

⋅

+

F

a

+

II stan graniczny: użytkowania

•

- odkształcenia konstrukcji utrudniające jej użytkowanie lub niedopuszczalne

ze względów estetycznych,

- nadmierne drgania pogarszjące komfort użytkowania obiektów

- miejscowe uszkodzenia (pęknięcia, wybrzuszenia) pogarszające estetykę

Kombinacje obciążeń:

- podstawowa

i

G

k

i

∑

Q

k

+

- długotrwała

i

G

k

i

∑

i

Q

k

i

Ψ

d

i

⋅

(

)

∑

+

Metoda stanów granicznych jest tzw. metodą półprobabilistyczną. Rozróżnia się 3 poziomy

obliczeń probabilistycznych:

- poziom 1, (półprobabilistyczny) niezależna kalibracja współczynników

γ

m

i

γ

f

,

- poziom 2, łączne kryterium niezawodności dla obciążeń i nośności,

- poziom 3, kryterium niezawodności całej konstrukcji.

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 30

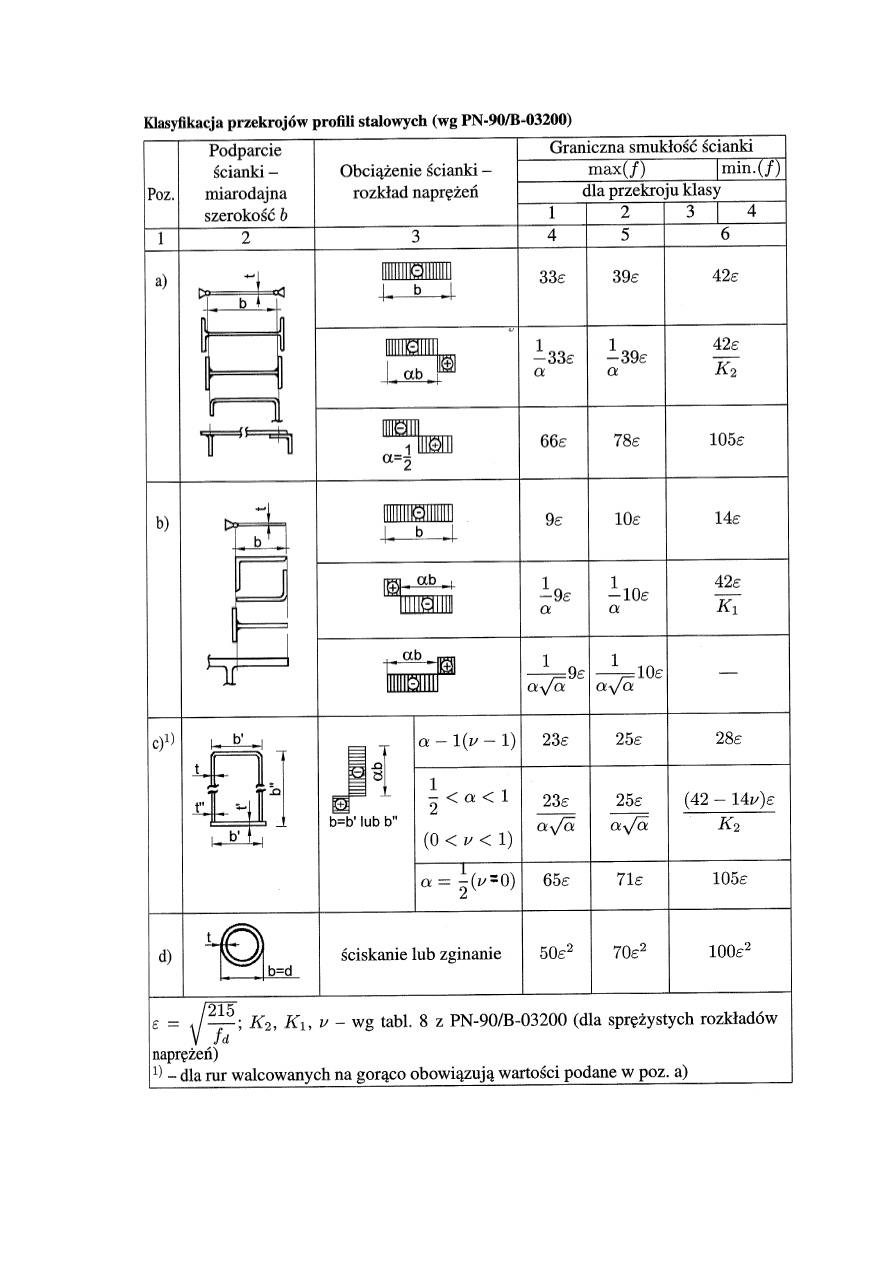
Wybrane zagadnienia z PN-90/B-03200

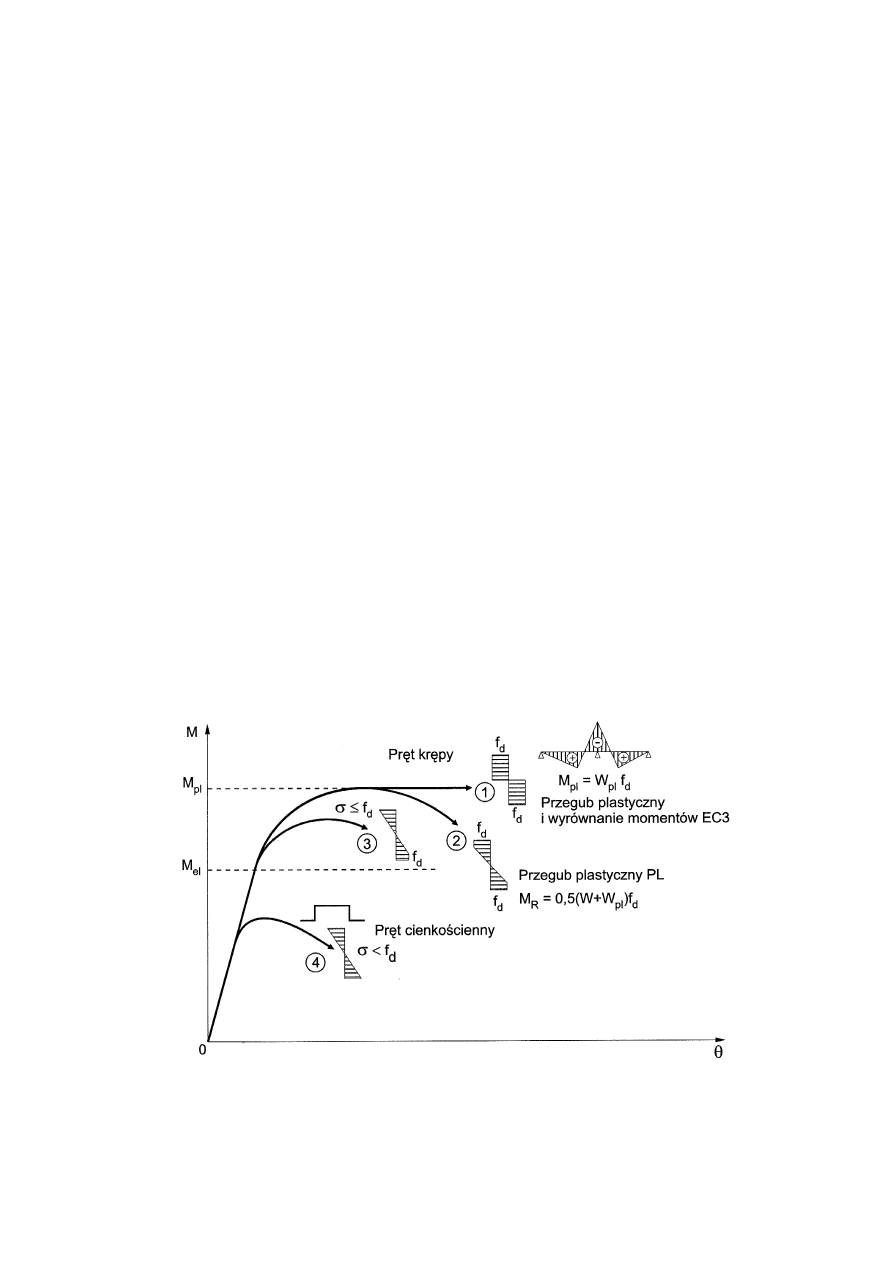
Klasyfikacja przekrojów

Klasa przekroju - stopień odporności elementu na miejscową utratę stateczności

Klasa 1. Przekroje klasy 1 mogą osiągać nośność uogólnionego przegubu plastycznego,

•

a w stanie pełnego uplastycznienia przy zginaniu wykazują zdolność do obrotu, niezbędną

do plastycznej redystrybucji momentów zginających.

Klasa 2. Przekroje klasy 2 mogą osiągać nośność uogólnionego przegubu plastycznego,

•

lecz wskutek miejscowej niestateczności plastycznej wykazują ograniczoną zdolność do

obrotu, uniemożliwiającą redystrybucję momentów zginających

Klasa 3. Przekroje klasy 3 charakteryzują się tym, że ich nośność jest uwarunkowana

•

początkiem uplastycznienia strefy ściskanej

Klasa 4. Przekroje klasy 4 tracą nośność przy największych naprężeniach ściskających

•

(lub średnich ścinających) mniejszych niż granica plastyczności

Klasyfikacja przekrojów odbywa się wg tablic 6 i 7 PN-90/B-03200

Ścieżki równowagi statycznej elementów zginanych o przekrojach 1,2,3,4 [11]

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 31

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 32

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 33

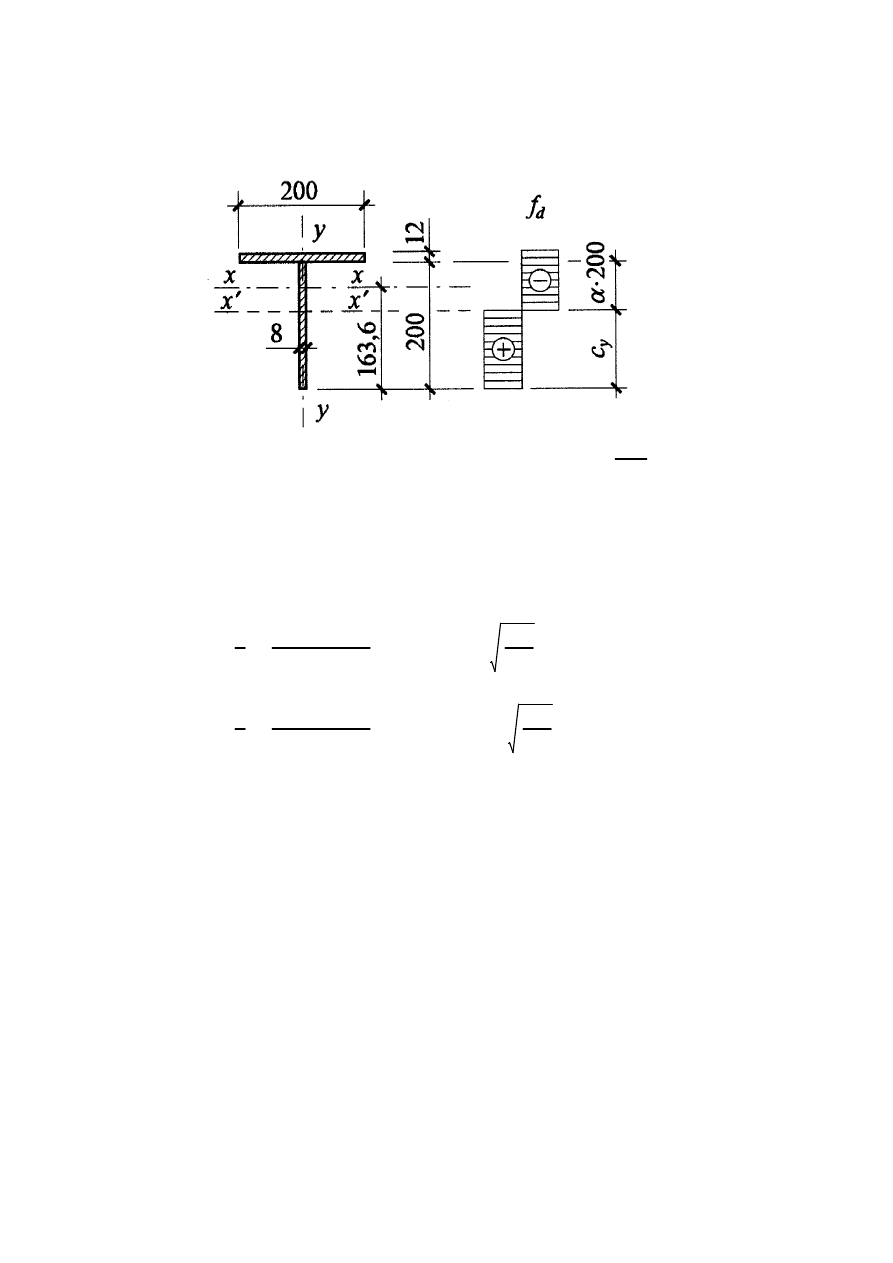
Przykład wg [13]

Ustalić klasę mimośrodowo ściskanego przekroju teowego z blach

[mm]

Dane:

- stal 18G2A o wytrzymałości

f

d

305MPa

=

30.5

kN

cm

2

=

- mimośród obciążenia N

e

y

10cm

=

Rozwiązanie:

Warunki smukłości pasa (jak dla elementu równomiernie ściskanego)

b

t

0.5 200

8

−

(

)

⋅

12

=

8

9

ε

⋅

>

=

9

215

305

⋅

=

7.56

=

b

t

0.5 200

8

−

(

)

⋅

12

=

8

10

ε

⋅

<

=

10

215

305

⋅

=

8.4

=

Środnik jest zginany, posiada strefę naprężeń ściskających i rozciągających. W celu

dokonania klasyfikacji należy określić współczynnik rozkładu naprężeń

α wyznaczający

zasięg strefy ściskanej. W przypadku klasy 1 lub 2 należy dokonać tego w stanie pełnego

uplastycznienia. W przypadku klasy 3 lub 4 należy rozpatrywać liniowo-sprężysty rozkład

naprężeń w przekroju. Osie obojętne stanu sprężytego i pełnego uplastycznienia (x oraz x')

przy zginaniu (ściskaniu mimośrodowym) przekrojów monosymetrycznych nie pokrywają się.

Położenie osi obojętnej w stanie sprężytym jest znane (y

o

=163.6mm). Położenie osi

obojętnej w stanie pełnego uplstycznienia należy obliczyć z warunków równowagi.

(uwaga dalej przyjęto wymiary w cm oraz naprężenia w kN/cm

2

)

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha

Konstrukcje metalowe

______________________________________________________________________________________________ 34

Pas spełniał warunki klasy 2, więc cały przekrój należy zaliczyć do klasy 2.

klasa 1

b

t

20

0.8

=

25

1

α α

⋅

9

⋅ ε

<

=

9

0.38

0.38

⋅

215

305

⋅

=

32.3

=

Warunek smukłości środnika

α

20

c

y

−

20

=

20

12.4

−

20

=

0.38

=

Można teraz obliczyć współczynnik

α

(drugi pierwiastek o wartości 40.3 cm odrzucamy)

c

y

12.4cm

=

skąd wyliczamy

24.4

−

c

y

2

⋅

1286.368 c

y

⋅

12200

−

+

oraz uporządkowaniu otrzymujemy zależność

10 1220

48.8c

y

−

(

)

⋅

24.4

−

c

y

2

798.368c

y

+

=

Po podstawieniu z równania (a) siły N

(b)

10 N

⋅

12.2

−

c

y

2

399.184c

y

+

12.2c

y

2

−

399.184c

y

+

=

24.4

−

c

y

2

798.368c

y

+

=

30.5 c

y

⋅ 0.8

⋅

16.36

0.5 c

y

⋅

−

(

)

⋅

12.2

−

c

y

2

⋅

399.184 c

y

⋅

+

=

wypadkowa naprężeń strefy rozciąganej

30.5

20 1.2

⋅

20

0.6

+

16.36

−

(

)

⋅

20

c

y

−

(

)

0.8

⋅

20

20

c

y

−

2

−

16.36

−













⋅

+













⋅

12.2

−

c

y

2

399.184c

y

+

=

wypadkowa naprężeń strefy ściskanej

- równanie momentów (względem osi środka ciężkości przekroju x-x)

(a)

N

1220

24.4c

y

−

24.4c

y

−

=

1220

48.8c

y

−

=

30.5 0.8

⋅

c

y

⋅

24.4c

y

=

wypadkowa naprężeń strefy rozciąganej

30.5 20 1.2

⋅

20 0.8

⋅

+

c

y

0.8

⋅

−

(

)

⋅

1220

24.4 c

y

⋅

−

=

wypadkowa naprężeń strefy ściskanej

- równanie sił

2005-03-07

______________________________________________________________________________________________

Politechnika Częstochowska Katedra Mechaniki Technicznej

Dr inż.S.Labocha